探索性因子分析课件
- 格式:ppt
- 大小:151.50 KB
- 文档页数:26


探索性因子分析法探索性因子分析(ExploratoryFactorAnalysis,简称EFA)是指使用相关分析的统计方法,旨在通过对一组变量之间的相关性来建立一个较小的变量集合,这些变量可以有效地表明以前未知的变量之间的相关性以及它们之间的潜在关系。
这个方法最初是由巴斯等人提出的,但现在已经成为一种常用的统计技术。
它已经广泛用于衡量政策,心理学和社会研究中的素质。
这种分析方法的基本思想是研究一组变量之间的相关性,以确定低级变量的几个组合,即因子。
这些因子可以用来解释变量之间的关系,以便更好地理解数据。
它试图理解数据中有多少潜在变量,这些变量应该占据什么位置。
EFA的统计分析流程大致如下:首先,将待分析的变量输入到统计分析软件中,然后进行因子载荷(factor loadings)分析。
据此,可以确定因子载荷矩阵,即每个变量对每个因子的影响程度。
接下来,对因子载荷进行提取,如主成分分析、因子旋转等,以达到有效的变量组合,并计算出每个因子的因子分数,以确定变量之间的关系。
有几种常用的因子旋转方法,包括oblimin旋转、varimax旋转和promax旋转。
oblimin旋转的目的是消除因子之间的相关性,当因子之间存在相关性时,这将对研究结果产生影响。
varimax旋转是另一种主要方式,使结果更加紧凑,减少被评价变量与任何单个因子的相关度,以获得更加清晰的因子分布情况。
promax旋转是varimax 旋转的一种变形,当变量之间存在同方差变换(OBL)时,可以使用promax旋转来消除这种变异。
EFA的研究可以给出关于变量结构的信息,这也可以帮助研究者更好地了解政策的作用、认知的发展及社会关系的情况。
它还可以作为一种确定一组变量之间关系的基础性方法,帮助研究者了解变量之间的相关性,以便更好地理解变量之间的关系。
此外,探索性因子分析也有一些缺点。
它需要大量的计算,运行时间可能会比较长。
另外,在角度变换时,很容易误把载荷系数反转,这会对结果产生不利影响。



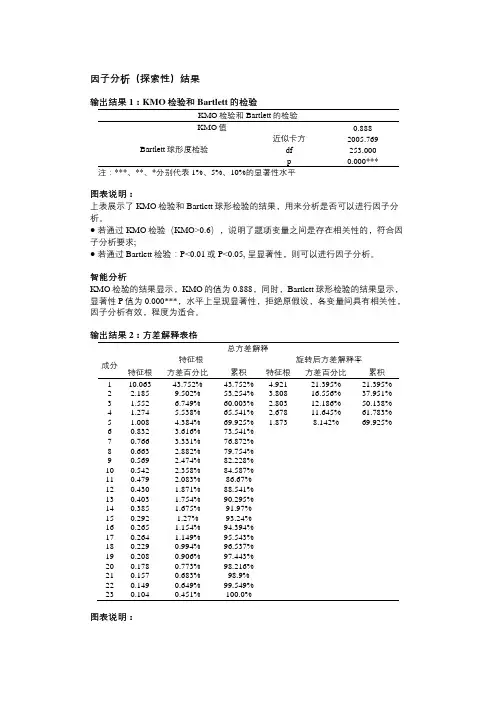
因子分析(探索性)结果输出结果1:KMO检验和Bartlett的检验KMO检验和Bartlett的检验KMO值0.888Bartlett球形度检验近似卡方2005.769 df 253.000p 0.000***注:***、**、*分别代表1%、5%、10%的显著性水平图表说明:上表展示了KMO检验和Bartlett球形检验的结果,用来分析是否可以进行因子分析。
● 若通过KMO检验(KMO>0.6),说明了题项变量之间是存在相关性的,符合因子分析要求;● 若通过Bartlett检验:P<0.01或P<0.05, 呈显著性,则可以进行因子分析。
智能分析KMO检验的结果显示,KMO的值为0.888,同时,Bartlett球形检验的结果显示,显著性P值为0.000***,水平上呈现显著性,拒绝原假设,各变量间具有相关性,因子分析有效,程度为适合。
输出结果2:方差解释表格总方差解释成分特征根旋转后方差解释率特征根方差百分比累积特征根方差百分比累积1 10.063 43.752% 43.752% 4.921 21.395% 21.395%2 2.185 9.502% 53.254% 3.808 16.556% 37.951%3 1.552 6.749% 60.003% 2.803 12.186% 50.138%4 1.274 5.538% 65.541% 2.678 11.645% 61.783%5 1.008 4.384% 69.925% 1.873 8.142% 69.925%6 0.832 3.616% 73.541%7 0.766 3.331% 76.872%8 0.663 2.882% 79.754%9 0.569 2.474% 82.228%10 0.542 2.358% 84.587%11 0.479 2.083% 86.67%12 0.430 1.871% 88.541%13 0.403 1.754% 90.295%14 0.385 1.675% 91.97%15 0.292 1.27% 93.24%16 0.265 1.154% 94.394%17 0.264 1.149% 95.543%18 0.229 0.994% 96.537%19 0.208 0.906% 97.443%20 0.178 0.773% 98.216%21 0.157 0.683% 98.9%22 0.149 0.649% 99.549%23 0.104 0.451% 100.0%图表说明:图表说明:● 碎石图是根据各主成分对数据变异的解释程度绘制的图。


探索性因子分析探索性因子分析(Exploratory Factor Analysis, EFA)是一种常用的统计方法,用于发现数据集中潜在的因子结构。
本文将探讨探索性因子分析的基本原理、应用领域以及分析步骤。
一、探索性因子分析的基本原理探索性因子分析的主要目标是通过对一组观测变量的统计分析,找出其中存在的共同的因素或维度,从而解释变量之间的相关关系。
其基本原理是将原始观测数据转化为较少数量的因子,以便更好地理解和解释数据。
探索性因子分析的核心假设是,一组观测变量可能是由一组隐含的共同因子所决定的。
每个共同因子代表一种概念或特征,而每个观测变量则表现出这些共同因子的不同强度。
通过探索性因子分析,我们可以识别出这些共同因子,从而更好地理解观测变量之间的关系。
二、探索性因子分析的应用领域探索性因子分析在各个学科和领域中都有广泛的应用。
以下列举几个常见的应用领域:1. 心理学:探索性因子分析在心理学中常用于测量和评估心理特质、人格特征和心理健康等方面。
通过分析心理测量问卷的数据,可以识别出隐藏在问卷题目背后的共同因子,进而得到更全面和准确的评估结果。
2. 教育研究:探索性因子分析可以用于分析教育测试成绩的数据,帮助研究人员了解学生的学习特征和学科能力,并发现不同因素对学生学业成绩的影响。
3. 市场调研:在市场调研中,探索性因子分析可以用于分析产品或服务的评价数据,帮助企业了解顾客需求和偏好,并提供科学依据为产品改进和市场策略制定。
4. 医学研究:在医学研究中,探索性因子分析可以用于分析疾病风险因素、病人症状和临床变量等数据,从而帮助医生和研究人员更好地了解和解释疾病发展的机制。
三、探索性因子分析的步骤进行探索性因子分析通常需要以下步骤:1. 收集数据:首先,需要收集与研究目的相关的数据。
这些数据可以是问卷调查、观察记录、实验结果或其他形式的数据。
2. 数据预处理:在进行因子分析之前,通常需要对数据进行预处理。



探索性因子分析法什么是探索性因子分析法?探索性因子分析法(Exploratory Factor Analysis,EFA)是一项用来找出多元观测变量的本质结构、并进行处理降维的技术。
因而,EFA能够将将具有错综复杂关系的变量综合为少数几个核心因子。
探索性因子分析法的起源因子分析法是两种分析形式的统一体,即验证性分析和纯粹的探索性分析。
英国的心理学家Charles Spearman在1904年的时候,提出单一化的智能因子(A Single Intellectual Factor)。
随着试验的深入,大量个体样本被分析研究,Spearman的单一智能因子理论被证明是不充分的。
同时,人们认识到有必要考虑多元因子。
20世纪30年代,瑞典心理学家Thurstone打破了流行的单因理论假设,大胆提出了多元因子分析(Multiple Factor Analysis)理论。
Thurstone在他的《心智向量》(Vectors of Mind,1935)一书中,阐述了多元因子分析理论的数学和逻辑基础。
探索性因子分析和验证性因子分析的异同[1]探索性因子分析和验证性因子分析相同之处两种因子分析都是以普通因子分析模型作为理论基础,其主要目的都是浓缩数据,通过对诸多变量的相关性研究,可以用假想的少数几个变量(因子、潜变量)来表示原来变量(观测变量)的主要信息。
图1所示即为最简单、也最为常见的因子模型,每个观测变量(指标)只在一个因子(潜变量)上负荷不为零,x1、x2 、x3是潜变量1的指标,x4、x5是潜变量2的指标。
将图1所示的因子模型推广至一般意义上的因子模型后,各观测变量x_i与m个公共因子1,2,...,m之间的关系可以用数学模型表示如下:x1 =111 +122 + ... +1mm +1......xk =k11 +k22 + ... +kmm +k其中:xi为各观测变量;i是公共因子;i是xi,的特殊因子,有时也称误差项,包括xi的唯一性因子和误差因子两部分;ij是公共因子的负载;m是公共因子1,2,...,m的个数,k是各观测变量x1,...,xk的个数,m k。