卷积神经网络CNN从入门到精通

课程大纲上课周（每周3课时）章节内容案例支持1.机器学习、深度学习与人工智能1第一章深度学习简介 2.深度学习与回归分析±及TenSOrFIOW安装 3.深度学习发展历程4.深度学习擅长领域5.安装Tenso1.神经网络模型介绍2.激活函数2第二章神经网络基础 3.神经网络的训练4.神经网络过拟合及处理方法1.神经网络的数据结构3第三章神经网络的 2.图像数据的存储与运算1、美食评分TensorFIow实现 3.线性回归模型的TensorFIow实现2、颜值打分第三章神经网络的TensorFIow实现1.逻辑回归模型的1、手写数字识别2、性别识别42.TensorFIow实现上机实验（一）1.卷积神经网络基本结构5第四章卷积神经网络 2.卷积与池化的通俗理解基础 3.卷积4.池化1.1eNet-51、手写数据识别6第五章经典卷积神经 2.AIexNet2、中文字体识网络（上）别：隶书和行楷1.VGG1×加利福尼亚理第五章经典卷积神经2.BatchNorma1ization技工学院鸟类数7网络（上）巧据库分类3.DataAugmentation技巧2、猫狗分类8第五章经典卷积神经上机实验（二）学生上机利用案例网络（上）实现经典网络9第六章经典卷积神经1、Inception1、花的三分类问题网络（T）2、ResNet2、F1OWer分类问题第六章经典卷积神经1、DenseNet1、性别区分10网络（T）2、MobiIeNet2、狗的分类3、迁移学习11第六章经典卷积神经上机实验（三）学生上机利用案例±1网络（T）实现经典网络12第七章深度学习用于1、词嵌入1、评论数据分析文本序列2、机器作诗初级：逻辑回归2、诗歌数据作诗13第七章深度学习用于1、机器作诗进阶1：RNN诗歌数据作诗文本序列IΛ第七章深度学习用于1、机器作诗进阶2：1STM诗歌数据作诗文本序列15第七章深度学习用于机器翻译原理中英文翻译文本序列第七章深度学习用于上机实验（四）学生上机利用案例16机器自动作诗或翻文本序列译。

cnn流程
深度学习中卷积神经网络（Convolutional Neural Network，简
称CNN）是一种流行的深度学习模型，用于图像分类和识别。

CNN被用
来提取和分类图像中的不同特征，并将这些特征连接在一起以产生最
终的识别结果。

CNN的主要工作流程是：第一步是卷积操作，将输入的图像数据
转换为适合其它神经网络处理的抽象特征；其次是用池化（pooling）
去除噪声，减少映射计算量。

这最多包括两层，分别称为Subsampling 和Pooling；第三步则是把这些抽象特征用于全链接卷积神经网络（FCN）；最后进入分类器，进行识别操作。

具体地说，CNN由输入层、卷积层、池化层、多层感知机和输出
层构成。

输入层与原输入图像数据一致；卷积层进行卷积并提取特征；池化层则会在保留重要特征的同时减少数据量；多层感知机（MLP）对
抽象特征进行分类；最后，输出层将分类结果反馈给用户。

综上，CNN的主要工作流程是：采用卷积操作提取图像数据的特征，通过池化去除噪声；使用全链接卷积神经网络（FCN）分析抽象特征；将抽象特征输入到多层感知机中进行分类；最后，将分类结果反
馈给用户。

CNN是目前用于图像分类和识别的有效技术，由于其效率高、预测正确率高、能够处理大量的特征，所以被广泛应用于自动驾驶、
医学图像处理和视觉机器人等领域。

⼀⽂看懂卷积神经⽹络-CNN（基本原理独特价值实际应⽤）卷积神经⽹络 – CNN 最擅长的就是图⽚的处理。

它受到⼈类视觉神经系统的启发。

CNN 有2⼤特点：能够有效的将⼤数据量的图⽚降维成⼩数据量能够有效的保留图⽚特征，符合图⽚处理的原则⽬前 CNN 已经得到了⼴泛的应⽤，⽐如：⼈脸识别、⾃动驾驶、美图秀秀、安防等很多领域。

CNN 解决了什么问题？在 CNN 出现之前，图像对于⼈⼯智能来说是⼀个难题，有2个原因：图像需要处理的数据量太⼤，导致成本很⾼，效率很低图像在数字化的过程中很难保留原有的特征，导致图像处理的准确率不⾼下⾯就详细说明⼀下这2个问题：需要处理的数据量太⼤图像是由像素构成的，每个像素⼜是由颜⾊构成的。

现在随随便便⼀张图⽚都是 1000×1000 像素以上的，每个像素都有RGB 3个参数来表⽰颜⾊信息。

假如我们处理⼀张 1000×1000 像素的图⽚，我们就需要处理3百万个参数！1000×1000×3=3,000,000这么⼤量的数据处理起来是⾮常消耗资源的，⽽且这只是⼀张不算太⼤的图⽚！卷积神经⽹络 – CNN 解决的第⼀个问题就是「将复杂问题简化」，把⼤量参数降维成少量参数，再做处理。

更重要的是：我们在⼤部分场景下，降维并不会影响结果。

⽐如1000像素的图⽚缩⼩成200像素，并不影响⾁眼认出来图⽚中是⼀只猫还是⼀只狗，机器也是如此。

保留图像特征图⽚数字化的传统⽅式我们简化⼀下，就类似下图的过程：图像简单数字化⽆法保留图像特征图像的内容假如有圆形是1，没有圆形是0，那么圆形的位置不同就会产⽣完全不同的数据表达。

但是从视觉的⾓度来看，图像的内容（本质）并没有发⽣变化，只是位置发⽣了变化。

（本质）并没有发⽣变化，只是位置发⽣了变化所以当我们移动图像中的物体，⽤传统的⽅式的得出来的参数会差异很⼤！这是不符合图像处理的要求的。

⽽ CNN 解决了这个问题，他⽤类似视觉的⽅式保留了图像的特征，当图像做翻转，旋转或者变换位置时，它也能有效的识别出来是类似的图像。

【机器学习基础】卷积神经⽹络（CNN）基础最近⼏天陆续补充了⼀些“线性回归”部分内容，这节继续机器学习基础部分，这节主要对CNN的基础进⾏整理，仅限于基础原理的了解，更复杂的内容和实践放在以后再进⾏总结。

卷积神经⽹络的基本原理 前⾯对全连接神经⽹络和深度学习进⾏了简要的介绍，这⼀节主要对卷积神经⽹络的基本原理进⾏学习和总结。

所谓卷积，就是通过⼀种数学变换的⽅式来对特征进⾏提取，通常⽤于图⽚识别中。

既然全连接的神经⽹络可以⽤于图⽚识别，那么为什么还要⽤卷积神经⽹络呢？（1）⾸先来看下⾯⼀张图⽚： 在这个图⽚当中，鸟嘴是⼀个很明显的特征，当我们做图像识别时，当识别到有“鸟嘴”这样的特征时，可以具有很⾼的确定性认为图⽚是⼀个鸟类。

那么，在提取特征的过程中，有时就没有必要去看完整张图⽚，只需要⼀⼩部分就能识别出⼀定具有代表的特征。

因此，使⽤卷积就可以使某⼀个特定的神经元（在这⾥，这个神经元可能就是⽤来识别“鸟嘴”的）仅仅处理带有该特征的部分图⽚就可以了，⽽不必去看整张图⽚。

那么这样就会使得这个神经元具有更少的参数（因为不⽤再跟图⽚的每⼀维输⼊都连接起来）。

（2）再来看下⾯⼀组图⽚：上⾯两张图⽚都是鸟类，⽽不同的是，两只鸟的“鸟嘴”的位置不同，但在普通的神经⽹络中，需要有两个神经元，⼀个去识别左上⾓的“鸟嘴”，另⼀个去识别中间的“鸟嘴”： 但其实这两个“鸟嘴”的形状是⼀样的，这样相当于上⾯两个神经元是在做同⼀件事情。

⽽在卷积神经⽹络中，这两个神经元可以共⽤⼀套参数，⽤来做同⼀件事情。

（3）对样本进⾏⼦采样，往往不会影响图⽚的识别。

如下⾯⼀张图： 假设把⼀张图⽚当做⼀个矩阵的话，取矩阵的奇数⾏和奇数列，可看做是对图⽚的⼀种缩放，⽽这种缩放往往不会影响识别效果。

卷积神经⽹络中就可以对图⽚进⾏缩放，是图⽚变⼩，从⽽减少模型的参数。

卷积神经⽹络的基本结构如图所⽰： 从右到左，输⼊⼀张图⽚→卷积层→max pooling（池化层）→卷积层→max pooling（池化层）→......→展开→全连接神经⽹络→输出。

⼀⽂带你了解CNN（卷积神经⽹络）⽬录前⾔⼀、CNN解决了什么问题？⼆、CNN⽹络的结构2.1 卷积层 - 提取特征卷积运算权重共享稀疏连接总结：标准的卷积操作卷积的意义1x1卷积的重⼤意义2.2 激活函数2.3 池化层(下采样) - 数据降维，避免过拟合2.4 全连接层 - 分类，输出结果三、Pytorch实现LeNet⽹络3.1 模型定义3.2 模型训练（使⽤GPU训练）3.3 训练和评估模型前⾔ 在学计算机视觉的这段时间⾥整理了不少的笔记，想着就把这些笔记再重新整理出来，然后写成Blog和⼤家⼀起分享。

⽬前的计划如下（以下⽹络全部使⽤Pytorch搭建）：专题⼀：计算机视觉基础介绍CNN⽹络(计算机视觉的基础)浅谈VGG⽹络，介绍ResNet⽹络（⽹络特点是越来越深）介绍GoogLeNet⽹络（⽹络特点是越来越宽）介绍DenseNet⽹络（⼀个看似⼗分NB但是却实际上⽤得不多的⽹络）整理期间还会分享⼀些⾃⼰正在参加的⽐赛的Baseline专题⼆：GAN⽹络搭建普通的GAN⽹络卷积GAN条件GAN模式崩溃的问题及⽹络优化 以上会有相关代码实践，代码是基于Pytorch框架。

话不多说，我们先进⾏专题⼀的第⼀部分介绍，卷积神经⽹络。

⼀、CNN解决了什么问题？ 在CNN出现之前，对于图像的处理⼀直都是⼀个很⼤的问题，⼀⽅⾯因为图像处理的数据量太⼤，⽐如⼀张512 x 512的灰度图，它的输⼊参数就已经达到了252144个，更别说1024x1024x3之类的彩⾊图，这也导致了它的处理成本⼗分昂贵且效率极低。

另⼀⽅⾯，图像在数字化的过程中很难保证原有的特征，这也导致了图像处理的准确率不⾼。

⽽CNN⽹络能够很好的解决以上两个问题。

对于第⼀个问题，CNN⽹络它能够很好的将复杂的问题简单化，将⼤量的参数降维成少量的参数再做处理。

也就是说，在⼤部分的场景下，我们使⽤降维不会影响结果。

⽐如在⽇常⽣活中，我们⽤⼀张1024x1024x3表⽰鸟的彩⾊图和⼀张100x100x3表⽰鸟的彩⾊图，我们基本上都能够⽤⾁眼辨别出这是⼀只鸟⽽不是⼀只狗。

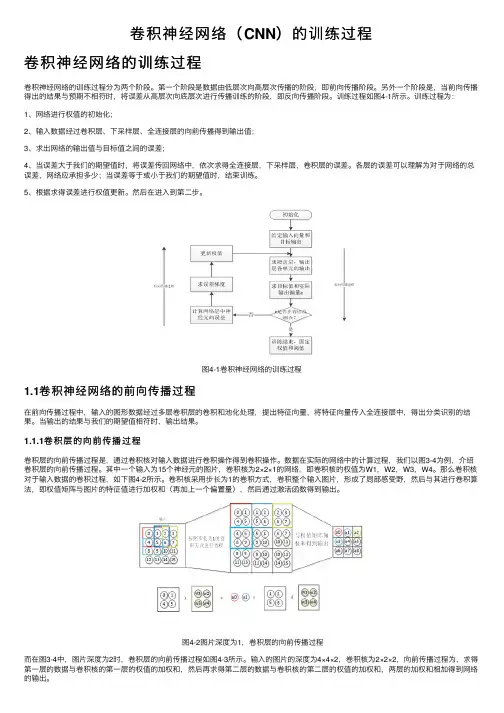
卷积神经⽹络（CNN）的训练过程卷积神经⽹络的训练过程卷积神经⽹络的训练过程分为两个阶段。

第⼀个阶段是数据由低层次向⾼层次传播的阶段，即前向传播阶段。

另外⼀个阶段是，当前向传播得出的结果与预期不相符时，将误差从⾼层次向底层次进⾏传播训练的阶段，即反向传播阶段。

训练过程如图4-1所⽰。

训练过程为：1、⽹络进⾏权值的初始化；2、输⼊数据经过卷积层、下采样层、全连接层的向前传播得到输出值；3、求出⽹络的输出值与⽬标值之间的误差；4、当误差⼤于我们的期望值时，将误差传回⽹络中，依次求得全连接层，下采样层，卷积层的误差。

各层的误差可以理解为对于⽹络的总误差，⽹络应承担多少；当误差等于或⼩于我们的期望值时，结束训练。

5、根据求得误差进⾏权值更新。

然后在进⼊到第⼆步。

图4-1卷积神经⽹络的训练过程1.1卷积神经⽹络的前向传播过程在前向传播过程中，输⼊的图形数据经过多层卷积层的卷积和池化处理，提出特征向量，将特征向量传⼊全连接层中，得出分类识别的结果。

当输出的结果与我们的期望值相符时，输出结果。

1.1.1卷积层的向前传播过程卷积层的向前传播过程是，通过卷积核对输⼊数据进⾏卷积操作得到卷积操作。

数据在实际的⽹络中的计算过程，我们以图3-4为例，介绍卷积层的向前传播过程。

其中⼀个输⼊为15个神经元的图⽚，卷积核为2×2×1的⽹络，即卷积核的权值为W1，W2，W3，W4。

那么卷积核对于输⼊数据的卷积过程，如下图4-2所⽰。

卷积核采⽤步长为1的卷积⽅式，卷积整个输⼊图⽚，形成了局部感受野，然后与其进⾏卷积算法，即权值矩阵与图⽚的特征值进⾏加权和（再加上⼀个偏置量），然后通过激活函数得到输出。

图4-2图⽚深度为1，卷积层的向前传播过程⽽在图3-4中，图⽚深度为2时，卷积层的向前传播过程如图4-3所⽰。

输⼊的图⽚的深度为4×4×2，卷积核为2×2×2，向前传播过程为，求得第⼀层的数据与卷积核的第⼀层的权值的加权和，然后再求得第⼆层的数据与卷积核的第⼆层的权值的加权和，两层的加权和相加得到⽹络的输出。

CNN（卷积神经网络）详解卷积神经网络（Convolutional Neural Network，CNN）是一种前馈神经网络，用于处理具有类似网格结构的数据。

这种网络结构在计算机视觉领域中应用非常广泛，包括图像识别、语音识别等领域。

CNN采用卷积层、池化层和全连接层等多种不同的层来提取特征。

一、卷积层卷积层是CNN的核心，也是最基本的层，它可以检测不同的特征，比如边缘、颜色和纹理等。

通常情况下，卷积层的输入是一个彩色或者灰度的图像，输出则是不同数量的“特征图”。

每个特征图对应一个特定的特征。

卷积层有一个非常重要的参数，叫做卷积核（Kernel），也就是滤波器。

卷积核是一个小的矩阵，它在输入数据的二维平面上滑动，将每个位置的像素值与卷积核的对应位置上的值相乘，然后将结果相加得到卷积层的输出。

通过不同的卷积核可以检测出不同的特征。

二、池化层池化层是CNN中的另一种重要层，它可以对卷积层的输出做降维处理，并且能够保留特征信息。

池化层通常是在卷积层之后加上的，其作用是将附近几个像素点合并成一个像素点。

这样做的好处是可以减小数据量，同时也可以使特征更加鲁棒。

池化层通常有两种类型，分别是最大池化和平均池化。

最大池化是从相邻的像素中寻找最大值，即将一个矩阵划分成多个小矩阵，然后寻找每个小矩阵中的最大值，最后将每个小矩阵中的最大值组成的矩阵作为输出。

平均池化则是简单地取相邻像素的平均值作为输出。

三、全连接层全连接层，也叫做密集连接层，是CNN中的最后一层，它将池化层输出的结果转化成一个一维的向量，并将其送入神经网络中进行分类或者回归预测。

全连接层通常使用softmax或者sigmoid等激活函数来输出分类结果。

四、CNN的应用CNN在计算机视觉领域有着广泛的应用，比如图像分类、物体检测、人脸识别、文字识别等。

其中最常见的应用就是图像分类，即将一张图片分为不同的目标类别。

通过卷积层和池化层不断地提取出图像的特征，然后送进全连接层对不同的类别进行分类。

卷积神经网络(CNN,ConvNet)及其原理详解卷积神经网络（CNN，有时被称为ConvNet）是很吸引人的。

在短时间内，它们变成了一种颠覆性的技术，打破了从文本、视频到语音等多个领域所有最先进的算法，远远超出了其最初在图像处理的应用范围。

CNN 由许多神经网络层组成。

卷积和池化这两种不同类型的层通常是交替的。

网络中每个滤波器的深度从左到右增加。

最后通常由一个或多个全连接的层组成：图1 卷积神经网络的一个例子Convnets 背后有三个关键动机：局部感受野、共享权重和池化。

让我们一起看一下。

局部感受野如果想保留图像中的空间信息，那么用像素矩阵表示每个图像是很方便的。

然后，编码局部结构的简单方法是将相邻输入神经元的子矩阵连接成属于下一层的单隐藏层神经元。

这个单隐藏层神经元代表一个局部感受野。

请注意，此操作名为“卷积”，此类网络也因此而得名。

当然，可以通过重叠的子矩阵来编码更多的信息。

例如，假设每个子矩阵的大小是5×5，并且将这些子矩阵应用到28×28 像素的MNIST 图像。

然后，就能够在下一隐藏层中生成23×23 的局部感受野。

事实上，在触及图像的边界之前，只需要滑动子矩阵23 个位置。

定义从一层到另一层的特征图。

当然，可以有多个独立从每个隐藏层学习的特征映射。

例如，可以从28×28 输入神经元开始处理MNIST 图像，然后（还是以5×5 的步幅）在下一个隐藏层中得到每个大小为23×23 的神经元的k 个特征图。

共享权重和偏置假设想要从原始像素表示中获得移除与输入图像中位置信息无关的相同特征的能力。

一个简单的直觉就是对隐藏层中的所有神经元使用相同的权重和偏置。

通过这种方式，每层将从图像中学习到独立于位置信息的潜在特征。

理解卷积的一个简单方法是考虑作用于矩阵的滑动窗函数。

在下面的例子中，给定输入矩阵I 和核K，得到卷积输出。

将3×3 核K（有时称为滤波器或特征检测器）与输入矩阵逐元素地相乘以得到输出卷积矩阵中的一个元素。

卷积神经网络CNN从入门到精通卷积神经网络算法的一个实现前言从理解卷积神经到实现它，前后花了一个月时间，现在也还有一些地方没有理解透彻，CNN还是有一定难度的，不是看哪个的博客和一两篇论文就明白了，主要还是靠自己去专研，阅读推荐列表在末尾的参考文献。

目前实现的CNN在MINIT数据集上效果还不错，但是还有一些bug，因为最近比较忙，先把之前做的总结一下，以后再继续优化。

卷积神经网络CNN是Deep Learning的一个重要算法，在很多应用上表现出卓越的效果，[1]中对比多重算法在文档字符识别的效果，结论是CNN优于其他所有的算法。

CNN在手写体识别取得最好的效果，[2]将CNN应用在基于人脸的性别识别，效果也非常不错。

前段时间我用BP神经网络对手机拍照图片的数字进行识别，效果还算不错，接近98%，但在汉字识别上表现不佳，于是想试试卷积神经网络。

1、CNN的整体网络结构卷积神经网络是在BP神经网络的改进，与BP类似，都采用了前向传播计算输出值，反向传播调整权重和偏置；CNN与标准的BP最大的不同是：CNN中相邻层之间的神经单元并不是全连接，而是部分连接，也就是某个神经单元的感知区域来自于上层的部分神经单元，而不是像BP那样与所有的神经单元相连接。

CNN的有三个重要的思想架构：局部区域感知权重共享空间或时间上的采样局部区域感知能够发现数据的一些局部特征，比如图片上的一个角，一段弧，这些基本特征是构成动物视觉的基础[3]；而BP中，所有的像素点是一堆混乱的点，相互之间的关系没有被挖掘。

CNN中每一层的由多个map组成，每个map由多个神经单元组成，同一个map 的所有神经单元共用一个卷积核（即权重），卷积核往往代表一个特征，比如某个卷积和代表一段弧，那么把这个卷积核在整个图片上滚一下，卷积值较大的区域就很有可能是一段弧。

注意卷积核其实就是权重，我们并不需要单独去计算一个卷积，而是一个固定大小的权重矩阵去图像上匹配时，这个操作与卷积类似，因此我们称为卷积神经网络，实际上，BP也可以看做一种特殊的卷积神经网络，只是这个卷积核就是某层的所有权重，即感知区域是整个图像。

深度学习——带你通俗理解卷积神经⽹络（CNN）卷积神经⽹络（CNN）基础知识⽂章⽬录1.前⾔ 如果说深度神经⽹络模型中的“明星”是谁？那么⾮卷积神经⽹络莫属。

下⾯给⼤家简单介绍⼀下CNN的基础知识。

其中CNN基础主要涉及卷积层、池化层、全连接层在卷积神经⽹络扮演的⾓⾊、实现的具体的功能和⼯作原理。

2.卷积层 1.主要作⽤：对输⼊的数据进⾏特征提取。

2.⼯具：卷积核——完成对数据提取的功能。

3.卷积核是怎么处理数据数据的呢？我们知道卷积核其实是⼀个指定窗⼝⼤⼩的扫描器，通过⼀次⼜⼀次地扫描输⼊的数据，来提取数据中的特征。

那么在通过卷积核处理后，就可以识别出图像中的重要特征了。

4.下⾯讲解卷积核的定义：⼀、 假定有⼀张32* 32*3的输⼊图像，其中32 * 32是图像的⾼度和宽度，3是指图像具有R，G，B三个⾊彩通道。

⼆、我们定义⼀个5 * 5 * 3的卷积核 ，其中3是指卷积核的深度，对应之前输⼊图像的三个彩⾊通道。

（⽬的：当卷积核窗⼝在输⼊图像上滑动时，能够⼀次在三个彩⾊通道上同时进⾏卷积操作）三、 常⽤的卷积核5 *5和3 *3我们知道了卷积核后，那么怎么进⾏卷积操作呢？ 现在我们定义步长为对卷积核的窗⼝进⾏滑动 下图为⼀个步长为2的卷积核经过⼀次滑动窗⼝位置变化情况 仔细观察不难发现，在上⾯的输⼊图像的最外界多了⼀圈全为0的像素，这其实就是⼀种⽤于提升卷积效果的边界像素扩充的⽅法共有两种⽅式进⾏填充Same和Valid1.Same在输⼊图像的最外界加上指定层数的值全为0的像素边界：为了让输⼊图像的全部像素能被滑动窗⼝捕捉。

2.Valid直接对输⼊图像进⾏卷积，不对输⼊图像进⾏任何的前期处理和图像填充。

缺点就是会导致部分像素点不嫩被滑动窗⼝捕捉。

通过对卷积过程的计算，可以得出卷积通⽤公式⽤于计算输⼊图像经过⼀轮卷积操作后的输出图像的宽度和⾼度的参数 其中W，H分别代表图像的宽度和⾼度的值；下标input代表输⼊图像的相关参数；下标output表⽰输出图像的相关参数，filter代表卷积核的相关参数，S代表卷积的步长，P（padding）代表在图像边缘增加的边界像素层数。

卷积神经网络发展进程卷积神经网络的发展，最早可以追溯到1962年，Hubel和Wiesel 对猫大脑中的视觉系统的研究。

1980年，一个日本科学家福岛邦彦(Kunihiko Fukushima)提出了一个包含卷积层、池化层的神经网络结构。

在这个基础上，Yann Lecun将BP算法应用到这个神经网络结构的训练上，就形成了当代卷积神经网络的雏形。

其实最初的CNN效果并不算好，而且训练也非常困难。

虽然也在阅读支票、识别数字之类的任务上有一定的效果，但由于在一般的实际任务中表现不如SVM、Boosting等算法好，因此一直处于学术界的边缘地位。

直到2012年，ImageNet图像识别大赛中，Hinton组的AlexNet引入了全新的深层结构和Dropout方法，一下子把error rate 从25%降低到了15%，这颠覆了图像识别领域。

AlexNet有很多创新，尽管都不是很难的方法。

其最主要的结果是让人们意识到原来那个福岛邦彦提出的、Yann LeCun优化的LeNet 结构原来是有很大改进空间的：只要通过一些方法能够加深这个网络到8层左右，让网络表达能力提升，就能得到出人意料的好结果。

顺着AlexNet的思想，LeCun组2013年提出了一个DropConnect，把error rate降低到了11%。

而NUS的颜水成组则提出了一个重要的Network in Network(NIN)方法，NIN的思想是在原来的CNN结构中加入了一个1*1 conv层，NIN的应用也得到了2014年Imagine另一个挑战——图像检测的冠军。

Network in Network更加引发了大家对CNN 结构改变的大胆创新。

因此，两个新的架构Inception和VGG在2014年把网络加深到了20层左右，图像识别的error rate(越小越好)也大幅降低到6.7%，接近人类错误率的5.1%。

2015年，MSRA的任少卿、何恺明、孙剑等人，尝试把Identity加入到卷积神经网络中提出ResNet。

卷积神经网络CNN从入门到精通卷积神经网络算法的一个实现前言从理解卷积神经到实现它，前后花了一个月时间，现在也还有一些地方没有理解透彻，CNN还是有一定难度的，不是看哪个的博客和一两篇论文就明白了，主要还是靠自己去专研，阅读推荐列表在末尾的参考文献。

目前实现的CNN在MINIT数据集上效果还不错，但是还有一些bug，因为最近比较忙，先把之前做的总结一下，以后再继续优化。

卷积神经网络CNN是Deep Learning的一个重要算法，在很多应用上表现出卓越的效果，[1]中对比多重算法在文档字符识别的效果，结论是CNN优于其他所有的算法。

CNN在手写体识别取得最好的效果，[2]将CNN应用在基于人脸的性别识别，效果也非常不错。

前段时间我用BP神经网络对手机拍照图片的数字进行识别，效果还算不错，接近98%，但在汉字识别上表现不佳，于是想试试卷积神经网络。

1、CNN的整体网络结构卷积神经网络是在BP神经网络的改进，及BP类似，都采用了前向传播计算输出值，反向传播调整权重和偏置；CNN及标准的BP最大的不同是：CNN中相邻层之间的神经单元并不是全连接，而是部分连接，也就是某个神经单元的感知区域来自于上层的部分神经单元，而不是像BP那样及所有的神经单元相连接。

CNN的有三个重要的思想架构：局部区域感知权重共享空间或时间上的采样局部区域感知能够发现数据的一些局部特征，比如图片上的一个角，一段弧，这些基本特征是构成动物视觉的基础[3]；而BP中，所有的像素点是一堆混乱的点，相互之间的关系没有被挖掘。

CNN中每一层的由多个map组成，每个map由多个神经单元组成，同一个map 的所有神经单元共用一个卷积核（即权重），卷积核往往代表一个特征，比如某个卷积和代表一段弧，那么把这个卷积核在整个图片上滚一下，卷积值较大的区域就很有可能是一段弧。

注意卷积核其实就是权重，我们并不需要单独去计算一个卷积，而是一个固定大小的权重矩阵去图像上匹配时，这个操作及卷积类似，因此我们称为卷积神经网络，实际上，BP也可以看做一种特殊的卷积神经网络，只是这个卷积核就是某层的所有权重，即感知区域是整个图像。

CNN-训练流程卷积神经⽹络（CNN）训练流程1、图像预处理（1）尺度调整：将不同⼤⼩的训练样本集图像尺⼨调整为48*48（2）对⽐度变换：将图像对⽐度归⼀化的三种⽅法A.将三个彩⾊空间的像素围绕平均像素强度线性变换加减⼀个标准偏差。

B.将三个彩⾊空间的像素围绕平均像素强度线性变换加减两个个标准偏差。

C.Contrast-limited Adaptive Histogram Equalization (CLAHE)对⽐受限的⾃适应直⽅图均衡化。

第三种对⽐度变换产⽣的效果最好。

图像扭曲：图像的位移，旋转度和尺度变换⼤⼩值都是在特定范围均匀分布的，在正负10%范围内。

2、卷积神经⽹络处理流程Our plain feed-forward CNN architecture is trained using on-line gradient descent. Images from the training set might be translated, scaled and rotated, whereas only the original images are used for validation. Training ends once the validation error is zero (usually after 10 to 50 epochs). Initial weights are drawn from a uniform random distribution in the range [?0.05, 0.05]. Each neuron’s activation function is a scaled hyperbolic tangent。

⽤在线梯度下降算法训练CNN，当有效误差为零训练结束（通常在10—50代之后），初始权重均匀分布在[-0.05—0.05]随机产⽣。

每⼀个神经元的激励函数为双曲正切函数。