压缩感知重构算法

基于图像结构模型的压缩感知图像重构方法随着数字图像在各个领域的广泛应用，如视频监控、医学影像以及移动通信等，对图像传输和存储的要求也越来越高。

然而，由于图像数据量庞大，传输和存储的成本也随之增加。

为了解决这一问题，压缩感知（Compressed Sensing，CS）技术被提出并逐渐得到应用。

压缩感知技术的基本思想是在图像采集中对图像进行压缩，即不直接采集完整的图像数据，而是对其进行稀疏采样，然后通过稀疏的采样数据来重构完整的图像。

而图像结构模型就是其中一种常用的重构方法之一。

图像结构模型是一种基于图像自身的特性进行建模和重构的方法。

它利用图像的边缘、纹理和结构等特征来提取图像信息，从而实现更加准确和高质量的图像重构。

下面将介绍基于图像结构模型的压缩感知图像重构方法的具体步骤和原理。

一、图像结构模型的建立在压缩感知图像重构过程中，首先需要建立图像结构模型。

这个步骤涉及到对图像的稀疏表示，常用的方法有小波变换、稀疏表示字典以及图像分割等。

小波变换是一种常用的图像分析和压缩方法，通过将图像进行小波变换来提取图像的频域信息，进而实现图像的稀疏表示。

稀疏表示字典则是通过提前建立一个字典，将图像的局部结构进行编码，从而实现图像的稀疏表示。

图像分割是将图像划分为若干个小块，每个小块可以看做是具有相似结构的局部区域，从而实现图像的稀疏表示。

二、图像重构算法建立好图像结构模型后，下一步就是利用稀疏采样数据对图像进行重构。

常用的图像重构算法有基于最小二乘法的估计（Least Squares，LS）、基于迭代阈值法的估计（Iterative Shrinkage-Thresholding Algorithm，ISTA）以及基于广义估计最小二乘法的估计（Generalized Estimation of Signal and Noise，GESPAR）等。

LS方法是一种常见的图像重构算法，它通过将图像重构问题转换成一个最小二乘问题，通过最小化重构图像与原始图像之间的欧式距离来进行重构。

基于压缩感知的信号重构算法研究共3篇基于压缩感知的信号重构算法研究1基于压缩感知的信号重构算法研究随着信息技术的发展以及现代通信系统的广泛应用，人们对于信号重构算法的研究也越来越深入。

其中，基于压缩感知的信号重构算法受到了广泛关注。

本文将从以下四个方面来探讨该算法的研究。

一、压缩感知的基本原理压缩感知的核心思想是将一个高维信号（如图像、音频等）映射到一个较低维的空间中，然后再通过一个线性投影方式将数据压缩。

利用测量矩阵可以将压缩后的数据重构到原来的高维空间中，并且能够利用未知信号的稀疏性完成恢复过程。

这种低维的表示方式可以使数据占用的空间大大减小，因此压缩感知成为了高效的信号采样方式。

二、常见的压缩感知算法常见的压缩感知算法包括OMP算法、CoSaMP算法、MPCP算法等。

其中OMP算法是一种迭代算法，用于寻找稀疏表示向量。

CoSaMP算法考虑到了噪声的影响，能够更准确地进行稀疏重构。

MPCP算法则是多向量压缩感知的拓展，用于处理多个信号的联合稀疏性问题。

三、压缩感知在图像压缩方面的应用基于压缩感知的信号重构算法在图像压缩方面的应用也是较为广泛的。

传统的JPEG和PNG等图像压缩算法虽然能够将图像进行压缩，但是重构后的图像质量较差，并且对于稀疏性较强的图像处理能力有限。

基于压缩感知的算法能够更好地处理稀疏性强的图像，同时也能够提高图像的显示效果。

四、压缩感知在音频处理方面的应用除了在图像处理方面的应用，基于压缩感知的信号重构算法在音频处理方面也具有广泛的应用前景。

例如在音频采样、去噪、提取声音等方面都有着极为广泛的应用。

此外，利用压缩感知的技术，人们还可以用较小的存储空间存储大量音乐等高质量音频数据。

综上所述，基于压缩感知的信号重构算法是一种高效且优越的信号处理方法，具有较广泛的应用前景。

在未来的研究中，我们可以结合更多的数据处理技术来提高算法的效率和精度基于压缩感知的信号重构算法在信号处理中具有广泛应用前景，能够更好地处理稀疏性较强的信号，并提高信号质量。

.1 压缩感知部分压缩感知算法主要可分为三类：贪婪迭代算法、凸凸优化（或最优化逼近方法）和基于贝叶斯框架提出的重构算法。

由于第三类方法注重信号的时间相关性，不适合图像处理问题，故目前的研究成果主要集中在前两类中。

目前已实现6中算法，分别为正交匹配追踪法（OMP）、迭代硬阈值法（IHT）、分段正交匹配追踪法（StOMP）、分段弱正交匹配追踪法（SwOMP）、广义正交匹配追踪（GOMP）、基追踪法（BP）。

1.1 正交匹配追踪法（OMP）在正交匹配追踪OMP中，残差是总与已经选择过的原子正交的。

这意味着一个原子不会被选择两次，结果会在有限的几步收敛。

OMP的算法如下(1)用x表示你的信号，初始化残差e0=x；(2)选择与e0内积绝对值最大的原子，表示为φ1；(3)将选择的原子作为列组成矩阵Φt，定义Φt列空间的正交投影算子为通过从e0减去其在Φt所张成空间上的正交投影得到残差e1；(4)对残差迭代执行(2)、(3)步；其中I为单位阵。

需要注意的是在迭代过程中Φt为所有被选择过的原子组成的矩阵，因此每次都是不同的，所以由它生成的正交投影算子矩阵P每次都是不同的。

(5)直到达到某个指定的停止准则后停止算法。

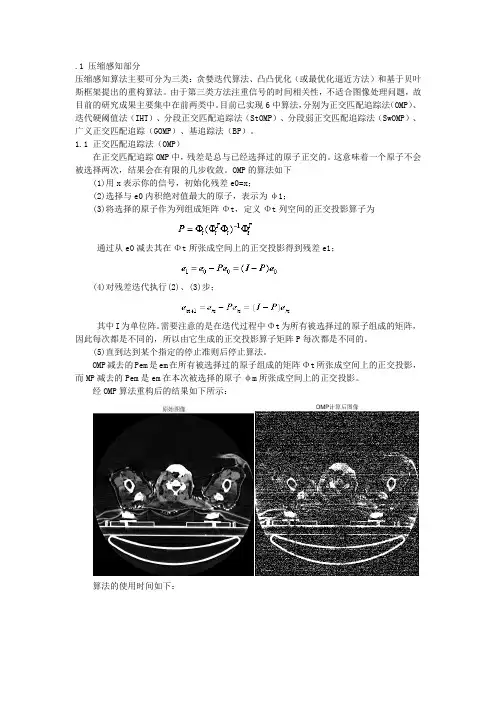
OMP减去的Pem是em在所有被选择过的原子组成的矩阵Φt所张成空间上的正交投影，而MP减去的Pem是em在本次被选择的原子φm所张成空间上的正交投影。

经OMP算法重构后的结果如下所示：算法的使用时间如下：1.2 迭代硬阈值法（IHT）目标函数为这里中的M应该指的是M-sparse，S应该指的是Surrogate。

这里要求：之后我们利用式对目标函数进行变形。

接着便是获得极值点：利用该式进行迭代可以得到极值点，我们需要的是最小值。

此时目标函数的最小值就得到了。

此时便得到我们需要的公式：我们要保证向量y的稀疏度不大于M，即，为了达到这一目标，要保留最大的M项（因为是平方，所以要取绝对值absolute value），剩余的置零（注意这里有个负号，所以要保留最大的M项）。

压缩感知重构算法——SP算法SP（subspace pursuit）算法是压缩感知中⼀种⾮常重要的贪婪算法，它有较快的计算速度和较好的重构概率，在实际中应⽤较多。

本⽂给出了SP算法的matlab代码，以及相应的测试函数。

参考⽂献：Dai W, Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction[J]. Information Theory, IEEE Transactions on, 2009, 55(5): 2230-2249.⽂献下载地址：Matlab代码：SP_paper.mfunction x=SP_paper(Phi,y,K)%SP算法%获取Phi矩阵的⾏数和列数[M,N]=size(Phi);%初始化步骤%将Phi的每列与y做相关，得到⼀个N*1的矩阵(列向量)correlation=Phi'*y;%对correlation取绝对值后排序，按从⼤到⼩的顺序[var,pos] = sort(abs(correlation),'descend');%声明⼀个空集T，⽤于记录Phi的列数标值T=[];T=union(T,pos(1:K));y_r=resid_paper(y,Phi(:,T));%迭代%使⽤如下形式的do---while结构% while(1)% if(condition)% break;% end% endcount=1;while(1)%根据残差计算待增加的列数，得到T_addcorrelation=Phi'*y_r;[var,pos] = sort(abs(correlation),'descend');T_add=union([],pos(1:K));%合并已有的T和T_addT=union(T,T_add);%x_p=((Phi(:,T)'*Phi(:,T))\eye(length(T)))*Phi(:,T)'*y;%proj_paper(y,Phi(:,T));%更新下标记录T[var,pos] = sort(abs(x_p),'descend');%取前K个最⼤值T=union([],T(pos(1:K)));%计算新的残差y_r_n=resid_paper(y,Phi(:,T));%判断是否退出循环,且置为最⼤迭代100次if(norm(y_r_n)>=norm(y_r) || count>100)break;end%若不退出循环,进⾏新⼀轮的迭代y_r=y_r_n;count=count+1;end%退出循环后，做最后的数据输出x=zeros(N,1);x(T)=((Phi(:,T)'*Phi(:,T))\eye(length(T)))*Phi(:,T)'*y;endfunction y_r=resid_paper(y,Phi)%计算y在Phi上的投影残差%获取矩阵Phi的⾏数和列数,M没有⽤[M,N]=size(Phi);%判断矩阵(Phi'*Phi)是否可逆if(rank(Phi'*Phi)~=N)error('矩阵不可逆');endy_p=Phi*((Phi'*Phi)\eye(N))*Phi'*y;y_r=y-y_p;end%%%%%%%%%%%%%%%%%%%%%%%%dataGen.mfunction [y,Phi,x]=dataGen(M,N,K)% 产⽣贪婪算法所需要的数据%⽣成-1/+1的原始信号xx = zeros(N,1);q = randperm(N); %y=randperm(n),是把1到n这些数随机打乱得到的⼀个数字序列。

压缩感知的重构算法算法的重构是压缩感知中重要的一步，是压缩感知的关键之处。

因为重构算法关系着信号能否精确重建，国内外的研究学者致力于压缩感知的信号重建，并且取得了很大的进展，提出了很多的重构算法，每种算法都各有自己的优缺点，使用者可以根据自己的情况，选择适合自己的重构算法，大大增加了使用的灵活性，也为我们以后的研究提供了很大的方便。

压缩感知的重构算法主要分为三大类：1.组合算法2.贪婪算法3.凸松弛算法每种算法之中又包含几种算法，下面就把三类重构算法列举出来。

组合算法：先是对信号进行结构采样，然后再通过对采样的数据进行分组测试，最后完成信号的重构。

(1) 傅里叶采样（Fourier Representaion）(2) 链式追踪算法（Chaining Pursuit）(3) HHS追踪算法（Heavy Hitters On Steroids）贪婪算法：通过贪婪迭代的方式逐步逼近信号。

(1) 匹配追踪算法（Matching Pursuit MP）(2) 正交匹配追踪算法（Orthogonal Matching Pursuit OMP）(3) 分段正交匹配追踪算法（Stagewise Orthogonal Matching Pursuit StOMP）(4) 正则化正交匹配追踪算法（Regularized Orthogonal Matching Pursuit ROMP）(5) 稀疏自适应匹配追踪算法（Sparisty Adaptive Matching Pursuit SAMP）凸松弛算法：(1) 基追踪算法（Basis Pursuit BP）(2) 最小全变差算法（Total Variation TV）(3) 内点法（Interior-point Method）(4) 梯度投影算法（Gradient Projection）(5) 凸集交替投影算法（Projections Onto Convex Sets POCS）算法较多，但是并不是每一种算法都能够得到很好的应用，三类算法各有优缺点，组合算法需要观测的样本数目比较多但运算的效率最高，凸松弛算法计算量大但是需要观测的数量少重构的时候精度高，贪婪迭代算法对计算量和精度的要求居中，也是三种重构算法中应用最大的一种。

正交半迭代硬阈值(OSIHT)压缩感知重构算法杨爱萍;刘华平;何宇清;栗改【摘要】信号重构是压缩感知过程中的重要环节,迭代硬阈值(IHT)算法因具有较好的重构性能被广泛应用,但其收敛速度比较慢.近期提出的半迭代硬阈值算法(SIHT)虽然可实现快速收敛,但对测量矩阵的尺度缩放非常敏感,依赖性强,大大限制了其应用范围.受OMP对MP算法改进启发,对SIHT算法进行改进,提出了正交半迭代硬阈值(OSIHT)重构算法.该算法不仅取消了对测量矩阵的依赖性,还有效改善了图像重构质量,减少运行时间.【期刊名称】《计算机工程与应用》【年(卷),期】2016(052)005【总页数】5页(P79-83)【关键词】压缩感知;重构算法;迭代阈值;半迭代法【作者】杨爱萍;刘华平;何宇清;栗改【作者单位】天津大学电子信息工程学院,天津300072;天津大学电子信息工程学院,天津300072;天津大学电子信息工程学院,天津300072;天津大学电子信息工程学院,天津300072【正文语种】中文【中图分类】TP391近年来，Candès和Donoho提出的压缩感知（CS）理论[1-4]，突破了传统采样定理的束缚，在获取信号的同时对数据进行适当的压缩，避免了传统采样压缩的资源浪费，缓解了信号采样、传输和存储过程中所面临的越来越大的压力，为信号采集技术带来了革命性的进展。

压缩感知理论主要包括：信号的稀疏表示、测量矩阵设计和信号的重构算法。

信号重构是由测量值及投影矩阵重构原始信号，是压缩感知理论的必备手段，是压缩感知处理过程最重要的环节。

信号压缩感知重构算法研究已经取得了不少的成果，其中典型的算法有凸松弛方法[5-6]、贪婪方法[7-9]、迭代阈值算法[10-12]等。

其中，迭代阈值算法因迭代简单、可单分量处理且具有较好的重构性能而被广泛应用。

但是传统的迭代阈值类算法具有较慢的收敛速度，文献[12]基于半迭代加速技术提出的半迭代硬阈值算法（Semi-Iterative Hard Thresholding algorithm，SIHT），可实现快速收敛，但该算法对测量矩阵的尺度缩放非常敏感，有很强的依赖性，在很大程度上限制了其应用范围。

浅谈压缩感知（⼆⼗七）：压缩感知重构算法之稀疏度⾃适应匹
配追踪（SAMP）
主要内容：
1. SAMP的算法流程
2. SAMP的MATLAB实现
3. ⼀维信号的实验与结果
4. 稀疏度K与重构成功概率关系的实验与结果
⼀、SAMP的算法流程
前⾯所述⼤部分OMP及其前改算法都需要已知信号的稀疏度K，⽽在实际中这个⼀般是不知道的，基于此背景，稀疏度⾃适应匹配追踪(Sparsity Adaptive MP)被提出。

SAMP不需要知道稀疏度K，在迭代循环中，根据新残差与旧残差的⽐较来确定选择原⼦的个数。

SAMP的算法流程：
三、⼀维信号的实验与结果
四、稀疏数K与重构成功概率关系的实验与结果
六、参考⽂章。