当前位置：文档之家 › 自动控制原理之伯德图

自动控制原理之伯德图

  • 格式：pptx
  • 大小：374.87 KB
  • 文档页数：45

下载文档原格式

  / 45

合集下载

自动控制原理3第三节典型环节的频率特性

自动控制原理3第三节典型环节的频率特性

左图是不同阻尼系数情况下的 对数幅频特性和对数相频特性 图。上图是不同阻尼系数情况 下的对数幅频特性实际曲线与 渐近线之间的误差曲线。
1 2T 1 T 2 T 5 T 10 T
1 5T
Saturday, November 05, 2016
15
微分环节的频率特性
⒌ 微分环节的频率特性： 微分环节有三种：纯微分、一阶微分和二阶微分。传递函 数分别为： G( s) s
05, 2016
12
振荡环节的波德图
2 T ( ) tg 相频特性： 1 T 2 2
1
几个特征点： 0, ( ) 0;
1 , ( ) ; , ( ) 。 T 2
由图可见：
K 10, T 1, 0.3 10 G ( j ) 2 s 0.6s 1 1 o T
1
幅频特性为： 相频特性为：
A( )
(1 T 2 2 )2 (2T )2 2 T ( ) tg 1 1 T 2 2
L( ) 20 log A( ) 20 log (1 T 2 2 ) 2 (2 T ) 2 对数幅频特性为：
低频段渐近线： T 1时，L( ) 0 高频段渐近线： T 1时， L( ) 20 log (T 2 2 ) 2 40 log T 1 两渐进线的交点 o 称为转折频率。斜率为-40dB/Dec。 T Saturday, November
1 2
T
时，无谐振峰值。当
M p A( p )

1 2
1 0.707时， p 0 。 2
时，有谐振峰值。
1 2 1 2
1 当 0 ， A(0 ) ， 。 L ( ) 20 lg 2 0 2

典型环节伯德图ppt课件

典型环节伯德图ppt课件

节相比是以
为对称，相角的变化范围是 至 。
Bode如图5-22所示
编辑版pppt
20
八滞后环节
滞后环节的频率特性是: 其对数幅频特性和相频特性分别为:
滞后环节伯德图如图5-23
所示。其对数幅频特性与
ω无关，是一条与ω轴重合
的零分贝线。滞后相角由
式（5-92）计算，分别与
滞后时间常数τ和角频率ω
成正比。
积分环节的相频特性是:
(5-69)
是一条与ω无关，值为-900 且平行于ω轴的直线。积分环节 的对数幅频特性和相频特性如图
5-12所示。
编辑版pppt
(5-68)
6
当有n个积分环节串联时，即:
其对数幅频特性为:
是一条斜率为-n×20dB/dec ，且在ω=1（弧度/秒）处过 零分贝线（ω轴）的直线。
相频特性是一条与ω无关， 值为-n×900 且与ω轴平行 的直线。两个积分环节串联 的Bode图如图5-13所示。
图5-13 两个积分环编节辑版串p联pp的t Bode图
7
三惯性环节 惯性环节的频率特性是:
其对数幅频特性是:
用两条直线近似描述惯性环节的对数幅频特性, 即在
的低频段时，
在
的高频段时
，与零分贝线重合； 是一条斜率为
(5-62)
幅值的总分贝数为:
(5-63)
放大环节的相频特性是:
(5-64)
如图5-11所示，它是一条与角频率ω无 关且与ω轴重合的直线。
编辑版pppt
4
二积分环节 积分环节的频率特性是: 其幅频特性为:
对数幅频特性是:
编辑版pppt
5
设
，则有:

自动控制原理知识点汇总

自动控制原理知识点汇总

自动控制原理总结第一章 绪 论技术术语1. 被控对象:是指要求实现自动控制的机器、设备或生产过程。

2. 被控量：表征被控对象工作状态的物理参量(或状态参量)，如转速、压力、温度、电压、位移等。

3. 控制器：又称调节器、控制装置，由控制元件组成，它接受指令信号，输出控制作用信号于被控对象。

4. 给定值或指令信号r(t)：要求控制系统按一定规律变化的信号，是系统的输入信号。

5. 干扰信号n(t)：又称扰动值，是一种对系统的被控量起破坏作用的信号。

6. 反馈信号b(t)：是指被控量经测量元件检测后回馈送到系统输入端的信号。

7. 偏差信号e(t)：是指给定值和被控量的差值，或指令信号和反馈信号的差值。

闭环控制的主要优点：控制精度高，抗干扰能力强。

缺点：使用的元件多，线路复杂，系统的分析和设计都比较麻烦。

对控制系统的性能要求 :稳定性 快速性 准确性稳定性和快速性反映了系统的过渡过程的性能。

准确性是衡量系统稳态精度的指标，反映了动态过程后期的性能。

第二章 控制系统的数学模型拉氏变换的定义:-0()()e d st F s f t t +∞=⎰几种典型函数的拉氏变换1.单位阶跃函数1(t)2.单位斜坡函数3.等加速函数4.指数函数e -at5.正弦函数sin ωt6.余弦函数cos ωt7.单位脉冲函数(δ函数) 拉氏变换的基本法则 1.线性法则 2.微分法则 3.积分法则1()d ()f t t F s s ⎡⎤=⎣⎦⎰L4.终值定理()lim ()lim ()t s e e t sE s →∞→∞==5.位移定理00()e()sf t F s ττ--=⎡⎤⎣⎦Le ()()atf t F s a ⎡⎤=-⎣⎦L传递函数：线性定常系统在零初始条件下，输出信号的拉氏变换和输入信号的拉氏变换之比称为系统(或元部件)的传递函数。

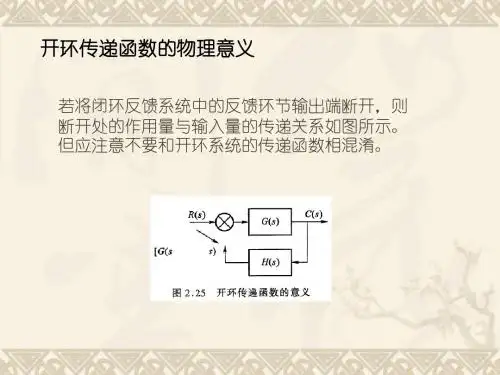
动态结构图及其等效变换 1.串联变换法则 2.并联变换法则 3.反馈变换法则4.比较点前移“加倒数”；比较点后移“加本身”。

第五章5_2 Bode图 自动控制原理 浙江大学考研资料

第五章5_2 Bode图 自动控制原理 浙江大学考研资料
ω 1 2 8 10 decades decades decades 20 80 100
5
Bode plots (Logarithmic plots )
Bode图（对数坐标图）
Bode图（对数频率特性曲线）： 对数频率特性曲线由对数幅频曲线和对数相频曲线组成 对数频率特性曲线的横坐标：按logω分度，单位为弧度/秒（rad/s） 对数幅频曲线的纵坐标：按LmG(jω)=20log|G(jω)|线性分度，单位是分贝 对数相频曲线的纵坐标：按Φ(ω)线性分度，单位为度
Lm j 20 log j 20 log
dB
Angle 90º jω
对数幅频曲线为一条斜线，其斜率为 6dB/octave 或者 20dB/decade. 相角恒等于 +90º.
-90º (jω)-1
ω
10
Bode plots (Logarithmic plots )
2 1 1 1 2 Lm 1 j 2 j Lm Lm n 1 jT1 1 jT2 n
1
(1+j (1 jωT1)-1 (1 (1+j jωT2)-1
1
Angle 1/T1 -90º -180º
17
1/T2 ω
2 1 1 1 2 Angle1 j 2 j Angle Angle n 1 jT1 1 jT2 n
Wintersweet
2
Bode plots (Logarithmic plots )
Bode图（对数坐标图）
对数坐标图的优点 1) 将乘积和除法的数学操作转化为加法和减法; 2) 传递函数的获取大多采用图表法，而不是分析法; 3) 半对数坐标扩展了低频段 首先运用直线近似的方法来获得系统的近似特性，然后修正直线， 提高精度. 对数坐标图 足够多的数据 极坐标图

典型环节传递函数及伯德图

典型环节传递函数及伯德图

1 T
10 T

L( )(dB)
0 0.01
( ) G( j ) 90
0.1 1 10

20
20dB / dec
j
40

( )()
0 90 60 30 0 0.01 0.1 1 10

４.惯性环节 （一阶积分环节，是一个相位滞后环节）

惯性环节的特点：当输入量突变时，输出量不会突变，只能按指数 规律逐渐变化，即具有惯性。 惯性环节的微分方程:
比例环节功能框图
1.比例环节（放大环节）
G( j ) K , L( ) 20lg G( j ) 20lg K G( s) K G( j ) K G( j ) K 0 ( ) G( j ) 0
L( )(dB)
20lgK j 0 K 0 0.1 1 10
1
转折频率
1 T
渐近线 1
10 T
0

0 -20

实际幅相曲线
( )()
0 .1 1 T
20dB / dec

0.707
1 T
0 -45
1 T
10
1 T

5 一阶微分环节
特点：此环节的输出量不仅与输入量本身有关，而且与输 入量的变化率有关。
方块图为:
R( s )
τs + 1
C (s)
６.振荡环节
G jω 1 2 2 L ω 20lg 1 T ω 2 2 T jω 2ζ T jω 1

2ζ Tω
2
2
ω t g1
2ζ Tω 2 2 1 T ω

自动控制原理第五章频域分析法

自动控制原理第五章频域分析法
mn 122
谐振峰值
Am(m) 2
1
12
振荡环节的对数频率特性
L ()2l0 oG g (j) 2l0 o(g 1 n 2 2)24 2 n 2 2
n L()0低频渐近线是零分贝线。
n L ( ) 4 0lo g (/ n) 4 0lo g (T ) n 1 /T
高频段是一条斜率为- 40/dB的直线，和零分
幅频特性的谐振峰值和谐振角频率：
G(ju)
1
(1u2)242u2
d G d (j) u u 0 ,u r 1 22 ( 1 /2 0 .7)0
r n12 2 ( 1/ 20 .7) 0
幅频特性的谐振角频率和谐振峰值：
rn1 22, M r G (jr) 1 /21 2
谐振频率
1 / T , L () 2l0 o1 g2 T 2 2l0 o 1 0 g ( d)B
在频率很低时，对数幅频曲线可用0分贝线近似。
1 / T , L ( ) 2l0 o1 g 2 T 2 2l0 o T g
当频率很高时，对数幅频曲线可用一条直线近似，直
线斜率为-20dB/dec，与零分贝线相交的角频率为 1/T 。
( )
0 0.1 1 10
0 o 0.1 1 10
45o
20
90o
对数坐标刻度图
注意：
➢纵坐标是以幅值对数分贝数刻度的，是均匀的；横 ➢ 坐标按频率对数标尺刻度，但标出的是实际的值， ➢ 是不均匀的。 ——这种坐标系称为半对数坐标系。 ➢在横轴上，对应于频率每增大10倍的范围，称为十 ➢ 倍频程(dec)，如1-10，5-50，而轴上所有十倍频 程 ➢ 的长度都是相等的。 ➢为了说明对数幅频特性的特点，引进斜率的概念， ➢ 即横坐标每变化十倍频程〔即变化〕所对应的纵 坐

自动控制原理：第六章频域分析法——伯特图及稳定性分析

自动控制原理：第六章频域分析法——伯特图及稳定性分析

0.1
0.05
0.05
0.1 0.3
(1 T 2 2
j2T)1
0.7
1
1
10
/ n
(ω) arctan[(2ζωT)/ (1 ωT2 )] 相角：0°~-180°
6.4 系统开环频率特性-典型环节的伯德图特性：
令
dA ( ) d
0,得
谐振
20
10
Bode Diagram 转折频率
0 K 0
90
K 0 180
101
100
101
102
/(rad/sec)
6.4 系统开环频率特性-典型环节的伯德图
2) 积分环节( j )1，微分环节( j )
Bode Diagram 20
1 j
L() /(dB)
积分
A( ω ) 1 ,( ω ) 90
ω
0 j
20
微分 A(ω) ω,(ω) 90
6.3 频率特性图示法-对数幅相频率特性曲线
6.3.3 对数幅相特性曲线（尼科尔斯（N.B.Nichols）曲线）
横坐标为相位()
纵坐标为对数幅值L()=20lgA()
绘制过程：
0
L() /(dB)
从伯德图中分别读取各频率 10 下L()和()的值，
20
在尼科尔斯坐标系中确定相
应的点并将频率作为参变 30 量标于各点旁，
r n 1 2 2
A(r ) Am 2
1
1 2
L() /(dB)
0
-10 -20
(1 T 22
j2T)1
0.05 0.1 0.3
-30
0.7
1 -40

自动控制原理第五章

自动控制原理第五章

•表5-1 RC网络的幅频特性和相频特性数据

A( )
( )
0 1 0
1 0.707
45
2 0.45
5 0.196

0
63.4 78.69 90
图5-2 RC网络的幅频和相频特性
图5-3 RC网络频率特性的幅相曲线
对数频率特性图又称伯德图（Bode图），包 括对数幅频特性和对数相频特性两条曲线， 其中，幅频特性曲线可以表示一个线性系 统或环节对不同频率正弦输入信号的稳态 增益；而相频特性曲线则可以表示一个线 性系统或环节对不同频率正弦输入信号的 相位差。对数频率特性图通常绘制在半对 数坐标纸上，也称单对数坐标纸。
图5-20控制系统结构图
将系统的开环频率特性函数按典型环节划分， 可以分解为： ( j 1) ( ( j ) 2 ( j ) 1) k
m1 m2
G ( j ) H ( j )
k
2 l
2
l l
( j )
0
k 1 n1
( i s 1) ( 2 ( j ) 2 2 j j ( j ) 1) j
图5-19 Ⅱ型三阶系统幅相频率特性图
讨论更一般的情况，对于如图5-20所示的闭 环控制系统结构图，其开环传递函数为 G( s) H ( s) ，可以把系统的开环频率特性写作如 下的极坐标形式或直角坐标形式：
G( j)H ( j) G( j)H ( j) e j () P() jQ()
•图5-6积分环节频率特性的极坐标图
在伯德图上，积分环节的对数频率特性为
L( ) lg A( ) lg G( j ) lg ( ) 2
图5-7积分环节的伯德图

自动控制原理第五章第二部分

自动控制原理第五章第二部分

当L(w=0时：
L(w
)

20
lg
K
w
0K
wv
I型系统
斜率为-20db/dec的低频段渐近线或其延长线与横轴的 交点的频率值与开环放大系数K相等。
II型系统
斜率为-40db/dec的低频段渐近线或其延长线与横轴的 交点的频率值的平方与开环放大系数K相等。
例1:已知某最小相位系统由频率响应实验获得的对数幅 频曲线如图所示，试确定其传递函数。
3.开环对数幅频特性：
L(w)
60
40dB / dec
40
转折频率 w1 1
w2 2
w3 20
环节 惯性 一阶微分
振荡
20
60dB / dec
0
0.1
12
10 20
100 w
20
40dB / dec
40
80dB / dec
传递函数的频域实验确定
1.频率响应实验
Asinwt
L(w )
20dB / dec
0dB / dec
20
20dB / dec
0
0.1
1
20
w
40dB / dec
解： (1)确定系统积分环节的个数
低频段的渐近线为-20dB/dec 1
(2)确定系统传递函数
K ( 1 s 1)
G(s)
0.1 s(s 1)( 1
s 1)
20
L(w )
一阶微分环节 二阶微分环节
一点+一斜率确定初始段渐近线
(4)从低频渐近线开始，沿w 增大的方向，每遇到一个
转折频率改变一次渐近线斜率，直到绘出转折频率最高 的环节为止；

第5章4——Bode图

第5章4——Bode图

2

1 2 n
2
n
2 arc tg n 2 1 2 n
0 0 ( ) 90 n 180
autocumt@ 22
振荡环节L()
L()dB 40 20 0dB -20
(rad / s)
10 -2
10 -1
1
10
0
2 3 4
10
1
autocumt@
自动控制原理
对数分度：
lg 2 0.301
lg 3 0.4771 lg 4 2lg 2 0.602 lg 5 0.699 lg 6 lg 3 lg 2 0.778
lg 7 0.845 lg 8 3 lg 2 0.903 lg 9 2 lg 3 0.954
（）º
(rad / s)
10 -2
autocumt@
10 -1
3
100
10
1
20 10 0
自动控制原理
L() dB -10
-20 -30 -40 900 450

( )
00 0 -450 -900
-1350

完 整 图 二 合 一
-1800
10 -2
autocumt@
[-20] 0.1 0.2
1
2
10 20
[-20]
100
16
5-4 对数频率特性——Bode图
（5）一次微分环节
传递函数： G（S） TS＋ 1 频率特性： G ( j ) Tj 1
0 0 1 相频特性 ( ) arctanT 45 T 90

自动控制原理基础伯德图

自动控制原理基础伯德图

使用MATLAB 绘制频率特性曲线姓名 黄勇 班级 16电气本三 学号 4702160186一、频率特性在定义谐波输入下，输出响应中与输入同频率的谐波分量与谐波输入的幅值之比A(ω)为幅频特性，相位之差）（ωϕ为相频特性，并称其指数表达形式：()()()j G j A e ϕωωω=为系统的频率特性。

总结上述我们可知：频率特性由两个部分组合而成，分别是幅频特性和相频特性。

稳态系统的输出信号与输入信号的相位之差我们称其为相频特性。

稳态系统输出与输入的幅值之比称为幅频特性。

另外频率响应对稳定系统和不稳定系统都适应，其中稳定系统的频率特性可以通过实验的方法确定。

二、频率特性的几何表示法⏹ 幅相频率特性曲线简称幅相特性曲线，或幅相特性，或极坐标图。

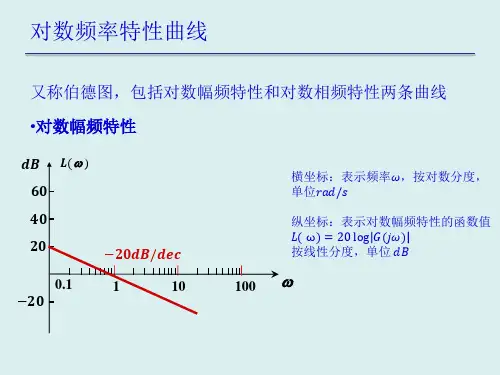
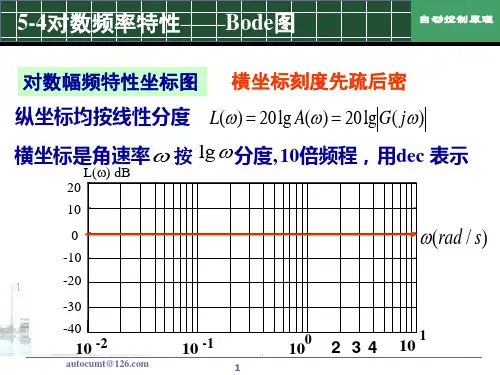
⏹ 对数频率特性曲线又称为伯德曲线或伯德图。

⏹ 对数幅相曲线又称为尼科尔斯曲线或尼科尔斯图。

三、惯性环节频率特性的绘制惯性环节的表达式为： ()11G s Ts =+T 的取值分别为2、4、7，使用MATLAB 软件绘制MATLABA的函数指令如下：指令说明：num为分子指令；den为分母指令；此次画图调用了伯德图画法（bode指令）。

绘制图如下：T=2时。

MATLABA的函数指令如下：绘制图如下：同理当T=4时。

MATLABA的函数指令如下：绘制图如下：四、振荡环节频率特性的绘制振荡环节的传递函数为： ()221=21nnGs ssζωω++在201取值，本次取值分别为0.1 0.3 0.5 0.707 0.85 0.91 1。

方法一：使用伯德图画MATLAB函数程序指令如下：MATLAB图形显示如下：方法二：使用奈奎斯特图画取值分别为0.1 0.3 0.5 0.707 0.85 0.91 1。

MATLAB函数程序指令如下：MATLAB图形显示如下：。

自动控制原理之伯德图

自动控制原理之伯德图
系统开环频率特性的绘制
画出各串联典型环节相频特性，将它们相加后得到系统开环相频特开环系统对数幅频特性图
01
L
02
5.4 系统开环频率特性的绘制
以后每遇到一个交接频率，就改变一次渐近线斜率。 每当遇到 环节的交接频率时，渐近线斜率
增加-20dB/十倍频； 每当遇到 环节的交接频率时，斜率增加
+20dB/十倍频； 每当遇到 环节的交接频率时，
通过A点作一条-20NdB/十倍频的直线，其中N为系统的无差阶数，直到第一个交接频率w1。如果w1<1，则低频渐近线的延长线经过A点。
确定交接频率w1、w2、w3……，标在角频率w轴上。
在w＝1处，量出幅值20lgK，其中K为系统开环放大系数。(在图中标出相应的字母，如A点)
二、绘制系统开环频率特性伯德图的步骤
斜率增加-40dB/十倍频。
系统开环频率特性的绘制
5
⑤ 绘出用渐近线表示的对数幅频特性以后，如果需要，可以进行修正。通常只需修正交接频率处以及交接频率的二倍频和1/2倍频处的幅值就可以了。 对于一阶项，在交接频率处的修正值为±3dB； 在交接频率的二倍频和1/2倍频处的修正值为±1dB。 对于二阶项，在交接频率处的修正值可由公式 求出。
5.4 系统开环频率特性的绘制
系统开环对数幅频特性L(ω)通过0分贝线，即 时的频率 称为穿越频率。穿越频率 是开环对数相频特性的一个很重要的参量。
01
02
03
绘制开环系统对数相频特性时，可分环节绘出各分量的对数相频特性，然后将各分量的纵坐标相加，就可以得到系统的开环对数相频特性。

开环伯德图绘制

开环伯德图绘制
于是有： ω = K ⇒ ω0 = K ν
ν
75
《自动控制原理》电子教案
（5）绘制中频段 首先在横坐标轴上将转折频率按从低到高的顺序标出各转折频率。然后，依次在各转折频率处改变 直线的斜率 ，改变的多少取决于转折处环节的性质，如惯性环节的斜率为 − 20dB dec ，振荡环节为
− 40dB dec ，一阶微分环节为 + 20dB dec ，二阶微分环节为 + 40dB dec 等等。 例：已知单位反馈控制系统的开环传递函数为 GK ( s) = 100( s + 2) s( s + 1)(s + 20) ，试绘制其开环
ω
2
由图可知： 解得wc=4，
小结丗对最小相位系统、幅频特性与相频特性的关系
如果幅频特性的斜率为－１对应的相角为－ｐｉ／２； 如果幅频特性的斜率为－ｋ对应的相角为－ｐｉ＊ｋ／２．
77
L(ω ) = 20 lg K − 20 ×ν × lg ω ω =1 = 20 lg K
③低频段直线（或其延长线）与零分贝线（横轴）的交点频率为 ω0 = K ，对于 I 型系统交点频
ν
1
率为 ω0 = K ，II 型系统交点频率为 ω0 =
1
K ；这是因为由低频段的幅频方程，可得到
L(ω ) = 20 lg K − 20 ×ν × lg ω = 0 ⇒ 20 lg K = 20 ×ν × lg ω = 20 lg ων
⎧ L (ω ) = −20 lg 1 + ω 2 − 20 lg lg 1 + 4ω 2 ⎧ϕ (ω ) = arctgω − arctg 2ω ⎪ 1 1 ，⎨ ⎨ 2 2 ⎩ϕ 2 (ω ) = −arctgω − arctg 2ω ⎪ L2 (ω ) = −20 lg 1 + ω − 20 lg lg 1 + 4ω ⎩

自动控制理频域伯德图

自动控制理频域伯德图


Lω 20lg1 ＝0 dB
——低频渐近线为一条0dB的水平直线。
Lω 20lg 1 Tn ω
2

2 2
2ζ T ω
n
2
高频段，即ωTn>>1时
L() 20lg( Tn ) 40lg(Tn )
2 2
当ω增加10倍
ωTn 40 40lgωTn L() 40lg10
相频与ω无关，值为-90°且平行于横轴的直线。
L ( )
20 0
20 0.1 10
1

( )
0 90
0.1
1
10

3 微分因子
G jω jω
微分环节是积分环节的倒数，它们的 曲线斜率和相位移也正好相差一个负号。
L ( )
20
0
20
0.1 20
1
10

( )
90
L() 40lg Tn 40lg1 0(dB)
即高频渐近线是一条斜率为-40dB/dec的直线。 当 ωω 1 时
n
Tn
说明
ω ωn
1 Tn
为二阶系统(振荡环节)的转折频率。

。10
0
0.1
0.2 0. 3
L ( )
dB
-40dB/dec
0 .7 1
10
系统 的相频特性为 90 arctan arctan 2 10
0
W=0
90
0
W=1
W=10 W=无穷大
110.860
123.70
0 90

控制系统的伯德图分析——自动控制原理

控制系统的伯德图分析——自动控制原理
() 0
伯德图
c
GMb>0
g
PM>0 Kg>1
PM -180
稳定闭环系统的GM和PM
奈氏图 jIm
L()
伯德图
c 1
0 GMb<0
c
ReΒιβλιοθήκη PM()0g
1
PM<0 Kg
-180
PM
Kg<1
不稳定闭环系统的GM和PM
GM，PM常作为控制系统的频域设计指标。
GM，PM大表明相对稳定性好,但响应速度低。 GM，PM小表明相对稳定性差,但响应速度高。 过大或过小都不好，较好的经验值为：
0时有低频渐近线方程
L( ) 20 lg K 20 lg K p
1
斜率=0， 与实轴无交点。
T
(2) N=1 (1型系统)
G( j)H ( j) K j (Tj 1)
L( ) 20 lg K 20 lg 20 lg T 2 2 1
0时有低频渐近线方程
L( ) 20 lg K 20 lg 20 lg K v 20 lg
斜率=-40 db/dec，交点: K a
L ()
1 T
Ka
-40db/dec
1
T Ka
L ()
1 T
Ka
-40db/dec
1
Ka
T
三、 伯德图与稳态误差的关系
表5-2 系统类型和低频渐近线特征
系统类型 斜率
0
0
1 -20
2 -40
L(=1) 与L=0的交点
20 lg K无p 交点
20 lg Kv
Kv
20 lg K a
Ka
斜率=-20 db/dec，交点: =Kv

经典控制Bode稳定判据

经典控制Bode稳定判据
5· 4 Bode（伯德）稳定判 据
•Nyquist稳定判据是利用开环频率特性G(K)的极 坐标图(Nyquist图）来判定闭环系统的稳定性。 •如果将开环极坐标图改画为开环对数坐标图，即 Bode图，同样可以利用它来判定系统的稳定性。 •这种方法称为对数频率特性判据，简称为对数判据 或Bode判据，它实质上是Nyquist判据的引申。
• 正穿越 • 负穿越
• 半次正穿越
• 半次负穿越
二、穿越的概念(Bode)
• 在开环对数幅频特性为正值的频率范围内， 沿ω 增加的方向，对数相频特性曲线自下 而上穿过-1800线为正穿越； • 沿ω 增加的方向，对数相频特性曲线自上 而下穿过-1800线为负穿越。 • 若对数相频特性曲线自-1800线开始向上， 为半次正穿越； • 对数相频特性曲线自-1800线开始向下，为 半次负穿越。
5.5系统的相对稳定性
相对稳定性——稳定裕量
Im
G0 ( j g )
幅值裕量 相角裕量
c • -1
Im
kg
-1 g
c •
•
Re
g
•
Re
kg
G 0 ( j g )
幅值穿越频率 相位穿越频率
c
g
G0 ( jc ) 1
( j g ) 1800Βιβλιοθήκη 一、相位裕度• 定义
一、Nyquist图和Bode图的对应关系
• Bode图与Nyquist图的对应关系： • （1）Nyquist图上的单位园 — Bode图 幅频特性上的0dB线 • （2）Nyquist图上的负实轴 — Bode图 相频特性上的-1800线
2个重要频率
• Nyquist轨迹与单位圆交点的频率，即对数 幅频特性曲线与横轴交点的频率，亦即输 入与输出幅值相等时的频率（开环输入与 输出的量纲相同），称为剪切频率或幅值 穿越频率、幅值交界频率，记为ω c。 • Nyquist轨迹与负实轴交点的频率，亦即对 数相频特性曲线与横轴交点的频率，称为 相位穿越频率或相位交界频率，记为ω g。

第五章1 控制系统的频域分析(频率特性与BODE图)

第五章1 控制系统的频域分析(频率特性与BODE图)
ϕ(ω) = −arctg (ωT )
自动控制原理
幅相频率特性画法举例
画出二阶系统 G ( s ) = 112
的幅相频率特性
s (1 + 0 .02 s )
自动控制原理
2. 伯德图(Bode图)
如将系统频率特性G(jω ) 的幅值和相角分别绘在半对数坐
标图上,分别得到对数幅频特性曲线（纵轴：对幅值取分贝数
自动控制原理
极坐标图(Polar plot)，幅相频率特性曲线，幅相曲线 当ω在0～∞变化时,相量G(jω) 的幅值和相角随ω而变化,与 此对应的相量G(jω) 的端点在复平面 G(jω) 上的运动轨迹 就称为幅相频率特性曲线或 Nyqusit曲线。画有 Nyqusit曲 线的坐标图称为极坐标图或Nyqusit图。（ ω在0～－∞变化 对称于实轴） 奈奎斯特(N.Nyquist)在1932年基于极坐标图阐述了反馈系统 稳定性
这些幅频特性曲线将通过点
自动控制原理
0dB,ω = 1
L(ω ) = 20 lg 1 = −20 lg ω (dB ) jω
ϕ (ω ) = −90°
Magnitude (dB)
Phas e (deg)
20 10
0 -10 -20 -30 -40 -89
-89.5
-90
-90.5
-91
-1
10
Bode Diagram of G(jw )=1/(jw )
(a) 幅频特性
自动控制原理
ϕ(ω) = −arctgTω
自动控制原理
输出与输入的相位之差
(b)相频特性
Uo (s) = G(s) = 1
Uo ( jω) = G( jω) = 1 = 1

孙炳达版 《自动控制原理》第5章 控制系统的频率特性分析法-4

孙炳达版 《自动控制原理》第5章 控制系统的频率特性分析法-4

渐近线
5.4 系统开环频率特性绘制
相频特性表达式为
ω
φ(ω)/° -40
-80 -120 -160 -200 -240
arctan 0.25 arctan
5.4 系统开环频率特性绘制
对渐近线进行误差修正 在振荡环节转折处，ζ=0.4/(2*0.5)=0.4， 修正值+6dB； 在惯性环节转折处，修正值-3dB。
40
L(ω)/dB
精确曲线
20dB 1
+6dB
20
0 -20 -40
-40dB/dec ω1=2 ω2=4
振荡
-3dB
10
惯性
ω /s-1
-60dB/dec
1 2 3
5.4 系统开环频率特性绘制
一、极坐标图 方法一： 根据不同的ω值，计算出相应的P(ω)和Q(ω)或A(ω) 和φ (ω) ，并在直角坐标平面上描出相应的点，然 后用光滑线段连接各点。 方法二：利用典型环节的频率特性，步骤为 (1)分别计算出各典型环节的幅频特性和相频特性； (2)各典型环节的幅频特性相乘得到系统的幅频特性， 各典型环节的相频特性相加得到系统的相频特性。 (3)给出不同的ω值，计算出相应的A(ω)和φ (ω)，描点 连线。
5.4 系统开环频率特性绘制
起点 G(0) 15 j 零虚频特性为0，解得 1 / 2 将此代入实频特性，求 得与实轴交点为-3.33。
终点
G() 0 j 0
根据幅相频率特性曲线的起 点、与实轴交点及终点，幅 相频率特性曲线如图所示。
5.4 系统开环频率特性绘制
10 例 设系统的频率特性为 Gk ( j ) j ( j 0.2 1)( j 0.05 1)

15 第十五讲 伯德图

15 第十五讲 伯德图

1
(1−ω
2
/ω
2 2 n
)
+ 4ς ω / ω
2 2 2 2 2
2 n
Mdb = −20log10
−1
(1−T ω
)
+ 4ς 2T 2ω2
2ςTω ϕ (ω) = − tan 1−ω2Tω2
1) 低频渐近线:
当ωT << 1时，即 ω << 1/T， 1/T→转折频率 MdB = 0dB
Mdb -40db/dec ω
• 步骤 1: 计算转折频率。
1+ s → ωb =1rad / s
1 → ωb =1rad / s s 1 → ωb = 2 rad / s 1 1+ s 2
Kdb = 20lg 10 = 20 dB
步骤 2: 确定要画的频率范围。 所有转折频率都在1~10rad/s的这个十倍频程内， 所以此伯德图将在以下范围内绘制：
0.1 1.0 10
ω
φ
+90
1+s
+45
0 10
-45
1 s
-90
1 1 1+ s 2
图.SP.15.1.6
步骤8: 将所有环节的相角相叠加。
φ
+90
0.1 1.0 10
ω
+45
0
合成相位i
-45
-90
图.SP.15.1.6
MATLAB 仿真
10(1+ s) G(s) = 1 s1+ s 2
sys=tf([10 10],[0.5 1 0]); bode(sys) pause
H(s) =1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2020 12:43:14 AM00:43:142020/12/12
• 11、自己要先看得起自己，别人才会看得起你。12/12/
谢 谢 大 家 2020 12:43 AM12/12/2020 12:43 AM20.12.1220.12.12
• 12、这一秒不放弃，下一秒就会有希望。12-Dec-2012 December 202020.12.12
• 13、无论才能知识多么卓著，如果缺乏热情，则无异 纸上画饼充饥，无补于事。Saturday, December 12, 2020
12-Dec-2020.12.12
• 14、我只是自己不放过自己而已，现在我不会再逼自 己眷恋了。20.12.1200:43:1412 December 202000:43
斜率增加-40dB/十倍频。
5.4 系统开环频率特性的绘制
⑤ 绘出用渐近线表示的对数幅频特性以后，如果需要，可以进
行修正。通常只需修正交接频率处以及交接频率的二倍频和 1/2倍频处的幅值就可以了。
对于一阶项，在交接频率处的修正值为±3dB；
在交接频率的二倍频和1/2倍频处的修正值为±1dB。
对于二阶项，在交接频率处的修正值可由公式 20lg 1
•
8、业余生活要有意义，不要越轨。20 20年12 月12日 星期六 12时43 分14秒 00:43:1 412 December 2020
•
9、一个人即使已登上顶峰，也仍要自 强不息 。上午 12时43 分14秒 上午12 时43分 00:43:1 420.12. 12
• 10、你要做多大的事情，就该承受多大的压力。12/12/
5.4 系统开环频率特性的绘制
二、绘制系统开环频率特性伯德图的步骤
① 确定交接频率w1、w2、w3……，标在角频率w轴上。
② 在w＝1处，量出幅值20lgK，其中K为系统开环放大系数。 (在图中标出相应的字母，如A点)
③ 通过A点作一条-20NdB/十倍频的直线，其中N为系统的 无差阶数，直到第一个交接频率w1。如果w1<1，则低频渐 近线的延长线经过A点。
5.4 系统开环频率特性的绘制
④ 以后每遇到一个交接频率，就改变一次渐近线斜率。 每当遇到 1 环节的交接频率时，渐近线斜率 jT j 1 增加-20dB/十倍频；
每当遇到 ( jTi 1) 环节的交接频率时，斜率增加
+20dB/十倍频；
每当遇到
( j)2
2 n
2 n
j
2 n
环节的交接频率时，
求出。
2
系统开环对数幅频特性L(ω)通过0分贝线，即 L(c ) 0 或 A(c ) 1
时的频率c 称为穿越频率。穿越频率c 是开环对数相频
特性的一个很重要的参量。
5.4 系统开环频率特性的绘制
⑥ 画出各串联典型环节相频特性，将它们相加后得到 系统开环相频特性。
绘制开环系统对数相频特性时，可分环节绘 出各分量的对数相频特性，然后将各分量的纵坐 标相加，就可以得到系统的开环对数相频特性。
•
6、意志坚强的人能把世界放在手中像 泥块一 样任意 揉捏。 2020年 12月12 日星期 六上午 12时43 分14秒 00:43:1 420.12. 12
•
7、最具挑战性的挑战莫过于提升自我 。。20 20年12 月上午 12时43 分20.1 2.1200: 43Dece mber 12, 2020
40dB / dec
20dB / dec
20dB / dec
D
开环系统对数幅频特性图 60dB / dec
•
1、有时候读书是一种巧妙地避开思考 的方法 。20.1 2.1220. 12.12Sa turday, December 12, 2020
•
2、阅读一切好书如同和过去最杰出的 人谈话 。00:4 3:1400: 43:1400 :4312/ 12/2020 12:43:14 AM
例5-12 已知系统的开环传递函数为
G(s)H (s)
K (1 s) 1 1
LL( )
s T1s 1 T2 s 2
1
2T2 s 1 (T1
T2 )
dB ()
AB
20dB / dec
20 log K
渐近特性
20dB /
40dB / dec
1
T2
C
•
3、越是没有本领的就越加自命不凡。 20.12.1 200:43: 1400:4 3Dec-20 12-Dec-20
•
4、越是无能的人，越喜欢挑剔别人的 错儿。 00:43:1 400:43: 1400:4 3Saturday, December 12, 2020
•
5、知人者智，自知者明。胜人者有力 ，自胜 者强。 20.12.1 220.12. 1200:4 3:1400: 43:14D ecembe r 12, 2020