有限元理论基础
- 格式:doc
- 大小:213.50 KB
- 文档页数:13

有限元的理论基础有限元方法的基础是变分原理和加权余量法,其基本求解思想是把计算域划分为有限个互不重叠的单元,在每个单元内,选择一些合适的节点作为求解函数的插值点,将微分方程中的变量改写成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式,借助于变分原理或加权余量法,将微分方程离散求解。
采用不同的权函数和插值函数形式,便构成不同的有限元方法。
1.加权余量法:是指采用使余量的加权函数为零求得微分方程近似解的方法称为加权余量法。
(Weigh ted residual method WRM )是一种直接从所需求解的微分方程及边界条件出发,寻求边值问题近似解的数学方法。
加权余量法是求解微分方程近似解的一种有效的方法。
设问题的控制微分方程为:在V 域内 在S 边界上式中 :L 、B ——分别为微分方程和边界条件中的微分算子;f 、g ——为与未知函数u 无关的已知函数域值;u ——为问题待求的未知函数 ()0B u g -=(5.1.2)()0L u f -=(5.1.1)混合法对于试函数的选取最方便,但在相同精度条件下,工作量最大。
对内部法和边界法必须使基函数事先满足一定条件,这对复杂结构分析往往有一定困难,但试函数一经建立,其工作量较小。
无论采用何种方法,在建立试函数时均应注意以下几点:(1)试函数应由完备函数集的子集构成。
已被采用过的试函数有幂级数、三角级数、样条函数、贝赛尔函数、切比雪夫和勒让德多项式等等。
(2)试函数应具有直到比消除余量的加权积分表达式中最高阶导数低一阶的导数连续性。
(3)试函数应与问题的解析解或问题的特解相关联。
若计算问题具有对称性,应充分利用它。
显然,任何独立的完全函数集都可以作为权函数。
按照对权函数的不同选择得到不同的加权余量计算方法,主要有:配点法、子域法、最小二乘法、力矩法和伽辽金法。
其中伽辽金法的精度最高。
2、虚功原理——平衡方程和几何方程的等效积分“弱”形式虚功原理包含虚位移原理和虚应力原理,是虚位移原理和虚应力原理的总称。

有限元理论基础及应用有限元理论是应用于工程计算领域的一种数值分析方法,它是通过将连续的结构或物体分割成有限数量的离散单元,然后在每个单元上进行近似计算,最终得到整个结构或物体的近似解。
有限元理论广泛应用于结构分析、流体力学、电磁场分析等领域,是工程计算的重要工具。
有限元理论的基础是有限元方法,它将连续的结构或物体以网格的形式划分成一系列有限的单元,通过在每个单元内进行节点位移或其他物理量的近似表示,建立起离散的数学模型。
在有限元方法中,常用的单元形状包括线元、三角形单元、四边形单元等。
每个单元的节点之间通过连接的方式形成整个结构的网格。
有限元理论的基本原理是将连续的物理问题转化为离散的代数问题,通过求解代数方程组得到数值结果。
其基本步骤包括:1.离散化:将连续的结构或物体划分为离散的单元,并在每个单元上建立近似解。
2.建立单元方程:根据结构或物体的本构关系、边界条件等,建立每个单元的方程。
3.组装:根据单元之间的连接方式,将每个单元的方程组装成整个结构或物体的方程。
4.边界条件处理:考虑边界条件对结构或物体的约束作用,修改方程。
5.求解代数方程组:将边界条件处理后的方程组进行求解,得到数值解。
有限元理论的应用非常广泛,主要包括:1.结构分析:有限元方法在结构力学领域的应用非常广泛,可以用于预测结构的应力、变形、疲劳寿命等。
例如,在建筑工程中,可以使用有限元方法对建筑结构进行静力分析,以确保结构的稳定性和安全性。
2.流体力学:有限元方法在流体力学领域的应用包括流体流动、传热、空气动力学等方面。
通过将流体分割成离散的单元,并建立流体的动量方程、能量方程等,可以模拟和预测流体的各种特性。
3.电磁场分析:有限元方法可以用于模拟和分析电磁场的分布、辐射、散射等现象。
在电子器件设计中,有限元方法可以用于预测电磁场的影响和优化设计。
此外,有限元方法还应用于声学、热力学、生物力学等领域。
它的优势包括模拟结果的准确性、适用于复杂几何形状和边界条件、计算速度较快等。




一、里兹法与迦辽金法(摘自电磁场有限元方法 金建铭) 1. 里兹法里兹法是一种变分方法,其中边值问题用变分表达式(也称泛函)表示,泛函的极小值对应于给定边界条件下的控制微分方程。
通过求泛函相对于其变量的极小值可得到近似解。
2. 伽辽金法伽辽金法属于残数加权方法类型,它通过对微分方程的残数求加权的方法得到方程的解。
若u是方程的近似解,将u 代入方程可得到非零的残数: r Luf =- u的最佳近似应能使残数r 在Ω内所有点上有最小值。
残数加权方法要求: 0i i R rd ωΩ=Ω=⎰这里i R 表示残数的加权积分,i ω是所选的加权函数。
在伽辽金法中,加权函数与近似解展开中所用的函数相同。
通常,这样可得到最精确的解。
二、有限元方法里兹法和伽辽金法中,在整个解域内找出能表示或至少近似表示问题真实解的试探函数是非常重要的。
然而对于许多问题,这个步骤是十分困难的,对二维和三维问题尤其如此。
为此,我们可将整个区域划分成小子域,并应用定义在每个子域上的试探函数。
因为子域是小区域,因而在每一子域内函数的变化不大,所以定义在子域上的试探函数通常比较简单。
这正是有限元法的基本思想。
应用里兹法的过程通常称为里兹有限元法或变分有限元法,而应用伽辽金方法的过程通常称为伽辽金有限元方法。
有限元法与经典里兹法和伽辽金法的不同之处是在试探函数的公式上。
在经典里兹法和伽辽金法中,试探函数由定义在全域上的一组基函数组成。
这种组合必须能够(至少近似)表示真实解,也必须满足适当的边界条件。
在有限元法中,试探函数是由定义在组成全域的子域上的一组基函数构成。
因为子域很小,所以定义在子域上的基函数能够十分简单。
三、关于形函数(摘自有限元法在电磁计算中的应用 张榴晨)对于一个待求的微分方程,用一组线性独立的尝试函数i ψ和待定系数i C 来表示方程的近似解,并用加权余数法(迦辽金法)来求解这些待定系数。
求解待定系数的代数方程组为:1[]1,2,,ni j i j i d C q d j n ψψψΩΩ=∇∇Ω=Ω=∑⎰⎰这里j ψ为所选择的加权函数,应用迦辽金法时,所选取的加权函数即为尝试函数。

有限元法的理论基础有限元法是一种离散化的数值计算方法,对于结构分析而言,它的理论基础是能量原理。
能量原理表明,在外力作用下,弹性体的变形、应力和外力之间的关系受能量原理的支配,能量原理与微分方程和定解条件是等价的。
下面介绍有限元法中经常使用的虚位移原理和最小势能原理。
1.虚位移原理虚位移原理又称虚功原理,可以叙述如下:如果物体在发生虚位移之前所受的力系是平衡的(物体内部满足平衡微分方程,物体边界上满足力学边界条件),那么在发生虚位移时,外力在虚位移上所做的虚功等于虚应变能(物体内部应力在虚应变上所做的虚功)。
反之,如果物体所受的力系在虚位移(及虚应变)上所做的虚功相等,则它们一定是平衡的。
可以看出,虚位移原理等价于平衡微分方程与力学边界条件。
所以虚位移原理表述了力系平衡的必要而充分的条件。
虚位移原理不仅可以应用于弹性性力学问题,还可以应用于非线性弹性以及弹塑性等非线性问题。
2.最小势能原理最小势能原理可以叙述为:弹性体受到外力作用时,在所有满足位移边界条件和变形协调条件的可以位移中,真实位移使系统的总势能取驻值,且为最小值。
根据最小势能原理,要求弹性体在外力作用下的位移,可以满足几何方程和位移边界条件且使物体总势能取最小值的条件去寻求答案。
最小势能原理仅适用于弹性力学问题。
2.2有限元法求解问题的基本步骤弹性力学中的有限元法是一种数值计算方法,对于不同物理性质和数学模型的问题,有限元法的基本步骤是相同的,只是具体方式推导和运算求解不同,有限元求解问题的基本步骤如下。
2.2.1问题的分类求解问题的第一步就是对它进行识别分析,它包含的更深层次的物理问题是什么?比如是静力学还是动力学,是否包含非线性,是否需要迭代求解,要从分析中得等到什么结果等。
对这些问题的回答会加深对问题的认识与理解,直接影响到以后的建模与求解方法的选取等。
2.2.2建模在进行有限元离散化和数值求解之值,我们为分析问题设计计算模型,这一步包括决定哪种特征是所要讨论的重点问题,以便忽略不必要的细节,并决定采用哪种理论或数学公式描述结果的行为。


有限元理论基础 2.1 数值模拟技术2.1.1数值模拟技术简介在工程技术领域中许多力学问题和场问题,实质上就是在一定的边界条件下求解一些微分方程。
对于少数简单问题,人们可以通过建立它们的微分方程与边界约束求出该问题的解析解。
但是对于比较复杂的数学方程问题以及不规则的边界条件通过激吻戏法往往难以求解,而需要借助各种数值模拟方法活的相应的工程数值解,这就是所谓的数值模拟技术。
在实际工程领域中,用数值模拟技术可以对复杂的工程结构进行受力和响应分析,这样可以在设计或者加工前预知实体结构工作状态下的大概情况。
目前在工程实际应用中,常用的数值求解方法有:有限单元法、有限差分法、边界元等但从实用性和使用范围来说,有限单元法则是随着计算机技术的发展而被广泛应用的一种行之有效的数值计算方法。
2.2.2 有限元法有限元法是一种基于能量原理的数值计算方法,是解决工程实际问题的一种有效的数值计算工具。
它是里茨法的另一种表示形式,它可应用里茨法分析的所有弹性理论。
限元法是处理连续的结构体离散或有限个单元集合,也就是将连续的求解域离散为一定数量的单元集合体。
且每个单元都具有一定的节点,相邻单元通过节点相互连续,同时使用等效节点力代替作用于单元上的力和选定场函数的节点值作为基本未知量。
并在每一单元中假设一个近似插值函数以表示单元中场函数的分布规律:进而利用力学中的某些变分原理去建立用以求解节点未知量的有限元法方程,从而将一个连续域中的无限自由度问题化为离散域中的有限自由度问题。
求解后,可利用解出的节点值和设定的插值函数确定整个单元集体上的场函数。
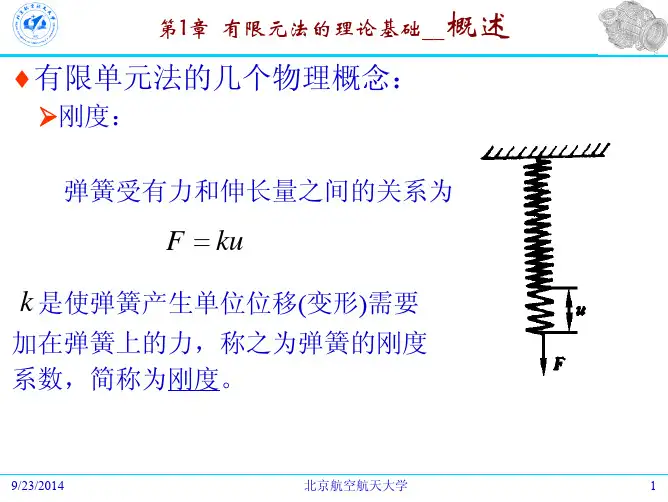
有限元求解问题中的单元分析:tt ta k F = 式中::tF 单元节点作用力。
tK :单元刚度矩阵。
t a :单元节点位移。
通过单元分析确定单元刚度矩阵,建立单元节点作用力和单元为伊关系。
有限元求解问题时建立的结构整体平衡方程:P KU = 式中:P —结构整体等效点力载荷 K —结构总体刚度矩阵 U —结构节点位移阵列 单元内力的计算:tDBa =σ式中:D —弹性矩阵 P —应变矩阵整个结构的有限元分析就是一句上述方程而进行的具体的有限元求解过程如图2.2有限元法的基础理论 2.2.1 有限元法理论在有限元法中,单元的应变—位移关系可表示为:Bu t = 式中:t —应变向量 u —位移向量B —应变—位移变换矩阵单元的应力—应变关系表示为:εσD = 式中:σ—应力向量 D —材料相关系数 在线弹性材料条件下,D 矩阵是一个常量:在非线性弹性材料中,D 矩阵上市应变t 的函数。
(ANSYS 软件)的理论基础-基本方程,边界条件。
基本方程:描述应力状态的平衡方程描述应变状态的几何方程 -----有限元计算的核心思想。
描述应力应变关系的本构方程 对应的边界条件。
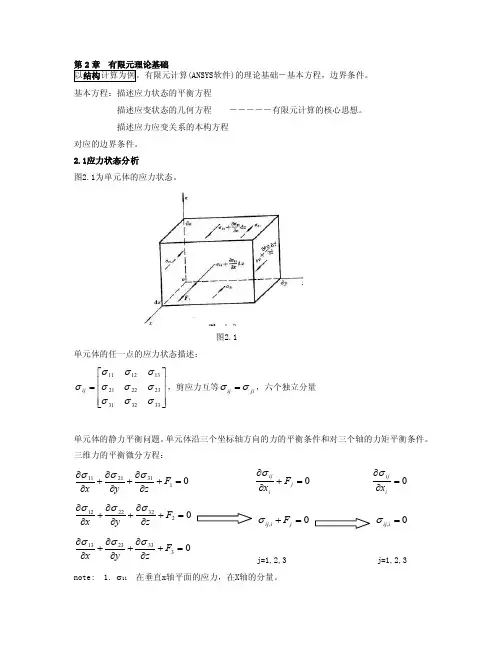
2.1应力状态分析图2.1为单元体的应力状态。
图2.1 单元体的任一点的应力状态描述:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211σσσσσσσσσσij ,剪应力互等ji ij σσ=,六个独立分量单元体的静力平衡问题。
单元体沿三个坐标轴方向的力的平衡条件和对三个轴的力矩平衡条件。
三维力的平衡微分方程:1312111=+∂∂+∂∂+∂∂F z y x σσσ 0=+∂∂j i ij F x σ 0=∂∂i ij x σ2322212=+∂∂+∂∂+∂∂F z y x σσσ0,=+j i ij F σ0,=i ij σ 03332313=+∂∂+∂∂+∂∂F z y x σσσ j=1,2,3 j=1,2,3note: 1. σ11 在垂直x 轴平面的应力,在X 轴的分量。
2. F 为体力,包括:重力、磁力、惯性力,与物体的质量成正比。
F i 为I 轴的体力分量。
3.物体表面单位面积的面力T 三个分量为T x ,T y ,T z ,或T 1,T 2,T 3,应力σ的三个分量σx ,σy ,σz 或σ1,σ2,σ3 应力边界条件:332313232221223121111σσσσσσσσσ++=++=++=T T T 3,2,1===i T T iji ji i σσ表达作用在物体表面单位面积丧的面力T 与物体内的应力分量之间的关系。
2.2 应变状态分析 图2.2为单元体的应变状态。
图2.2单元体的一点的应变状态的张量描述:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211εεεεεεεεεεεεεεεεεεεzz zy zx yz yy yxxz xy xxij 与应力状态相似。
第二章有限元法的基本原理有限元法吸取了有限差分法中的离散处理内核,又继承了变分计算中选择试探函数并对区域积分的合理方法。
有限元法的理论基础是加权余量法和变分原理,因此这里首先介绍加权余量法和变分原理。
2.1等效积分形式与加权余量法加权余量法的原理是基于微分方程等效积分的提法,同时它也是求解线性和非线性微分方程近似解的一种有效方法。
在有限元分析中,加权余量法可以被用于建立有限元方程,但加权余量法本身又是一种独立的数值求解方法。
2.1.1微分方程的等效积分形式工程或物理学中的许多问题,通常是以未知场函数应满足的微分方程和边界条件的形式提出来的,可以一般地表示为未知函数u 应满足微分方程组⎛A 1(u )⎫ ⎪A (u )= A 2(u )⎪=0(在Ω内)(2-1) M ⎪⎝⎭域Ω可以是体积域、面积域等,如图2-1所示。
同时未知函数u 还应满足边界条件⎛B 1(u )⎫ ⎪B (u )= B 2(u )⎪=0(在Γ内)(2-2)M ⎪⎝⎭要求解的未知函数u 可以是标量场(例如压力或温度),也可以是几个变量组成的向量场(例如位移、应变、应力等)。
A ,B 是表示对于独立变量(例如空间坐标、时间坐标等)的微分算子。
微分方程数目应和未知场函数的数目相对应,因此,上述微分方程可以是单个的方程,也可以是一组方程。
所以在以上两式中采用了矩阵形式。
以二维稳态的热传导方程为例,其控制方程和定解条件如下:A (φ)=∂∂φ∂∂φ(k )+(k )+q =0(在Ω内)(2-3)∂x ∂x ∂y ∂y⎧φ-φ=0⎪B(φ)=⎨∂φ-q=0⎪k⎩∂n (在Γφ上)(在Γq上)(2-4)这里φ表示温度(在渗流问题中对应压力);k是流度或热传导系数(在渗流问题中对应流度K/μ);φ和q是边界上温度和热流的给定值(在渗流问题中分别对应边界上的压力和边界上的流速);n是有关边界Γ的外法线方向;q是源密度(在渗流问题中对应井的产量)。
有限元基础理论考试复习资料1.有限元分析的步骤是怎样的?答:(1)力学模型的确定,建立积分方程。
(2)将结构进行离散化,包括单元划分、结点编号、单元编号、结点坐标计算、位移约束条件确定。
(3)单元函数确定,等效结点力的计算。
(4)单元分析,刚度矩阵的计算,先逐个计算单元刚度,再组装成整体刚度矩阵。
(5)总体分析,建立整体平衡方程,引入约束条件,求解结点位移。
(6)由结点位移计算单元应变及应力。
2.有限元(FEM)离散化体现在哪几个方面?答:1.物体本身离散化2.边界条件离散化3.载荷离散化3.有限单元法的基本思想是什么?答:有限单元法的基本思想是将物体(即连续的求解域)离散成有限个且按一定方式相互联结在一起的单元的组合,来模拟或逼近原来的物体,从而将一个连续的无限自由度问题简化为离散的有限自由度问题求解的一种数值分析法。
4.什么是单元离散化?答:离散化既是将连续体用假想的线或面分割成有限个部分,各部分之间用有限个点相连。
每个部分称为一个单元,连接点称为结点。
5.连续体结构分析有哪几种基本假定?答:(1)连续性假设;(2)完全弹性假设;(3)均匀性假设;(4)各向同性假设;(5)小变形假设。
6.形函数是什么?有什么性质?答:反映单元内位移分布状态,称为位移的形态函数,简称形函数。
其有如下性质:1)形函数在各单元节点上的值,具有“本点是1、他点我零”的性质。
2)在单元内任意一点上,三个形函数之和等于1。
3)三角形单元任意一条边上的形函数,仅与该边的两端点坐标有关。
7.什么是单元,节点,节点力,节点位移,节点载荷,体力,载荷,面力,集中力,位移,应力,应变?答:单元:即原始结构离散后,满足一定几何特性和物理特性的最小结构域。
节点:定义于单元上的特殊点,或单元之间的联系点。
节点力:单元与单元间通过节点的相互作用力。
节点位移:在节点处度量的结构位移。
节点载荷:作用于节点上的外载(等效)。
体力:分布于整个弹性体体积内的外力。
有限元理论基础有限元理论基础2.1 数值模拟技术2.1.1数值模拟技术简介在工程技术领域中许多力学问题和场问题,实质上就是在一定的边界条件下求解一些微分方程。
对于少数简单问题,人们可以通过建立它们的微分方程与边界约束求出该问题的解析解。
但是对于比较复杂的数学方程问题以及不规则的边界条件通过激吻戏法往往难以求解,而需要借助各种数值模拟方法活的相应的工程数值解,这就是所谓的数值模拟技术。
在实际工程领域中,用数值模拟技术可以对复杂的工程结构进行受力和响应分析,这样可以在设计或者加工前预知实体结构工作状态下的大概情况。
目前在工程实际应用中,常用的数值求解方法有:有限单元法、有限差分法、边界元等但从实用性和使用范围来说,有限单元法则是随着计算机技术的发展而被广泛应用的一种行之有效的数值计算方法。
2.2.2 有限元法有限元法是一种基于能量原理的数值计算方法,是解决工程实际问题的一种有效的数值计算工具。
它是里茨法的另一种表示形式,它可应用里茨法分析的所有弹性理论。
限元法是处理连续的结构体离散或有限个单元集合,也就是将连续的求解域离散为一定数量的单元集合体。
且每个单元都具有一定的节点,相邻单元通过节点相互连续,同时使用等效节点力代替作用于单元上的力和选定场函数的节点值作为基本未知量。
并在每一单元中假设一个近似插值函数以表示单元中场函数的分布规律:进而利用力学中的某些变分原理去建立用以求解节点未知量的有限元法方程,从而将一个连续域中的无限自由度问题化为离散域中的有限自由度问题。
求解后,可利用解出的节点值和设定的插值函数确定整个单元集体上的场函数。
有限元求解问题中的单元分析:t tt akF=式中::t F单元节点作用力。
tK:单元刚度矩阵。
ta:单元节点位移。
通过单元分析确定单元刚度矩阵,建立单元节点作用力和单元为伊关系。
有限元求解问题时建立的结构整体平衡方程:PKU=式中:P—结构整体等效点力载荷K—结构总体刚度矩阵U—结构节点位移阵列单元内力的计算:tDBa=σ式中:D—弹性矩阵P—应变矩阵整个结构的有限元分析就是一句上述方程而进行的具体的有限元求解过程如图结构离散生引入约束输出节计算并输结构总体结构节点求解线性2.2有限元法的基础理论2.2.1 有限元法理论在有限元法中,单元的应变—位移关系可表示为:But=式中:t—应变向量u—位移向量B—应变—位移变换矩阵单元的应力—应变关系表示为:εσD=式中:σ—应力向量D—材料相关系数在线弹性材料条件下,D矩阵是一个常量:在非线性弹性材料中,D矩阵上市应变t的函数。
有限元刚度方程为:PKu=式中:P—结构总体刚度矩阵K—单元刚度矩阵其中单元刚度矩阵K为:⎰=vt DBdV BK式中:V—积分域对于非线性弹性材料而言,D矩阵和单元刚度矩阵K均是应变t和位移u的函数。
在小变形问题中,矩阵B与位移u没有相关关系。
而在大变形问题时,矩阵B和单元刚刚度矩阵K则均是位移u的函数。
在轮胎分析中,轮胎由于充气和垂直载荷等作用,轮胎结构会产生较大的变形,轮胎集合结构的这种变形属于集合非线性问题。
轮胎结构本身又是多种材料构成的复合体,其材料属性既有各向同性又有各项异性,这属于材料非线性问题。
在轮胎的静态解触、自由滚动和动态接触状态下,轮胎与路面之间的接触,又涉及到接触非线性问题提。
2.2.2应力—应变理论有限元是里茨法的另一种表示形式,它可应用里茨法分析的所有弹性理论,而应力—应变理论则是里茨分析法的弹性理论的基础。
因此在有限元分析中,一般使用弹性理论俺就载荷作用下物体中的内力状态和变形规律。
1.应力物体收到外力的作用时发生变形,这种变形改变了物体内各分子间的间距,在物体内形成了一个内立场。
当内力和外力相互平衡时,变形不再继续,物体达到稳定平衡状态。
这种由于物体受外力的作用因其物体的变形,而导致内部各部分之间因相对位置改变而因其的相互作用,这种相互作用成为内力。
所谓应力,就是指分布内力系在物体内某一点处的强弱的相互作用。
为了研究物体内某一点C 处的内力,假设用以经过点C 的截面mm 将物体分开,在这选取包含点C 的一个部分进行研究。
如图2.2所示。
围绕点C 取微笑面积A ∆,A ∆上存在着分布内力系的合力F ∆,如图2.2b 所示。
F ∆的大小和方向与点C 的位置和A ∆的大小密切相关。
A F ∆∆与的比值成为平均应力。
A F P m∆∆= m P 为一矢量,表示在A ∆范围内,单位面积上内力的平均集度,称作平均应力。
随着A ∆的逐渐变小,m P 的大小和方向都将逐渐变化。
当A ∆趋近于零时,m P 的大小和方向都将趋近于一定极限P ,即C 点应力P 为A Fp p A m A ∆∆==→∆→∆00lim lim应力P 是分布内力系F ∆在点C 处的集度,反应了分布内力系F ∆在点C 处的强弱成都。
对于应力P ,威力表征其与无提议的形变或者材料的相关性,通常将应力P 分解成垂直于截面的分量正应力σ和切与截面的分量切应力τ。
2. 应变应变表示物体收到外力的作用时发生变形的强弱程度。
在图2.2a 中,物体中的M 点因变形位移到'M 点,'MM 为无体统变形时M 点的位移。
这里假设物体受到约束,没有刚性位移,M 点的位移全是由变形引起的,假想在M 点附近取平面与坐标平面平行的正六面体(当正六面体的边长趋于无限小时为单元体),设该六面体的棱边边长分别为zy x l l l ,,。
变形后其边长和棱边夹角都发生微小变化将单元体投影到xy 平面,如图2.3b 所示。
变形前单元体平行于x 轴的边长长度为x l ,变形后,点M 和点N 分别位移到'M 点和'N 点。
''N M 的长度为x lx ∆+,且MN N M x -=∆''比值:x m l x MNMN N M ∆=-=''ε 表示单元体边长x l 的平均长度变化,成为平均应变。
当MN 长度趋近于0时,则mε的极限为:x N MN m l x MN MN N M ∆=-=→→00lim ''lim ε2.2.3 大变形的有限元数学描述在轮胎结构分析中,轮胎变形问题属于集合非线性范畴,此时小变形情况下的几何方程不再适合轮胎的结构分析,为此必须重新定义新的平衡方程。
这主要是方程和平衡方程不能消除刚性运动的影响,从而无法度量大变形物体的形态。
在度量物体的变形时,需要选取一个特定的结构为基准在变形问题中,一般有两种参考构型。
设初始时刻t=0,时质点坐标为()3,2,1=i X i ,iX 表示任意时刻t 质点的位置。
当选择初始构型为参考构型时则iX 为自变量。
u x X -= 应变表达式为:⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂+∂∂=⎪⎪⎭⎫ ⎝⎛-∂∂∂∂=j k i k i j j i v j k i k v X u X u X u X u X x X x E 2121δ式中:vE 为格林应变 j kk i v x X X x ∂∂∂∂=δ为克朗内记号。
若选择现时构型,即i x 作为自变量,其应变表达式为:⎪⎪⎭⎫ ⎝⎛∂∂∂∂-∂∂+∂∂=⎪⎪⎭⎫ ⎝⎛∂∂∂∂-=j k i k i j j i j ki k v v x u x u x u x u x x X x e 2121δ 式中:v e 为阿尔曼西应变。
2.2.4 大变形状态下的平衡方程描述在变形情况下,应力是和应变相关的,在外部载荷的作用下,物体发生形变,并在变形后重新达到平衡。
因此,用变形后状态即现时构型构成的Cauchy 应力平衡方程更是合适。
设物体在现时构型中占据的区域为V ,它的边界为A ,其中A 由ut A A ,两部分构成,同事设现时构型的单位体积的体积载荷和表面载荷分别为ii q p ,,如图所示。
这时在区域V 的Cauchy 应力平衡方程为:0=+∂∂j j u p x σ应力边界条件:j j u q n=σ 式中:j n 为现时构型边界i A 的外法线方向余弦。
结合Cauchy 应力张量和Kirchohoff 应力张量可以将大变形问题的平衡方程表述为:01001001dV u p dA u q E S j V j A A v v ⎰⎰⎰+=δδδ 2.2.5 大变形增量问题轮胎的充气和与路面接触分析都与其变形过程有着密切关系,对于这些非线性问题要想获得一个合适解,就必须采用增量法。
所谓增量法,即将时间历程离散或时间序列,即132,1,,,0+=n n t t t t t t 在t t t i i ∆+→的增量阶段,需要选用一个参考构型,一般使用两种方式:一种是完全拉格朗日方程,即选取某一时刻t 的构型为参考构型。
通常在轮胎这类大变形问题中,一般选用拉格朗日方程求解比较合适。
2.2.6接触问题在轮胎的静态接触、自由滚动和动态接触状态下,轮胎与路面之间发生接触行为。
在ANSYS 中,接触属于一种高度的状态非线性行为,它是状态非线性类型中一个特殊而又比较重要的子集部分。
接触问题主要体现在(1)接触区域的大小、相互接触物体的相对位置以及接触的具体状态事先都是都是未知的;(2)接触无提议之间不可相互侵入,接触界面间的法向作用只存在压力,切向可以滑移,这些条件共同构成高度非线性的单边性不等式约束。
在状态非线性分析中,刚度矩阵[K]相关于位移矩阵[x]。
()[]{}[]F x x K =式中:力与位移的关系是非线性的。
其关系如图所示接触一般分为刚—柔接触和柔柔接触,接触方式一般分为三种形式:面面接触、点面接触和点点接触。
轮胎路面接触属于典型的刚—柔面面接触。
在刚柔面面接触中,需要把一个个面设置为“目标”面,而把另一个面设置为“接触面”,通常选择刚性路面为“目标面”,而接触面选择柔性的胎面花纹表面。
这两个面共同组成“接触对”,使用相同的实常数号,有限元程序则是通过这组相同的实常数号来识别该接触对。
接触分析中,接触区域需要同时满足运动和力学两方面约束条件。
运动约束条件是指接触的两个物体在接触边界上法向无相对运动,即无提议之间不存在相互渗透。
力学约束是指接触面法向方向上只能存在接触压力,而在接触面的切向方向上会产生大小相等方向相反的摩擦力。
两个接触物体在接触过程中可能会出现三种情形:粘式、滑移和分离。
粘式指接触的两个无提议在接触点粘在一处,不存在相对运动。
滑移是指接触的两个物体在接触边界上发生切向运动。
分离是指两个接触的物体在变形前存在接触,但在变形后发生分离。
23本章小结:。