优化建模练习题解答

解 设分别购买饲料A B C D E 各i x 个单位，每单位营养成分为ij a ，单价为j c ，每天对营养成分的需要量为j b 。

⎪⎩⎪⎨⎧=≥===∑∑==5,4,3,2,1,03,2,1,..min 5151i x j b x a t s x c f ii ji ij i ii model : title ex1; sets :s1/1..5/:c,x; s2/1..3/:b; link(s1,s2):a; endsets data :c=2 7 4 3 8; b=700 30 100; a=; enddatamin =@sum (s1:c*x);@for (s2(j):@sum (s1(i):a(i,j)*x(i))>b(j));end每天购买饲料D 39.743kg,E 25.641k ，最少费用324.359元.解 设分别生产三种产品i x 个单位。

model : title ex2;max =3000*x1+2000*x2+2900*x3; 8*x1+2*x2+10*x3<300; 10*x1+5*x2+8*x3<400; 2*x1+13*x2+10*x3<420; end分别生产22.5,23.2,7.3个单位，利润最大，为135266.7元。

设备B 的单位租金为300元，高于影子价格266.67元，所以不合算。

产品Ⅰ的单位利润在（3000-1454.55,3000+333.33）上变化都不用改变生产计划。

3.队员选拔问题 某校篮球队准备从十名预备队员中选择五名作为正式队员，队员的各种情况如下表：队员号码 身高（厘米） 技术分 位置1 185 8.6 中锋2 186 9 中锋3 193 8.4 中锋 4 190 9.5 中锋5 182 9.1 前锋6 184 9 前锋7 188 8.1 前锋 8 186 7.8 后卫9 190 8.2 后卫 10 192 9.2 后卫队员的挑选要满足下面条件： （1）至少补充一名前锋。

练习1、求解下列线性规划问题。

（1）()131********max 43112.22233332436400,1,2,3,4i f x x x s tx x x x x x x x x x i =--++-=+=-+=≥= （2）()123123123max 23.2222320,1,2i f x x x x s tx x x x x x x i =---+≤-+-≤-≥=（3）()1231212312max 564.22553415100,1,2,3i f x x x x s tx x x x x x x x i =+++≤++≤+≤≥=（4）12312312312123min 33..25231612,,0x x x s t x x x x x x x x x x x -++-+≤-+≤+≤≥ （5）1212312412515max 2..506221,,0x x s t x x x x x x x x x x x +++=-++=++=≥ （6）()123412341234max 30354045..34647043658001,2,3,4i x x x x s t x x x x x x x x x i ++++++≤+++≤≥=2、建立线性规划模型，求解下列问题。

（1）某工厂生产甲、乙两种产品。

已知生产甲种产品t 1需耗A 种矿石t 10、B 种矿石t 5、煤t 4；生产乙种产品t 1需耗A 种矿石t 4、B 种矿石t 4、煤t 9。

每t 1甲种产品的利润是600元，每t 1乙种产品的利润是1000元。

工厂在生产这两种产品的计划中要求消耗A 种矿石不超过t 300、B 种矿石不超过t 200、煤不超过t 360。

甲、乙两种产品应各生产多少，能使利润总额达到最大？（2）设有A 1，A 2两个香蕉基地，产量分别为60吨和80吨，联合供应B 1，B 2，B 3三个销地的销售量经预测分别为50吨、50吨和40吨。

第一、填空题1.组成优化设计数学模型的三要素是设计变量 、 目标函数 、 约束条件。

2.函数()22121212,45f x x x x x x =+-+在024X ⎡⎤=⎢⎥⎣⎦点处的梯度为120-⎡⎤⎢⎥⎣⎦，海赛矩阵 为2442-⎡⎤⎢⎥-⎣⎦3.目标函数是一项设计所追求的指标的数学反映，因此对它最基本的要能用 来评价设计的优劣，，同时必须是设计变量的可计算函数。

4.建立优化设计数学模型的基本原则是确切反映工程实际问题，的基础上力求简洁。

5.约束条件的尺度变换常称规格化，这是为改善数学模型性态常用的一种方法。

6.随机方向法所用的步长一般按加速步长法来确定，此法是指依次迭代的步 长按一定的比例递增的方法。

7.最速下降法以负梯度方向作为搜索方向，因此最速下降法又称为梯度法，其收敛速度较 慢 。

8.二元函数在某点处取得极值的充分条件是()00f X ∇=必要条件是该点处的海赛矩阵正定9.拉格朗日乘子法的基本思想是通过增加变量将等式约束优化问题变成无 约束优化问题，这种方法又被称为升维法。

10改变复合形形状的搜索方法主要有反射，扩，收缩，压缩11坐标轮换法的基本思想是把多变量 的优化问题转化为单变量的优化问题 12．在选择约束条件时应特别注意避免出现相互矛盾的约束，，另外应当尽量减少不必要的约束。

13．目标函数是n 维变量的函数，它的函数图像只能在n+1,空间中描述出来，为了在n 维空间中反映目标函数的变化情况，常采用目标函数等值面的方法。

14.数学规划法的迭代公式是1k k k k X X d α+=+，其核心是建立搜索方向，和计算最正确步长15协调曲线法是用来解决设计目标互相矛盾的多目标优化设计问题的。

16.机械优化设计的一般过程中，建立优化设计数学模型是首要和关键的一步，它是取得正确结果的前提。

二、名词解释1．凸规划对于约束优化问题()min f X..s t ()0j g X ≤(1,2,3,,)j m =⋅⋅⋅若()f X 、()j g X (1,2,3,,)j m =⋅⋅⋅都为凸函数，则称此问题为凸规划。

实验03 简单的优化模型（2学时）（第3章简单的优化模型）1. 生猪的出售时机p63~65目标函数（生猪出售纯利润，元）：Q(t) = ( 8 – g t )( 80 + rt ) – 4t – 640其中，t≥ 0为第几天出售，g为每天价格降低值（常数，元/公斤），r为每天生猪体重增加值（常数，公斤）。

求t使Q(t)最大。

1.1（求解）模型求解p63(1) 图解法绘制目标函数Q(t) = ( 8 – g t )( 80 + rt ) – 4t – 640的图形（0 ≤t≤ 20）。

其中，g=0.1, r=2。

从图形上可看出曲线Q(t)的最大值。

(2) 代数法对目标函数Q(t) = ( 8 – g t )( 80 + rt ) – 4t – 640用MATLAB求t使Q(t)最大。

其中，r, g是待定参数。

（先对Q(t)进行符号函数求导，对导函数进行符号代数方程求解）然后将代入g=0.1, r=2，计算最大值时的t和Q(t)。

要求：①编写程序绘制题(1)图形。

②编程求解题(2).③对照教材p63相关内容。

相关的MATLAB函数见提示。

★要求①的程序和运行结果：★要求②的程序和运行结果：1.2（编程）模型解的的敏感性分析p63~64对1.1中(2)所求得的符号表达式t(r,g)，分别对g和r进行敏感性分析。

(1) 取g=0.1，对t(r)在r=1.5:0.1:3上求r与t的关系数据，绘制r与t 的关系图形（见教材p65）。

(2) 取r=2，对t(g)在g=0.06:0.01:0.15上求g与t的关系数据，绘制g 与t的关系图形（见教材p65）。

要求：分别编写(1)和(2)的程序，调试运行。

★给出(1)的程序及运行结果：★给出(2)的程序及运行结果：2.（编程）冰山运输模型求解p77~81按函数调用顺序。

(1) 每立方米水所需费用),(),(),(000V u W V u S V u Y =u 为船速，V 0为冰山的初始体积。

例1（任务分配问题）某车间有甲、乙两台机床，可用于加工三种工件。

假定这两台车床的可用台时数分别为800和900，三种工件的数量分别为400、600和500，且已知用不同车床加工单位数量不同工件所需的台时数和加工费用如下表。

问怎样分配车床的加工任务，才能既满足加工工件的要求，又使加工费用最低？解：设在甲车床上加工工件1、2、3的数量分别为321,,x x x ，在乙车床上加工工件1、2、3的数量分别为654,,x x x 。

建立以下线性规划模型：6543218121110913m in x x x x x x z +++++=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=≥≤++≤++=+=+=+6,,2,1,09003.12.15.08001.14.0500600400..654321635241 i x x x x x x x x x x x x x t s i例2 某厂每日8小时的产量不低于1800件。

为了进行质量控制，计划聘请两种不同水平的检验员。

一级检验员的标准为：速度25件/小时，正确率98%，计时工资4元/小时；二级检验员的标准为：速度15件/小时，正确率95%，计时工资3元/小时。

检验员每错检一次，工厂要损失2元。

为使总检验费用最省，该工厂应聘一级、二级检验员各几名？ 解： 设需要一级和二级检验员的人数分别为21,x x 人,则应付检验员的工资为：因检验员错检而造成的损失为：故目标函数为：约束条件为：线性规划模型：212124323848x x x x +=⨯⨯+⨯⨯21211282)%5158%2258(x x x x +=⨯⨯⨯⨯+⨯⨯⨯2121213640)128()2432(m in x x x x x x z +=+++=⎪⎪⎩⎪⎪⎨⎧≥≥≤⨯⨯≤⨯⨯≥⨯⨯+⨯⨯0,0180015818002581800158258212121x x x x x x 213640m in x x z +=例3 投资问题某单位有一批资金用于四个工程项目的投资，用于各工程项目时所得到得净收益（投入资金的百分比）如下表所示：由于某种原因，决定用于项目A 的投资不大于其它各项投资之和；而用于项目B 和C 的投资要大于项目D 的投资。

数学建模与优化考试试题题目一：某市的公交公司需要对公交车的发车时间进行调整，以满足市民的出行需求，并尽量减少公交车的等待时间和拥挤情况。

为了有效地解决这个问题，我们使用数学建模和优化的方法进行分析。

1. 问题描述某市公交车的运营时间为早上6点至晚上10点，每天间隔一段固定的时间发车。

公交车站点数量为M，每个站点的上下客时间为Ti。

现有数据显示，在早高峰时段（7点至9点）和晚高峰时段（17点至19点）市民出行需求较大，其他时间段市民出行需求较小。

公交公司希望尽量减少市民的等待时间和公交车的拥挤情况，提高出行效率。

因此，需要调整公交车的发车时间以适应市民的出行需求。

2. 模型建立建立一个数学模型来分析最优的公交车发车时间。

首先，我们将问题简化为一个最小化等待时间和最小化拥挤度的目标函数。

然后，通过对每个站点发车时间的调整，最大限度地优化这个目标函数。

3. 数据收集与分析为了准确建立模型，需要收集和分析以下数据：- 各个站点在早高峰时段和晚高峰时段的平均上下客时间；- 各个站点在各个时间段的客流量统计数据；- 公交车到站时间的统计数据。

4. 模型求解利用收集到的数据和已经建立的数学模型，可以通过数学优化算法求解最优的公交车发车时间。

该算法将最小化等待时间和拥挤度作为目标函数，并考虑到市民出行需求的变化。

5. 结果分析与改进根据模型求解的结果，可以进行结果分析，并对公交车发车时间进行进一步的调整和优化。

同时，还可以对模型进行改进，如引入更多的因素，如天气、节假日等。

题目二：某工厂需要优化生产线的排布和生产策略，以提高生产效率和降低成本。

为了完成这个任务，我们使用数学建模和优化的方法进行分析。

1. 问题描述该工厂的生产线包括多个工作站，每个工作站都有不同的生产能力和工作时间。

目前，生产线的排布和生产策略并不完善，导致生产效率低下和成本较高。

工厂希望通过优化生产线的排布和生产策略，提高生产效率，降低成本。

2. 模型建立建立一个数学模型来分析最优的生产线排布和生产策略。

《数学建模》课程作业题一13第五章优化模型•优化问题1、已知某工厂计划生产I, 11,111三种产品，各产品需要在A, B,C 设备上 加工，有模型得建立及求解：设生产I, 11,111产品xl, x2,x3件z 为所获得得利润。

于就是数学模型如下:利用mail a b 求解（附录一）得到最优值Z =1 3 5、2667（千元）, 生产方案如下表.生产I, I I, III 产品分别为2 3 , 23,7利润最大为125、2667千元.（2）若为了增加产量，可租用别得工厂设备B,每月可租用60台，租金1、8万 元，租用B 设备就是否划算？ 模型得建立及求解：租用别得工厂设备B 以后模型为：利用matlab 求解（附录二）得到最优值Z 二129（千元）， 生产方案如下表。

生产I, II, IH 产品分别为31, 28, 0利润最大为129千元.（3）若另有俩种新产品IV 、V,其中新产品IV 需用设备A 为12台时，B 为 5台时,C 为10台时,单位产品盈利2、1千元;新产品V 需用设备A 为4台时，B 为4台时，C 为12台时，单位产品盈利1、87千元，如A,B, C 得设备台时不 增加,这两种新产品投产在经济上就是否划算？ 模型得建立及求解：添加两个新产品IV 、V 后，IV 、V 对应得产品数分别为x4,x5,建立模型如下: 利用ma t lab 求解（附录三）得到最优值Z =136、96 2 5 （千元），生产方案如下告产I, II, III, IV, V产品分别为27, 16, 0, 0, 14利润最大为136、962 5千兀。

（4）对产品工艺重新进行设计，改进结构、改进后生产每件产品I需用设备A为9台时，设备B为12台时，设备C为4台时，单位盈利4、5千元,这时对原计划有何影响？模型得建立及求解：改进结构后，建立得模型如下：利用mat la b求解（附录四）得到最优值Z二1 53、1 618 （千元），生产方案如下表.生产I,II, III产品分别为23, 2 5, 0利润最大为153、1618千元。

lingo优化模型例题
以下是一道优化模型的例题，题目如下：
某公司的成本函数为 C(x) = 100x + 2000/x + 5000，其中 x 为产量。

该公司希望通过调整产量来最小化成本。

问该公司应该生产多少数量的产品才能使成本最低？
解题步骤如下：
1. 定义变量：设 x 为产量。

2. 建立目标函数：成本函数 C(x) = 100x + 2000/x + 5000。

3. 建立约束条件：无约束条件。

4. 建立优化模型：采用最小化模型。

minimize C(x)
subject to x > 0
5. 编写LINGO代码：
SETS:
N /x/;
ENDSETS
VARIABLES:
X;
ENDVARIABLES
OBJECTIVE:
MIN = 100*X + 2000/X + 5000;
END
END
6. 运行LINGO代码，得到最优解 X 的值即为该公司应该生产的产量。

注意：由于该模型只有一个变量和一个目标函数，并且无约束条件，所以优化问题比较简单，可以直接使用LINGO编写代码求解。

对于更复杂的优化模型，可能需要添加更多的变量、约束条件和目标函数，并使用适当的算法进行求解。

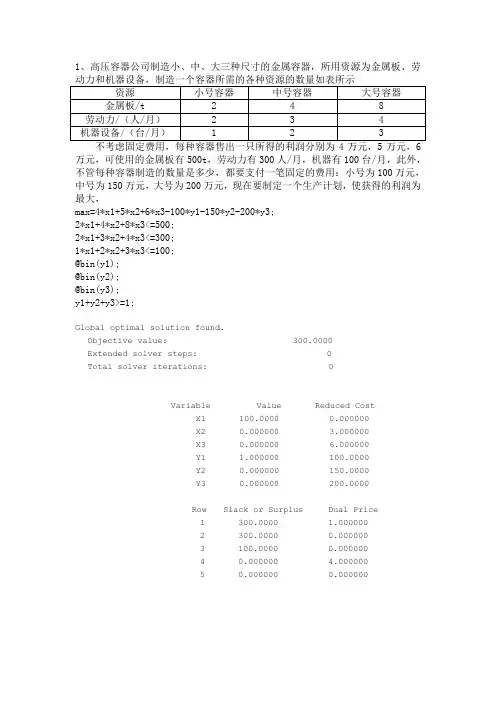
1、高压容器公司制造小、中、大三种尺寸的金属容器，所用资源为金属板、劳万元，可使用的金属板有500t，劳动力有300人/月，机器有100台/月，此外，不管每种容器制造的数量是多少，都要支付一笔固定的费用：小号为100万元，中号为150万元，大号为200万元，现在要制定一个生产计划，使获得的利润为最大，max=4*x1+5*x2+6*x3-100*y1-150*y2-200*y3;2*x1+4*x2+8*x3<=500;2*x1+3*x2+4*x3<=300;1*x1+2*x2+3*x3<=100;@bin(y1);@bin(y2);@bin(y3);y1+y2+y3>=1;Global optimal solution found.Objective value: 300.0000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostX1 100.0000 0.000000X2 0.000000 3.000000X3 0.000000 6.000000Y1 1.000000 100.0000Y2 0.000000 150.0000Y3 0.000000 200.0000Row Slack or Surplus Dual Price1 300.0000 1.0000002 300.0000 0.0000003 100.0000 0.0000004 0.000000 4.0000005 0.000000 0.0000002、安排4个人去做4项不同的工作,每个工人完成各项工作所消耗的时间（单位：（2）如果在（1）中在增加一项工作E，甲、乙、丙、丁四人完成工作E的时间分别为17,20,15,16分钟，那么应指派这四人干哪四项工作，使得这四人总的消耗时间为最少？min=20*x11+19*x12+20*x13+28*x14+18*x21+24*x22+27*x23+20*x24+26*x31+16 *x32+15*x33+18*x34+17*x41+20*x42+24*x43+19*x44;x11+x12+x13+x14=1;x21+x22+x23+x24=1;x31+x32+x33+x34=1;x41+x42+x43+x44=1;x11+x21+x31+x41=1;x12+x22+x32+x42=1;x13+x23+x33+x43=1;x14+x24+x34+x44=1;@bin(x11);@bin(x12);@bin(x13);@bin(x14);@bin(x21);@bin(x22);@bin(x23);@bin(x24);@bin(x31);@bin(x32);@bin(x33);@bin(x34);@bin(x41);@bin(x42);@bin(x43);@bin(x44);Global optimal solution found.Objective value: 71.00000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostX11 0.000000 20.00000X12 1.000000 19.00000X13 0.000000 20.00000X14 0.000000 28.00000X21 0.000000 18.00000X22 0.000000 24.00000X23 0.000000 27.00000X24 1.000000 20.00000X31 0.000000 26.00000X32 0.000000 16.00000X33 1.000000 15.00000X34 0.000000 18.00000X41 1.000000 17.00000X42 0.000000 20.00000X43 0.000000 24.00000X44 0.000000 19.00000Row Slack or Surplus Dual Price1 71.00000 -1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.000000min=20*x11+19*x12+20*x13+28*x14+17*x15+18*x21+24*x22+27*x23+20*x24+20 *x25+26*x31+16*x32+15*x33+18*x34+15*x35+17*x41+20*x42+24*x43+19*x44+1 6*x45;x11+x12+x13+x14+x15=1;x21+x22+x23+x24+x25=1;x31+x32+x33+x34+x35=1;x41+x42+x43+x44+x45=1;x11+x21+x31+x41<=1;x12+x22+x32+x42<=1;x13+x23+x33+x43<=1;x14+x24+x34+x44<=1;x15+x25+x35+x45<=1;@bin(x11);@bin(x12);@bin(x13);@bin(x14);@bin(x15);@bin(x21);@bin(x22);@bin(x23);@bin(x24);@bin(x25);@bin(x31);@bin(x32);@bin(x33);@bin(x34);@bin(x35);@bin(x41);@bin(x42);@bin(x43);@bin(x44);@bin(x45);Objective value: 68.00000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced Cost X11 0.000000 20.00000 X12 1.000000 19.00000 X13 0.000000 20.00000 X14 0.000000 28.00000 X15 0.000000 17.00000 X21 1.000000 18.00000 X22 0.000000 24.00000 X23 0.000000 27.00000 X24 0.000000 20.00000 X25 0.000000 20.00000X31 0.000000 26.00000X32 0.000000 16.00000X33 1.000000 15.00000X34 0.000000 18.00000X35 0.000000 15.00000X41 0.000000 17.00000X42 0.000000 20.00000X43 0.000000 24.00000X44 0.000000 19.00000X45 1.000000 16.00000Row Slack or Surplus Dual Price1 68.00000 -1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 1.000000 0.00000010 0.000000 0.0000003、一个公司考虑到北京、上海、广州和武汉四个城市设立库房，这些库房负责向华北、华中、华南三个地区供货，每个库房每月可处理货物1000件。

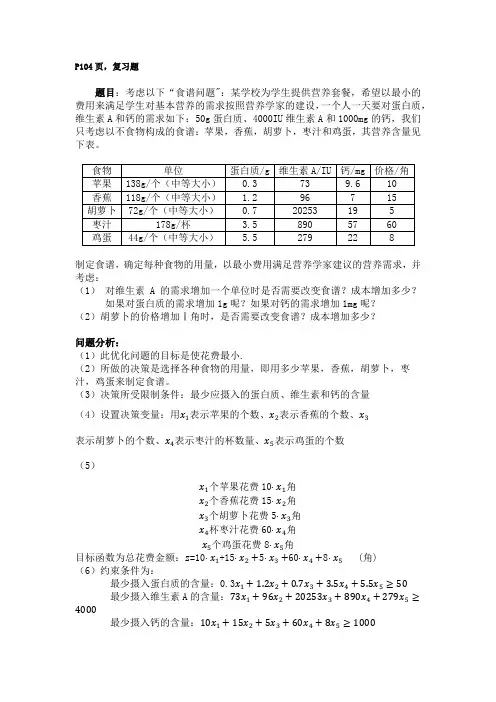
P104页，复习题题目：考虑以下“食谱问题"：某学校为学生提供营养套餐，希望以最小的费用来满足学生对基本营养的需求按照营养学家的建设，一个人一天要对蛋白质，维生素A和钙的需求如下：50g蛋白质、4000IU维生素A和1000mg的钙，我们只考虑以不食物构成的食谱：苹果，香蕉，胡萝卜，枣汁和鸡蛋，其营养含量见下表。

制定食谱，确定每种食物的用量，以最小费用满足营养学家建议的营养需求，并考虑：（1）对维生素A的需求增加一个单位时是否需要改变食谱？成本增加多少？如果对蛋白质的需求增加1g呢？如果对钙的需求增加1mg呢？（2）胡萝卜的价格增加Ⅰ角时，是否需要改变食谱？成本增加多少？问题分析：（1）此优化问题的目标是使花费最小.（2）所做的决策是选择各种食物的用量，即用多少苹果，香蕉，胡萝卜，枣汁，鸡蛋来制定食谱。

（3）决策所受限制条件：最少应摄入的蛋白质、维生素和钙的含量（4）设置决策变量：用x1表示苹果的个数、x2表示香蕉的个数、x3表示胡萝卜的个数、x4表示枣汁的杯数量、x5表示鸡蛋的个数（5）x1个苹果花费10·x1角x2个香蕉花费15·x2角x3个胡萝卜花费5·x3角x4杯枣汁花费60·x4角x5个鸡蛋花费8·x5角目标函数为总花费金额：z=10·x1+15·x2+5·x3+60·x4+8·x5 (角)（6）约束条件为：最少摄入蛋白质的含量：0.3x1+1.2x2+0.7x3+3.5x4+5.5x5≥50最少摄入维生素A的含量：73x1+96x2+20253x3+890x4+279x5≥4000最少摄入钙的含量：10x1+15x2+5x3+60x4+8x5≥1000非负约束：x 1,x 2,x 3,x 4,x 5≥0优化模型：minz =10x 1+15x 2+5x 3+60x 4+8x 5s.t. 0.3x 1+1.2x 2+0.7x 3+3.5x 4+5.5x 5≥5073x 1+96x 2+20253x 3+890x 4+279x 5≥4000 9.6x 1+7x 2+19x 3+57x 4+22x 5≥1000 x 1,x 2,x 3,x 4,x 5≥0由线性规划模型的定义，容易得到线性规划的性质：1. 比例性 每个决策变量的对目标函数的“贡献”与该决策变量的取值成正比；每个决策变量对每个约束条件右端项的“贡献”，与该决策变量的取值成正比.2. 可加性 各个决策变量对目标函数的“贡献”，与其他决策变量的取值无关；各个决策变量对每个约束条件右端项的“贡献”，与其他决策变量的取值无关.3. 连续性 每个决策变量的取值是连续的. 考察本题，实际上隐含下面的假设 ：1.购买苹果、香蕉、胡萝卜、枣汁、鸡蛋每个（杯）的花费是与各自的用量无关的常数；苹果、香蕉、胡萝卜、枣汁、鸡蛋每个（杯）所包含的蛋白质、维生素、钙的含量是与各自的用量无关的常数.（线性规划性质1—比例性）2.购买苹果、香蕉、胡萝卜、枣汁、鸡蛋每个（杯）的花费是与它们相互间用量无关的常数；苹果、香蕉、胡萝卜、枣汁、鸡蛋每个（杯）所包含的蛋白质、维生素A 、钙的含量是与它们相互间的用量无关的常数. （线性规划性质2—可加性）3. 购买苹果、香蕉、胡萝卜、枣汁、鸡蛋的数量都是实数. (线性规划性质3—连续性) 模型求解：（决策变量是5维的，不适用图解法求解模型）软件求解：线性规划模型：min z=10x1+15x2+5x3+60x4+8x5s.t. 0.3x1+1.2x2+0.7x3+3.5x4+5.5x5≥5073x1+96x2+20253x3+890x4+279x5≥40009.6x1+7x2+19x3+57x4+22x5≥1000x1,x2,x3,x4,x5≥0模型全局最优解：(Global optimal solution)x1=0x2=0x3=49.38272x4=0x5=2.805836z的最优值为269.3603角用LINGO 软件求解，得到如下输出：结果分析：1. 3个约束条件的右端项可视为3种资源：蛋白质含量、维生素A 含量、钙含量.LINGO 的输出项Row Slack or Surplus ，给出了3种资源在最优解下的剩余.2.目标函数可视为“支出（成本）”，紧约束的“资源”增加1单位时，“支出”的增加由LINGO 的输出项 Dual Price 给出。

3.数学建模之优化模型实例3.优化模型实例数学建模资料优化建模例1 钢管下料问题某钢管零售商从钢管厂进货，将钢管按照顾客的要求切割后售出。

从钢管厂进货时得到的原料钢管都是19米长。

1) 现有一客户需要50根4米长、20根6米长和15根8米长的钢管。

应如何下料最节省？2) 零售商如果采用的不同切割模式太多，将会导致生产过程的复杂化，从而增加生产和管理成本，所以该零售商规定采用的不同切割模式不能超过3种。

此外，该客户除需要1)中的三种钢管外，还需要10根5米长的钢管。

应如何下料最节省？数学建模资料优化建模问题1)的求解问题分析首先，应当确定哪些切割模式是可行的。

所谓一个切割模式，是指按照客户需要在原料钢管上安排切割的一种组合。

例如，我们可以将19米长的钢管切割成3根4米长的钢管，余料为7米显然，可行的切割模式是很多的。

其次，应当确定哪些切割模式是合理的。

通常假设一个合理的切割模式的余料不应该大于或等于客户需要的钢管的最小尺寸。

在这种合理性假设下，切割模式一共有7种，如表1所示。

数学建模资料优化建模表1 钢管下料的合理切割模式4米钢管根数6米钢管根数8米钢管根数余料(米) 4 0 0 3 3 1 0 1 2 0 1 3模式1 模式2 模式3 模式4 模式5 模式6 模式71 1 0 02 13 00 1 0 23 1 1 3数学建模资料优化建模问题化为在满足客户需要的条件下，按照哪些种合理的模式，切割多少根原料钢管，最为节省。

而所谓节省，可以有两种标准，一是切割后剩余的总余料量最小，二是切割原料钢管的总根数最少。

下面将对这两个目标分别讨论。

数学建模资料优化建模模型建立决策变量用xi 表示按照第i种模式(i=1, 2, 。

, 7) 切割的原料钢管的根数，显然它们应当是非负整数。

决策目标以切割后剩余的总余料量最小为目标，则由表1可得Min Z13x1 x2 3x3 3x4 x5 x6 3x7(32)以切割原料钢管的总根数最少为目标，则有Min Z 2 x1 x2 x3 x4 x5 x6 x7(33)下面分别在这两种目标下求解。

优化类数学建模及求解问题描述：假设有一个大型商场，为了最大化利润，商场希望能够合理安排商品的销售时间以及每种商品的折扣幅度，以吸引更多的顾客前来购物。

商场现有n种商品，每种商品每天的销售量受多种因素影响，例如天气、节假日、竞争对手等。

为了优化销售策略，商场希望能够找到一种最优的商品销售时间和折扣策略。

模型假设：1. 假设每个商品的销售时间只有一种，且每天只能销售一次。

2. 假设每个商品每天的销售量是固定的，不受其他商品的影响。

3. 假设每种商品的销售价格和折扣幅度可以调整。

4. 假设商场的成本与销售量成正比，且折扣越多，成本越高。

模型建立：设第i种商品在第j天销售时的销售量为Xi_j，折扣幅度为Dj。

由于每种商品每天的销售量是固定的，因此可以根据历史数据估计出每个商品每天的销售量。

假设每个商品的进货成本为Ci，销售价格为Pi，折扣后的销售价格为P_Dj。

根据商场的成本与销售量成正比，可得到以下方程：C_i * Xi_j + D_j * P_Dj = Y_j其中Y_j表示第j天的总销售额。

为了最大化利润，商场的目标函数可以设定为总销售额的函数，即：Maximize: Σ_j Y_jSubject to: D_j >= Dj_min (最小折扣)D_j <= Dj_max (最大折扣)P_Dj >= P_min (最低销售价格)P_Dj <= P_max (最高销售价格)其中Dj_min和Dj_max分别表示折扣的下限和上限，P_min和P_max分别表示最低和最高销售价格。

此外，还需要满足一些约束条件，例如每种商品的销售时间和折扣策略必须是唯一的，不能重复使用同一策略。

模型求解：由于这是一个复杂的优化问题，需要使用高级的数学建模方法进行求解。

可以使用一些高级的优化软件包（如LINGO、CVX等）进行求解。

在求解过程中，需要将历史数据输入到软件中，并设置好约束条件和目标函数。

1、高压容器公司制造小、中、大三种尺寸的金属容器，所用资源为金属板、劳 动力和机器设备，制造一个容器所需的各种资源的数量如表所示不考虑固定费用，每种容器售出一只所得的利润分别为4万元，5万元，6万 元，可使用的金属板有500t ，劳动力有300人/月，机器有100台/月，此外，不管每 种容器制造的数量是多少，都要支付一笔固定的费用：小号为100万元，中号为150 万元，大号为200万元，现在要制定一个生产计划，使获得的利润为最大， max=4*x1 +5*x2+6*x3-100*y1 -150*y2-200*y3; 2*x1 +4*x2+8*x3<=500; 2*x1 +3*x2+4*x3<=300; 1 *X1 +2*X2+3*X3<=100; @bi n(y1); @bi n( y2);@bin( y3); y1 +y2+y3>=1; Global optimal soluti on found.Objective value: Exte nded solver steps: Total solver iterati ons:Variable Value Reduced Cost X1 100.0000 0.000000 X2 0.000000 3.000000 X3 0.000000 6.000000 Y1 1.000000 100.0000 Y2 0.000000 150.0000 Y30.000000200.0000Row 1 Slack or Surplus Dual Price 300.0000 1.000000 2 300.0000 0.000000 3 100.0000 0.000000 4 0.000000 4.000000 50.0000000.000000300.00002、安排4个人去做4项不同的工作，每个工人完成各项工作所消耗的时间(单位：分钟)如表：(2) 如果在(1)中在增加一项工作E,甲、乙、丙、丁四人完成工作E的时间分别为17,20,15,16分钟，那么应指派这四人干哪四项工作，使得这四人总的消耗时间为最少？min =20*x11 + 19*x12+20*x13+28*x14+18*x21 +24*x22+27*x23+20*x24+26*x31 +16*x32+15*x33+18*x34+17*x41 +20*x42+24*x43+19*x44;x11+x12+x13+x14=1;x21+x22+x23+x24=1;x31+x32+x33+x34=1;x41+x42+x43+x44=1;x11+x21+x31+x41=1;x12+x22+x32+x42=1;x13+x23+x33+x43=1;x14+x24+x34+x44=1;@bin (x11);@bin (x12);@bin (x13);@bin (x14);@bin (x21);@bin (x22);@bin (x23);@bin (x24);@bin (x31);@bin (x32);@bin (x33);@bin (x34);@bin (x41);@bin (x42);@bin (x43); @bin (x44);Global optimal solution found. Objective value: 71.00000Extended solver steps 0 Total solver iterations:Variable Value Reduced Cost X11 0.000000 20.00000 X12 1.000000 19.00000 X13 0.000000 20.00000 X14 0.000000 28.00000 X21 0.000000 18.00000 X22 0.000000 24.00000 X23 0.000000 27.00000 X24 1.000000 20.00000 X31 0.000000 26.00000 X32 0.000000 16.00000 X33 1.000000 15.00000 X34 0.000000 18.00000 X41 1.000000 17.00000 X42 0.000000 20.00000 X430.000000 24.00000 X440.00000019.00000Row Slack or Surplus Dual Price 1 71.00000 2 0.000000 3 0.000000 4 0.000000 5 0.000000 6 0.000000 7 0.000000 8 0.000000 90.000000min =20*x11 +19*x12+20*x13+28*x14+17*x15+18*x21 +24*x22+27*x23+20*x24+20 *x25+26*x31 +16*x32+15*x33+18*x34+15*x35+17*x41 +20*x42+24*x43+19*x44+1 6*x45; x11+x12+x13+x14+x15=1; x21+x22+x23+x24+x25=1; x31+x32+x33+x34+x35=1;-1.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000x41+x42+x43+x44+x45=1;x11 +x21 +x31 +x41 <=1;x12+x22+x32+x42<=1;x13+x23+x33+x43v=1;x14+x24+x34+x44<=1;x15+x25+x35+x45<=1;@bin (x11);@bin (x12);@bin (x13);@bin (x14);@bin (x15);@bin (x21);@bin (x22);@bin (x23);@bin (x24);@bin (x25);@bin (x31);@bin (x32);@bin (x33);@bin (x34);@bin (x35);@bin (x41);@bin (x42);@bin (x43);@bin (x44);@bin (x45);Objective value: 68.00000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostX11 0.000000 20.00000X12 1.000000 19.00000X13 0.000000 20.00000X14 0.000000 28.00000X15 0.000000 17.00000X21 1.000000 18.00000X22 0.000000 24.00000X23 0.000000 27.00000X24 0.000000 20.00000X25 0.000000 20.00000X31 0.000000 26.00000X320.000000 16.00000X33 1.000000 15.00000X340.000000 18.00000X35 0.000000 15.00000X41 0.000000 17.00000X42 0.000000 20.00000X43 0.000000 24.00000X44 0.000000 19.00000X451.000000 16.00000DualRow Slack or Surplus Prii1 68.00000 -1.0000002 0.000000 0.0000003 0.000000 0.00000040.000000 0.00000050.000000 0.0000006 0.000000 0.00000070.000000 0.0000008 0.000000 0.0000009 1.000000 0.00000010 0.000000 0.0000003、一个公司考虑到北京、上海、广州和武汉四个城市设立库房，这些库房负责向华北、华中、华南三个地区供货，每个库房每月可处理货物1000件。

数学建模动态优化模型例题例题：动态投资组合优化假设有一个投资者，在每年初都需要重新配置其投资组合。

该投资者面临两个主要问题：首先，选择在哪些资产上进行投资；其次，在每个资产上分配多少资金。

假设该投资者有n个不同的资产可供选择，每个资产的预期收益率和风险不同。

此外，该投资者还有一个总共可投资的资金总额B。

为了最大化预期收益并控制风险，投资者希望找到一个最优的投资组合。

假设每年初的投资组合决策可以视为一个动态优化问题。

投资者可以在每个年初选择不同的投资组合来适应市场的变化。

投资者需要考虑以下因素：1. 资产的预期收益率和风险。

2. 投资组合的总收益率和风险。

3. 投资组合在不同时间点的波动。

数学建模：1. 定义变量：- x(i, t): 在第t年开始时投资于第i个资产的金额。

- r(i): 第i个资产的预期年收益率。

- σ(i): 第i个资产的年波动率。

- R(t): 第t年的总投资组合收益率。

- Σ(t): 第t年的总投资组合波动率。

2. 约束条件：- ∑(i=1 to n) x(i, t) = B，总投资金额等于可投资的资金总额。

3. 目标函数：- max ∑(t=1 to T) R(t)，总收益最大化。

4. 模型建立：- 目标函数为最大化投资组合的总收益。

- 约束条件为总投资金额等于可投资的资金总额。

- 根据预期收益率和波动率，计算每一年投资组合的收益率和波动率。

- 使用动态规划等方法，通过逐年调整投资组合来找到最优解。

以上是一个简化的动态投资组合优化模型。

在实际应用中，还需要考虑更多的因素，例如纳税规则、市场交易成本等。

此外，还需要根据实际情况进行数据收集、参数估计和模型求解。

练习题一1、建立优化模型应考虑哪些要素“答：决策变量、目标函数和约束条件。

2、讨论优化模型最优解的存在性、迭代算法的收敛性及停顿准则。

答：针对一般优化模型，讨论解的可行域，假设存在一()()min ()..0,1,2, 0,1,,i j f x s t g x i m h x j p≥===L L D 点，对于均有则称为优化模型最优解，最优解存在；*X D ∈X D ∀∈*()()f X f X ≤*X 迭代算法的收敛性是指迭代所得到的序列，满足，(1)(2)(),,,K X X X L L (1)()()()K K f X f X +≤则迭代法收敛；收敛的停顿准则有，，(1)()k k x x ε+-<(1)()()k k k x x xε+-<，，等等。

()()(1)()k k f x f x ε+-<()()()(1)()()k k k f x f x f x ε+-<()()k f x ε∇<练习题二1、*公司看中了例2.1中厂家所拥有的3种资源R 1、R2、和R 3，欲出价收购〔可能用于生产附加值更高的产品〕。

如果你是该公司的决策者，对这3种资源的收购报价是多少？〔该问题称为例2.1的对偶问题〕。

解：确定决策变量对3种资源报价作为本问题的决策变量。

123,,y y y 确定目标函数问题的目标很清楚——“收购价最小〞。

确定约束条件资源的报价至少应该高于原生产产品的利润，这样原厂家才可能卖。

因此有如下线性规划问题：123min 170100150w y y y =++*2、研究线性规划的对偶理论和方法〔包括对偶规划模型形式、对偶理论和对偶单纯形法〕。

答：略。

3、用单纯形法求解以下线性规划问题：〔1〕⎪⎪⎩⎪⎪⎨⎧≥≤+-≤++≤-++-=0,,43222..min32131321321321x x x x x x x x x x x t s x x x z ；〔2〕⎪⎪⎩⎪⎪⎨⎧=≥=++=+-=+-+-=)5,,2,1(052222..4min 53243232132 i x x x x x x x x x x t s x x z i 解：〔1〕引入松弛变量*4，*5，*6c j →1-11C B基b*1*2*3*4*5*60*421[1]-21000*532110100*64-101001c j -z j1-11因检验数σ2<0，故确定*2为换入非基变量，以*2的系数列的正分量对应去除常数列，最小比值所在行对应的基变量*4作为换出的基变量。

习题六1、某工厂生产四种不同型号的产品，而每件产品的生产要经过三个车间进行加工，根据该厂现有的设备和劳动力等生产条件，可以确定各车间每日的生产能力（折合成有效工时来表示）。

现将各车间每日可利用的有效工时数，每个产品在各车间加工所花费的工时数及每件产品可获得利润列成下表：试确定四种型号的产品每日生产件数,,,,4321x x x x 使工厂获利润最大。

2、在车辆拥挤的交叉路口，需要合理地调节各车道安置的红绿灯时间，使车辆能顺利、有效地通过。

在下图所示的十字路口共有6条车道，其中d c b a ,,,是4条直行道，f e ,是两条左转弯道，每条车道都设有红绿灯。

按要求制定这6组红绿灯的调节方案。

首先应使各车道的车辆互不冲突地顺利驶过路口，其次希望方案的效能尽量地高。

即各车道总的绿灯时间最长，使尽可能多的车辆通过。

da bc提示：将一分钟时间间隔划分为4321,,,d d d d 共4个时段，()()()f J b J a J ,,, 为相应车道的绿灯时间。

()d J3、某两个煤厂A 和B 每月进煤量分别为60吨和100吨，联合供应三个居民区C 、D 、E 。

这三个居民区每月对煤的需求量依次分别是50吨、70吨、40吨。

煤厂A 与三个居民区C 、D 、E 的距离分别为10公里、5公里和6公里。

煤厂B 与三个居民区C 、D 、E 的距离分别为4公里、8公里和12公里。

问如何分配供煤量可使运输总量达到最小？4、某工厂制造甲、乙两种产品，每种产品消耗煤、电、工作日及获利润如下表所示。

现有煤360吨，电力200KW.h ，工作日300个。

请制定一个使总利润最大的生产计划。

5、棉纺厂的主要原料是棉花，一般要占总成本的70%左右。

所谓配棉问题，就是要根据棉纱的质量指标，采用各种价格不同的棉花，按一定的比例配制成纱，使其既达到质量指标，又使总成本最低。

棉纱的质量指标一般由棉结和品质指标来决定。

这两项指标都可用数量形式来表示。