2017圆柱圆锥奥数练习题.docx

圆柱与圆锥练习一、填空。

1、把一个圆柱体削成一个最大的圆锥体，削去部分的体积是40立方厘米，问原来圆柱的体积是（）立方厘米。

2、正方形木块的棱长是10厘米，将其加工成一个最大的圆柱形木块，圆柱形木块的体积是（）立方厘米。

3、一个圆柱的高是5厘米，侧面展开是一个长为31.4厘米的长方形。

这个圆柱的体积是（）厘米。

4、一个长方形的长是5厘米，宽是2厘米，以其中的一条边为轴旋转一周，可以得到一个圆柱，圆柱的体积最大是（）立方厘米。

5、一个圆柱削成一个最大的圆锥后，削去本分的体积比圆锥体积多30立方厘米，则原来圆柱的体积是（）立方厘米。

二、解决问题。

1、把一个长、宽、高分别为9厘米、7厘米、3厘米的长方体铁块和一个棱长为5厘米的正方体铁块，熔铸成一个底面直径为10厘米的圆锥形铁块。

求圆锥形铁块的高。

2、在一只底面直径是30厘米的圆柱形木桶里，有一个直径为10厘米的圆柱形钢材浸没在水里，当钢材从桶里取出来时，桶里的水下降了3厘米。

这段钢材长为多少？3、圆柱形容器A 和B 的深度相等，底面半径分别为3厘米和4厘米把A 容器装满水，然后把水倒入B 容器，水深比B 容器的高的四分之三少1.2厘米。

B 容器的深度是多少厘米？4、用铁皮做一个如下图所示空心零件（单位：厘米），需用铁皮多少平方厘米？2724 45、一个圆柱形玻璃杯内盛有水，水面高2.5厘米，玻璃杯内侧的底面积是72平方厘米。

在这个杯中放进棱长6厘米的正方体铁块后，水面没有淹没铁块，这时水面高多少厘米？6、一个底面半径是10厘米的圆柱形玻璃杯中，装有10厘米深的水。

将一个底面半径4厘米、高6厘米的圆锥形铅锤放入杯子中，杯中的水面上升了多少厘米？7、有一个底面直径为20厘米的圆柱形容器里，盛有一些水。

把一个底面半径为3厘米的圆锥形铅锤完全浸没在水中，水面上升0.3厘米，铅锤的高是多少厘米？8、把一个底面直径为2厘米、高为6厘米的圆柱形钢材熔铸成一个圆锥体，这个圆锥的底面积是15平方厘米，它的高是多少厘米？。

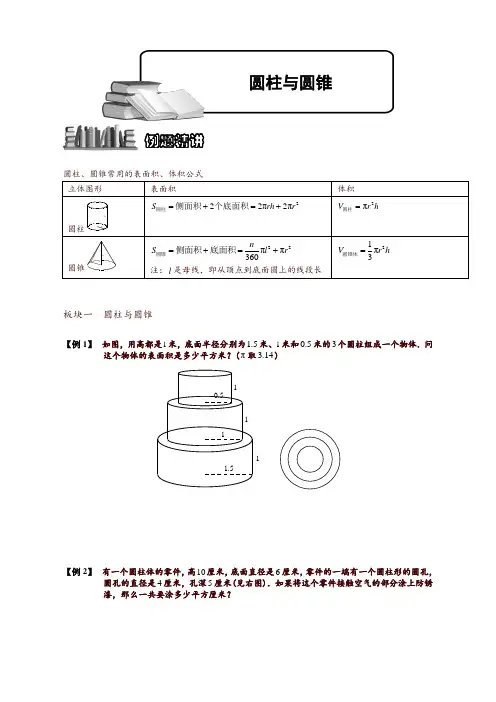
圆柱、圆锥常用的表面积、体积公式板块一 圆柱与圆锥【例 1】 如图，用高都是1米，底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体．问这个物体的表面积是多少平方米？(π取3.14)1【例 2】 有一个圆柱体的零件，高10厘米，底面直径是6厘米，零件的一端有一个圆柱形的圆孔，圆孔的直径是4厘米，孔深5厘米(见右图)．如果将这个零件接触空气的部分涂上防锈漆，那么一共要涂多少平方厘米？例题精讲圆柱与圆锥【例 3】(希望杯2试试题)圆柱体的侧面展开，放平，是边长分别为10厘米和12厘米的长方形，那么这个圆柱体的体积是________立方厘米．(结果用π表示)【例 4】如右图，是一个长方形铁皮，利用图中的阴影部分，刚好能做成一个油桶(接头处忽略不计)，求这个油桶的容积．(π 3.14=)【巩固】如图，有一张长方形铁皮，剪下图中两个圆及一块长方形，正好可以做成1个圆柱体，这个圆柱体的底面半径为10厘米，那么原来长方形铁皮的面积是多少平方厘米？(π 3.14=)【例 5】把一个高是8厘米的圆柱体，沿水平方向锯去2厘米后，剩下的圆柱体的表面积比原来的圆柱体表面积减少12.56平方厘米．原来的圆柱体的体积是多少立方厘米？【巩固】一个圆柱体底面周长和高相等．如果高缩短4厘米，表面积就减少50.24平方厘米．求这个圆柱体的表面积是多少？【例 6】一个圆柱体形状的木棒，沿着底面直径竖直切成两部分．已知这两部分的表面积之和比) 圆柱体的表面积大22008cm，则这个圆柱体木棒的侧面积是________2cm．(π取3.14【巩固】已知圆柱体的高是10厘米，由底面圆心垂直切开，把圆柱分成相等的两半，表面积增加了40平方厘米，求圆柱体的体积．(π3=)【例 7】一个圆柱体的体积是50.24立方厘米，底面半径是2厘米．将它的底面平均分成若干个扇形后，再截开拼成一个和它等底等高的长方体，表面积增加了多少平方厘米？(π 3.14=)【例 8】右图是一个零件的直观图．下部是一个棱长为40cm的正方体，上部是圆柱体的一半．求这个零件的表面积和体积．【例 9】输液100毫升，每分钟输2.5毫升．如图，请你观察第12分钟时图中的数据，问：整个吊瓶的容积是多少毫升？【例 10】一个拧紧瓶盖的瓶子里面装着一些水(如图)，由图中的数据可推知瓶子的容积是_______ 立方厘米．(π取3.14)(单位：厘米)【巩固】一个酒精瓶，它的瓶身呈圆柱形(不包括瓶颈)，如图．已知它的容积为26.4π立方厘米．当瓶子正放时，瓶内的酒精的液面高为6厘米；瓶子倒放时，空余部分的高为2厘米．问：瓶内酒精的体积是多少立方厘米？合多少升？【巩固】一个酒瓶里面深30cm，底面内直径是10cm，瓶里酒深15cm．把酒瓶塞紧后使其瓶口向下倒立这时酒深25cm．酒瓶的容积是多少？(π取3)253015【巩固】一个盖着瓶盖的瓶子里面装着一些水，瓶底面积为10平方厘米，(如下图所示)，请你根据图中标明的数据，计算瓶子的容积是＿＿＿＿＿＿．【巩固】一个透明的封闭盛水容器，由一个圆柱体和一个圆锥体组成，圆柱体的底面直径和高都是12厘米．其内有一些水，正放时水面离容器顶11厘米，倒放时水面离顶部5厘米，那么这个容器的容积是多少立方厘米？(π3)5cm【例 11】 (希望杯2试试题)如图，底面积为50平方厘米的圆柱形容器中装有水，水面上漂浮着一块棱长为5厘米的正方体木块，木块浮出水面的高度是2厘米．若将木块从容器中取出，水面将下降________厘米．【例 12】 有两个棱长为8厘米的正方体盒子，A 盒中放入直径为8厘米、高为8厘米的圆柱体铁块一个，B 盒中放入直径为4厘米、高为8厘米的圆柱体铁块4个，现在A 盒注满水，把A 盒的水倒入B 盒，使B 盒也注满水，问A 盒余下的水是多少立方厘米？【例 13】 兰州来的马师傅擅长做拉面，拉出的面条很细很细，他每次做拉面的步骤是这样的：将一个面团先搓成圆柱形面棍，长1.6米．然后对折，拉长到1.6米；再对折，拉长到1.6米……照此继续进行下去，最后拉出的面条粗细(直径)仅有原先面棍的164．问：最后马师傅拉出的这些细面条的总长有多少米？(假设马师傅拉面的过程中．面条始终保持为粗细均匀的圆柱形，而且没有任何浪费)【例 14】一个圆柱形容器内放有一个长方形铁块．现打开水龙头往容器中灌水．3分钟时水面恰好没过长方体的顶面．再过18分钟水灌满容器．已知容器的高为50厘米，长方体的高为20厘米，求长方体底面面积与容器底面面积之比．【例 15】一只装有水的圆柱形玻璃杯，底面积是80平方厘米，高是15厘米，水深8厘米．现将一个底面积是16平方厘米，高为12厘米的长方体铁块竖放在水中后．现在水深多少厘米？【巩固】一只装有水的圆柱形玻璃杯，底面积是80平方厘米，高是15厘米，水深10厘米．现将一个底面积是16平方厘米，高为12厘米的长方体铁块竖放在水中后．现在水深多少厘米？【巩固】一只装有水的圆柱形玻璃杯，底面积是80平方厘米，高是15厘米，水深13厘米．现将一个底面积是16平方厘米，高为12厘米的长方体铁块竖放在水中后．现在水深多少厘米？【例16】一个圆柱形玻璃杯内盛有水，水面高2.5厘米，玻璃杯内侧的底面积是72平方厘米．在这个杯中放进棱长6厘米的正方体铁块后，水面没有淹没铁块．这时水面高多少厘米？【例17】一个盛有水的圆柱形容器，底面内半径为5厘米，深20厘米，水深15厘米．今将一个底面半径为2厘米，高为17厘米的铁圆柱垂直放入容器中．求这时容器的水深是多少厘米？【例18】有甲、乙两只圆柱形玻璃杯，其内直径依次是10厘米、20厘米，杯中盛有适量的水．甲杯中沉没着一铁块，当取出此铁块后，甲杯中的水位下降了2厘米；然后将铁块沉没于乙杯，且乙杯中的水未外溢．问：这时乙杯中的水位上升了多少厘米？【巩固】有一只底面半径是20厘米的圆柱形水桶，里面有一段半径是5厘米的圆柱体钢材浸在水中．钢材从水桶里取出后，桶里的水下降了6厘米．这段钢材有多长？【例19】一个盛有水的圆柱形容器底面内半径为5厘米，深20厘米，水深15厘米．今将一个底面半径为2厘米，高为18厘米的铁圆柱垂直放人容器中．求这时容器的水深是多少厘米?【例20】如图11-7，有一个圆柱和一个圆锥，它们的高和底面直径都标在图上，单位是厘米．那么，圆锥体积与圆柱体积的比是多少?【例21】一个圆锥形容器高24厘米，其中装满水，如果把这些水倒入和圆锥底面直径相等的圆柱形容器中，水面高多少厘米？【例22】(”希望杯”一试六年级)如图，圆锥形容器中装有水50升，水面高度是圆锥高度的一半，这个容器最多能装水升．【例23】如图，甲、乙两容器相同，甲容器中水的高度是锥高的13，乙容器中水的高度是锥高的23，比较甲、乙两容器，哪一只容器中盛的水多？多的是少的的几倍？乙甲【例 24】张大爷去年用长2米、宽1米的长方形苇席围成容积最大的圆柱形粮囤．今年改用长3米宽2米的长方形苇席围成容积最大的圆柱形的粮囤．问：今年粮囤的容积是去年粮囤容积的多少倍?【例 25】(仁华考题)如图，有一卷紧紧缠绕在一起的塑料薄膜，薄膜的直径为20厘米，中间有一直径为8厘米的卷轴，已知薄膜的厚度为0.04厘米，则薄膜展开后的面积是平方米．【巩固】图为一卷紧绕成的牛皮纸，纸卷直径为20厘米，中间有一直径为6厘米的卷轴．已知纸的厚度为0.4毫米，问：这卷纸展开后大约有多长？【巩固】如图，厚度为0.25毫米的铜版纸被卷成一个空心圆柱(纸卷得很紧，没有空隙)，它的外直径是180厘米，内直径是50厘米．这卷铜版纸的总长是多少米？【例26】(人大附中分班考试题目)如图，在一个正方体的两对侧面的中心各打通一个长方体的洞，在上下底面的中心打通一个圆柱形的洞．已知正方体边长为10厘米，侧面上的洞口是边长为4厘米的正方形，上下底面的洞口是直径为4厘米的圆，求此立体图形的表面积和体积．板块二旋转问题【例 27】 如图，ABC 是直角三角形，AB 、AC 的长分别是3和4．将ABC ∆绕AC 旋转一周，求ABC ∆扫出的立体图形的体积．(π 3.14=)CB A 43【例 28】 已知直角三角形的三条边长分别为3cm ，4cm ，5cm ，分别以这三边轴，旋转一周，所形成的立体图形中，体积最小的是多少立方厘米？(π取3.14)【巩固】如图，直角三角形如果以BC 边为轴旋转一周，那么所形成的圆锥的体积为16π，以AC边为轴旋转一周，那么所形成的圆锥的体积为12π，那么如果以AB 为轴旋转一周，那么所形成的几何体的体积是多少？ABC【例 29】 如图，ABCD 是矩形，6cm BC =，10cm AB =，对角线AC 、BD 相交O ．E 、F 分别是AD 与BC 的中点，图中的阴影部分以EF 为轴旋转一周，则白色部分扫出的立体图形的体积是多少立方厘米？(π取3) A BA B【巩固】(华杯赛决赛试题)如图，ABCD 是矩形，6cm BC =，10cm AB =，对角线AC 、BD 相交O ．图中的阴影部分以CD 为轴旋转一周，则阴影部分扫出的立体的体积是多少立方厘米？BA【例 30】 如图，从正方形ABCD 上截去长方形DEFG ，其中AB=1厘米，DE=12厘米，DG=13厘米。

圆柱与圆锥练习二概念整理：1. 圆柱特征：两个相等的圆形底面，无数条高，曲面围成的侧面（可能是长方形、正方形、平行四边形、不规则图形）侧面积：S=Ch表面积：S= C×(r+h) S＝=S侧+2S底= 2πrh＋2πr2体积：V=Sh 体积＝侧面积÷2×半径S = V÷h h = V÷S 2. 圆锥：特征：一个圆形底面，一条高，曲面围成的侧面（展开后是扇形）体积：体积=底面积×高÷3 高=体积×3÷底面积高=体积×3÷底面积V＝πr2h÷3ShV31h＝3V÷S S＝3V÷h3.圆柱与圆锥的体积关系(1)等底等高的圆柱与圆锥,圆柱的体积是3份，圆锥的体积是1份.它们的体积和4份，它们的体积差2份(2)等底等积的圆柱与圆锥,圆锥的高是3份，圆柱的高是1份.它们高的和4份，它们高的差2份。

(3)等高等积的圆柱与圆锥圆锥的底面积是3份，圆柱的底面积是1份.它们底面积的和4份，底面积的积差2份。

4.圆柱转化成近似的长方体的过程中,(1)高不变 (2)体积不变 (3)底面积不变 (4)表面积多出2个长方形,长=高,宽=半径5、沿着圆柱的直径切开，多出2个长方形，长=高，宽=直径6、平行于圆柱的上下底面切开，多出2个圆7、三角形、长方形、正方形、梯形旋转形成的形体，一定要确定形体找准高和半径。

8、长方形做成无底的圆柱形管子，以长作为底面周长，体积大9、圆柱与圆锥的高、底面积和体积的关系的应用采用列表法相等的用1表示10、圆柱削成一个最大的圆锥，说明是圆柱和圆锥是等底等高11、长方体和正方体削成最大的圆柱或圆锥，而是要找准圆柱或圆锥的底和高圆柱和圆锥的练习二1. （1）一个圆柱的高减少2厘米侧面积就减少50.24平方厘米，它的体积减少多少立方厘米？1、（2）一个圆柱的高增加3分米，侧面积就增加56.52平方分米，它的体积增加多少立方分米？2.（1）一个圆柱体木块，底面半径是8厘米，高是30厘米。

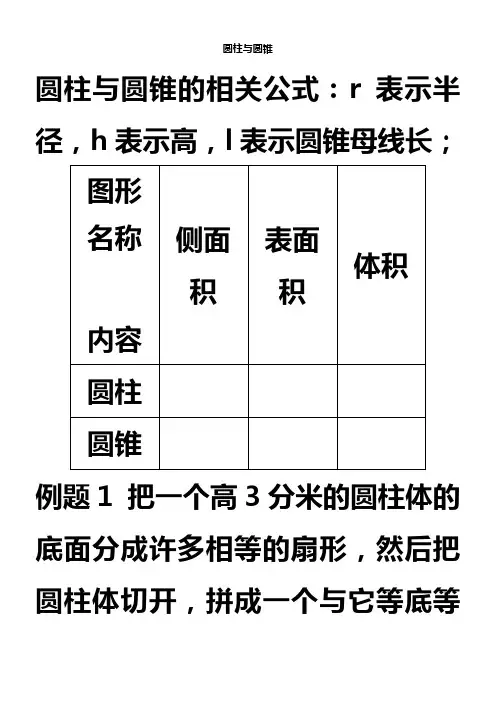
圆柱与圆锥圆柱与圆锥的相关公式：r表示半径，h表示高，l表示圆锥母线长；图形名称内容侧面积表面积体积圆柱圆锥例题1 把一个高3分米的圆柱体的底面分成许多相等的扇形，然后把圆柱体切开，拼成一个与它等底等高的近似长方体，它的表面积比圆柱体的表面积增加了36平方分米，求这个圆柱体的体积。

例题2 求下图中图形按图中所示方向旋转一周后所形成的立体图形的体积。

（单位：厘米）随堂练习：1.有内半径分别为1厘米和4厘米且深度相等的圆柱形容器A 和B ，把A 容器装满水，再倒入B 容器里，水的深度比容器深度的43还低3厘米，容器的深度是多少0101厘米？2.高都是1米，底面半径分别是0.5米、1米和1.5米的三个圆柱组成的几何体如图，求这个物体的表面积。

例题3 如图，一张扇形薄铁片，弧长18.84分米，它能够围成一个高4分米的圆锥，试求圆锥的容积。

（接缝处忽略不计）例题4 如图，圆锥形容器中装有3升水，水面高度正好是圆锥子高度的一半，这个容器还能装多少升水？h随堂练习：1.埃及著名的胡夫胡夫金字塔为正四棱锥形，正方形底座边长为230.4米，塔高146.7米，假定建筑金字塔所用材料全部是石灰石，每立方米重2700千克，那么胡夫金字塔的总重量是多少千克？2.一个底面半径是6厘米的圆锥体形金属铸件，放进棱长15厘米的正方形体一容器中的水中，这个铸件全部被水浸没，容器中的水面纟原来升高1.2厘米，求这个圆锥体的高（精确到0.1厘米）例题5 如图，在圆锥中，AB和BC 长均为10厘米，底面周长为10 厘米，有一只小虫准备从A点出发，沿着锥面爬到线段BC，那么它爬行的最短距离是多少厘米？例题6 一个长方体木块，长、宽、高分别是6厘米，8厘米，10厘米，把它加工成一个最大的圆锥体，这个圆锥体的体积是多少立方厘米？随堂练习：1.下图是一个立方体图形的侧面展开图（单位：厘米），求这个立体图形的表面积和体积。

2.两个同样材料做成的球A 和B ，一个实心，一个空心，A 的直径为7，重量为22，B 的直径为10.6，重量为33.3，问哪个球是实心球？（球体体积积=334r ） 3.一个草垛，上面是一个圆锥，底面周长是6.24米，圆锥的高是0.6米；下面是一个圆台，下底面周长为4.71米，圆台的高是1.5米。

圆锥的体积练习一．有关圆柱、圆锥体积关系的练习1．仔细观察,哪个圆柱的体积是圆锥的的3倍。

（单位：cm）2．等底等高的圆柱和圆锥,圆柱的体积是圆锥的（），圆锥的体积是圆柱的（），圆柱的体积比圆锥大( ），圆锥的体积比圆柱小（）。

3．一个圆柱和圆锥等底等高，它们的体积一共60立方厘米，那么，圆柱的体积是（）立方厘米,圆锥的体积是( )立方厘米。

4．等底等高的圆柱和圆锥，圆柱的体积比圆锥大10立方米，圆柱的体积是（），圆锥的体积是（ )。

5．一个圆柱和一个圆锥等底等高，圆锥的体积比圆柱的体积少0。

8立方分米，那么,圆锥的体积是（）立方分米,圆柱的体积是（）立方分米。

6．等底等高的圆柱和圆锥，如果先在圆锥容器中注满水，水面高12厘米，再全部倒入圆柱形容器中，水面高（）厘米;如果先在圆柱容器中注满水,再把水倒入圆锥形容器直到注满，这时圆柱形容器中的水面高（）厘米。

1．把一个体积是282。

6立方厘米的铁块熔铸成一个底面半径是6厘米的圆锥形机器零件，求圆锥零件的高。

2、一个无盖的圆柱形水桶,底面直径20厘米，高30厘米,制造这样一对水桶，至少要多少铁皮?如果用这对水桶盛水，能盛多少千克？（每升水重1千克，得数保留整千克）3．一个圆锥形的小麦堆，底面周长是 12.56米，高是2.7米，现在把这些小麦放到圆柱形的粮囤中去，恰好占这粮囤容积的78。

5%。

已知粮囤底面的周长是9。

42米，求这个粮囤的高。

(得数保留两位小数）4、大厅内有8根同样的圆柱形木柱，每根高5米，底面周长是3.2米，如果每千克油漆可漆4.5平方米，漆这些木柱需油漆多少千克？ (得数保留两位小数)5．一个装满玉米的圆柱形粮囤，底面周长6.28米，高2米。

如果将这些玉米堆成一个高1米的圆锥形的玉米堆，圆锥底面积是多少平方米？6、一个圆柱体和一个圆锥体等底等高，它们的体积相差50。

24立方厘米。

如果圆锥体的底面半径是2厘米，这个圆锥体的高是多少厘米？7．建筑工地运来9。

圆柱圆锥常见题型归纳训练题一、公式转换圆柱和圆锥的关系：1. 等底等高的情况下，圆柱体积是圆锥体积的倍。

2. 等底等高的情况下，圆锥体积是圆柱体积的。

3. 等底等高的情况下，圆锥体积比圆柱体积少。

4. 等底等高的情况下，圆柱体积比圆锥体积多倍。

5. 圆柱与圆锥等底等体积，圆锥的高是圆柱的倍。

6. 圆柱与圆锥等高等体积，圆锥的底面积是圆柱的倍。

基本题型a求表面积：1，一个圆柱的侧面积是25.12平方厘米，底面半径是2厘米，求该圆柱的表面积是多少？求体积：2.一个圆柱型粮囤，底面半径是4米，高2米，若每立方米粮食重500千克，求该粮囤能装多少千克粮食？求侧面积3.一座大厦有四根同样的圆柱，已知圆柱的底面周长是15.7dm，高10m，如果要把圆柱的侧面都包裹上彩布，至少需彩布多少平方分米?4逆推求高一个圆柱，表面积是345.4平方厘米，底半径是5厘米，求它的高。

二，切割拼接问题，表面积增加或减少1.基本公式：a.横切：切面是圆，表面积增加2倍底面积，即S增=2πR2b.竖切（过直径）：切面是长方形（如果h=2R，切面为正方形），该长方形的长是圆柱的高，宽是圆柱的底面直径，表面积增加两个长方形的面积，即S增=4Rh基本题型1，把一长为1.6米的圆柱截成3段后，表面积增加了9.6平方米，求圆柱原来的体积？2，把长为20分米的圆柱沿着底面直径劈开，表面积增加了80平方分米，求该圆柱原来的表面积是多少？3.圆柱长2米，把它截成相等的4段后，表面积增加了18.84平方厘米，求每段的体积是多少？4.把3个一样的圆柱，连成一个大圆柱，长9厘米，表面积减少12.56平方分米，求原来每个圆柱的体积是多少立方厘米？5、把两个底面直径都是4厘米，长都是4分米圆柱形钢材焊接成一个长的圆柱形钢材，焊接成的圆柱形钢材的表面积比原来两个小圆柱形钢材的表面积之和减少了多少？6、一根2米长的圆柱形木料, 横截面的半径是10厘米, 沿横截面的直径垂直锯开, 分成相等的两块, 每块的体积和表面积各是多少?三．放入或拿出物体，水面上升或下降。

---------------------------------------------------------------最新资料推荐------------------------------------------------------圆柱与圆锥(奥数)圆柱与圆锥 1. 求下图中图形按图中所示方向旋转一周后所形成的立体图形的体积。

（单位：厘米） 2.有内半径分别为 1 厘米和 4 厘米且深度相等的圆柱形容器 A 和 B，把 A 容器装满水，再倒入 B 容器里，水的深度比容器深度的43还低 3 厘米，容器的深度是多少厘米？ 3.高都是 1 米，底面半径分别是 0.5 米、 1 米和1.5 米的三个圆柱组成的几何体如图，求这个物体的表面积。

4. 如图，一张扇形薄铁片，弧长 18.84 分米，它能够围成一个高 4 分米的圆锥，试求圆锥的容积。

（接缝处忽略不计） 5 如图，圆锥形容器中装有 3 升水，水面高度正好是圆锥子高度的一半，这个容器还能装多少升水？ 6.埃及著名的胡夫胡夫金字塔为正四棱锥形，正方形底座边长为 230.4 米，塔高 146.7 米，假定建筑金字塔所用材料全部是石灰石，每立方米重 2700 千克，那么胡夫金字塔的总重量是多少千克？ 0.8 1.5 0.5 1.2 h 7.一个底面半径是 6 厘米的圆锥体形金属铸件，放进棱长 15 厘米的正方形体一容器中的水中，这个铸件全部被水浸没，容器中的水面纟原来升高 1.2 厘米，求这个圆锥体的高（精确到 0.1 厘米） 8. 在圆锥中， AB 和 BC 长均为 10 厘米，底面周长为厘米，有一只小虫准备从 A 点1 / 3出发，沿着锥面爬到线段 BC，那么它爬行的最短距离是多少厘米？9. 一个长方体木块，长、宽、高分别是 6 厘米， 8 厘米， 10 厘米，把它加工成一个最大的圆锥体，这个圆锥体的体积是多少立方厘米？ 10.两个同样材料做成的球 A 和 B，一个实心，一个空心， A 的直径为 7，重量为 22， B 的直径为 10.6，重量为33.3，问哪个球是实心球？（球体体积积） 11.将一根直径是 20 厘米，长 2 米的圆木，锯成截面为最大的正方形的方木，要锯去多少木料？ 12.在底面半径是 10 厘米的圆柱形杯中，装有 7 厘米高的水，把一小块铁浸入水中，这时水上升到9 厘米，问这块铁的体积多大？ 13 一根水管，内直径 20 厘米，水在管内的流速是每秒 4 米，每秒可以流过多少立方米的水？14.一个圆柱被挖掉一个圆锥，圆锥高是圆柱高的3为 6 厘米米，则剩余的体积是多少？（精确到 0.01） 2，底面半径为 2 厘米，圆柱高 15.有一个下面是圆柱体，上面是圆锥体的容器，圆柱体的高度是 10 厘米，圆锥体的高度是 6 厘米，容器内的液面度度是 7 厘米，当将这个容器倒过来放时，从圆锥的尖到液面的高是多少厘米？ 16.有两个边长为 8 厘米的正方体盒子。

立體圖形 表面積體積 圓柱h r 222π2πS rh r =+=+圆柱侧面积个底面积2πV r h =圆柱 圓錐h r 22ππ360n S l r =+=+圆锥侧面积底面积 注：l 是母線，即從頂點到底面圓上的線段長21π3V r h =圆锥体板塊一 圓柱與圓錐【例 1】 如圖，用高都是1米，底面半徑分別為1.5米、1米和0.5米的3個圓柱組成一個物體．問這個物體的表面積是多少平方米？(π取3.14)11111.50.5【例 2】 有一個圓柱體的零件，高10釐米，底面直徑是6釐米，零件的一端有一個圓柱形的圓孔，圓孔的直徑是4釐米，孔深5釐米(見右圖)．如果將這個零件接觸空氣的部分塗上防銹漆，那麼一共要塗多少平方釐米？例題精講圓柱與圓錐【例 3】(希望杯2試試題)圓柱體的側面展開，放平，是邊長分別為10釐米和12釐米的長方形，那麼這個圓柱體的體積是________立方釐米．(結果用π表示)【例 4】如右圖，是一個長方形鐵皮，利用圖中的陰影部分，剛好能做成一個油桶(接頭處忽略不計)，求這個油桶的容積．(π 3.14=)【鞏固】如圖，有一張長方形鐵皮，剪下圖中兩個圓及一塊長方形，正好可以做成1個圓柱體，這個圓柱體的底面半徑為10釐米，那麼原來長方形鐵皮的面積是多少平方釐米？(π 3.14=)【例 5】把一個高是8釐米的圓柱體，沿水準方向鋸去2釐米後，剩下的圓柱體的表面積比原來的圓柱體表面積減少12.56平方釐米．原來的圓柱體的體積是多少立方釐米？【鞏固】一個圓柱體底面周長和高相等．如果高縮短4釐米，表面積就減少50.24平方釐米．求這個圓柱體的表面積是多少？【例 6】一個圓柱體形狀的木棒，沿著底面直徑豎直切成兩部分．已知這兩部分的表面積之和比圓柱體的表面積大22008cm，則這個圓柱體木棒的側面積是________2cm．(π取3.14)第2题【鞏固】已知圓柱體的高是10釐米，由底面圓心垂直切開，把圓柱分成相等的兩半，表面積增加了40平方釐米，求圓柱體的體積．(π3=)【例 7】一個圓柱體的體積是50.24立方釐米，底面半徑是2釐米．將它的底面平均分成若干個扇形後，再截開拼成一個和它等底等高的長方體，表面積增加了多少平方釐米？(π 3.14=)【例 8】右圖是一個零件的直觀圖．下部是一個棱長為40cm的正方體，上部是圓柱體的一半．求這個零件的表面積和體積．【例 9】 輸液100毫升，每分鐘輸2.5毫升．如圖，請你觀察第12分鐘時圖中的數據，問：整個吊瓶的容積是多少毫升？【例 10】 一個擰緊瓶蓋的瓶子裏面裝著一些水(如圖)，由圖中的數據可推知瓶子的容積是_______ 立方釐米．(π取3.14) 8(单位：厘米)4106【鞏固】一個酒精瓶，它的瓶身呈圓柱形(不包括瓶頸)，如圖．已知它的容積為26.4π立方釐米．當瓶子正放時，瓶內的酒精的液面高為6釐米；瓶子倒放時，空餘部分的高為2釐米．問：瓶內酒精的體積是多少立方釐米？合多少升？【鞏固】一個酒瓶裏面深30cm，底面內直徑是10cm，瓶裏酒深15cm．把酒瓶塞緊後使其瓶口向下倒立這時酒深25cm．酒瓶的容積是多少？(π取3)253015【鞏固】一個蓋著瓶蓋的瓶子裏面裝著一些水，瓶底面積為10平方釐米，(如下圖所示)，請你根據圖中標明的數據，計算瓶子的容積是＿＿＿＿＿＿．【鞏固】一個透明的封閉盛水容器，由一個圓柱體和一個圓錐體組成，圓柱體的底面直徑和高都是12釐米．其內有一些水，正放時水面離容器頂11釐米，倒放時水面離頂部5釐米，那麼這個容器的容積是多少立方釐米？(π3 )5cm【例 11】(希望杯2試試題)如圖，底面積為50平方釐米的圓柱形容器中裝有水，水面上漂浮著一塊棱長為5釐米的正方體木塊，木塊浮出水面的高度是2釐米．若將木塊從容器中取出，水面將下降________釐米．【例 12】有兩個棱長為8釐米的正方體盒子，A盒中放入直徑為8釐米、高為8釐米的圓柱體鐵塊一個，B盒中放入直徑為4釐米、高為8釐米的圓柱體鐵塊4個，現在A盒注滿水，把A盒的水倒入B盒，使B盒也注滿水，問A盒餘下的水是多少立方釐米？【例 13】蘭州來的馬師傅擅長做拉麵，拉出的麵條很細很細，他每次做拉麵的步驟是這樣的：將一個麵團先搓成圓柱形面棍，長1.6米．然後對折，拉長到1.6米；再對折，拉長到1.6米……照此繼續進行下去，最後拉出的麵條粗細(直．問：最後馬師傅拉出的這些細麵條的總長有多少徑)僅有原先面棍的164米？(假設馬師傅拉麵的過程中．麵條始終保持為粗細均勻的圓柱形，而且沒有任何浪費)【例 14】一個圓柱形容器內放有一個長方形鐵塊．現打開水龍頭往容器中灌水．3分鐘時水面恰好沒過長方體的頂面．再過18分鐘水灌滿容器．已知容器的高為50釐米，長方體的高為20釐米，求長方體底面面積與容器底面面積之比．【例 15】一只裝有水的圓柱形玻璃杯，底面積是80平方釐米，高是15釐米，水深8釐米．現將一個底面積是16平方釐米，高為12釐米的長方體鐵塊豎放在水中後．現在水深多少釐米？【鞏固】一只裝有水的圓柱形玻璃杯，底面積是80平方釐米，高是15釐米，水深10釐米．現將一個底面積是16平方釐米，高為12釐米的長方體鐵塊豎放在水中後．現在水深多少釐米？【鞏固】一只裝有水的圓柱形玻璃杯，底面積是80平方釐米，高是15釐米，水深13釐米．現將一個底面積是16平方釐米，高為12釐米的長方體鐵塊豎放在水中後．現在水深多少釐米？【例 16】一個圓柱形玻璃杯內盛有水，水面高2.5釐米，玻璃杯內側的底面積是72平方釐米．在這個杯中放進棱長6釐米的正方體鐵塊後，水面沒有淹沒鐵塊．這時水面高多少釐米？【例 17】一個盛有水的圓柱形容器，底面內半徑為5釐米，深20釐米，水深15釐米．今將一個底面半徑為2釐米，高為17釐米的鐵圓柱垂直放入容器中．求這時容器的水深是多少釐米？【例 18】有甲、乙兩只圓柱形玻璃杯，其內直徑依次是10釐米、20釐米，杯中盛有適量的水．甲杯中沉沒著一鐵塊，當取出此鐵塊後，甲杯中的水位下降了2釐米；然後將鐵塊沉沒於乙杯，且乙杯中的水未外溢．問：這時乙杯中的水位上升了多少釐米？【鞏固】有一只底面半徑是20釐米的圓柱形水桶，裏面有一段半徑是5釐米的圓柱體鋼材浸在水中．鋼材從水桶裏取出後，桶裏的水下降了6釐米．這段鋼材有多長？【例 19】一個盛有水的圓柱形容器底面內半徑為5釐米，深20釐米，水深15釐米．今將一個底面半徑為2釐米，高為18釐米的鐵圓柱垂直放人容器中．求這時容器的水深是多少釐米?【例 20】如圖11-7，有一個圓柱和一個圓錐，它們的高和底面直徑都標在圖上，單位是釐米．那麼，圓錐體積與圓柱體積的比是多少?【例 21】一個圓錐形容器高24釐米，其中裝滿水，如果把這些水倒入和圓錐底面直徑相等的圓柱形容器中，水面高多少釐米？【例 22】(”希望杯”一試六年級)如圖，圓錐形容器中裝有水50升，水面高度是圓錐高度的一半，這個容器最多能裝水升．，乙容器中水的【例 23】如圖，甲、乙兩容器相同，甲容器中水的高度是錐高的13，比較甲、乙兩容器，哪一只容器中盛的水多？多的是少高度是錐高的23的的幾倍？乙甲【例 24】張大爺去年用長2米、寬1米的長方形葦席圍成容積最大的圓柱形糧囤．今年改用長3米寬2米的長方形葦席圍成容積最大的圓柱形的糧囤．問：今年糧囤的容積是去年糧囤容積的多少倍?【例 25】(仁華考題)如圖，有一卷緊緊纏繞在一起的塑膠薄膜，薄膜的直徑為20釐米，中間有一直徑為8釐米的卷軸，已知薄膜的厚度為0.04釐米，則薄膜展開後的面積是平方米．20cm8cm100cm【鞏固】圖為一卷緊繞成的牛皮紙，紙卷直徑為20釐米，中間有一直徑為6釐米的卷軸．已知紙的厚度為0.4毫米，問：這卷紙展開後大約有多長？【鞏固】如圖，厚度為0.25毫米的銅版紙被卷成一個空心圓柱(紙卷得很緊，沒有空隙)，它的外直徑是180釐米，內直徑是50釐米．這卷銅版紙的總長是多少米？【例 26】(人大附中分班考試題目)如圖，在一個正方體的兩對側面的中心各打通一個長方體的洞，在上下底面的中心打通一個圓柱形的洞．已知正方體邊長為10釐米，側面上的洞口是邊長為4釐米的正方形，上下底面的洞口是直徑為4釐米的圓，求此立體圖形的表面積和體積．板塊二旋轉問題【例 27】如圖，ABC是直角三角形，AB、AC的長分別是3和4．將ABC∆繞AC旋轉一周，求ABC∆掃出的立體圖形的體積．(π 3.14=)CB A4 3【例 28】 已知直角三角形的三條邊長分別為3cm ，4cm ，5cm ，分別以這三邊軸，旋轉一周，所形成的立體圖形中，體積最小的是多少立方釐米？(π取3.14)【鞏固】如圖，直角三角形如果以BC 邊為軸旋轉一周，那麼所形成的圓錐的體積為16π，以AC 邊為軸旋轉一周，那麼所形成的圓錐的體積為12π，那麼如果以AB 為軸旋轉一周，那麼所形成的幾何體的體積是多少？ABC【例 29】 如圖，ABCD 是矩形，6cm BC =，10cm AB =，對角線AC 、BD 相交O ．E 、F 分別是AD 與BC 的中點，圖中的陰影部分以EF 為軸旋轉一周，則白色部分掃出的立體圖形的體積是多少立方釐米？(π取3)A BA B【鞏固】(華杯賽決賽試題)如圖，ABCD 是矩形，6cm BC =，10cm AB =，對角線AC 、BD 相交O ．圖中的陰影部分以CD 為軸旋轉一周，則陰影部分掃出的立體的體積是多少立方釐米？B A【例 30】 如圖，從正方形ABCD 上截去長方形DEFG ，其中AB=1釐米，DE=12釐米，DG=13釐米。

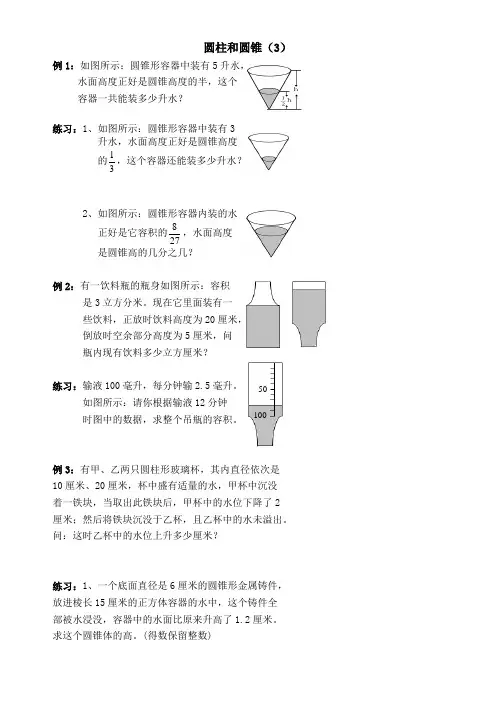
圆柱和圆锥（3）例1：如图所示：圆锥形容器中装有5升水，水面高度正好是圆锥高度的半，这个容器一共能装多少升水？练习：1、如图所示：圆锥形容器中装有3升水，水面高度正好是圆锥高度的31，这个容器还能装多少升水？2、如图所示：圆锥形容器内装的水正好是它容积的278，水面高度 是圆锥高的几分之几？例2：有一饮料瓶的瓶身如图所示：容积是3立方分米。

现在它里面装有一些饮料，正放时饮料高度为20厘米，倒放时空余部分高度为5厘米，问瓶内现有饮料多少立方厘米？练习：输液100毫升，每分钟输2.5毫升。

如图所示：请你根据输液12分钟时图中的数据，求整个吊瓶的容积。

例3：有甲、乙两只圆柱形玻璃杯，其内直径依次是10厘米、20厘米，杯中盛有适量的水，甲杯中沉没着一铁块，当取出此铁块后，甲杯中的水位下降了2厘米；然后将铁块沉没于乙杯，且乙杯中的水未溢出。

问：这时乙杯中的水位上升多少厘米？练习：1、一个底面直径是6厘米的圆锥形金属铸件，放进棱长15厘米的正方体容器的水中，这个铸件全部被水浸没，容器中的水面比原来升高了1.2厘米。

求这个圆锥体的高。

(得数保留整数) 501002、有A 、B 两个容器，原来A 容器里装有2000毫升水，B 容器是空的。

现在往两个容器以每分钟400毫升的流量注入水，4分钟后两个容器的水面高相等。

已知B 的底面半径为2厘米，求A 的底面直径是多少？能力检测：1、一个酒精瓶，它的瓶身呈圆柱形（不包括瓶颈）。

已知它的容积是32π立方厘米，当瓶子正放时瓶内酒精的高度是6厘米，瓶子倒放时空余部分是2厘米。

问瓶内酒精体积是多少立方厘米？合多少升？2、如图所示：已知容器内水深是容器高度的43，如果容器中还能再装37升水，求容器中 现在水的体积。

3、一个圆柱形木块，切成4块（如图1），表面积增加48平方厘米；切成3块（如图2），表面积增加50.24平方厘米；削成一个最大的圆锥（如图3），体积减少了多少立方厘米？4、有甲、乙两个容器，先将甲容器注满水，然后将水倒入乙 容器，乙容器水深多少厘米？ 图26 10 4 105、一个圆柱形水桶的底面周长是12.56厘米，把一个底面半径是1厘米的圆锥形铅锤浸没在桶里水中，水面升高0.2厘米，求铅锤的高。

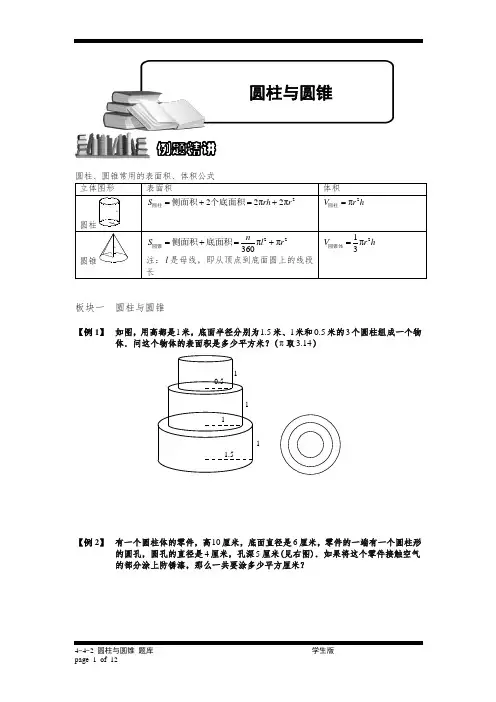
立体图形 表面积体积 圆柱hr222π2πS rh r =+=+圆柱侧面积个底面积2πV r h =圆柱圆锥h r22ππ360nS l r =+=+圆锥侧面积底面积 注：l 是母线，即从顶点到底面圆上的线段长21π3V r h =圆锥体板块一 圆柱与圆锥【例 1】 如图，用高都是1米，底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体．问这个物体的表面积是多少平方米？(π取3.14)11111.50.5【例 2】 有一个圆柱体的零件，高10厘米，底面直径是6厘米，零件的一端有一个圆柱形的圆孔，圆孔的直径是4厘米，孔深5厘米(见右图)．如果将这个零件接触空气的部分涂上防锈漆，那么一共要涂多少平方厘米？例题精讲圆柱与圆锥【例 3】(希望杯2试试题)圆柱体的侧面展开，放平，是边长分别为10厘米和12厘米的长方形，那么这个圆柱体的体积是________立方厘米．(结果用π表示)【例 4】如右图，是一个长方形铁皮，利用图中的阴影部分，刚好能做成一个油桶(接头处忽略不计)，求这个油桶的容积．(π 3.14=)【巩固】如图，有一张长方形铁皮，剪下图中两个圆及一块长方形，正好可以做成1个圆柱体，这个圆柱体的底面半径为10厘米，那么原来长方形铁皮的面积是多少平方厘米？(π 3.14=)【例 5】把一个高是8厘米的圆柱体，沿水平方向锯去2厘米后，剩下的圆柱体的表面积比原来的圆柱体表面积减少12.56平方厘米．原来的圆柱体的体积是多少立方厘米？【巩固】一个圆柱体底面周长和高相等．如果高缩短4厘米，表面积就减少50.24平方厘米．求这个圆柱体的表面积是多少？【例 6】一个圆柱体形状的木棒，沿着底面直径竖直切成两部分．已知这两部分的表面积之和比圆柱体的表面积大22008cm，则这个圆柱体木棒的侧面积是)________2cm．(π取3.14【巩固】已知圆柱体的高是10厘米，由底面圆心垂直切开，把圆柱分成相等的两半，表面积增加了40平方厘米，求圆柱体的体积．(π3=)【例 7】一个圆柱体的体积是50.24立方厘米，底面半径是2厘米．将它的底面平均分成若干个扇形后，再截开拼成一个和它等底等高的长方体，表面积增加了多少平方厘米？ (π 3.14=)【例 8】右图是一个零件的直观图．下部是一个棱长为40cm的正方体，上部是圆柱体的一半．求这个零件的表面积和体积．【例 9】输液100毫升，每分钟输2.5毫升．如图，请你观察第12分钟时图中的数据，问：整个吊瓶的容积是多少毫升？【例 10】一个拧紧瓶盖的瓶子里面装着一些水(如图)，由图中的数据可推知瓶子的容积是_______ 立方厘米．(π取3.14)8(单位：厘米)4106【巩固】一个酒精瓶，它的瓶身呈圆柱形(不包括瓶颈)，如图．已知它的容积为26.4π立方厘米．当瓶子正放时，瓶内的酒精的液面高为6厘米；瓶子倒放时，空余部分的高为2厘米．问：瓶内酒精的体积是多少立方厘米？合多少升？【巩固】一个酒瓶里面深30cm，底面内直径是10cm，瓶里酒深15cm．把酒瓶塞紧后使其瓶口向下倒立这时酒深25cm．酒瓶的容积是多少？(π取3)253015【巩固】一个盖着瓶盖的瓶子里面装着一些水，瓶底面积为10平方厘米，(如下图所示)，请你根据图中标明的数据，计算瓶子的容积是＿＿＿＿＿＿．【巩固】一个透明的封闭盛水容器，由一个圆柱体和一个圆锥体组成，圆柱体的底面直径和高都是12厘米．其内有一些水，正放时水面离容器顶11厘米，倒放时水面离顶部5厘米，那么这个容器的容积是多少立方厘米？(π3)5cm【例 11】(希望杯2试试题)如图，底面积为50平方厘米的圆柱形容器中装有水，水面上漂浮着一块棱长为5厘米的正方体木块，木块浮出水面的高度是2厘米．若将木块从容器中取出，水面将下降________厘米．【例 12】有两个棱长为8厘米的正方体盒子，A盒中放入直径为8厘米、高为8厘米的圆柱体铁块一个，B盒中放入直径为4厘米、高为8厘米的圆柱体铁块4个，现在A盒注满水，把A盒的水倒入B盒，使B盒也注满水，问A盒余下的水是多少立方厘米？【例 13】兰州来的马师傅擅长做拉面，拉出的面条很细很细，他每次做拉面的步骤是这样的：将一个面团先搓成圆柱形面棍，长1.6米．然后对折，拉长到1.6米；再对折，拉长到1.6米……照此继续进行下去，最后拉出的面条粗细(直径)仅有原先面棍的164．问：最后马师傅拉出的这些细面条的总长有多少米？(假设马师傅拉面的过程中．面条始终保持为粗细均匀的圆柱形，而且没有任何浪费)【例 14】一个圆柱形容器内放有一个长方形铁块．现打开水龙头往容器中灌水．3分钟时水面恰好没过长方体的顶面．再过18分钟水灌满容器．已知容器的高为50厘米，长方体的高为20厘米，求长方体底面面积与容器底面面积之比．【例 15】一只装有水的圆柱形玻璃杯，底面积是80平方厘米，高是15厘米，水深8厘米．现将一个底面积是16平方厘米，高为12厘米的长方体铁块竖放在水中后．现在水深多少厘米？【巩固】一只装有水的圆柱形玻璃杯，底面积是80平方厘米，高是15厘米，水深10厘米．现将一个底面积是16平方厘米，高为12厘米的长方体铁块竖放在水中后．现在水深多少厘米？【巩固】一只装有水的圆柱形玻璃杯，底面积是80平方厘米，高是15厘米，水深13厘米．现将一个底面积是16平方厘米，高为12厘米的长方体铁块竖放在水中后．现在水深多少厘米？【例 16】一个圆柱形玻璃杯内盛有水，水面高2.5厘米，玻璃杯内侧的底面积是72平方厘米．在这个杯中放进棱长6厘米的正方体铁块后，水面没有淹没铁块．这时水面高多少厘米？【例 17】一个盛有水的圆柱形容器，底面内半径为5厘米，深20厘米，水深15厘米．今将一个底面半径为2厘米，高为17厘米的铁圆柱垂直放入容器中．求这时容器的水深是多少厘米？【例 18】有甲、乙两只圆柱形玻璃杯，其内直径依次是10厘米、20厘米，杯中盛有适量的水．甲杯中沉没着一铁块，当取出此铁块后，甲杯中的水位下降了2厘米；然后将铁块沉没于乙杯，且乙杯中的水未外溢．问：这时乙杯中的水位上升了多少厘米？【巩固】有一只底面半径是20厘米的圆柱形水桶，里面有一段半径是5厘米的圆柱体钢材浸在水中．钢材从水桶里取出后，桶里的水下降了6厘米．这段钢材有多长？【例 19】一个盛有水的圆柱形容器底面内半径为5厘米，深20厘米，水深15厘米．今将一个底面半径为2厘米，高为18厘米的铁圆柱垂直放人容器中．求这时容器的水深是多少厘米?【例 20】如图11-7，有一个圆柱和一个圆锥，它们的高和底面直径都标在图上，单位是厘米．那么，圆锥体积与圆柱体积的比是多少?【例 21】一个圆锥形容器高24厘米，其中装满水，如果把这些水倒入和圆锥底面直径相等的圆柱形容器中，水面高多少厘米？【例 22】 (”希望杯”一试六年级)如图，圆锥形容器中装有水50升，水面高度是圆锥高度的一半，这个容器最多能装水 升．【例 23】 如图，甲、乙两容器相同，甲容器中水的高度是锥高的13，乙容器中水的高度是锥高的23，比较甲、乙两容器，哪一只容器中盛的水多？多的是少的的几倍？甲乙【例 24】 张大爷去年用长2米、宽1米的长方形苇席围成容积最大的圆柱形粮囤．今年改用长3米宽2米的长方形苇席围成容积最大的圆柱形的粮囤．问：今年粮囤的容积是去年粮囤容积的多少倍?【例 25】 (仁华考题)如图，有一卷紧紧缠绕在一起的塑料薄膜，薄膜的直径为20厘米，中间有一直径为8厘米的卷轴，已知薄膜的厚度为0.04厘米，则薄膜展开后的面积20cm8cm100cm【巩固】图为一卷紧绕成的牛皮纸，纸卷直径为20厘米，中间有一直径为6厘米的卷轴．已知纸的厚度为0.4毫米，问：这卷纸展开后大约有多长？【巩固】如图，厚度为0.25毫米的铜版纸被卷成一个空心圆柱(纸卷得很紧，没有空隙)，它的外直径是180厘米，内直径是50厘米．这卷铜版纸的总长是多少米？【例 26】(人大附中分班考试题目)如图，在一个正方体的两对侧面的中心各打通一个长方体的洞，在上下底面的中心打通一个圆柱形的洞．已知正方体边长为10厘米，侧面上的洞口是边长为4厘米的正方形，上下底面的洞口是直径为4厘米的圆，求此立体图形的表面积和体积．板块二 旋转问题【例 27】 如图，ABC 是直角三角形，AB 、AC 的长分别是3和4．将ABC ∆绕AC 旋转一周，求ABC ∆扫出的立体图形的体积．(π 3.14=)CB A 43【例 28】 已知直角三角形的三条边长分别为3cm ，4cm ，5cm ，分别以这三边轴，旋转一周，所形成的立体图形中，体积最小的是多少立方厘米？(π取3.14)【巩固】如图，直角三角形如果以BC 边为轴旋转一周，那么所形成的圆锥的体积为16π，以AC 边为轴旋转一周，那么所形成的圆锥的体积为12π，那么如果以AB 为轴旋转一周，那么所形成的几何体的体积是多少？ABC【例 29】 如图，ABCD 是矩形，6cm BC =，10cm AB =，对角线AC 、BD 相交O ．E 、F 分别是AD 与BC 的中点，图中的阴影部分以EF 为轴旋转一周，则白色部分扫出的立体图形的体积是多少立方厘米？(π取3)A BA B【巩固】(华杯赛决赛试题)如图，ABCD 是矩形，6cm BC =，10cm AB =，对角线AC 、BD相交O．图中的阴影部分以CD 为轴旋转一周，则阴影部分扫出的立体的体积是多少立方厘米？BA【例 30】 如图，从正方形ABCD 上截去长方形DEFG ，其中AB=1厘米，DE=12厘米，DG=13厘米。

圆柱与圆锥(奥数)一、圆柱与圆锥1．将一根长16分米的圆柱形钢材截成三段较短的圆柱形，其表面积增加了24 平方分米，这根钢材原来的体积是多少？【答案】解：24÷4=6（平方分米）16×6=96（立方分米）答：这根钢材原来的体积是96立方分米。

【解析】【分析】将一根圆柱形钢材截成三段，增加了四个底面积，据此求出圆柱形钢材的底面积，再用底面积乘高即可求出这根钢材的体积。

2．下面各题只列综合算式或方程，不计算。

（1）四、五年级一共要栽220棵树。

四年级有3个班，每班栽28棵，剩下的分给五年级四个班，平均每班栽多少棵?（2）一种华为牌手机原价每部2580元，网上限时抢购每部1680元，网购每部手机降价百分之多少?（3）做一节底面直径为0.35m，长为3.5m的圆柱形通风管，需要多少平方米铁皮?【答案】（1）解：方法一：解：设平均每班栽x棵。

28×3+4x=220方法二：（220-28×3）÷4（2）解：（2580-1680）÷2580×100%（3）解：3.14×0.35×3.5【解析】【分析】（1）根据题意可知，此题可以用方程解答，设平均每班栽x棵，用四年级每班栽的棵数×四年级的班数+五年级每班栽的棵数×五年级的班数=四年级和五年级一共栽的总棵数，据此列方程；还可以用（四年级、五年级一共栽的棵数-四年级每班栽的棵数×四年级的班数）÷五年级的班数=五年级每班栽的棵数，据此列式解答；（2）根据题意可知，用（原价-现价）÷原价×100%=降价百分之几，据此列式解答；（3）圆柱形通风管没有上下底面，已知圆柱的底面直径和高，求圆柱的侧面积，用公式：圆柱的侧面积=底面周长×高，据此列式解答.3．一个圆锥体形的沙堆，底面周长是25.12米，高1.8米，用这堆沙在8米宽的公路上铺5厘米厚的路面，能铺多少米？【答案】解：5厘米＝0.05米沙堆的底面半径：25.12÷（2×3.14）＝25.12÷6.28＝4（米）沙堆的体积： ×3.14×42×1.8＝3.14×16×0.6＝3.14×9.6＝30.144（立方米）所铺沙子的长度：30.144÷（8×0.05）＝30.144÷0.4＝75.36（米）．答：能铺75.36米。

范文 .范例 .参考（四）例 1、（圆柱和圆锥的特征）圆柱和圆锥分别有什么特点？圆柱圆锥底两个底面完全相同，都是圆一个底面，是圆形。

面形。

曲面，沿高剪开，展开后是曲面，沿顶点到底面圆周上的一条线侧面长方形。

段剪开，展开后是扇形。

两个底面之间的距离，有无高顶点到底面圆心的距离，只有一条。

数条。

例 2、求下面立体图形的底面周长和底面积。

半径 3 厘米直径10米例 3、判断：圆柱和圆锥都有无数条高。

例 4、（圆柱的侧面积）体育一个圆柱，底面直径是 5 厘米，高是12 厘米。

求它的侧面积。

例 6、（辨析）一个无盖的圆柱铁皮水桶，底面直径是30 厘米，高是50 厘米。

做这样一个水桶，至少需用铁皮6123 平方厘米。

例 7、（考点透视）一个圆柱的侧面积展开是一个边长15.7 厘米的正方形。

这个圆柱的表面积是多少平方厘米？例 8、（考点透视）一个圆柱形的游泳池，底面直径是10 米，高是 4 米。

在它的四周和底部涂水泥，每千克水泥可涂 5 平方米，共需多少千克水泥？例9、（考点透视）把一个底面半径是 2 分米，长是 9 分米的圆柱形木头锯成长短不同的三小段圆柱形木头，表面积增加了多少平方分米？4、求下列圆柱体的侧面积（1）底面半径是 3 厘米，高是 4 厘米。

（3）底面周长是 12.56 厘米，高是 4 厘米。

5、求下列圆柱体的表面积（1）底面半径是 4 厘米，高是 6 厘米。

（3）底面周长是 25.12 厘米，高是 8 厘米。

6、用铁皮制作一个圆柱形烟囱，要求底面直径是 3 分米，高是 15 分米，制作这个烟囱至少需要铁皮多少平方分米？（接头处不计，得数保留整平方分米）7、请你制作一个无盖圆柱形水桶，有以下几种型号的铁皮可供搭配选择。

8、一个圆柱形蓄水池，底面周长是25.12 米，高是 4 米，将这个蓄水池四周及底部抹上水泥。

如果每平方米要用水泥20 千克，一共要用多少千克水泥？一、圆柱体积1、求下面各圆柱的体积。

【数学】圆柱与圆锥(奥数)一、圆柱与圆锥1．如图，这是用塑料薄膜覆盖的蔬菜大棚，长15米，横截面是一个直径为2米的半圆。

大棚内的空间有多大?【答案】解：3.14×（2÷2）2×15÷2=23.55（立方米）答：大棚内的空间有23.55立方米。

【解析】【分析】观察图可知，大棚的形状是一个圆柱的一半，要求大棚内的空间大小，用圆柱的体积÷2=大棚内的空间大小，据此列式解答.2．工厂要生产一节烟囱，烟囱长2.5m，横截面是直径为40cm的圆。

（1）做一节烟囱一共需要铁皮多少平方米?（接头处忽略不计）（2）如果烟囱中充满废气，一节烟囱中最多可以容纳废气多少立方米?【答案】（1）解：40cm=0.4m3.14×0.4×2.5=3.14（m2）答：做一节烟囱一共需要铁皮3.14平方米。

（2）解：3.14×（0.4÷2）2×2.5=0.314（m3）答：一节烟囱中最多可以容纳废气0.314立方米。

【解析】【分析】1cm=0.01m，（1）做一节烟囱一共需要铁皮的平方米数=这节烟囱横截面的周长×长，其中这节烟囱横截面的周长=横截面的半径×2×π；（2）一节烟囱中最多可以容纳废气的立方米数=这节烟囱的容积=πr2h。

据此代入数据作答即可。

3．一个圆锥形沙堆，底面周长是31.4米，高是1.2米．每立方米黄沙重2吨，这堆黄沙重多少吨？【答案】解：底面半径：31.4÷（2×3.14）＝31.4÷6.28＝5（米）这堆沙子的总重量： ×3.14×52×1.2×2＝3.14×25×0.4×2＝78.5×0.4×2＝31.4×2＝62.8（吨）答：这堆黄沙重62.8吨。

【解析】【分析】用底面周长除以圆周率的2倍即可求出底面半径。

圆柱与圆锥(奥数)(1)一、圆柱与圆锥1．一个底面半径为12厘米的圆柱形杯中装有水，手里浸泡了一个底面直径是12厘米，高是18厘米的圆锥体铁块，当铁块从杯中取山来时，杯中的水面会下降多少厘米??【答案】解： ×3.14×（12÷2）2×18÷（3.14×122）= ×3.14×36×18÷（3.14×144）=1.5（厘米）答：桶内的水将下降1.5厘米。

【解析】【分析】水面下降部分水的体积就是圆锥的体积，根据圆锥的体积公式先计算出圆锥体铁块的体积，也就是水面下降部分水的体积。

用水面下降部分水的体积除以杯子的底面积即可求出水面下降的高度。

2．工厂要生产一节烟囱，烟囱长2.5m，横截面是直径为40cm的圆。

（1）做一节烟囱一共需要铁皮多少平方米?（接头处忽略不计）（2）如果烟囱中充满废气，一节烟囱中最多可以容纳废气多少立方米?【答案】（1）解：40cm=0.4m3.14×0.4×2.5=3.14（m2）答：做一节烟囱一共需要铁皮3.14平方米。

（2）解：3.14×（0.4÷2）2×2.5=0.314（m3）答：一节烟囱中最多可以容纳废气0.314立方米。

【解析】【分析】1cm=0.01m，（1）做一节烟囱一共需要铁皮的平方米数=这节烟囱横截面的周长×长，其中这节烟囱横截面的周长=横截面的半径×2×π；（2）一节烟囱中最多可以容纳废气的立方米数=这节烟囱的容积=πr2h。

据此代入数据作答即可。

3．如下图，爷爷的水杯中部有一圈装饰，是悦悦怕烫伤爷爷的手特意贴上的。

这条装饰圈宽5cm，装饰圈的面积是多少cm2?【答案】解：3.14×6×5＝94.2（cm²）答：装饰圈的面积是94.2cm2。

圆柱与圆锥(奥数)一、圆柱与圆锥1．一根圆柱形木材长20分米，把它截成3段，表面积增加了12.56平方分米。

这根木材体积是多少立方米?【答案】解：12.56÷4×20=62.8（立方分米）=0.0628（立方米）答：这根木材体积是0.0628立方米。

【解析】【分析】将圆柱形木材截成3段，增加了4个底面积，用增加的表面积除以4即可求出圆柱的底面积，然后用底面积乘高即可求出这根圆柱形木材的体积。

2．在建筑工地上有一个近似于圆锥形状的沙堆，测得底面直径4米，高1.5米．每立方米沙大约重1.7吨，这堆沙约重多少吨？（得数保留整吨数）【答案】解：圆锥的体积： ×[3.14×（4÷2）2]×1.5＝ ×1.5×12.56＝6.28（立方米）这堆沙的吨数：1.7×6.28＝10.676（吨）≈11（吨）答：这堆沙约重11吨。

【解析】【分析】这堆沙大约的重量=这堆沙的体积×每立方米大约的重量，其中这堆沙的体积=圆锥的体积=πr2h，得数要保留整数，就是把得出的数的十分位上的数进行“四舍五入”即可。

3．求下图（单位：厘米）钢管的体积。

【答案】解：10÷2=5（厘米）；8÷2=4（厘米）；3.14×（52-42）×100=3.14×（25-16）×100=3.14×9×100=28.26×100=2826（立方厘米）.【解析】【分析】根据题意可知，这根钢管的体积=底面积×高，底面是一个圆环，根据圆环的面积S=π（R2-r2），据此先求出底面积，然后乘钢管的长度，即可得到这根钢管的体积，据此列式解答.4．一个圆锥形沙堆，底面周长12.56m，高9m，如果每立方米沙约重1.5吨，这堆沙有多少吨？【答案】解：12.56÷3.14÷2=2（m）3.14×2²×9××1.5=3.14×4×3×1.5=3.14×18=56.52（吨）答：这堆沙有56.52吨。

第 1圆柱与圆锥的相关奥数体一、填空。

1、把一个圆柱体削成一个最大的圆锥体，削去部分的体积是40立方厘米，问原来圆柱的体积是（ ）立方厘米。

2、正方形木块的棱长是10厘米，将其加工成一个最大的圆柱形木块，圆柱形木块的体积是（ ）立方厘米。

3、一个圆柱的高是5厘米，侧面展开是一个长为31.4厘米的长方形。

这个圆柱的体积是（ ）厘米。

4、一个长方形的长是5厘米，宽是2厘米，以其中的一条边为轴旋转一周，可以得到一个圆柱，圆柱的体积最大是（ ）立方厘米。

5、一个圆柱削成一个最大的圆锥后，削去本分的体积比圆锥体积多30立方厘米，则原来圆柱的体积是（ ）立方厘米。

二、解决问题。

1、把一个长、宽、高分别为9厘米、7厘米、3厘米的长方体铁块与一个棱长为5厘米的正方体铁块，熔铸成一个底面直径为10厘米的圆锥形铁块。

求圆锥形铁块的高。

2、在一只底面直径是30厘米的圆柱形木桶里，有一个直径为10厘米的圆柱形钢材浸没在水里，当钢材从桶里取出来时，桶里的水下降了3厘米。

这段钢材长为多少？4、圆柱形容器A 与B 的深度相等，底面半径分别为3厘米与4厘米。

把A 容器装满水，然后把水倒入B 容器，水深比B 容器的高的 少1.2厘米。

B 容器的深度是多少厘米？2、用铁皮做一个如下图所示空心零件（单位：厘米），需用铁皮多少平方厘米？ 4328、一个圆柱形玻璃杯内盛有水，水面高2.5厘米，玻璃杯内侧的底面积是72平方厘米。

在这个杯中放进棱长6厘米的正方体铁块后，水面没有淹没铁块，这时水面高多少厘米？7、一个底面半径是10厘米的圆柱形玻璃杯中，装有10厘米深的水。

将一个底面半径4厘米、高6厘米的圆锥形铅锤放入杯子中，杯中的水面上升了多少厘米？5、有一个底面直径为20厘米的圆柱形容器里，盛有一些水。

把一个底面半径为3厘米的圆锥形铅锤完全浸没在水中，水面上升0.3厘米，铅锤的高是多少厘米？6、把一个底面直径为2厘米、高为6厘米的圆柱形钢材熔铸成一个圆锥体，这个圆锥的底面积是15平方厘米，它的高是多少厘米？第2 页。

【精品】小学奥数教程∶圆柱与圆锥计算题一、圆柱与圆锥1．一个圆柱形的汽油桶，底面半径是2分米，高是5分米，做这个桶至少要用多少平方分米的铁皮？它的容积是多少升？【答案】解：3.14×22×2+3.14×2×2×5=3.14×4×2+3.14×4×5=25.12+62.8=87.92（dm2）3.14×22×5=62.8（dm3）62.8dm3=62.8L答：做这个桶至少要用87.92平方分米的铁皮。

它的容积是62.8升。

【解析】【分析】需要铁皮的面积就是油桶的表面积，用底面积的2倍加上侧面积就是表面积，圆柱的侧面积=底面周长×高；圆柱的容积=底面积×高，根据公式计算即可。

2．求圆柱的表面积和圆锥的体积。

（1）（2）【答案】（1）解：2×3.14×3×4+2×3.14×32=103.62（cm2）（2）解：【解析】【分析】（1）圆柱的表面积=圆柱的底面积×2+圆柱的侧面积，圆柱的底面积=πr2，圆柱的侧面积=圆柱的底面周长×高，圆柱的底面周长=2πr；（2）圆锥的体积=πr2h。

3．一根圆柱形木材长20分米，把它截成3段，表面积增加了12.56平方分米。

这根木材体积是多少立方米?【答案】解：12.56÷4×20=62.8（立方分米）=0.0628（立方米）答：这根木材体积是0.0628立方米。

【解析】【分析】将圆柱形木材截成3段，增加了4个底面积，用增加的表面积除以4即可求出圆柱的底面积，然后用底面积乘高即可求出这根圆柱形木材的体积。

4．在建筑工地上有一个近似于圆锥形状的沙堆，测得底面直径4米，高1.5米．每立方米沙大约重1.7吨，这堆沙约重多少吨？（得数保留整吨数）【答案】解：圆锥的体积： ×[3.14×（4÷2）2]×1.5＝ ×1.5×12.56＝6.28（立方米）这堆沙的吨数：1.7×6.28＝10.676（吨）≈11（吨）答：这堆沙约重11吨。