动态规划_例题众多_详细讲解

动态规划算法的详细原理及使用案例一、引言动态规划是一种求解最优化问题的算法，它具有广泛的应用领域，如机器学习、图像处理、自然语言处理等。

本文将详细介绍动态规划算法的原理，并提供一些使用案例，以帮助读者理解和应用这一算法的具体过程。

二、动态规划的基本原理动态规划算法通过将问题分解为多个子问题，并利用已解决子问题的解来求解更大规模的问题。

其核心思想是利用存储技术来避免重复计算，从而大大提高计算效率。

具体来说，动态规划算法通常包含以下步骤：1. 定义子问题：将原问题分解为若干个子问题，这些子问题具有相同的结构，但规模更小。

这种分解可以通过递归的方式进行。

2. 定义状态：确定每个子问题的独立变量，即问题的状态。

状态具有明确的定义和可计算的表达式。

3. 确定状态转移方程：根据子问题之间的关系，建立状态之间的转移方程。

这个方程可以是简单的递推关系式、递归方程或其他形式的方程。

4. 解决问题：使用递推或其他方法，根据状态转移方程求解每个子问题，直到获得最终解。

三、动态规划的使用案例1. 背包问题背包问题是动态规划算法的经典案例之一。

假设有一个背包，它能容纳一定重量的物品，每个物品有对应的价值。

目的是在不超过背包总重量的前提下，选取最有价值的物品装入背包。

这个问题可以通过动态规划算法来求解。

具体步骤如下：（1）定义问题：在不超过背包容量的限制下，选取物品使得总价值最大化。

（2）定义状态：令dp[i][j]表示将前i个物品放入容量为j的背包中所能获得的最大价值。

（3）状态转移方程：dp[i][j] = max(dp[i-1][j-w[i]]+v[i], dp[i-1][j])，其中w[i]为第i个物品的重量，v[i]为第i个物品的价值。

（4）解决问题：根据状态转移方程依次计算每个子问题的解，并记录最优解，直到获得最终答案。

2. 最长公共子序列最长公共子序列（Longest Common Subsequence，简称LCS）是一种经典的动态规划问题，它用于确定两个字符串中最长的共同子序列。

动态规划运筹学例题动态规划是运筹学中常用的一种优化技术，它利用规划、三角函数和其他数学技术来解决日常生活中的各种问题，比如最优路线问题、最优资源分配问题、最优出行路线问题等。

本文将通过一个例题，来介绍动态规划的基本思想，以及如何利用动态规划来解决问题。

例题一：已知一条路线，由A点到B点，有N个途经的节点，每个节点之间的距离已知。

求从A到B的最短路线。

按照动态规划的思想，首先将该问题分解为若干个子问题，并根据子问题的解来解决原问题，这种分解和解决问题的方式称为动态规划。

对于上面的问题，可以将其分解为N个子问题，分别是从A到第1个节点、从第1个节点到第2个节点、从第2个节点到第3个节点，以此类推，最后一个子问题是从第N-1个节点到B点的最短路程。

将上面的N个子问题中，从第i个节点到B点的最短路程记为d[i]，由于从第i个节点到B点可能经过i+1、i+2、……、N-1节点，因此要找到d[i]，只需要找到经过i+1、i+2、……、N-1节点的最短路程即可，即求d[i]=Min{d[i+1]+length[i][i+1],d[i+2]+length[i][i+2],…,d[N-1]+length[i][N-1]}，其中length[i][j]是第i个节点到第j个节点的距离。

以上就是动态规划的解题步骤，它能将原问题分解成若干个子问题，并找到最优解。

对于本例来说，通过上述步骤，就可以得到从A 到B的最短路程。

这种分解和求解问题的方法是动态规划，可以用来解决许多类似的问题，如：1）最优路线问题；2）旅行推销员问题；3）硬币找零问题。

动态规划的一大特点是，他能很好地将问题分解为多个子问题，并能从子问题的解中求解出最优解。

总之，动态规划是一种很有用的优化技术，它可以有效解决各种运筹学问题。

它不仅可以帮助我们解决许多具体问题，而且还能使我们更好地理解问题及其解法。

动态规划算法详解及经典例题⼀、基本概念（1）⼀种使⽤多阶段决策过程最优的通⽤⽅法。

（2）动态规划过程是：每次决策依赖于当前状态，⼜随即引起状态的转移。

⼀个决策序列就是在变化的状态中产⽣出来的，所以，这种多阶段最优化决策解决问题的过程就称为动态规划。

假设问题是由交叠的⼦问题所构成，我们就能够⽤动态规划技术来解决它。

⼀般来说，这种⼦问题出⾃对给定问题求解的递推关系中，这个递推关系包括了同样问题的更⼩⼦问题的解。

动态规划法建议，与其对交叠⼦问题⼀次重新的求解，不如把每⼀个较⼩⼦问题仅仅求解⼀次并把结果记录在表中（动态规划也是空间换时间的）。

这样就能够从表中得到原始问题的解。

（3）动态规划经常常使⽤于解决最优化问题，这些问题多表现为多阶段决策。

关于多阶段决策：在实际中，⼈们经常遇到这样⼀类决策问题，即因为过程的特殊性，能够将决策的全过程根据时间或空间划分若⼲个联系的阶段。

⽽在各阶段中。

⼈们都须要作出⽅案的选择。

我们称之为决策。

⽽且当⼀个阶段的决策之后，经常影响到下⼀个阶段的决策，从⽽影响整个过程的活动。

这样，各个阶段所确定的决策就构成⼀个决策序列，常称之为策略。

因为各个阶段可供选择的决策往往不⽌⼀个。

因⽽就可能有很多决策以供选择，这些可供选择的策略构成⼀个集合，我们称之为同意策略集合（简称策略集合）。

每⼀个策略都对应地确定⼀种活动的效果。

我们假定这个效果能够⽤数量来衡量。

因为不同的策略经常导致不同的效果，因此，怎样在同意策略集合中选择⼀个策略，使其在预定的标准下达到最好的效果。

经常是⼈们所关⼼的问题。

我们称这种策略为最优策略，这类问题就称为多阶段决策问题。

（4）多阶段决策问题举例：机器负荷分配问题某种机器能够在⾼低两种不同的负荷下进⾏⽣产。

在⾼负荷下⽣产时。

产品的年产量g和投⼊⽣产的机器数量x的关系为g=g(x)，这时的年完善率为a，即假设年初完善机器数为x，到年终时完善的机器数为a*x(0<a<1)；在低负荷下⽣产时，产品的年产量h和投⼊⽣产的机器数量y 的关系为h=h(y)。

动态规划练习题[题1] 多米诺骨牌（DOMINO）问题描述：有一种多米诺骨牌是平面的，其正面被分成上下两部分，每一部分的表面或者为空，或者被标上1至6个点。

现有一行排列在桌面上：顶行骨牌的点数之和为6+1+1+1=9；底行骨牌点数之和为1+5+3+2=11。

顶行和底行的差值是2。

这个差值是两行点数之和的差的绝对值。

每个多米诺骨牌都可以上下倒置转换，即上部变为下部，下部变为上部。

现在的任务是，以最少的翻转次数，使得顶行和底行之间的差值最小。

对于上面这个例子，我们只需翻转最后一个骨牌，就可以使得顶行和底行的差值为0，所以例子的答案为1。

输入格式：文件的第一行是一个整数n（1〈=n〈=1000〉，表示有n个多米诺骨牌在桌面上排成一行。

接下来共有n行，每行包含两个整数a、b（0〈=a、b〈=6，中间用空格分开〉。

第I+1行的a、b分别表示第I个多米诺骨牌的上部与下部的点数（0表示空）。

输出格式：只有一个整数在文件的第一行。

这个整数表示翻动骨牌的最少次数，从而使得顶行和底行的差值最小。

[题2] Perform巡回演出题目描述:Flute市的Phlharmoniker乐团2000年准备到Harp市做一次大型演出,本着普及古典音乐的目的,乐团指挥L.Y.M准备在到达Harp市之前先在周围一些小城市作一段时间的巡回演出,此后的几天里,音乐家们将每天搭乘一个航班从一个城市飞到另一个城市,最后才到达目的地Harp市(乐团可多次在同一城市演出).由于航线的费用和班次每天都在变,城市和城市之间都有一份循环的航班表,每一时间,每一方向,航班表循环的周期都可能不同.现要求寻找一张花费费用最小的演出表.输入: 输入文件包括若干个场景.每个场景的描述由一对整数n(2<=n<=10)和k(1<=k<=1000)开始,音乐家们要在这n个城市作巡回演出,城市用1..n标号,其中1是起点Flute市,n是终点Harp市,接下来有n*(n-1)份航班表,一份航班表一行,描述每对城市之间的航线和价格,第一组n-1份航班表对应从城市1到其他城市(2,3,...n)的航班,接下的n-1行是从城市2到其他城市(1,3,4...n)的航班,如此下去.每份航班又一个整数d(1<=d<=30)开始,表示航班表循环的周期,接下来的d个非负整数表示1,2...d天对应的两个城市的航班的价格,价格为零表示那天两个城市之间没有航班.例如"3 75 0 80"表示第一天机票价格是75KOI,第二天没有航班,第三天的机票是80KOI,然后循环:第四天又是75KOI,第五天没有航班,如此循环.输入文件由n=k=0的场景结束.输出:对每个场景如果乐团可能从城市1出发,每天都要飞往另一个城市,最后(经过k天)抵达城市n,则输出这k个航班价格之和的最小值.如果不可能存在这样的巡回演出路线,输出0.样例输入: 样例输出：3 6 4602 130 150 03 75 0 807 120 110 0 100 110 120 04 60 70 60 503 0 135 1402 70 802 32 0 701 800 0[题3] 复制书稿（BOOKS）问题描述：假设有M本书（编号为1，2，…M），想将每本复制一份，M本书的页数可能不同（分别是P1，P2，…PM）。

Floyd算法是一种用来寻找图中所有节点对之间最短路径的算法，它的核心思想是动态规划。

Floyd算法的基本原理是：假设图中有n个节点，将所有节点对之间的最短路径长度初始化为它们之间的直接连线长度，然后逐步更新这些距离，直到得到所有节点对之间的最短路径。

在本文中，我们将通过四个例题a1、a2、a3、a4来讲解Floyd算法的具体应用，以帮助读者更好地理解和掌握这一算法。

1. 例题a1【题目】有一个带权有向图，节点数为n，边数为m，求图中任意两点之间的最短路径长度。

【输入】第一行为两个整数n和m，分别表示节点数和边数。

接下来m行，每行包含三个整数a、b、c，表示图中存在一条从节点a到节点b的有向边，边的权值为c。

【输出】输出一个n×n的矩阵，其中第i行第j列的元素表示节点i到节点j的最短路径长度。

如果两点之间不存在路径，则输出一个特定的值（例如9999）。

【样例】输入：5 71 2 21 3 32 3 22 4 53 4 13 5 64 5 3输出：0 2 3 7 99999 0 2 5 89999 9999 0 3 69999 9999 9999 0 39999 9999 9999 9999 0【分析】根据给定的图和节点数，首先初始化一个n×n的矩阵，然后将直接连线的路径长度填入矩阵中。

接下来，利用Floyd算法逐步更新矩阵中的最短路径长度，直到得到所有节点对之间的最短路径长度。

2. 例题a2【题目】有一个带权有向图，节点数为n，边数为m，求图中是否存在负权环。

【输入】第一行为两个整数n和m，分别表示节点数和边数。

接下来m行，每行包含三个整数a、b、c，表示图中存在一条从节点a到节点b的有向边，边的权值为c。

【输出】若存在负权环，则输出"存在负权环"，否则输出"不存在负权环"。

【样例】输入：3 31 2 -12 3 -23 1 -3输出：存在负权环【分析】我们可以利用Floyd算法求出图中任意两点之间的最短路径长度，然后再验证是否存在负权环。

动态规划动态规划是运筹学的一个分支，它是解决多阶段决策过程最优化问题的一种方法。

该方法是由美国数学家贝尔曼(R．Bellman)等人在本世纪50年代初提出的。

他们针对多阶段决策问题的特点，提出了解决这类问题的“最优化原理”，并成功地解决了生产管理、工程技术等方面的许多实际问题，从而建立了运筹学的一个新分支——动态规划。

他的名著《动态规划》于1957年出版，该书是动态规划的第一本著作。

动态规划是现代企业管理中的一种重要决策方法，在工程技术、经济管理、工农业生产及军事及其它部们都有广泛的应用，并且获得了显著的效果。

动态规划可用于解决最优路径问题、资源分配问题、生产计划与库存问题、投资分配问题、装载问题、设备更新与维修问题、排序问题及生产过程的最优控制等。

由于它所具有独特的解题思路，在处理某些优化问题时，常常比线性规划或非线性规划方法更有效。

第一节动态规划的基本方法多阶段决策的实际问题很多，下面通过具体例子，说明什么是动态规划模型及其求解方法。

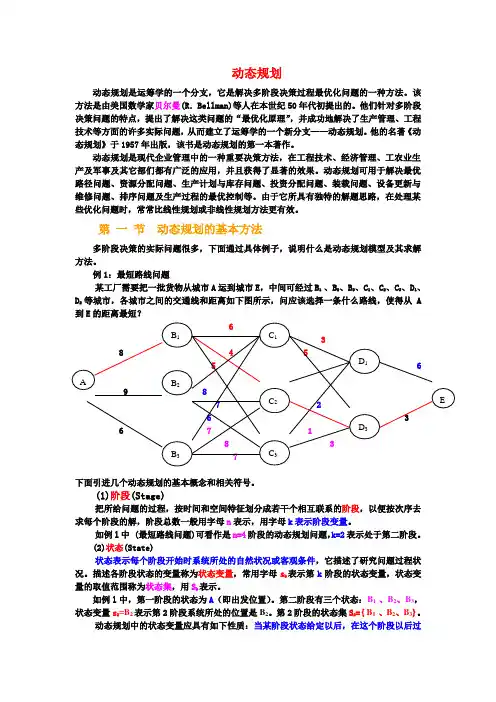
例1：最短路线问题某工厂需要把一批货物从城市A运到城市E，中间可经过B1 、B2、B3、C1、C2、C3、D1、D2等城市，各城市之间的交通线和距离如下图所示，问应该选择一条什么路线，使得从A到E的距离最短？下面引进几个动态规划的基本概念和相关符号。

(1)阶段(Stage)把所给问题的过程，按时间和空间特征划分成若干个相互联系的阶段，以便按次序去求每个阶段的解，阶段总数一般用字母n表示，用字母k表示阶段变量。

如例l中 (最短路线问题)可看作是n=4阶段的动态规划问题，k=2表示处于第二阶段。

(2)状态(State)状态表示每个阶段开始时系统所处的自然状况或客观条件，它描述了研究问题过程状况。

描述各阶段状态的变量称为状态变量，常用字母sk表示第k阶段的状态变量，状态变量的取值范围称为状态集，用Sk表示。

如例l中，第一阶段的状态为A（即出发位置）。

第二阶段有三个状态：B1 、B2、B3，状态变量s2=B2表示第2阶段系统所处的位置是B2。

floyd算法的例题讲解Floyd算法，也称为Floyd-Warshall算法，是一种用于解决所有点对最短路径问题的动态规划算法。

它能够找出图中任意两个节点之间的最短路径，并计算出最短路径的长度。

下面以一个具体的例题来讲解Floyd算法的应用。

假设我们有一个带权有向图，表示城市之间的道路网络，图中的节点表示城市，边上的权重表示两个城市之间的距离。

我们的目标是找出任意两个城市之间的最短路径。

给定以下带权有向图的邻接矩阵表示：A B C DA 0 3 ∞7B ∞0 2 ∞C 5 ∞0 1D ∞∞12 0其中，∞表示两个城市之间没有直接的道路连接。

我们可以使用Floyd算法来解决这个问题。

首先，我们初始化一个与邻接矩阵相同的矩阵，称为距离矩阵。

初始时，距离矩阵的值等于邻接矩阵的值。

接下来，我们使用三重循环来逐步更新距离矩阵的值。

循环变量k表示中转节点，i和j 表示起点和终点。

具体的算法步骤如下：对于每对节点i和j，如果存在中转节点k，尝试更新距离矩阵的值：dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])。

重复执行步骤1，直到遍历完所有的节点对(i, j)和中转节点k。

按照上述算法步骤，我们来计算最短路径的距离矩阵。

初始时，距离矩阵与邻接矩阵相同。

对于k = A：更新dist[A][B] = min(dist[A][B], dist[A][A] + dist[A][B]) = min(∞, 0 + 3) = 3。

更新dist[A][C] = min(dist[A][C], dist[A][A] + dist[A][C]) = min(∞, 0 + ∞) = ∞。

更新dist[A][D] = min(dist[A][D], dist[A][A] + dist[A][D]) = min(∞, 0 + 7) = 7。

对于k = B：更新dist[B][A] = min(dist[B][A], dist[B][B] + dist[B][A]) = min(∞, 0 + ∞) = ∞。

常见动态规划题⽬详解1.爬楼梯题⽬描述：假设你正在爬楼梯。

需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。

你有多少种不同的⽅法可以爬到楼顶呢？注意：给定 n 是⼀个正整数。

⽰例 1：输⼊： 2输出： 2解释：有两种⽅法可以爬到楼顶。

1. 1 阶 + 1 阶2. 2 阶⽰例 2：输⼊： 3输出： 3解释：有三种⽅法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶2. 1 阶 + 2 阶3. 2 阶 + 1 阶实现代码：class Solution {public:int climbStairs(int n) {vector<int> a(n);a[0] = 1;a[1] = 2;if(n == 1){return 1;}if(n == 2){return 2;}for(int i = 2; i < n;i++){a[i] = a[i - 1] + a[i - 2];}return a[n - 1];}};2.变态跳台阶题⽬描述：⼀只青蛙⼀次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。

求该青蛙跳上⼀个n级的台阶总共有多少种跳法。

实现代码：class Solution {public:int jumpFloorII(int number) {if(number == 0){return 0;}int total = 1;for(int i = 1; i < number; i++){total *= 2;}return total;}};3.n年后⽜的数量题⽬描述：假设农场中的母⽜每年会产⽣⼀头⼩母⽜，并且永远不会死。

第⼀年农场中只有⼀头成熟的母⽜，第⼆年开始，母⽜开始⽣⼩母⽜，每只⼩母⽜三年之后成熟⼜可以⽣⼩母⽜，给定整数N，求N年后母⽜的数量。

实现代码：class solution{　public: int f(int n){ if(n < 1){ return 0; } if(n == 1|| n== 2||n == 3){ return n; } int res = 3; int pre = 2; int prepre = 1; int tmp1=0; int tmp2 = 0; for(int i = 4;i < n;i++){ tmp1 = res; tmp2 = pre; res = pre + prepre; pre = tmp1; prepre = tmp2; } return res; }};4.矩形覆盖题⽬描述：我们可以⽤2*1的⼩矩形横着或者竖着去覆盖更⼤的矩形。

动态规划经典例题动态规划关键在于填表以及输出过程(个⼈理解)算法思想把原问题分解成若⼲个简单的⼦问题，保存已解决的⼦问题答案，避免重复计算。

动态规划常应⽤于有重叠⼦问题和最优⼦结构性质的问题。

⼦问题最优从⽽达到全局最优。

算法基本步骤找出最优解的性质递归的定义最优值以⾃底向上的⽅式计算最优值根据计算最优值的信息构造最优解经典案例⼀ 0/1背包问题import java.util.Scanner;import static sun.misc.Version.println;public class Dp{int n,v;//物品数量和容积int value[];int weight[];int dp[][];//dp[i][j]表⽰i个物品，容积为j时得到的最⼤价值public void Maxvalue(){for(int i=1;i<=n;i++){for(int j=0;j<=v;j++){//注意下标还有别的写法if(j>=weight[i]){dp[i][j]=Math.max(value[i]+dp[i-1][j-weight[i]], //拿了第i个dp[i-1][j]);//没拿}else{dp[i][j]=dp[i-1][j];}}}for(int i=0;i<=n;i++){for(int j=0;j<=v;j++){System.out.print(dp[i][j] + " ");}System.out.println();}}public void BestResult(int n,int v){boolean isAdd[]=new boolean[n+1];//记录物品是否拿了for(int i=n;i>=1;i--){ // 倒序if(dp[i][v]==dp[i-1][v]){isAdd[i]=false;}else{isAdd[i]=true;}v-=weight[i];}for(int i=1;i<=n;i++){//把结果正序输出System.out.println(i+"是"+isAdd[i]);}}public void Init(){Scanner sc =new Scanner (System.in);n=sc.nextInt();v=sc.nextInt();weight=new int [n+1];value=new int [n+1];dp=new int[n][v];for(int i=1;i<=n;i++){weight[i]=sc.nextInt();}for(int i=1;i<=n;i++){value[i]=sc.nextInt();}}public static void main(String[] args){Dp bag=new Dp();bag.Init();bag.Maxvalue();bag.BestResult(bag.n,bag.v);}}经典例题⼆矩阵连乘问题public class dp_matrix {int j=6;int p[];int s[][];//记录断点kint dp[][];//最⼩代价public dp_matrix() {p=new int[]{10,15,25,35,20,10,40};s=new int[j][j];dp=new int[j][j];}public void dp_matrix(){for(int i=0;i<j;i++){dp[i][i]=0;}for(int r=2;r<=j;r++){for(int i=0;i<=j-r;i++){int n=i+r-1;dp[i][n]=dp[i+1][n]+p[i]*p[i+1]*p[n+1];//i<js[i][n]=i;//在i+1分的for(int k=i+1;k<n;k++){int key=dp[i][k]+dp[k+1][n]+p[i]*p[k+1]*p[n];//注意下标if(key<dp[i][n]){dp[i][n]=key;//更新s[i][n]=k;// 更新}}}}}public void traceBack(int i ,int j){if(i==j){System.out.print(i);}else{System.out.print("(");traceBack(i,s[i][j]);traceBack(s[i][j]+1,j);System.out.print(")");}}public static void main(String[] args){dp_matrix matrix=new dp_matrix();matrix.dp_matrix();matrix.traceBack(0,5);}}经典例题三最长公共⼦序列public class Dp_Lcs {public void Maxlength(){String []m={"a","b","c","d"};String []n={"b","c","d"};int x=m.length;int y=n.length;int [][] dp=new int[m.length+1][n.length+1];//dp[i][j]表⽰xi与yi两个序列最长公共⼦序列的长度 int[][] s=new int[m.length][n.length];//s[i][j]⽤来储存m[i]与n[j]之间的关系for(int i=0;i<=x;i++){//初始化dp[i][0]=0;}for(int i=0;i<=y;i++){dp[0][i]=0;}for(int i=1;i<=x;i++){for(int j=1;j<=y;j++){if(m[i-1]==(n[j-1])){ //相等时dp[i][j]=dp[i-1][j-1]+1;//参照图s[i-1][j-1]=1;}else {dp[i][j]=Math.max(dp[i-1][j], dp[i][j-1]);if(dp[i][j]==dp[i-1][j]){s[i-1][j-1]=-1;}else s[i-1][j-1]=0;}}}for(int i=0;i<x;i++){for(int j=0;j<y;j++){System.out.print(s[i][j]);}System.out.println();}for(int i=0;i<x+1;i++){for(int j=0;j<y+1;j++){System.out.print(dp[i][j]);}System.out.println();}System.out.println("最长为"+" ");LCS(s,m,x,y);}public void LCS(int[][] s, String[] m, int i, int j){//{递归遍历s[i][j]if(i == 0 || j == 0){ return;}switch (s[i-1][j-1]) {case 1:LCS(s,m,i - 1, j - 1);System.out.println(m[i-1]+ " ");break;case 0:LCS(s,m,i - 2, j);break;default:LCS(s,m,i, j-2);break;}}public static void main(String[] args) { Dp_Lcs a=new Dp_Lcs();a.Maxlength();}}。

动态规划算法题（5题）1、题⽬描述（⽹易）有 n 个学⽣站成⼀排，每个学⽣有⼀个能⼒值，⽜⽜想从这 n 个学⽣中按照顺序选取 k 名学⽣，要求相邻两个学⽣的位置编号的差不超过d，使得这 k 个学⽣的能⼒值的乘积最⼤，你能返回最⼤的乘积吗？输⼊描述:每个输⼊包含 1 个测试⽤例。

每个测试数据的第⼀⾏包含⼀个整数 n (1 <= n <= 50)，表⽰学⽣的个数，接下来的⼀⾏，包含 n 个整数，按顺序表⽰每个学⽣的能⼒值 ai（-50 <= ai <= 50）。

接下来的⼀⾏包含两个整数，k 和 d (1 <= k <= 10, 1 <= d <= 50)。

输出描述:输出⼀⾏表⽰最⼤的乘积。

试题分析：本题要使⽤动态规划来解，动态规划的特点：1.求解的是最优化问题；2.可以分解为最优⼦结构本题可以先求解在第i个学⽣的位置下，j（j<K）个学⽣的能⼒值的最⼤值，得到所有学⽣位置下j个学⽣的能⼒值的最⼤值；在j个学⽣的情况下，得到j+1个学⽣的最⼤值，样例输出： 10 8 7 2 -7 9 5 4 10 -7 1 3 3输出： 630如上，第⼀步先计算k=2的情况：7:在d=3的情况下，最⼤最⼩值都为562:在d=3的情况下，最⼤值为16，最⼩值为14-7:在d=3的情况下，最⼤值为-14，最⼩值为-56......得到第⼀趟的结果k=3的情况下（这⾥以第⼀趟的结果为基础，只有这样就不需要考虑第⼀趟中d=3的限制）：2:在d=3的情况下，最⼤最⼩值都为112（56*2）-7:在d=3的情况下，最⼤值为-98（14*-7）最⼩值为-392（56*-7）9:在d=3的情况下，最⼤值为504（56*9）最⼩值为-504（-56*9）......得到第⼆趟的结果返回最⼤值就是最后的结果#-*- coding:utf-8 -*-n=input()array=[int(i) for i in raw_input().split()]k,d=[int(i) for i in raw_input().split()]# n=36array_max=array_min=array#轮询k-1趟即可for i in range(0,k-1):_max=[-float('inf')]*n#将最⼤值的数组赋值⽆穷⼩_min=[float('inf')]*n#将最⼩值的数组赋值⽆穷⼤for j in range(i+1,n):if j<=d+i:#下⾯对应的min、max都是考虑到array[j]为负值的情况下temp_max = max(max(ii*array[j] for ii in array_max[i:j]),max(ii*array[j] for ii in array_min[i:j]))temp_min = min(min(ii*array[j] for ii in array_max[i:j]),min(ii*array[j] for ii in array_min[i:j]))else:temp_max = max(max(ii*array[j] for ii in array_max[j-d:j]),max(ii*array[j] for ii in array_min[j-d:j]))temp_min = min(min(ii*array[j] for ii in array_max[j-d:j]),min(ii*array[j] for ii in array_min[j-d:j]))_max[j]=temp_max_min[j]=temp_minarray_max=_maxarray_min=_minprint array_maxprint array_minprint max(array_max)2、题⽬描述（腾讯）：腾讯⼤厦有39层，你⼿⾥有两颗⼀抹⼀眼的玻璃珠。