高中数学 三角恒等变换 3_1 两角和与差的正弦、余弦和正切公式 3_1_1 两角差的余弦公式互动课堂学案

高中数学第三章三角恒等变换3-1两角和与差的正弦余弦和正切公式3-1-1两角差的余弦公式3-1-2两角和与差的正弦余弦正切公式自我检测新人教A 版必修43.1.2 两角和与差的正弦、余弦、正切公式自我小测1.的值为( )ππsin 1212-A ．0B ． C. D ．2 2．已知，，那么等于( )2tan()5αβ+=π1tan()44β-=πtan()4α+ A. B.C. D.131813223223183．在△ABC 中，若sin(B ＋C)＝2sin Bcos C ，那么这个三角形一定是( )A ．锐角三角形B ．钝角三角形C ．直角三角形D ．等腰三角形 4．(2011浙江高考，理6)若，，，π02α<<π02β-<<π1cos()43α+=πcos()42β-=( )．cos()2βα+A ．B ．C ．D 5．若α，β均为锐角，且，，则cos β＝__________.1cos 7α=11cos()14αβ+=- 6．A ，B ，C 是△ABC 的三个内角，且tan A ，tan B 是方程3x2－5x ＋1＝0的两个实数根，则△ABC 是__________三角形．7．已知α，β∈(0，π)，，，求2α－β的值．1tan()2αβ-=1tan 7β=- 8．若，，且，求cos(α＋β)的值．3π5sin()413α+=π3cos()45β-=π3π044αβ<<<<9已知向量a ＝(cos α，sin α)，b ＝(cos β，sin β)，.13-=a b (1)求cos(α－β)的值；(2)若，且，求sin α的值．π02α<<π02β-<<4sin 5β=- 参考答案1答案：C 解析：，故选πππππππsin 2(cos cos sin sin )2cos 12126126124-=-==2答案：C解析：ππtan()tan ()()44ααββ⎡⎤+=+--⎢⎥⎣⎦21πtan()tan()3544π21221tan()tan()1454αββαββ-+--===++-+⨯. 3答案：D解析：∵sin(B ＋C)＝2sin Bcos C ，∴sin Bcos C ＋cos Bsin C ＝2sin Bcos C ， 移项整理得：sin Bcos C －cos Bsin C ＝0，。

3.1.3 二倍角的正弦、余弦、正切公式疱工巧解牛知识•巧学 一、倍角公式1.公式的推导：倍角公式是和角公式的特例，只要在和角公式中令α=β，就可得出相应的倍角公式.sin(α+β)=sin αcos β+cos αsin β−−→−=βα令sin2α=2sin αcos α；cos(α+β)=cos αcos β-sin αsin β−−→−=βα令cos2α=cos 2α-sin 2α.由于sin 2α+cos 2α=1，显然，把sin 2α=1-cos 2α代入cos2α=cos 2α -sin 2α，得cos2α=cos 2α-sin 2α=cos 2α-(1-cos 2α)=2cos 2α-1.同理，消去cos 2α，得cos2α=1-2sin 2α. tan(α+β)=αααβαβαβα2tan 1tan 22tan tan tan 1tan tan -=−−→−∙-+=令. 综上，我们把公式叫做二倍角公式.2.二倍角公式中角α的范围由任意角的三角函数的定义可知S 2α、C 2α中的角α是任意的，但公式T 2α即tan2α=αα2tan 1tan 2-中的角是有条件限制的. 要使tan2α有意义，需满足1-tan 2α≠0且tan α有意义.当tan α有意义时，α≠2π+k π(k∈Z )；当1-tan 2α≠0，即tan α≠±1时，α≠±4π+k π(k∈Z ).综上,可知要使T 2α有意义，需α≠±4π+k π且α≠2π+k π(k∈Z ).特别地，当α=2π+k π(k∈Z )时，虽然tan α的值不存在，但tan2α的值是存在的，这时求tan2α的值，可用诱导公式进行，即tan2(2π+k π)=tan(π+2k π)=tan π=0. 学法一得 二倍角的切函数是用单角的切函数表示出来的，它的角α除了使解析式有意义外，还应使函数自身也有意义. 3.倍角公式中的倍角是相对的二倍角公式不仅仅可用于将2α作为α的2倍的情况，对于两个角的比值等于2的情况都成立，如8α是4α的二倍角，4α是2α的二倍角，3α是23α的二倍角，2α是4α的二倍角，3α是6α的二倍角等. 在运用倍角公式对半角的三角函数进行变换时，无论正用还是逆用，都可直接使用这一公式.例6cos6sin23sinααα=，6cos 26sin 6cos 3cos222αααα=-=-1=1-2sin26α；sin3α·cos3α=21 (2sin3αcos3α)=21sin6α；cos 22α-sin 22α=cos4α；ααα3sin 4123cos 23sin 21=；︒-︒35tan 135tan 22=tan70°等. 4.倍角公式的几种变形形式(sin α±cos α)2=1±sin2α；1+cos2α=2cos 2α；1-cos2α=2sin 2α；cos 2α=22cos 1α+；sin 2α=22cos 1α-. 学法一得 我们常把1+cos α=2cos 22α，1-cos α=2sin 22α称为升幂换半角公式，利用该公式消去常数项，便于提取公因式化简三角函数式；把cos 2α=22cos 1α+，sin 2α=22cos 1α-称为降幂换倍角公式，利用该公式能使之降次，便于合并同类项化简三角函数式.倍角公式给出了α的三角函数与2α的三角函数之间的关系.对于该公式不仅要会正用，还应会逆用和变用.5.倍角公式与和角公式的内在联系只有理清公式的来龙去脉及公式的变形形式，才能及时捕捉到有价值的信息，完成问题的解答.典题•热题知识点一 直接应用倍角公式求值 例1 求下列各式的值：(1)2sin15°sin105°；(2)︒-15sin 731432；(3)︒-︒5.22tan 15.22tan 2；(4)12cos24cos 24sin πππ. 解：(1)原式=2sin15°·sin(90°+15°)=2sin15°cos15°=sin30°=21.(2)原式=143(1-2sin 215°)=143cos30°=283323143=⨯. (3)原式=.2112145tan 215.22tan 15.22tan 2212=⨯=︒=︒-︒∙. (4)原式=8121416sin 4112cos 12sin 21=⨯==πππ.方法归纳 倍角公式中的角是相对的，对它应该有广义上的理解，即112cos 2sin22++=n n nααα(n∈N *)，12sin 2cos 2cos212+-=+n n nααα(n∈N *)，1212tan 12tan 22tan++-=n n nααα(n∈N *).知识点二 利用倍角公式给值求值例2 已知x∈(2π-，0)，cosx=54，则tan2x 等于( ) A.247 B.247- C.724 D.724- 思路分析：运用三角函数值在各个象限的符号及倍角公式求解. 解法一：∵x∈(2π-，0)，cosx=54， ∴sinx=53)54(1cos 122-=--=--x . 由倍角公式sin2x=2sinxcosx=2524-，cos2x=2cos 2x-1=2×(54)2-1=257. 得tan2x=7242cos 2sin -=x x .解法二：∵x∈(2π-，0)，cosx=54， ∴sinx=53)54(1cos 122-=--=--x .∴tanx=43cos sin -=x x . ∴tan2x=724)43(1)43(2tan 1tan 222-=---⨯=-xx . 答案：D方法归纳 ①解好选择题的关键在于能否针对题目的特点，选择合理而适当的解法，最忌对任何题目都按部就班地演算求解，小题大做，应力求做到“小题小做”“小题巧做”. ②像这种从题目的条件出发，通过正确地运算推理，得出结论，再与选择肢对照确定选项的方法叫做定量计算法；像这样通过对题干和选择肢的关系进行观察、分析，再运用所学知识，通过逻辑推理作出正确选择的方法叫做定性分析法. 例3 已知sin(4π+α)sin(4π-α)=161，α∈(2π，π)，求sin4α的值.思路分析：要求sin4α的值，根据倍角公式可知只需求出sin2α、cos2α的值或sin α、cos α的值即可.由于(4π+α)+(4π-α)=2π，可运用二倍角公式求出cos2α的值. 解：由题设条件得sin(4π+α)sin(4π-α)=sin(4π+α)cos ［2π-(4π-α)］ =sin(4π+α)cos(4π+α)=21sin(2π+2α)=21cos2α=61，∴cos2α=31.∵α∈(2π，π)，∴2α∈(π，2π).又∵cos2α=31>0，∴2α∈(23π，2π).∴sin2α=322)31(12cos 122-=--=--α. ∴sin4α=2sin2α·cos2α=2×92431)322(-=⨯-. 例4 已知cos(4π+x)=53，47127ππ<<x ，求x x x tan 1sin 22sin 2-+的值. 思路分析：由于结论中同时含有切、弦函数，所以可先对结论切化弦，化简后不难发现，只需求出sin2x 和tan(4π+x)的值即可，注意到2(4π+x)=2π+2x ，这样通过诱导公式就容易找到sin2x 同cos(4π+x)的关系了. 解：∵47127ππ<<x ，∴πππ2465<+<x .又∵cos(4π+x)=53>0，∴23π＜4π+x ＜2π.∴sin(4π+x)=54)53(1)4(cos 122-=--=+--x π，345354)4cos()4sin()4tan(-=-=++=+x x x πππ.∵sin2x=-cos2(4π+x)=1-2cos 2(4π+x)=25725181=-， ∴原式=x x x x x x x x x x x xx x x sin cos )sin (cos 2sin sin cos cos sin 2cos 2sin cos sin 1sin 22sin 22-+=-∙+∙=-+7528)34(257)4tan(2sin tan 1tan 12sin -=-⨯=+∙=-+∙=x x x x x π.例5 在△ABC 中，已知AB=AC=2BC(如图3-1-10)，求角A 的正弦值.图3-1-10思路分析：由于所给三角形是等腰三角形，所以可通过底角的三角函数值或顶角一半的三角函数值来求解.解：作AD⊥BC 于点D ，设∠BAD=θ，那么A=2θ.∵BD=21BC=41AB ，∴sin θ=41=AB BD . ∵0＜2θ＜π，∴0＜θ＜2π.于是cos θ=415)41(1sin 122=-=-θ. 故sinA=sin2θ=2sin θcos θ=815415412=⨯⨯. 巧解提示:作AD⊥BC 于点D ，∵BD=21BC=41AB,又∵AB=AC， ∴∠B=∠C.∴cosB=cosC=41=AB BD . ∵0＜B ＜2π，∴sinB=415.又∵A+B+C=π，∴A=π-(B+C)=π-2B. ∴sinA=sin(π-2B)=sin2B=2sinBcosB=815414152=⨯⨯. 方法归纳 在△ABC 中，由于A+B+C=π，所以A=π-(B+C)，222CB A +-=π.由诱导公式可知：sinA=sin(B+C)；cosA=-cos(B+C)；tanA=-tan(B+C)；2cot 2tan ;2sin 2cos ;2cos 2sinCB AC B A C B A +=+=+=. 任意变换A 、B 、C 的位置，以上关系式仍然成立. 例6 已知sin 22α+sin2αcos α-cos2α=1，α∈(0，2π)，求sin α、tan α的值. 思路分析：已知是二倍角，所求的结论是单角；已知复杂，结论简单，因此可从化简已知入手，推出求证的结论.解：把倍角公式sin2α=2sin αcos α，cos2α=2cos 2α-1代入已知得4sin 2αcos 2α+2sin αcos 2α-2cos 2α=0，即2cos 2α(2sin 2α+sin α-1)=0，即2cos 2α(2sin α-1)(sin α+1)=0.∵α∈(0，2π)，∴sin α+1≠0，cos 2α≠0. ∴2sin α-1=0，即sin α=21.又∵α∈(0,2π),∴α=6π.∴tan α=33.知识点三 利用倍角公式化简三角函数式例7 利用三角公式化简sin50°(1+3tan10°).思路分析：本题给我们的感觉是无从下手，很难看出有什么公式可直接利用.从角的角度去分析，10°、50°除了它们的和60°是特殊角外，别无特点；从函数名称的角度去分析，由于该式子有弦，有切，我们可从化切为弦入手去尝试解决，转化成弦函数.通分后出现asin θ+bcos θ的形式，由于3是一特殊角的三角函数值，可把它拼凑成两角和(差)的正、余弦展开式的形式逆用公式求值.若把50°转化成(60°-10°)从同一角入手，也可以求值. 解：原式=sin(60°-10°)(1+3tan10°)=(23cos10°-21sin10°)(1+3tan10°) =23cos10°+23cos10°tan10°-21sin 10°-23sin10°tan10° =23cos10°+sin10°-23sin10°·tan10°=23(cos10°-︒︒10cos 10sin 2)+sin10° =︒︒︒+︒∙=︒+︒︒∙10cos 10cos 10sin 33220cos 2310sin 10cos 20cos 23 ︒︒+︒∙∙=︒︒+︒∙=10cos 20sin 2120cos 233322310cos 20sin 3320cos 23180sin 80sin 10cos 80sin 10cos 20sin 60cos 20cos 60sin =︒︒=︒︒=︒︒︒+︒︒=.巧解提示:原式=︒︒+︒∙︒=︒︒+︒10cos )10sin 2310cos 21(250sin )10cos 10sin 31(50sin ︒︒︒+︒︒︒=10cos 10sin 30cos 10cos 30sin 50sin 2110cos 10cos 10cos 80sin 10cos 40sin 40cos 2=︒︒=︒︒=︒︒︒=.方法归纳 对于三角整式，基本思路是降次、消项和逆用公式；对三角分式，基本思路是分子与分母约分或逆用公式；对二次根式，要设法使被开方数升次，通过开方进行化简.另外，还可用切割化弦、变量代换、角度归一等方法.对于形如1±sin α、1±cos α的形式，我们可采取升幂换半角的形式，消去常数项1，通过提取公因式化简有理式或通过开方化简无理式. 例8 求cos20°cos40°cos60°cos80°的值. 解：由于cos60°=21，所以原式=21cos20°cos40°cos80° ︒︒︒︒︒∙=20sin 80cos 40cos 20cos 20sin 21 ︒︒︒∙=︒︒︒︒∙=20sin 80cos 80sin 8120sin 80cos 40cos 40sin 41 16120sin 160sin 161=︒︒∙=. 方法归纳 对于可化为cos αcos2αcos4α…cos2n-1α(n∈N 且n>1)的三角函数式，由于它们的角是以2为公比的等比数列，可将分子、分母同乘以最小角的正弦，运用二倍角公式进行化简.巧解提示:此外，本题也可构造一对偶式求解. 设M=cos20°·cos40°·cos60°·cos80°， N=sin20°·sin40°·sin60°·sin80°， 则MN=161sin40°·sin80°·sin120°·sin160° =161sin20°·sin40°·sin60°·sin80° =161N ，∴M=161,即cos20°·cos40°·cos60°·cos80°=161. 知识点四 利用倍角公式证明三角恒等式例9 求证：θθθθθθ2tan 14cos 4sin 1tan 24cos 4sin 1-++=-+. 证明：原式等价于1+sin4θ-cos4θ=αθ2tan 1tan 2-(1+sin4θ+cos4θ)， 即1+sin4θ-cos4θ=tan2θ(1+sin4θ+cos4θ). ① 而①式右边=tan2θ(1+cos4θ+sin4θ)=θθ2cos 2sin(2cos 22θ+2sin2θcos2θ)=2sin2θcos2θ+2sin 22θ =sin4θ+1-cos4θ=左边. 所以①式成立，原式得证.例10 求证：︒=︒-︒10sin 3240cos 140sin 322.思路分析：由于分母是三角函数值平方的形式，通分后转化成3cos 240°-sin 240°，按平方差公式展开得(3cos40°+sin40°)(3cos40°-sin40°)，恰好是两个辅助角公式的形式，可运用三角函数的和差公式求值；此外，也可对它的分母降幂换倍角进行化简. 证明：左边=︒∙︒︒-︒︒+︒=︒︒︒-︒40cos 40sin )40sin 40cos 3)(40sin 40cos 3(40cos 40sin 40sin 40cos 3222222 2)40cos 40sin 2()40sin 2140cos 23(2)40sin 2140cos 23(24︒︒︒-︒⨯︒+︒⨯= ︒︒︒-︒︒︒︒+︒︒=80sin )40sin 60cos 40cos 60)(sin 40sin 60cos 40cos 60(sin 162︒︒-︒︒+︒=80sin )4060sin()4060sin(162︒=︒︒︒⨯=︒︒=︒︒︒=10sin 3210cos 10cos 10sin 21680sin 20sin 1680sin 20sin 100sin 162=右边， 所以原式成立.方法归纳 对于三角函数式的化简、求值和证明，可从角的角度、运算的角度或函数名称的角度去考虑，其中通过通分，提取公因式、约分、合并同类项等运算的手法去化简是非常必要的.例11 已知3sin 2α+2sin 2β=1，3sin2α-2sin2β=0，求证：cos(α+2β)=0.思路分析：从求证的结论看，cos(α+2β)的展开式中含有cos α、cos2β、sin α、sin2β这样的函数值.由已知条件结合倍角公式的特点，恰好能转化出cos2β、sin2β这样的函数值.证明：由3sin 2α+2sin 2β=1，得1-2sin 2β=3sin 2α，∴cos2β=3sin 2α. 又∵sin2β=23sin2α， ∴cos(α+2β)=cos αcos2β-sin αsin2β=cos α·3sin 2α-sin α·23sin2α=23sin αsin 2α-23sin αsin2α=0. 方法归纳 首先观察条件与结论的差异，从解决某一差异入手.确定从结论开始，通过变换将已知条件代入得出结论；或通过变换已知条件得出结论；或同时将条件与结论变形，直到找到它们间的联系.如果上述方法都难奏效的话，可采用分析法；如果已知条件含有参数，可采用消去参数法；如果已知条件是连比的式子，可采用换元法，等等. 问题•探究 材料信息探究问题 倍角和半角公式：sin α=2tan12tan22αα+，cos α=2tan12tan 122αα+-，tan α=2tan12tan 22αα-，这组公式称为“万能公式”，那么“万能公式”是怎样来的？它真的是“万能”的吗？探究过程:万能公式是一组用tan2α来表示sin α、cos α和tan α的关系式. 这组公式可以利用二倍角公式推导，其中正切tan α=2tan 12tan22αα-，可以由倍角公式直接获得；正弦、余弦只要在倍角公式中添加分母，再分子、分母同除以cos 22α可得： 2tan 12tan22cos 2sin 2cos 2sin 22cos 2sin 2sin 222ααααααααα+=+==， 2tan 12tan 12cos 2sin 2sin 2cos 2sin 2cos cos 22222222ααααααααα+-=+-=-=. 这组“万能公式”为一类三角函数的求值提供了一座方便可行的桥梁，如要计算cos α或sin(α+β)的值，可以先设法求得tan2α或2tan βα+的值.由于公式中涉及角的正切，所以使用时要注意限制条件，即要保证式子有意义.探究结论:所谓的“万能”，是说不论角α的哪一种三角函数，都可以表示成tan 2α的有理式，这样就可以把问题转化为以tan 2α为变量的“一元有理函数”，即如果令tan 2α=t ，则sin α、cos α和tan α均可表达为关于t 的分式函数，这就实现了三角问题向代数问题的转化，为三角问题用代数方法求解提供了一条途径.如ta n15°+cot15°=tan15°+=︒+︒=︒15tan 115tan 15tan 12430sin 2115tan 15tan 222=︒=+︒︒，就较方便的解决了问题.再如求函数2sin cos +=x x y 的值域.令t x=2tan ，则t∈R ，利用万能公式有sinx=212t t +,cosx=2211t t +-，所以=+++-=21211222t t t t y 222221t t t ++-，由此可以建立关于t 的一次或二次函数(2y+1)t 2+2yt+2y-1=0，进一步分类讨论可得函数的值域.。

[ 介绍学习 ] 高中数学第三章三角恒等变换 3.1 两角和与差的正弦余弦和正切公式 3.1.2 两角和与差的正弦[k12]两角和与差的正弦、余弦和正切公式疱工巧解牛知识 ?巧学一、两角和的余弦公式1.比较 cos( α- β) 与 cos( α+β) ，依据α+β与α- β之间的联系：α +β=α-(- β) ，则由两角差的公式得 cos( α+β)=cos ［α-(- β)］=cosαcos( - β)+sin αsin( - β)=cos αcosβ-sin αsin β,即cos( α+β)=cos αcosβ - sin αsin β.学法一得这种以 - β代β的变换角的方式在三角函数的恒等变形中有侧重要应用，同时也启迪我们要辩证地对待和角与差角 . 在公式C(α-β)中，因为角α、β是随意角，所以在C(α+β)中，角α、β也是随意角 .2.用两点间的距离公式推导 C(α+β).图 3-1-5如图 3-1-5 ，在直角坐标系 xOy 内作单位圆O，以 O为极点，以 x 轴的非负半轴为始边，作出角α、 - β，使角α、 - β的终边分别交单位圆于点 P2、P4，再以 OP2为始边，作角β，使它的终边交单位圆于点 P3，这样就出现了α、β、α+β这样的角，设角α、- β的始边交单位圆于点 P1，则 P1(1 ，0). 设 P2(x ，y) ，依据随意角的三角函数的定义，有 sin α=y，cosα=x，即P2(cos α， sin α) ；同理 , 可得 P3(cos( α+β) ，sin( α+β)) ， P4(cos(- β) ，sin(- β)).由整个作图过程可知△P3OP1≌△P2OP4，所以|P1P3|=|P2P4|.|P 1P3| 2=|P2P4| 2，即［cos( α+β)-1］2+sin 2(α+β)=22［cos(- β)- cosα］ +［sin(- β)- sin α］ .依据同角三角函数的基本关系, 整理得 2-2cos( α+β)=2 - 2(cos αcosβ - sin αsin β) ，即 cos( α+β)=cos αcosβ - sin αsin β.3.利用向量的数目积推导 C(α+β).图 3-1-6如图3-1-6 ，在平面直角坐标系xOy 内作单位圆，以 Ox 为始边作角α、 - β，它们与单位圆的交点分别为 A、B.显然，OA =(cosα,sinα ),OB=(cos(-β ),sin(- β )).根据向量数目积的定义，有OA·OB=(cos α,sin α) ·(cos( - β),sin( - β))=cos αc os(- β)+sin αsin( - β)=cos αcosβ - sin αsin β.于是 cos( α+β)=cos αcosβ - sin αsin β.学法一得①在办理问题的过程中，把有待解决或难解决的问题，经过某种转变，归纳为一类已经解决或比较简单解决的问题，最后求得原问题的解，这种思想方法叫做化归思想 .②以随意角的三角函数的定义为载体，我们推导了同角的三角函数的基本关系式、引诱公式和两角和的余弦公式 . 熟记公式中角、函数的摆列次序及式中的正负号是正确使用公式的重点 .记忆要诀公式右端的两部分为同名三角函数之积，连结符号与左侧的连结符号相反 . 二、两角和与差的正弦1.公式的推导[k12]sin( α- β)=cos［ - ( α- β) ］=cos［(- α)+ β］22=cos( - α)cos β -sin(- α)sin β=sin αcos 22β- cosαsin β.在上边的公式中，以 - β代β，即可获得sin( α+β)=sin αcosβ+cosαsin β.2.和差公式是引诱公式的推行，引诱公式是和差公式的特例 . 如sin(2 π- α)=sin2 πcosα - cos2πsin α=0×cosα- 1×sin α=- sin α.当α 或β 中有一个角是的整数倍时，往常使2用引诱公式较为方便；上边公式中的α、β 均为随意角 .误区警告公式对分派律不建立，即sin( α±β )≠sin α± sin β，学习时必定要注意这一点 .学法一得公式使用时不单要会正用，还要能够逆用，如化简sin( α+β)cos β - cos( α+β)sin β，不要将sin( α+β) 和 cos( α+β) 睁开，而应该整体观察，进行以下变形：sin( α+β)cos β - cos( α+β)sin β=sin［( α+β)- β］=sin α，这也表现了数学中的整体原则 .记忆要诀记忆时要与两角和与差的余弦公式差别开来，两角和与差的正弦公式的右端的两部分为异名三角函数之积，连结符号与左侧的连结符号相同 .三、两角和与差的正切1.公式的推导利用两角和的正弦、余弦公式，能够推导出两角和的正切公式：tan( α+β)=sin()sin cos cos sin，当cos()cos cos sin sincosαcosβ≠0时，我们能够将上式的分子、分母同时除以 cosαcosβ，即得用 tan α和 tan β表示的公式：tan( α+β)= tan tan，在上边的公式中，以- β1 tan tan代β，可得两角差的正切公式：tan( α- β)= tan tan.1 tan tan2.公式建立的条件要能应用公式，第一要使公式自己存心义，即 tan α、 tan β存在 . 并且 1+tan αtan β的值不为零，所以可得α、β 需知足的条件：α≠ kπ+, β≠ kπ+，α+β≠ kπ+或222α- β≠ kπ+，以上 k∈ Z. 当 tan α、 tan β、2tan( α±β ) 不存在时，能够改用引诱公式或其余方法解决 .学法一得两角和与差的正切相同不单能够正用，并且能够逆用、变形用，逆用和变形用都是化简三角恒等式的重要手段，如tan α+tanβ=tan( α+β)(1 - tan αtan β)就能够解决诸如tan15 °+tan30 °+tan15 °tan30 °的问题 . 所以在办理问题时要注意观察式子的特色，奇妙运用公式或其变形，使变换过程简单明了.典题 ?热题知识点一所求角可表示成两个特别角的和、差例 1 求 sin75 °,tan15 °的值 .解：sin75 °=sin(45 °+30°)=sin45 °cos30°+cos 45°sin30 °[k12]= 232162；22224tan15 °=tan(60 ° - 45°)= tan 60tan 4531231tan 60 tan 4513，或13tan15 °=tan(45 °- 30°)=tan 45tan 303231tan 45tan 30313.例 2求 sin 7cos15 sin8的值 .cos7sin15 sin8思路剖析：察看被求式的函数名称的特色和角的特色，此中7°=15° - 8°， 15°=8°+7°，8°=15°- 7°. 不论采纳哪一种代换方式，都可减少角的个数 . 利用和角或差角公式睁开，进行约分、化简、求值 . 若用 7°=15°- 8°代换，分子、分母是二次齐次式；若用15°=8°+7°或8°=15°- 7°代换，分子、分母将会出现三次式，明显选择后者更好，不如比较一下.答案：原式 = sin 7cos(78 ) sin 8cos7sin(78 ) sin 8sin 7cos7 cos8 sin 8sin 7? sin 2 8sin 7 (1sin 2 8 )cos7cos8 sin 8 cos7sin 7 cos8 sin 8cos7? sin 2 8cos7 (1sin2 8 )sin 7cos8 sin 8[k12]sin 7 ?cos 2 8 cos7 cos8 sin 8 sin 7 cos8 cos7 sin 8 cos7 ? cos 2 8sin 7 cos8 sin 8cos7 cos8sin 7 sin 8sin15 tan1523.cos15巧解提示 : 原式 =sin(158 )cos15 ? sin 8cos(15 8 )sin15 ? sin 8sin15 ? cos8cos15 ? sin 8 cos15 ? sin8 cos15 ?cos8sin15 ? sin 8sin15 ? sin8sin15 ? cos8=tan15 °=tan(45 ° - 30°)cos15 ? cos83tan 45 tan 30 13.3 21 tan 45 ? tan 30313方法概括 三角函数式的构造一般由角、 三角函数符号及运算符号三部分构成 . 所以三角恒等变换常常第一找寻式子所包括的各个角之间的联系，并以此为依照选择能够联系它们的适合公式，这是三角恒等变换的重要特色 . 不论是化简、求值，仍是证明，其结果应按照以下几个原则：①能求值的要求值；②三角函数的种类尽可能少；③角的种类尽可能少；④次数尽可能低；⑤尽可能不含根号和分母 .知识点二 已知 α、β 的三角函数值，求 α±β 的三角函数值例 3 已知 sin α=1，求 cos(+α) 的值 .33[k12]思路剖析：因为是个特别角，所以依据 C (α+β)3的睁开式，只要求出cos α 的值即可 . 因为条件1只告诉了 sin α= ，没有明确角 α 所在的象限，3所以应分类议论， 先求 cos α 的值，再代入睁开式确立 cos(+α) 的值 .3解：∵ sin α=1>0，∴α 位于第一、二象限 .3当 α 是第一象限角时， cos α=1 (1)22 2，33∴cos(3 +α)=coscos α-sin3sin α=31 22 3 1 2 2 3 ;23 236同理，当 α 是第二象限角时， cos α=22，3∴cos(3+α)=2 33.6方法概括解这种给值求值问题的重点是先分清 S ( α±β) 、C (α±β)、T ( α±β) 的睁开式中所需要的条件，联合题设，明确谁是已知的，谁是待求的 . 此中在利用同角三角函数的基本关系求值时， 应先解决与已知拥有平方关系的三角函数值 . 可是，关于 cos( π+α) 、cos( +α) 这样的函数求2[k12]值，因为它们的角与的整数倍有关，所以无需2按它们的睁开式求值，直接利用引诱公式可能更简单 .例 4 已知 cos( α -)=1，sin(- β)=2，并且29232＜α＜π， 0＜β＜，求cos的值 .22思路剖析：察看给出的角2() (2) ，联合2公式C(α-β)睁开式的特色，只要利用同角三角函数的基本关系计算出 sin( α- ) 、cos( - β) 的22值即可 .解：∵＜α＜π，0＜β＜，∴＜＜，0 22422＜＜.2 4∴＜α - ＜π， - ＜ - β＜ .42422又∵ cos( α-2)=91＜0，∴22.∴sin() 1 sin 2 ()1( 1)2 4 5.2299同理，∵ sin(- β)= 2>0，∴02.232∴ cos()1sin 2 () 1 (2)2 5 .22332cos[() ( )]22=cos( α-2)cos(- β)+sin( α- )sin(- β)2221 5 4 52 7 5 .9 3 93 27例 5 在△ ABC 中， sinA= 3 ,cosB= 5，求 cosC.5 13思路剖析：此题主要观察三角形中的三角函数问题 . 若不注意“△ ABC ”这个条件，就会产生多解，所以解这种问题时必定要注意尽量压缩角的范围，避开分类议论， 同时要注意结论能否切合题意 .解：∵cosB= 52 , ∴B ∈( ,) 且 sinB= 12.13 2 4213∵sinA=3 23 52 , ∴A ∈(0, 4) ∪( , π).43) ，则3若 A ∈( , π),B ∈( ,2 A+B ∈( π, ) 与44 2A+B+C=π 矛盾，∴A (34, π). 所以 A ∈(0,) 且 cosA=4.45从而cosC=cos ［π-(A+B)］=-cos(A+B)=-cosAcosB+sinAsinB=4 5 3 12 16 5 13 5 13 65例 6 如图 3-1-7 ，已知向量OP =(3,4) 绕原点旋转45°到 OP′的地点，求点 P′(x ′,y ′) 的坐标 .图 3-1-7思路剖析：此题相当于已知角α 的三角函数值，求α+45°的三角函数值 . 解：设∠ xOP=α.2234因为 |OP|= 34 5 ，所以cosα=,sin α= .55因为x′=5cos( α+45°)=5(cos αcos45° - sin αsin 45°)5( 324 2 )2，52522同理 , 可求得 y′=5sin( α+45°)= 7 2，所以2P′(22 , 722 ).方法概括①已知角α 的某一三角函数值和角α 所在的象限，则角α 的其余三角函数值独一；已知角α 的某一三角函数值，不知角α 所在的象限，应先分类议论，再求α 的其余三角函数值.②一般地，90°±α，270°±α的三角函数值，等于α 的余名函数值，前面加上一个把α 当作锐角时原函数值的符号，它的证明也可经过两角和、差的三角函数式进行 . ③在给值求值的题型中，要灵巧办理已知与未知的关系，合理进行角的变换，使所求角能用已知角表示出来，所求角的三角函数值能用已知角的三角函数值表示出来 .知识点三已知三角函数值求角例 7 已知 sin α=5，sin β=10 , 且α、β都是510锐角，求α+β的值 .思路剖析： (1) 依据已知条件可先求出α+β的某个三角函数值，如 cos( α+β).(2) 由两角和的余弦公式及题设条件知只要求出 cosα、cosβ即可 .(3) 因为α、β都是锐角，所以 0＜α +β＜π ,y=cosx 在(0, π) 上是减函数，进而依据cos( α+β) 的值即可求出α+β的值 .解：∵ sin α=5 ,sin β=10，且α、β都是锐510角，∴ cosα=1 sin2 2 55，cosβ= 1 sin231010.∴c os( α+β)=cos αcosβ - sin αsin β= 25310510 2 .5105102又∵ 0＜α +β＜π , ∴α +β= .4方法概括给值求角的一般步骤是：①确立所求角的范围；②找到该范围内拥有单一性的某一三角函数值；③先找到一个与之有关的锐角，再由引诱公式导出所求角的值 .知识点四利用两角和、差的三角函数公式证明恒等式例 8 已知 3sin β=sin(2 α+β)，求证：tan( α+β)=2tan α.思路剖析：察看条件等式和结论等式中的角，条件中含有β、2α+β，结论中含有α+β、α，若从条件下手，可采纳角的变换，β=( α+β)- α，2α+β=( α+β)+ α，睁开后转变成齐次整式，约分得出结论 .证明：∵3sin β=3sin ［ ( α+β)- α］=3sin( α+β)cos α - 3cos( α+β)sin α，sin(2 α+β)=sin［( α+β)+ α］[k12]=sin( α+β)cos α+cos( α+β)sin α，又 3sin β=sin(2 α+β) ，∴3sin( α+β)cos α - 3cos( α+β)sin α=sin(α+β)cos α+cos( α+β)sin α.∴2sin( α+β)cos α=4cos( α+β)sin α.∴t an( α+β)=2tan α.方法概括对条件恒等式的证明，若条件复杂，可从化简条件下手得出结论；若结论复杂，可化简结论得出条件；若条件和结论都较为复杂，可同时化简它们，直到找到它们间的联系 .知识点五变用两角和差的三角函数公式化简求值例 9 用和、差公式证明tan12 °+tan18 °+33 tan12 °· tan18 °=3 .3解∵：tan12tan18=tan(12 °+18°)=tan30 °=3，1 tan12? tan183∴tan12 °+tan18 °=33 (1- tan12 °· tan18 °) ，即左边[k12]= 3 (1- tan12 °tan18 °)+3 tan12 °tan18 °=3 333=右侧 .∴t an12 °+tan18 °+3 tan12 °· tan18 °=3 .33方法概括三角公式经过等价变形，可正用，可逆用，也可变用，主假如经过对函数构造式的变形与对角的分、拆、组合来实现的 .例 10 求(1+tan1 °)(1+tan2 °)(1+tan3 °)(1+tan45 °) 的值 .解：因为α+β=45°时，tan( α+β)=tan tan=1，所以1tan tantan α+tan β+tan αtan β=1，即(1+tan α)(1+tan β)=2.于是(1+tan1 °)(1+tan44 °)=(1+tan2 °)(1+tan43°)==(1+tan22 °)(1+tan23 °)=2.又因为 1+tan45°=2，所以原式 =223.方法归纳当α+β=kπ+,k ∈ Z时，4(1+tan α)(1+tan β)=2 ；当α+β=kπ -,k ∈Z时，4(1+tan α)(1+tan β)=2tan αtan β.问题 ?研究思想方法研究问题 1 在三角恒等变换中，三角公式众多，公式变换也是解决问题的有效手段，在应用这些公式时要注意些什么问题？研究过程 : 使用任何一个公式都要注意它的逆向变换、多向变换，这是灵巧使用公式所一定的，特别是面对那么多三角公式，把这些公式变活，显得更为重要，这也是学好三角函数的基本功 .如： cos( α- β)cos β- sin( α- β)sin β化简为 __________.将α- β看作一个角，β 看作另一个cos( α- β)cos β - sin(α-角,则β)sin β=cos［(α- β)+ β］ =cosα.解答此题时不单利用角的变换：α=( α- β)+ β，同时运用了公式的逆向变换 .探究结论:两角和的正切公式tan(α+β)=tan tan.除了掌握其正向使用之1 tan tan外，还需掌握以下变换：1- tanαtanβ=tan tan；tan() tanα+tan β=tan(α+β)(1- tanαtanβ)；tan αtan βtan( α+β)=tan( α+β)- tan α -ta nβ等 . 两角和的正切公式的三种变形要熟习，其在此后解题中常常使用，要能灵巧办理 .问题 2 2004 年重庆高考有一题为：求函数 y=sin4x+ 2 3 sinxcosx-cos 4x 的最小正周期和最小值，并写出该函数在［ 0, π］上的单一递加区间.该函数变形后就需要用到形如asinx+bcosx(a 、b 不一样时为零 ) 的式子的变换，我们称之为协助角变换，那么怎样进行协助角变换？研究过程 : 形如 asinx+bcosx(a 、b 不一样时为零 )的式子能够引入协助角变形为Asin(x+ φ) 的形式.asinx+bcosx=22(a sin x b cosx) ,a b2222a b a b令 cosφ=2ab 2 ,sinφ=a2b 2，则a b原式= a2b2(sinxcosφ +cosxsinφ )= a2 b 2sin(x+ φ).( 此中φ角所在象限由 a、b 的符号确立，φ 角的值由 tan φ=b确立，常常取φ=arctan b ).a a研究结论 : 协助角变换是三角变形的重要形式，它的应用十分宽泛，特别是在数学中求三角函数的最值及物理学中间波的合成时，都是重要的工具. 比如2sinx-3cosx ，就能够利用这一结论将其化为一个三角函数的形式，进而确立其最值，因为 a=2,b=-3,A= a 2b213，所以2sinx-3cosx=13 sin(x+φ)，(此中φ 在第四象限，且 tan φ=32 ) ，所以 2sinx-3cosx的最大值是13 ，最小值是13 .。

3．1.3 二倍角的正弦、余弦、正切公式学习目标 1.会用两角和的正弦、余弦、正切公式推导出二倍角的正弦、余弦、正切公式. 2.能熟练运用二倍角的公式进行简单的恒等变换并能灵活地将公式变形运用．知识点一 二倍角公式的推导思考1 二倍角的正弦、余弦、正切公式就是用α的三角函数表示2α的三角函数的公式．根据前面学过的两角和与差的正弦、余弦、正切公式，你能推导出二倍角的正弦、余弦、正切公式吗？答案 sin2α＝sin(α＋α)＝sin αcos α＋cos αsin α ＝2sin αcos α；cos2α＝cos(α＋α)＝cos αcos α－sin αsin α ＝cos 2α－sin 2α； tan2α＝tan(α＋α)＝2tan α1－tan 2α(α≠π2＋k π，2α≠π2＋k π，k ∈Z )． 思考2 根据同角三角函数的基本关系式sin 2α＋cos 2α＝1，你能否只用sin α或cos α表示cos2α？答案 cos2α＝cos 2α－sin 2α＝cos 2α－(1－cos 2α)＝2cos 2α－1； 或cos2α＝cos 2α－sin 2α＝(1－sin 2α)－sin 2α＝1－2sin 2α.知识点二 二倍角公式的变形 1．公式的逆用2sin αcos α＝sin2α，sin αcos α＝12sin2α，cos 2α－sin 2α＝cos_2α，2tan α1－tan 2α＝tan2α. 2．二倍角公式的重要变形——升幂公式和降幂公式 升幂公式1＋cos2α＝2cos 2α，1－cos2α＝2sin 2α， 1＋cos α＝2cos 2α2,1－cos α＝2sin 2α2.降幂公式cos 2α＝1＋cos2α2，sin 2α＝1－cos2α2.1．sin α＝2sin α2cos α2.( √ )2．cos4α＝cos 22α－sin 22α.( √ ) 3．对任意角α，tan2α＝2tan α1－tan 2α.( × ) 提示 公式中所含各角应使三角函数有意义．如α＝π4及α＝π2，上式均无意义.类型一 给角求值 例1 (1)计算：cos2π12－sin 2π12； 考点 应用二倍角公式化简求值 题点 利用余弦的二倍角公式化简求值 解 原式＝cos π6＝32.(2)计算：1－tan 275°tan75°；考点 应用二倍角公式化简求值 题点 利用正切的二倍角公式化简求值解 1－tan 275°tan75°＝2·1－tan 275°2tan75°＝2·1tan150°＝－2 3.(3)计算：cos20°cos40°cos80°. 考点 应用二倍角公式化简求值 题点 利用正弦的二倍角公式化简求值解 原式＝12sin 20°·2sin 20°cos 20°cos 40°cos 80°＝12sin 20°·sin 40°·cos 40°cos 80°＝122sin 20°sin 80°cos 80° ＝123sin 20°·sin 160°＝sin 20°23sin 20°＝18. 反思与感悟 对于给角求值问题，一般有两类(1)直接正用、逆用二倍角公式，结合诱导公式和同角三角函数的基本关系对已知式子进行转化，一般可以化为特殊角．(2)若形式为几个非特殊角的三角函数式相乘，则一般逆用二倍角的正弦公式，在求解过程中，需利用互余关系配凑出应用二倍角公式的条件，使得问题出现可以连用二倍角的正弦公式的形式．跟踪训练1 (1)cos π7cos 3π7cos 5π7的值为( )A.14B ．－14C.18D ．－18考点 应用二倍角公式化简求值 题点 利用正弦的二倍角公式化简求值 答案 D解析 cos π7cos 3π7cos 5π7＝cos π7·⎝ ⎛⎭⎪⎫－cos 4π7·⎝ ⎛⎭⎪⎫－cos 2π7＝2sin π7cos π7cos 2π7cos4π72sinπ7＝sin 2π7cos 2π7cos 4π72sin π7＝sin 4π7cos4π74sinπ7＝sin8π78sinπ7＝－18.(2)12－cos 2π8＝________； 考点 应用二倍角公式化简求值 题点 利用余弦的二倍角公式化简求值答案 －24解析 原式＝12⎝ ⎛⎭⎪⎫1－2cos 2π8＝－12cos π4＝－24.类型二 给值求值例2 (1)若sin α－cos α＝13，则sin2α＝________.考点 应用二倍角公式化简求值 题点 综合应用二倍角公式化简求值 答案 89解析 (sin α－cos α)2＝sin 2α＋cos 2α－2sin αcos α＝1－sin2α＝⎝ ⎛⎭⎪⎫132，即sin2α＝1－⎝ ⎛⎭⎪⎫132＝89.(2)若tan α＝34，则cos 2α＋2sin2α等于( )A.6425B.4825C ．1D.1625考点 应用二倍角公式化简求值 题点 综合应用二倍角公式化简求值 答案 A解析 cos 2α＋2sin 2α＝cos 2α＋4sin αcos αcos 2α＋sin 2α＝1＋4tan α1＋tan 2α. 把tan α＝34代入，得cos 2α＋2sin 2α＝1＋4×341＋⎝ ⎛⎭⎪⎫342＝42516＝6425.故选A.引申探究在本例(1)中，若改为sin α＋cos α＝13，求sin2α.解 由题意，得(sin α＋cos α)2＝19，∴1＋2sin αcos α＝19，即1＋sin 2α＝19，∴sin 2α＝－89.反思与感悟 (1)条件求值问题常有两种解题途径：①对题设条件变形，把条件中的角、函数名向结论中的角、函数名靠拢；②对结论变形，将结论中的角、函数名向题设条件中的角、函数名靠拢，以便将题设条件代入结论． (2)一个重要结论：(sin θ±cos θ)2＝1±sin 2θ.跟踪训练2 (1)(2017·石家庄高一检测)若sin(π－α)＝13，且π2≤α≤π，则sin2α的值为( ) A ．－429B ．－229C.229D.429考点 二倍角的正弦、余弦、正切公式 题点 利有二倍角公式求二倍角的正弦值 答案 A解析 因为sin(π－α)＝13，所以sin α＝13，又因为π2≤α≤π，所以cos α＝－1－sin 2α＝－223，所以sin2α＝2sin αcos α＝2×13×⎝ ⎛⎭⎪⎫－223＝－429. (2)已知α为锐角，若cos ⎝ ⎛⎭⎪⎫α＋π6＝35，则cos ⎝ ⎛⎭⎪⎫2α－π6＝________.考点 应用二倍角公式化简求值 题点 综合应用二倍角公式化简求值 答案2425解析 因为α为锐角，cos ⎝ ⎛⎭⎪⎫α＋π6＝35>0， 所以α＋π6为锐角，sin ⎝ ⎛⎭⎪⎫α＋π6＝45， 则sin ⎝ ⎛⎭⎪⎫2α＋π3＝2sin ⎝⎛⎭⎪⎫α＋π6cos ⎝ ⎛⎭⎪⎫α＋π6＝2×45×35＝2425.又cos ⎝ ⎛⎭⎪⎫2α－π6＝sin ⎝ ⎛⎭⎪⎫2α＋π3，所以cos ⎝ ⎛⎭⎪⎫2α－π6＝2425. 类型三 利用二倍角公式化简证明 例3 (1)化简：1＋sin2θ－cos2θ1＋sin2θ＋cos2θ.考点 应用二倍角公式化简求值 题点 利用二倍角公式化简三角函数式 解 方法一 原式＝－cos 2θ＋sin 2θ＋cos 2θ＋sin 2θ＝2sin 2θ＋2sin θcos θ2cos 2θ＋2sin θcos θ＝2sin θθ＋cos θ2cos θθ＋sin θ＝tan θ.方法二 原式＝θ＋cos θ2－2θ－sin 2θθ＋cos θ2＋2θ－sin 2θ＝θ＋cos θθ＋cos θ－θ－sin θθ＋cos θθ＋cos θ＋θ－sin θ＝2sin θ2cos θ＝tan θ.(2)求证：4sin αcos α1＋cos2α·cos 2αcos 2α－sin 2α＝tan2α. 考点 三角恒等式的证明 题点 三角恒等式的证明证明 左边＝2sin 2α2cos 2α·cos 2αcos 2α＝tan 2α＝右边． 反思与感悟 三角函数式化简、证明的常用技巧 (1)特殊角的三角函数与特殊值的互化．(2)对于分式形式，应分别对分子、分母进行变形处理，有公因式的提取公因式后进行约分． (3)对于二次根式，注意二倍角公式的逆用． (4)利用角与角之间的隐含关系，如互余、互补等．(5)利用“1”的恒等变形，如tan 45°＝1，sin 2α＋cos 2α＝1等． 跟踪训练3 α为第三象限角，则1＋cos2αcos α－1－cos2αsin α＝________.考点 应用二倍角公式化简求值 题点 利用二倍角公式化简三角函数式 答案 0解析∵α为第三象限角，∴cosα<0，sinα<0，∴1＋cos2αcosα－1－cos2αsinα＝2cos2αcosα－2sin2αsinα＝－2cosαcosα－－2sinαsinα＝0.1．(2017·山东)已知cos x ＝34，则cos2x 等于( )A ．－14B.14C ．－18D.18考点 二倍角的正弦、余弦、正切公式 题点 利用二倍角公式求二倍角的余弦值 答案 D解析 cos2x ＝2cos 2x －1＝2×⎝ ⎛⎭⎪⎫342－1＝18.故选D.2．sin15°sin75°的值是( ) A.12B.32C.14D.34考点 二倍角的正弦、余弦、正切公式 题点 利用二倍角公式求二倍角的正弦值 答案 C解析 sin15°sin75°＝sin15°cos15°＝12sin30°＝14.3．sin4π12－cos 4π12等于( ) A ．－12B ．－32C.12D.32考点 应用二倍角公式化简求值 题点 利用余弦的二倍角公式化简求值 答案 B 解析 原式＝⎝⎛⎭⎪⎫sin 2π12＋cos 2π12·⎝ ⎛⎭⎪⎫sin 2π12－cos 2π12 ＝－⎝⎛⎭⎪⎫cos2π12－sin 2π12＝－cos π6＝－32. 4.3tanπ81－tan2π8＝________.考点 应用二倍角公式化简求值题点 利用正切的二倍角公式化简求值 答案 32解析 原式＝32×2tanπ81－tan2π8＝32tan ⎝ ⎛⎭⎪⎫2×π8＝32tan π4＝32. 5．证明：sin α＋11＋sin α＋cos α＝12tan α2＋12.考点 三角恒等式的证明 题点 三角恒等式的证明证明 ∵左边＝2tanα21＋tan2α2＋11＋2tan α21＋tan 2 α2＋1－tan2α21＋tan2α2＝tan2α2＋2tan α2＋11＋tan 2α2＋2tan α2＋1－tan2α2＝⎝ ⎛⎭⎪⎫tan α2＋122tan α2＋2＝12⎝ ⎛⎭⎪⎫tan α2＋1＝12tan α2＋12＝右边， ∴原等式成立．1．对于“二倍角”应该有广义上的理解，如：8α是4α的二倍；6α是3α的二倍；4α是2α的二倍；3α是32α的二倍；α2是α4的二倍；α3是α6的二倍；α2n 是α2n ＋1的二倍(n ∈N *)．2．二倍角余弦公式的运用在二倍角公式中，二倍角的余弦公式最为灵活多样，应用广泛．常用形式：①1＋cos2α＝2cos 2α；②cos 2α＝1＋cos2α2；③1－cos2α＝2sin 2α；④sin 2α＝1－cos2α2.一、选择题1．已知α是第三象限角，cos α＝－513，则sin2α等于( )A ．－1213B.1213C ．－120169D.120169考点 二倍角的正弦、余弦、正切公式 题点 利用二倍角公式求二倍角的正弦值 答案 D解析 由α是第三象限角，且cos α＝－513，得sin α＝－1213，所以sin 2α＝2sin αcos α＝2×⎝ ⎛⎭⎪⎫－1213×⎝ ⎛⎭⎪⎫－513＝120169，故选D.2．(2017·全国Ⅲ)已知sin α－cos α＝43，则sin2α等于( )A ．－79B ．－29C.29D.79考点 应用二倍角公式化简求值 题点 利用正弦的二倍角公式化简求值 答案 A解析 ∵sin α－cos α＝43，∴(sin α－cos α)2＝1－2sin αcos α＝1－sin2α＝169，∴sin2α＝－79.故选A.3．已知α为锐角，且满足cos2α＝sin α，则α等于( ) A ．30°或60° B ．45° C ．60°D ．30°考点 应用二倍角公式化简求值 题点 利用余弦的二倍角公式化简求值答案 D解析 因为cos2α＝1－2sin 2α，故由题意，知2sin 2α＋sin α－1＝0，即(sin α＋1)(2sin α－1)＝0.因为α为锐角，所以sin α＝12， 所以α＝30°.故选D.4．已知x ∈⎝ ⎛⎭⎪⎫－π2，0，cos x ＝45，则tan2x 等于( ) A.724B ．－724C.247D ．－247考点 二倍角的正弦、余弦、正切公式题点 利用二倍角公式求二倍角的正切值答案 D解析 由cos x ＝45，x ∈⎝ ⎛⎭⎪⎫－π2，0，得sin x ＝－35， 所以tan x ＝－34， 所以tan2x ＝2tan x 1－tan 2x ＝2×⎝ ⎛⎭⎪⎫－341－⎝ ⎛⎭⎪⎫－342＝－247，故选D. 5.2－sin 22＋cos4的值是( )A ．sin2B ．－cos2 C.3cos2D ．－3cos2考点 应用二倍角公式化简求值题点 利用余弦的二倍角公式化简求值答案 D解析 原式＝1＋cos 22＋2cos 22－1＝3cos 22＝－3cos2. 6．函数f (x )＝cos2x ＋6cos ⎝ ⎛⎭⎪⎫π2－x 的最大值为( ) A ．4B ．5C ．6D ．7考点 应用二倍角公式化简求值题点 综合应用二倍角公式化简求值答案 B解析 f (x )＝1－2sin 2x ＋6sin x ＝－2⎝⎛⎭⎪⎫sin x －322＋112，所以当sin x ＝1时，f (x )的最大值为5.7．已知α为第二象限角，sin α＋cos α＝33，则cos2α等于( ) A ．－53B ．－59C.59D.53 考点 应用二倍角公式化简求值题点 综合应用二倍角公式化简求值答案 A解析 由题意得(sin α＋cos α)2＝13， ∴1＋sin 2α＝13，sin 2α＝－23. ∵α为第二象限角，∴cos α－sin α<0.又∵sin α＋cos α>0，∴cos α<0，sin α>0，且|cos α|<|sin α|，∴cos 2α＝cos 2α－sin 2α<0，∴cos 2α＝－1－sin 22α ＝－1－⎝ ⎛⎭⎪⎫－232＝－1－49＝－53，故选A. 二、填空题8．sin6°sin42°sin66°sin78°＝________. 考点 应用二倍角公式化简求值题点 利用正弦的二倍角公式化简求值答案 116解析 原式＝sin6°cos48°cos24°cos12° ＝sin6°cos6°cos12°cos24°cos48°cos6° ＝sin96°16cos6°＝cos6°16cos6°＝116. 9．已知θ∈(0，π)，且sin ⎝⎛⎭⎪⎫θ－π4＝210，则tan2θ＝________. 考点 二倍角的正弦、余弦、正切公式题点 利用二倍角公式求二倍角的正切值答案 －247解析 由sin ⎝ ⎛⎭⎪⎫θ－π4＝210， 得22(sin θ－cos θ)＝210，即sin θ－cos θ＝15.解方程组⎩⎪⎨⎪⎧sin θ－cos θ＝15，sin 2θ＋cos 2θ＝1，得⎩⎪⎨⎪⎧ sin θ＝45，cos θ＝35或⎩⎪⎨⎪⎧ sin θ＝－35，cos θ＝－45.因为θ∈(0，π)，所以sin θ>0，所以⎩⎪⎨⎪⎧sin θ＝－35cos θ＝－45不合题意，舍去，所以tan θ＝43，所以tan2θ＝2tan θ1－tan 2θ＝2×431－⎝ ⎛⎭⎪⎫432＝－247.10．若1＋tan α1－tan α＝2018，则1cos2α＋tan2α＝________.考点 应用二倍角公式化简求值题点 综合应用二倍角公式化简求值答案 2018解析 1cos2α＋tan2α＝1cos2α＋sin2αcos2α＝1＋sin2αcos2α＝α＋sin α2cos 2α－sin 2α＝cos α＋sin αcos α－sin α＝1＋tan α1－tan α＝2018.11．已知tan θ2＝3，则1－cos θ＋sin θ1＋cos θ＋sin θ＝________.考点 应用二倍角公式化简求值题点 综合应用二倍角公式化简求值答案 3解析 1－cos θ＋sin θ1＋cos θ＋sin θ＝2sin 2θ2＋2sin θ2cos θ22cos 2θ2＋2sin θ2cos θ2 ＝2sin θ2⎝ ⎛⎭⎪⎫sin θ2＋cos θ22cos θ2⎝⎛⎭⎪⎫cos θ2＋sin θ2＝tan θ2＝3. 三、解答题12．(2017·山东青岛城阳一中期中考试)已知3sin β＝sin(2α＋β)，且α≠k π2，α＋β≠π2＋k π(k ∈Z )，求证：tan(α＋β)＝2tan α. 考点 三角恒等式的证明题点 三角恒等式的证明证明 因为sin β＝sin[(α＋β)－α]＝sin(α＋β)cos α－cos(α＋β)sin α； sin(2α＋β)＝sin[(α＋β)＋α]＝sin(α＋β)cos α＋cos(α＋β)·sin α，所以3sin(α＋β)cos α－3cos(α＋β)sin α＝sin(α＋β)cos α＋cos(α＋β)sin α， 即sin(α＋β)cos α＝2cos(α＋β)sin α.又α≠k π2，α＋β≠π2＋k π(k ∈Z )， 所以cos α≠0，cos(α＋β)≠0.于是等式两边同除以cos(α＋β)·cos α，得tan(α＋β)＝2tan α.13．化简：＋sin α＋cos α⎝⎛⎭⎪⎫sin α2－cos α22＋2cos α(180°<α<360°)．考点 应用二倍角公式化简求值题点 综合应用二倍角公式化简求值解 原式＝⎝ ⎛⎭⎪⎫2cos 2α2＋2sin α2cos α2⎝ ⎛⎭⎪⎫sin α2－cos α24cos 2α2＝2cos α2⎝ ⎛⎭⎪⎫cos α2＋sin α2⎝ ⎛⎭⎪⎫sin α2－cos α22⎪⎪⎪⎪⎪⎪cos α2＝cos α2⎝ ⎛⎭⎪⎫sin 2α2－cos 2α2⎪⎪⎪⎪⎪⎪cos α2＝－cos α2cos α⎪⎪⎪⎪⎪⎪cos α2. 因为180°<α<360°，所以90°<α2<180°， 所以cos α2<0，所以原式＝cos α. 四、探究与拓展14．等腰三角形一个底角的余弦值为23，那么这个三角形顶角的正弦值为________． 考点 应用二倍角公式化简求值题点 利用正弦的二倍角公式化简求值答案 459解析 设A 是等腰△ABC 的顶角，则cos B ＝23， sin B ＝1－cos 2B ＝1－⎝ ⎛⎭⎪⎫232＝53. 所以sin A ＝sin(180°－2B )＝sin2B＝2sin B cos B ＝2×53×23＝459. 15．已知函数f (x )＝cos ⎝⎛⎭⎪⎫2x ＋π3＋sin 2x －cos 2x ＋23sin x cos x . (1)化简f (x )；(2)若f (α)＝17，2α是第一象限角，求sin2α. 考点 应用二倍角公式化简求值题点 综合应用二倍角公式化简求值解 (1)f (x )＝12cos2x －32sin2x －cos2x ＋3sin2x ＝32sin2x －12cos2x ＝sin ⎝⎛⎭⎪⎫2x －π6. (2)f (α)＝sin ⎝⎛⎭⎪⎫2α－π6＝17，2α是第一象限角， 即2k π<2α<π2＋2k π(k ∈Z )，∴2k π－π6<2α－π6<π3＋2k π(k ∈Z )， ∴cos ⎝⎛⎭⎪⎫2α－π6＝437， ∴sin2α＝sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫2α－π6＋π6 ＝sin ⎝ ⎛⎭⎪⎫2α－π6·cos π6＋cos ⎝⎛⎭⎪⎫2α－π6·sin π6 ＝17×32＋437×12＝5314.。

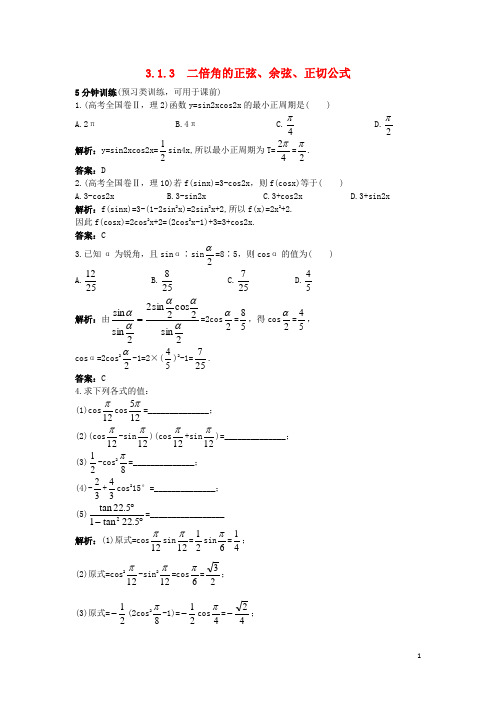
3.1.3 二倍角的正弦、余弦、正切公式5分钟训练(预习类训练，可用于课前)1.(高考全国卷Ⅱ，理2)函数y=sin2xcos2x 的最小正周期是( )A.2πB.4πC.4π D.2π 解析：y=sin2xcos2x=21sin4x,所以最小正周期为T=42π=2π.答案：D2.(高考全国卷Ⅱ，理10)若f(sinx)=3-cos2x ，则f(cosx)等于( )A.3-cos2xB.3-sin2xC.3+cos2xD.3+sin2x解析：f(sinx)=3-(1-2sin 2x)=2sin 2x+2,所以f(x)=2x 2+2.因此f(cosx)=2cos 2x+2=(2cos 2x-1)+3=3+cos2x. 答案：C3.已知α为锐角，且sinα∶sin 2α=8∶5，则cosα的值为( ) A.2512 B.258 C.257 D.54 解析：由2sin2cos2sin 22sin sin ααααα==2cos 2α=58，得cos 2α=54， cosα=2cos 22α-1=2×(54)2-1=257. 答案：C4.求下列各式的值：(1)cos 12πcos 125π=______________； (2)(cos 12π-sin 12π)(cos 12π+sin 12π)=______________；(3)21-cos 28π=______________； (4)-32+34cos 215°=______________；(5)︒-︒5.22tan 15.22tan 2=_________________解析：(1)原式=cos 12πsin 12π=21sin 6π=41；(2)原式=cos212π-sin 212π=cos 6π=23； (3)原式=21-(2cos 28π-1)=21-cos 4π=42-；(4)-32+34cos 215°=32(2cos 215°-1)=32cos30°=33；(5)原式=21tan45°=21. 答案：(1)41 (2)23 (3)42- (4)33 (5)2110分钟训练(强化类训练，可用于课中) 1.若tanx=2，则tan2(x-4π)等于( ) A.34 B.-34 C.43 D.43- 解析：tan(2x-2π)=-tan(2π-2x)=-cot2x=x 2tan 1-,而tan2x=4122-⨯=-34,∴原式=43.答案：C2.当0＜x ＜2π时，函数f(x)=x x x 2sin sin 82cos 12++的最小值为( )A.2B.32C.4D.34解析：f(x)=x x x x cos sin 2sin 8cos 222+=x tan 1+4tanx≥42=4，当且仅当tanx=21时，取“=”.答案：C3.化简cos72°cos36°=________________. 解析：原式=︒︒=︒︒︒=︒︒•︒︒36sin 4144sin 36sin 472sin 72cos 236sin 236sin 236cos 72cos =41. 答案：414.在△ABC 中，tanA+tanB+33+tanAtanB 且sinAcosA=43，判断三角形的形状. 解：由sinAcosA=43，得21sin2A=43，即sin2A=23， ∴2A=60°或120°.∴A=30°或60°.又由tanA+tanB=3-(1-tanAtanB)，得tan(A+B)=3tan tan 1)tan tan 1(3-=---BA B A ，∴A+B=120°.当A=30°时，B=90°，tanB 无意义，∴A=60°,B=60°，即三角形为等边三角形. 5.平面上两塔相距120 m ，一人分别在两塔的底部测得一塔顶的仰角为另一塔顶仰角的2倍，又在两塔底的连线中点测得两塔顶的仰角互余.求两塔的高.解析：如图所示，设两塔的高分别为x m 、y m ，且∠ADB=α，∠AMB=θ.由题意，得∠CBD=2α，∠AMC=90°， ∠AMB=∠MCD=θ， 所以x=60tanθ，y=θtan 60， x=120tan α，y=120tan2α.所以⎪⎪⎩⎪⎪⎨⎧-==.12012,360022x x y xy 解得x=40，y=90.答：两塔高分别是90 m 和40 m.6.(2006高考北京卷，理15)已知函数f(x)=xx cos )42sin(21π--， (1)求f(x)的定义域；(2)设α是第四象限的角，且tanα=-34，求f(α)的值. 解：(1)由cosx≠0,得x≠kπ+2π(k ∈Z ). 故f(x)的定义域为{x|x≠kπ+2π,k ∈Z }.(2)因为tanα=54-,cosα=53，且α为第四象限的角，所以sinα=54-,cosα=53.故f(α)=αααααααπαcos 2cos 2sin 1cos )2cos 222sin 22(21cos )42sin(21+-=--=--=ααααcos cos sin 2cos 22-=2(cosα-sinα)=514. 30分钟训练(巩固类训练，可用于课后) 1.已知θ是第三象限的角，若sin 4θ+cos 4θ=95，那么sin2θ等于( ) A.322 B.322- C.32 D.-32解析：(sin 2θ+cos 2θ)2=sin 4θ+cos 4θ+2sin 2θcos 2θ=sin 4θ+cos 4θ+21(sin2θ)2，而(sin 2θ+cos 2θ)2=1，可以得到sin2θ=±322，又由于θ是第三象限的角，所以sin2θ=322. 答案：A2.已知tanα=71，tanβ=2π，0＜α＜β＜2π,则α+2β等于( ) A.45π B.4π C.45π或4π D.47π解析：∵tan2β=43tan 1tan 2=-ββ，∴tan(α+2β)=28314371-+=1.∵tanα=71＜1,∴0＜α＜4π.tan2β=43＜1,∴0＜2β＜4π.∴0＜α+2β＜43π.∴α+2β=4π.答案：B3.(2006高考上海卷，理17)求函数y=2cos(x+4π)cos(x-4π)+3sin2x 的值域和最小正周期.解：y=2(cosxcos4π-sinxsin 4π)(cosxcos 4π-sinxsin 4π)+3sin2x =cos 2x-sin 2x+3sin2x=cos2x+3sin2x=2sin(2x+6π).∴原函数的值域是［-2,2］，周期T=22π=π. 4.化简︒-+︒+10sin 110sin 1. 解：原式=︒︒-︒+︒+︒︒+︒+︒5cos 5sin 25cos 5sin 5cos 5sin 25cos 5sin 2222=|sin5°+cos5°|+|sin5°-cos5°|=sin5°+cos5°+cos5°-sin5°=2cos5°. 5.求sin10°sin30°sin50°sin70°的值.解：原式=21cos20°cos40°cos80° =︒︒︒=︒︒︒=︒︒︒︒︒20sin 1680cos 80sin 2880cos 40cos 40sin 220sin 480cos 40cos 20cos 20sin 2 =16120sin 16160sin =︒︒. 6.已知sin 22α+sin2αcos α-cos2α=1，α∈(0,2π)，求sin α,tan α.解：由题意知4sin 2αcos 2α+2sin αcos 2α-2cos 2α=0，即2cos 2α(2sin α-1)(sin α+1)=0. 又α∈(0,2π)，∴sinα+1≠0,cos 2α≠0. 由2sin α-1=0得sin α=21，∴α=6π,tan α=33.7.已知sin(α-4π)=1027，cos2α=257，求sin α及tan(α+3π).解：由sin(α-4π)=1027,得22(sin α-cos α)=1027，即sin α-cos α=57. ① 又由cos2α=257得cos 2α-sin 2α=257，即(cos α+sin α)(cos α-sin α)=257，∴cosα+sin α=-51. ②由①②得sin α=53，cos α=54-,∴tanα=-43.tan(α+3π)=1132548343344331433tan 313tan -=+-=+-=-+αα. 8.当x∈［-2π,2π］时，求f(x)=sin 2x+2sinxcosx+3cos 2x 的周期、最大值及此时的x 值. 解：f(x)=1+cos2x+1+sin2x=2sin(2x+4π)+2.周期T=π.当x ∈［-2π,2π］时，2x+4π∈［-43π,45π］,sin(2x+4π)∈［-1,1］. ∴f(x)∈［22-,22+］.∴f(x)max =22+.由2x+4π=2k π+2π得x=k π+8π. 又∵x∈［-2π,2π］，∴x=8π,即当x=8π时，f(x)的最大值为22+.9.(2006高考安徽卷，理17)已知43π＜α＜π,tanα+cosα=310-.(1)求tanα的值；(2)求)4sin(282cos 112cos2sin82sin 522πααααα--++的值.解：(1)∵tanα+cosα=310-,∴3tan 2α+10tanα+3=0,解得tanα=-31或tanα=-3.∵43π＜α＜π,∴-1＜tanα＜0.∴tanα=-31.(2)∵tanα=-31,∴)4(sin 282cos 112cos2sin82sin 522παααααα--++=451tan 3tan 4cos sin 82cos 16sin 4)2cos 2(sin 522-=-+=--+•+++αααααααα. 10.(2006高考四川卷，理17)已知A 、B 、C 是△ABC 三内角，向量m =(-1,3)，n =(cosA,sinA),且m ·n =1. (1)求角A ； (2)若BB B22sin cos 2sin -+1=-3，求tanC. 解：(1)∵m ·n =1,∴(-1,3)·(cosA,sinA)=1,即3sinA-cosA=1,2(sinA·23-cosA·21)=1,sin(A-6π)=21. ∵0＜A ＜π,-6π＜A-6π＜65π,∴A-6π=6π.∴A=3π.(2)由题知BB B B 22sin cos cos sin 21-+=-3，整理得sin 2B-sinBcosB-2cos 2B=0. ∵cosB≠0,∴tan 2B-tanB-2=0. ∴tanB=-2或tanB=-1.而tanB=-1使cos 2B-sin 2B=0，舍去. ∴tanB=2.∴tanC=tan［π-(A+B)］=-tan(A+B)=11358321322tan tan 1tan tan +=-+⨯-=-+-B A B A .。

【2019最新】高中数学第三章三角恒等变换3-1两角和与差的正弦余弦和正切公式3-1-3二倍角的正弦余弦正切公式一课后集训 二倍角的正弦、余弦、正切公式 1课后集训基础达标1.sin 212π-cos 212π等于（ ） A.23 B.43 C.-23 D.43- 解析：原式=-（cos 212π-sin 212π）=-cos 6π=-23.∴应选C. 答案：C 2.已知sin α+cos α=31，则sin2α的值是（ ） A.98 B.-98 C.917 D.-917 解析：将sin α+cos α=31两边平方得：1+sin2α=91，∴sin2α=-98.应选B. 答案：B 3.︒--︒+100cos 1100cos 1等于（ ）A.-2cos5°B.2cos5°C.-2sin5°D.2sin5° 解析：︒-︒=︒--︒+50sin 250cos 2100cos 1100cos 122 =2(cos50°-sin50°) =2×2（cos45°cos50°-sin45°sin50°）=2cos95°=-2sin5°.∴应选C.答案：C4.sin15°sin30°sin75°的值等于（ ） A.43 B.83 C.81 D.41 解析：原式=sin15°·sin30°·cos15° =21·sin30°·（2sin15°·cos15°）=41·sin30°=81. 答案：C 5.cos5π·cos π52的值等于（ ） A.41 B.21 C.2 D.4 解析：原式=5sin 252cos 5cos 5sin 2ππππ∙∙ =.415sin 254sin 2115sin 252cos 5sin ==∙2πππππ ∴应选A.答案：A6.cos （α+β）cos β+sin （α+β）sin β=53，则cos2α等于（ ） A.257 B.2518 C.257- D.2518- 解析：由cos （α+β）cos β+sin （α+β）sin β=53 得：cos α=53. ∴cos2α=2cos 2α-1=2×259-1=-257， ∴应选C.答案：C综合运用7.设f （tanx ）=tan2x ，则f （2）的值等于（ ） A.54 B.-34 C.32- D.4 解析：∵f（tanx ）=xx 2tan 1tan 2-， ∴f（2）=22122-⨯=-34. ∴应选B.答案：B8.(2005全国Ⅲ，8)αααα2cos cos 2cos 12sin 22∙+等于（ ） A.tan α B.tan2α C.1 D.21解析：原式=αααααα2cos 2sin 2cos cos cos 22sin 222=∙=tan2α. 答案：B9.已知sin （θ-4π）=53，则θθ22tan 1tan 1-+等于（ ） A.2425 B.±2425 C.2524 D.±2524 解析：∵θθθθθθθθθ2cos 1cos sin cos cos sin cos tan 1tan 122222222=-+=-+， 由sin （θ-4π）=53， 得22（sin θ-cos θ）=53， 两边平方得：sin2θ=257，∴cos2θ=±2524. ∴原式=252425241±=±. 故应选B.答案：B拓展探究10.化简cos α·cos 2α·cos 22α·cos 32α·…·cos 12-n α. 解析：只要注意到每相邻两角之间具有倍数关系，变用二倍角正弦公式即可. 解：原式同乘除因式sin 12-n α，然后逐次使用倍角公式解得原式=12sin 22sin -n n a α. 备选习题11.已知sin （x-4π)=-31，则sin2x 的值等于（ ） A.911 B.97 C.-911 D.97- 解析：由于sin2x=cos （2π-2x ） =cos2（4π-x ）=cos2（x-4π）4=1-2×（31-）2=97. ∴应选B.答案：B12.函数y=sin （x-6π）cosx 的最小值是_______________. 解析：y=sin （x-6π）cosx =（sinx·cos 6π-cosx·sin 6π）cosx =23sinxcosx-21cos 2x =43sin2x-41（1+cos2x ） =43sin2x-41cos2x-41 =21（23sin2x-21cos2x ）-41 =21sin （2x-6π）-41. ∴函数最小值为43-. 答案：43- 13.（1）已知sinx=215-，求sin2（x-4π）的值. （2）已知sin α+cos α=33（0＜α＜π），求cos2α的值. （3）已知sin （4π-α）sin （4π+α）=62（0＜α＜2π），求sin2α的值. 解析：（1）sin2（x-4π） =sin （2x-2π）2=-cos2x=2sin 2x-1=2（215-）2-1=2-5.（2）由sin α+cos α=33得（sin α+cos α）2=31，∴2sin αcos α=32-.又0＜α＜π，∴sin α＞0，cos α＜0.∵（sin α-cos α）2=1-2sin αcos α =1+3532=，∴sin α-cos α=315.∴cos2α=cos 2α-sin 2α=（cos α+sin α）（cos α-sin α） =-315×33=35-.（3）∵sin（4π-α）=sin ［2π-（4π+α）］=cos （4π+α） ∴62=sin （4π-α）sin （4π+α）=sin （4π+α）cos （4π+α） =21sin （2π+2α）=21cos2α.∴cos2α=32.∵0＜α＜2π，∴0＜2α＜π.∴sin2α=37)2(cos 12=-α. 14.化简：)4(sin )4tan(21cos 222απαπα+--. 解：原式=)4(cos )4cos()4sin(21cos 222απαπαπα-∙--- =.12cos 2cos 2cos 1cos 2)4cos()4sin(21cos 222==-=-∙--αααααπαπα 15.已知tan （α+4π）=2，则cos2α+3sin 2α+tan2α=______________. 解析：∵tan（α+4π）=1+ααtan 1tan 1-+=2， ∴tan α=31. 于是cos2α+3sin 2α+tan2α=cos 2α-sin 2α+3sin 2α+αα2tan 1tan 2- =cos 2α+2sin 2α+911312-⨯=20374391191219832tan 1tan 2122=++⨯+=+++αα. 答案：2037 16.已知cos （4π+α）=53，π1217＜α＜47π，求αααtan 1)tan 1(2sin -+的值. 解：sin2α=-cos （2π+2α） =-cos ［2（4π+α）］=-［2cos 2（4π+α）-1］=-［2×（53）2-1］=257， απαπααtan 4tan 1tan 4tan tan 1tan 1-+=-+ =tan （4π+α）.∵π1217＜α＜47π，∴35π＜4π+α＜2π. ∴sin（4π+α）=-54. ∴tan（4π+α）=-34. ∴7528)34(257tan 1)tan 1(2sin -=-⨯=-+ααα.。

3.1.3 二倍角的正弦、余弦、正切公式（二）课堂导学三点剖析1.二倍角公式在证明题中的应用【例1】 求证:x x cos 22sin （1+tanx·tan 2x ）=tanx. 思路分析：本题的目标是把等式的左端统一成角x 的正切函数.可能用的公式有sin2x=2sinxcosx ，tan 2x =x x x x x x x sin cos 12cos 2sin 22sin 22cos 2sin2-==. 证法1：左端=x x x cos 2cos sin 2（1+xx x x sin cos 1cos sin -•) =sinx （1+xx cos cos 1-） =xx cos sin =tanx=右端. 证法2：左端=x x x x x x x x x x x x x x x cos sin 2tan 2cos cos 2sin cos 2cos sin 2)2tan(2tan tan cos 22sin =••=--• =x x cos sin =tanx=右端. 温馨提示证明恒等式就是要根据所证等式两端的特征（结构、名称、角度等）来选择最佳方法，本题就是抓住左右两端的次数差异作为突破口，使问题得以解决.2.二倍角公式在化简题中的应用【例2】 已知函数f （x ）=cos 4x-2sinxcosx-sin 4x.（1）求f （x ）的最小正周期；（2）若x∈［0，2π］，求f （x ）的最大值，最小值. 解：（1）因为f （x ）=cos 4x-2sinxcosx-sin 4x=（cos 2x+sin 2x ）（cos 2x-sin 2x ）-sin2x =cos2x-sin2x=2cos （2x+4π），所以f （x ）的最小正周期T=22π=π. （2）因为0≤x≤2π，所以4π≤2x+4π≤π45. 当2x+4π=4π时，cos （2x+4π）取得最大值22； 当2x+4π=π时，cos （2x+4π）取得最小值-1. 所以f （x ）在［0，2π］上的最大值为1， 最小值为2-.温馨提示（1）将cos2x-sin2x 变形为sin （4π-2x ），也会有同样的结果; （2）像这类高次三角函数，首先利用倍角公式通过降幂化为y=Asin （ωx+φ）或y=Acos （ωx+φ）（A ，ω，φ均为常数，A ＞0）的形式，然后再求周期和最值.3.公式的综合、灵活运用【例3】 已知函数f （x ）=3-sin 2x+sinxcosx （1）求f （625π）的值； （2）设α∈（0，π），f （2α）=41-23，求sinα的值 解：（1）∵sin 625π=21，cos 625π=23， ∴f（625π）=-3sin 2625π+sin 625πcos 625π=0 （2）f （x ）=23cos2x-23+21sin2x ∴f（2α）=23cos α+21sin α-23=41-23， 16sin 2α-4sin α-11=0解得sin α=8531±. ∵α∈（0，π），∴sinα＞0故sinα=8531+ 温馨提示要注意公式变形的重要性，不能死记公式，更不能只会正用，同时逆用、变形也要学会只有灵活运用公式，才能灵活解决问题各个击破类题演练1求证：3+cos4α-4cos2α=8sin 4α.证法1：∵左边=2+1+cos4α-4cos2α=2+2cos 22α-4cos2α=2（cos 22α-2cos2α+1）=2（cos2α-1）2=2（-2sin 2α）2=8sin 4α=右边.∴等式成立.证法2：右边=2×4sin 4α=2（1-cos2α）2=2（1-2cos2α+cos 22α）=2-4cos2α+2cos 22α =2-4cos2α+1+cos4α=3+cos4α-4cos2α=左边.∴等式成立.变式提升1 求证:.tan 14cos 4sin 1tan 24cos 4sin 12θθθθθθ-++=-+ 证明：左边=θθθtan 24sin )4cos 1(+- =θθθθθcos sin 22cos 2sin 22sin 22+=θθθθθsin sin cos 2)2cos 2(sin 2+ =2cos 2θ（sin2θ+cos2θ） 右边=θθθ2tan 14sin )4cos 1(-++ =θθθθθθ2222cos sin cos 2cos 2sin 22cos 2•-+ =θθθθθ2cos 2cos )2sin 2(cos 2cos 2•+ =2cos 2θ（sin2θ+cos2θ）∴左边=右边，故等式成立.类题演练2设函数f （x ）=sin 2x+3sinxcosx+α， （1）写出函数f （x ）的单调递增区间;（2）求f （x ）的最小正周期.解：（1）f （x ）=2322cos 1+-x sin2x+a =23sin2x-21cos2x+a+21 =sin （2x-6π）+a+21, 2k π-2π≤2x -6π≤2kπ+2π，k∈Z ， k π-6π≤x≤kπ+3π,k∈Z , ∴f（x ）的单调递增区间是［kπ-6π，kπ+3π］，k∈Z （2）T=222πωπ==π， ∴f（x ）的最小正周期为π.变式提升2已知函数y=sin2x-2（sinx+cosx ）+a 2设t=sinx+cosx ，t 为何值时，函数y 取得最小值；解：∵t=sinx+cosx=2sin （x+4π），-2≤t≤2， ∴t 2=1+2sinxcosx=1+sin2x ，sin2x=t 2-1，∴y=t 2-1-2t+a 2=（t-1）2+a 2-2∵-2≤t≤2，∴当t=1时，函数y 取得最小值a 2-2类题演练3 已知α为第二象限角，且sinα=415，求12cos 2sin )4sin(+++ααπα的值. 解：∵sinα=415，α为第二象限角，∴cosα=-41. ∴sin2α=2sinαcosα=815-. ααπαπαααπα2cos 22sin 4sin cos 4cos sin 12cos 2sin )4sin(++=+++ =151230)41(28152241224152--=-⨯+-⨯-⨯ =.2151)115(2-=--变式提升3函数f （x ）=sin 2（x+4π）-sin 2（x-4π）是（ ） A.周期为π的偶函数 B.周期为π的奇函数C.周期为2π的偶函数D.周期为2π的奇函数解析：f （x ）=2)22cos(12)22cos(1ππ---+-x x =22sin 122sin 1x x --+=sin2x.∴T=22 =π,f（x ）为奇函数. 答案：B。

3.1.3 二倍角的正弦、余弦、正切公式互动课堂疏导引导1.二倍角公式(1)二倍角公式的正弦、余弦、正切公式sin2α=2sin αcos α,(S 2α)cos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α,(C 2α)tan2α=αα2tan 1tan 2-,(T 2α) 这组公式要记准、记熟、用活.下面给出这组公式的推导:∵sin(α+β)=sin αcos β+cos αsin β,当α=β时,有sin2α=2sin αcos α.∵cos(α+β)=cos αcos β-sin αsin β,当α=β时,有cos2α=cos 2α-sin 2α=2cos 2α-1(sin 2α=1-cos 2α)=1-2sin 2α(cos 2α=1-sin 2α).∵tan(α+β)=βαβαtan tan 1tan tan -+, 当α=β时,有tan2α=αα2tan 1tan 2-. 公式S 2α、C 2α中,α∈R ,公式T 2α中的α≠21k π+4π且α≠k π+2π (k∈Z ). 从上面的公式推导中可以看到二倍角公式是和角公式的特殊情况.(2)关于倍角公式应注意的几个问题:①推导思路:在正弦、余弦、正切的和角公式中,令两角相等,就得相应倍角公式.由此,倍角公式是和角公式的特例.②公式的适用范围:公式S 2α、C 2α中,角α可以为任意角,但公式T 2α只有当α≠2π+k π及α≠4π+2πk (k∈Z )时才成立,否则不成立.当α=2π+k π,k∈Z ,虽然tan α的值不存在,但tan2α的值是存在的,这时求tan2α的值可利用诱导公式.③对于“二倍角”要有广义理解,如4α是2α的2倍;α作为2α的2倍;2α作为4α的2倍;3α作为23α的2倍;3α作为6α的2倍等. 2.二倍角公式的变形(1)公式逆用2sin αcos α=sin2α,sin αcos α=21sin2α,cos α=ααsin 22sin 2,cos 2α-sin 2α=cos2α,αα2tan 1tan 2-=tan2α. (2)公式的逆向变换及有关变形1±sin2α=sin 2α+cos 2α±2sin αcos α=(sin α±cos α)2,1+cos2α=2cos 2α,1-cos2α=2sin 2α,cos 2α=22cos 1α+,sin 2α=22cos 1α-. 活学巧用1.已知sin α+cos α=31,且0＜α＜π,求sin2α、cos2α、tan2α的值. 解析:方法一:∵sin α+cos α=31,∴sin 2α+cos 2α+2sin αcos α=91.∴sin2α=98-且sin αcos α=94-＜0. ∵0＜α＜π,sin α＞0,∴cos α＜0.∴sin α-cos α＞0.∴sin α-cos α=3172sin 1)cos (sin 2=-=-ααα. ∴cos2α=cos 2α-sin 2α=(sin α+cos α)(cos α-sin α)=31×(-317)=917-. tan2α=171782cos 2sin =αα. 方法二:∵sin α+cos α=31,平方得sin αcos α=94-, ∴sin α、cos α可看成方程x 2-31x 94-=0的两根, 解方程x 2-31x 94-=0,得x 1=6171+,x 2=6171-.∵α∈(0,π),∴sin α＞0.∴sin α=6171+, cos α=6171-.∴sin2α=2sin αcos α=98-,cos2α=cos 2α-sin 2α=917-,tan2α=171782cos 2sin =αα. 答案:sin2α=98-,cos2α=917-,tan2α=17178. 2.已知函数f(x)=cos 4x-2sinxcosx-sin 4x.(1)求f(x)的最小正周期;(2)若x∈［0, 2π］,求f(x)的最大值、最小值. 解析:f(x)=(cos 2x+sin 2x)(cos 2x-sin 2x)-sin2x =cos2x-sin2x=2cos(2x+4π). (1)T=22π=π. (2)0≤x≤2π,0≤2x≤π,4π≤2x+4π≤45π,-1≤cos(2x+4π)≤22,∴-2≤2cos(2x+4π)≤1.∴f(x)max =1,f(x)min =-2.答案:(1)π;(2)f(x)max =1,f(x)min =-2.3.已知函数y=21cos 2x+23sinxcosx+1,x∈R .当函数y 取得最大值时,求自变量x 的集合. 解析:y=21cos 2x+23sinxcosx+1=41(2cos 2x-1)+41+43(2sinxcosx)+1 =21(cos2xsin 6π+sin2xcos 6π)+45=21sin(2x+6π)+45.y 取得最大值必须且只需2x+6π=2π+2k π,k∈Z ,即x=6π+k π,k∈Z .所以量x 的集合为{x|x=6π+k π,k∈Z }.。

3.1.2 两角和与差的正弦21．两角和与差的正弦公式两角和的正弦公式：sin(α＋β)＝sin αcos β＋cos αsin β，(Sα＋β)两角差的正弦公式：sin(α－β)＝sin αcos β－cos αsin β.(Sα－β)【自主测试1－1】sin 7°cos 37°－cos 7°sin 37°的值是( )A．－12B．12C．32D．－32答案：A【自主测试1－2】sin 105°＝________.答案：6＋242．旋转变换公式已知点P(x，y)，与原点的距离保持不变，逆时针旋转θ角到点P′(x′，y′)，则有⎩⎪⎨⎪⎧x′＝x cos θ－y sin θ，y′＝x sin θ＋y cos θ.【自主测试2－1】已知点M(－1,6)，与坐标原点保持距离不变，按顺时针旋转90°得到点M′的坐标为________．答案：(6,1)【自主测试2－2】已知向量OBuuu r＝(1,3)，绕原点按逆时针旋转60°得到向量'OBu u u u r的坐标为________．答案：⎝⎛⎭⎪⎫1－332，3＋323．辅助角公式形如a sin x＋b cos x(a，b不同时为0)的式子可以化为一个三角函数式．即a sin x＋b cos x＝a2＋b2sin(x＋φ)，其中cos φ＝aa2＋b2，sin φ＝ba2＋b2.【自主测试3－1】函数y＝sin x＋cos x的最小正周期是( )A．π2B．π C．2π D．4π解析：∵y＝sin x＋cos x＝2⎝⎛⎭⎪⎫22sin x＋22cos x＝2⎝⎛⎭⎪⎫cosπ4sin x＋sinπ4cos x＝2sin⎝⎛⎭⎪⎫x＋π4，∴最小正周期为T ＝2π1＝2π.答案：C【自主测试3－2】已知3cos x －sin x ＝－65，则sin ⎝ ⎛⎭⎪⎫π3－x ＝( ) A ．45 B ．－45 C ．35 D ．－35 答案：D1．对两角和与差的正弦公式的正确理解 剖析：(1)公式中的α，β均为任意角． (2)与两角和与差的余弦公式一样，公式对分配律不成立，即sin(α±β)≠sin α±sinβ.(3)和差公式是诱导公式的推广，诱导公式是和差公式的特例．如sin(2π－α)＝sin 2πcos α－cos 2πsin α＝0×cos α－1×sin α＝－sin α，当α或β中有一个角是π2的整数倍时，通常使用诱导公式较为方便． (4)使用任何一个公式都要注意它的逆向、多向变换，还要掌握整体思想等，这是灵活使用公式的前提，特别是三角函数公式．如化简sin(α＋β)cos β－cos(α＋β)sin β，不要将sin(α＋β)和cos(α＋β)展开，而是采用整体思想，进行如下变形：sin(α＋β)cos β－cos(α＋β)sin β＝sin[(α＋β)－β]＝sin α，这也体现了数学中的整体原则．(5)记忆时要与两角和与差的余弦公式区别开来，两角和与差的余弦公式的右端的两部分为同名三角函数的积，连接符号与左边的连接符号相反；两角和与差的正弦公式的右端的两部分为异名三角函数的积，连接符号与左边的连接符号相同．归纳总结两角和与差的正、余弦公式虽然形式、结构不同．但它们的本质是相同的：cos(α＋β)cos(α－β)sin(α＋β),sin(α－β)，所以在理解公式的基础上，只要记住中心公式cos(α＋β)的由来及其表达方式就可掌握其他三个公式了．这要作为一种数学思想、一个数学方法来仔细加以体会．2．解读辅助角公式剖析：(1)a sin x ＋b cos x (a ，b 不同时为0)中的角x 必须为同一个角，否则不成立． (2)通过化单角(x )为复角(x ＋θ)，达到减少函数名称，合二为一的目的．最终化为一个(复)角的一种三角函数，有利于进一步研究相关性质．(3)化简的形式不唯一． 由于选用的辅助角不一样，所以化简的结果也会不相同，这实际上是由化简过程中采用的公式决定的．如f (x )＝3sin x ＋cos x 可以写成f (x )＝2sin ⎝⎛⎭⎪⎫x ＋π6还可以写成f (x )＝2cos ⎝⎛⎭⎪⎫x －π3.3．有关三角函数的最值问题的求法剖析：一般地，三角函数的求最值问题可归结为以下几种情况： (1)形如y ＝A sin(ωx ＋φ)＋B 的函数，利用sin α的值域求最值；(2)形如y ＝a sin x ＋bc cos x ＋d的函数，可通过数形结合法，将y 看成是两点连线的斜率，确定斜率的最值即可；(3)可化为形如y ＝a (sin x －b )2＋c 或y ＝a (cos x －b )2＋c 的函数，利用换元法转化为二次函数在特定区间上的最值问题；(4)求形如f (x )＝a sin x ＋b cos x (ab ≠0)的函数的最值，通常化归为求函数y ＝A sin(ωx ＋φ)⎝⎛⎭⎪⎫tan φ＝b a 的最值．题型一 利用两角和与差的正弦公式求值【例题1】已知cos φ＝45，在下列情况下，分别求sin ⎝ ⎛⎭⎪⎫π3－φ的值． (1)φ∈⎝ ⎛⎭⎪⎫0，π2；(2)φ∈⎝ ⎛⎭⎪⎫3π2，2π. 分析：在已知cos φ＝45和φ的取值范围的前提下，要求sin ⎝ ⎛⎭⎪⎫π3－φ，只需把sin φ求出再应用公式即可得出．解：(1)∵cos φ＝45，φ∈⎝ ⎛⎭⎪⎫0，π2，∴sin φ＝1－cos 2φ＝35，∴sin ⎝ ⎛⎭⎪⎫π3－φ＝sin π3cos φ－cos π3sin φ＝32×45－12×35＝43－310. (2)∵cos φ＝45，φ∈⎝ ⎛⎭⎪⎫3π2，2π， ∴sin φ＝－1－cos 2φ＝－35，∴sin ⎝ ⎛⎭⎪⎫π3－φ＝sin π3cos φ－cos π3sin φ＝32×45－12×⎝ ⎛⎭⎪⎫－35＝43＋310. 反思在cos φ已知的前提下，sin φ要根据φ的取值范围才能唯一确定．如果φ不能确定，则一定要分情况讨论．题型二 三角函数式的化简【例题2】化简：sin A ＋2Bsin B－2cos(A ＋B )．分析：解答本题若用两角和与差的正余弦公式展开，则计算复杂．对题中各角之间的关系进行分析后，我们选定(A ＋B )和B 作为基本量，则有A ＋2B ＝(A ＋B )＋B ，抓住了这些关系后，再恰当地运用公式，问题便不难解决了．解：原式＝sin[A ＋B ＋B ]－2cos A ＋B sin Bsin B＝sin A ＋B cos B －cos A ＋B sin B sin B＝sin[A ＋B －B ]sin B ＝sin A sin B.反思在做三角函数题时，角度变换是三角恒等变换的首选方法，但具体怎样来变换，我们主要是分析它们之间的关系，以便通过角度变换，减少不同角的个数．这其中，寻找一个或几个基本量是快速定位这类题目解法的关键．题型三 公式在三角形中的应用【例题3】在△ABC 中，若sin A ＝35，cos B ＝513，求cos C ．分析：借助C ＝π－A －B 转化，再利用公式求解．解：∵cos B ＝513，∴B 为锐角，∴sin B ＝1－cos 2B ＝1213.∵sin A ＝35，0＜A ＜π，∴当A 为锐角时，cos A ＝1－sin 2A ＝45，此时cos C ＝cos[π－(A ＋B )]＝－cos(A ＋B )＝sin A sin B －cos A cos B ＝1665，当A 为钝角时，sin A ＝35＜32，∴A ＞120°.又∵cos B ＝513＜12，∴B ＞60°，∴A ＋B ＞180°与三角形内角和等于180°矛盾．∴cos C ＝1665.反思解决与三角形有关的问题时要注意： (1)三角形的内角和等于180°；(2)创设条件使之能运用两角和与两角差的三角函数公式； (3)常用结论：A ＋B ＋C ＝180°，sin(A ＋B )＝sin C ，cos(A ＋B )＝－cos C ，sin A ＋B 2＝cos C2，cos A ＋B 2＝sin C 2，tan(A ＋B )＝－tan C ．〖互动探究〗若把本例中的“cos B ”改为“sin B ”，结果又如何？解：∵sin A ＝35，0＜A ＜π，∴当A 为锐角时，cos A ＝1－sin 2A ＝45.∵sin B ＝513＜35＝sin A ，∴B 为锐角，∴cos B ＝1－⎝ ⎛⎭⎪⎫5132＝1213，∴cos C ＝－cos(A ＋B )＝sin A sin B －cos A cos B ＝35×513－45×1213＝－3365， 当A 为钝角时，cos A ＝－45，cos B ＝1213，∴cos C ＝－cos(A ＋B )＝sin A sin B －cos A cos B ＝35×513－⎝ ⎛⎭⎪⎫－45×1213＝6365.题型四 辅助角公式的应用【例题4】已知函数f (x )＝sin x －3cos x ，x ∈R . (1)求f (x )的最小正周期与值域；(2)求f (x )的单调递增区间．分析：解答本题时，可把a sin x ＋b cos x 化简成a 2＋b 2sin(x ＋θ)的形式求解．解：f (x )＝sin x －3cos x ＝2⎝ ⎛⎭⎪⎫12sin x －32cos x＝2⎝ ⎛⎭⎪⎫sin x cos π3－cos x sin π3＝2sin ⎝ ⎛⎭⎪⎫x －π3，x ∈R . (1)T ＝2π1＝2π，f (x )的值域为[－2,2]．(2)由2k π－π2≤x －π3≤2k π＋π2(k ∈Z )，得2k π－π6≤x ≤2k π＋5π6(k ∈Z )．所以f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤2k π－π6，2k π＋5π6(k ∈Z )． 反思研究形如f (x )＝a sin x ＋b cos x 的函数的性质，都要先把其化为整体角的正弦函数形式或余弦函数形式，方法是提取a 2＋b 2，逆用公式S α±β，C α±β，特别注意角的范围对三角函数值的影响．题型五 易错辨析 【例题5】已知向量MN u u u u r＝(3，－1)，将此向量绕其始点，顺时针旋转30°后所得向量MN ′→的坐标为________．错解：由旋转变换公式得⎩⎪⎨⎪⎧x ′＝x cos 30°－y sin 30°，y ′＝x sin 30°＋y cos 30°，即⎩⎪⎨⎪⎧x ′＝33＋12，y ′＝3－32，所以MN ′→＝⎝ ⎛⎭⎪⎫33＋12，3－32.错因分析：没有考虑到是顺时针旋转30°，在代入公式时，角的度数为－30°. 正解：由旋转变换公式得 ⎩⎪⎨⎪⎧x ′＝3cos －30°－－1sin －30°，y ′＝3sin －30°＋－1cos －30°，即⎩⎪⎨⎪⎧x ′＝33－12，y ′＝－3＋32，所以MN ′→＝⎝ ⎛⎭⎪⎫33－12，－3＋32.1．(2012·山东邹城质检)sin 75°cos 30°－cos 75°sin 30°的值为( )A ．1B ．12C ．22D ．32答案：C2．已知sin(α＋β)＝14，sin(α－β)＝13，则tan α∶tan β＝( )A ．－17B ．17C ．－7D ．7解析：由sin(α＋β)＝14，sin(α－β)＝13，得sin αcos β＋cos αsin β＝14，①sin αcos β－cos αsin β＝13.②由①＋②，得2sin αcos β＝712.③由①－②，得2cos αsin β＝－112.④故由③④，得tan αtan β＝－7.答案：C3．(2012·山东鱼台期末)在△ABC 中，如果sin A ＝2sin C cos B ，那么这个三角形是( )A ．锐角三角形B ．直角三角形C ．等腰三角形D ．等边三角形 答案：C4．sin α＋30°－sin α－30°cos α＝________.解析：sin α＋30°－sin α－30°cos α＝sin αc os 30°＋cos αsin 30°－sin αcos 30°－cos αsin 30°cos α＝2cos αsin 30°cos α＝2sin 30°＝1.答案：15．若3sin x －3cos x ＝23sin(x ＋φ)，φ∈(－π，π)，则φ＝________.解析：3sin x －3cos x ＝23⎝ ⎛⎭⎪⎫32sin x －12cos x＝23(sin x cos φ＋cos x sin φ)＝23sin(x ＋φ)，∴cos φ＝32，sin φ＝－12.又φ∈(－π，π)，∴φ＝－π6.答案：－π66．是否存在x 使得函数y ＝sin(x ＋10°)＋cos(x ＋40°)存在最小值？若存在，求出x ；若不存在，请说明理由．解：∵x ＋40°＝(x ＋10°)＋30°，∴y ＝sin(x ＋10°)＋cos[(x ＋10°)＋30°]＝sin(x ＋10°)＋cos(x ＋10°)cos 30°－sin(x ＋10°)sin 30° ＝12sin(x ＋10°)＋cos 30°cos(x ＋10°) ＝sin 30°sin(x ＋10°)＋cos 30°cos(x ＋10°) ＝cos(x ＋10°－30°)＝cos(x －20°)．∵－1≤cos(x －20°)≤1，∴函数的值域为[－1,1]， ∴当y min ＝－1时，x －20°＝k ·360°＋180°，k ∈Z ， 此时，x ＝k ·360°＋200°，k ∈Z .。

3.1.3 二倍角的正弦、余弦、正切公式（一）
课前导引
问题导入
从特殊到一般和从一般到特殊，这是人们正确认识客观事物的认识规律，也是处理数学问题的重要思想方法.从这一思想出发，我们知道两角和的正弦为：sin （α+β）=sinαcosβ+cosαsinβ，那么现在我们令α=β，在这种特殊情况下我们可以得到公式sin2α=2sinαcosα，同理其余几种三角函数也可以做类似的推理，本节我们就来研究一下有关倍角的公式.你能利用上述知识解决下面的问题吗？
已知sinα=
135，α∈（2
π，π），求sin2α，cos2α，tan2α的值. 思路分析：∵sinα=135，α∈（2π，π）， ∴cosα=.13
12)135(1sin 122-=--=--α ∴sin2α=sin（α+α）=sinαcosα+cosαsinα=2sinαcosα=169
120-， cos2α=cos 2α-sin 2
α=169
119， tan2α=1191202cos 2sin -=αα. 知识预览
1.二倍角正弦公式S 2α：sin2α=2sin αcos α.
2.二倍角余弦公式C 2α：cos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α.
3.二倍角正切公式T 2α：tan2α=αα2tan 1tan 2-.。