菱形十二面体 作法

素描几何体——十二面体教学目标:要求学生掌握物体的基本造型个性、理解物体的结构与基本透视。

教学重点:物体的形状个性、结构、透视教学难点:物体的分面、透视教学过程:一、石膏十二面体就是隶属于石膏几何形体训练的其中一个内容,它的特点为:块面齐整、造型简练、明暗表现清楚的几大特点,所以在素描练习中具有重要的地位,下面就它的结构特点与素描画法做一个简单的介绍。

二、结构特点这节课所介绍的多面体的基本形为五边形,而多面体则由十二个五边形所组成,每个五边形的各条边均与其她的五边形相连,形成一个完整的多面体,结构清楚、明暗效果直接明了,让画者很容易的区分黑白灰的层次感觉,便于绘画练习。

三、素描画法十二面体的素描画法具体分为一下几个步骤:第一步,考虑画面的构图,也就就是说把十二面体在纸上画多大,画在什么位置上。

第二步,用直线画出大的形状。

这个步骤画的时候用线不要太重,以便于后边几个步骤中能够进行修理。

第三步画出具体形状。

在进行这个步骤的绘画练习时,要把您所能瞧到的五边形全部绘画出来,但同时要注意,由于角度的不同,所瞧到的五边形也发生了很大的变化,既各边的长短在视觉上有了很大的差异。

第四步就是画出明暗效果,在十二面体的明暗表现时,由于它的块面特点,所以较为容易区分,不必要再先铺设大的色块,直接表现即可。

但就是再画的时候要注意每一个五边形,由于距离光线的远近不同,五边形本身也就会出现明暗的深浅变化,一般离光近的一边重,其它边要逐渐变浅。

第五步就是进行画面上的调整,在这个环节,要求画者要根据画面应有的效果去对画面进行修正,也就就是说要添加一些细节部分,去除掉一些繁琐的内容。

这样一幅十二面体的素描就画了出来。

四、作业石膏几何体——十二面体临摹五、作品欣赏。

SkewbUltimate十二面体魔方还原公式
Skewb Ultimate的复原步骤：
第一步，固定一个棱为顶，解决其周围四个顶角位置，底下的四个自然也就对位；
第二步，解决四个顶角的色向；
第三步，解决其余五个棱位置；
第四步，解决剩下棱的色向；
第五步，解决底角的色向。

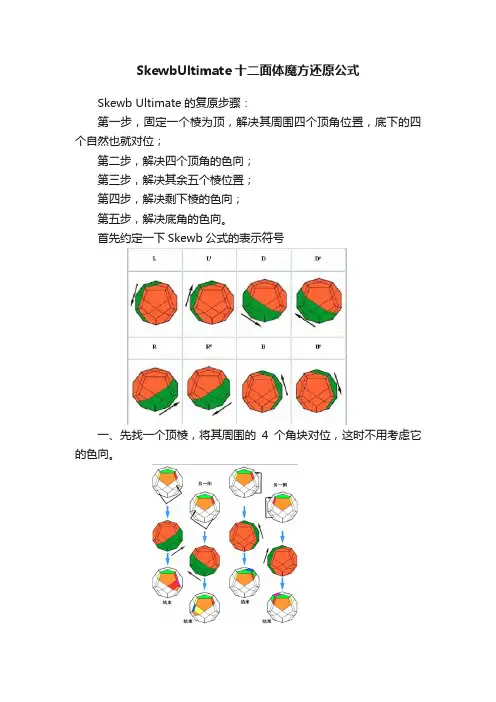
首先约定一下Skewb公式的表示符号
一、先找一个顶棱，将其周围的4个角块对位，这时不用考虑它的色向。

如果两角都在上半个球体且需要交换时，用下面的转法：
魔方公式表示：D B D
二、对好四个顶角的色向
此时一个棱周围的4个角的位置已正确，余下的4个
的位置必定也已正确。

现在要将角的色向翻对，使之与第一个棱的色向相符
公式表示：D R D' R'
反时针:
公式表示：D' L' D L
另一种情况（另一侧角）
公式表示：R B R' B'
反时针
公式表示：R' D' R D
三、对好其余五个棱的位置
现在顶角的位置和色向都已正确，而另外4个的位置也已正确，余下的5个棱的位置有可能不对，下一步
的目标是先使它们的位置正确，稍后再来使之对色。

不改变顶角而交换棱块的转法如下：
下面的两种转法都将使两对棱互换。

公式表示：1)D' R D R'
2)R' B R B'
执行上面二者中任一种转法一次的结果：两对棱交换，且角翻转120度;
执行上面二者中任一种转法两次的结果：两对棱不交。

哈密顿周游世界问题菱形十二面体The Hamiltonian cycle problem, also known as the Traveling Salesman Problem, is a classic problem in graph theory that aims to find the most efficient route that visits every vertex exactly once and returns to the starting point.哈密顿周游世界问题，也被称为旅行推销员问题，是图论中的一个经典问题，旨在找到访问每个顶点一次且返回起点的最有效路径。

This problem is notoriously difficult and has been studied extensively in the field of computer science and combinatorial optimization. The complexity of finding the optimal Hamiltonian cycle increases exponentially with the number of vertices in the graph.这个问题极具挑战性，在计算机科学和组合优化领域得到了广泛研究。

寻找最优哈密顿周期的复杂度随着图中顶点数量的增加呈指数增长。

One interesting variation of the Hamiltonian cycle problem is the rhombic dodecahedron, a polyhedron with twelve faces, each of which is a rhombus. Finding a Hamiltonian cycle on a rhombicdodecahedron involves traversing all twelve rhombic faces exactly once without backtracking.一个有趣的变体是菱形十二面体的哈密顿周游问题，菱形十二面体是一个每个面都是菱形的多面体。

单元（章节）课题结构素描本节课题十二面体结构画法三维目标知识与技能：要求学生掌握物体的基本造型个性、理解物体的结构和基本透视过程与方法：通过示范与讲解，在听讲中理解其结构与画法，在实践中进一步掌握画法。

情感、态度价值观：在学习中提升绘画技能，在实践中树立信心。

提炼的课题十二面体由于块面较多，结构复杂，对学生来说比较难，特别是在造型与观察中存在形体不准，观察方法单一。

教学重难点教学重点：物体的形状个性、结构、透视。

教学难点：物体的分面、透视。

教学过程导入示范与讲解一、十二面体的特点石膏十二面体是隶属于石膏几何形体训练的其中一个内容，它的特点为：块面齐整、造型简练、明暗表现清楚的几大特点，所以在素描练习中具有重要的地位，下面就它的结构特点和素描画法做一个简单的介绍二、结构特点这节课所介绍的多面体的基本形为五边形，而多面体则由十二个五边形所组成，每个五边形的各条边均与其他的五边形相连，形成一个完整的多面体，结构清楚、明暗效果直接明了，让画者很容易的区分黑白灰的层次感觉，便于绘画练习。

（如图）三、结构画法（示范与讲解）十二面体的素描画法具体分为一下几个步骤：第一步，考虑画面的构图，也就是说把十二面体在纸上画多大，画在什么位置上。

第二步，用直线画出大的形状。

这个步骤画的时候用线不要太重，以便于后边几个步骤中能够进行修理。

（如图）第三步画出具体形状。

在进行这个步骤的绘画练习时，要把你所能看到的五边形全部绘画出来，但同时要注意，由于角度的不同，所看到的五边形也发生了很大的变化，既各边的长短在视觉上有了很大的差异。

组织学生开展实践操作。

菱形的作法原理菱形作为一种几何图形，是由两个等边且相互垂直的倒三角形组成的。

在这里，我们将介绍菱形的构造原理和一些基本的数学知识。

首先，让我们回顾一下等边三角形的性质。

等边三角形是一种所有边长都相等的三角形。

在等边三角形ABC中，每个角度都为60度，因此它是一个正三角形。

现在，我们要构造一个菱形。

假设我们已经有一个等边三角形ABC。

首先，我们选择一个边作为菱形的对角线。

假设我们选择边AB作为对角线。

然后，我们通过将边AB平分并延长，将三角形ABC划分为两个等腰三角形ACD和BCD。

在这里，点D是边AB的中点。

接下来，我们需要找到菱形的四个顶点。

顶点A可以通过将边AC的延长线与边BD的交点找到。

同样地，顶点B可以通过将边BC的延长线与边AD的交点找到。

顶点C和D就是菱形对角线的中点。

现在，我们已经确定了菱形的顶点A、B、C和D。

我们可以连接这些顶点，得到一个菱形。

由于菱形的两个三角形是等边的，所以菱形的相邻边长也相等。

通过菱形的构造过程，我们可以看到菱形与等边三角形有着密切的关系。

菱形的对角线是等边三角形的两个边的延长线，而菱形的顶点是等边三角形的两个边的交点。

此外，菱形还有一些其他有趣的性质。

例如，菱形的对角线互相垂直，并且对角线的中点也是菱形的中心点。

此外，菱形的内角度数为360度，因此它是一个凸多边形。

菱形在几何图形中具有广泛的应用。

它可以用来构造平行四边形、菱形网络和菱形格子等。

此外，菱形还可以用来解决一些几何问题，例如求解菱形的面积和周长。

总之，菱形的作法原理可以通过等边三角形的构造过程来理解。

通过将等边三角形划分为两个等腰三角形，并通过连接对角线的两个端点，我们可以构造出一个菱形。

记住菱形的性质和特点，可以帮助我们更好地利用和应用菱形。

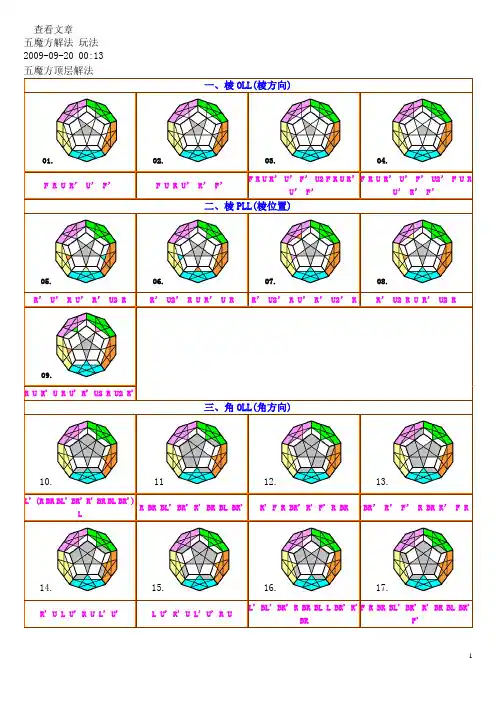
查看文章五魔方解法玩法2009-09-20 00:1301.02.F R U R’ U’ F’ F U R U’ R’ F’R’ U’ F’ U2 F R UU’ F’F R U R’ U’ F’ U2’ F U RU’ R’ F’二、棱棱位置)06.R’ U’ R U’ R’ U2 R R’ U2’ R U R’ U R R’ U2’ R U’ R’ U2’ R R’ U2 R U R’ U2 R09.R U R' U R U' R' U2 R U2 R'BR BL' BR' R' BR BL BR')LR BR BL' BR' R' BR BL BR'R' F R BR' R' F' R BR BR’ R’ F’ R BR R’ F RR' U L U' R U L' U'L U' R' U L' U' R U L' BL' BR' R BR BL L BR' R'BRF R BR BL' BR' R' BR BL BR'F'F (R U R’ U’) 3F’BL'BR' R' BR BL BR' yF R BR' R' F' R BRR’ U’ (R U R’ U’)2R U2’ R’BL' BR' R' BR BL BR' y2’R' F R BR' R' F' R BRF (R U R’ U’) 3F’ y R BRBL' BR' R' BR BL BR'BL' BR' R' BR BL BR'R BR BL' BR' R' BR BL BR'R’ U2’（R U R’ U’）R’ U2’ （R U R’ U’）R U’ R’R U R' U R U' R' U2 R U2' R'U R U' R' U2 R U2 R'524好/翻13：F R U--R’ U’ F’514好/翻23：F U R--U’ R’ F’5好/翻1234：(F R U--R’ U’ F’) U2 (F R U--R’ U’ F’)1/5好，234正：(R’ U’ R U’ )(R’ U2 R)1/5好，234负：(R’ U2’ R )(U R’ U R)1/3好，245正：(R’U2’R U’)(R’U2’R)1/3好，245负：(R’U2 R U)(R’U2 R)1/2/3好，4-5换：(R’ U2 R U )(R’ U2 R)3好，1-5/2-4换：(R U R' U )(R U' R' U2 )(R U2 R')△//正负(在两侧)：(F /R r′R’/ F’)( R r R’)△//负正(都在下边)：L' (R r l' r'--R' r l r') LT//正负(在两侧)：R’ (F’ L’ F/ R /F’ L F)T//负正(都在下边)：(R' F R )(r'/ R' F' R/ r)一//正正正(左同向)：(F U' r' U )(F’ U' r U)一//负负负(右同向)：(R' U L U')( R U L' U' )V//正正正(左同向)：L' l' (r' R r )l L (r' R' r)V//负负负(右同向)：R (r l L’ l’)(r’ l L l’) R’1好：2正3正4负5负(同底左右下)：(L U2’ L’U’)(L U L’ U’)2 (L U2’ L’)1好：2正3负4正5负(左右两侧)：L (F U F’ U’) 3 L’1好：2正3负4负5正(同底左右上)：L (F U F’ U’) 3 L’(R r l' r' )(R' r l r')1好：2负3负4正5正(左右上/左右侧)：F (R r’ R’) F’ (R r R’) (l’ r l) L’(l’ r’ l) L 1好：2负3正4负5正(右同向/左上左下)：l L F L’ l’ L F L F’ L F R’ F’ L’ F R 1好：2负3正4正5负(左同向/右上右下)：(R r l' r' )(R' r l r') (F R r’ R’ )(F’ R r R’ ) 3正(同方向/左向)：(R U R' U )(R U' R' U2 )(R U2' R' U )(R U' R' U2 )(R U2 R' )3负(同方向/右向)：(R U2’ R’ U2’)(R U R’ U’)(R U2 R’ U2’ )（R U R’ U’）R U’ R’11。

正十二面体及其延伸绘制教程
最近事情比较多，只能抽空解答下部分后台提问，本部分内容为回答“正十二面体和棱形十二面体怎么画？”，在此分别以与讲解，本部分为正十二面体绘制教程及其延伸（卡线及晶格），由于时间有限，仅提供思路，供参考，望有用！
[PS：注我们分享的实例模型是随时动态更新的，逐渐增多，运用前，本身的max是17故此最好是16或17的软件，并已确保vray 渲染器已经安装好，在利用模型前可以选择直接打开或者导入自己自建场景，导入或合并等]
最终效果如下：
正文如下：
直接在顶视图创建个异面体（扩展基本体），在修改面板中系列中选择“十二面体/二十面体”，将系列参数中的Q由0改为1，回车，即可得到正十二面体。

添加材质，简单渲染如下：
延伸一：进一步转化成可编辑多边形，选中所有边切角，可以变得更加圆滑，效果如下：
延伸二：回归原来的正十二面体，加多边形修改器，点击细化两次，点击修改器中晶格修改器，选择仅来自顶点的节点，节点选择二十面体，修改半径值至合适，点击段数2-3段，下面平滑选中，并原地复制一个，整体缩放一次后（两个套在一起）渲染如下：
抱歉，凑点字数。

正十二面体折法
正十二面体是一种由 12 个面组成的正多面体，它由一个正方体切割而来。

以下是一种简单的折法:
1. 将一张方形纸对角线对折，然后展开，使对角线相交于一点。

2. 将纸张沿着相交点对折，使得纸张中心线与对角线重合。

3. 将纸张向左侧折叠一半，然后向右侧展开。

4. 将纸张向右侧折叠一半，然后向左侧展开。

5. 将纸张向上方折叠一半，然后向下方展开。

6. 将纸张向下方折叠一半，然后向上方展开。

7. 将纸张向左侧折叠一半，然后向右侧展开。

8. 将纸张向右侧折叠一半，然后向左侧展开。

9. 将纸张向上方折叠一半，然后向下方展开。

10. 将纸张向下方折叠一半，然后向上方展开。

11. 将纸张向左侧折叠一半，然后向右侧展开。

12. 将纸张向右侧折叠一半，然后向左侧展开。

完成后，正十二面体就会出现啦！。