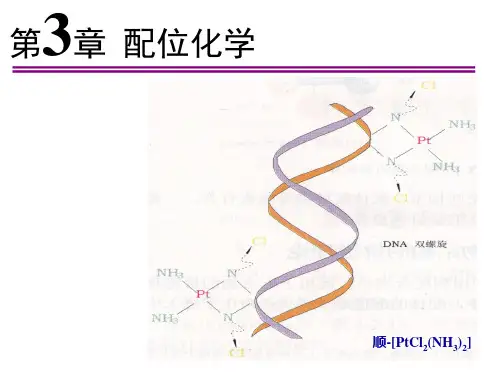
配位化学第三章

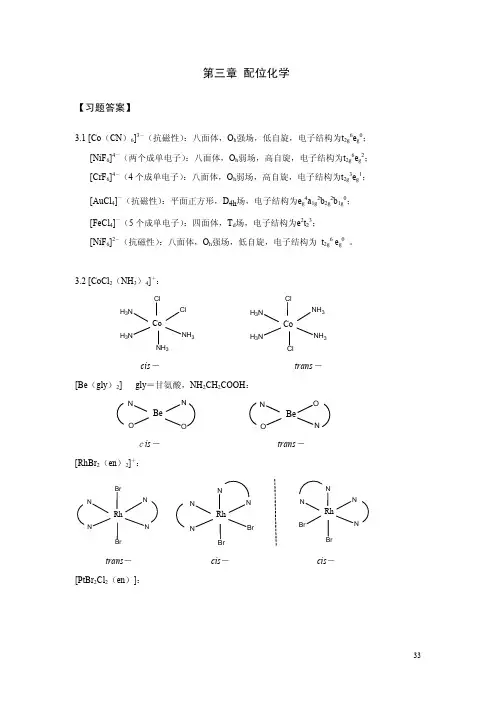
第三章 配位化学【习题】3.1 试判断下列配离子的几何构型和电子结构：[Co（CN）6]3－（抗磁性）；[NiF6]4－（两个成单电子）；[CrF6]4－（4个成单电子）；[AuCl4]－（抗磁性）；[FeCl4]－（5个成单电子）；[NiF6]2－（抗磁性）3.2 画出下列各配合物（配离子）所有可能的异构体：[CoCl2（NH3）4]＋，[Be（gly）2]，[RhBr2（en）2]＋，[PtBr2Cl2（en）]，[Ir（C2O4）2Cl2]3－，[Cr（gly）3]，[Pt（gly）2]（gly＝glycine，甘氨酸）3.3 已知配合物[M（A－B）2]和[M（A－B）2X2]型的配合物都是旋光活性的，请分别画出它们的几何结构。

3.4 紫红色的[Ti（H2O）6]3＋在可见区的吸收光谱如教材中例题3－1的图所示，其最大吸收峰位置对应于20.3×103 cm－1，并在该最大吸收峰位置的右边（低频方向）出现一个肩峰，试用晶体场理论解释上述肩峰的由来。

3.5 下列配离子中哪些属于高自旋构型？（a）Mn（H2O）62＋；（b）Fe（H2O）63＋；（ｃ）Co（NH3）63＋；（ｄ）Co（H2O）62＋；（ｅ）CoCl42－；（ｆ）Fe（CN）64－3.6 下列配合物或配离子中属于低自旋构型的是（a）Fe（H2O）63＋；（b）Co（H2O）62＋；（c）Co（H2O）63＋；（d）CoF63－3.7 对于CoF63－配离子，下面的哪项论述是正确的？（a）CoF63－的晶体场分裂能大；（b）F－为强场配体；（c）CoF63－是顺磁性的；（d）所有论述都不正确。

3.8 下列配离子中，哪一种可能产生Jahn－Teller效应？（a）Fe（CN）64－；（b）Fe（H2O）62＋；（c）Cr（H2O）63＋；（d）Co（NH3）63＋；3.9 试画出配合物[Co（NO2）3（NH3）3]可能存在的几何异构体。

第三章配合物在溶液中的稳定性作业1.下列各组中，哪种配体与同一种中心离子形成的配合物稳定性较高，为什么？（1）Cl- , F-和Al3+（2）Br-，I-和Hg2+（3）2CH3NH2,en和Cu2+（4）Br-，F- 和Ag+（5）RSH,ROH和Pt2+（6）Cl-，OH-和Si4+（7）RSH,ROH和Mg2+解(1)F-与Al3+形成配合物更稳定，因为F-电负性大，离子半径更小（2）I-与Hg2+更稳定，因为碘离子的电负性较大，离子半径更小（3 ）2CH3NH2与Cu2+形成的配合物更稳定，因为它的碱性比en更强与形成的配合物更稳定（4）Br-与Ag+形成的配合物更稳定，因为与Ag+形成配合物Br-变形性比F-强（5）RSH与Pt2+形成配合物更稳定，因为在与Mg2+形成配合物时S 的半径小于O的半径（6）OH-与Si4+形成的配合物更稳定，因为在与Si4+形成配合物时OH-的电荷比更多（7）RSH与Mg2+形成配合物更稳定，因为在与Mg2+形成配合物时S 的半径小于O的半径2.写出下列，配体与中心离子形成的配合物的稳定次序。

解（1）CH3NH2，en，NH2-NH2，NH2-OH和Cu2+en > CH3NH2 > NH2-NH2 > NH2OH（2）R3CCOOH，CH3COOH，Cl3CCOOH，I3CCOOH和Fe3+ R3CCOOH > CH3COOH > I3CCOOH > Cl3CCOOH（3）NH3，NH2-NH2，NH2-OH，R-OH和Ag+NH3 > NH2-NH2 > NH2-OH > R-OH（4）N, NH2与Zn2+N>NH2（5）NH2O2N,NH2CH3,NH2NO2与Cu2+NH2 CH3>NH2NO2>NH2O2N（6）NOH，NOHCH3与Ni2+NOHCH3>NOHCH33．下列二组试剂与同一种金属离子形成螯合物时，估计lg k的大小次序：解：（1）NH 2NO 2NH2CH3NH2NO2 2 > 3 > 1（2）1. 2.3. 4.3 > 2 > 1 > 4（3）M(en)3，M(Pn)3，M(dien)2M(en)3 > M(dien)2 > M(Pn)34.解释下列各胺与Cu（II）形成配离子稳定性的差别：配体lgk1(25oC)乙二胺10.551,2-二氨基丙烷10.651,3-二氨基丙烷9.981,2,3,-三氨基丙烷11.1解：当配位原子相同时，配体碱性越强，越易给出电子，形成的配合物往往越稳定。

第三节群表示的基及群的表示一、基本概念1、基：群元素作用的对象称为与它相应的群表示的基。

基可以有各种类型，如矢量（x，y，z），波函数（p x，p y，p z）2、群的表示：选定群表示的基以后，则分子点群中的每一个元素都与一个矩阵相对应，这些矩阵构成的矩阵群可以看作是点群的一个表示。

* 群的表示不是唯一的。

二、群的表示（可约与不可约表示）1、可约表示1）定理：设一组矩阵（E，A，B，C…）构成一个群的表示。

若对每个矩阵进行同样的相似变换：E´=X-1EXA´=X-1AXB´=X-1BX…………..则（E´，A´，B´……）也是群的一个表示。

证明（封闭性）：若AB = CA´B´ = (X-1AX)(X-1BX) = X-1A(XX-1)BX = X-1(AB)X = X-1CX = C´若每个矩阵A´，B´，C´, … 均按同样的方式划分成方块，则可证明，每个矩阵的对应方块可以单独地相乘：A1´B1´=C1´A2´B2´=C2´A3´B3´=C3´………..因此各组矩阵E1´，A1´，B1´，C1´, …E2´，A2´，B2´，C2´, ……………………….本身都是一个群的表示。

因为用矩阵X可以把每个矩阵变换为一个新矩阵，所有新的矩阵按照同样的方式给出两个或多个低维表示。

因此我们称（E，A，B，C,…）为可约表示。

2、不可约表示若找不到矩阵X，按照上述方式约化给定表示的所有矩阵，这种表示称为不可约表示。

不可约表示具有特殊的重要性。

三、广义正交定理1、向量的正交1）向量及其标积。

向量的定义：向量标积：AθBA·B = A·Bcosθ2）向量正交若A·B = 0，则称A与B正交。