高一数学必修3(人教版)课后强化训练(含详解)：1.1.2.3

1. 1. 1KHQHZY 课后强化作业 一、选择题 i •下列关于算法的说法正确的有 ____________ 个.（） ① 求解某一类问题的算法是惟一的. ② 算法必须在有限步操作之后停止. ③ 算法的每一步操作必须是明确的，不能有歧义或模糊. ④ 算法执行后一定产生确定的结果. A . 1 B . 2 C . 3 D . 4 ［答案］C ［分析］由算法特性知，算法具有有穷性、确定性、可输出性，故①计算c =工i a 2 + b 2;③输出斜边长c 的值. 其中正确的顺序号是（ ）［答案］D 3 .使用计算机解题的步骤由以下几部分构成⑤ 编写程序 正确的顺序为（A .④①③②⑤B .④①③⑤②C .④③②①⑤D .④①②③⑤［答案］B4 .以下关于算法的说法正确的是 （ ）A ．描述算法可以有不同的方式，可用形式语言也可用其它语言B •算法可以看成按照要求设计好的有限的确切的计算序列，并且这样的步骤或序列只能解决当前问2 .已知直角三角形两条直角边长 a 、b ,求斜边长c 的一个算法分为以下三步: ②③④均对，选C. ②输入直角三角形两直角边长 a 、b 的值; A .①②③ B .②③①C .①③②D .②①③①寻找解题方法 ②调试运行 ③设计正确算法 ④正确理解题意题C •算法过程要一步一步执行，每一步执行的操作必须确切，不能含混不清，而且经过有限步或无限步后能得出结果D •算法要求按部就班地做，每一步可以有不同的结果[答案] A[分析] 算法可以看成按照要求设计好的有限的确切的计算序列，并且这样的步骤或计算序列能够解决一类问题.算法过程要求一步一步执行，每一步执行的操作，必须确切，只能有惟一结果，而且经过有限步后，必须有结果输出后终止，描述算法可以有不同的语言形式，如自然语言、框图语言及形式语言等.5 .下列四种自然语言叙述中，能称作算法的是（）A •在家里一般是妈妈做饭B •做米饭需要刷锅、淘米、添水、加热这些步骤C •在野外做饭叫野炊D •做饭必须要有米[答案] B[分析] 算法是做一件事情或解决一个问题等的程序或步骤，故选B.6 •阅读下面的四段话，其中不是解决问题的算法的是（）A .求1 X 2X 3的值，先计算1X 2= 2，再计算2X 3 = 6，最终结果为6B •解一元一次方程的步骤是去分母、去括号、移项、合并同类项、未知数的系数化为1C .方程x2— 1 = 0有两个实数根D•某同学判断直线与圆的位置关系时，第一步求圆心C的坐标和半径r，第二步求C到直线的距离，第三步比较d与r的大小，第四步下结论.[答案] C7 .给出下列算法：第一步，输入正整数n（n>1）.第二步，判断n是否等于2,若n=2,则输出n；若n>2,则执行第三步.第三步，依次从2到n—1检验能不能整除n,若不能整除n,则执行第四步；若能整除n,则执行第第四步,输出n.则输出的n 的值是（）A ．奇数B ．偶数C •质数D •合数［答案］ C［分析］根据算法可知n = 2时，输出n的值2;若n = 3，输出n的值3;若n = 4,2能整除4，则重新输入n的值……，故输出的n的值为质数.&已知两个单元分另U存放了变量x和y,下面描述交换这两个变量的值的算法中正确的为（）A ．S1把x 的值给y ; S2把y 的值给x.B ．S1把x 的值给t; S2把t 的值给y; S3 把y 的值给x.C．S1把x 的值给t; S2把y 的值给x; S3 把t 的值给y.D．S1把y 的值给x , S2把x 的值给t; S3 把t 的值给y.［答案］C［分析］为了达到交换的目的，需要一个中间变量t，通过t使两个变量来交换S i先将x的值赋给t（这时存放x的单元可以再利用）;S2再将y的值赋给x（这时存放y的单元可以再利用）；S3最后把t的值赋给y,两个变量x和y的值便完成了交换.［点评］这好比有一碗酱油和一碗醋•我们要把这两碗盛装的物品交换过来，需要一个空碗（即t）;先把醋（或酱油）倒入空碗,再把酱油（或醋）倒入原来盛醋（或酱油）的碗,最后把倒入空碗中的醋（或酱油）倒入原来盛酱油（或醋）的碗，就完成了交换.二、填空题9 •在计算机上能够求解方程组，是因为计算机安装有计算软件，而软件的核心是________ .［答案］算法10．一个算法步骤如下：S1 S 取值0, i 取值1.S2如果i W 10,则执行S3,否则执行S3计算S+ i，并让S取计算结果的值.S4计算i + 2,并让i取计算结果的值.55 转去执行S2.56 输出S.运行以上步骤输出的结果为S= __________ .［答案］25［分析］由以上算法可知：S= 1 + 3+ 5+ 7 + 9 = 25.11 •请说出下面算法要解决的问题__________ •第一步，输入三个数，并分别用a、b、c表示；第二步，比较a与b的大小，如果a<b,则交换a与b的值;第三步，比较a与c的大小，如果a<c,则交换a与c的值;第四步，比较b与c的大小，如果b<c,则交换b与c的值;第五步，输出a、b、c.［答案］输入三个数a, b, c,并按从大到小顺序输出.［分析］第一步是给a、b、c赋值.第二步运行后a>b.第三步运行后a>c.第四步运行后b>c, ••• a>b>c.第五步运行后，显示a、b、c的值，且从大到小排列.12. 已知A（x i, y i）, B（X2,沁，求直线AB的斜率的一个算法如下：51 输入X1、y“ X2、y2 的值.52 计算A x=X2 - X1, A y= y2 - y1S3若A X = 0,则输出斜率不存在，否则（A丰0）, k= ___ ① ___ .S4输出斜率k.则①处应填 _________ .A y［答案］A X三、解答题13. 写出求方程ax2+ bX+ c= 0（a^ 0）的根的算法.［分析］S1给出（输入）a、b、c的值（a^ 0）.2S2 计算A= b —4ac.—b+ —b —: A2a .S3如果A <Q则输出方程无实数解，结束算法，否则（A 0）X1= 2a ,S4 输出X1 , X2.S5结束.14. 写出求任意给出的4个数a、b、c、d的平均数的一个算法.［分析］第一步，输入这4个数a、b、c、d的值；第二步，计算S= a+ b+ c+ d;第三步，计算v = S；第四步，输出v的值.|2x—1, x W 015. 设计算法，给定任一x的值，求y的值，其中y= 2彳 -.x2+ 1, x>0［分析］第一步，输入x的值；第二步，判断x是否大于零，若x>0，执行第三步；否则，执行第四步；第三步，计算y= x2+1的值，转去执行第五步；第四步，计算y= 2x—1的值；第五步，输出y的值.16. 设计一个算法，求两底面半径分别为4和12,且高为6的圆台的表面积.［分析］第一步，输入两底面半径r, R,高h和圆周率n的值.第二步，计算I = (R-r)2+ h2.第三步，计算S= T R2 + n2+ n R+ r)l.第四步，输出表面积S.17. 某人带着一只狼和一只羊及一捆青菜过河，只有一条船，船仅可载重此人和狼、羊及青菜中的一种，没有人在的时候，狼会吃羊，羊会吃青菜.设计安全过河的算法.S6人自己［分析］S1人带羊过河.S2人自己返回.S3人带青菜过河.S4人带羊返回.S5人带狼过河.返回.S7人带羊过河.。

§1.1 习题课课时目标1.理解并掌握画程序框图的规则.2.在具体问题的解决过程中，理解程序框图的三种基本逻辑结构.3.能正确选择并运用三种逻辑结构框图表示具体问题的算法．1．下列关于程序框图的描述①对于一个算法来说程序框图是唯一的；②任何一个框图都必须有起止框；③程序框图只有一个入口，也只有一个出口；④输出框一定要在终止框前．其中正确的有()A．1个B．2个C．3个D．4个答案 B解析②、③正确，对于一个算法来说，程序框图不唯一，与设计有关，故①错．输入输出的位置，不一定在开始和结束处，故④错．2．某程序框图如图所示，该程序运行后输出的k的值是()A．4 B．5C．6 D．7答案 A解析 当k ＝0时，S ＝0S ＝1k ＝1，当S ＝1时，S ＝1＋21＝3k ＝2，当S ＝3时，S ＝3＋23＝11<100k ＝3，当S ＝11时，k ＝4，S ＝11＋211>100，故k ＝4.3．如图是一个算法的程序框图，该算法所输出的结果是( )A.12B.23C.34D.45 答案 C解析 运行第一次的结果为n ＝0＋11×2＝12；第二次n ＝12＋12×3＝23；第三次n ＝23＋13×4＝34.此时i ＝4程序终止， 即输出n ＝34.4．阅读下边的程序框图，若输出s 的值为－7，则判断框内可填写( )A ．i<3?B ．i<4?C ．i<5?D ．i<6? 答案 D解析 i ＝1，s ＝2；s ＝2－1＝1，i ＝1＋2＝3； s ＝1－3＝－2，i ＝3＋2＝5； s ＝－2－5＝－7，i ＝5＋2＝7.因输出s 的值为－7，循环终止，故判断框内应填“i<6？”． 5．求边长为3,4,5的直角三角形的内切圆半径的算法为： 第一步 输入__________________； 第二步 计算r ＝a ＋b －c2；第三步 输出r.答案 a ＝3，b ＝4，c ＝56．根据下面的程序框图操作，使得当成绩不低于60分时，输出“及格”，当成绩低于60分时，输出“不及格”，则框1中填________，框2中填________．答案 是 否解析 由x≥60与及格对应知1处填是，则2处填否．一、选择题1．一个完整的程序框图至少包含( ) A ．终端框和输入、输出框 B ．终端框和处理框 C ．终端框和判断框D ．终端框、处理框和输入、输出框答案 A解析一个完整的程序框图至少需包括终端框和输入、输出框．2．下列程序框图表示的算法是()A．输出c，b，a B．输出最大值C．输出最小值D．比较a，b，c的大小答案 B解析根据程序框图可知，此图应表示求三个数中的最大数．3．用二分法求方程的近似根，精确度为δ，用直到型循环结构的终止条件是() A．|x1－x2|>δ B．|x1－x2|<δC．x1<δ<x2D．x1＝x2＝δ答案 B解析直到型循环结构是先执行、再判断、再循环，是当条件满足时循环停止，因此用二分法求方程近似根时，用直到型循环结构的终止条件为|x1－x2|<δ.4．阅读如图所示的程序框图，运行相应的程序，则输出的i值等于()A ．2B ．3C ．4D ．5 答案 C S=0→i ＝1→a ＝2 →S ＝2→i ＝2→a ＝8 →S ＝10→i ＝3→a ＝24 →S ＝34→i ＝4→输出i ＝4.5．如图给出的是计算12＋14＋16＋…＋1100的值的一个程序框图，其中判断框内应填入的条件是( )A ．i≥49?B ．i≥50?C ．i≥51?D ．i≥100? 答案 C解析 i ＝1时，S ＝0＋12＝12，i ＝2时，S ＝12＋14，…，i ＝50时，S ＝12＋14＋16＋…＋1100，当i ＝51时结束程序，故选C. 6．读如图所示的程序框图则循环体执行的次数为( )A ．50B ．49C ．100D ．99 答案 B解析 ∵i ＝i ＋2，∴当2＋2n≥100时循环结束此时n ＝49，故选B. 二、填空题7．直到型循环结构框图为________．答案 ②8．已知下列框图，若a ＝5，则输出b ＝________.答案 26解析 因a ＝5，所以5>5不成立， 判断框执行“否”，即b ＝52＋1＝26.9．执行如图所示的程序框图，若输入x ＝4，则输出y 的值为________．答案 －54解析 当输入x ＝4时， 计算y ＝12x －1，得y ＝1.不满足|y －x|<1.于是得x ＝1， 此时y ＝12－1＝－12，不满足|－12－1|<1，此时x ＝－12，又推得y ＝－54.这样|y －x|＝|－54＋12|＝34<1，执行“是”，所以输出的是－54.三、解答题10．已知点P 0(x 0，y 0)和直线l ：Bx ＋By ＋C ＝0，写出求点P 0到直线l 的距离d 的算法并画出程序框图．解 (1)用数学语言来描述算法：第一步，输入点的坐标x 0，y 0，输入直线方程的系数即常数B ，B ，C ； 第二步，计算z 1＝Bx 0＋By 0＋C ； 第三步，计算z 2＝B 2＋B 2； 第四步，计算d ＝|z 1|z 2； 第五步，输出d.(2)用程序框图来描述算法，如图：11．画出求满足12＋22＋32＋…＋i 2>106的最小正整数n 的程序框图． 解 程序框图如下：能力提升12．一队士兵来到一条有鳄鱼的深河的左岸．只有一条小船和两个小孩，这条船只能承载两个小孩或一个士兵．试设计一个算法，将这队士兵渡到对岸，并将这个算法用程序框图表示．解第1步，两个儿童将船划到右岸；第2步，他们中一个上岸，另一个划回来；第3步，儿童上岸，一个士兵划过去；第4步，士兵上岸，让儿童划回来；第5步，如果左岸没有士兵，那么结束，否则转第1步．程序框图如图所示．13．某工厂2010年生产轿车200万辆，技术革新后预计每年的产量比上一年增加5%，问最早哪一年生产的轿车超过300万辆？试设计算法并画出相应的程序框图．解算法如下：第一步：n＝2 010；第二步：a＝200；第三步：T＝0.05a；第四步：a＝a＋T；第五步：n＝n＋1；第六步：若a>300，输出n.否则执行第三步．程序框图：2．画程序框图必须遵守一些共同的规则：(1)使用框图的符号要标准．(2)框图一般按从上到下、从左到右的顺序画．(3)除了判断框外，大多数框图符号只有一个进入点和一个退出点，判断框是唯一具有超过一个退出点的框图符号．(4)判断框有两种：一种是“是”与“否”两个分支的判断，而且有且仅有两个结果；另一种是多分支判断，有几种不同的结果，这种判断框中学阶段很少用到．(5)在图形符号内描述的语言要简练清楚．。

新人教版高中数学必修3 全册同步测试题及解析答案篇一:高一数学必修3全册各章节课堂同步习题（详解答案）第一章算法初步1.1算法与程序框图1.1.1算法的概念班次姓名［自我认知］:1.下面的结论正确的是（）.A.一个程序的算法步骤是可逆的B. 一个算法可以无止境地运算下去的C.完成一件事情的算法有且只有一种D. 设计算法要本着简单方便的原则2.下面对算法描述正确的一项是（）. A.算法只能用自然语言来描述B.算法只能用图形方式来表示C.同一问题可以有不同的算法D.同一问题的算法不同，结果必然不同3.下面哪个不是算法的特征（）A.抽象性B.精确性C. 有穷性D.唯一性4.算法的有穷性是指（）A.算法必须包含输出B.算法中每个操作步骤都是可执行的C.算法的步骤必须有限D.以上说法均不正确5.早上从起床到出门需要洗脸刷牙(5min)、刷水壶(2min)、烧水(8min)、泡面(3min)、吃饭(lOmin)、听广播(8min)几个步骤，从下列选项中选最好的一种算法()A.S1洗脸刷牙、S2 刷水壶、S3烧水、S4泡面、S5吃饭、S6听广播 B.S1刷水壶、S2烧水同时洗脸刷牙、S3泡面、S4吃饭、S5听广播 C. S1刷水壶、S2烧水同时洗脸刷牙、S3泡面、S4吃饭同时听广播D.S1吃饭同时听广播、S2泡面；S3烧水同时洗脸刷牙；S4刷水壶6.看下面的四段话，其中不是解决问题的算法是()A.从济南到北京旅游，先坐火车,再坐飞机抵达B.解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1C.方程x2?l?0有两个实根D.求1+2+3+4+5的值，先计算1+2=3,再计算3+3=6,6+4=10,10+5=15,最终结果为15 7.已知直角三角形两直角边长为a,b,求斜边长c的一个算法分下列三步：①计算c?a,b的值；③输出斜边长c的值，其中正确的顺序是()A.①②③B.②③①C.①③②D.②①③［课后练习］:8.若f?x?在区间?a,b?内单调，且f?a??f?b??O,则f?x?在区间?a,b?内()A.至多有一个根B.至少有一个根C.恰好有一个根D.不确定9.已知一个学生的语文成绩为89,数学成绩为96,外语成绩为99.求他的总分和平均成绩的一个算法为：第一步：取A=89 ,B=96 ,C=99；第二步：①；第三步：②;第四步：输出计算的结果.10.写出求1+2+3+4+5+6+7+100的一个算法.可运用公式l+2+3+?+n= 第一步①；第二步②;第三步输出计算的结果.11.写出Ix2x3x4x5x6的一个算法.12.写出按从小到大的顺序重新排列x,y,z三个数值的算法. n（n?l）直接计算.21.1. 2程序框图［自我认知］:1 •算法的三种基本结构是（）A.顺序结构、条件结构、循环结构B.顺序结构、流程结构、循环结构C.顺序结构、分支结构、流程结构D .流程结构、循环结构、分支结构2 .程序框图中表示判断框的是（）A.矩形框B.菱形框D.圆形框D.椭圆形框3.如图⑴、（2）,它们都表示的是输出所有立方小于1000的正整数的程序框图，那么应分别补充的条件为（）（1）33(2)3A.⑴n>1000 ? (2)n<1000 ?B.⑴n<1000 ?⑵n>1000 ?C.(Dn<1000?⑵n>1000 ?D. (l)n<1000 ?(2)n<1000?4.算法共有三种逻辑结构，即顺序逻辑结构,条件逻辑结构和循环逻辑结构，下列说法正确的是()A.—个算法只能含有一种逻辑结构B.一个算法最多可以包含两种逻辑结构C. 一个算法必须含有上述三种逻辑结构D.—个算法可以含有上述三种逻辑结构的任意组合［课后练习］:5.给出以下一个算法的程序框图(如下图所示)，该程序框图的功能是()A.求输出a,b,c三数的最大数B.求输出a,b,c三数的最小数3333C.将a,b,c按从小到大排列D.将a,b,c按从大到小排列第5题图第6题图6.右边的程序框图（如上图所示），能判断任意输入的数x 的奇偶性：其中判断框内的条件是A.m?O?B.x?O ?C.x?l ?D.m?l?7.在算法的逻辑结构中，要求进行逻辑判断，并根据结果进行不同处理的是哪种结构（）A.顺序结构B.条件结构和循环结构C.顺序结构和条件结构D.没有任何结构?x2?l（x?0）8.已知函数f?x???，设计一个求函数值的算法，并画出其程序框图（x?0）?2x?l1.1.2程序框图（第二课时）［课后练习］:班次姓名1 . 如图⑴的算法的功能是.输出结果i=,i+2=.2.如图⑵程序框图箭头a指向①处时，输出s=.箭头a指向②处时，输出s=.3.如图⑷所示程序的输出结果为s=132,则判断中应填A、i>10? B、i>ll? C、i<ll?D、i>12? 4.如图⑶程序框图箭头b指向①处时，输出s=.箭头b指向②处时, 输出S= _________5、如图⑸是为求1-1000的所有偶数的和而设计的一个程序空白框图，将空白处补上。

1．1．2．1一、选择题1．下列关于程序框图的说法中正确的个数是( )①用程序框图表示算法直观、形象，容易理解②程序框图能够清楚地展现算法的逻辑结构，也就是通常所说的一图胜万言③在程序框图中，起止框是任何流程不可少的④输入和输出框可用在算法中任何需要输入、输出的位置A．1个B．2个C．3个D．4个[答案] D[解析] 由程序框图定义可知，①②③④都正确．2．在程序框图中，算法中间要处理数据或计算，可分别写在不同的( )A．处理框内B．判断框内C．输入、输出框内D．终端框内[答案] A[解析] 由处理框的意义可知，对变量进行赋值，执行计算语句，处理数据，结果的传送等都可以放在处理框内，∴选A.3．在画程序框图时如果一个框图需要分开来画，要在断开处画上( )A．流程线B．注释框C．判断框D．连结点[答案] D4．在程序框图中，一个算法步骤到另一个算法步骤的连接用( )A．连结点B．判断框C．流程线D．处理框[答案] C[解析] 流程线的意义是流程进行的方向，一个算法步骤到另一个算法步骤表示的是流程进行的方向，故选C.而连结点是当一个框图需要分开来画时，在断开处画上连结点．判断框是根据给定条件进行判断，处理框是赋值、计算、数据处理、结果传送，所以A、B、D都不对．5．下面是求方程ax2＋bx＋c＝0(a≠0)的根的程序框图．则判断框内(1)处应填的条件为( )A．Δ>0? B．Δ≥0?C．Δ<0? D．Δ≤0?[答案] C[解析] 判断框中条件(1)满足时，输出方程无实数解，故判断的条件应为Δ<0.6．(08·宁夏海南文)下面的程序框图，如果输入三个实数a，b，c，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的( )A．c>x?B．x>c?C．c>b?D．b>c?[答案] A[解析] x 开始取a 的值，经过第一次判断后，x 取a 与b 中较大的值，又最后输出的是三个数a ，b ，c 中的最大值为x ，故第二次判断的条件应为c >x ？，故选A.7．如图，若f (x )＝x 2，g (x )＝log 2x ，输入x 的值为0.25，则输出结果为( )A ．0.24B ．－2C ．2D ．－0.25[答案] B[解析] 由框图知，h (x )是f (x )与g (x )中的较小值，∵f (0.25)＝0.252＝116，g (0.25)＝log 20.25＝－2，∴h (0.25)＝－2.8．如图所示的程序框图运行后输出结果为12，则输入的x 值为( )A ．－1B.22C.12 D ．－1或22[答案] D[解析] 程序框图表示的是求分段函数f (x )＝⎩⎪⎨⎪⎧x 2 x ≥142xx ≤0log 12x 0<x <14的函数值，由⎩⎪⎨⎪⎧x 2＝12x ≥14得，x ＝22；由⎩⎪⎨⎪⎧2x ＝12x ≤0得，x ＝－1.又⎩⎪⎨⎪⎧log 12x ＝120<x <4无解，故选D.二、填空题9．(09·上海理)某算法的程序框图如图所示，则输出量y 与输入量x满足的关系式是______________________．[答案] y ＝⎩⎪⎨⎪⎧2x(x ≤1)x －2 (x >1)[解析] 由程序框图可知，当x >1时，y ＝x －2；当x ≤1时，y ＝2x， ∴输出量y 与输入量x 满足的关系式是y ＝⎩⎪⎨⎪⎧2x(x ≤1)x －2 (x >1).10．读下列流程图填空：(1)流程图(1)的算法功能是________________． (2)流程图(2)的算法功能是________________． (3)流程图(3)的算法功能是________________． (4)流程图(4)的算法功能是________________． [答案] (1)求输入的两个实数a 与b 的和．(2)求以输入的两个正数a ，b 为直角边长的直角三角形斜边的长． (3)求输入两数a ，b 的差的绝对值． (4)求函数f (x )＝|x －3|＋1，即分段函数f (x )＝⎩⎪⎨⎪⎧x －2 (x >3)4－x (x ≤3)的函数值．11．判断正整数x 的奇偶性的程序框图如下，则①处应为________．[答案] r ＝1?[点评] (1)想一想，若在判断框内的条件改为r ＝0，则上面的程序框图如何修改？(将是与否互换)(2)r 为x 除以2的余数可表示为r ＝x MOD 2.12．(2010·广州市)某算法的程序框如图所示，若输出结果为12，则输入的实数x 的值是________．[答案]2[解析] 当x ≤1时，y ＝x －1≤0，∵输出结果为12，∴x >1，∴log 2x ＝12，∴x ＝ 2.三、解答题13．画出求坐标平面内两点A (a ，b )，B (c ，d )之间距离的程序框图． [解析]14．为了加强居民的节水意识，某市制定了以下生活用水收费标准：每户每月用水未超过7立方米时，每立方米收费1.0元，并加收0.2元的城市污水处理费；超过7立方米的部分，每立方米收费1.5元，并加收0.4元的城市污水处理费．设某户每月用水量为x 立方米，应交纳水费y 元，请你设计一个输入用水量、输出应交水费额的算法，画出程序框图．[解析] y 与x 之间的函数关系式为：y ＝⎩⎪⎨⎪⎧1.2x (0≤x ≤7)1.9x －4.9 (x >7)算法设计如下：S 1 输入每月用水量x ；S 2 判断输入的x 是否超过7；若x >7，则应交水费y ＝1.9x －4.9；否则应交纳水费y ＝1.2x ；S 3 输出应交水费y .程序框图如图所示．15．试描述判断圆(x －a )2＋(y －b )2＝r 2和直线Ax ＋By ＋C ＝0(A 2＋B 2≠0)位置关系的算法，画出流程图．[解析] 直线与圆的位置关系有三种，相离、相切、相交．如果圆心到直线的距离d 大于r ，则直线与圆相离；d ＝r ，则直线与圆相切；d <r ，则直线与圆相交．因此，我们可以先求出圆心到直线的距离d ，然后再和r 相比较．因此需用条件分支结构来描述．第一步：输入圆心的坐标a 、b 和半径r ，直线方程的系数A 、B 、C ； 第二步：计算z 1＝Aa ＋Bb ＋C ； 第三步：计算z 2＝A 2＋B 2； 第四步：计算d ＝|z 1|z 2；第五步：如果d >r 则相离；如果d ＝r 则相切；如果d <r 则相交． 程序框图如图所示．。

1．2．1一、选择题1．关于赋值语句需要注意的事项中不正确的是( )A ．赋值号左边只能是变量名字，而不是表达式B ．赋值号左、右不能对换C ．不能利用赋值语句进行代数式的演算D ．赋值号与数学中的等号的意义相同[答案] D[解析] 关于赋值语句中一定要注意的事项是把赋值号与数学中的等号区分开，它们的意义不相同．2．下列所给的式子，前一个是算术式子，后一个是QBASIC 语言中的对应式子，正确的有________个．( )①e 5：e ^5②334：3^3/4 ③lg7：LOG 10(7)④3：SQR(3)⑤|x －3|：ABS(x －3)A ．1B ．2C ．3D ．4 [答案] C[解析] 在QBASIC 语言中幂底数为e 时有专用符号exp ( )，如e x 表达为exp (x )．∴e 5应为exp (5)；当幂指数为分式等代数式时，应加括号，乘方优先于乘除，∴334应为3^(3/4)；常用对数的指令为LOG 10( )，故(3)正确；④⑤都正确，∴选C.3．赋值语句“x ＝x ＋1”的正确解释为( )A ．x 的值与x ＋1的值可能相等B ．将原来x 的值加上1后，得到的值替换原来x 的值C ．这是一个错误的语句D ．此表达式经过移项后，可与x ＝x －1功能相同[答案] B4．以下给出的赋值语句中，正确的有________个．( )①3＝B ②x ＋y ＝0③A ＝B ＝－2 ④T ＝T *T⑤A ＝A ＋1A ．0B ．1C ．2D ．3[答案] C[解析] 根据赋值语句特点知，①②③都不对，赋值号左边应该是一个变量，故①②不对；一个赋值语句一次只能给一个变量赋值，不能出现两个以上“＝”号，∴③不对，④⑤正确．5．运行下面程序，输出结果为( )程序：a ＝3b ＝5a ＝a ＋bb ＝a \bPRINT a ，bA ．3,5B ．8，53C ．8,1D ．8，85 [答案] C[解析] 第3,4两句给a ，b 重新赋值后a ＝8，b ＝1，∴选C.[点评] a \b 表示整数a 除以整数b 所得的整数商．6．下列程序若输出的结果为4，则输入的x 值可能是( )[答案] D[解析] 由x 2＋2x ＋1＝4得，x ＝1或x ＝－3.7．执行下列算法语句后的结果(x MOD y 表示整数x 除以整数y 的余数)为( )INPUT “x ，y ＝”；x ，yA ＝x *yB ＝x MOD yC＝A*y＋BPRINT A，B，CEND(运行时从键盘上输入16和5)．A．A＝80，B＝1，C＝401B．A＝80，B＝3，C＝403C．A＝80，B＝3.2，C＝403.2D．A＝80，B＝3.2，C＝404[答案] A[解析]第一句输入x＝16，y＝5，第二句A＝xy＝80，第三句B取x除以y的余数，∴B ＝1，故选A.8．已知函数f(x)＝x2－1，g(x)＝2x＋3，下面程序是求f(g(0))＋g(f(0))的值的算法语句：x＝0g＝2]①y1＝ff＝x*x－1g＝____②____y2＝gy＝y1＋y2PRINT yEND则①、②处应填入的表达式为()[答案] B[解析]由算法语句知，y1＝f(g(0))，g＝g(0)，故①处应为g*g－1，同理②处应为2]二、填空题9．写出下列程序运行的结果输出结果为________．输出结果为________．[答案](1)128(2)a＝1，b＝0，c＝－1(3)f＝48，g＝99(4)a＝10，b＝20，c＝30，a＝20，b＝30，c＝20.[解析](1)执行第三、四句后，a＝4，b＝－2，执行第五句后，a＝4×(－2)4×4＝128，故输出a的值为128；(2)执行第三句后，c＝－1，执行第四句后，b＝0，故输出a＝1，b＝0，c＝－1；(3)第一句输入a值2，第二句f＝a2－1＝3，第三句g＝2a＋3＝7，第四句f＝g2－1＝48，第五句g＝2f＋3＝99，最后输出f＝48，g＝99.(4)第一句输入a＝10，b＝20，c＝30，第二句输出a＝10，b＝20，c＝30，第三句a＝20，第四句b＝30，第五句c＝20，第六句输出a＝20，b＝30，c＝20.10．写出下列程序的运行结果：(3)x ＝－31.24y ＝INT(x )x ＝ABS(y )x ＝x MOD3PRINT xEND运行结果为________．(注：INT(x )表示不超过x 的最大整数)[答案] (1)4 (2)4 (3)2[解析] (1)对A 重复赋值，A 总是取最后赋出的值，故依次执行后为，A ＝－26→A ＝－20→A ＝4，因此最后输出A 的值4.(2)第一句x ＝3，第二句y ＝x 3＝27，第三句给x 重新赋值后x ＝53，第四句给y 重新赋值后y ＝27＋535＝16，第五句x ＝4，第六句输出x 的值4. (3)第一句x ＝－31.24，第二句y ＝－32，第三句给x 重新赋值x ＝|y |＝32，第四句给x 重新赋值为32除以3的余数2，最后输出x 的值为2.11．(09·江苏理)下图是一个算法的流程图，最后输出的W ＝________.[答案] 22[解析] 由程序框图知，运行过程为：S ＝0，T ＝1，S ＝1；不满足S ≥10，故T ＝3，S ＝8；不满足S ≥10，故T ＝5，S ＝17；此时满足S ≥10，故W ＝22，输出W 的值后结束．三、解答题12．编写一个程序，求用长度为l 的细铁丝分别围成一个正方形和一个圆时所围成的正方形和圆的面积．要求输入l 的值，输出正方形和圆的面积(π取3.14)．[解析] 设围成的正方形的边长为a ，依题意4a ＝l ，a ＝l 4，所以正方形的面积为S 1＝⎝⎛⎭⎫l 42＝l 216；同理若设围成的圆的半径为R ，则2πR ＝l ，R ＝l 2π，所以圆的面积为S 2＝πR 2＝π⎝⎛⎭⎫l 2π2＝l 24π.因此可以用顺序结构实现这一算法，采用INPUT 语句输入l 的值，利用赋值语句得到面积，最后输出两个面积．程序如下：13．某粮库3月4日存粮50000kg,3月5日调进粮食30000kg,3月6日调出全部存粮的一半，求每天的库存粮食数，画出程序框图．[解析] 库存的粮食数每天都在变，可以设置一个变量来表示每天的库存粮食数． 程序框图如图所示．程序：a＝50000PRINT“3月4日存粮数”；aa＝a＋30000PRINT“3月5日存粮数”；aa＝a/2PRINT“3月6日存粮数”；aEND.14．读下列程序，写出运行结果．a＝－6，b＝2，a＝ABS(a)，b＝b^2a＝a＋b，c＝a－2][解析]运行以上程序依次得到：a＝－6，b＝2→a＝6，b＝4→a＝10，c＝2→a＝5，b＝9→b＝3.最后输出a，b，c的值：5,3,2.15．已知直线方程为Ax＋By＋C＝0(A·B≠0)，试编写一个程序，要求输入符合条件的A、B、C的值，输出该直线在x轴、y轴上的截距和直线的斜率．[解析]INPUT A、B、CM＝(－C)/AN＝(－C)/Bk＝(－A)/BPRINT“该直线在x轴上的截距为：”MPRINT“该直线在y轴上的截距为：”NPRINT“该直线的斜率为：”k END。

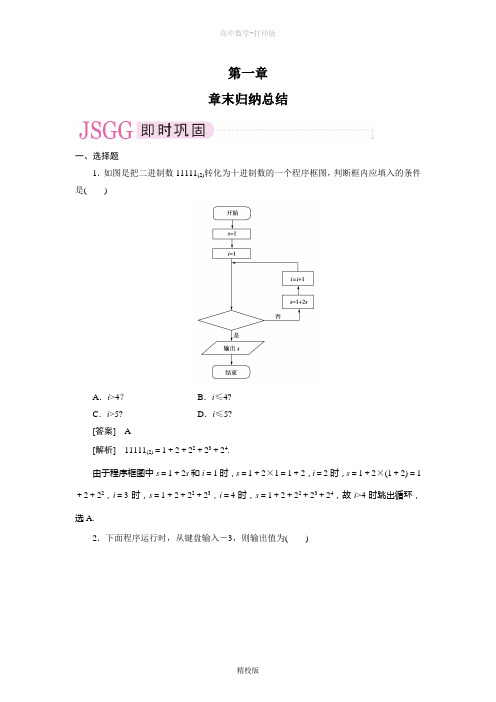
第一章章末归纳总结一、选择题1．如图是把二进制数11111(2)转化为十进制数的一个程序框图，判断框内应填入的条件是()A．i>4？B．i≤4?C．i>5? D．i≤5?[答案] A[解析]11111(2)＝1＋2＋22＋23＋24.由于程序框图中s＝1＋2s和i＝1时，s＝1＋2×1＝1＋2，i＝2时，s＝1＋2×(1＋2)＝1＋2＋22，i＝3时，s＝1＋2＋22＋23，i＝4时，s＝1＋2＋22＋23＋24，故i>4时跳出循环，选A.2．下面程序运行时，从键盘输入－3，则输出值为()A ．－3B ．3C ．1D ．－1[答案] D[解析] 由程序知，当x >0时，y ＝1；否则，当x ＝0时，y ＝0；当x <0时，y ＝－1. ∴y ＝⎩⎨⎧1 (x >0)0(x ＝0)－1 (x <0).3．如图，该程序运行后输出结果为( )A ．14B ．16C ．18D ．64[答案] B[解析] A 初值为10，步长为－1，到A ＝3循环最后一次，A ＝2时，输出S ，每循环一次，S 的值增加2，故最后结果为S ＝16.[点评] 注意程序项的改变引起结论的变化，请思考在下述情形下输出结果分别是多少？①S＝S＋2与A＝A－1交换前后次序．②S＝S＋2改为S＝A＋2.③A＝A－1改为A＝A－2.④S＝S＋2改为S＝S＋A.⑤S＝S＋2改为S＝S＋2]4．(2010·福建文，6)阅读右图所示的程序框图，运行相应的程序，输出的i值等于()A．2 B．3C．4 D．5[答案] C[解析]S＝0i＝1a＝1·21＝2S＝0＋2＝2i＝1＋1＝2a＝2·22＝8S＝2＋8＝10i＝2＋1＝3a＝3·23＝24S＝10＋24＝34i＝3＋1＝4∵S ＝34>11所以输出的i 值等于4.二、填空题5．(2010·北京文，9)已知函数y ＝⎩⎪⎨⎪⎧log 2x ， x ≥2，2－x ， x <2.如图表示的是给定x 的值，求其对应的函数值y 的程序框图．①处应填写________；②处应填写________．[答案] x <2，y ＝log 2x[解析] 根据分段函数解析式及程序框图知，当满足x <2时，执行y ＝2－x ，故判断框中条件为x <2，不满足条件x <2，即x ≥2时，y ＝log 2x ，故②中为y ＝log 2x .三、解答题6．用后测试型语句编写一个程序，输出使1＋4＋7＋…＋n ≥300成立的最小的正整数n .[解析] 用S 表示累加的和，i 表示每次加的数，则i 步长为3.若S <300则继续加，S ≥300则输出最小整数n 的值．S ＝0i ＝1DOS ＝S ＋ii ＝i ＋3LOOP UNTIL S >＝300n ＝i －3PRINT nEND[点评]由于循环体中S＝S＋i与i＝i＋3的顺序是计算S后，i又加上了3，故满足条件时，i的值比实际要求的n值大3，故n＝i－3.若将程序语句改为：S＝1i＝1DOi＝i＋3S＝S＋iLOOP UNTIL S>＝300PRINT____①____END则①处应输出的结果是什么呢？这里语句若改为先S＝S＋i，后i＝i＋3可以吗？。

2021-2022年高中数学课后强化训练（含详解）2.1.3 新人教版必修3一、选择题1．某社区有500个家庭，其中高收入家庭125户，中等收入家庭280户，低收入家庭95户．为了调查社会购买力的某项指标，要从中抽取1个容量为100户的样本，记作①；某学校高一年级有12名女排运动员，要从中选出3名调查学习负担情况，记作②.那么完成上述两项调查应采用的抽样方法是( ) A．①用简单随机抽样法；②用系统抽样法B．①用分层抽样法；②用简单随机抽样法C．①用系统抽样法；②用分层抽样法D．①用分层抽样法；②用系统抽样法[答案] B[解析] 对于①，总体由高收入家庭、中等收入家庭和低收入家庭差异明显的3部分组成，而所调查的指标与收入情况密切相关，所以应采用分层抽样法．对于②，总体中的个体数较少，而且所调查内容对12名调查对象是“平等”的，所以适宜采用简单随机抽样法．2．简单随机抽样、系统抽样和分层抽样之间的共同点是( )A．都是从总体中逐个抽取B．将总体分成几部分，按事先确定的规则在各部分抽取C．抽样过程中每个个体被抽到的机会是相等的D．将总体分成几层，然后各层按照比例抽取[答案] C[解析] 由三种抽样方法的定义可知，在抽样过程中，每个个体被抽到的机会相等，∴选C.3．(08·重庆文)某校高三年级有男生500人，女生400人，为了解该年级学生的健康情况，从男生中任意抽取25人，从女生中任意抽取20人进行调查，这种抽样方法是( )A．简单随机抽样法B．抽签法C．随机数表法D．分层抽样法[答案] D4．一个年级有12个班，每个班同学从1～50排学号，为了交流学习经验，要求每班学号为14的同学参加交流活动，这里运用的是什么抽样方法( ) A．分层抽样B．抽签法C．随机数表法D．系统抽样[答案] D[解析] 实际上是把总体分成12个部分，从每个部分都抽取学号为14的学生．这正是系统抽样的方法．5．某工厂生产A、B、C三种不同型号的产品，产品的数量之比依次为347.现在用分层抽样的方法抽出容量为n的样本，样本中A号产品有15件，那么样本容量n为( )A．50 B．60C．70 D．80[答案] C[解析] 由分层抽样定义知，3＋4＋7n ＝315，∴n＝70，故选C.6．(09·陕西文)某单位共有老、中、青职工430人，其中青年职工160人，中年职工人数是老年职工人数的2倍．为了解职工的身体状况，现采用分层抽样方法进行调查，在抽取的样本中有青年职工32人，则该样本中的老年职工人数为( )A．9 B．18C．7 D．36[答案] B[解析] 由题意知青、中、老职工的人数分别为160、180、90，∴三者比为16：18：9，∵样本中青年职工32人，∴老年职工人数为18，故选B.7．xx年某市共有30万公务员参加计算机等级考试，为了分析考试情况，评卷人员对其中1000名公务员的成绩进行分析，下列说法中正确的是( ) A．30万公务员是总体B．每名参加考试的公务员的考试成绩是个体C．1000名公务员是总体的一个样本D．1000名公务员是样本的容量[答案] B[解析] 30万公务员的计算机考试成绩是总体，30万是总体容量，其中每名参加考试的公务员的考试成绩是个体，1000名公务员的成绩是样本，1000是样本容量，∴选B.8．在某班元旦晚会上，现场的一个游戏要求从观众中选出5人参与，下列抽样方法最合适的是( )A．分层抽样B．系统抽样C．随机数表法D．抽签法[答案] D[解析] 元旦晚会上的游戏，该班任何一个人参与都可以，故不需要分层抽样，人数不太多不需要系统抽样，故用简单随机抽样即可，这种情形下，用抽签法更合适．9．采用分层抽样的方法抽取一个容量为45的样本，高一年级被抽取20人，高三年级被抽取10人，高二年级共有300人，则这个学校共有高中学生____人．( )A．1350 B．675C．900 D．450[答案] C[解析] 高二年级被抽取的人数为45－20－10＝15，则每层的抽样比为15300＝120，所以学生总数为45÷120＝900，即这个学校共有高中学生900人．10．某单位有老年人28人，中年人54人，青年人81人．为了调查它们的身体状况，从他们中抽取容量为36的样本，最适合抽取样本的方法是( ) A．简单随机抽样B．系统抽样C．分层抽样D．先从老年人中剔除1人，再用分层抽样[答案] D[解析] 总体总人数为28＋54＋81＝163(人)．样本容量为36，由于总体由差异明显的三部分组成，考虑用分层抽样．若按36163取样本，无法得到整解．故考虑先剔除1人，抽取比例变为36162＝29.则中年人取54×29＝12(人)，青年人取81×29＝18(人)，先从老年人中剔除1人，老年人取27×29＝6(人)，组成容量为36的样本．二、填空题11．某地区有农民、工人、知识分子家庭共计xx户，其中农民家庭1 600户，工人家庭303户．现要从中抽出容量为40的样本，则在整个抽样过程中，可以用到下列抽样方法中的________．(将你认为正确的选项的序号都填上)①简单随机抽样②系统抽样③分层抽样[答案] ①②③[解析] 为了保证抽样的合理性，应对农民、工人、知识分子分层抽样；在各层中采用系统抽样和简单随机抽样．抽样时还要先用简单随机抽样剔除多余个体．12．(08·天津文)一个单位共有职工200人，其中不超过45岁的有120人，超过45岁的有80人．为了调查职工的健康状况，用分层抽样的方法从全体职工中抽取一个容量为25的样本，应抽取超过45岁的职工________人．[答案] 1013．(09·广东文)某单位200名职工的年龄分布情况如图所示，现要从中抽取40名职工作样本，用系统抽样法，将全体职工随机按1～200编号，并按编号顺序平均分为40组(1～5号，6～10号…，196～200号)．若第5组抽出的号码为22，则第8组抽出的号码应是________．若用分层抽样方法，则40岁以下年龄段应抽取________人．[答案] 37,20[解析] 由分组可知，抽号的间隔为5，又因为第5组抽出的号码为22，所以第8组抽出的号码为22＋(8－5)×5＝37.40岁以下年龄段的职工数为200×0.5＝100，则应抽取的人数为40200×100＝20人．14．(08·湖南文)从某地区15000位老人中随机抽取500人，其生活能否自理的情况如下表所示.男女能178278不能2321[答案] 60[解析] 男性比女性多15000500×(23－21)＝60(人)．三、解答题15．某班有40名男生，25名女生，已知男、女身高有明显不同，现欲调查平均身高．准备抽取130.采用分层抽样方法，抽取男生1人，女生1人，你认为这种做法妥当否？如果让你来调查，你准备怎样做？[解析] 由于取样比例数过小，仅抽取2人，很难准确反映总体情况，况且男、女生差异较大，抽取人数相同，也不尽合理，故此法不妥当．抽取人数太多，失去了抽样调查的统计意义，取样太少，不能准确反映真实情况，考虑到本题应采用分层抽样及男、女生各自的人数，故按51抽取更妥贴，即男生抽取8人，女生抽取5人，各自用抽签法或随机数法抽取组成样本．16．某校在校高中学生有1600人，其中高一学生520人，高二学生500人，高三学生580人．如果想通过抽查其中的80人来调查学生的消费情况，考虑到学生的年级高低消费情况有明显差别，而同一年级内消费情况差异较小，问应当采用何种抽样方法？高三学生中应抽查多少人？[分析] 各部分之间有明显差别是分层抽样的依据．至于各层内用什么方法抽样，是灵活自主的，可系统抽样，也可简单随机抽样．本题只问采用何种抽样方法，而不必答出如何抽样的过程．[解析] 因为不同年级的学生消费情况有明显的差别，所以应采用分层抽样．由于520∶500∶580＝26∶25∶29，于是将80分成26∶25∶29的三部分，该三部分各抽个体数分别为26x,25x,29x，则26x＋25x＋29x＝80，解得x＝1.故高三年级中应抽取29人．17．一批产品中，有一级品100个，二级品60个，三级品40个，分别用系统抽样法和分层抽样法，从这批产品中抽取一个容量为20的样本．[解析] (1)系统抽样方法：将200件产品编号为1～200，然后将编号分成20个部分，在第1部分中用简单随机抽样法抽取一件产品．如抽到5号，那么得到的20个编号为5号，15号，25号，…，195号的样本．(2)分层抽样方法：因为100＋60＋40＝200，20200＝110，所以100×110＝10,60×110＝6,40×110＝4.因此在一级品、二级品和三级品中分别抽取10件，6件和4件，即得到所需样本．18．对某单位1000名职工进行某项专门调查，调查的项目与职工任职年限有关，人事部门提供了如下资料：请根据上述资料，设计一个样本容量为总体容量的110的抽样方案．[解析] 在这个问题中，总体是某单位的1000名职工，并且已经知道人数的分布情况，可以用分层抽样法抽取样本．把总体分三层，任职5年以下抽取个体数30010＝30，任职5～10年的抽取个体数50010＝50，任职10年以上的抽取个体数200×110＝20，用系统抽样方法或简单随机抽样方法在各层中抽取以上数目的样本．25212 627C 扼24319 5EFF 廿39946 9C0A 鰊 I36821 8FD5 迕+aw28422 6F06 漆36374 8E16 踖Q29399 72D7 狗20023 4E37 丷。

高一数学必修3人教版课后强化训练含详解：第三章章末归纳总结优化方案教考资源网第三章章末归纳总结一、选择题1．掷一颗骰子，出现偶数点或出现不小于4的点数的概率是2A.35答案]A[解析]对立事件为出现1点或3点，22∴＝156，则判断框中应填B．3D．－221世纪教育网--中国最大型、最专业的中小学教育资源门户网站。

自于资源最齐全的２１世纪教育网A．i≥10C．i≤11[答案]DB．i≥11D．i≥12[解析]根据处理框中，um＝um×i，um初值为1，i初值为13，∴第一次判断后执行循环体得到um＝13≠156；i＝12应进行第二次循环；第二次循环后um＝13×12＝156，i＝11；此时作出判断，条件不满足跳出循环，输出um的值156，故条件为i≥12 9．如图，汉诺塔问题是指有3根杆子A、B、C，B杆上有若干碟子，把所有碟子从B杆移到A杆上，每次只能移动一个碟子，大的碟子不能叠在小的碟子上面．把B杆上的4个碟子全部移到A 杆上，最少需要移动次．A．12C．17[答案]B[解析]将4个碟子按从小到大顺序编号为1,2,3,4号．用—→M表示第i号碟子移到M杆上．如②—→B表示第2号碟子移到B杆上，要保证大碟不能叠在小碟的上面，最少需要移动15次，下面是移动的步骤．S1①—→CS6：②—→CS11：①—→BS2②—→AS7：①—→CS12：③—→AS3①—→AS8：④—→AS13：①—→CS4③—→CS9：①—→AS14：②—→AS5①—→BS10：②—→BS15：①—→A∴选B10．登上一个四级的台阶，每步最多2阶，可以选择的方式共有________种．A．3B．4C．5D．6[答案]C[解析]将四级台阶从下到上依次编号为1,2,3,4，登上台阶的方式为①1—→2—→3—→4，②1—→2—→4，③1—→3—→4，④2—→3—→4，⑤2—→4其中1—→3—→4表示第一步上第一阶，第二步上第三阶，第三步上第四阶，其余类推．∴选C11．以下程序运行后输出结果为IN＝t/aEND程序运行时，从键盘输入a＝18，b＝30A．6B．90C．540D．15[答案]B[解析]这是求从键盘输入的两个正整数a，b的最小公倍数的程序，程序先求a与b的积t和用等值算法求a，b的最大公约数，最后用t与最大公约数的商即m表示两数的最小公倍数并输出，选B12．运行以下程序输出结果为＝0T＝0i＝1DOT＝T＋i＝＋Ti＝i＋1LOO与“75”比较，如果m小于75，则输出mS2如果序列中还有其他数，重复S1S3在序列中一直到没有可比的数为止．18．本题满分12分平面上一条直线将平面分成2块，2条直线最多可以将平面分成4块，设n条直线最多可以将平面分成fn 块，可以证明fn满足关系式fn＋1＝fn＋n＋1n≥1，写出应用此关系式求f10的程序．[解析]由题意可知f1＝2，f2＝4，据递推关系式fn＋1＝fn ＋n＋1n≥1可以递推出f3＝7，f4故可用循环语句来完成程序．用变量表示fn，初值＝f1，输出值＝f10，即f9＋9＋1，故控制循环的变量n，初值为1，步长1，终值为9程序为：＝2n＝1DO21世纪教育网--中国最大型、最专业的中小学教育资源门户网站。

1．3．2一、选择题1．两个整数490和910的最大公约数是( )A ．2B ．10C ．30D ．70[答案] D[解析] 490＝72×2×5,910＝13×7×2×5，∴最大公约数为7×2×5＝70.2．用秦九韶算法计算多项式f (x )＝3x 6＋4x 5＋5x 4＋6x 3＋7x 2＋8x ＋1当x ＝0.4时的值时，需要做乘法和加法的次数分别是( )A ．6,6B ．5,6C ．5,5D ．6,5[答案] A[解析] 秦九韶算法中最多需用加法和乘法的次数，由多项式的次数n 可知，∴选A.3．已知f (x )＝3x 3＋2x 2＋x ＋4，则f (10)＝( )A ．3214B ．3210C ．2214D ．90[答案] A[解析] ∴答案A.4．将二进制数1101化为十进制数为( )A ．10B ．11C ．12D ．13[答案] D[解析] 1101(2)＝1×23＋1×22＋0×21＋1＝13.5．以下各数中有可能是五进制数的为( )A ．55B ．106C ．732D ．2134[答案] D[解析] 五进制数只需0,1,2,3,4五个数字．6．下列二进制数中最大的数是( )A ．111(2)B ．1001(2)C ．110(2)D ．101(2)[答案] B[解析] 据k 进制数的位置原则知，四位数一定大于三位数，故选B.也可以先把它化为十进制数，再比较．7．如图所示的程序框图输出的结果是( )A.34B.45C.56D.67 [答案] C[解析] i ＝1≤4满足条件，执行第一次循环后，A ＝23，i ＝2；i ＝2≤4满足条件，执行第二次循环后，A ＝34，i ＝3； i ＝3≤4满足条件，执行第三次循环后，A ＝45，i ＝4；i ＝4≤4满足条件，执行第四次循环后，A ＝56，i ＝5；i ＝5≤4不满足条件，跳出循环，输出A ＝56. 8．用秦九韶算法求多项式f (x )＝12＋35x －8x 2＋79x 3＋6x 4＋5x 5＋3x 6的值，当x ＝－4时，v 4的值为( )A ．－57B ．124C ．－845D ．220[答案] D[解析] 依据秦九韶算法有v 0＝a 6＝3，v 1＝v 0x ＋a 5＝3×(－4)＋5＝－7，v 2＝v 1x ＋a 4＝－7×(－4)＋6＝34，v 3＝v 2x ＋a 3＝34×(－4)＋79＝－57，v 4＝v 3x ＋a 2＝－57×(－4)＋(－8)＝220.9．二进制数算式1010(2)＋10(2)的值是( )A ．1011(2)B ．1100(2)C ．1101(2)D ．1000(2)[答案] B[解析] 1010(2)＋10(2)＝(1×23＋0×22＋1×21＋0×20)＋(1×21＋0×20)＝12＝1100(2)，故选B.[点评] 可以按进位制原则，直接象通常的十进制加法一样计算．注意k 进制是满k 进1.10．下列各数中最小的数为( )A ．101011(2)B ．1210(3)C ．110(8)D ．68(12)[答案] A[解析] 101011(2)＝1×25＋1×23＋1×2＋1＝43,1210(3)＝1×33＋2×32＋1×3＝48,110(8)＝1×82＋1×8＝72,68(12)＝6×12＋8＝80，故选A.[点评] 相同进位制数的大小可以看位数，按“位值”原则比较大小，如132(4)>123(4),101(2)>11(2)，但不同进位制的数之间比较大小，不适用“位值”原则，一般都是先化为十进制数再比较大小．二、填空题11．秦九韶算法是我国南宋数学家________在他的代表作________中提出的一种用于计算一元n 次多项式的值的方法．[答案] 秦九韶 《数书九章》12．(1)十进制数化为k 进制数是采取________，即用k 连续去除十进制数或所得的商，最后将余数________写出．(2)k 进制数化为十进制数是把k 进制数写成________________的形式，再计算出结果即可．[答案] (1)除k 取余法 倒排(2)各位上的数字与k 的幂的乘积之和13．完成下列进位制之间的转化．(1)10231(4)＝________(10)；(2)235(7)＝________(10)；(3)137(10)＝________(6)；(4)1231(5)＝________(7)；(5)213(4)＝________(3)；(6)1010111(2)＝________(4)．[答案] (1)301 (2)124 (3)345 (4)362 (5)1110 (6)1113.[解析] (1)10231(4)＝1×44＋0×43＋2×42＋3×4＋1＝301(10)，∴10231(4)＝301(10)．(2)235(7)＝2×72＋3×7＋5＝124(10)，∴235(7)＝124(10)． (3)∴137(10)＝345(6)．(4)1231(5)＝1×53＋2×52＋3×5＋1＝191(10)，∴1231(5)＝362(7)．(5)213(4)＝2×42＋1×4＋3＝39(10)，∴213(4)＝1110(3)．(6)1010111(2)＝1×26＋0×25＋1×24＋0×23＋1×22＋1×2＋1＝87(10)，∴1010111(2)＝1113(4)．三、解答题14．若10y 1(2)＝x 02(3)，求数字x ，y 的值及与此两数等值的十进制数．[分析] 由二进制及三进制可知，y ∈{0,1}，x ∈{1,2}，将二进制数和三进制数都转化为十进制数，再由两数相等及x 、y 的取值范围可得出x 、y 的值．[解析] ∵10y 1(2)＝x 02(3)，∴1×23＋0×22＋y ×2＋1＝x ×32＋0×3＋2，将上式整理得9x －2y ＝7，由进位制的性质知，x ∈{1,2}，y ∈{0,1}，当y ＝0时，x ＝79(舍)， 当y ＝1时，x ＝1.∴x ＝y ＝1，已知数为102(3)＝1011(2)，与它们相等的十进制数为1×32＋0×3＋2＝11.15．(1)用秦九韶算法计算多项式f (x )＝x 6－12x 5＋60x 4－160x 3＋240x 2－192x ＋64当x ＝2时的值．并用前测试型循环语句写出算法．(2)用秦九韶算法求多项式f (x )＝x 7－2x 6＋3x 3－4x 2＋1当x ＝2时的函数值．并用后测试型循环语句写出算法．[解析] (1)先将多项式f (x )进行改写：f (x )＝x 6－12x 5＋60x 4－160x 3＋240x 2－192x ＋64＝(((((x －12)x ＋60)x －160)x ＋240)x －192)·x ＋64.然后由内向外计算得：v 0＝1，v 1＝v 0x ＋a 5＝1×2－12＝－10，v 2＝v 1x ＋a 4＝－10×2＋60＝40，v 3＝v 2x ＋a 3＝40×2－160＝－80，v 4＝v 3x ＋a 2＝－80×2＋240＝80，v 5＝v 4x ＋a 1＝80×2－192＝－32，v 6＝v 5x ＋a 0＝－32×2＋64＝0.∴多项式f (x )当x ＝2时的值为f (2)＝0.算法程序为：n ＝6i＝0WHILE i<＝nINPUT“ai＝”；a(i)i＝i＋1WENDx＝2i＝1v＝a(n)WHILE i<＝nv＝v*x＋a(n－i)i＝i＋1WENDPRINT“f(2)＝”；vEND想一想就解决这个具体问题的算法还可以简化吗？(2)先将多项式f(x)进行改写：f(x)＝x7－2x6＋3x3－4x2＋1＝((((((x－2)x＋0)x＋0)x＋3)x－4)x＋0)x＋1由内向外逐次计算：v0＝1，v1＝v0x＋a6＝1×2－2＝0，v2＝v1x＋a5＝0×2＋0＝0，v3＝v2x＋a4＝0×2＋0＝0，v4＝v3x＋a3＝0×2＋3＝3，v5＝v4x＋a2＝3×2－4＝2，v6＝v5x＋a1＝2×2＋0＝4.v7＝v6x＋a0＝4×2＋1＝9.故多项式f(x)当x＝2时的值为f(2)＝9.算法程序为：INPUT“n，an，x＝”；n，v，xi＝n－1DOINPUT“ai＝”；av＝v*x＋ai＝i－1LOOP UNTIL i<0PRINT vEND运行时输入a0＝1，a1＝0，a2＝－4，a3＝3，a4＝a5＝0，a6＝－2，a7＝1.16．试将二进制数101 101 101(2)转化为八进制数．[解析]可先将二进制数转化为十进制数，再转化为八进制数．101 101 101(2)＝1×28＋0×27＋1×26＋1×25＋0×24＋1×23＋1×22＋0×21＋1×20＝256＋64＋32＋8＋4＋1＝365.又365＝8×45＋5,45＝8×5＋5,5＝8×0＋5，∴365(10)＝555(8)．因此二进制数101 101 101(2)化为八进制数等于555(8)．17．若六进制数13m502(6)化为十进制数等于12710，求数字m.[解析]由于13m502(6)＝1×65＋3×64＋m×63＋5×62＋0×61＋2×60＝216m＋11846，所以令12710＝216m＋11846，解得m＝4.所以数字m＝4.*18.若三位数ABC满足ABC＝A3＋B3＋C3，则称ABC为水仙花数，例如13＋53＋33＝1＋125＋27＝153，则称153为水仙花数．编写一个程序，输出100～999中的所有水仙花数．[分析]解决本题的关键是寻求满足关系式的ABC，A为百位数字，B是十位数字，C是个位数字．A取值从1到9，B和C取值从0到9，可用(100A＋10B＋C)表示三位数ABC.用条件100A＋10B＋C＝A3＋B3＋C3控制输出．[解析]程序如下：[点评]可以用“MOD”与“\”编写程序如下：a＝100b＝aWHILE a<＝999C＝a MOD 10a＝a\10B＝a MOD 10A＝a\10T＝A^3＋B^3＋C^3IF T＝b，THENPRINT bEND IFb＝b＋1a＝bWENDEND。

2021-2022年高中数学课后强化训练（含详解）2.1.1 新人教版必修3一、选择题1．某校期末考试后，为了分析该校高一年级1000名学生的学习成绩，从中随机抽取了100名学生的成绩单，就这个问题来说，下面说法中正确的是( ) A．1000名学生是总体B．每名学生是个体C．每名学生的成绩是所抽取的一个样本D．样本的容量是100[答案] D[解析] 1000名学生的成绩是统计中的总体，每个学生的成绩是个体，被抽取的100名学生的成绩是一个样本，其样本的容量为100.2．关于简单随机抽样的特点，有以下几种说法，其中不正确的是( )A．要求总体中的个体数有限B．从总体中逐个抽取C．这是一种不放回抽样D．每个个体被抽到的机会不一样，与先后顺序有关[答案] D[解析] 简单随机抽样，除具有A、B、C三个特点外，还具有：是等可能抽样，各个个体被抽取的机会相等，与先后顺序无关．3．某校高一共有10个班，编号1至10，某项调查要从中抽取三个班作为样本，现用抽签法抽取样本，每次抽取一个号码，共抽3次，设五班第一次被抽到的可能性为a，第二次被抽到的可能性为b，则( )A．a＝310，b＝29B．a＝110，b＝19C．a＝310，b＝310D．a＝110，b＝110[答案] C[解析] 由简单随机抽样的定义知，每个个体在每次抽取中都有相同的可能性被抽到，故五班在每次抽样中被抽到的可能性都是3 10.4．简单随机抽样的结果( )A．完全由抽样方式所决定B．完全由随机性所决定C．完全由人为因素所决定D．完全由计算方法所决定[答案] B[解析] 据简单随机抽样的定义，总体中每个个体被抽到的机会相等，因此抽样结果只与随机性有关，∴选B.5．在简单随机抽样中，某一个个体被抽中的可能性( )A．与第几次抽样有关，第1次抽中的可能性要大些B．与第几次抽样无关，每次抽中的可能性都相等C．与第几次抽样有关，最后一次抽中的可能性大些D．与第几次抽样无关，每次都是等可能的抽取，但各次抽取的可能性不一样[答案] B[解析] 据简单随机抽样的定义可知，某一个个体被抽中的可能性与第几次抽样无关，每次都是等可能的抽取，各次抽到的可能性也都相同，∴选B.6．从总数为N的一批零件中抽取一个容量为30的样本，若每个零件被抽取的可能性为25%，则N为( )A．150 B．200C．100 D．120[答案] D[解析] ∵每个个体被抽到机会相等，都是30N＝0.25，∴N＝120.7．下列抽样方法是简单随机抽样的是( )A．从整数集中，逐个抽取100个检验是否为奇数B．从某车间包装的传送带上，每隔30分钟抽一包产品，称其重量是否合格C．某学校分别从行政人员、教师、后勤人员中抽取2人、14人、4人调查对学校机构改革的意见D．从8台电脑中不放回地随机抽取2台进行质量检验[答案] D8．某校有40个班，每班50人，每班选派3人参加“学代会”，在这个问题中样本容量是( )A．40 B．50C．120 D．150[答案] C二、填空题9．一次体育运动会，某代表团有6名代表参加，欲从中抽取一人检查是否服用兴奋剂，抽检人员将6名队员名字编号为1～6号，然后抛掷一枚骰子，朝上的一面是几就抽检几号对应的队员，问这种抽检方式是简单随机抽样吗？(答是或不是)________．[答案] 是[解析] 抛掷一颗均匀骰子，各面向上的机会是均等的，故每名队员被抽到的机会相等．10．高一(1)班有50名同学，现要从中抽取6名同学参加一个讨论会，每位同学的机会均等．我们可以把50名同学的学号写在小球上，放在一个不透明的袋子中，充分搅拌后，再从中逐个抽取6个小球，从而抽取6名参加讨论会的同学．这种抽样方法是简单随机抽样吗？(答是或不是)________．[答案] 是[解析] 据抽签法的定义知，上述抽样方法是抽签法，∴是简单随机抽样．11．某大学为了支援西部教育事业，现从报名的18名志愿者中选取6人组成志愿小组．用抽签法设计抽样方案如下：S将18名志愿者编号，号码为1,2， (18)1S将号码分别写在一张纸条上，揉成团，制成号签；2S将号签放入一个不透明的袋子中，并充分搅匀；3S________________________________________；4S所得号码对应的志愿者就是志愿小组的成员．5则S4步骤应为______________________________．[答案] 从袋子中依次抽出6个号签，记录下上面的编号．三、解答题12．从30个足球中抽取10个进行质量检测，说明利用随机数法抽取这个样本的步骤及公平性．[解析] 步骤如下：第一步：首先将30个足球编号：00,01,02， (29)第二步：在随机数表中随机选一数作为开始，如从第9行第17列的数0开始．第三步：从选定的数0开始向右读(也可以向左、向上、向下等)，读取一个二位数字07，由于07<29，将它取出；读取82，由于82>29，将它去掉．按照这种方式继续向右读，取出的二位数字若与前面已有的相同，也将它去掉，这样又得到15,00,13，…，依次下去，直到样本的10个号码全部取出．这样就得到一个容量为10的样本．公平性在于：(1)随机数表中每个位置上出现哪一个数是等可能的；(2)从30个足球的总体中抽到哪一个个体的号码也是机会均等的．基于以上两点，利用随机数表抽取样本保证了各个个体被抽到的机会是相等的．13．为了缓解城市的交通拥堵情况，某大城市准备出台限制私家车的政策．为此要进行民意调查．某个调查小组调查了一些拥有私家车的市民，你认为这样的调查结果会怎样？[解析] 一个城市的交通状况的好坏将直接影响着生活在这个城市中的每个人，关系到每个人的利益，为了调查这个问题，在抽样时应当关注到各种人群，既要抽到拥有私家车的市民，也要抽到没有私家车的市民．调查时，如果只对拥有私家车的市民进行调查，结果一定是片面的，不能代表所有市民的意愿．因此，在调查时，要对生活在该市的所有市民进行随机地抽样调查，不要只关注到拥有私家车的市民．14．一个学生在一次竞赛中要回答的8道题是这样产生的：从15道物理题中随机抽3道；从20道化学题中随机抽3道；从12道生物题中随机抽2道．请用随机抽样法确定这个学生所要回答的三门学科的题的序号(物理题的编号为1～15，化学题的编号为16～35，生物题的编号为36～47)．[解析] S1将物理题编号调整为01,02,03，…，15；其余两种题号不变；S在随机数表中任选一数作为开始，任选一方向作为读数方向；2S从选取的数开始，按指定方向，每次读取2位，凡不在01～47之间的数3跳过去不读，前面已读过的也跳过去不读，从01～15中，读取3个号码为止，从16～35中，读取3个号码为止，从36～47中读取2个号码为止；S读取号码对应的序号就是所要回答问题的编号．4[点评] (1)选取的初始数字不同，读取号码则不同，方向不同，号码也不同，但都合乎问题要求，如选择第6行第3个数字开始向右读数，号码为06,04,12；22,17,23；39,43.若选取第3行第5个数字开始向下读取，读到下方后返回从上向下读，则为03,04,12；16,18,15；42,36.(2)本题用抽签法需将三签符号分开，分别抽取．15．因为样本是总体的一部分，是由某些个体所组成的，尽管对总体具有一定的代表性，但并不等于总体，为什么不把所有个体考察一遍，使样本就是总体？[解析] 如果样本就是总体，抽样调查就变成普查了，尽管确实真实地反映了实际情况，但不是统计的基本思想，其操作性、可行性、人力、物力等方面，都会有制约因素存在．何况有些调查是有破坏性的．如考察一批玻璃的抗碎能力、灯泡的使用寿命等，如果进行普查这批玻璃和灯泡就全部报费了，因此为了又能了解总体的真实情况，又不需要把总体中每个个体都调查一番，人们才想到研究统计．16．现从10架钢琴中抽取4架进行质量检验，写出用抽签法抽样的过程．[解析] S1将10架钢琴编号，号码是0,1， (9)S将号码分别写在一张纸条上，揉成团，制成号签；2S将得到的号签放入一个不透明的袋子中，并充分搅匀；3S从袋子中依次抽取4个号签，并记录上面的编号；4S所得号码对应的4架钢琴就是要抽取的对象．x 36983 9077 遷37791 939F 鎟837429 9235 鈵\ml35643 8B3B 謻u34219 585AB 薫32518 7F06 缆 25012 61B4 憴。