「精品」高中数学第一章立体几何初步1.7.3球的表面积和体积课件北师大版必修2(1)
- 格式:ppt
- 大小:13.37 MB
- 文档页数:33


2018-2019高中数学第一章立体几何初步1.7.2 棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积1.7.3 球的表面积和体积学案北师大版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019高中数学第一章立体几何初步1.7.2 棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积1.7.3 球的表面积和体积学案北师大版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019高中数学第一章立体几何初步1.7.2 棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积1.7.3 球的表面积和体积学案北师大版必修2的全部内容。
7.2 棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积7。
3 球的表面积和体积学习目标1。
理解柱体、锥体、台体的体积公式(重点);2.理解球的表面积和体积公式(重点);3。
能运用体积公式求解有关的体积问题,并且熟悉台体与柱体和锥体之间的转换关系(重、难点).知识点一柱、锥、台体的体积公式几何体体积公式柱体圆柱V柱体=ShS—柱体底面积h—柱体的高棱柱锥体圆锥V锥体=错误!ShS—锥体底面积h—锥体的高棱锥台体圆台V台体=错误!(S上+S下+错误!)·h S上、S下-台体的上、下底面面积,h—高棱台简单组合体分割成几个几何体,其表面积如何变化?其体积呢?提示表面积变大了,体积不变.知识点二球的体积公式与表面积公式1.球的体积公式V=错误!πR3(其中R为球的半径).2。
球的表面积公式S=4πR2.【预习评价】球有底面吗?球面能展开成平面图形吗?提示球没有底面,球的表面不能展开成平面。
题型一柱体、锥体、台体的体积【例1】(1)一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m3.解析由所给三视图可知,该几何体是由相同底面的两个圆锥和一个圆柱组成,底面半径为1 m,圆锥的高为1 m,圆柱的高为2 m,因此该几何体的体积V=2×错误!×π×12×1+π×12×2=错误!π(m3).答案错误!π(2)在四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,2AB=3CD,M为AE的中点,设E-ABCD 的体积为V,那么三棱锥M-EBC的体积为多少?解如图,设点B到平面EMC的距离为h1,点D到平面EMC的距离为h2。

2018-2019学年高中数学第一章立体几何初步1.7.3 球的表面积和体积训练案北师大版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019学年高中数学第一章立体几何初步1.7.3 球的表面积和体积训练案北师大版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019学年高中数学第一章立体几何初步1.7.3 球的表面积和体积训练案北师大版必修2的全部内容。
1.7.3 球的表面积和体积[A。
基础达标]1.用一平面去截体积为43π的球,所得截面的面积为π,则球心到截面的距离为( ) A.2 B。
错误!C.错误!D.1解析:选C。
由已知得球的半径为R=错误!,又πr2=π,所以r=1,所以d=错误!=错误!.2.如图是某几何体的三视图,则该几何体的体积为( )A.9π+42 B.36π+18C.错误!π+12D.错误!π+18解析:选D。
由三视图可知,该几何体是一个球体和一个长方体的组合体.其中,V球=错误!π·(错误!)3=错误!,V长方体=2×3×3=18。
所以V总=错误!π+18。
3.一个几何体的三视图如图所示,其中主视图和左视图是腰长为4的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是()A.12πB.24πC.32πD.48π解析:选D.由三视图可知该几何体是有一条侧棱垂直于底面的四棱锥.其中底面ABCD是边长为4的正方形,高为4,该几何体的所有顶点在同一球面上,则球的直径为错误!×4=4错误!,即球的半径为23,所以该球的表面积是4π(2错误!)2=48π.4.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A.9πB.10πC.11πD.12π解析:选D。
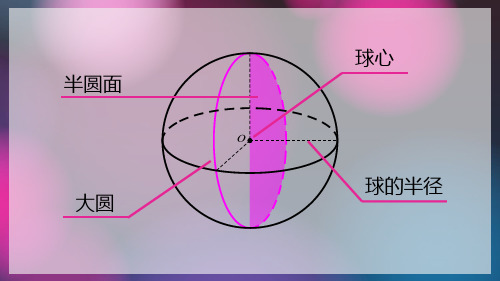


球的体积和表面积一、教学目标1、知识与技能:⑴通过对球的体积和面积公式的推导,了解推导过程中所用的基本数学思想方法:“分割——求和——化为准确和”,有利于同学们进一步学习微积分和近代数学知识。
⑵能运用球的面积和体积公式灵活解决实际问题。
⑶培养学生的空间思维能力和空间想象能力。
2、过程与方法:通过球的体积和面积公式的推导,从而得到一种推导球体积公式V=34πR 3和面积公式S=4πR 2的方法,即“分割求近似值,再由近似和转化为球的体积和面积”的方法,体现了极限思想。
3、情感与价值观:通过学习,使我们对球的体积和面积公式的推导方法有了一定的了解,提高了空间思维能力和空间想象能力,增强了我们探索问题和解决问题的信心。
二、教学重点、难点重点:引导学生了解推导球的体积和面积公式所运用的基本思想方法。
难点:推导体积和面积公式中空间想象能力的形成。
三、学法和教法1、学法:学生通过阅读教材,发挥空间想象能力,了解并初步掌握“分割、求近似值、再由近似值的和转化为球的体积和面积”的解题方法和步骤。
2、教法:探究讨论法四、教学过程(一)、创设情景1、教师提出问题:球既没有底面,也无法像在柱体、锥体和台体那样展开成平面图形,那么怎样来求球的表面积与体积呢?引导学生进行思考。
2、教师设疑:球的大小是与球的半径有关,如何用球半径来表示球的体积和面积?激发学生推导球的体积和面积公式。
(二)、探究新知1.球的体积:如果用一组等距离的平面去切割球,当距离很小之时得到很多“小圆片”,“小圆片”的体积的体积之和正好是球的体积,由于“小圆片”近似于圆柱形状,所以它的体积也近似于圆柱形状,所以它的体积有也近似于相应的圆柱和体积,因此求球的体积可以按“分割——求和——化为准确和”的方法来进行。
步骤:第一步:分割如图:把半球的垂直于底面的半径OA作n 等分,过这些等分点,用一组平行于底面的平面把半球切割成n 个“小圆片”,“小圆片”厚度近似为nR ,底面是“小圆片”的底面。