当前位置：文档之家 › 机械设计第九版 濮良贵 课后习题答案

机械设计第九版 濮良贵 课后习题答案

  • 格式：doc
  • 大小：5.44 MB
  • 文档页数：57

下载文档原格式

  / 57

合集下载

濮良贵机械设计第九版课后 习题答案.(DOC)

濮良贵机械设计第九版课后 习题答案.(DOC)
⑨计算大、小齿轮的，并加以比较
取 ⑩由弯曲强度确定的最大转矩
（4）齿轮传动的功率 取由接触强度和弯曲强度确定的最大转矩中的最小值 即
第十一章 蜗杆传动 习题答案
11-1 试分析图11-26所示蜗杆传动中各轴的回转方向、蜗轮轮齿的螺旋 方向及蜗杆、蜗轮所受各力的作用位置及方向。
[解] 各轴的回转方向如下图所示，蜗轮2、4的轮齿螺旋线方向均为右 旋。蜗杆、蜗轮所受各力的作用位置及方向如下图
第十章 齿轮传动 习题答案
10-1 试分析图10-47所示的齿轮传动各齿轮所受的力（用受力图表示各 力的作用位置及方向）。
[解] 受力图如下图：
补充题：如图（b），已知标准锥齿轮，标准斜齿轮 ，若中间轴上两齿轮所受轴向力互相抵消，应为多少？并计算2、3齿轮
各分力大小。 [解] （1）齿轮2的轴向力：
[解] 螺栓组受到剪力F和转矩，设剪力F分在各个螺栓上的力为，转矩T 分在各个螺栓上的分力为
（a）中各螺栓轴线到螺栓组中心的距离为r，即r=125mm 由（a）图可知，最左的螺栓受力最大
（b）方案中
由（b）图可知，螺栓受力最大为
5-10
第六章 键、花键、无键连接和销连接 习题答案
6-3 在一直径的轴端，安装一钢制直齿圆柱齿轮（如下图），轮毂宽 度，工作时有轻微冲击。试确定平键的尺寸，并计算其允许传递的最大 扭矩。
⑤由图10-21d按齿面硬度查得小齿轮的接触疲劳强度极限；大齿轮 的接触疲劳强度极限。 ⑥齿数比 ⑦计算应力循环次数
⑧由图10-19取接触疲劳寿命系数 ⑨计算接触疲劳许用应力
取失效概率为，安全系数
2）计算 ①计算小齿轮分度圆直径，代入中较小值
②计算圆周速度
③计算尺宽
④计算尺宽与齿高之比

濮良贵机械设计第九版课后习题答案解析汇总之欧阳文创编

濮良贵机械设计第九版课后习题答案解析汇总之欧阳文创编

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN3-2已知材料的力学性能为MPa260=s σ，MPa1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

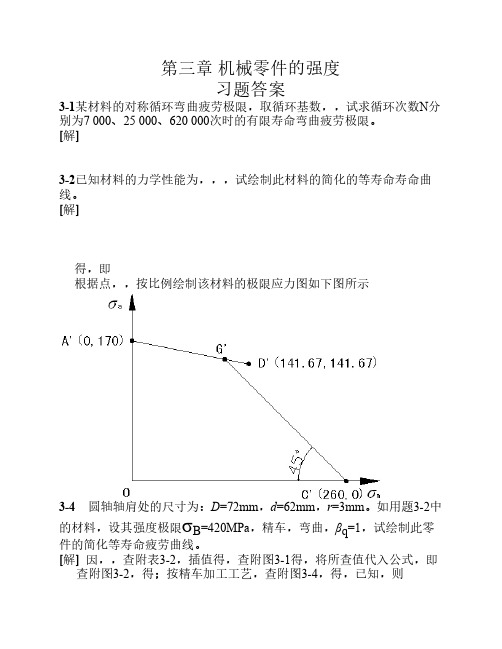
[解] )170,0('A )0,260(C得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②Cσ=m ，求出该截面的计算安全系数ca S 。

[解] 由题3-4可知35.2,2.0MPa,260MPa,170s 1-====σσK Φσσ（1）C r =工作应力点在疲劳强度区，根据变应力的循环特性不变公式，其计算安全系数 （2）C σ=m工作应力点在疲劳强度区，根据变应力的平均应力不变公式，其计算安全系数第五章螺纹连接和螺旋传动习题答案5-5图5-49是由两块边板和一块承重板焊接的龙门起重机导轨托架。

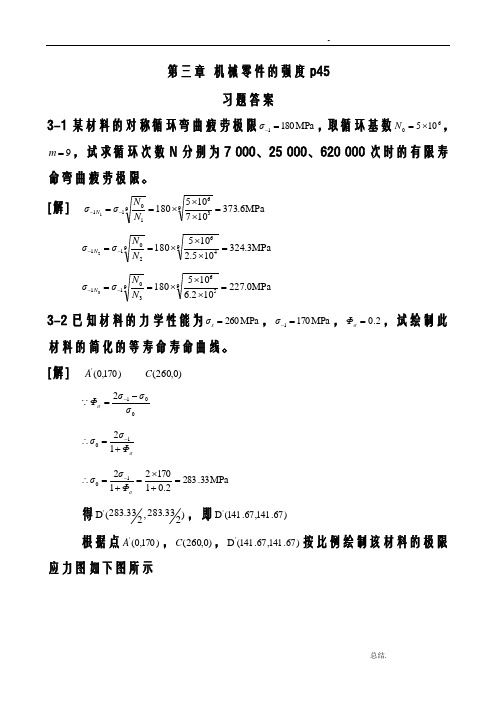
机械设计课后习题答案濮良贵

机械设计课后习题答案濮良贵

第三章 机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσNMPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解])170,0('A)0,260(C012σσσΦσ-=-σΦσσ+=∴-1210MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==dD ，067.0453==d r，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q σσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

濮良贵机械设计第九版课后习题答案解析

濮良贵机械设计第九版课后习题答案解析

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-1210 MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ 得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4圆轴轴肩处的尺寸为：D=72mm，d=62mm，r=3mm。

如用题3-2中的材料，设其强度极限σB=420MPa，精车，弯曲，βq=1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==dD，067.0453==dr，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq，将所查值代入公式，即()()69.1188.178.0111k=-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=qβ，则35.211191.0175.069.1111k=⨯⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫⎝⎛-+=qσσσσββεK()()()35.267.141,67.141,0,260,35.2170,0DCA∴根据()()()29.60,67.141,0,260,34.72,0DCA按比例绘出该零件的极限应力线图如下图3-5如题3-4中危险截面上的平均应力MPa20m=σ，应力幅MPa20a=σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

机械设计第九版课后答案濮良贵第10单元课后习题10-8答案

机械设计第九版课后答案濮良贵第10单元课后习题10-8答案

KAFt1 / b 1.25 4693 / 27.72 N/mm 211 .63N/mm >100N/mm 查表 10-3 得出间载荷分配系数 KF 1.2 ③由表 10-4 用插值法查得 KH 1.347 （用外插法求的） ，结合 b/h=4.575 查图 10-3 得 KF 1.298 。
由图 10-23 查取接触疲劳寿命系数 KHN1 1.17 、KHN2 1.25 。 （此处取的是机械设计第九版 10-23 中的第一条曲线，读者可根据材料不同自行取其它曲线） 取失效概率为 1%、安全系数 S=1，由式（10-14）得
N1 60n1jLh 60 14460 1 100 6.876 10 7
t n
arccosz cos / z 2h cos arccos23 cos20.562 / 23 2 1 cos14 30.30
at1 1 t 1 an *
arccosz cos / z 2h cos arccos73 cos20.562 / 73 2 1 cos14 24.21
b t
/ cos 2 1.632 / cos 213.140 1.721
v b
③由式（10-19） ，可得计算弯曲疲劳强度的螺旋角系数 Y 。
Y 0.25 0.75 / v 0.25 0.75 / 1.721 0.686 Y 1
Hlim1 1.17 600 MPa 702MPa S 1 H 2 KHZ2 Hlim2 1.25 550 MPa 687.5MPa S 1
K
H 1
HZ1
取 H 1 和 H 2 中的较小值作为该齿轮副的接触疲劳许用应力，既

第九版机械设计濮良贵课后习题答案

第九版机械设计濮良贵课后习题答案

第三章 机械 零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳 极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数 N分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN M P a 3.324105.2105180946920112=⨯⨯⨯==--N N σσN M P a 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学 性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-121M P a 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图 如下图所示3-4 圆轴轴肩处的 尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等 寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q σσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例 绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截 面的计算安全系数ca S 。

机械设计课后习题答案濮良贵

机械设计课后习题答案濮良贵

第三章 机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσNMPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解])170,0('A)0,260(C012σσσΦσ-=-ΘσΦσσ+=∴-1210MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ 得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==dD，067.0453==d r，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q σσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

机械习题答案

机械习题答案
2 2
2 ⑵若 M＜0：螺栓 4 和 5 所受的工作载荷最大，其值 F3 为 F3 = Ml1 (4l12 + 4l 2 )
1 8
FΣy
y
FΣ FΣx
h
x
l
l1
l2
l2
l1
2 7
3 6
4 5
4)受力最大的螺栓及其所受到的最大作用力 Fmax： ⑴若 M≥0：螺栓 1 和 8 所受的作用力最大，其值 Fmax 为：
《机械设计》 （第九版）
濮良贵主编
习题参考答案（第 5 章）
5-4.图 5-49 所示的底板螺栓组连接受外力 FΣ的作用，外力 FΣ作用在包含 x 轴并垂直于底板接合 面的平面内。试分析底板螺栓组的受力情况，并判断哪个螺栓受力最大，保证连接安全工作 的必要条件有哪些？ 解：1、受力简化： 1)FΣ向 x 和 y 轴分解，得水平分力 FΣx 铅垂 分力 FΣy 2)FΣx 向接全面简化，得作用在接合面上的横 向载荷 FΣx 和顺时针倾覆力矩 M1=FΣx×h 3)FΣy 向接合面对称中心简化，得轴向载荷 FΣy 和逆时针倾覆力矩 M2=FΣy×l 4)螺栓组的受力情况： 综上，底板螺栓组受以下三种载荷的作用： ⑴横向载荷 FΣx，作用方向：水平向右 ⑵轴向载荷 FΣy，作用方向：铅垂向上 ⑶倾覆力矩 M：M=M1-M2。M≥0，底板受顺时针倾覆力矩作用 M＜0，底板受逆时针倾覆力矩作用 2、受力分析： 1)受横向载荷 FΣx 作用： 每个螺栓所受的工作剪力 F1=FΣx/8，方向向右。 2)受轴向载荷 FΣy 作用： 每个螺栓所受的工作拉力 F2=FΣy/8，方向向上。 3)受倾覆力矩 M 作用： ⑴若 M≥0：螺栓 1 和 8 所受的工作载荷最大，其值 F3 为 F3 = Ml1 (4l1 + 4l 2 )

机械设计课后习题答案濮良贵

机械设计课后习题答案濮良贵

第三章 机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσNMPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C 0012σσσΦσ-=-ΘσΦσσ+=∴-1210MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==dD，067.0453==d r，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q σσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

机械设计课后习题答案濮良贵

机械设计课后习题答案濮良贵

第三章 机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσNMPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解])170,0('A)0,260(C012σσσΦσ-=-σΦσσ+=∴-1210MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D=72mm，d=62mm，r=3mm。

如用题3-2中的材料，设其强度极限σB=420MPa，精车，弯曲，βq=1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==dD，067.0453==dr，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq，将所查值代入公式，即()()69.1188.178.0111k=-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=qβ，则35.211191.0175.069.1111k=⨯⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫⎝⎛-+=qσσσσββεK()()()35.267.141,67.141,0,260,35.2170,0DCA∴根据()()()29.60,67.141,0,260,34.72,0DCA按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa20m=σ，应力幅MPa20a=σ，试分别按①Cr=②Cσ=m，求出该截面的计算安全系数caS。

濮良贵第九版版机械设计习题答案解析

濮良贵第九版版机械设计习题答案解析

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-121MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-3一圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

材料为40CrNi ，设其强度极限σB =900MPa ，屈服极限750MPa s σ=试计算周健的弯曲有效应力集中系数k σ。

[解] 因1.16D d =，0.048rd=，查附表3-2，插值得 1.995σα=，查附图3-1得78.0≈σq ，将所查值代入公式，即()()k 1110.78 1.9951 1.896σσσq α=+-=+⨯-=3-4圆轴轴肩处的尺寸为：D =54mm ，d =45mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB=420MPa ，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得0.7σε=；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则k 11 1.691111 2.510.70.911σσσσq K εββ⎛⎫⎛⎫=+-=+-⨯= ⎪ ⎪⎝⎭⎝⎭()()()170141.670,,260,0,141.67,2.512.51A C D ∴根据()()()0,67.73,260,0,141.67,56.44A C D 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

濮良贵第九版版机械设计习题答案及解析

濮良贵第九版版机械设计习题答案及解析

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-121MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-3一圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

材料为40CrNi ，设其强度极限σB =900MPa ，屈服极限750MPa s σ=试计算周健的弯曲有效应力集中系数k σ。

[解] 因1.16D d =，0.048rd=，查附表3-2，插值得 1.995σα=，查附图3-1得78.0≈σq ，将所查值代入公式，即()()k 1110.78 1.9951 1.896σσσq α=+-=+⨯-=3-4圆轴轴肩处的尺寸为：D =54mm ，d =45mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB=420MPa ，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得0.7σε=；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则k 11 1.691111 2.510.70.911σσσσq K εββ⎛⎫⎛⎫=+-=+-⨯= ⎪ ⎪⎝⎭⎝⎭()()()170141.670,,260,0,141.67,2.51 2.51A C D ∴ 根据()()()0,67.73,260,0,141.67,56.44A C D 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

濮良贵第九版机械设计习题及解析

濮良贵第九版机械设计习题及解析

WORD 格式 可编写第三章 机械部件的强度习题答案3-1 某资料的对称循环波折疲倦极限σ1180MPa ，取循环基数 N 0 5 106 ， m 9 ，试求循环次数 N分别为 7 000 、 25 000 、 620 000 次时的有限寿命波折疲倦极限。

[ 解 ]σ1N 1σ1 9N 0 180 95 106373.6MPaN 17 103σ1N 2σ1 9 N 018095 106324.3MPaN 22.5 10 4σ1N 3σ19 N 018095 106227.0MPaN 36.2 10 53-2 已知资料的力学性能为 σs260MPa ， σ1 170MPa ， Φσ 0.2 ，试绘制此资料的简化的等寿命寿命曲线。

[ 解 ]A ' (0,170)C( 260,0)σ1σΦσ2 0σ0σ2σ11 Φσσ2σ1 2 170283.33MPa1 Φσ 1 0.2得 D '(283.332 ,283.332) ，即 D ' (141.67,141.67)依照点 A ' (0,170) ， C (260,0) ， D ' (141.67,141.67) 按比率绘制该资料的极限应力求以以下列图所示3-3 一圆轴轴肩处的尺寸为： D =72mm ， d =62mm ， r =3mm 。

资料为 40CrNi ，设其强度极限σB=900MPa ，信服WORD 格式可编写极限 σ750MPa 试计算周健的波折有效应力集中系数k 。

s[解] 因D1.16 ，r0.048 ，查附表 3-2 ，插值得σ1.995 ，查附图 3-1 得 q σ0.78 ，将所查值dd代入公式，即k σ 1 q σ σ 1 1 0.78 1.995 1 1.8963-4 圆轴轴肩处的尺寸为： D =54mm ， d =45mm ， r =3mm 。

如用题 3-2 中的资料，设其强度极限σ B=420MPa ，试绘制此部件的简化等寿命疲倦曲线。

机械设计课后习题答案濮良贵

机械设计课后习题答案濮良贵

第三章 机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解]MPa 6.373107105180936910111=⨯⨯⨯==--N N σσNMPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C0012σσσΦσ-=-ΘσΦσσ+=∴-1210 MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ 得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q σσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

濮良贵机械设计第九版课后习题答案解析汇总之欧阳家百创编

濮良贵机械设计第九版课后习题答案解析汇总之欧阳家百创编

第三章 机械零件的强度欧阳家百（2021.03.07）习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

[解] 由题3-4可知35.2,2.0MPa,260MPa,170s 1-====σσK Φσσ （1）C r =工作应力点在疲劳强度区，根据变应力的循环特性不变公式，其计算安全系数 （2）C σ=m工作应力点在疲劳强度区，根据变应力的平均应力不变公式，其计算安全系数第五章 螺纹连接和螺旋传动习题答案5-5 图5-49是由两块边板和一块承重板焊接的龙门起重机导轨托架。

机械设计课后习题答案濮良贵

机械设计课后习题答案濮良贵

机械设计课后习题答案濮良贵第三章机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-ζ，取循环基数60105?=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111===--N N ζζN M P a 3.324105.2105180946920112===--N N ζζNM P a 0.227102.6105180956930113===--N N ζζN 3-2已知材料的力学性能为MPa 260=s ζ，MPa 1701=-ζ，2.0=ζΦ，试绘制此材料的简化的等寿命寿命曲线。

[解])170,0('A)0,260(C012ζζζΦζ-=-ζΦζζ+=∴-1210M P a 33.2832.0117021210=+?=+=∴-ζΦζζ 得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.145 54==dD ，067.0453==d r，查附表3-2，插值得88.1=αζ，查附图3-1得78.0≈ζq ，将所查值代入公式，即()()69.1188.178.0111k =-?+=-α+=ζζζq查附图3-2，得75.0=ζε；按精车加工工艺，查附图3-4，得91.0=ζβ，已知1=q β，则35.211191.0175.069.1111k = ??-+= ??-+=q ζζζζββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =ζ，应力幅MPa 20a =ζ，试分别按①C r =②C ζ=m ，求出该截面的计算安全系数ca S 。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第三章 机械零件的强度3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσNMPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解])170,0('A)0,260(C012σσσΦσ-=-ΘσΦσσ+=∴-1210MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==dD，067.0453==d r，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q σσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

[解] 由题3-4可知35.2,2.0MPa,260MPa,170s 1-====σσK Φσσ（1）C r =工作应力点在疲劳强度区，根据变应力的循环特性不变公式，其计算安全系数28.2202.03035.2170m a 1-=⨯+⨯=+=σΦσK σS σσca（2）C σ=m工作应力点在疲劳强度区，根据变应力的平均应力不变公式，其计算安全系数()()()()81.1203035.2202.035.2170m a m 1-=+⨯⨯-+=+-+=σσσσca σσK σΦK σS第五章螺纹连接和螺旋传动5-1 分析比较普通螺纹、管螺纹、梯形螺纹和锯齿形螺纹的特点，各举一例说明它们的应用靠螺纹密封的联接螺纹梯形螺纹牙型为等腰梯形，牙侧角3o，内外螺纹以锥面巾紧不易松动，工艺较好，牙根强度高，对中性好最常用的传动螺纹锯齿形螺纹牙型不为等腰梯形，工作面的牙侧角3o，非工作面的牙侧角30o。

外螺纹牙根有较大的圆角，以减少应力集中。

内外螺纹旋合后，大径处无间隙，便于对中。

兼有矩形螺纹传动效率高和梯形螺纹牙根旨度高的特点只能用于单向受力的螺纹联接或螺旋传动，如螺旋压力机5-2 将承受轴向变载荷的联接螺栓的光杆部分做得细些有什么好处？答：可以减小螺栓的刚度，从而提高螺栓联接的强度。

5-3 分析活塞式空气压缩气缸盖联接螺栓在工作时的受力变化情况，它的最大应力，最小应力如何得出？当气缸内的最高压力提高时，它的最大应力，最小应力将如何变化？解：最大应力出现在压缩到最小体积时，最小应力出现在膨胀到最大体积时。

当汽缸内的最高压力提高时，它的最大应力增大，最小应力不变。

5-4 图5-49所示的底板螺栓组联接受外力FΣ作用在包含x轴并垂直于底板接合面的平面内。

试分析底板螺栓组的受力情况，并判断哪个螺栓受力最大？堡证联接安全工作的必要条件有哪些？5-5 图5-49是由两块边板和一块承重板焊接的龙门起重机导轨托架。

两块边板各用4个螺栓与立柱相连接，托架所承受的最大载荷为20kN，载荷有较大的变动。

试问：此螺栓连接采用普通螺栓连接还是铰制孔用螺栓连接为宜？为什么？Q215，若用M6×40铰孔用螺栓连接，已知螺栓机械性能等级为8.8，校核螺栓连接强度。

[解] 采用铰制孔用螺栓连接为宜因为托架所受的载荷有较大变动，铰制孔用螺栓连接能精确固定被连接件的相对位置，并能承受横向载荷，增强连接的可靠性和紧密性，以防止受载后被连接件间出现缝隙或发生相对滑移，而普通螺栓连接靠结合面产生的摩擦力矩来抵抗转矩，连接不牢靠。

（1）确定M 6×40的许用切应力[τ]由螺栓材料Q215，性能等级8.8，查表5-8，可知MPa 640][s =σ，查表5-10，可知0.5~5.3][=τS()MPa 128~86.1820.5~5.3640][][][s ===τ∴τS σMPa 67.4265.1640][s ===p p S σσ （2）螺栓组受到剪力F 和力矩（FL T =），设剪力F 分在各个螺栓上的力为i F ，转矩T 分在各个螺栓上的分力为j F ，各螺栓轴线到螺栓组对称中心的距离为r ,即mm 27545cos 2150=︒=rkN2510275810300208 kN 5.220818133=⨯⨯⨯⨯===⨯==∴--r FL F F F j i 由图可知，螺栓最大受力kN 015.945cos 255.22)25(5.2cos 22222max =︒⨯⨯⨯++=++=θF F F F F j i j i()][319106410015.9423320max τ>=⨯⨯π⨯=π=τ∴-d F][8.131104.1110610015.9333min 0max p p σL d F σ<=⨯⨯⨯⨯==∴--故M 6×40的剪切强度不满足要求，不可靠。

5-6 已知一个托架的边板用6个螺栓与相邻的机架相连接。

托架受一与边板螺栓组的垂直对称轴线相平行、距离为250mm 、大小为60kN 的载荷作用。

现有如图5-50所示的两种螺栓布置形式，设采用铰制孔用螺栓连接，试问哪一种布置形式所用的螺栓直径最小？为什么？[解] 螺栓组受到剪力F 和转矩，设剪力F 分在各个螺栓上的力为i F ，转矩T 分在各个螺栓上的分力为j F（a ）中各螺栓轴线到螺栓组中心的距离为r ，即r =125mmkN 2010125610250606 kN 1060616133=⨯⨯⨯⨯===⨯==∴--r FL F F F ji由（a ）图可知，最左的螺栓受力最大kN 302010max =+=+=j i F F F （b ）方案中kN 10606161=⨯==F FikN 39.24101252125421252101252125102506062223223612max612maxmax =⨯⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⨯+⎪⎭⎫ ⎝⎛⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯===---==∑∑i ii ij rFLr rMr F 由（b ）图可知，螺栓受力最大为kN 63.335239.24102)39.24(10cos 22222max =⨯⨯⨯++=++=θF F F F F j i j i []直径较小）布置形式所用的螺栓可知采用（由a F d τπ≥∴max04 5-7 图5-52所示为一拉杆螺纹联接。

已知拉丁所受的载荷F=56KN,载荷稳定，拉丁材料为Q235钢，试设计此联接。

5-8 两块金属板用两个M12的普通螺栓联接。

若接合面的摩擦系数f=0.3,螺栓预紧力控制在其屈服极限的70%。

螺栓用性能等级为4.8的中碳钢制造，求此联接所能传递的横向载荷。

5-9受轴向载荷的紧螺栓联接，被联接钢板间采用橡胶垫片。

已知螺栓预紧力Fo=15000N,当受轴向工作载荷F＝10 000N时，求螺栓所受的总拉力及被联接件之间的残余预紧力。

5-10图5-24所示为一汽缸盖螺栓组联接。

已知汽缸内的工作压力P=0~1MPa，缸盖与缸体均为钢制，直径D1=350mm,D2=250mm.上、下凸缘厚均为25mm.试设计此联接。

5-11 设计简单千斤顶（参见图5-41）的螺杆和螺母的主要尺寸。

起重量为40000N，起重高度为200mm,材料自选。

(1) 选作材料。

螺栓材料等选用45号钢。

螺母材料选用ZCuA19Mn2,查表确定需用压强[P]=15MPa.(2)确定螺纹牙型。

梯形螺纹的工艺性好，牙根强度高，对中性好，本题采用梯形螺纹。

（3）按耐磨性计算初选螺纹的中径。

因选用梯形螺纹且螺母兼作支承，故取，根据教材式（5-45）得按螺杆抗压强度初选螺纹的内径。

根据第四强度理论，其强度条件为但对中小尺寸的螺杆，可认为，所以上式可简化为式中，A为螺杆螺纹段的危险截面面积，;S为螺杆稳定性安全系数，对于传力螺旋，S=3.5-5.0;对于传导螺旋，S=2.5-4.0;对于精密螺杆或水平螺杆，S>4.本题取值为5.故（5）综合考虑，确定螺杆直径。

比较耐磨性计算和抗压强度计算的结果，可知本题螺杆直径的选定应以抗压强度计算的结果为准，按国家标准GB/T5796-1986选定螺杆尺寸参数：螺纹外径d=44mm,螺纹内径d1=36mm,螺纹中径d2=40.5mm,螺纹线数n=1,螺距P=7mm.(6)校核螺旋的自锁能力。

对传力螺旋传动来说，一般应确保自锁性要求，以避免事故。

本题螺杆的材料为钢，螺母的材料为青铜，钢对青铜的摩擦系数f=0.09(查《机械设计手册》)。

因梯形螺纹牙型角,所以因,可以满足自锁要求。

注意：若自锁性不足，可增大螺杆直径或减沾上螺距进行调整。

（7）计算螺母高度H.因选所以H=,取为102mm.螺纹圈数计算：z=H/P=14.5螺纹圈数最好不要超过10圈，因此宜作调整。

一般手段是在不影响自锁性要求的前提下，可适当增大螺距P,而本题螺杆直径的选定以抗压强度计算的结果为准，耐磨性已相当富裕，所以可适当减低螺母高度。

现取螺母高度H=70mm,则螺纹圈数z=10,满足要求。

（8）螺纹牙的强度计算。

由于螺杆材料强度一般远大于螺母材料强度，因此只需校核螺母螺纹的牙根强度。

根据教材表5-13，对于青铜螺母,这里取30MPa,由教材式（5-50）得螺纹牙危险截面的剪切应力为满足要求螺母螺纹根部一般不会弯曲折断，通常可以不进行弯曲强度校核。