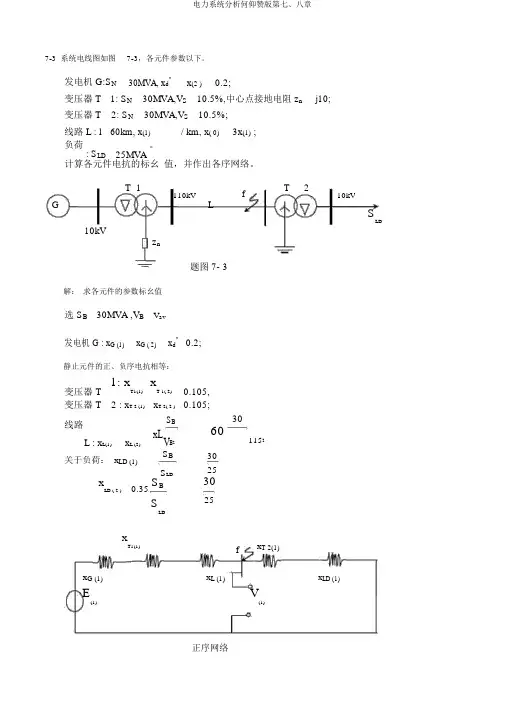
7-3 系统电线图如图7-3，各元件参数如下。
值，并作出各序网络。
计算各元件电抗的标幺。
负荷线路变压器中心点接地电阻变压器发电机MVA S x x km x km l L V MVA S T j z V MVA S T x x MVA S G LD S N n S N d N 25:;3,/4.0,60:%;5.10,30:2;
10%,5.10,30:1;
2.0,30:)1()0()1()2("
==Ω====-===-===
解：求各元件的参数标幺值 av B B V V MVA S ==,30选 ;2.0:"
)2()1(===d G G x x x G 发电机
静止元件的正、负序电抗相等： 0544
.0115
304.060:;105.0:2,105.0:12
2
)2()1()2(2)1(2)2(1)1(1=⨯
⨯=====-==-B
B L L T T T T V S xL
x x L x x T x x T 线路变压器变压器
42
.025
3035.035
.044
.125
302.12
.1)2()1(=⨯
===⨯==LD
B LD LD
B LD S S x S S x 对于负荷：
3
-7
题图正序网络
7-5电力系统接线如图7-5，1f 发生接地短路，作出系统的零序等值网络。
题图中1～17为原件编号。
解：
零序网络
负序网络
11
零序网路
8-1简单系统如题图8-l 所示。
已知元件参数如下。
%,
5.10,60:;19.0,1
6.0,60:)2("
=====S N d N V MVA S T x x MVA S G 变压器发电机
在f 点分别发生单相接地、两相短路、两相短路接地和三相短路时，试计算短路点短路电流的有名值，并进行比较分析。
解：kA kA V S I E V V MVA S B
B B av B B 301226.0115
3603,05.1,,60=⨯=
====则选
105.0295.0105.019.0265
.0105.016.0105
.019
.016.0)0()0()2()2()2()1()1()1()0()2()1()2("
)1(===+=+==+=+=======T ff T G ff T G ff T T T G d G x x x x x x x x x x x x x x 所以
()。
由本题可知：)2()3()1()1,1()
1()3()1,1()1()
1,1()1,1(2
2
)0()
2()
0()2()
1,1()
0()2()0()2()
1,1()
2()1()2()
0()2()1()1(194.1301226.0265
.005.1437.1301226.007744
.0265.005.15554.15554.1)
105.0295.0(105.0295.0131307744
.0105
.0295.0105.0295.09783.0301226.0295
.0265.005.13342686.1301226.0105
.0295.0265.005
.133f
f
f
f
B ff f
B ff f
ff ff ff ff ff ff ff ff B ff ff f
B ff ff ff f
I
I
I I
kA
kA I x E I
kA
kA I x x Em
I
x x
x x m
x x x x x kA
kA I x x E I
kA
kA I x x x E
I
>>>=⨯==
=⨯+⨯=
+=
=+⨯-⨯=
+-⨯=
=+⨯=
+==⨯+⨯=
+=
=⨯++⨯=
++=
∆
∆
G
kV 10kV
110f
1
-8题图
8-2 上题系统中，若变压器中性点经30欧姆的电抗接地，做题所列各类短路的计算，并对两题计算的结
果做分析比较。
解：kA kA V S I E V V MVA S B
B B av B B 301226.0115
3603,05.1,,60=⨯=
=
===则选
5133
.013611.03105.03295.0105.019.0265
.0105.016.013611.0115
603030
105.019
.016.0)0()0()2()2()2()1()1()1(2
2)0()2()1()2("
)1(=⨯+=+==+=+==+=+==⨯
========n T ff T G ff T G ff B
B n T T T G d G X x x x x x x x x V
S X x x x x x x 所以
中性点接地电阻只对接地故障有影响，故重算接地短路电流 ()
电流大大减小。
电抗增大很多，使接地
中性点接地电抗使零序
kA
I
kA
kA I x x Em
I x x
x x m
x x x x x kA I
kA
kA I x x x E
I f
B ff f
ff ff ff ff ff ff ff ff f B ff ff ff f
194.1062.1301226.01873
.0265.005.15181.15181.1)
5133.0295.0(5133.0295.013131873
.05133
.0295.05133.0295.09783.0884.0301226.05133
.0295.0265.005
.133)3()
1,1()1()
1,1()1,1(2
2
)0()
2()
0()2()
1,1()
0()2()0()2()
1,1()2()
0()2()1()1(==⨯+⨯=
+=
=+⨯-⨯=
+-⨯=
=+⨯=
+=
==⨯++⨯=
++=
∆
∆
8-3 简单系统如题图8-3所示。
已知元们参数如下。
;
2211,%,5.10,50:;
05.1,2.0,50:"
]0[)2("
Ω======接法，中心点接地电抗
变压器发电机d Y V MVA S T E x x MVA S G S N d N 。
在f 点分别发生bc 两相短路，计算短路点各相电流，并画出bc 两相的电流、电压向量图。
解：kA kA V S I E V V MVA S B
B B
av B B 25102.0115
3503,9005.1,,500]0[=⨯=
=∠===则选
35453
.008318.03105.03305
.0105.02.0305
.0105.02.008318.0115
502222
105.02
.02.0)0()0()2()2()2()1()1()1(2
2
)0()2()1()2("
)1(=⨯+=+==+=+==+=+==⨯
========n T ff T G ff T G ff B
B n T T T G d G X x x x x x x x x V
S X x x x x x x 所以
两相接地短路电流 0
0721.1721.10
721.1721
.1)
305.0305.0(05.1)
()0()2()1()0()1()2()2()1(]
0[)1(=+-=++==-=-==+=
+=
fa fa fa fa fa fa fa ff ff fa I I I I I I I j j x x j E I 所以
kA
I I kA kA I j kA
I I I I I I I I fb
fc fa fa fa fa B
fb fb fb fb 0
)1(0
)0(0
)2(0
)1()0()2()1(90748.0)90(748.025102.0325102.0)01120
1)120(1()(∠=-=-∠=⨯-=⨯∠⋅+∠⋅+-∠⋅=++=
kV 10G
kV
110f
3
-8题图
kV V V
kV V V kV kV j V I x j V V V V V fb
fc
fa
fa B
fa ff B fa fa fa fa )90(364.60)90(364.602
190728.120115721.1305.022)(000
)1()2()0()2()1(-∠==-∠=-=∠=⨯⨯⨯==++=
向量图。
