下载文档原格式
题目高中数学复习专题讲座指数函数、对数函数问题 高考要求指数函数、对数函数是高考考查的重点内容之一，本节主要帮助考生掌握两种函数的概念、图象和性质并会用它们去解决某些简单的实际问题 重难点归纳(1)运用两种函数的图象和性质去解决基本问题 此类题目要求考生熟练掌握函数的图象和性质并能灵活应用(2)综合性题目 此类题目要求考生具有较强的分析能力和逻辑思维能力(3)应用题目 此类题目要求考生具有较强的建模能力 典型题例示范讲解例1已知过原点O 的一条直线与函数y =log 8x 的图象交于A 、B 两点，分别过点A 、B 作y 轴的平行线与函数y =log 2x 的图象交于C 、D 两点(1)证明 点C 、D 和原点O 在同一条直线上； (2)当BC 平行于x 轴时，求点A 的坐标命题意图 本题主要考查对数函数图象、对数换底公式、对数方程、指数方程等基础知识，考查学生的分析能力和运算能力知识依托 (1)证明三点共线的方法 k OC =k OD (2)第(2)问的解答中蕴涵着方程思想，只要得到方程(1)，即可求得A 点坐标错解分析 不易考虑运用方程思想去解决实际问题技巧与方法 本题第一问运用斜率相等去证明三点共线；第二问运用方程思想去求得点A 的坐标(1)证明 设点A 、B 的横坐标分别为x 1、x 2,由题意知 x 1>1,x 2>1,则A 、B 纵坐标分别为log 8x 1,log 8x 2 因为A 、B 在过点O 的直线上，所以228118log log x x x x =,点C 、D 坐标分别为(x 1,log 2x 1),(x 2,log 2x 2), 由于log 2x 1=2log log 818x ===2log log log ,log 38282218x x x 3log 8x 2, 所以OC 的斜率 k 1=118212log 3log x x x x =, OD 的斜率 k 2=228222log 3log x x x x =， 由此可知 k 1=k 2,即O 、C 、D 在同一条直线上(2)解 由BC 平行于x 轴知 log 2x 1=log 8x 2即 log 2x 1=31log 2x 2,代入x 2log 8x 1=x 1log 8x 2得x 13log 8x 1=3x 1log 8x 1, 由于x 1>1知log 8x 1≠0,∴x 13=3x 1又x 1>1,∴x 1=3,则点A 的坐标为(3，log 83)例2在xOy 平面上有一点列P 1(a 1,b 1),P 2(a 2,b 2),…,P n (a n ,b n )…,对每个自然数n 点P n 位于函数y =2000(10a )x(0<a <1)的图象上，且点P n ,点(n ,0)与点(n +1,0)构成一个以P n 为顶点的等腰三角形(1)求点P n 的纵坐标b n 的表达式；(2)若对于每个自然数n ,以b n ,b n +1,b n +2为边长能构成一个三角形，求a 的取值范围；(3)设C n =lg(b n )(n ∈N *),若a 取(2)中确定的范围内的最小整数，问数列{C n }前多少项的和最大？试说明理由命题意图 本题把平面点列，指数函数，对数、最值等知识点揉合在一起，构成一个思维难度较大的综合题目，本题主要考查考生对综合知识分析和运用的能力知识依托 指数函数、对数函数及数列、最值等知识错解分析 考生对综合知识不易驾驭，思维难度较大，找不到解题的突破口技巧与方法 本题属于知识综合题，关键在于读题过程中对条件的思考与认识，并会运用相关的知识点去解决问题解 (1)由题意知 a n =n +21,∴b n =2000(10a )21n(2)∵函数y =2000(10a )x(0<a <10)递减， ∴对每个自然数n ,有b n >b n +1>b n +2则以b n ,b n +1,b n +2为边长能构成一个三角形的充要条件是b n +2+b n +1>b n ,即(10a )2+(10a)－1>0, 解得a <－5(1+2)或a >5(5－1) ∴5(5－1)<a <10(3)∵5(5－1)<a <10,∴a =7∴b n =2000(107)21+n 数列{b n }是一个递减的正数数列，对每个自然数n ≥2,B n =b n B n －1于是当b n ≥1时，B n <B n －1,当b n <1时，B n ≤B n －1,因此数列{B n }的最大项的项数n 满足不等式b n ≥1且b n +1<1,由b n =2000(107)21+n ≥1得 n ≤20 8 ∴n =20例3设f (x )=log 2xx -+11,F (x )=x-21+f (x ) (1)试判断函数f (x )的单调性，并用函数单调性定义，给出证明；(2)若f (x )的反函数为f －1(x ),证明 对任意的自然数n (n ≥3),都有f －1(n )>1+n n ; (3)若F (x )的反函数F －1(x ),证明 方程F －1(x )=0有惟一解解 (1)由xx-+11>0,且2－x ≠0得F (x )的定义域为(－1，1)， 设－1＜x 1＜x 2＜1,则 F (x 2)－F (x 1)=(122121x x ---)+(11222211log 11log x x x x -+--+) )1)(1()1)(1(log )2)(2(212122112x x x x x x x x -++-+---=,∵x 2－x 1>0,2－x 1>0,2－x 2>0,∴上式第2项中对数的真数大于1 因此F (x 2)－F (x 1)>0,F (x 2)>F (x 1),∴F (x )在(－1，1）上是增函数(2)证明 由y =f (x )=xx -+11log 2得 2y =1212,11+-=-+y y x x x ,∴f －1(x )=1212+-x x ,∵f (x )的值域为R ，∴f -－1(x )的定义域为R当n ≥3时，f -1(n )>1221111221112121+>⇔+->+-⇔+>+-⇔+n n n n n n n n n n 用数学归纳法易证2n >2n +1(n ≥3),证略(3)证明 ∵F (0)=21,∴F －1(21)=0,∴x =21是F －1(x )=0的一个根 假设F －1(x )=0还有一个解x 0(x 0≠21),则F -1(x 0)=0,于是F (0)=x 0(x 0≠21) 这是不可能的，故F -1(x )=0有惟一解学生巩固练习1 定义在(－∞,+∞)上的任意函数f (x )都可以表示成一个奇函数g (x )和一个偶函数h (x )之和，如果f (x )=lg(10x +1),其中x ∈(－∞,+∞),那么( )A g (x )=x ,h (x )=lg(10x +10－x +2)B g (x )=21［lg(10x +1)+x ］,h (x )= 21［lg(10x +1)－x ］ C g (x )=2x ,h (x )=lg(10x +1)－2xD g (x )=－2x ,h (x )=lg(10x +1)+2x2 当a >1时，函数y =log a x 和y =(1－a )x 的图象只可能是( )3 已知函数f (x )=⎩⎨⎧<<--≥)02()(log )0( 22x x x x 则f -－1(x －1)=_________4 如图，开始时，桶1中有a L 水，t 分钟后剩余的水符合指数衰减曲线y 1=ae －nt ,那么桶2中水就是y 2=a －ae －nt ,假设过5分钟时，桶1和桶2的水相等，则再过_________分钟桶1a 5 设函数f (x )=log a (x －3a )(a >0且a ≠1),当点P (x ,y )是函数y =f (x )图象上的点时，点Q (x －2a ,－y )是函数y =g (x )图象上的点(1)写出函数y =g (x )的解析式；(2)若当x ∈［a +2,a +3］时，恒有|f (x )－g (x )|≤1,试确定a 的取值范围 6 已知函数f (x )=log a x (a >0且a ≠1),(x ∈(0,+∞)),若x 1,x 2∈(0,+∞),判断21［f (x 1)+f (x 2)］与f (221x x +)的大小，并加以证明 y 2=a-ae -nty 1=ae -nt桶2桶17 已知函数x ,y 满足x ≥1,y ≥1 log a 2x +log a 2y =log a (ax 2)+log a (ay 2)(a >0且a ≠1),求log a (xy )的取值范围8 设不等式2(log 21x )2+9(log 21x )+9≤0的解集为M ，求当x ∈M 时函数f (x )=(log 22x )(log 28x )的最大、最小值参考答案1 解析 由题意 g (x )+h (x )=lg(10x +1) ①又g (－x )+h (－x )=lg(10－x +1) 即－g (x )+h (x )=lg(10－x +1) ②由①②得 g (x )=2x ,h (x )=lg(10x +1)2x 答案 C2 解析 当a >1时，函数y =log a x 的图象只能在A 和C 中选，又a >1时，y =(1－a )x 为减函数答案 B3 解析 容易求得f -－1(x )=⎩⎨⎧<-≥)1(2)1( log 2x x x x,从而 f －1(x －1)=⎩⎨⎧<-≥--).2( ,2)2(),1(log 12x x x x答案 ⎩⎨⎧<-≥--)2( ,2)2(),1(log 12x x x x4 解析 由题意，5分钟后，y 1=ae－nt,y 2=a －ae－nt,y 1=y 2∴n =51l n 2 设再过t 分钟桶1中的水只有8a , 则y 1=ae －n (5+t )=8a ,解得t =10答案 105 解 (1)设点Q 的坐标为(x ′,y ′),则x ′=x －2a ,y ′=－y 即x =x ′+2a ,y =－y ′ ∵点P (x ,y )在函数y =log a (x －3a )的图象上，∴－y ′=log a (x ′+2a －3a ),即y ′=log aax -21,∴g (x )=log a x -1 (2)由题意得x －3a =(a +2)－3a =－2a +2>0;a x -1=aa -+)3(1>0,又a >0且a ≠1,∴0＜a ＜1,∵|f (x )－g (x )|=|log a (x －3a )－log aax -1| =|log a (x 2－4ax +3a 2)|·|f (x )－g (x )|≤1,∴－1≤log a (x 2－4ax +3a 2)≤1,∵0＜a ＜1,∴a +2>2a f (x )=x 2－4ax +3a 2在［a +2,a +3］上为减函数， ∴μ(x )=log a (x 2－4ax +3a 2)在［a +2,a +3］上为减函数，从而［μ(x )］max =μ(a +2)=log a (4－4a ),［μ(x )］mi n =μ(a +3)=log a (9－6a ),于是所求问题转化为求不等式组⎪⎩⎪⎨⎧≤--≥-<<1)44(log 1)69(log 10a a a aa 的解由log a (9－6a )≥－1解得0＜a ≤12579-, 由log a (4－4a )≤1解得0＜a ≤54, ∴所求a 的取值范围是0＜a6 解 f (x 1)+f (x 2)=log a x 1+log a x 2=log a x 1x 2,∵x 1,x 2∈(0,+∞),x 1x 2≤(221x x +)2(当且仅当x 1=x 2时取“=”号)， 当a >1时，有log a x 1x 2≤log a (221x x +)2,∴21log a x 1x 2≤log a (221x x +)，21(log a x 1+log a x 2)≤log a 221x x +, 即21[f (x 1)+f (x 2)］≤f (221x x +)(当且仅当x 1=x 2时取“=”号) 当0＜a ＜1时，有log a x 1x 2≥log a (221x x +)2,∴21(log a x 1+log a x 2)≥log a 221x x +,即21［f (x 1)+f (x 2)］≥f (221x x +)(当且仅当x 1=x 2时取“=”号）7 解 由已知等式得 log a 2x +log a 2y =(1+2log a x )+(1+2log a y ), 即(log a x －1)2+(log a y －1)2=4,令u =log a x ,v =log a y ,k =log a xy ,则(u －1)2+(v －1)2=4(uv ≥0),k =u +v 在直角坐标系uOv 内，圆弧(u －1)2+(v －1)2=4(uv ≥0)与平行直线系v =－u +k 有公共点， 分两类讨论(1)当u ≥0,v ≥0时，即a >1时，结合判别式法与代点法得1+3≤k ≤2(1+2);(2)当u ≤0,v ≤0,即0＜a ＜1时，同理得到2(1－2)≤k ≤1－综上，当a >1时，log a xy 的最大值为2+22，最小值为1+3；当0＜a ＜1时，log a xy 的最大值为1－3，最小值为2－8 解 ∵2(21log x )2+9(21log x )+9≤0∴(221log x +3)( 21log x +3)≤0 ∴－3≤21log x 23 即21log (21)－3≤21log x ≤21log (21)23-∴(21)23-≤x ≤(21)－3,∴22≤x ≤8即M ={x |x ∈［22,8］}又f (x )=(log 2x －1)(log 2x －3)=log 22x －4log 2x +3=(log 2x －2)2－1∵22≤x ≤8,∴23≤log 2x ≤3 ∴当log 2x =2,即x =4时y mi n =－1;当log 2x =3,即x =8时，y max =0课前后备注。
第五节 指数与指数函数(1)了解指数函数模型的实际背景.(2)理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算.(3)理解指数函数的概念,理解指数函数的单调性,掌握指数函数图象通过的特殊点. (4)知道指数函数是一类重要的函数模型.1.指数幂的概念(1)根式的概念:根式的概念 符号表示 备注如果① x n =a ,那么x 叫做a 的n 次方根n>1且n ∈N *当n 为奇数时,正数的n 次方根是一个② 正数 ,负数的n 次方根是一个③ 负数 √a n0的n 次方根是0当n 为偶数时,正数的n 次方根有④ 两个 ,它们互为⑤ 相反数±√a n负数没有偶次方根(2)两个重要公式:√a n n ={ ⑥ a ,n 为奇数,|a|={⑦ a (a ≥0),⑧ -a (a <0),n 为偶数; (√a n)n =⑨ a (注意a 必须使√a n有意义). 2.有理数指数幂 (1)分数指数幂的表示: (i)正数的正分数指数幂:a m n=⑩ √a m n(a>0,m,n ∈N *,n>1). (ii)正数的负分数指数幂: a -m n=1a m n=√a mn(a>0,m,n ∈N *,n>1).(iii)0的正分数指数幂是 0 ,0的负分数指数幂无意义. (2)有理数指数幂的运算性质: (i)a r a s = a r+s (a>0,r,s ∈Q). (ii)(a r )s = a rs (a>0,r,s ∈Q). (iii)(ab)r = a r b r (a>0,b>0,r ∈Q). 3.指数函数的图象与性质a>10<a<1图象定义域 R 值域(0,+∞) 性质过定点 (0,1)当x>0时, y>1 ; 当x<0时,当x>0时, 0<y<1 ; 当x<0时, y>10<y<1 在(-∞,+∞)上是 单调增函数在(-∞,+∞)上是 单调减函数▶提醒 (1)当指数函数的底数a 的大小不确定时,需分a>1和0<a<1两种情况进行讨论.(2)指数函数的图象恒过点(0,1),(1,a),(-1,1a ),依据这三点的坐标可得到指数函数的大致图象.指数函数的图象与底数大小的关系.下图是指数函数(1)y=a x ,(2)y=b x ,(3)y=c x ,(4)y=d x 的图象,底数a,b,c,d 与1之间的大小关系为c>d>1>a>b>0.由此我们可得到以下规律:在第一象限内,指数函数y=a x (a>0,且a ≠1)的图象越高,底数越大.1.判断正误(正确的打“√”,错误的打“✕”). (1)√a n n与(√a n)n 都等于a(n ∈N *).( ) (2)函数y=23x 与y=2x+1都不是指数函数.( ) (3)若a m <a n (a>0,且a ≠1),则m<n.( ) (4)当a<0时,(a 2)32=a 3.()(5)函数y=21+2x 是减函数.( ) (6)函数y=11+3的值域是(0,1).( )答案 (1)✕ (2)✕ (3)✕ (4)✕ (5)√ (6)√2.函数f(x)=2|x-1|的大致图象是( )答案 B 3.函数y=√1-(12)1x的定义域是.答案 (0,+∞)4.已知函数f(x)=a x-2+2的图象恒过定点A,则点A 的坐标为 . 答案 (2,3)5.若指数函数f(x)=(a-2)x 为减函数,则实数a 的取值范围为 . 答案 (2,3)指数幂的运算命题方向一 根式与指数幂典例1 (1)3√a ·√a 45(a>0)的值是( )A.1B.aC.a 15D.a 1710(2)化简:√3-2√2+√(1-√2)33+√(1-√2)44+√5-2√6= . (3)1.5-13×(-76)0+814×√24+(√23×√3)6-√(-23)23= .答案 (1)D (2)√3-1 (3)110命题方向二 化简求值典例2 化简下列各式: (1)(235)+2-2×(214)-12-(0.01)0.5;(2)56a 13b -2·(-3a -12b -1)÷(4a 23b -3)12;(3)(a 23b -1-12a -12b 13√56.解析(1)原式=1+14×(49)12-(1100)12=1+14×23-110=1+16-110=1615.(2)原式=-52a -16b -3÷(4a 23·b -3)12=-54a -16b -3÷(a 13b -32) =-54a -12b -32=-54·√3=-5√ab 4ab =-54a -12b -32.(3)原式=a -13b 12a -12b 13a 16b 56=a-13-12-16·b12+13-56=1a .规律总结指数幂运算的一般原则(1)有括号的先算括号里的,无括号的先进行指数运算. (2)先乘除后加减,负指数幂化成正指数幂的倒数.(3)底数是负数的,先确定符号;底数是小数的,先化成分数;底数是带分数的, 先化成假分数.(4)若是根式,则化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运算性质来解答. ▶提醒 运算结果不能同时含有根号和分数指数幂,也不能既有分母又含有负指数,形式力求统一. 1-1 化简:(1)(√23×√3)6+(-2 018)0-4×(1649)-12+√(3-π)44 ; (2)a 32-1a+a 12+1-a+a 12a 12+1+a -1a 12-1;(3)√a 13√a 12√a (a>0).解析 (1)(√23×√3)6+(-2 018)0-4×(1649)-12+√(3-π)44=108+1-7+π-3=99+π . (2)原式=(a 12-1)·(a+a 12+1)a+a 12+1-a 32-a+a-a12-a32+a12-a+1a-1=a12-1-1-aa-1=a12.(3)a>0,√a 13√a12√a=√a13√a12·a12=√a13·√a=√a13·a12=√a56=a512.指数函数的图象及应用典例3(1)函数f(x)=-3|x|+1的大致图象是()(2)若曲线|y|=2x+1与直线y=b没有公共点,则b的取值范围是.(3)若函数y=a x-m+n-3(a>0且a≠1)的图象恒过定点(3,2),则m+n=.答案(1)A(2)[-1,1](3)7解析(1)因为函数f(x)=-3|x|+1,所以f(-x)=-3|-x|+1=-3|x|+1=f(x),即函数为偶函数,其图象关于y轴对称,故排除B,D.当x=0时,f(0)=-30+1=0,即函数图象过原点,故排除C.故选A.(2)作出曲线|y|=2x+1(如图),要使该曲线与直线y=b没有公共点,只需-1≤b≤1.◆探究(变条件)本例(2)中若曲线y=|2x-1|与直线y=b有两个公共点,求b的取值范围.解析曲线y=|2x-1|与直线y=b如图所示.由图象可得,b的取值范围是(0,1).方法技巧应用指数函数图象的4个技巧(1)画指数函数y=a x(a>0,且a≠1)的图象,应抓住三个关键点:(1,a),(0,1),(-1,1a).(2)已知函数解析式判断其图象一般是取特殊点,判断所给的图象是否过这些点,若不满足,则排除.(3)对于有关指数型函数的图象问题,一般是从最基本的指数函数的图象入手,通过平移、伸缩、对称变换得到.特别地,当底数a与1的大小关系不确定时,应注意分类讨论.(4)有关指数方程、不等式问题往往利用相应的指数型函数图象,数形结合求解.2-1(1)函数y=a x-a-1(a>0,且a≠1)的图象可能是()(2)已知函数f(x)=a x-2+7(a>0且a≠1)的图象恒过定点P,若定点P在幂函数g(x)的图象上,则幂函数g(x)的图象是()(3)若关于x的方程|a x-1|=2a(a>0,且a≠1)有两个不等实根,则a的取值范围是.)答案(1)D(2)D(3)(0,12解析(2)由题意知,f(2)=a2-2+7=8,定点P(2,8),设幂函数g(x)=xα,将P(2,8)代入得2α=8,故α=3,即g(x)=x3,故选D.(3)方程|a x-1|=2a(a>0,且a≠1)有两个不等实根转化为函数y=|a x-1|的图象与y=2a的图象有两个交点.当0<a<1时,如图①,所以0<2a<1,即0<a<1;2当a>1时,如图②,而y=2a>1,不符合要求.所以0<a<12.指数函数的性质及应用命题方向一 比较指数幂的大小典例4 (1)已知a=(12)23,b=2-43,c=(12)12,则下列关系式中正确的是()A.c<a<bB.b<a<cC.a<c<bD.a<b<c(2)设a=0.230.32,b=20.01,c=0.320.23,则a,b,c 的大小关系为 . 答案 (1)B (2)a<c<b 解析(1)b=(12)43,而函数y=(12)x在R上为减函数,43>23>12,所以(12)43<(12)23<(12)12,即b<a<c.(2)0.230.32<0.230.23<0.320.23<1<20.01,所以a<c<b.命题方向二 解简单指数型不等式典例5 (1)已知函数f(x)=(12)x,则不等式f(a 2-4)>f(3a)的解集为( ) A.(-4,1) B .(-1,4) C.(1,4) D.(0,4) (2)已知(13)3x+1>91-x ,则x 的取值范围是 .(3)已知4x -2x+1-8<0,则x 的取值范围是 . 答案 (1)B (2)(-∞,-3) (3)(-∞,2)命题方向三 指数函数性质的综合应用典例6 (1)函数f(x)=(12)-x 2+2x的值域为( )A.(-∞,12] B.(0,12]C.[12,+∞) D.[2,+∞)(2)函数f(x)=e x -1e +1(e 为自然对数的底数)的值域为( ) A.(-1,1) B.(-1,+∞) C.(-∞,1)D.(-1,0)∪(0,1)(3)若函数y=√2+x -x 2的定义域为A,则函数y=4x -2x+1(x ∈A)的值域为 . 答案 (1)C (2)A (3)[-1,8] 解析 (2)f(x)=e x -1e x +1=1+-2e x +1,因为e x >0,所以e x +1>1,所以-2<-2e x +1<0,所以-1<1+-2e x +1<1,即f(x)的值域为(-1,1),所以选A.(3)由2+x-x 2≥0,解得-1≤x ≤2,所以A=[-1,2].函数y=4x -2x+1= 22x -2·2x =(2x -1)2-1,x ∈[-1,2],则12≤2x ≤4,当2x =1,即x=0时,y min =-1;当2x =4,即x=2时,得y max =8,所以-1≤y ≤8.所以函数y=4x -2x+1(x ∈A)的值域是[-1,8]. 典例7 (1)函数f(x)=(12)-x 2+2x+1的单调减区间为 .(2)已知奇函数f(x)=a-2e x +1(a ∈R,e 为自然对数的底数). (i)判断f(x)的单调性(不用证明);(ii)若对任意实数x, f(x)>m 2-4m+2恒成立,求实数m 的取值范围. 答案 (1)(-∞,1] 解析 (1)设u=-x 2+2x+1, ∵y=(12)u为减函数,∴函数y=(12)-x 2+2x+1的减区间即函数u=-x 2+2x+1的增区间.又u=-x 2+2x+1的增区间为(-∞,1], ∴所求减区间为(-∞,1].(2)(i)f(x)是R 上的单调递增函数. (ii)∵f(x)为奇函数,∴f(-x)=-f(x),∴a-2e -x +1=-a+2e x +1,∴2a=2,∴a=1,∴f(x)=1-2e x +1,令t=e x +1,∵e x >0, ∴t>1,又g(t)=1-2t 在(1,+∞)上为增函数,∴-1<g(t)<1,即-1<f(x)<1,当f(x)>m 2-4m+2对任意实数x 恒成立时, 有m 2-4m+2≤-1,即m 2-4m+3≤0,∴1≤m ≤3,故实数m 的取值范围是[1,3]. 规律总结(1)利用指数函数的性质比较大小或解不等式,最重要的是“同底”原则.(2)求解与指数函数有关的复合函数问题,要明确复合函数的构成,涉及值域、单调区间、最值等问题时,要借助“同增异减”这一性质分析判断. 3-1 不等式(12)x 2+ax<(12)2x+a -2恒成立,则a 的取值范围是 .答案 (-2,2) 3-2 求函数f(x)=3√x2-5x+4的定义域、值域及单调区间.解析 解不等式x 2-5x+4≥0,得x ≤1或x ≥4,所以函数y=f(x)的定义域为(-∞,1]∪[4,+∞).因为2-5x +4≥0,∴f(x)=3√x2-5x+4≥30=1,则函数y=f(x)的值域为[1,+∞).令u=2-5x +4,由二次函数的性质可知,u=√x 2-5x +4在区间(-∞,1]上单调递减,在区间[4,+∞)上单调递增,y=3u 为增函数,故函数y=f(x)的单调递减区间为(-∞,1],单调递增区间为[4,+∞).A 组 基础题组1.已知a>0,√a 23=( )A.a 12B.a 32C.a 23D.a 13答案 D2.若3<a<4,则化简√(3-a)2+√(4-a)44的结果是( ) A.7-2a B.2a-7 C.1 D.-1 答案 C 3.设y 1=40.9,y 2=80.48,y 3=(12)-1.5,则( )A.y 3>y 1>y 2B.y 2>y 1>y 3C.y 1>y 2>y 3D.y 1>y 3>y 2答案 D4.设2x =8y+1,9y =3x-9,则x+y 的值为( ) A.18B.21C.24D.27答案 D 5.设a 12-a -12=m,则a 2+1a=( )A.m 2-2B.2-m 2C.m 2+2D.m 2答案 C 将a 12-a -12=m 两边平方得,(a 12-a -12)2=m 2,即a-2+a -1=m 2,所以a+a -1=m 2+2,即a+1a =m 2+2⇒a 2+1a=m 2+2.故选C.6.函数f(x)=51-|2x+4|的单调递增区间为( ) A.[-2,+∞) B.[-32,+∞) C.(-∞,-32] D.(-∞,-2]答案 D 由题意知,函数f(x)的定义域为R,设u=g(x)=1-|2x+4|,则g(x)={-2x -3,x >-2,2x +5,x ≤-2,则g(x)在(-2,+∞)上单调递减,在(-∞,-2]上单调递增,因为y=5u 在R 上单调递增,所以根据复合函数的单调性,可得函数f(x)的单调递增区间为(-∞,-2]. 7.已知函数f(x)=3x -3-x ,则f(x)( ) A.是偶函数,且在R 上是增函数 B.是奇函数,且在R 上是增函数 C.是偶函数,且在R 上是减函数 D.是奇函数,且在R 上是减函数答案 B 函数f(x)的定义域为R, f(-x)=3-x-(13)-x =(13)x-3x =-f(x),∴函数f(x)是奇函数.又y=3x 在R 上是增函数,函数y=(13)x在R 上是减函数,∴函数f(x)=3x-(13)x在R 上是增函数. 8.函数f(x)=(12)x 2+2x+3值域为( )A.[14,+∞) B.(-∞,14] C.(0,14] D.[0,14]答案 C 令t=x 2+2x+3,则t=(x+1)2+2≥2,y=(12)t为减函数,所以y ≤(12)2=14,结合y=(12)t>0,可得C 选项.9.函数y=2x2x +1(x ∈R)的值域为( ) A.(0,+∞) B.(0,1) C.(1,+∞)D.(0,12)答案 B y=2x2x +1=2x +1-12x +1=1-12x +1,∵0<12x +1<1,∴-1<-12x +1<0, ∴0<1-12x +1<1,即0<y<1,即函数的值域为(0,1),故选B.10.对不同的a>0且a ≠1,函数f(x)=a 4-2x +3的图象必过一个定点A,则点A 的坐标是 . 答案 (2,4)解析 根据指数函数的图象恒过定点(0,1),可令4-2x=0,得x=2,∴f(2)=a 0+3=4,∴点A 的坐标是(2,4).11.若关于x 的方程22x -2x+1+a=0在[0,1]内有解,则实数a 的取值范围是 . 答案 [0,1]解析 由22x -2x+1+a=0得a=2x+1-22x ,令2x =t,则a=2t-t 2=-(t-1)2+1,∵x ∈[0,1],∴t ∈[1,2],∴当t=1时,a 取得最大值1,当t=2时,a 取得最小值0, ∴0≤a ≤1.12.已知函数f(x)=10x -10-x10x +10-x . (1)判断函数的奇偶性;(2)证明: f(x)在定义域内是增函数; (3)求f(x)的值域.解析 (1)因为f(x)的定义域为R, 且f(-x)=10-x -10x10-x +10x =-f(x),所以f(x)是奇函数.(2)证明:f(x)=10x -10-x 10x +10-x =102x -1102x +1=1-2102x +1, 任取x 1,x 2∈R,且x 2>x 1,则 f(x 2)-f(x 1)=(1-2102x 2+1)-(1-2102x 1+1) =2×102x 2-102x 1(102x 2+1)(102x 1+1).因为x 2>x 1,所以102x 2-102x 1>0,又102x 2+1>0,102x 1+1>0,所以f(x 2)-f(x 1)>0,即f(x 2)>f(x 1),所以函数f(x)在定义域内是增函数. (3)令y=f(x),由y=10x -10-x 10x +10-x ,解得102x=1+y 1-y,因为102x >0,所以-1<y<1,即函数f(x)的值域是(-1,1).B 组 提升题组1.已知函数f(x)=|2x -1|,a<b<c,且f(a)>f(c)>f(b),则下列结论中,一定成立的是( ) A.a<0,b<0,c<0 B.a<0,b ≥0,c>0 C.2-a <2cD.2a +2c <2答案 D 作出函数f(x)=|2x -1|的图象,如图中实线所示,因为a<b<c,且f(a)>f(c)>f(b),所以结合图象知f(a)<1,a<0,0<f(c)<1,0<c<1,∴0<2a <1,1<2c <2,∴f(a)=|2a -1|=1-2a , f(c)=|2c -1|=2c -1. 又f(a)>f(c),即1-2a >2c -1, ∴2a +2c <2,故选D.2.已知函数f(x)=1e +1-12,则f(x)是( ) A.奇函数,且在R 上是增函数 B.偶函数,且在(0,+∞)上是增函数 C.奇函数,且在R 上是减函数 D.偶函数,且在(0,+∞)上是减函数答案 C f(x)的定义域为R,关于原点对称, f(-x)=1e -x +1-12 =e xe x +1-12,有f(-x)+f(x)=0,所以f(x)是奇函数,又易知f(x)是减函数.故选C.3.设a>0,且a ≠1,函数y=a 2x +2a x -1在[-1,1]上的最大值是14,则实数a 的值为 . 答案 13或3解析 令t=a x (a>0,且a ≠1),则原函数化为y=f(t)=(t+1)2-2(t>0). ①当0<a<1,x ∈[-1,1]时,t=a x ∈[a,1a ],此时f(t)在[a,1a ]上为增函数.所以f(t)max =f (1a )=(1a +1)2-2=14.所以(1a +1)2=16,解得a=-15 (舍去)或a=13. ②当a>1,x ∈[-1,1]时,t=a x ∈[1a ,a],此时f(t)在[1a ,a]上是增函数.所以f(t)max =f(a)=(a+1)2-2=14,解得a=3或a=-5(舍去). 综上可得a=13或3.4.已知函数f(x)=2|x-2|-1在区间[0,m]上的值域为[0,3],则实数m 的取值范围是 . 答案 [2,4]解析 函数f(x)=2|x-2|-1的图象的对称轴为x=2,且在(-∞,2]上单调递减,在(2,+∞)上单调递增,由函数f(x)=2|x-2|-1在区间[0,m]上的值域为[0,3],知0≤m-2≤2,即m ∈[2,4]. 5.已知函数f(x)=1-42a x +a (a>0,且a ≠1)是定义在(-∞,+∞)上的奇函数. (1)求a 的值; (2)求函数f(x)的值域;(3)当x ∈(0,1]时,tf(x)≥2x -2恒成立,求实数t 的取值范围. 解析 (1)因为f(x)是定义在(-∞,+∞)上的奇函数,所以f(-x)=-f(x). 即1-42a -x +a =-1+42a x +a , 所以a=2. (2)记y=f(x), 即y=2x -12x +1,所以2x =1+y1-y .由2x >0,得1+y1-y >0,解得-1<y<1.所以f(x)的值域为(-1,1). (3)由tf(x)≥2x-2得t2x -t2x +1≥2x -2,即(2x )2-(t+1)2x +t-2≤0. 令u=2x ,因为x ∈(0,1], 所以u ∈(1,2].即当u ∈(1,2]时,u 2-(t+1)u+t-2≤0恒成立. 所以{12-(t +1)×1+t -2≤0,22-(t +1)×2+t -2≤0,解得t ≥0.故t 的取值范围是[0,+∞).快乐分享，知识无界！感谢您的下载!由Ruize收集整理！。
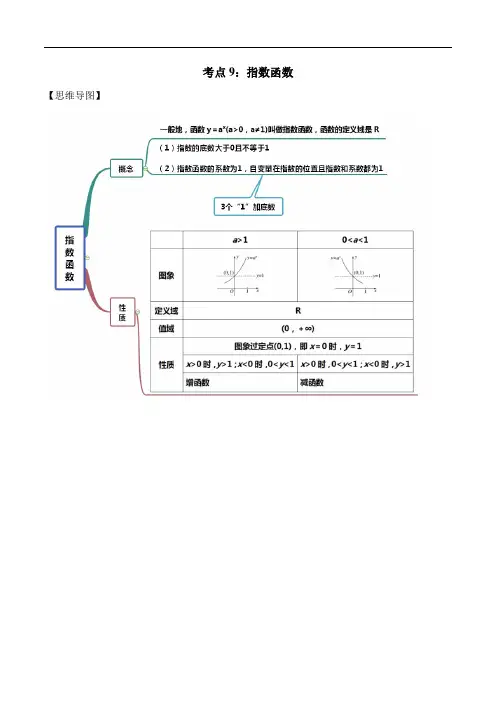
考点9：指数函数【思维导图】【常见考法】考法一：定义辨析1．下列函数：①2yx ；②()2x y =-；③12x y +=；④()1x y a =-（1a >且2a ≠）.其中，指数函数的个数是 。
2．若函数1((2)x y x a =-是自变量）是指数函数，则a 的取值范围是 。
3．若函数21()(33)()22x f x a a a =-++-是指数函数，则实数a 的值为_________．考法二：定义域1．函数f(x)=的定义域为 。
2．函数()422x x f x =--______________．3．设函数f （x ）x 44-，则函数f （x 4）的定义域为 。
4. 函数y 1x a -的定义域是(－∞，0]，则a 的取值范围为 。
5．已知f （x ）2x 2ax a 31+--的定义域为R ，则实数a 的取值范围是______．考法三：单调性1．函数2212x x y --+=-的单调递增区间为 。
2．函数243()2x x f x --=的单调减区间为 。
3．已知函数1()2xf x ⎛⎫= ⎪⎝⎭，则不等式()24(3)f a f a ->的解集为 。
4.若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是 。
5．，，则，，的大小关系为 。
6．已知3413a ⎛⎫= ⎪⎝⎭，1213b ⎛⎫= ⎪⎝⎭，12c π=，则a b c 、、 的大小关系 。
7．0.81.1512log 2,2,,2a b c -⎛⎫=== ⎪⎝⎭已知则a b c 、、的大小关系是 。
考法四：值域1．设函数()()121x f x x R =∈+,则它的值域为 。
2．函数221()2x x y -+=的值域是 。
3．函数1425x x y +=--在[1,2]上值域为 。
4．已知实数0a >且1a ≠,若函数6,2(),2x x x f x a x -≤⎧=⎨>⎩的值域为[4,)+∞,则a 的取值范围是 。
【考点预测】1.指数及指数运算(1)高中数学53个题型归纳与方法技巧总结篇专题09指数与指数函数根式的定义：一般地，如果n x a =，那么x 叫做a 的n 次方根，其中(1n >，)n N *∈，n 称为根指数，a 称为根底数．(2)根式的性质：当n 为奇数时，正数的n 次方根是一个正数，负数的n 次方根是一个负数.当n 为偶数时，正数的n 次方根有两个，它们互为相反数.(3)指数的概念：指数是幂运算(0)n a a ≠中的一个参数，a 为底数，n 为指数，指数位于底数的右上角，幂运算表示指数个底数相乘.(4)有理数指数幂的分类①正整数指数幂()n n a a a a a n N *=⋅⋅⋅⋅∈个；②零指数幂01(0)a a =≠；③负整数指数幂1(0nn aa a-=≠，)n N *∈；④0的正分数指数幂等于0，0的负分数指数幂没有意义．(5)有理数指数幂的性质①+(0m n m n a a a a >=，m ，)n Q ∈；②()(0m n m n a a a >=，m ，)n Q ∈；③()(0mm mab a a b >=，0b >，)m Q ∈(0mn a a >=，m ，)n Q ∈．2.指数函数⑥既不是奇函数，也不是偶函数【方法技巧与总结】1.指数函数常用技巧(1)当底数大小不定时，必须分“1a >”和“01a <<”两种情形讨论．(2)当01a <<时，x →+∞，0y →；a 的值越小，图象越靠近y 轴，递减的速度越快．当1a >时x →+∞，0y →；a 的值越大，图象越靠近y 轴，递增速度越快．(3)指数函数x y a =与1()xy a=的图象关于y 轴对称．【题型归纳目录】题型一：指数运算及指数方程、指数不等式题型二：指数函数的图像及性质题型三：指数函数中的恒成立问题题型四：指数函数的综合问题【典例例题】题型一：指数运算及指数方程、指数不等式例1．（2022·四川凉山·三模（文））计算：)2ln31e 1lg 4lg 0.254-⎛⎫+-++= ⎪⎝⎭______．例2．（2022·河北邯郸·一模）不等式10631x x x --≥的解集为___________.例3．（2022·陕西·榆林市教育科学研究所模拟预测（理））甲､乙两人解关于x 的方程220x x b c -+⋅+=，甲写错了常数b ，得到的根为2x =-或x =217log 4，乙写错了常数c ，得到的根为0x =或1x =，则原方程的根是（）A ．2x =-或2log 3x =B ．1x =-或1x =C ．0x =或2x =D ．1x =-或2x =例4．（2022·全国·高三专题练习（文））已知函数()f x 是定义在R 上的奇函数，当0x ≥时，()4322x x f x a =-⨯+．则关于x 的不等式()6f x ≤-的解集为（）A ．(,2]-∞-B ．(,1]-∞-C ．[)()2,00,2- D ．[)()2,02,-⋃+∞例5．（2022·全国·高三专题练习）化简：（1）126016(2018)449-⎛⎫+--⨯ ⎪⎝⎭（2111332ab a b -⎫⎪⎭a >0，b >0).（3）312211122211111a a aa a a a a -+--++++-.【方法技巧与总结】利用指数的运算性质解题.对于形如()f x a b =，()f x a b >，()f x a b <的形式常用“化同底”转化，再利用指数函数单调性解决；或用“取对数”的方法求解.形如20xx a Ba C ++=或2)00(x x a Ba C ++ 的形式，可借助换元法转化二次方程或二次不等式求解.题型二：指数函数的图像及性质例6．（2022·浙江绍兴·模拟预测）函数2()()-+=-x xx m f x a a ，的图象如图所示，则（）A ．0,01<<<m aB ．0,1<>m aC ．0,01m a ><<D ．0,1>>m a 例7．（2022·全国·高三专题练习）函数()21xf x m =--恰有一个零点，则m 的取值范围是（）A ．()1,+∞B ．{}()01,∞⋃+C ．{}[)01,∞⋃+D ．[)1,+∞例8．（2022·四川省泸县第二中学模拟预测（文））函数()11e xf x -=+，下列关于函数()f x 的说法错误的是（）A ．函数()f x 的图象关于原点对称B ．函数()f x 的值域为()0,1C ．不等式()12f x >的解集是()0,∞+D ．()f x 是增函数例9．（2022·河南·三模（文））已知()1f x -为定义在R 上的奇函数，()10f =，且()f x 在[)1,0-上单调递增，在[)0,∞+上单调递减，则不等式()250xf -<的解集为（）A ．()22,log 6B ．()()2,12,log 6-∞⋃C ．()2log 6,+∞D ．()()21,2log 6,⋃+∞例10．（2022·新疆阿勒泰·三模（理））函数11x y a -=+图象过定点A ，点A 在直线()31,0mx ny m n +=>>上，则121m n+-最小值为___________.例11．（2022·北京·高三专题练习）已知()212221x x xf x a +=+-+（其中a R ∈且a 为常数）有两个零点，则实数a 的取值范围是___________.例12．（2022·全国·高三专题练习）已知函数()22x x f x k -=+⋅（k 为常数，k ∈R ）是R 上的奇函数．(1)求实数k 的值；(2)若函数()y f x =在区间[]1,m 上的值域为15,4n ⎡⎤⎢⎥⎣⎦，求m n +的值．【方法技巧与总结】解决指数函数有关问题，思路是从它们的图像与性质考虑，按照数形结合的思路分析，从图像与性质找到解题的突破口，但要注意底数对问题的影响.题型三：指数函数中的恒成立问题例13．（2022·北京·高三专题练习）设()f x 是定义在R 上的偶函数，且当0x ≤时，()2xf x -=，若对任意的[],1x m m ∈+，不等式()()2f x f x m -≥恒成立，则正数m 的取值范围为（）A ．m 1≥B ．1mC ．01m <<D ．01m <≤例14．（2022·北京·高三专题练习）已知函数()33x xf x -=-．(1)利用函数单调性的定义证明()f x 是单调递增函数；(2)若对任意[]1,1x ∈-，()()24f x mf x ⎡⎤+≥-⎣⎦恒成立，求实数m 的取值范围．例15．（2022·全国·高三专题练习（文））已知函数()3(21xf x a a =-+为实常数).（1）讨论函数()f x 的奇偶性，并说明理由；（2）当()f x 为奇函数时，对任意[]1,6x ∈，不等式()2xuf x ≥恒成立，求实数u 的最大值.例16．（2022·全国·高三专题练习（文））已知函数1()421x x f x a +=-+ ．（1）若函数()f x 在[0x ∈，2]上有最大值8-，求实数a 的值；（2）若方程()0f x =在[1x ∈-，2]上有解，求实数a 的取值范围．例17．（2022·全国·高三专题练习）已知函数2()f x x =，1()2xg x m⎛⎫=- ⎪⎝⎭（1）当[1,3]x ∈-时，求()f x 的值域；（2）若对[]0,2x ∀∈，()1g x 成立，求实数m 的取值范围；（3）若对[]10,2x ∀∈，2[1,3]x ∃∈-，使得12()()g x f x 成立，求实数m 的取值范围．【方法技巧与总结】已知不等式能恒成立求参数值(取值范围)问题常用的方法：（1）函数法：讨论参数范围，借助函数单调性求解；（2）分离参数法：先将参数分离，转化成求函数的值域或最值问题加以解决；（3）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图象，利用数形结合的方法求解．题型四：指数函数的综合问题例18．（2022·天津河西·二模）已知定义在R 上的函数()f x 满足：①()2()0f x f x -+=；②()()20f x f x ---=；③在[]1,1-上的解析式为()[](]πcos ,1,021,0,1x x f x x x ⎧∈-⎪=⎨⎪-∈⎩，则函数()f x 与函数1()2xg x ⎛⎫= ⎪⎝⎭的图象在区间[]3,3-上的交点个数为()A ．3B ．4C ．5D ．6例19．（2022·北京·二模）若函数()()223,02,0xx f x x x a⎧+≤⎪=⎨-<≤⎪⎩的定义域和值域的交集为空集，则正数a 的取值范围是（）A ．(]0,1B ．()0,1C ．()1,4D ．()2,4例20．（2022·甘肃省武威第一中学模拟预测（文））已知函数()4sin 22x x f x =++，则124043202220222022f f f ⎛⎫⎛⎫⎛⎫+++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭______．例21．（2022·全国·高三专题练习）已知函数()f x 的定义域为R ，满足()()121f x f x +=-，且当(]1,1x ∈-时，()12x f x -=，则()2020f =______．例22．（2022·辽宁·建平县实验中学模拟预测）已知函数()221010,231,2x x x f x x x --⎧-≤⎪=⎨-->⎪⎩，则不等式()()10f x f x +-<的解集为___________.例23．（2022·江西·二模（文））设函数()2,111,12x a x f x x x --⎧≤⎪=⎨-+>⎪⎩，若()1f 是函数()f x 的最大值，则实数a 的取值范围为_______．【过关测试】一、单选题1．（2022·北京通州·模拟预测）已知函数1()33xxf x ⎛⎫=- ⎪⎝⎭，则()f x （）A ．是偶函数，且在R 是单调递增B ．是奇函数，且在R 是单调递增C ．是偶函数，且在R 是单调递减D ．是奇函数，且在R 是单调递减2．（2022·安徽淮南·二模（理））1947年，生物学家Max Kleiber 发表了一篇题为《body size and metabolicrate 》的论文，在论文中提出了一个克莱伯定律：对于哺乳动物，其基础代谢率与体重的34次幂成正比，即340F c M =，其中F 为基础代谢率，M 为体重．若某哺乳动物经过一段时间生长，其体重为原来的10倍，则基础代谢率1.7783≈）（）A ．5.4倍B ．5.5倍C ．5.6倍D ．5.7倍3．（2022·陕西·西安中学模拟预测（文））英国著名数学家布鲁克-泰勒以微积分学中将函数展开成无穷级数的定理著称于世.在数学中，泰勒级数用无限连加式来表示一个函数，泰勒提出了适用于所有函数的泰勒级数，并建立了如下指数函数公式：23e 126!nxx x x x n =+++++++ ，其中R,N x n ∈∈的近似值为（精确到0.01）（）A ．1.63B ．1.64C ．1.65D ．1.664．（2022·河南洛阳·二模（文））已知函数()()1331,1log 52,1x x f x x x +⎧-≥⎪=⎨-+-<⎪⎩，且()2f m =-，则()6f m +=（）A ．26B ．16C ．－16D ．－265．（2022·四川成都·三模（理））若函数()9x f x =0x ，则()0091xx -=（）．A ．13B ．1CD ．26．（2022·河南·开封高中模拟预测（文））若关于x 的不等式()221xxa x ⋅>+∈R 有实数解，则实数a 的取值范围是（）A ．()1,+∞B ．()2,+∞C ．[)1,+∞D ．[)2,+∞7．（2022·四川·内江市教育科学研究所三模（理））已知函数()f x 满足：对任意x ∈R ，1122f x f x ⎛⎫⎛⎫+=-- ⎪ ⎪⎝⎭⎝⎭．当[1,0)x ∈-时，()31x f x =-，则()3log 90=f （）A ．19B ．19-C ．1727D ．1727-8．（2022·上海宝山·二模）关于函数131()(22xx f x x =-⋅和实数,m n 的下列结论中正确的是（）A ．若3m n -<<，则()()f m f n <B ．若0m n <<，则()()f m f n <C ．若()()f m f n <，则22m n <D ．若()()f m f n <，则33m n <二、多选题9．（2022·湖南·模拟预测）在同一直角坐标系中，函数x y a =与()log 2a y x =-的图象可能是（）A ．B ．C ．D ．10．（2022·全国·模拟预测）已知0a b >>，下列选项中正确的为（）A 1=，则1a b －＜B ．若221a b －＝，则1a b －＜C ．若22=1a b -，则1a b －＜D ．若22log log 1a b -=，则1a b －＜11．（2022·广东肇庆·模拟预测）若a b >，则下列不等式中正确的有（）A ．0a b ->B ．22a b>C ．ac bc>D ．22a b >12．（2022·全国·模拟预测）已知函数14sin ,01()2,1x x x f x x x -<≤⎧=⎨+>⎩，若存在三个实数，使得()()()123f x f x f x ==，则（）A ．123x x x ++的取值范围为()2,3B ．()23x f x 的取值范围为5,23⎛⎫ ⎪⎝⎭C ．123x x x 的取值范围为51,362⎛⎫⎪⎝⎭D ．()13x f x 的取值范围为1,23⎛⎫⎪⎝⎭三、填空题13．（2022·安徽淮北·一模（理））2log142-⎛⎫++= ⎪⎝⎭___________.14．（2022·四川·模拟预测（理））已知两个条件：①,,()()()a b f a b f a f b ∈+=⋅R ；②()f x 在(0,)+∞上单调递减.请写出一个同时满足以上两个条件的函数____________.15．（2022·河南·模拟预测（文））函数()1423x x f x +=-+在1,2⎛⎤-∞ ⎥⎝⎦的值域为______．16．（2022·山西·二模（理））已知函数()322x xx f x -=-给出下列结论：①()f x 是偶函数；②()f x 在()0, +上是增函数；③若0t >，则点()(),t f t 与原点连线的斜率恒为正．其中正确结论的序号为______．四、解答题17．（2022·全国·高三专题练习）由于突发短时强降雨，某小区地下车库流入大量雨水.从雨水开始流入地下车库时进行监测，已知雨水流入过程中，地下车库积水量y （单位：3m ）与时间t （单位：h ）成正比，雨停后，消防部门立即使用抽水机进行排水，此时y 与t 的函数关系式为25ty k ⎛⎫=⨯ ⎪⎝⎭（k 为常数），如图所示.(1)求y 关于t 的函数关系式；(2)已知该地下车库的面积为25602m ，当积水深度小于等于0.05m 时，小区居民方可入内，那么从消防部门开始排水时算起，至少需要经过几个小时以后，小区居民才能进入地下车库？18．（2022·全国·高三专题练习）（1）计算：1294⎛⎫- ⎪⎝⎭（﹣9.6）0﹣22327283--⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭；（2）已知1122a a-+=3，求22112a a a a --++++的值．19．（2022·全国·高三专题练习）已知a >0，且a ≠1，若函数y ＝|ax －2|与y ＝3a 的图象有两个交点，求实数a 的取值范围．20．（2022·全国·高三专题练习）设函数()(0x x f x ka a a -=->且1)a ≠是定义域为R 的奇函数；（1）若()10f >，判断()f x 的单调性并求不等式(2)(4)0f x f x ++->的解集；（2）若()312f =，且22()4()x xg x a a f x -=+-，求()g x 在[1,)+∞上的最小值．21．（2022·北京·高三专题练习）定义在D 上的函数()f x ，如果满足:对任意,x D ∈存在常数0,M >都有()M f x M -≤≤成立，则称()f x 是D 上的有界函数，其中M 称为函数()f x 的上界.已知()422x x f x a =+⋅-.（1）当2a =-时，求函数()f x 在()0,∞+上的值域，并判断函数()f x 在()0,∞+上是否为有界函数﹐请说明理由﹔（2）若函数()f x 在(),0-∞上是以2为上界的有界函数，求实数a 的取值范围.22．（2022·全国·高三专题练习）已知函数()(0,0,1,1)x x f x a b a b a b =+>>≠≠.(1)设12,2a b ==，求方程()2f x =的根；(2)设12,2a b ==，若对任意x ∈R ，不等式()()26f x f x m ≥-恒成立，求实数m 的最大值；(3)若01,1a b <<>，函数()()2g x f x =-有且只有1个零点，求ab 的值.。
2021年高考数学一轮复习《指数及指数函数》精选练习一、选择题1.当2－x 有意义时，化简x 2－4x ＋4－x 2－6x ＋9的结果为( )A.2x －5B.－2x －1C.－1D.5－2x2.计算（2n ＋1）2×（12）2n ＋14n ×8－2(n ∈N *)的结果是( )A.164B.22n ＋5C.2n 2－2n ＋6 D.(12)2n －73.已知x 2＋x －2=22，且x>1，则x 2－x －2的值为( )A.2或－2B.－2C. 6D.24.下列各式中错误的是（ ） A.21153151(1)a a a a --⋅⋅=>B.()269463(,0)a b a b a b ---⋅=⋅> C.12211133342423424(,0)x y x y x y y x y --⎛⎫⎛⎫⎛⎫--=> ⎪⎪⎪⎝⎭⎝⎭⎝⎭D.113324115324153(,,0)525a b cac a b c a b c ---=->5.若2<a<3，化简442)3()2(a a -+-的结果是( )A.5-2aB.2a-5C.1D.-16.当x -2有意义时，化简964422+--+-x x x x 的结果是( )A.2x-5B.-2x-1C.-1D.5-2x7.将322-化简成不含根号的式子是( ) A.212- B.512- C.312- D.322-8.设m a a =--2121，则a a 12+等于( )A.m 2－2B.2－m 2C.m 2＋2D.m 29.若f(x)=－x 2＋2ax 与g(x)=(a ＋1)1－x 在区间[1，2]上都是减函数，则a 的取值范围是() A.(0.5,1] B.(0,0.5] C.[0，1] D.(0，1]10.函数y=16－4x 的值域是( )A.[0，＋∞)B.[0，4]C.[0，4)D.(0，4)11.函数y=2x －8的定义域为( )A.(－∞，3)B.(－∞，3]C.(3，＋∞)D.[3，＋∞)12.若函数f(x)=2x＋12x －a 是奇函数，则使f(x)＞3成立的x 的取值范围为( )A.(－∞，－1)B.(－1,0)C.(0,1)D.(1，＋∞)13.已知a=30.2，b=0.2－3，c=(－3)0.2，则a ，b ，c 的大小关系为( )A.a ＞b ＞cB.b ＞a ＞cC.c ＞a ＞bD.b ＞c ＞a14.函数y=|2x －1|的大致图象是( )15.已知f(x)=a －x (x>0且a ≠1)，且f(－2)>f(－3)，则a 的取值范围是( )A.(0，＋∞)B.(1，＋∞)C.(－∞，1)D.(0,1)16.函数f(x)=a x －3＋1(a>0，且a ≠1)的图象恒过定点P ，则定点P 的坐标为() A.(3,3) B.(3,2) C.(3,6) D.(3,7)17.已知函数f(x)=5|x|，g(x)=ax 2－x(a ∈R)，若f[g(1)]=1，则a=( )A.1B.2C.3D.－118.函数y=2x2x ＋1的值域是( )A.(0，1)B.(0，1]C.(0，＋∞)D.[0，＋∞)19.函数f(x)=3－x －1的定义域、值域分别是( )A.定义域是R ，值域是RB.定义域是R ，值域是(0，＋∞)C.定义域是R ，值域是(－1，＋∞)D.以上都不对20.函数y=xax|x|(0<a<1)的图象的大致形状是( )二、填空题21.函数y=a x(－2≤x ≤3)的最大值为2，则a=________.22.已知函数f(x)满足f(x)=⎩⎪⎨⎪⎧f （x ＋2），x<0，2x ，x ≥0，则f(－7.5)的值为________. 23.已知集合A={x|1≤2x<16}，B={x|0≤x<3，x ∈N}，则A ∩B=________.24.已知函数f(x)是定义在R 上的奇函数，当x ＞0时，f(x)=1－2－x ，则不等式f(x)＜－12的解集是______. 25.函数f(x)=a 2x －3a x ＋2(a>0，且a ≠1)的最小值为________.26.若函数f(x)=a x (a ＞0，a ≠1)在[－1,2]上的最大值为4，最小值为m ，且函数g(x)=(1－4m)x 2在[0，＋∞)上是增函数，则a=________.27.若函数y=a 2x ＋2a x －1(a ＞0且a ≠1)在[－1,1]上的最大值为14，则a 的值为________.28.已知函数f(x)=22x ＋1＋ax ，则f(2 022)＋f(－2 022)=________. 29.若函数f(x)=⎩⎪⎨⎪2－x （x ≥2），则f(－3)的值为________. 30.当x ∈[－1，1]时，函数f(x)=3x －2的值域为________.31.若f(x)=⎩⎪⎨⎪⎧ a x ，x>1，⎝ ⎛⎭⎪⎫4－a 2x ＋2，x ≤1是R 上的单调递增函数，则实数a 的取值范围为________． 32.已知f(x)=x 2，g(x)=(0.5)x －m.若对任意x 1∈[－1,3]，总存在x 2∈[0,2]，使得f(x 1)≥g(x 2)成立，则实数m 的取值范围是____________________.33.若函数f(x)= 2x 2＋2ax －a －1的定义域为R ，则a 的取值范围是________.34.函数f(x)=⎩⎪⎨⎪⎧ ⎝⎛⎭⎪⎫4－a 2x ＋2，x ≤1a x ，x>1在R 上单调递增，则实数a 取值范围为________.35.函数f(x)=错误!未找到引用源。
指数及指数函数高考复习题1若点(a,9)在函数y ＝3x的图象上，则tana π6的值为( )A ．0 B.33C ．1 D. 3 2函数164x y =-的值域是 ( )（A ）[0,)+∞ （B ）[0,4] （C ）[0,4) （D ）(0,4)3设232555322555a b c ===（）,（），（），则a ，b ，c 的大小关系是( )（A ）a ＞c ＞b （B ）a ＞b ＞c （C ）c ＞a ＞b （D ）b ＞c ＞a4下列四类函数中，个有性质“对任意的x >0，y >0，函数f (x )满足f （x ＋y ）＝f （x ）f （y ）”的是 ( )（A ）幂函数 （B ）对数函数 （C ）指数函数 （D ）余弦函数5.化简)31()3)((656131212132b a b a b a ÷-的结果（ ）A ．a 6B ．a -C ．a 9-D ．29a6已知函数()f x 满足：x ≥4,则()f x ＝1()2x ；当x ＜4时()f x ＝(1)f x +，则2(2log 3)f +＝（ ）A.124 B.112 C.18 D.387. 不等式4x －3·2x ＋2<0的解集是( )A ．{x |x <0}B ．{x |0<x <1}C ．{x |1<x <9}D ．{x |x >9}8．若关于x 的方程|a x－1|＝2a (a >0，a ≠1)有两个不等实根，则a 的取值范围是( )A ．(0,1)∪(1，＋∞) B．(0,1) C ．(1，＋∞) D．(0，12)9(理)函数y ＝|2x－1|在区间(k －1，k ＋1)内不单调，则k 的取值范围是( )A ．(－1，＋∞)B ．(－∞，1)C ．(－1,1)D ．(0,2)10(理)若函数y ＝2|1－x |＋m 的图象与x 轴有公共点，则m 的取值范围是( )A ．m ≤－1B ．－1≤m <0C ．m ≥1D ．0<m ≤111．函数f (x )＝x 12 －(12)x的零点个数为( )A ．0B ．1C ．2D ．312(理)已知函数⎩⎨⎧>≤--=-7,7,3)3()()6(x a x x a x f x 若数列{a n }满足a n ＝f (n )(n ∈N *)，且{a n }是递增数列，则实数a 的取值范围是( )A ．[94，3)B ．(94，3) C ．(2,3) D ．(1,3)13．设函数f (x )＝|2x－1|的定义域和值域都是[a ，b ](b >a )，则a ＋b 等于( )A ．1B ．2C ．3D ．414．已知函数⎪⎩⎪⎨⎧>-≤=1),1(log 1,)21()(2x x x x f x，则f (x )≤12的解集为________． 15．若函数⎪⎪⎩⎪⎪⎨⎧>≤=0,10,)31()(x xx x f x则不等式|f (x )|≥13的解集为________． 16．函数y ＝a x ＋2012＋2011(a >0且a ≠1)的图象恒过定点________．17．设f (x )是定义在实数集R 上的函数，满足条件y ＝f (x ＋1)是偶函数，且当x ≥1时，f (x )＝2x－1，则f (23)、f (32)、f (13)的大小关系是________．18．若定义运算a *b ＝⎩⎪⎨⎪⎧aa <b ，b a ≥b ，则函数f (x )＝3x *3－x的值域是________．19．定义区间[x 1，x 2]的长度为x 2－x 1，已知函数f (x )＝3|x |的定义域为[a ，b ]，值域为[1,9]，则区间[a ，b ]的长度的最大值为______，最小值为______．20.设函数f(x)=,求使f(x)≥2 的x 的取值范围.21．(文)(2011·上海吴淞中学月考)已知函数f (x )＝a ·2x ＋a －22x＋1是奇函数．(1)求a 的值；(2)判断函数f (x )的单调性，并用定义证明；(3)求函数的值域．22．(文)已知f (x )是定义在R 上的奇函数，且当x ∈(0,1)时，f (x )＝2x4x ＋1.(1)求f (x )在(－1,1)上的解析式； (2)证明：f (x )在(0,1)上是减函数．[]的值，求实数上的最大值是在函数且设a a a y a a x x 141,1-12,10.232-+=≠24.已知f (x )＝aa 2－1(a x －a －x)(a >0且a ≠1)．(1)判断f (x )的奇偶性； (2)讨论f (x )的单调性； (3)当x ∈[－1,1]时，f (x )≥b 恒成立，求b 的取值范围．指数及指数函数高考复习题答案1[答案] D[解析] 由点(a,9)在函数y ＝3x图象上知3a＝9，即a ＝2，所以tan a π6＝tan π3＝ 3. 2解析：[)40,0164161640,4x x x >∴≤-<∴-∈3.A 【解析】25y x =在0x >时是增函数，所以a c >，2()5xy =在0x >时是减函数，所以c b >。
[练案9］第六讲指数与指数函数A组基础巩固一、单选题1．化简：(a错误!b错误!）·(3a错误!b错误!)÷（错误!a错误!b错误!）等于（ C ）A．6a B．－aC．9a D．9a2[解析] 原式＝错误!×a错误!b错误!＝9a。
故选C。
2．(2020·海南中学模拟)已知函数f（x)＝4＋2a x－1(a>1且a≠1)的图象恒过点P，则点P的坐标是( A )A．（1,6) B．(1,5)C．（0,5) D．(5,0)［解析] 当x＝1时，f（1)＝6，与a无关,所以函数f（x)＝4＋2a x －1的图象恒过点P（1,6）．故选A。
3．（2020·德州一模)已知a＝（错误!)错误!，b＝（错误!）错误!，c＝(错误!）错误!,则（ D ）A．a<b〈c B．c〈b<aC．c<a〈b D．b〈c〈a[解析] 因为y＝(错误!)x在R上为减函数，错误!〉错误!,所以b〈c.又因为y＝x错误!在（0，＋∞)上为增函数，错误!>错误!,所以a>c,所以b<c 〈a。
故选D。
4．(2020·山东菏泽联考）函数y＝（错误!）2x－x2的值域为（ A ) A．［错误!,＋∞）B．(－∞，错误!］C．（0，错误!] D．（0,2］［解析] 设t＝2x－x2，t≤1，所以y＝(错误!）t，t≤1，所以y∈[错误!,＋∞），故选A.5．（2020·辽宁模拟）若函数f(x）＝a|2x－4｜（a>0，0≠1)满足f （1）＝错误!，则f(x）的单调递减区间是( B ）A．(－∞,2]B．［2,＋∞）C．［－2,＋∞)D．（－∞，－2］［解析］由f(1)＝错误!得a2＝错误!.又a>0，所以a＝错误!,因此f（x)＝(错误!)|2x－4|。
因为y＝|2x－4｜在［2,＋∞)上单调递增，所以f(x）的单调递减区间是［2，＋∞）．故选B.二、多选题6．（2020·河北保定调研改编）函数y＝(a2－4a＋4)a x是指数函数，则a的值不可以是（ACD )A．4 B．3C．2 D．1[解析] 由指数函数的定义知a2－4a＋4＝1且a≠1，解得a＝3，故选A、C、D。
精品题库试题文数1.(河北省衡水中学2021届高三下学期二调)已知都是概念在R上的函数，，，且，且，．假设数列的前n 项和大于62，那么n的最小值为（）[解析] 1.因为，因此为增函数，即，因为，因此，解得，，，，得，最小值为6.2.(吉林省实验中学2021届高三年级第一次模拟考试) 已知函数，那么使函数有零点的实数的取值范围是（）A.B.C.D.[解析] 2.当时，由，得，因此，当时，由，得，而为增函数，因此，综上得或．3.(吉林省长春市2021届高中毕业班第二次调研测试) 已知命题：函数的图象恒过定点；命题：假设函数为偶函数，那么函数的图像关于直线对称，那么以下命题为真命题的是A．B．C．D．[解析] 3.的图象恒过，那么为假命题；假设函数为偶函数，即的图象关于轴对称，的图象即图象整体向左平移一个单位取得，因此的图象关于直线对称，那么为假命题；参考四个选项可知，选.4.(山东省潍坊市2021届高三3月模拟考试) 函数与(且) 在同一直角坐标系下的图象可能是[解析] 4.为偶函数，排除A项，当时，的周期，排除C项，当时，的周期，排除B项.5.（成都市2021届高中毕业班第一次诊断性检测）计算1og5＋所得的结果为(A) (B) 2(C) (D) 1[解析] 5.原式6.（天津七校联考高三数学（文）学科试卷）已知集合，，那么（）A. B. C. D.[解析] 6. 由，得，因此，7.(2021天津市滨海新区五所重点学校高三联考，5,5分) 设，，，那么的大小关系是()[解析] 7. ，，，因此.8.(2021年湖北七市高三4月联合考试，8,5分) 概念：函数的概念域为D, 若是关于任意的，存在唯一的，使得(其中c为常数）成立，那么称函数在D上的几何均值为c，那么以下函数在其概念域上的“几何均值” 能够为2的是()A. B.C. (e为自然对数的底）D.[解析] 8.A中，，那么，当时，，因此A不是；B中，，那么，当时，，因此现在不存在，因此B不是；C中，，那么，因此，因此，因此关于任意的，存在唯一的，因此C是；D中，，那么，当时，，因此0=2，因此现在不存在，因此D不是.9.(2021北京海淀区5月模拟卷，2,5分) 已知，，，那么的大小关系为()A. B. C. D.[解析] 9.，由于，因此，因此，因此.10.(2021年辽宁五校协作体高三第二次模拟，2,5分) 函数的图象必然过点（）A.（1,1）B.（1,2）C.（2,0）D.（2, -1）[解析] 10.令，得，因此当时，，因此函数的图象必然过点（1,2）.11.(2021年天津市高三第六次联考，5,5分) 设，，，那么()A. B. C. D.[解析] 11. ，，由于，因此，因此，因此.12.(2021山东，5,5分). 函数f(x) =+的概念域为()A. (-3,0]B. (-3,1]C. (-∞, -3) ∪(-3,0]D. (-∞, -3) ∪(-3,1][解析] 12.由题意知解得-3< x≤0, 因此函数f(x) 的概念域为(-3,0]. 应选A.13.(重庆市杨家坪中学2021届高三下学期第一次月考) 方程的实数解为______.[解析] 13.因为，因此或（舍），得，即.14.(江西省红色六校2021届高三第二次联考) 概念在R上的奇函数知足：当时，，那么在R上，函数零点的个数为.[解析] 14.因为为上的奇函数，因此，当时，令，得，同一坐标系下作出与的图像，由图象可知两函数只有一个交点，即当时，为增函数，因此只有一个零点，依照对称性函数在时只有一个零点，因此一共３个零点．15.（重庆南开中学高2021级高三1月月考)实数知足，那么的最大值是。
