并联电阻公式的推导法.

电阻在串联和并联中的规律和公式
（实用版）
目录
1.串联电路的电阻规律和公式
2.并联电路的电阻规律和公式
3.电阻串联和并联的实际应用
正文
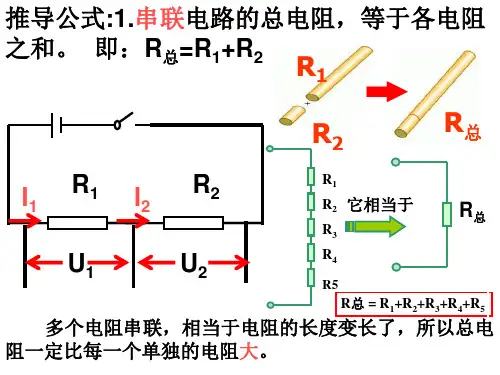
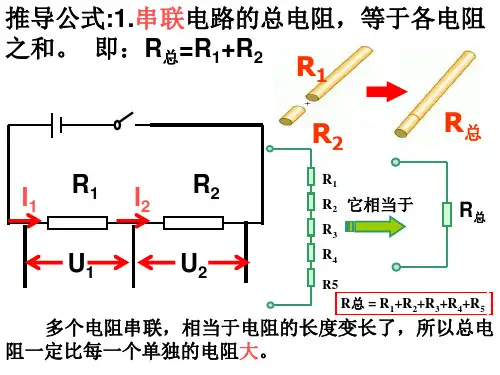
一、串联电路的电阻规律和公式
串联电路是指多个电阻依次排列在同一电路中，电流在各个电阻之间是相等的。

根据欧姆定律，电阻的计算公式为 R=U/I，其中 R 代表电阻，U 代表电压，I 代表电流。

在串联电路中，总电阻等于各电阻之和，即R_total=R1+R2+R3+...+Rn。

二、并联电路的电阻规律和公式
并联电路是指多个电阻同时连接在电路的两个分支上，电压在各个电阻之间是相等的。

根据基尔霍夫定律，并联电路的总电阻公式为
1/R_total=1/R1+1/R2+1/R3+...+1/Rn。

化简后得到
R_total=R1*R2*R3*...*Rn/(R1+R2+R3+...+Rn)。

三、电阻串联和并联的实际应用
电阻串联和并联在实际电路中应用广泛，例如在家庭用电、工业生产等领域。

在串联电路中，电阻值越大，电流越小，总电阻等于各电阻之和。

在并联电路中，电阻值越小，电流越大，总电阻的倒数等于各电阻阻值的倒数之和。

第1页共1页。

两个电阻并联的总电阻公式
电阻是电路中的一种基本元件，用来阻碍电流的流动。

在电路中，电阻的并联是一种常见的电路连接方式。

当两个电阻并联时，总电阻的计算公式为：
1/Rt = 1/R1 + 1/R2
其中，Rt表示总电阻，R1和R2分别表示两个电阻的电阻值。

这个公式的意义是，当两个电阻并联时，总电阻等于它们的倒数之和的倒数。

也就是说，两个电阻并联后，总电阻会变小，电路中的电流会增大。

为了更好地理解这个公式，我们可以通过一个简单的例子来说明。

假设有两个电阻，它们的电阻值分别为2欧姆和3欧姆。

将它们并联起来，求总电阻。

根据公式，我们可以得到：
1/Rt = 1/R1 + 1/R2
1/Rt = 1/2 + 1/3
1/Rt = 5/6
Rt = 6/5
因此，两个电阻并联后的总电阻为1.2欧姆。

从这个例子中可以看出，当两个电阻并联时，总电阻小于它们中的任何一个电阻。

这是因为电阻并联后，电路中的电流会增大，从而降低了电路的总电阻。

除了两个电阻并联的情况，当电路中有多个电阻并联时，总电阻的计算公式也可以通过类似的方法得到。

具体来说，可以将所有电阻的倒数相加，然后再将结果取倒数，即可得到总电阻。

电阻并联是一种常见的电路连接方式，可以有效地降低电路的总电阻，从而增大电路中的电流。

通过总电阻的计算公式，我们可以更好地理解电阻并联的原理，为电路的设计和分析提供帮助。

串联并联电阻计算公式
并联电阻计算公式是计算两个或多个电阻并联时的总阻值的一种公式。

并联电阻计算公式通常表示为R
3，...，Rn的形式，其中n表示与电阻并联的数量。

并联电阻计算公式可以用来计算电路中的总阻值，以及电路中未知电阻的大小。

为此，计算并联电阻的公式是：总阻=1/(1/R1+1/R2+1/R3+...+1/Rn)
这个公式可以用来计算任何数量的电阻，但是应当注意，只有当两个电阻并联时，总阻才能用1/R1+1/R2的形式表示。

并联电阻计算公式可以帮助设计电路，例如，如果要设计一个电路，使电流从一个电源流过一个电路，可以使用该公式来计算需要添加的电阻的总阻值。

并联电阻计算公式也可以用来计算电池的阻抗和电容量，以及电路中可以提供的最大电流。

此外，并联电阻计算公式还可以用来计算电路中的等效阻值。

例如，如果一个电路中有两个电阻，可以使用该公式来计算等效电阻的值，从而知道电路的总阻值。

总而言之，并联电阻计算公式是一种非常有用的公式，它可以用来计算电路中的总阻值，以及确定电路中可以提供的最
大电流和电容量。

它还可以用来计算电路中等效阻值，以及设计电路时需要添加的电阻的总阻值。

并联电阻计算公式并联电阻的计算公式是：1/R=1/R1+1/R2+1/R3+...+1/Rn其中，R1、R2、R3...Rn为并联电路中的各个电阻值。

在并联电路中，电流可选择流过不同的分支，从而形成不同的电阻路径。

所有的电阻并联在一起，等效为一个总电阻。

并联电阻的总电阻值小于其中的最小电阻值。

我们可以通过以下步骤计算并联电阻：1.列举出所有的电阻值。

例如，一个并联电路包含3个电阻，分别为10欧姆、20欧姆、30欧姆。

2.使用并联电阻的计算公式。

将每个电阻的倒数相加，并将结果取倒数。

在这个例子中：1/R=1/10+1/20+1/303.计算倒数的和。

1/R=3/30+2/30+1/301/R=6/301/R=1/5将等式两边取倒数：R=5欧姆因此，这个并联电路的总电阻是5欧姆。

并联电阻的计算方法非常简单，只需要将每个电阻的倒数相加，并将结果取倒数即可。

这个公式适用于任意数量的电阻。

需要注意的是，在计算并联电路的总电阻时，最好将所有电阻的单位统一，例如都使用欧姆。

如果电阻的单位不同，需要先将其转换为相同的单位，然后再进行计算。

并联电阻的概念在实际电路中有着广泛的应用。

例如，在家庭电路中，多个电器可以并联连接到电源线路，这样每个电器可以独立地工作而不会受到其他电器的影响。

在电子设备中，也常常会使用并联电路来提供稳定的电流供应。

总之，并联电阻的计算公式为1/R=1/R1+1/R2+1/R3+...+1/Rn，其中R1、R2、R3...Rn为并联电路中的各个电阻值。

通过将每个电阻的倒数相加，并将结果取倒数，可以得到并联电路的总电阻值。

2个电阻并联公式在我们的电学世界里，电阻可是个非常重要的角色。

今天咱们就来聊聊两个电阻并联的公式。

想象一下，你家里的电路就像是一个复杂的交通网络，电流就像来来往往的车辆。

电阻呢，就像是道路上的关卡，会限制车辆的通行。

当有两个电阻并联在一起时，电流就有了更多的选择，就像车辆可以选择不同的道路通行一样。

两个电阻并联的公式是：1/R 并 = 1/R₁ + 1/R₂。

这里的 R₁和 R₂分别代表两个电阻的阻值，R 并则是它们并联后的等效电阻。

比如说，有一个电阻 R₁是 3 欧姆，另一个电阻 R₂是 6 欧姆。

咱们来算算它们并联后的等效电阻 R 并。

首先，按照公式 1/R 并 = 1/3 + 1/6 。

咱们先算 1/3 + 1/6 ，通分一下，得到 2/6 + 1/6 = 3/6 ，约分后就是 1/2 。

所以 1/R 并 = 1/2 ，那么 R 并 = 2 欧姆。

这就好比两条道路，一条比较通畅，电阻小，通过它比较容易，就像 3 欧姆的电阻；另一条道路比较狭窄，电阻大，通过它比较困难，就像 6 欧姆的电阻。

当这两条道路并行时，电流就会选择更容易通过的路径，整体的通行效果就相当于一个 2 欧姆电阻的效果。

在实际生活中，我们也能看到电阻并联的例子。

比如，你家里的多个电器同时工作，它们就相当于并联在电路中。

像电视、冰箱、电灯等等，它们各自有不同的电阻，但通过并联的方式，都能正常地从电源获取电流，同时工作。

再举个例子，假如你有两个手电筒，每个手电筒里面都有一个电阻。

当你把它们的电路并联起来，一起打开，你会发现它们的亮度和单独打开一个时是不一样的。

这就是因为电阻并联改变了电路中的电流和电压分布。

总之，两个电阻并联的公式虽然看起来简单，但它却在电学中有着广泛的应用。

只要我们掌握了这个公式，就能更好地理解和处理电路中的各种问题。

无论是解决家里电器的小故障，还是进行更复杂的电路设计，都能派上用场。

希望大家能真正掌握这个公式，让电学知识为我们的生活带来更多的便利和乐趣！。

三电阻并联后的总电阻公式在电学中，电阻是指电流通过时，电压与电流之间的比值。

当电路中存在多个电阻时，可以将它们连接成不同的方式，如串联和并联，从而改变电路的总电阻。

我们来讨论三个电阻的并联。

并联电路是指将多个电阻连接在一起，共享相同的电压源。

设三个电阻分别为R₁、R₂和R₃，并联后的总电阻为R。

并联电路中，每个电阻都受到相同的电压，所以可以利用欧姆定律计算总电阻。

在并联电路中，总电流等于三个电阻上的电流之和，即：I=I₁+I₂+I₃通过欧姆定律，我们可以得到：V/R=V/R₁+V/R₂+V/R₃其中，V为电压源的电压。

将V约掉，上述公式可以简化为：1/R=1/R₁+1/R₂+1/R₃这就是三个电阻并联后的总电阻公式。

根据这个公式，我们可以计算任意三个电阻并联的总电阻。

下面我们来通过例题来进一步理解这个总电阻公式。

假设有三个电阻分别为R₁=4Ω、R₂=6Ω和R₃=8Ω，请计算并联后的总电阻R。

根据上述公式：1/R=1/R₁+1/R₂+1/R₃1/R=1/4+1/6+1/8为了计算方便，我们可以先求得分数的最小公倍数：最小公倍数=4×6×8=192然后将每个分数的分子调整为最小公倍数：1/R=48/192+32/192+24/192相加得到：1/R=104/192接下来，我们需要求得的是R的倒数，即R的倒数等于104/192，所以R=192/104继续化简：R=24/13≈1.846Ω因此，三个电阻并联后的总电阻为1.846Ω。

这个例题展示了如何使用并联电阻的总电阻公式来计算三个电阻并联后的总电阻。

同样的方法也适用于更多电阻并联的情况。

总之，在电路中，通过并联电阻的总电阻公式，我们可以计算多个电阻并联后电路的总电阻。

这个公式是通过欧姆定律和电压在并联电路中的共享性质推导而来的。

熟练掌握总电阻公式可以帮助我们更好地理解电路中电阻的行为，并在实际问题中应用。

并联电路等效电阻公式推导
+-
R 2i
图 一 两个电阻的并联电路如图一所示，在图一中，我们把R1与R2的并联电阻值用R 表示，它又可以称为两并联电阻的等效电阻。

利用欧姆定律I=U R 可以写出图一中表示电流关系的公式1； U
R =U
R1+U
R2 （公式1）
把这个式子中的电压U 削去，就得
1
R =1
R1+1
R2（公式2）
将公式2等式右边的两项通分后得到
1
R = R2
R1R2 +R1
R1R2 =R1+R2
R1R2 (公式3)
将公式3两边取倒数就得到
R = R1R2
R1+R2 (公式4)
公式4就是两并联电阻的等效电阻计算公式。

如果有三个
电阻并联时，也可以先将任意两个电阻用公式4计算出一个等效电阻值R ，然后再将它与第三个电阻并联计算。

更多电阻并联则以此类推。

二〇二四年九月十五日。