1.4.正方形组成的图形

立体图形三视图及展开图一、知识点(一)三视图在观察物体的时候，我们往往可以从不同的角度进行观察，角度不同，看到的风景就会不同。

比如：我们可以从正面看、上面看、左面看，看到的图形分别称为正视图、俯视图和左视图，并且容易发现：正面看和后面看，上面看和下面看，左面看和右面看得到的图形是相同的。

对于较复杂的立体图形，通过三视图法往往可以很方便地计算出表面积(二)正方体的展开图展开后由上、下、左、右、前、后六个正方形面组成，这六个正方形面的面积都相等，我们采用不同的剪开方法，共可以得到下面(三)长方体的展开图：观察上图可以发现，长方体的展开图由6个长方形组成，相对面的面积相等，即S上＝S下＝长×宽，S左＝S右＝宽×高，S前＝S后＝长×高。

(四)判断图形折叠后能否围成长方体或正方体的方法判断一个图形折叠后能否围成正方体或长方体，首先，要依据它们各自展开图的特点判断；其次，可以运用空间想象或实际操作进一步判断。

二、题型(一)展开图与对立面【例1.1】水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示，如下图，是一个正方体的平面展开图，若图中的“似”表示正方体的前面，“锦”表示右面，“程”表示下面。

则“祝”、“你”、“前”分别表示正方体的________________________。

【答案】后面、上面、左面【解析】易知“你”、“程”相对，“前”、“锦”相对，“祝”、“似”相对，因此“祝”、“你”、“前”分别表示正方体的后面、上面、左面。

【例1.2】一个数学玩具的包装盒是正方体，其表面展开图如下。

现在每方格内都填上相应的数字。

已知将这个表面展开图沿虚线折成正方体后，相对面的两数之和为“3”，则填在A、B、C内的三个数字依次是___________。

【答案】3、1、2【解析】面上的数是“0”，与“B”相对的面上的数是“2”，与“C"相对的面上的数是“1”。

认识长方形、正方形、圆、平行四边形和三角形教材第2页的例1、第3页的“做一做”及练习一的第1、第2、第3、第6题。

1.能直观认识长方形、正方形、三角形、平行四边形和圆这些平面图形,能够辨认和区别这些图形。

2.通过画各种平面图形,使学生直观感受各种平面图形的特征。

3.初步培养学生的观察能力、动手操作能力和用数学交流的能力。

4.感受现实生活与数学的联系。

知道长方形、正方形、圆、平行四边形和三角形的形状及名称,并能辨认和区别这些图形。

每组一袋各种形状的物体和图形、课件、投影等。

老师说物体名称,学生拿出相应的物体。

1.画一画,揭示概念。

(1)出示长方体积木。

提问:谁知道这个长方体的面是什么形状的?学生回答后老师板书:长方形老师用长方体积木在黑板上画一个长方形。

(2)以小组为单位,利用实物学具,照老师的样子沿着物体表面的边缘画出图形。

(3)把小组中画得好的图形进行整理,投影展示,并给这些图形起个名字。

(4)揭示概念。

老师拿出大小和颜色不同的图形展示长方形、正方形、三角形、平行四边形和圆，并按顺序板书它们的名称。

2.仔细观察,感知特点。

(1)自己观察,两人互说自己的感受和发现。

(2)汇报交流:长方形是有的边长,有的边短。

正方形的4条边一样长。

三角形有3条边。

平行四边形有4条边。

圆是一条首尾相连的封闭曲线……学生如果还说出其他特征要给予肯定。

如:长方形对边相等……(3)重点区分圆和球。

当学生把圆说成球时,老师马上拿出准备好的球,沿横截面切开,让学生感受到球的横截面是一个圆。

圆和球是两个不同的概念。

3.形成表象,初步建立空间观念。

(1)由实物抽象出图形。

课件显示“长方体”,然后抽象出长方体的一个面——长方形。

用同样的方法抽象出正方形、三角形、平行四边形和圆。

(2)记忆想象。

①出示长方形、正方形、三角形、平行四边形和圆,先让学生辨认,然后把长方形、正方形、三角形和圆贴在黑板上。

②让学生闭上眼想一想这四种图形的样子。

1、展览厅内要用相同的正方体木块搭成一个三视图如图所示的展台，则此展台共需这样的正方体______块1.1下面图形是由小正方体木块搭成的几何体的三视图示意图,则该几何体的实物图形是什么模样的?它由多少个小正方体木块搭成.请用小木块实地操作一下吧!正视图左视图俯视图1.2如图是由一些相同的小正方体构成的立体图形的三种视图．那么构成这个立体图形的小正方体有1.3用小立方块搭成的几何体，主视图和俯视图如下，问这样的几何体有多少可能？它最多需要多少小立方块，最少需要多少小立方块，请画出最少和最多时的左视图；1.4下图是一个立体图形的三视图，这个图形是由一些相同的小正方体搭成的，这些小正方体的个数是（）1.5根据图12所给出的几何体的三视图，试确定几何体中小正方体的数目的范围.俯视图左视图主视图第3题图俯视图左视图正视图俯视图左视图主视图主视图俯视图图121.6如图10是由四个相同的小立方体组成的立体图形的主视图和左视图，那么原立体图形可能是 ．（把下图中正确的立体图形的序号都填在横线上）1.7用小立方块搭一个几何体,使得它的主视图和俯视图如图所示,这样的几何体只有一种吗?它最少要多少个立方块?最多要多少个立方块?1.8如图1－30是由几个小立方块所搭几何体的俯视图和左视图，请摆出这个几何体，再根据它画出主视图。

（10分）1.9用小立方体搭一个几何体，使它的主视图和俯视图如图所示，这样的几何体只有一种吗？它最多需要多少个小立方体？它最少需要多少个小立方体？请你画出这两种情况下的左视图。

2、立方体木块的六个面分别标有数字1、2、3、4、5、6，下图是从不同方向观察这个立方体木块看到的数字情况，数字1和5对面的数字的和是 ．2.1如图1－14所示，在正方体能见到的面上写上数1、2、3，按两种方法展开后如图（一）、图（二）。

请在展开图的其它各面上写上适当的数，使得相对的面上两数的和等于７(5分)3、左图中的立方体展开后，应是右图中的（ ）.图10主视图左视图①②③④主视图 俯视图 左视图 俯视图图1－30 12 3图1－14 主视图 俯视图3.1将左边的正方体展开能得到的图形是 （ ）3.2小丽制作了一个如下左图所示的正方体礼品盒，其对面图案都相同，那么这个正方体的平面展开图可能是 （ ）（A ） （B ） （C ） （D ）3.3明明用纸（如下图左）折成了一个正方体的盒子，里面装了一瓶墨水，混放在下面的盒子里，只凭观察，选出墨水在哪个盒子中（ ）3.4下面四个图形都是由相同的六个小正方形纸片组成（如图5），小正方形上分别贴有北京2008年奥运会吉祥物五个福娃（贝贝、晶晶、欢欢、迎迎、妮妮）的卡通画和奥运五环标志，如果分别用“贝、晶、欢、迎、妮”五个字来表示五个福娃，那么折叠后能围成如图所示正方体的图形是（ ）.3.5下面四个图形中，经过折叠能围成如图3只有三个面上印有图案的正方体纸盒的是（ ）4、画出下列几何体的三种视图（A ）（B ）（C ）（D ）AB C DA ．B ． D ． 图35、我们知道，对于一些立体图形问题，常把它转化为平面图形来研究和处理.棱长为a 的正方体摆成如图16所示的形 状. 问：（1）有几个正方体；（2）摆成如图16形式后，表面积是多少？5.1如图，是无盖长方体盒子的表面展开图(重叠部分不计)，则盒子的容积为( )6、把大小相同的小正方体摆成如图所示的形状,从上向下数,第一层1个,第二层3个,……,按这种规律摆放,求第五层的正方体个数.想一想:第n 层呢?22320012003)21(24)23(3)5.0(292)1(-⨯÷-÷⎥⎦⎤⎢⎣⎡-⨯--⨯+÷- (－1)3－(1－21)÷3×[2―(―3)2] 12622)68(3317666⨯+-⨯-⨯- （-14）2÷（-12）4×（-1）8-（138 +213 -334）×24()⎪⎭⎫⎝⎛----+⎪⎭⎫ ⎝⎛-⋅-21221232-÷41583 -14-（1-0.5）×13 ×[2-(-3)2]6322111(0.5)[2(3)]0.5338---÷⨯-----）（-1+3-5+7-9+11-…-1997+1999观察与探索：填空：图815 3111111111111 , , , ,......21223634124545-==-==-==-==⨯⨯用适当方法计算： 1111 (12233499100)++++⨯⨯⨯⨯ 变式：1、2、观察下列算式，并进行计算。

第六单元测试卷（二）时间:60分钟满分:100分分数:一、填空题。

（14分）1. 一个角有( )个顶点,( )条边。

2. 三角板上的最大的角是( )角,比这个角小的是( )角,比这个角大的是( )角。

3. 三角板上有( )个直角,( )个锐角,( )个钝角。

4. 长方形的对边( ),四个角都是( );正方形的四条边都( ),四个角都是( )。

5. 平行四边形,两组对边( ),易( )。

二、下图中是角的在括号里画“√”。

（16分）( ) ( ) ( )( ) ( ) ( ) ( ) ( )三、把下列图形归类。

（14分）长方形:( ) 正方形:( ) 平行四边形:( )四、数出下列图形中角的个数。

（12分）( )个( )个( )个五、写出下列各角是什么角。

（12分）( )角( )角( )角( )角六、解决问题。

（32分）1. 用一张长12厘米、宽9厘米的长方形纸,剪一个最大的正方形。

正方形的边长是几厘米?剩下的纸至少还可以剪几个最大的小正方形?（7分）2. 在下面的方格纸上画一个正方形、一个长方形和一个平行四边形。

（8分）3. 看图填空。

（9分）三角形有( )个,平行四边形有( )个,长方形有( )个。

4. 在下面的图形中你能找出几个锐角?几个直角和几个钝角?（8分）参考答案一、1. 122. 直锐钝3. 1204. 相等直角相等直角5.相等变形二、(√)( )(√)(√)(√)(√)(√)( )三、④⑦①⑥②③四、657五、钝直锐锐六、1. 9厘米3个 2. 略 3. 183 34. 4个锐角,3个直角,2个钝角。

第六单元过关检测卷一、我会填。

(每空1分，共10分)1．《典中点》的封面有( )个角，这些角都是( )角。

2．钟面上( )时整和( )时整，时针和分针成直角。

3．红领巾有1个( )角，2个( )角。

4．在长10厘米、宽8厘米的长方形中剪一个最大的正方形，正方形的边长是( )厘米。

5.是( )形，有( )个钝角，( )个锐角。

专题1.4 四边形章末重难点题型【沪科版】【考点1 多边形的对角线】【方法点拨】从n边形的一个顶点出发，最多能画（n-3）条对角线，这些对角线能把n边形分成（n-2）个三角形。

共2)3(nn条对角线.【例1】（2019秋•杏花岭区校级期末）在研究多边形的几何性质时．我们常常把它分割成三角形进行研究．从八边形的一个顶点引对角线，最多把它分割成三角形的个数为（）A．5B．6C．7D．8【变式2-1】（2019春•泰安期中）从多边形一条边上的一点（不是顶点）处出发，连接各个顶点得到2019个三角形，则这个多边形的边数为（）A．2020B．2019C．2018D．2017【变式2-2】（2019春•东昌府区期末）多边形的一个顶点处的所有对角线把多边形分成了11个三角形，则经过这一点的对角线的条数是（）A．8B．9C．10D．11【变式2-3】一个凸n边形的边数与对角线条数的和小于20，且能被5整除，则n为（）A．4B．5C．6D．5或6【考点2 多边形的内角和与外角和】【方法点拨】多边形的外角和固定不变为360°，多边形的内角和为180（n-2）(其中n为边数）.【例2】（2019秋•仁怀市期末）一个正多边形，它的一个内角恰好是一个外角的4倍，则这个正多边形的边数是（）A．八B．九C．十D．十二【变式2-1】（2019秋•博白县期末）已知多边形的每个内角都是108°，则这个多边形是（）A．五边形B．七边形C．九边形D．不能确定【变式2-2】（2019秋•定州市期末）如图，∠1，∠2，∠3是五边形ABCDE的3个外角，若∠A+∠B＝220°，则∠1+∠2+∠3＝（）A．140°B．180°C．220°D．320°【变式2-3】（2019秋•恩施市期末）一个多边形截去一个角后，形成的另一个多边形的内角和是1620°，则原来多边形的边数是（）A．10B．11C．12D．10或11或12【考点3 平面镶嵌】【方法点拨】几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．【例3】（2019春•洛江区期末）商店出售下列形状的地砖：①长方形；②正方形；③正五边形；④正六边形．若只选购其中某一种地砖镶嵌地面，可供选择的地砖共有（）A．1种B．2种C．3种D．4种【变式3-1】（2019春•上蔡县期末）在现实生活中，铺地最常见的是用正方形地板砖，某小区广场准备用多种地板砖组合铺设，则能够选择的组合是（）A．正三角形，正方形B．正方形，正六边形C．正五边形，正六边形D．正六边形，正八边形【变式3-2】（2019春•泉州期末）下列组合不能密铺平面的是（）A．正三角形、正方形和正六边形B．正三角形、正方形和正十二边形C．正三角形、正六边形和正十二边形D．正方形、正六边形和正十二边形【变式3-3】（2019春•卧龙区期末）下列能铺满地面的组合有（）①正十二边形，正三角形的组合；②正六边形，正方形的组合；③正六边形，正方形，正三角形的组合；④正八边形，正五边形的组合；⑤正十二边形，正方形，正三角形的组合．A．1个B．2个C．3个D．4个【考点4 平行四边形的性质】【方法点拨】解题的关键是掌握平行四边形的性质：①边：平行四边形的对边相等．②角：平行四边形的对角相等．③对角线：平行四边形的对角线互相平分．【例4】（2019春•沙坪坝区期中）如图，平行四边形ABCD中，∠DAB的平分线AE交CD于E，DC＝5，BC＝3，则EC的长是（）A．1B．1.5C．2D．3【变式4-1】（2019春•巴南区期中）已知▱ABCD的周长为32cm，对角线AC、BD相交于点O，若△BOC 的周长比△AOB的周长大4cm，则AD的长是（）A．4cm B．6cm C．8cm D．10cm【变式4-2】（2019春•闽侯县期中）如图，在平行四边形ABCD中，∠BAD的平分线交CD于点G，AD ＝AE．若AD＝5，DE＝6，则AG的长是（）A．6B．8C．10D．12【变式4-3】（2019春•谢家集区期中）如图，平行四边形ABCD的对角线相交于点O，且AD＞AB，过点O作OE⊥AC交AD于点E，连接CE．若平行四边形ABCD的周长为20，则△CDE的周长是（）A．10B．11C．12D．13【考点5 平行四边形的判定条件】【方法点拨】平行四边形的判定，关键是掌握判定定理：（1）两组对边分别平行的四边形是平行四边形．（2）两组对边分别相等的四边形是平行四边形．（3）一组对边平行且相等的四边形是平行四边形．（4）两组对角分别相等的四边形是平行四边形．（5）对角线互相平分的四边形是平行四边形．【例5】（2019春•鄂城区期中）下列条件中，能判定四边形ABCD为平行四边形的个数是（）①AB∥CD，AD＝BC；②AB＝CD，AD＝BC；③∠A＝∠B，∠C＝∠D；④AB＝AD，CB＝CDA．1个B．2个C．3个D．4个【变式5-1】（2019春•常熟市期中）在四边形ABCD中，对角线AC、BD相交于点O，下列条件中不一定能判定这个四边形是平行四边形的是（）A．AB∥DC，AD＝BC B．∠BAD＝∠BCD，∠ABC＝∠ADCC．OA＝OC，OB＝OD D．AB＝DC，AD＝BC【变式5-2】（2019春•北京校级期中）已知四边形ABCD中，AC、BD交于点O，给出条件①AD∥BC且AB＝CD，②AB＝CD且OA＝OC，③∠DAB＝∠DCB且OA＝OC，④∠DAB＝∠DCB且OB＝OD，其中能判定四边形ABCD是平行四边形的有（）A．0个B．1个C．2个D．3个【变式5-3】（2018•雁江区模拟）在四边形ABCD中，AC与BD相交于点O，如果只给出条件“AB∥CD”，那么还不能判定四边形ABCD为平行四边形，给出以下六个说法中，正确的说法有（）（1）如果再加上条件“AD∥BC”，那么四边形ABCD一定是平行四边形；（2）如果再加上条件“AB＝CD”，那么四边形ABCD一定是平行四边形；（3）如果再加上条件“∠DAB＝∠DCB”那么四边形ABCD一定是平行四边形；（4）如果再加上“BC＝AD”，那么四边形ABCD一定是平行四边形；（5）如果再加上条件“AO＝CO”，那么四边形ABCD一定是平行四边形；（6）如果再加上条件“∠DBA＝∠CAB”，那么四边形ABCD一定是平行四边形．A．3个B．4个C．5个D．6个【考点6 平行四边形的判定及性质】【例6】（2019春•越秀区校级期中）如图，在平行四边形ABCD中，∠BAD和∠DCB的平分线AE，CF 分别交BC，AD于点E，F，点M，N分别是AE，CF的中点，连接FM，EN（1）求证：BE＝DF；（2）求证：四边形FMEN是平行四边形．【变式6-1】（2019春•香坊区校级期中）已知：如图，四边形ABCD是平行四边形，E，F是对角线AC上的两点，AE＝CF．（1）求证：四边形DEBF是平行四边形；（2）如果AE＝EF＝FC，请直接写出图中所有面积等于四边形DEBF的面积的三角形．【变式6-2】（2019春•鄂城区期中）已知：如图，在▱ABCD中，点E、F在AC上，且AF＝CE，点G、H 分别在AB、CD上，且AG＝CH，AC与GH相交于点O．（1）求证：EG∥FH；（2）GH、EF互相平分．【变式6-3】（2018春•青山区期中）如图，▱ABCD的对角线AC、BD相交于点O，且E、F、G、H分别是AO、BO、CO、DO的中点．（1）求证：四边形EFGH是平行四边形；（2）若AC+BD＝36，AB＝12，求△OEF的周长．【考点7 三角形的中位线】【例7】（2019秋•长春期中）如图，在四边形ABCD中，P是对角线BD的中点，E，F分别是AB，CD的中点，AD＝BC，∠PEF＝18°，则∠PFE的度数是（）A．9°B．18°C．27°D．36°【变式7-1】（2019春•相城区期中）如图，△ABC中，AB＝9，D、E分别是AB、AC的中点，点F在DE 上，且DF＝3EF，当AF⊥BF时，BC的长是（）A．9B．10.5C．12D．18【变式7-2】（2019春•嘉祥县期中）如图，四边形ABCD中，∠A＝90°，AB＝12，AD＝5，点M、N分别为线段BC、AB上的动点（含端点，但点M不与点B重合），点E、F分别为DM、MN的中点，则EF长度的可能为（）A．2B．5C．7D．9【变式7-3】（2019春•庐阳区期末）如图，△ABC的周长为17，点D，E在边BC上，∠ABC的平分线垂直于AE，垂足为点N，∠ACB的平分线垂直于AD，垂足为点M，若BC＝6，则MN的长度为（）A．B．2C．D．3【考点8 菱形的性质】【方法点拨】菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线都平分一组对角。

一．规则拼接图形求周长1．拼接过程中拼一次减少两个长或两个宽； 2．通过大图形寻找内部图形长、宽倍数关系； 3．环形问题考虑外周长和内周长． 二．代数法求周长设未知数求周长，把未知的边设成未知数，找出等量关系，列出方程，求出未知数即可．重难点：代数法求周长，设未知量很关键．题模一：拼接图形求周长例1.1.1如图所示，内部正方形的周长为24厘米．根据图中给出的数（单位：厘米），长方形的周长为_________厘米．例 1.1.2如图，八个同样大小的小长方形拼成一个大长方形，已知大长方形的周长为112厘几何第02讲_拼接图形求周长3142米，求小长方形的周长．例1.1.3如图，ABC，ADE，EFG均为正三角形，D、G分别为线段AC、AE的中点，线段AB长为8．则多边形ABCDEFG的周长为__________．例1.1.4图中阴影部分是正方形，那么最大长方形的周长是多少厘米？例1.1.5用12个边长为1的小正方形拼一个大长方形，这个长方形的周长最短是多少？例1.1.6如图，由一些相同的小长方形和一个小正方形拼成的大正方形．已知图中大正方形的周长为400，小正方的周长为240，求每个小长方形的周长是多少？题模二：代数法求周长例1.2.1如图，一个六边形的6个内角都是120 ，其连续四边的长依次是1，9，9，5厘米．求这个六边形的周长．例1.2.2如图，用正方形a 、b 、c 、d 、e 拼成一个长30厘米，宽22厘米的长方形，求正方形e 的面积．例1.2.3对于一个多边形，定义一种“生长”操作：如图1，将其一边AB 变成向外凸的折线ACDEB ，其中C 和E 是AB 的三等分点，C 、D 、E 三点可构成等边三角形．那么，一个边长是9的等边三角形，经过两次“生长”操作（如图2），得到的图形的周长是__________；经过四次“生长”操作，得到的图形的周长是__________．随练1.1如图，将一个边长为4厘米的正方形对折，再沿折线剪开，得到两个长方形．这两个长方形的周长之和比原来正方形的周长多______________厘米．1995B A A BE CD图1（1）（3）（2） 图244随练 1.2如图，在一个长方形中有一段阴影面积．如果阴影部分恰好是正方形，那么图中大长方形的周长是多少厘米？6厘米9厘米随练1.34个一样的宽为2厘米的长方形拼成一个大长方形．大长方形的周长是__________厘米．随练 1.4将一个周长为60厘米的正方形剪成周长相等的两块，如图，那么每块周长是___________厘米．随练 1.5如图，在一个长方形中有一段阴影部分．如果阴影部分恰好是正方形，那么图中大长方形的周长是多少厘米？6厘米9厘米随练1.6如图，蕾蕾家的菜园是一个由4块正方形的菜地和1个小长方形的水池组成的大长方形．如果每块菜地的面积都是20平方米且菜园的长为10米，那么菜园中水池（图中阴影部分）的周长是_______米．随练1.7一个六边形的六个内角都是120，并有连续的三边长均为6厘米．如果这个六边形的周长是32厘米，那么该六边形最长的边有多长．随练1.8如图是由9个等边三角形拼成的六边形，已知中间最小的等边三角形的边长是1，则这个六这形的周长是__________．作业1如图，8块相同的长方形地砖拼成一个长方形，求每块长方形地砖的长是多少厘米？作业2如图，五个相同的小正方形拼成一个大长方形，已知大长方形的周长为48厘米，求小长方形的周长．60cm作业3用两个与右图同样的三角形，可以拼出几个不同的平行四边形，其中周长最长的是__________厘米．作业4下图中的正方形被分成了4个相同的长方形，每个长方形的周长都是40厘米．求这个正方形的周长．作业5如图所示，在长方形ABCD 中，120AB 厘米，截去一个正方形EBCF 后，求剩下的长方形AEFD 的周长．作业6如图，5个相同的小长方形拼成一个大正方形．已知大正方形的周长比一个小长方形的周长多10厘米，那么小长方形的周长是_______厘米．765作业7如下图，四个一样的长方形拼成一个边长为10厘米的大正方形，中间形成了一个小正方形，每个长方形的周长是__________厘米．作业8如图，大正六边形内部有7个完全一样的小正六边形．阴影部分的周长是120（阴影部分周长由内、外两部分组成），那么大正六边形的周长是多少？作业9如图，一个六边形的6个内角都是120°，其四条边长如图所示，则这个六边形的周长是__________．作业10如图，在五边形中有一个角为60°，别的角都是120°．这个五边形的周长是_______．101023。

人教版五年级三角形和正方形专题练习题
以下是一些关于三角形和正方形的练题，适合五年级学生进行巩固和练。

1. 三角形练题
1.1 给定图形，判断其是否为三角形，并说明理由。

1.2 用两个直尺拼出正三角形。

1.3 用方格纸上的点组成一个直角三角形。

1.4 补全下面的等边三角形。

1.5 按要求填空：
- 一个三角形有____个顶点。

- 一个三角形有____条边。

- 一个三角形有____个角。

2. 正方形练题
2.1 判断下列图形是否为正方形，并说明理由。

2.2 画一个边长为4个单位长度的正方形。

2.3 计算下列正方形的周长和面积：
- 边长为5个单位长度的正方形。

- 边长为8个单位长度的正方形。

2.4 按要求填空：
- 一个正方形有____个顶点。

- 一个正方形有____条边。

- 一个正方形有____个角。

以上是关于三角形和正方形的练题，希望对五年级的学生有所帮助。

祝你练愉快，提高数学能力！
Note: Please replace the `triangle_a.png`, `triangle_b.png`, and
`square_a.png` with the actual images you want to use for the exercise questions.。

五年级图形知识点归纳总结在五年级的数学学习中，图形是一个重要的知识点。

通过学习图形的性质、分类和特征等内容，可以帮助学生提高空间意识和观察能力。

本文将对五年级图形知识点进行归纳总结，以帮助学生更好地理解和掌握这些内容。

一、平面图形1.1 三角形三角形是由三条边和三个内角组成的图形。

根据边长的不同，可以分为等边三角形、等腰三角形和普通三角形。

根据角度的不同，可以分为锐角三角形、钝角三角形和直角三角形。

三角形的内角和为180度。

1.2 矩形矩形是由四条边和四个内角组成的图形，相邻的内角互补，即相邻的内角和为180度。

矩形所有内角均为直角，且对立边相等。

矩形的周长可以通过公式：周长 = 2×(长+宽) 计算。

1.3 正方形正方形是一种特殊的矩形，它的四条边和四个内角都相等。

正方形的周长可以通过公式：周长 = 4×边长计算。

1.4 圆形圆形是由一条闭合曲线组成的图形，其中任意两点到圆心的距离相等，这个距离被称为半径。

圆形的周长可以通过公式：周长= 2×π×半径或周长= π×直径计算，其中π取3.14。

二、立体图形2.1 立方体立方体是由六个正方形的面组成的立体图形。

它有八个顶点、十二条边和六个面。

立方体的体积可以通过公式：体积 = 边长 ×边长 ×边长计算。

2.2 正方体正方体是一种特殊的立方体，它的六个面都是正方形。

正方体的体积可以通过公式：体积 = 边长 ×边长 ×边长计算。

2.3 圆柱体圆柱体是由一个圆形底面和一个平行于底面的圆形顶面以及连接两个底面的侧面组成的立体图形。

圆柱体的体积可以通过公式：体积 = 圆面积 ×高计算。

2.4 圆锥体圆锥体是由一个圆形底面和一个顶点连接底面上所有点的侧面组成的立体图形。

圆锥体的体积可以通过公式：体积 = 圆锥底面积 ×高 ÷ 3 计算。

2.5 球体球体是由所有离球心距离相等的点构成的立体图形。

4从三个方向看物体的形状1．观察下面的图片，从上面看到的是，从左面看到的是，从正面看到的是。

2．下列四个几何体中，从左面看为圆的是（）A．B．C．D．3．（2019•十堰）下面几何体中，其从正面看与从上面看相同的是（）A．B．C．D．4．（2019•梅州）如图所示几何体的从左面看为（）A．B．C．D．5．（2019•张家界）如图是由4个完全相同的小正方体组成的立体图形，则它的从上面看是（）A．B．C．D．6．（2019•盐城）如图是由6个棱长均为1的正方体组成的几何体，它的从正面看的面积为．6．（2019•百色）某几何体的三视图如图所示，则组成该几何体的小正方体的个数是．7．（2019•冷水江市校级模拟）如图是由大小相同的小正方体组成的简单几何体的从左面看和从上面看，那么组成这个几何体的小正方体的个数最少为个．8．某几何体是由几个棱长为1的小立方体搭成的，其三视图如图所示，则该几何体的表面积（包括下底面）为．同步小题12道一．选择题1．（2019•桂林）下列几何体分别从三个方向观察得到的图形相同的是（）A．圆柱 B．球C．圆锥 D．长方体2．（2019•娄底）下列几何体中，从正面看和从上面看都为矩形的是（）A．B．C．D．3．（2019•济宁）如图，几何体是由3个大小完全一样的正方体组成的，它的从左面看是（）A．B．C．D．4．（2019•常德）如图是由6个相同的小正方体搭成的几何体，那么这个几何体的从上面看是（）A．B．C．D．5．（2019•宁夏）由若干个相同的小正方体组合而成的一个几何体的三视图如图所示，则组成这个几何体的小正方形个数是（）A．3 B．4 C．5 D．66．（2019•自贡）如图是几何体的从上面看，所表示数字为该位置小正方体的个数，则该几何体的正视图是（）A．B．C．D．二．填空题7．如图，右边的两个图形分别是由左边的物体从两种不同的方向观察得到的，请在这两种平面图形的下面填写它们各是从什么方向看得到的｡①；②．8．如图所示的几何体是由一些小正方体组合而成的，若每个小正方体的棱长都是1，则该几何体从上面看的面积是．9．（2019•嘉善县模拟）如图，由五个小正方体组成的几何体中，若每个小正方体的棱长都是1，则该几何体的从正面看和从左面看的面积之和是．10．（2019•黄冈校级自主招生）如图是由几块相同的小正方体搭成的立体图形的三视图，则这个立体图形中小正方体共有块．三．解答题11．画出如图所示的几何体的从正面看、从左面看、从上面看：12．用小立方块搭成的几何体，从正面看和从上面看如下，问这样的几何体有多少可能？它最多要多少小立方块，最少要多少小立方块，画出最多、最少时的从左面看．答案：4从三个方向看物体的形状1．③②①2．解析：因为圆柱的从左面看是矩形，圆锥的从左面看是等腰三角形，球的从左面看是圆，正方体的从左面看是正方形，所以，从左面看是圆的几何体是球．故选C3．解析：A、圆柱从正面看是矩形，从上面看是圆；B、圆锥从正面看是三角形，从上面看是圆；C、正方体的从正面看与从上面看都是正方形；D、三棱柱的从正面看是矩形与从上面看都是三角形；故选：C4．解析：从左边看第一层一个小正方形，第二层一个小正方形，第三层一个小正方形，故选A5．解析：根据题意，从上面看原图形可得到．故选C6．解析：从正面看如图所示，∵由6个棱长均为1的正方体组成的几何体，∴从正面看的面积为5×12=5，答案5．6．解析：综合三视图，我们可得出，这个几何体的底层应该有4个小正方体，第二层应该有1个小正方体，因此搭成这个几何体的小正方体的个数为4+1=5个；答案：5．7．解析：由从上面看可以看出组成这个几何体的底面小正方体有4个，由从左面看可知第二层最少有1个，故组成这个几何体的小正方体的个数最少为：4+1=5（个），答案：5．8．解析：（1×1）×[（3+2+4）×2]=1×18=18．答：该几何体的表面积（包括下底面）为18．答案：18．同步小题12道1．解析：圆柱从正面看和从左面看为长方形，从上面看为圆形；球从正面、左面和上面看均为圆形；圆锥从正面看和从左面看为三角形，从上面看为带圆心的圆形；长方体从正面、左面和上面看均为长方形，但长方形的长宽不等．故选B2．解析：A、圆锥的从正面看是三角形，从上面看是带圆心的圆，故本选项错误；B、圆柱的从正面看是矩形、从上面看是矩形，故本选项正确；C、球的从正面看、从上面看都是圆，故本选项错误；D、三棱柱的从正面看为矩形和从上面看为三角形，故本选项错误．故选B3．解析：如图，几何体是由3个大小完全一样的正方体组成的，它的从左面看是故选D4．解析：从上面看易得上面第一层中间有1个正方形，第二层有3个正方形．下面一层左边有1个正方形，故选A．5．解析：综合三视图，我们可以得出，这个几何模型的底层有3+1=4个小正方体，第二有1个小正方体，因此搭成这个几何体模型所用的小正方体的个数是4+1=5个．故选C6．解析：从正面看，如图所示：．故选B7．解析：从正面看从左往右2列正方形的个数依次为2，1，∴②是从正面看得到的图形；从左面看从左往右2列正方形的个数依次为2，1，∴②是从左面看得到的图形；从上面看从左往右2列正方形的个数依次为2，1，且第2列的那个正方形应在上面一行，∴①是从上面看得到的图形；从右面看从左往右2列正方形的个数依次为1，2，不在上面的图形中，答案：从上面看；从正面看或从左面看．8．解析：从上边看第二层是三个小正方形，第一层左边一个小正方形，右边一个小正方形，该几何体从上面看的面积是3+2=5，答案：5．9．解析：该几何体的从正面看的面积为1×1×4=4，从左面看的面积是1×1×3=3，所以该几何体的从正面看和从左面看的面积之和是3+4=7，答案：7．10．解析：综合从正面看，从上面看，从左面看，底层有2+2+1=5个正方体，第二层有3个正方体，第三层有1个正方体，所以搭成这个几何体所用的小立方块的个数是5+3+1=9个．答案：9．11．解：作图如下：12．解析：有两种可能；有从正面看可得：这个几何体共有3层，由从上面看可得：第一层正方体的个数为4，由从正面看可得第二层最少为2块，最多的正方体的个数为3块，第三层只有一块，故：最多为3+4+1=8个小立方块，最少为个2+4+1=7小立方块．最多时的从左面看是：最少时的从左面看为：。

知识图谱-底和高的选取正方形对角线等腰直角三角形斜边面积与长度的相互转化几何第03讲_基本直线形底和高的选取错题回忆底和高的选取知识精讲一．正方形对角线我们把正方形沿对角线剪成两个一样的等腰直角三角形，再拼接成一个大的等腰直角三角形，总面积没有发生改变，由此可以得出正方形面积公式：正方形面积=．二．等腰直角三角形斜边等腰直角三角形的面积等于直角边长平方的一半．如果不知道直角边长，只知道斜边长，也能求出等腰直角三角形的面积：等腰直角三角形面积=．等腰直角三角形斜边上的高等于斜边的一半，而且斜边上的高还把等腰直角三角形分成了两个一模一样的小等腰直角三角形．三．面积与长度的相互转化我们已经学过基本直线形面积公式．已知三角形的底和高，我们很容易算出面积．如果已知三角形的面积和一条边的长度，就可以算出以这条边为底对应的高是多少；如果已知三角形的面积和一条高的长度，就可以算出与这条高所对应的底边的长度．这种反求的方法，在几何问题中是经常会遇到的．需要注意的是，已知三角形面积和底〔或高〕，求三角形高〔或底〕的时候，切记首先要“×2”．三点剖析重难点：等腰直角三角形面积公式，不要忘记除以4．题模精讲题模一正方形对角线例1.1、如图，已知正方形ABCD，对角线长10厘米．正方形ABCD的面积是多少平方厘米？答案：50解析：，所以正方形的面积是平方厘米．例1.2、如图，正方形ABCD被两条平行的直线截成了面积相等的三个部分，其中上、下两部分都是等腰直角三角形．已知两条截线的长度都是10厘米，那么整个正方形的面积是多少平方厘米？答案：75解析：最上方的三角形和最下方的两个等腰直角三角形可以拼成一个正方形，对角线是10厘米，所以这两个三角形的面积和是，三部分面积相等，所以这个图形的面积是平方厘米．例1.3、如图，已知正方形ABCD的边长是8厘米，E、F、G、H分别是边AD、AB、BC、CD的中点，连接E、F、G、H也得到一个正方形，请问正方形EFGH的面积是多少平方厘米？答案：32解析：外围的四个小三角形可以拼成一个正方形，这个正方形和正方形EFGH边长一样，所以大正方形的面积等于正方形EFGH面积的2倍，所以小正方形的面积是平方厘米．题模二等腰直角三角形斜边例2.1、一个等腰直角三角形，最长的边长为20厘米，它的面积是________平方厘米．答案：100解析：在等腰直角三角形中，，即平方厘米．例2.2、如图，△ABC与△ADE都是等腰直角三角形，BC长8cm，DE长4cm，求阴影部分的面积．答案：12解析：△ADE面积为，△ABC面积为，所以阴影部分的面积为．例2.3、如图，等腰直角三角形ABC中，斜边长8厘米．四边形CDEF为正方形，正方形CDEF的面积是多少平方厘米？答案：8解析：连接CE，四个一样的三角形组成了大三角形，所以正方形的面积是整个大三角形面积的一半，三角形ABC的面积是平方厘米，所以正方形的面积是平方厘米．例2.4、如下图，厘米，长方形BDEF中的厘米，阴影的面积是60平方厘米，则的面积是＿＿＿＿＿平方厘米．A、33B、32C、31D、30答案：D解析：已知平方厘米，所以平方厘米，厘米，所以厘米，所以的面积是平方厘米．选D．题模三面积与长度的相互转化例3.1、三角形面积是12平方米，其中底边是4米，那么高是__________米．答案：6解析：三角形面积＝底×高÷2，反过来高是：．例3.2、如图，ABCD是一个长10厘米，宽6厘米的长方形，三角形ADE的面积比三角形CEF的面积大10平方厘米，求CF的长．答案：4cm解析：如上图，△ADE的面积比△CEF的面积大10平方厘米，则△ADE与梯形ABCE 的面积和比△CEF与梯形ABCE的面积和也大10平方厘米，即长方形ABCD 的面积比△ABF的面积大10平方厘米．所以△ABF的面积为，，．例3.3、把小正方形的每边延长3厘米后，得到一个大正方形，大正方形的面积比小正方形的面积大48平方厘米．小正方形的面积是多少平方厘米？答案：25解析：面积差48平方厘米，其实就是4个小直角三角形的面积，所以每一个小正方形的面积是12平方厘米，小三角形的高是厘米，所以小正方形的边长是厘米，小正方形的面积是平方厘米．如图，直角三角形ABC的边长BC=3，AC=4，AB=5，DG垂直于AB且DG=1.2，求正方形CEDF的边长．答案：解析：连结DA、DB、DC．，而可表示为，故正方形CEDF的边长为．如下图，梯形ABCD的上底AD长5厘米，下底BC长12厘米．腰CD的长为8厘米，过B点向CD作出的垂线BE的长为9厘米，那么梯形ABCD的面积是多少？答案：51平方厘米解析：作出梯形的高DF，连接BD，那么BE正好是△BCD的高．在△BCD中，厘米，对应的高长9厘米，所以面积是平方厘米．再把BC看作底边，对应的高是DF，由三角形的面积反求高可得：厘米．在梯形ABCD中，上底和下底分别为5厘米和12厘米，高是厘米，所以面积为平方厘米．例3.6、如图，在长方形ABCD中，长，宽，，G是AD边上一点，假设△GEC的面积等于32，求HF的长．答案：4cm解析：，故，．例3.7、如下列图，直角梯形ABCD中，，，，且三角形AED、三角形FCD和四边形EBFD的面积相等，求三角形DEF 的面积．答案：解析：，，，所以．，所以．，．例3.8、如下图，正方形ABCD的边长是18，E是CD中点，且ABFH是长方形，两个阴影三角形面积相等．那么，四边形AEFB的面积是______．答案：216解析：由两个阴影部分面积相等，可以得出和，得出，得出，则．例3.9、图中有3个大小不同的正方形，其中大正方形的周长比小正方形的周长大8，大正方形的面积比中正方形的面积大12．大正方形的面积是多少？答案：49解析：因大正方形的周长比小正方形的周长大8，也就是说大正方形的每条边长度比小正方形的多．如下列图所示，图中这两段以粗线画出的线段长度相等，则每段的长度是．由于大正方形的面积比中正方形的面积大12．比较一下可知，如下列图中的4个阴影三角形的总面积为12，于是每个三角形的面积是．同时阴影三角形的一条直角边的长度为1，那么另一条直角边的长度就是．又大正方形的边长就是两条直角边的长度和，为．那么大正方形的面积为：．随堂练习随练1.1、如图，已知正方形ABCD，对角线长6厘米．正方形ABCD的面积是多少平方厘米？答案：18解析：,所以正方形的面积是平方厘米．随练1.2、如图，等腰直角三角形ABC中，斜边长8厘米．等腰直角三角形ABC的面积是多少平方厘米？答案：16解析：两个等腰直角三角形可以拼成一个正方形，所以等腰直角三角形ABC的面积是平方厘米．随练1.3、三角形底边是12米，高是11米，面积是__________平方米．答案：66解析：三角形面积＝底×高÷2，．随练1.4、如下图两个等腰直角三角形，恰好拼成一个直角梯形，已知较小的等腰直角三角形的斜边长6厘米，那么这个直角梯形的面积是多少平方厘米？答案：27解析：等腰直角三角形ABD的面积是平方厘米，三角形BCD的面积是平方厘米，所以梯形的面积是平方厘米．随练1.5、如下图，梯形ABCD的上底AD长8厘米，下底BC长16厘米．腰CD的长为8厘米，过B点向CD作出的垂线BE的长为10厘米，梯形ABCD的面积是多少平方厘米？答案：60解析：三角形BCD的面积是平方厘米，所以BC边上的高是厘米，所以梯形的高也是6厘米，梯形的面积是平方厘米．随练1.6、在长方形ABCD中，AB=8厘米，BC=12厘米，E、F、G分别为边AB、BC、CD的中点，H为AD边上任意一点，图中阴影部分的面积是________平方厘米．答案：36解析：整个图形被分成了3个三角形，每一个三角形的面积算出之后相加即可，所以整个阴影的面积是．随练1.7、如图在直角梯形ABDC中，ACE和BDE都是等腰直角三角形〔1〕如果△ACE的面积是8，△BDE的面积为18.请问：梯形ABDC的面积是多少？〔2〕如果△ACE的面积是9，△BDE的面积为16.请问：梯形ABDC的面积是多少？答案：〔1〕50〔2〕49解析：〔1〕，，所以梯形的面积是〔2〕，所以三角西的那个CED的面积是，梯形的面积是．随练1.8、如下图，平行四边形的一边长为15厘米，这条边上的高为6厘米，一条线段将此平行四边形分成了两部分，它们的面积相差18平方厘米．请问：其中梯形的上底是多少厘米？答案：3厘米解析：如下列图所示，从线段的顶点做边的平行线，把梯形又分成了一个三角形和一个小平行四边形，分割出的三角形显然和原来的三角形面积相等．那么最左边的小平行四边形的面积就是多出来的18平方厘米，又其高为6厘米，它的底边长又正好是所需求的梯形的上底长．所以，梯形的上底长为厘米．自我总结课后作业作业1、如下图是一个由正方形ABCD和等腰直角三角形BCE组成的梯形，三角形BCE 的斜边BE长8厘米，这个梯形的面积是多少平方厘米？答案：48解析：，所以三角形BCE的面积是，连接对角线发现正方形的面积是三角形BCE面积的2倍，所以梯形的面积是．作业2、如图，等腰直角三角形ABC中，斜边长6厘米．等腰直角三角形ABC的面积是多少平方厘米？答案：9两个等腰直角三角形可以拼成一个正方形，所以等腰直角三角形ABC的面积是平方厘米．作业3、如图，等腰直角三角形ABC中，斜边长10厘米．等腰直角三角形ABC的面积是多少平方厘米？答案：25解析：两个等腰直角三角形可以拼成一个正方形，所以等腰直角三角形ABC的面积是平方厘米．作业4、三角形底边是6米，高是8米，面积是__________平方米．答案：24三角形面积＝底×高÷2，．作业5、如下图，梯形ABCD的上底AD长4厘米，下底BC长8厘米．腰AB的长为4厘米，过C点向AB作出的垂线CE的长为6厘米，三角形ADC的面积是多少平方厘米？答案：18解析：三角形ABC的面积是厘米，根据三角形的面积公式可以求出三角形ABC的BC边上的高是厘米，所以梯形的高是3厘米，梯形的面积等于平方厘米．作业6、如下图，梯形ABCD的上底AD长6厘米，下底BC长12厘米．腰CD的长为9厘米，过B点向CD作出的垂线BE的长为8厘米，梯形ABCD的面积是多少平方厘米？答案：54解析：三角形BCD的面积是平方厘米，所以BC边上的高是厘米，所以梯形的高也是6厘米，梯形的面积是平方厘米．作业7、如图，平行四边形ABCD的边BC长10cm，直角三角形BCE的直角边EC长8cm，已知两块阴影部分的面积和比△EFG的面积大10cm2，求CF的长．答案：5cm解析：同时加上BCFG可知，梯形ABCD面积比△BCE面积大10cm2．直角三角形BCE的面积为，故．作业8、如下图，把小正方形的每边延长2厘米后，得到一个大正方形．大正方形的面积比小正方形的面积大36平方厘米，那么小正方形的边长是多少厘米？答案：7厘米解析：可以看出，大正方形恰好比小正方形多出了四个相同的直角三角形，而且直角三角形的一条直角边正好是延长出去的2厘米线段，图中空白部分的4个直角三角形面积总和为36平方厘米，每个三角形的面积为平方厘米．在这4个直角三角形中，较短的直角边长等于2厘米，那么较长的直角边长为厘米．所以小正方形的边长为厘米．作业9、如下图，ABCD是一个长方形，点E在CD延长线上．已知AB= 5，BC= 12，且△AFE的面积等于20，那么△CFE的面积等于多少？答案：60解析：已知，，那么△ABE的面积就是．又因为△AFE的面积是20，因此△ABF的面积是，AF的长度为．那么在△AFE中，ED是AF边上对应的高，所以ED的长度为．在△CEF中，底边，高，因此面积为．。

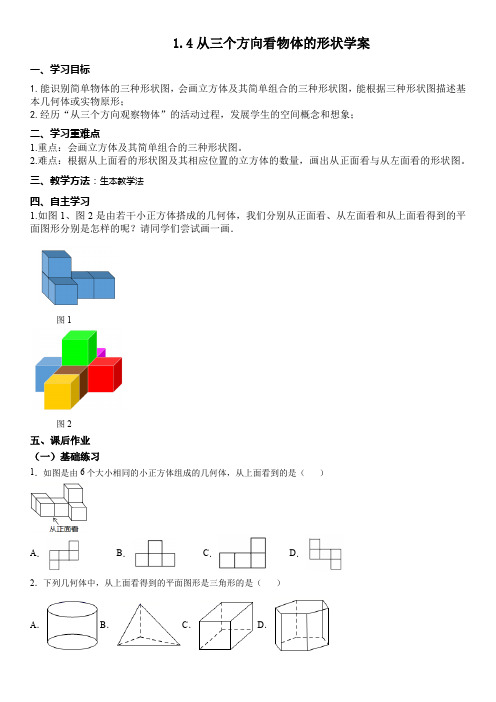
1.4从三个方向看物体的形状学案一、学习目标1.能识别简单物体的三种形状图，会画立方体及其简单组合的三种形状图，能根据三种形状图描述基本几何体或实物原形；2.经历“从三个方向观察物体”的活动过程，发展学生的空间概念和想象；二、学习重难点1.重点：会画立方体及其简单组合的三种形状图。

2.难点：根据从上面看的形状图及其相应位置的立方体的数量，画出从正面看与从左面看的形状图。

三、教学方法：生本教学法四、自主学习1.如图1、图2是由若干小正方体搭成的几何体，我们分别从正面看、从左面看和从上面看得到的平面图形分别是怎样的呢？请同学们尝试画一画．图1图2五、课后作业（一）基础练习1．如图是由6个大小相同的小正方体组成的几何体，从上面看到的是（）A．B．C．D．2．下列几何体中，从上面看得到的平面图形是三角形的是（）A．B．C．D．3．如图，由 5 个相同的小正方体组成的立体图形，分别从正面、左面、上面三个不用方向观察这个立体图形，你看不到哪个平面图形？（ ）A ．B ．C ．D ．4．用若干大小相同的小立方块搭成一个几何体，使得从正面和从上面看到这个几何体的形状如图所示，该几何体至多是用（ ）个小立方块搭成的．A ．5B ．6C ．7D ．8（二）巩固提升5．十个棱长为a 的正方体摆放成如图的形状，这个图形的表面积是（ ）A ．236aB ．36aC ．26aD ．230a6．如如如如如如如如如如如如如如如如如如如如如如如如如如如如如如如如_________如如如如如π如7．把边长为1厘米的6个相同正方体摆成如图的形式．（1）该几何体的体积是______3cm ，表面积是______2cm ；（2）在格纸中画出该几何体的主视图、左视图、俯视图；（3）如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的左视图和俯视图不变，那么最多可以再添加______个小正方体．（三）培优训练8．用相同的小立方体搭一个几何体，从正面、上面看到的形状图如图所示，从上面看到的形状图中小正方形的字母表示在该位置上小立方体的个数，请回答下列问题：（1）a ，b ，c 各表示的数字是几？（2）这个几何体最多由几个小立方体搭成？最少呢？（3）当1d e ==，2f =时，画出这个几何体从左面看得到的形状图.9．如图所示的某种玩具是由两个正方体用胶水粘合而成的，它们的棱长分别为1米和3 米，为了美观，现要在其表面喷涂油漆，已知喷涂1平方米需用油漆30克，那么喷涂这个玩具共需油漆________克．。

第三单元：观察物体第2课时：观察由几个相同正方体摆成的组合体班级：姓名: 等级:【基础训练】一、填空题。

1．是由_____个小正方体拼成的，从_____面看到的是，从_____面看到的是，从_____面看到的是。

2．下图的立体图形是由（________）个小正方体搭成，至少还需要（________）个同样的小正方体，才能搭成一个大正方体。

3．如图由（______）个小正方体拼成的，从正面看到的是（______）个小正方形组成的图形。

4．数一数下列物体是由几个小正方体拼成的。

（______）个（______）个5．下面这个图形由（________）个正方体组成，从（________）面和（________）面看到是一样的。

6．数一数，下面图形各是由几个小正方体摆成的？（______）个（______）个（______）个7．如图：上面的几何体是由8个小正方体拼成的，如果把这个图形的表面涂上红色，那么，（1）只有1个面涂红色的有________个小正方体；（2）只有2个面涂红色的有________个小正方体；（3）只有3个面涂红色的有________个小正方体；（4）只有4个面涂红色的有________个小正方体；（5）只有5个面涂红色的有________个小正方体．8．摆一摆，数一数，下面立体图形各是由几个小正方体拼成的。

二、选择题1．小强用同样大小的小正方体摆了一个长方体，从正面和上面看，看到的图形分别是如下图所示，小强摆这个长方体一共用了（）个小正方体。

A．12B．18C．242．如图，在墙角摆放着一些大小相同的正方体纸箱，只露一个面的正方体纸箱一共有（）个。

A．1B．2C．33．一个立体图形，从上面看到的形状是，从正面看到的形状是，从左面看到的形状是。

要搭成这个立体图形至少需要（）个小正方体。

A．4B．5C．6D．74．一个立体从上面看到的形状是，从右面看到的形状是，要搭成这样的立体，最少需要（）个同样大小的小正方体．A．7B．8C．9D．105．由若干个小正方体拼成的图形，从前面看是，从右面看是。

【寒假预习】人教版五年级数学下册寒假预习新课——第一单元（含答案）一、单选题1.4个小正方体摆成，再添一个同样的小正方体，从前面看是，有（）种不同的摆法。

A. 2B. 4C. 82.从侧面看到的形状是，这个立体图形是（）。

A. B. C.3.小明用几个棱长1厘来的小正方体木块摆了一个物体，从正面看是，从右面看是，从上面看是，这个物体的体积至少是（）立方厘米。

A. 4B. 5C. 6D. 74.下面物体中，从上面看是，从右面看是的是（）。

A. B. C. D.5.观察（）号立体图形，可以看到下面三个位置的形状。

A. B. C. D.6.在左边的立体图形中添一个小正方体，使其从左面看到的形状不变，符合要求的摆法是（）。

A. B. C.7.一个立体图形从上面看是，从正面看是。

要搭这样的立体图形，至少要用（）个小正方体。

A. 4B. 5C. 8D. 98.一个立体图形，从正面看是，从上面看是，搭成这个立体图形最少需要（）个小正方体。

A. 4B. 5C. 6D. 79.一个立体图形从上面、前面看到的图形都是，它至少是用（）个相同的小正方体搭成。

A. 4B. 5C. 610.一个立体图形，从正面看到图形是，从上面看到的图形是，从右面看到的图形是，这个立体图形可能是（）A. B. C. D.二、判断题11.一个物体从前面看到的图形是，它一定是由4个小正方体摆成的。

（）12.小明根据二个方向观察到的图形就能摆出原来的几何体。

（）13.小明用6个同样大的正方体摆成一个物体。

他从正面和上面看到的图形都是。

那么如果从侧面看摆成的物体，看到的图形是。

（）14.用5个同样大的正方体摆出的物体，从上面看是，一共有3种不同的摆法。

（）15.用几个小正方体搭成一个组合体，从正面看到形状是，那么这个组合体至少是用3个小正方体组成的。

（）16.某一由小正方体堆成的几何体，从上面看到的图形是，则这个几何体至少需要5个小正方体。

（）三、填空题17.一个物体由几个相同的正方体组成，从前而看形状是，从右面看形状是，这个物体至少由________个小正方体组成。

7单元跟踪检测卷一、填一填。

(每空1分，共21分)1．四边形有( )条直的边和( )个角。

2．(1)右面的图形中共有( )个四边形。

(2)( )是正方形，它有( )条相等的边，( )个直角。

(3)②和④是( )，它的( )相等，有4个( )。

3．右图中，两副同样的三角板，( )号三角板和( )号三角板可以拼成一个长方形；( )号三角板和( )号三角板可以拼成一个正方形。

4．比较下面每组图形的周长。

(1) (2)甲的周长乙的周长甲的周长乙的周长5．一块长方形玻璃长10分米，宽4分米，它的周长是( )分米。

6．一个正方形的边长是4厘米，周长是( )厘米；一个正方形的周长是4厘米，边长是( )厘米。

7．用四根分别长6厘米、4厘米、6厘米、4厘米的小棒可以摆成一个( )。

8．用一根长40厘米的绳子正好绕一个正方形镜框一周，这个镜框的边长是( )厘米。

9．一个长方形的长是2米，宽是30分米，它的周长是( )分米。

二、辨一辨。

(对的画“√”，错的画“×”)(每题2分，共10分) 1．因为的每个面都是四边形，所以也是四边形。

( ) 2．由4条线段组成的图形一定是四边形。

( ) 3．左图因为缺少了一部分，所以它没有周长。

( ) 4．告诉一个长方形的长与宽的和是12厘米，无法求这个长方形的周长，因为不知道这个长方形的长是多少，宽是多少。

( ) 5．用左边的两个完全一样的直角三角形可以拼成右边的一个长方形，因为一个三角形的周长是4＋3＋5＝12(厘米)，所以右边长方形的周长是12×2＝24(厘米)。

( )三、选一选。

(把正确答案的序号填在括号里)(每题2分，共10分) 1．下图中，你认为四边形最多的是( )。

2．猜右图信封中的卡片是( )。

A．长方形B．正方形C．长方形或正方形3．一个长方形的长是8厘米，宽是6厘米，它的周长是( )厘米。

A．14 B．28 C．484．下面用8个边长是1厘米的小正方形拼成的图形中，周长最短的是( )。

1.4.正⽅形组成的图形课内练习1．摆⼀摆，画⼀画，3个正⽅形组成的图形。

⼀共有（）个。

2. 摆⼀摆，画⼀画，4个正⽅形组成的图形。

⼀共有（）个。

3. 摆⼀摆，画⼀画，5个正⽅形组成的图形⼀共有12个，你能把它们都画出来吗？★4. 想⼀想，这12个五连块，除了⼀个外，其它都可以⽤哪些英⽂字母（印刷体）表⽰？1.4 正⽅形组成的图形⽼师的话：学会⽤相同的正⽅形拼组各种平⾯图形“多连块”，还要⽤多连块拼出新的⼏何图形。

8×9＋8＝ 5×3－3＝ 12÷6＋12＝ 45－25÷5＝ 80＋10×2＝ 49－7×7＝ 8×5×4＝ 60÷2÷3＝ 150＋280＝ 930－270＝ 900＋100＝ 640－80＝1.4 正⽅形组成的图形课后练习1.细⼼填⼀填。

（1）2个正⽅形组成的图形叫（），3个正⽅形可以组成（）种三连块，（）个正⽅形可以组成（）种四连块。

（2）⼀个三连块，⼀个四连块和⼀个五连块可以拼成⼀个（）×（）的正⽅形。

（3）找⼀找，填⼀填。

三连块：四连块：五连块：2. 耐⼼试⼀试。

⽤下⾯的多连块拼成⽅框⾥的图形，并⽤不同的⽔彩笔涂⾊表⽰。

3. 开⼼玩⼀玩。

⽤不同的多连块摆出4×4的正⽅形，你能摆出两种不同的摆法吗？220－130＝510－150＝720＋180＝63÷9×7＝18×2÷9＝50×6÷10＝120－120÷6＝28＋72÷9＝3×5÷3×5＝10＋6×10＝（）－240＝420（）＋410＝700 A.。