最新华理高数全部复习资料之重积分

高等数学定积分及重积分的方法与技巧第一部分 定积分的计算一、定积分的计算例1 用定积分定义求极限. )0(21lim 1>++++∞→a nn a a a a n . 解 原式=∫∑=⋅=∞→1011lim a ani n x n n i dx =aa x a +=++11111. 例2 求极限 ∫+∞→121lim xx n n dx .解法1 由10≤≤x ，知nn x x x ≤+≤210，于是∫+≤1210x x n ∫≤1n x dx dx .而∫10nx ()∞→→+=+=+n n n x dx n 0111101，由夹逼准则得∫+∞→1021lim xx n n dx =0. 解法2 利用广义积分中值定理()()x g x f ba ∫()()∫=b ax g f dx x dx （其中()x g 在区间[]b a ,上不变号）， ().1011112102≤≤+=+∫∫n n nn dx x dx xx x x由于11102≤+≤nx，即211nx+有界，()∞→→+=∫n n dx x n01110，故∫+∞→1021lim x x n n dx =0. 注 （1）当被积函数为()22,x a x R +或()22,a x x R −型可作相应变换.如对积分()∫++3122112xxdx，可设t x tan =；对积分()02202>−∫a dx x ax x a，由于()2222a x a x ax −−=−，可设t a a x sin =−.对积分dx e x ∫−−2ln 021，可设.sin t e x =−（2）()0,cos sin cos sin 2≠++=∫d c dt td t c tb t a I π的积分一般方法如下：将被积函数的分子拆项，[分子]=A[分母]+B[分母]′，可求出22dc bdac A ++=，22dc adbc B +−=. 则积分 ()220cos sin ln 2cos sin cos sin πππtd t c B A dt td t c t d t c B A I ++=+′++=∫.ln2dc B A +=π例3 求定积分()dx x x x ∫−1211arcsin分析 以上积分的被积函数中都含有根式，这是求原函数的障碍.可作适当变换，去掉根式. 解法1 ()dxx x x ∫−1211arcsin 2tx x t ==12121211212arcsin arcsin arcsin 21arcsin 2tt d t dt tt ==−∫∫.1632π=解法2 ()dx x x x∫−1211arcsin .163cos sin cos sin 2sin 2242242πππππ==⋅=∫u du u u uu u u x 小结 （定积分的换元法）定积分与不定积分的换元原则是类似的，但在作定积分换元()t x ϕ=时还应注意：（1）()t x ϕ=应为区间[]βα,上的单值且有连续导数的函数； （2）换限要伴随换元同时进行；（3）求出新的被尽函数的原函数后，无需再回代成原来变量，只要把相应的积分限代入计算即可.例4 计算下列定积分（1）∫+=2031cos sin sin πx x xdx I ， dx xx xI ∫+=2032cos sin cos π；（2）.1cos 226dx e xx ∫−−+ππ解 （1）∫+=2031cos sin sin πxx xdx I)(sin cos cos 2023du u u uu x −+−=∫ππ=.sin cos cos 223∫=+πI dx xx x故dx xx xx I I ∫++==203321cos sin cos sin 21π=()41cos cos sin sin 212022−=+−∫ππdx x x x x . （2）=I .1cos 226dx e x x ∫−−+ππ()dxe xdu e uu x x u ∫∫−−+=−+−=2262261cos 1cos ππππ+++=∫∫−−2222661cos 1cos 21ππππdx e x dx e x e I x x x.3252214365cos cos 21206226πππππ=×××===∫∫−xdxxdx这里用到了偶函数在对称取间上的积分公式以及公式：dx xdx n n∫∫=2020cos sin ππ()()()()()()=⋅×−×−−=×−×−−=偶数奇数n n n n n n n n n n ,22421331,1322431π小结 （1）常利用线性变换把原积分化为可抵消或可合并的易于积分的形式。

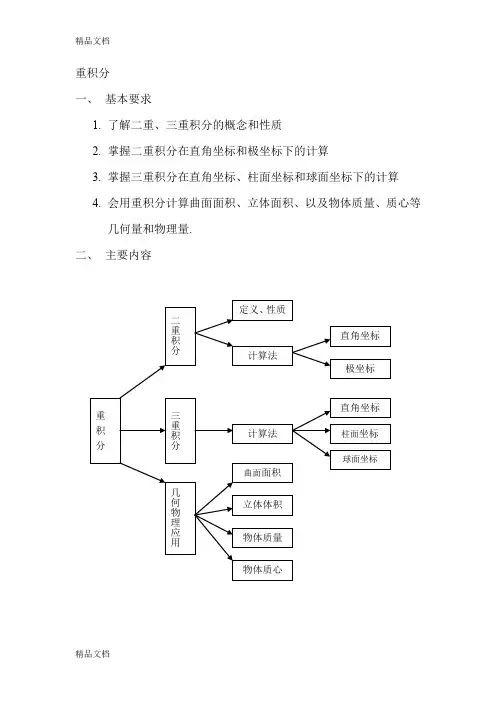
重积分一、基本要求1.了解二重、三重积分的概念和性质2.掌握二重积分在直角坐标和极坐标下的计算3.掌握三重积分在直角坐标、柱面坐标和球面坐标下的计算4.会用重积分计算曲面面积、立体面积、以及物体质量、质心等几何量和物理量.二、主要内容详细内容：1. 重积分定义：设(,)f x y 是有界闭域D 上的有界函数，将D 任意分成n 个小闭区域12,,,n σσσ∆∆∆，其中i σ∆也表示第i 个小闭区域的面积，在每个i σ∆上任取一点(,)i i ξη (1,2,,)i n =作和1(,)ni i i i f ξησ=∆∑，如果当各小区域的直径的最大值0λ→时，这和式的极限总存在，则称此极限为函数(,)f x y 在D 上的二重积分，记作(,)Df x y d σ⎰⎰，即1(,)l i m (,)ni i i i Df x y d f λσξησ→==∆∑⎰⎰ 2. 性质ⅰ) [](,)(,)(,)(,)DDDf x yg x y d f x y d g x y d αβσασβσ+=+⎰⎰⎰⎰⎰⎰ⅱ)1211(,)(,)(,)D D D D f x y d f x y d f x y d σσσ=+⎰⎰⎰⎰⎰⎰ⅲ)1DDd d σσσ==⎰⎰⎰⎰ (σ为D 的面积)ⅳ)如果在D 上，(,)(,)f x y g x y ≤，则有(,)(,)DDf x y dg x y d σσ≤⎰⎰⎰⎰ⅴ)设,M m 分别是(,)f x y 在闭区域D 上的最大值和最小值，σ是D 的面积，则有(,)Dm f x y d M σσσ≤≤⎰⎰ⅵ)(中值定理)设(,)f x y 在闭区域D 上连续，σ是D 的面积，则在D 上至少存在一点(,)ξη,使得(,)(,)Df x y d f σξησ=⎰⎰3. 直角坐标下计算二重积分ⅰ)积分区域{}12(,)()(),D x y x y x a x b φφ=≤≤≤≤ 则21()()(,)(,)bx a x Df x y d dx f x y dy φφσ=⎰⎰⎰⎰ⅱ) 积分区域{}12(,)()(),D x y y x y c y d ϕϕ=≤≤≤≤则21()()(,)(,)dy c y Df x y d dy f x y dx ϕϕσ=⎰⎰⎰⎰4. 极坐标下计算二重积分设积分区域D ：12()(),φθρφθαθβ≤≤≤≤ 则(,)(cos ,sin )DDf x y d f d d σρθρθρρθ=⎰⎰⎰⎰21()()(cos ,sin )d f d βφθαφθθρθρθρρ=⎰⎰5. 二重积分的几何意义：(,)Df x y d σ⎰⎰等于以D 为底，(,)z f x y =为顶的曲顶拄体的体积，(这里(,)0f x y ≥)物理意义：(,)Df x y d σ⎰⎰表示位于平面区域D ，面密度为(,)f x y 的薄片的质量.6. 三重积分定义：设(,,)f x y z 是有界闭域Ω上的有界函数，将Ω任意分成n 个小闭区域12,,,n v v v ∆∆∆，其中i v ∆也表示第i 个小闭区域的体积，在每个i v ∆上任取一点(,,)i i i ξηζ (1,2,,)i n =作和1(,,)nii i i i f ξηζσ=∆∑，如果当各小区域的直径的最大值0λ→时，这和式的极限总存在，则称此极限为函数(,,)f x y z 在Ω上的三重积分，记作(,,)f x y z dv Ω⎰⎰，即1(,,)l i m (,,)ni i i i i f x y z d v f vλξηζ→=Ω=∆∑⎰⎰⎰ 7. 直角坐标下计算三重积分ⅰ)积分区域{}12(,,)(,)(,),(,)xy x y z z x y z z x y x y D Ω=≤≤∈ 则21(,)(,)(,,)(,,)xyz x y z x y D f x y z dv dxdy f x y z dz Ω=⎰⎰⎰⎰⎰⎰21()()(,)(,)bx ax Df x y d dx f x y dy φφσ=⎰⎰⎰⎰ⅱ) 积分区域{}12(,,)(,),z x y z x y D c z c Ω=∈≤≤ 则21(,,)(,,)zc c D f x y z dv dz f x y z dxdy Ω=⎰⎰⎰⎰⎰⎰8.柱面坐标下计算二重积分设Ω：1212,()(),(,)(,)z z z αθβφθρφθρθρθ≤≤≤≤≤≤ 则(,,)f x y z dv Ω⎰⎰⎰2211()(,)()(,)(cos ,sin ,)z z d d f z dz βφθρθαφθρθθρρρθρθ=⎰⎰⎰9. 球面坐标下计算三重积分设Ω：1212,()(),(,)(,)r r r αθβφθφφθθφθφ≤≤≤≤≤≤ 则(,,)f x y z dv Ω⎰⎰⎰＝2211()(,)2()(,)sin (sin cos ,sin sin ,cos )r r d d f r r r r dr βφθθφαφθθφθφφφθφθφ=⎰⎰⎰10. 三重积分的物理意义：(,,)f x y z dv Ω⎰⎰⎰表示位于空间区域Ω，体密度为(,,)f x y z 的空间形体的质量. 11.对称区域上的奇偶函数积分ⅰ)若(,)f x y 为区域上D 的连续函数，D 关于y 轴对称，且1D 为D 位于y 轴右侧的子区域，则10(,)(,)2(,)(,)DD f x y x f x y d f x y d f x y x σσ⎧⎪=⎨⎪⎩⎰⎰⎰⎰，为的奇函数，为的偶函数ⅱ) 若(,,)f x y z 为Ω区域上的连续函数，Ω关于xy O 坐标面对称，1Ω为Ω位于xy O 坐标面上侧的部分，则10(,,)(,,)2(,,)(,,)f x y z f x y z dv f x y z dvf x y z ΩΩ⎧⎪=⎨⎪⎩⎰⎰⎰⎰⎰⎰，为z 的奇函数为z 的偶函数12.几何应用、物理应用曲面面积：xyD A =⎰⎰平面薄片的质心坐标：(,)(,)DDx x y d x x y d ρσρσ=⎰⎰⎰⎰， (,)(,)DDy x y d y x y d ρσρσ=⎰⎰⎰⎰空间物体的质心坐标：1(,,)x x x y z dv M ρΩ=⎰⎰⎰ ，1(,,)y y x y z dv MρΩ=⎰⎰⎰1(,,)z z x y z dv MρΩ=⎰⎰⎰其中(,,)M x y z dv ρΩ=⎰⎰⎰三、 重点与难点：1. 选择适当的坐标计算重积分.2. 根据被积函数及积分区域特点，选择适当的积分次序.3. 二次积分的积分次序变换.4. 利用对称区域上函数的奇偶性简化计算. 四、 例题1. 设(,)f x y 在[,]a b 上连续，证明不等式22()()()b b a a f x dx b a f x dx ⎡⎤≤-⎢⎥⎣⎦⎰⎰ 等号仅当()f x 为常数时成立.分析：利用“非负被积函数的二重积分非负”的性质来证明.在证明等号成立的条件时，用到了“非负连续函数的定积分为零，则此函数恒为零”的性质. 证明：因为[]20()()bba adx f x f y dy ≤-⎰⎰222()()2()()()bb baa ab a f x dx f x dx b a f y dy ⎡⎤=--+-⎢⎥⎣⎦⎰⎰⎰ 故有22()()()b ba a f x dxb a f x dx ⎡⎤≤-⎢⎥⎣⎦⎰⎰ 当()f x 为常数时，显然上述等号成立.反之，设上述等号成立，则[]2()()0bba a dx f x f y dy -=⎰⎰ 由于函数[]2()()()ba F x f x f y dy =-⎰是[,]ab 上非负连续函数， 故()0F x ≡，a x b ≤≤.特别()0F a =即[]2()()0ba f x f y dy -=⎰，又由于函数[]2()()()G y f x f y =-是[,]a b 上非负连续函数，故()0G x ≡，a y b ≤≤.因此()()f y f a ≡，a y b ≤≤ 即()f x 为常数.2. 在下列二次积分中改变积分次序 1)2111(,)x dx f x y dy --⎰⎰分析：积分域D ：211,1x y x -≤≤≤≤-，也表示为两个区域12,D D 的并，其中1D ：210,1y x y -≤≤≤≤- ：01,y x ≤≤≤≤解：2110111(,)(,)(,)x dx f x y dy dy f x y dx dy f x y dx ---=+⎰⎰⎰⎰2)311(,)x x dx f x y dy -⎰⎰分析：注意到当01x <<，3x x <，尽管这个二次积分并不是(,)f x y 在由y x =及3y x =所围区域上的二重积分，但是改变积分次序使之与原二次积分相等仍为可能.解：311(,)x x dx f x y dy -⎰⎰＝33110(,)(,)x x x x dx f x y dy dx f x y dy --⎰⎰⎰⎰ 3011(,)(,)x yx dx f x y dy dy f x y dx --=⎰⎰⎰31100(,)(,)x x y dx f x y dy dx f x y dx =⎰⎰⎰311(,)x x dx f x y dy -⎰⎰01(,)y dy f x y dx -=⎰10(,)y dx f x y dx -⎰11(,)ydy f x y dx -=⎰3. 计算下列二重积分1) 22()Dx y dxdy +⎰⎰，其中D 是,,y x y x a y a ==+=和3y a = (0)a >为边的平行四边形区域.分析：当y 从a 变到3a ，对每一固定的y ，x 从y a -变到y 故化为先对x 后对y 的二重积分较简单. 解：D ：3,a y a y a x y ≤≤-≤≤ 32222()()aya y a Dx y dxdy dy x y dx -+=+⎰⎰⎰⎰23324()1433aay y a ay dy a ⎡⎤-=+-=⎢⎥⎣⎦⎰ 2) 2Dy dxdy ⎰⎰，其中D 是由x 轴和摆线的第一拱(sin ),(1cos ),(02)x a t t y a t t π=-=-≤≤所围的区域分析：区域D ：02x a π≤≤，0()y x φ≤≤其中()y x φ=为摆线的直角坐标方程，显然当(sin )x a t t =-时，()(1cos ),(02)y x a t t φπ==-≤≤解： []2()2322001()3a x ay dxdy dx y dy x dx πφπφ==⎰⎰⎰⎰⎰23301(1cos )(1cos )3a t a t dt π=--⎰ ((sin ))x a t t =- 4280161sin 332a t dt π=⎰44882003232sin 2sin 33a a udu udu ππ==⋅⎰⎰ ()2tu = 4432753135238642212a a ππ⋅⋅⋅=⋅⋅=⋅⋅⋅3)2Dy x dxdy -⎰⎰，其中D ：11x -≤≤，02y ≤≤分析：将区域D 分成两块12,D D ，使被积函数21222(),(,)(,)y x x y D y x y xx y D ⎧--∈⎪-=⎨-∈⎪⎩再利用二重积分的关于积分域的可加性，分块计算 解：曲线2y x =将区域D 分成 ：11x -≤≤，20y x ≤≤ ：11x -≤≤，22x y ≤≤2Dy xdxdy -⎰⎰1222()()D D x y dxdy y x dxdy =-+-⎰⎰⎰⎰2221122101()()x x dx x y dy dx y x dy --=-+-⎰⎰⎰⎰114240(44)4615x dx x x dx=+-+=⎰⎰4)D⎰⎰,其中D :22224x y ππ≤+≤分析：当二重积分的积分域为圆域或扇形域，可考虑用极坐标解：220sin d d πππθρρρ=⋅⎰⎰⎰⎰22sin d πππρρρ=⋅⎰ 26π- 4.计算二重积分112111224y y xxy dy e dx dy e dx I =+⎰⎰⎰分析：由于被积函数的原函数不易求出，可考虑改变积分次序后再计算.解：设区域D ：211,2x x y x ≤≤≤≤21111223()82y y xx xxx De e d dx e dy x e e dx σI ===-=-⎰⎰⎰⎰⎰ 5.设一平面薄片位于双曲线221x y -=及0,1y y ==直线所围平面区域D ，且D 上任一点(,)x y 处的面密度为2x y ，求此薄片的质量. 分析：平面薄片的质量等于密度函数再区域上的二重积分，再利用区域对称化简计算.解：薄片的质量1222DD M x yd x yd σσ==⎰⎰⎰⎰31122200022(1)3dy x ydx y y dy ==+⎰⎰152222(1)1)1515y =+=6.求曲面z =夹在两曲面2222,2x y y x y y +=+=之间的那部分曲面的面积.分析：将所求的曲面投影到xoy 面计算最简单，投影域xy D 为曲线2222,2x y y x y y +=+=所围部分.解：投影域：xy D ：222y x y y ≤+≤由z =，知x y z z ==2xyxyD D S dxdy ==⎰⎰⎰⎰)4ππ=-=7.化二次积分1100(,)dx f x y dy ⎰⎰为极坐标形式的二次积分.分析：一般极坐标形式的二次积分为先对ρ后对θ的二次积分，当然也可化为先θ对后对ρ的二次积分. 解：区域可表示为1D ：10,04cos πθρθ≤≤≤≤及2D ：1,042sin ππθρθ≤≤≤≤1114cos 0(,)(cos ,sin )dx f x y dy d f d πθθρθρθρρ=⎰⎰⎰⎰12sin 04(cos ,sin )d f d πθπθρθρθρρ+⎰⎰积分域也可表示为1D ：01,02πρθ≤≤≤≤及2D ：110cosarcsinarc ρθρρ≤≤≤≤两部分.111200(,)(cos ,sin )dx f x y dy d f d πρρρθρθθ=⎰⎰⎰⎰＋1arcsin11arccos(cos ,sin )d f d ρρρρθρθθ⎰8.设函数()f x 在[0,1]上连续，并设10()f x dx A =⎰，求110()()x dx f x f y dy ⎰⎰. 分析：求解关键是利用二重积分对坐标轮换对称的性质，即区域D 的边界曲线方程关于,x y 对称，则有 (,)(,)DDf x y dxdy f y x dxdy =⎰⎰⎰⎰.解：变换积分次序得1110()()()()yxdx f x f y dy dy f x f y dx =⎰⎰⎰⎰10()()xdx f x f y dy =⎰⎰111112()()()()()()x xxdx f x f y dy dx f x f y dy dx f x f y dy =+⎰⎰⎰⎰⎰⎰1100()()dx f x f y dy =⎰⎰112()()f x dx f y dyA=⋅=⎰⎰∴11201()()2x dx f x f y dy A =⎰⎰ 9.求锥面z =和抛物面22z x y =+所围成的立体体积. 分析：求体积可用二重积分，也可用三重积分. 解一：投影域D ：221x y +≤()22DV x y d σ⎤=+⎦⎰⎰2120()6d d πθρρρρπ=-=⎰⎰解二：221120002()6V dv d d dz d πρρπθρρπρρρρΩ===-=⎰⎰⎰⎰⎰⎰⎰10.计算23xy z dxdydz Ω⎰⎰⎰，其中Ω是由,,1,0z xy y x x z ====所围成的区域分析：Ω在面xoy 上投影域D 如图所示，在D 上的点(,)x y ，0z xy =≥，在不知道曲面z xy =形状的情况下，也容易写出Ω的积分范围. 解：Ω：0,0,01z xy y x x ≤≤≤≤≤≤ 12323000xxyxy z dxdydz dx dy xy z dz Ω=⎰⎰⎰⎰⎰⎰1230001364x xyxdx y dy z dz ==⎰⎰⎰ 11.求22()x y z dv Ω++⎰⎰⎰，其中Ω是由曲面220y zx ⎧=⎨=⎩绕z 轴旋转一周而成的曲面与平面4z =所围成的立体.分析：Ω是由旋转曲面222x y z +=与4z =所围而成的立体，化三重积分的计算中可化为先对z 或后对z 的积分.解一：Ω：221()42x y z +≤≤，(,)xy x y D ∈，22:8xy D x y +≤ 22422221()2()()xyx y D x y z dv dxdy x y z dz +Ω++=++⎰⎰⎰⎰⎰⎰2242102350()528)82563d d z dzd πρθρρπρρρρρπ=+=+-=⎰⎰解二：Ω：04z ≤≤，(,)z x y D ∈，其中22:2z D x y z +≤ 422220()()zD x y z dv dz x y z dxdy Ω++=++⎰⎰⎰⎰⎰⎰4220420)42563dz d z d z dzπθρρρππ=+==⎰⎰⎰12.试将三重积分(,,)f x y z dv ΩI =⎰⎰⎰化为三次积分，其中Ω是由z =及1,2z z ==所围成的区域.分析：此题可分别化为直角坐标、柱面坐标和球面坐标下的三重积分，主要这个三重积分不可将它理解为(,,)f x y z 在大的圆锥区域积分减去小的圆锥区域积分.解：21(,,)zz dx dy f x y z dx -I =⎰⎰直2121(cos ,sin ,)d d f z dz πθρρρθρθI =⎰⎰⎰柱22201(cos ,sin ,)d d f z dz πρθρρρθρθ+⎰⎰⎰22101(cos ,sin ,)zdz d f z d πθρθρθρρ=⎰⎰⎰()!22sec 2!!400sec (sin cos ,sin sin ,cos )sin n r n r d d f r r r r dr ππφφθφφθφθφφ-I =⎰⎰⎰球13.设(,,)1()(,,)f x y z x y z f x y z dv Ω=+++⎰⎰⎰，其中Ω：2221,0x y z z ++≤≥分析：两边在Ω上求三重积分，解出(,,)f x y z dv Ω⎰⎰⎰即可.解：设(,,)f x y z dv A Ω=⎰⎰⎰，则 (,,)1()f x y z x A y z =+++[](,,)(1)()A f x y z dv x A y z dv dv A zdv ΩΩΩΩ==+++=+⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰22211200122(1)33x y z A zdz dxdy A z z dz πππ+≤-=+=+-⎰⎰⎰⎰ 234A ππ=+ 83(4)A ππ=-，故8(,,)1()3(4)f x y z x y z ππ=+++- 14.用定积分表示三重积分000()xyzdy dz f t dt ⎰⎰⎰分析：由于被积函数是t 的函数，故将,z t 积分次序变换后，把对z 的积分算出，再将,y t 的积分次序变换，又可把对y 的积分算出，最后保留对t 的积分式子. 解：0()()xy z x y ytdy dz f t dt dy dt f t dz =⎰⎰⎰⎰⎰⎰020()()()()1()()2x yx xt x dy f t y t dtdt f t y t dy f t x t dt =-=-=-⎰⎰⎰⎰⎰15.用重积分证明：由平面图形0,0()a x b y f x ≤≤≤≤≤绕x 轴和y 轴旋转所成的旋转体的体积分别是2()bx a V f x dx π=⎰和2()b y a V xf x dx π=⎰证明：曲线()y f x =绕x 轴旋转的旋转曲面方程：222()y z f x +=，a x b ≤≤在xoy 面上投影域为xy D ：,()()a x b f x y f x ≤≤-≤≤故所求体积()()b f x x a f x V dx dy -=⎰⎰(04bf x a dx =⎰⎰24()4ba f x dx π=⎰2()baf x dx π=⎰曲线()y f x =绕y轴旋转的旋转曲面方程：y f = 在xoz 面上投影域为zx D ：2222a x z b ≤+≤故所求体积0zx f y D V dzdx dy =⎰⎰⎰2()2()bf a b ad d dyf d πρθρρπρρρ==⎰⎰⎰⎰即2()by a V xf x dx π=⎰16.求曲面221z x y =++上点(1,1,3)M -处的切平面与曲面22z x y =+所围成的空间区域的体积V .分析：所围的空间区域在xoy 面上的投影域的确定以及如何在此投影域上积分是此题的关键.解：曲面221z x y =++在(1,1,3)M -处的法向量''(,,1)(2,2,1)M x y M n z z =-=--则切平面方程为2(1)2(1)2(3)0x y z --+--= 即221z x y =--所以切平面与曲面的交线22221z x y z x y =--⎧⎨=+⎩在xoy 面上的投影曲线为 22(1)(1)1x y z ⎧-++=⎨=⎩即所求空间在xoy 面上的投影域D 为22(1)(1)1x y -++≤故22221()DV x y x y dxdy ⎡⎤=---+⎣⎦⎰⎰221(1)(1)Dx y dxdy ⎡⎤=---+⎣⎦⎰⎰ 22221(1)x y x y dxdy +≤=--⎰⎰2120(1)2d d πθρρρπ=-=⎰⎰17.设球体占有闭区域Ω：2222x y z Rz ++≤，它在内部个点处的密度的大小等于该点到坐标原点距离的平方.试求这球体的质心.分析：由于Ω为球体，且被积函数出现222x y z ++项，故可用球面坐标计算，同时注意到区域Ω的对称性. 解：密度222(,,)x y z x y z ρ=++ 此球体的质量(,,)M x y z dv ρΩ=⎰⎰⎰222()x y z dv Ω=++⎰⎰⎰22cos 222sin R d d r r dr ππφθφφ=⋅⎰⎰⎰5555202322sin cos 515R R d πππφφφ=⋅=⎰由对称性易知0x y == 22211(,,)()z x y z dv z xy z dv MMρΩΩ==++⎰⎰⎰⎰⎰⎰而22cos 22222200()sin cos R z x y z dv d d d ππφθφφρρρρρΩ++=⋅⋅⎰⎰⎰⎰⎰⎰666720282sin cos 63R Rd πππφφφ=⋅=⎰∴54z R =即球体的质心：5(0,0,)4R 五、自测题(A)一、 选择题(3分⨯5＝15分)1. 设D 为221x y +≤在第一象限部分，二重积分2Dxy d σ⎰⎰可化为A)112dx xy dy ⎰⎰B) 1200dx dy ⎰C) 1200dx dy ⎰D) 20xy dy2. 设1()Dx y d σI =+⎰⎰,2sin()Dx y d σI =+⎰⎰,3tan()Dx y d σI =+⎰⎰,其中D 为三角形闭区域，三顶点分别为(0,0),(1,0),(0,1),则 A) 123I <I <I B) 213I <I <I C) 231I <I <I D)以上均不正确3. 设空间区域1Ω：2222,0x y z R z ++≤≥2Ω：2222,0,0,0x y z R x y z ++≤≥≥≥ 则 A)124xdv xdv ΩΩ=⎰⎰⎰⎰⎰⎰ B)124ydv ydv ΩΩ=⎰⎰⎰⎰⎰⎰C) 124zdv zdv ΩΩ=⎰⎰⎰⎰⎰⎰ D)124xyzdv xyzdv ΩΩ=⎰⎰⎰⎰⎰⎰4. 设平面薄片位于区域221x y +≤，密度函数为222(2)(2)x y x ρ=++，质心坐标为(,)x y ，则A) 0,0x y == B)0,0x y =≠ C) 0,0x y ≠= D)0,0x y ≠≠5. 设22()Dx y d σ+⎰⎰，D ：由2y x =，1x =，0y =所围，则化为极坐标形式的积分为 A)sec 3400d d πθθρρ⎰⎰B)1340d d πθρρ⎰⎰C) 3400d d πθρ⎰ D)sec 340tan sec d d πθθθθρρ⎰⎰二、 填空题(3分⨯5＝15分) 1.2224x x y d σ≤+≤⎰⎰＝2. 2sin sin 200cos d d πθαθθρθρ+⎰⎰＝3.利用重积分性质估计22(49)Dx y d σI =++⎰⎰，这里D :224x y +≤，那么 I∈ 4.积分222y xdx e dy -⎰⎰的值等于5.设Ω：224,01x y z +≤≤≤，则(sin cos 2)x y z dv Ω+⎰⎰⎰三、(10分) 计算二重积分1()x y x y dxdy +≤+⎰⎰四、 (10分) 改变下列积分次序. 1.220(,)xx dx f x y dy ⎰⎰ 2. ln 10(,)exdx f x y dy ⎰⎰五、 (10分) 证明()()000()()()ayam a x m a x dy e f x dx a x e f x dx --=-⎰⎰⎰六、 (10分) 计算三重积分()x y dv Ω+⎰⎰⎰，其中Ω是由曲面z =与z =所围区域.七、 (10分) 设(,)f x y 连续，且(,)(,)Df x y xy f x y dxdy =+⎰⎰，其中D 是由0y =，2y x =，1x =曲面与所围区域，求(,)f x y .八、 (10分) 求平面1xy z a b c++=被三坐标所割出的有限部分的面积.九、 (10分) 计算2z dv ΩI =⎰⎰⎰，Ω：2222221x y z a b c ++≤.自测题(B)三、 选择题(3分⨯5＝15分) 1. 在下列哪种情况下成立A) (,)(,)f x y f x y -=- B) (,)(,)f x y f x y -= C) (,)(,)f x y f x y --= D) (,)(,)f x y f x y -= 且(,)(,)f x y f x y -=2. 设D 由1x =，0y =，12x y +=，1x y +=，若[]31ln()Dx y dxdy I =+⎰⎰，32()Dx y dxdy I =+⎰⎰，[]33sin()Dx y dxdy I =+⎰⎰，则1I ，2I ，3I 之间的关系为A) 123I <I <I B) 321I <I <I C) 132I <I <I D) 312I <I <I 3.设(,)f x y 为连续函数，则00(,)axdx f x y dy ⎰⎰等于 A) 00(,)aydy f x y dx ⎰⎰ B) 0(,)a ay dy f x y dx ⎰⎰ C) 0(,)aya dy f x y dx ⎰⎰ D) 0(,)aady f x y dx ⎰⎰ 4.设平面区域{}(,),D x y a x a x y a =-≤≤≤≤，{}1(,)0,D x y x a x y a =≤≤≤≤则(cos sin )Dxy x y dxdy +⎰⎰等于A) 12cos sin D x ydxdy ⎰⎰ B) 12D xydxdy ⎰⎰C) 14(cos sin )D xy x y dxdy +⎰⎰ D)05.一物体占有空间区域Ω：2221,0x y z z ++≤≥，密度为(2)(2),x y z +-质心坐标，(,,)x y z 则A)0,0x y >> B) 0,0x y >> C) 0,0x y <> D) 0,0x y << 四、 填空题(3分⨯5＝15分) 1.22222()x y yf x y d σ+≤+⎰⎰的极坐标形式的二次积分为2.设区域D 由双曲线222()2x y xy +=，那么()Dx y d σ+⎰⎰等于3.设D ：222x y a +≤，Dxy dxdy ⎰⎰＝4.空间区域Ω是由平面1x y z ++=及三坐标面所围，将三重积分(,,)f x y z dv Ω⎰⎰⎰化为先对x ，再对y ，最后对z 的三重积分5.曲面1x y z ++=所围立体的体积是 三、(10分)计算221()Dx yf x y dxdy ⎡⎤++⎣⎦⎰⎰，其中D 是由3y x =，1y =，1x =-所围成的区域，()f x 为连续函数.十、 (10分)求椭球2222221x y z a b c++≤的体积十一、15分)将(,,)f x y z dv Ω⎰⎰⎰化为三次积分，其中Ω由22z x y =+，z =所围.十二、10分) 21xxdx ⎰⎰十三、10分) 求由2y ax =及x a = (0)a >所围图形关于直线y a =-的转动惯量. 八、(15分) 求222201lim(,)t x y t f x y d t σπ→+≤⎰⎰，其中(,)f x y 为连续函数.自测题(C)一、选择题(3分⨯5＝15分)1. 设D ：2214x y ≤+≤，则(,)D f x y d σ⎰⎰A)2121(,)(,)dx f x y dy dx f x y dy ---⎰⎰B)120104(,)(,)dx f x y dy dx f x y dy ⎡⎤-⎢⎥⎣⎦⎰⎰C) 2201(cos ,sin )d f d πθρθρθρρ⎰⎰D) 2012(cos ,sin )d f d πθρθρθρρ⎰⎰ 2. 设1Dx y dxdy I =+⎰⎰，22aDx y dxdy I =+⎰⎰ (0)a >，其中D ：1x y +≤，那么A) 120I -I > B) 120I -I <C) 120I -I = D) 12I -I 的符号与a 的取值有关3.设Ω：2222x y z R ++≤，2221()x y z dv ΩI =++⎰⎰⎰，则A) 543R πI = B)223()2x y dv ΩI =+⎰⎰⎰C) 223()2y z dv ΩI >+⎰⎰⎰ D) 223()2z x dv ΩI <+⎰⎰⎰ 4.设k D ：22()()2,1,2,3x k y k k -+-≤=，记2(3)kk D x y d σI =+-⎰⎰，则有A)123I =I ≠I B) 321I =I ≠I C) 132I =I ≠I D)以上都不正确5.设设Ω：2222x y z z ++≤，12z ≥，则f dxdydz Ω⎰⎰⎰A)123002()sin d f d ππφρρφρ⎰⎰ B)2cos 23002()sin d f d πφπφρρφρ⎰⎰C)111022dr f rdz π⎰⎰D)21022dz f rdr π⎰五、 填空题(3分⨯5＝15分)1.将柱面坐标三次积分42000(,,)dz d f z d πθρθρ⎰⎰化为先对z 后对ρ，θ的三次积分2.不等式22041z x y ≤≤+≤所表示的图形的体积为3.设Ω为2222x y z x ++≤则222()f x y z dv Ω++⎰⎰⎰在球面坐标下的三次积分为在柱面坐标下的三次积分为4.一旋转抛物面状容器装满水，再将水倒掉34，问容器内水面下降了 ％三、(15分)将二次积分变换积分次序 2210(,)x dx f x y dy I =⎰⎰六、 (15分)计算三次积分1000sin 1x yzdx dy dz z-⎰⎰⎰ 七、 (15分)用二重积分证明：平面曲线()0y f x =>，(0)a x b ≤≤≤绕x轴和y 轴旋转一圈所得的旋转曲面的面积分别是2(bx a S f x π=⎰和2by a S π=⎰ 八、 (15分)求曲面z =与222x z z +=所围立体的体积 九、 (10分)若(,)f x y 为区域D 上的连续函数，D 关于y 轴对称，且1D 为D 位于y 轴右侧的子区域，证明 0(,)(,)2(,)(,)DDf x y x f x y d f x y d f x y x σσ⎧⎪=⎨⎪⎩⎰⎰⎰⎰为的奇函数为的偶函数重积分自测题答案自测题(A)一、1.C 2.B 3.C 4.B 5.D二、1.3π 2.0 3.]ρπ[36，100 4. 41(1)2e -- 5.4π 三、43四、1)2420222(,)(,)yy y dy f x y dx dy f x y dx +⎰⎰⎰⎰2) 1(,)y eedy f x y dx ⎰⎰六、8π 七、18xy +九、3415abc π自测题(B)一、1.D 2.C 3.B 4.A 5.B 二、1.2sin 200()d f d πθθρρρ⎰⎰2.03.42a 4.111000(,,)z y zdz dy f x y z dx ---⎰⎰⎰5.43三、25- 四、43abc π五、7()36π-1 七、485a 八、(0,0)f自测题(C)一、1.C 2.A 3.B 4.A 5.D 二、1.222400(,,)d d f z dz πρθρρθ⎰⎰⎰2.8π3.2sin cos 2200sin ()d d f r r dr ππφθπθφφ-⎰⎰⎰2cos 220()d d f z dz πθπθρρρ-+⎰⎰4.50三、142001(,)(,)dy f x y dx dy f x y dx -⎰⎰四、1(1sin1)2-七、提示：将(,)Df x y d σ⎰⎰表示为在1D 上的二重积分.。

高考数学知识点精讲重积分与曲线积分的计算高考数学知识点精讲：重积分与曲线积分的计算在高考数学中，重积分与曲线积分是较为复杂但又十分重要的知识点。

理解和掌握它们的计算方法，对于解决许多数学问题以及在后续的高等数学学习中都具有关键意义。

一、重积分重积分包括二重积分和三重积分。

1、二重积分二重积分的几何意义是计算以给定的二元函数为曲顶的曲顶柱体的体积。

其计算的基本思想是将区域分割成小的矩形，然后对每个小矩形上的函数值进行近似求和，当分割越来越细时，这个和就趋近于二重积分的值。

在直角坐标系下，计算二重积分通常有两种积分顺序：先对 x 积分再对 y 积分，或者先对 y 积分再对 x 积分。

选择合适的积分顺序往往能简化计算。

例如，对于函数＼（f(x,y)＼）在区域＼（D\）上的二重积分，若＼（D\）可以表示为＼（a\leq x\leq b\），＼（＼varphi_1(x)＼leqy\leq ＼varphi_2(x)＼），则先对＼（y\）积分，化为累次积分：＼＼iint_D f(x,y)dxdy ＝＼int_a^b\！＼！＼left\int_{＼varphi_1(x)｝＾｛＼varphi_2(x)｝ f(x,y)dy\rightdx＼若＼（D\）可以表示为＼（c\leq y\leq d\），＼（＼psi_1(y)＼leq x\leq ＼psi_2(y)＼），则先对＼（x\）积分，化为累次积分：＼＼iint_D f(x,y)dxdy ＝＼int_c^d\！＼！＼left\int_{＼psi_1(y)｝＾｛＼psi_2(y)｝ f(x,y)dx\rightdy＼在极坐标系下，若＼（f(x,y) ＝ f(＼rho\cos\theta, ＼rho\sin\theta)＼），区域＼（D\）由极坐标方程表示，则二重积分可以化为：＼＼iint_D f(x,y)dxdy ＝＼int_{＼alpha}＾｛＼beta}＼！＼！＼int_{r_1(＼theta)｝＾｛r_2(＼theta)｝ f(＼rho\cos\theta, ＼rho\sin\theta)＼rho d\rho d\theta＼2、三重积分三重积分的几何意义是计算空间立体的质量。

第9章 重积分典型例题一、二重积分的概念、性质 1、二重积分的概念：d 01(,)lim(,)niiii Df x y f λσξησ→==∆∑⎰⎰其中：D ：平面有界闭区域，λ：D 中最大的小区域的直径（直径：小区域上任意两点间距离的最大值者），i σ∆：D 中第i 个小区域的面积2、几何意义：当(,)0f x y ≥时，d (,)Df x y σ⎰⎰表示以曲面(,)z f x y =为曲顶，D 为底的曲顶柱体的体积。

所以d 1Dσ⎰⎰表示区域D 的面积。

3、性质（与定积分类似）：:线性性、对积分区域的可加性、比较性质、估值性质、二重积分中值定理二、二重积分的计算1、在直角坐标系下计算二重积分（1） 若D 为X 型积分区域：12,()()a x b y x y y x ≤≤≤≤，则21()()(,)(,)by x ay x Df x y dxdy dx f x y dy =⎰⎰⎰⎰（2）若D 为Y 型积分区域：12,()()c y d x y x x y ≤≤≤≤，则21()()(,)(,)dx y cx yf x y dxdy dy f x y dx =⎰⎰（3X －型或者Y －型区域之和，如图，则123(,)(,)(,)(,)D D D f x y d x d y f x y d x d y f x y d x d y f x y d x d=++⎰⎰⎰⎰⎰⎰⎰（4（5）对称性的应用1(,)2(,),(,)0(,)DD f x y dxdy f x y dxdy f x y y D x f x y y ⎧=⎪⎨⎪⎩⎰⎰⎰⎰关于为偶函数区域关于轴对称， 关于为奇函数1(,)2(,),(,)0(,)D D f x y dxdy f x y dxdy f x y x D y f x y x ⎧=⎪⎨⎪⎩⎰⎰⎰⎰关于为偶函数区域关于轴对称， 关于为奇函数（6）积分顺序的合理选择：不仅涉及到计算繁简问题，而且又是能否进行计算的问题。

第12章 重积分内容提要（一）二重积分概念和性质1．二重积分定义：设二元函数),(y x f z =定义在有界闭区域D 上。

将D 任意划分成除公共边界外没有其它公共部分的n 个子区域i σ∆（n i ,,2,1 =），在每个i σ∆中任取一点),(i i ηξ（n i ,,2,1 =），作和式∑=∆ni ii i f 1),(σηξ。

令λ表示各子区域直径的最大值，若极限∑=→∆ni ii i f 10),(lim σηξλ存在，且极限值和区域D 的分割方式以及各子区域中点),(i i ηξ的取法无关，则称函数),(y x f z =在区域D 上可积，并称此极限为),(y x f z =在区域D 上的二重积分，记作⎰⎰Dy x f σd ),(，即∑⎰⎰=→∆ni ii i Df def y x f 1),(lim d ),(σηξσλ其中，),(y x f 称为被积函数，σd ),(y x f 为被积表达式，σd 为面积元素，x 、y 是积分变量，D 是积分区域，并称∑=∆ni ii if 1),(σηξ为积分和式。

2．二重积分的几何意义：设),(y x f z =在区域D 上连续，当0),(≥y x f 时，二重积分⎰⎰Dy x f σd ),(表示以曲面),(y x f z =为顶，底面区域是D 的曲顶柱体的体积。

3．性质 （1）线性性质若),(y x f ，),(y x g 在D 上可积，1k 和2k 为任意常数，则),(),(21y x g k y x f k +在D 上可积，且⎰⎰⎰⎰⎰⎰+=+DDDy x g k y x f k y x g k y x f kσσσd ),(d ),(d )],(),([2121。

（2）积分区域可加性质若21D D D =，且1D 和2D 除边界外没有公共部分，则),(y x f 在D 上可积的充要条件是),(y x f 在1D 和2D 上都可积，且⎰⎰⎰⎰⎰⎰+=21d ),(d ),(d ),(D D Dy x f y x f y x f σσσ。

§9. 4 重积分的应用 元素法的推广:有许多求总量的问题可以用定积分的元素法来处理. 这种元素法也可推广到二重积分的应用中. 如果所要计算的某个量U 对于闭区域D 具有可加性(就是说, 当闭区域D 分成许多小闭区域时, 所求量U 相应地分成许多部分量, 且U 等于部分量之和), 并且在闭区域D 内任取一个直径很小的闭区域d σ时, 相应的部分量可近似地表示为f (x , y )d σ 的形式, 其中(x , y )在d σ内, 则称f (x , y )d σ 为所求量U 的元素, 记为dU , 以它为被积表达式, 在闭区域D 上积分: ⎰⎰=Dd y x f U σ),(,这就是所求量的积分表达式. 一、曲面的面积设曲面S 由方程 z =f (x , y )给出, D 为曲面S 在xOy 面上的投影区域, 函数f (x , y )在D 上具有连续偏导数f x (x , y )和f y (x , y ). 现求曲面的面积A .在区域D 内任取一点P (x , y ), 并在区域D 内取一包含点P (x , y )的小闭区域d σ, 其面积也记为d σ. 在曲面S 上点M (x , y , f (x , y ))处做曲面S 的切平面T , 再做以小区域d σ的边界曲线为准线、母线平行于z 轴的柱面. 将含于柱面内的小块切平面的面积作为含于柱面内的小块曲面面积的近似值, 记为dA . 又设切平面T 的法向量与z 轴所成的角为γ , 则σγσd y x f y x f d dA yx ),(),(1cos 22++==, 这就是曲面S 的面积元素. 于是曲面S 的面积为σd y x f y x f A y x D),(),(122++=⎰⎰,或 d x d y yz x z A D22)()(1∂∂+∂∂+=⎰⎰.设dA 为曲面S 上点M 处的面积元素, dA 在xOy 面上的投影为小闭区域d σ, M 在xOy 面上的投影为点P (x , y ), 因为曲面上点M 处的法向量为n =(-f x , -f y , 1), 所以 σσd y x f y x f d dA y x ),(),(1||22++==n . 提示: dA 与xOy 面的夹角为(n ,^ k ), dA cos(n ,^ k )=d σ,n ⋅k =|n |cos(n ,^ k )=1, cos(n ,^ k )=|n |-1.讨论: 若曲面方程为x =g (y , z )或y =h (z , x ), 则曲面的面积如何求？d y d z zx y x A yzD⎰⎰∂∂+∂∂+=22)()(1,或 d z d x xy z y A zxD ⎰⎰∂∂+∂∂+=22)()(1. 其中D yz 是曲面在yOz 面上的投影区域, D zx 是曲面在zOx 面上的投影区域. 例1 求半径为R 的球的表面积.解 上半球面方程为222y x R z --=, x 2+y 2≤R 2.因为z 对x 和对y 的偏导数在D : x 2+y 2≤R 2上无界, 所以上半球面面积不能直接求出. 因此先求在区域D 1: x 2+y 2≤a 2 (a <R )上的部分球面面积, 然后取极限.d x d y y x R R a y x 222222--⎰⎰≤+⎰⎰-=πθ20022a r R r d r d R )(222a R R R --=π.于是上半球面面积为2222)(2lim R a R R R Ra ππ=--→.整个球面面积为 A =2A 1=4πR 2. 提示:222y x R x x z ---=∂∂, 222y x R y y z ---=∂∂, 22222)()(1y x R R y z x z --=∂∂+∂∂+. 解 球面的面积A 为上半球面面积的两倍. 上半球面的方程为222y x R z --=, 而222y x R x x z ---=∂∂, 222y x R y y z ---=∂∂,所以 22)()(12222yz x z A R y x ∂∂+∂∂+=⎰⎰≤+d x d y yx R R R y x 2222222--=⎰⎰≤+⎰⎰-=πρρρθ200222R R d d R 20224 4R R R R πρπ=--=.例2设有一颗地球同步轨道通讯卫星, 距地面的高度为h =36000km , 运行的角速度与地球自转的角速度相同. 试计算该通讯卫星的覆盖面积与地球表面积的比值(地球半径R =6400km).解 取地心为坐标原点, 地心到通讯卫星中心的连线为z 轴, 建立坐标系. 通讯卫星覆盖的曲面∑是上半球面被半顶角为α的圆锥面所截得的部分. ∑的方程为222y x R z --=, x 2+y 2≤R 2sin 2α. 于是通讯卫星的覆盖面积为⎰⎰⎰⎰--=∂∂+∂∂+=xy xy D D dxdy yx R R dxdy yz x z A 22222)()(1. 其中D xy ={(x , y )| x 2+y 2≤R 2sin 2α}是曲面∑在xOy 面上的投影区域. 利用极坐标, 得 )c o s 1(222s i n 022s i n 02220απρρρπρρρθααπ-=-=-=⎰⎰⎰R d R R d R R d A R R .由于hR R +=αcos , 代入上式得hR h R h R R R A +=+-=222)1(2ππ.由此得这颗通讯卫星的覆盖面积与地球表面积之比为%5.4210)4.636(21036)(24662≈⋅+⋅=+=h R h R A π. 由以上结果可知, 卫星覆盖了全球三分之一以上的面积, 故使用三颗相隔π32角度的通讯卫星就可以覆盖几乎地球全部表面. 二、质心设有一平面薄片, 占有xOy 面上的闭区域D , 在点P (x , y )处的面密度为ρ(x , y ), 假定μ(x , y )在D 上连续. 现在要求该薄片的质心坐标.在闭区域D 上任取一点P (x , y ), 及包含点P (x , y )的一直径很小的闭区域d σ(其面积也记为d σ), 则平面薄片对x 轴和对y 轴的力矩(仅考虑大小)元素分别为 dM x =y μ(x , y )d σ, dM y =x μ(x , y )d σ. 平面薄片对x 轴和对y 轴的力矩分别为 ⎰⎰=Dx d y x y M σμ),(, ⎰⎰=Dy d y x x M σμ),(.设平面薄片的质心坐标为) ,(y x , 平面薄片的质量为M , 则有 y M M x =⋅, x M M y =⋅ . 于是⎰⎰⎰⎰==DDyd y x d y x x MM x σμσμ),(),(, ⎰⎰⎰⎰==DDxd y x d y x y MM y σμσμ),(),(.在闭区域D 上任取包含点P (x , y )小的闭区域d σ(其面积也记为d σ), 则 平面薄片对x 轴和对y 轴的力矩元素分别为 dM x =y μ(x , y )d σ, dM y =x μ(x , y )d σ. 平面薄片对x 轴和对y 轴的力矩分别为 ⎰⎰=Dx d y x y M σμ),(, ⎰⎰=Dy d y x x M σμ),(.设平面薄片的质心坐标为) ,(y x , 平面薄片的质量为M , 则有 y M M x =⋅, x M M y =⋅ . 于是 ⎰⎰⎰⎰==DDyd y x d y x x MM x σμσμ),(),(, ⎰⎰⎰⎰==DDxd y x d y x y MM y σμσμ),(),(.提示: 将P (x , y )点处的面积元素d σ看成是包含点P 的直径得小的闭区域. D 上任取一点P (x , y ), 及包含的一直径很小的闭区域d σ(其面积也记为d σ), 则平面薄片对x 轴和对y 轴的力矩(仅考虑大小)元素分别为讨论: 如果平面薄片是均匀的, 即面密度是常数, 则平面薄片的质心(称为形心)如何求？求平面图形的形心公式为 ⎰⎰⎰⎰=DDd xd x σσ, ⎰⎰⎰⎰=DDd yd y σσ.例3 求位于两圆ρ=2sin θ 和ρ=4sin θ 之间的均匀薄片的质心.解 因为闭区域D 对称于y 轴, 所以质心) ,(y x C 必位于y 轴上, 于是0=x . 因为 ⎰⎰⎰⎰=DDd d yd θρθρσsin 2πρρθθθθπ7sin sin 4sin 220==⎰⎰d d ,πππσ31222=⋅-⋅=⎰⎰d D,所以3737===⎰⎰⎰⎰ππσσDD d yd y . 所求形心是)37 ,0(C .类似地, 占有空间闭区域Ω、在点(x , y , z )处的密度为ρ(x , y , z )(假宽ρ(x , y , z )在Ω上连续)的物体的质心坐标是 ⎰⎰⎰Ω=dv z y x x Mx ),,(1ρ, ⎰⎰⎰Ω=dv z y x y M y ),,(1ρ, ⎰⎰⎰Ω=dv z y x z M z ),,(1ρ,其中⎰⎰⎰Ω=dv z y x M ),,(ρ.例4 求均匀半球体的质心.解 取半球体的对称轴为z 轴, 原点取在球心上, 又设球半径为a , 则半球体所占空间闭区可表示为Ω={(x , y , z )| x 2+y 2+z 2≤a 2, z ≥0}显然, 质心在z 轴上, 故0==y x . ⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰ΩΩΩΩ==dv zdv dv dv z z ρρ83a =.故质心为)83 ,0 ,0(a .提示: Ω: 0≤r ≤a , 20πϕ≤≤, 0≤θ≤2π.⎰⎰⎰⎰⎰⎰=Ωa dr r d d dv 022020sin ϕθϕππ⎰⎰⎰=adr r d d 022020sin ππθϕϕ323a π=,⎰⎰⎰⎰⎰⎰⋅=Ωadr r r d d dv z 022020sin cos ϕϕθϕππ⎰⎰⎰=a dr r d d 0320202sin 21ππθϕϕ42214a ⋅⋅=π.三、转动惯量设有一平面薄片, 占有xOy 面上的闭区域D , 在点P (x , y )处的面密度为μ(x , y ), 假定ρ(x , y )在D 上连续. 现在要求该薄片对于x 轴的转动惯量和y 轴的转动惯量. 在闭区域D 上任取一点P (x , y ), 及包含点P (x , y )的一直径很小的闭区域d σ(其面积也记为d σ), 则平面薄片对于x 轴的转动惯量和y 轴的转动惯量的元素分别为 dI x =y 2μ(x , y )d σ , dI y =x 2μ(x , y )d σ .整片平面薄片对于x 轴的转动惯量和y 轴的转动惯量分别为σμd y x y I Dx ),(2⎰⎰=, σμd y x x I Dy ),(2⎰⎰=.例5 求半径为a 的均匀半圆薄片(面密度为常量μ)对于其直径边的转动惯量. 解 取坐标系如图, 则薄片所占闭区域D 可表示为 D ={(x , y )| x 2+y 2≤a 2, y ≥0}而所求转动惯量即半圆薄片对于x 轴的转动惯量I x , ⎰⎰⎰⎰⋅==DDx d d d y I θρρθρμσμ222sin⎰⎰⎰⋅==ππθθμρρθθμ024032s i n 4 s i n d a d d a2441241Ma a =⋅=πμ,其中μπ221a M =为半圆薄片的质量.类似地, 占有空间有界闭区域Ω、在点(x , y , z )处的密度为ρ(x , y , z )的物体对于x 、y 、z 轴的转动惯量为⎰⎰⎰Ω+=dv z y x z y I x ),,()(22ρ,⎰⎰⎰Ω+=dv z y x x z I y ),,()(22ρ,⎰⎰⎰Ω+=dv z y x y x I z ),,()(22ρ.例6 求密度为ρ的均匀球体对于过球心的一条轴l 的转动惯量.解 取球心为坐标原点, z 轴与轴l 重合, 又设球的半径为a , 则球体所占空间闭区域Ω={(x , y , z )| x 2+y 2+z 2≤a 2}.所求转动惯量即球体对于z 轴的转动惯量I z . ⎰⎰⎰Ω+=dv y x I z )(22ρθϕϕθϕθϕρd d r d r r r s i n )s i n s i n c o s s i n(2222222+=⎰⎰⎰Ωθϕϕρd d r d r 34s i n⎰⎰⎰Ω=dr r d d a ⎰⎰⎰=ππϕϕθρ200043 sin ρπ5158a =M a 252=, 其中ρπ334a M =为球体的质量.提示: x 2+y 2=r 2sin 2ϕcos 2θ+r 2sin 2ϕ sin 2θ=r 2sin 2ϕ.四、引力我们讨论空间一物体对于物体外一点P 0(x 0, y 0, z 0)处的单位质量的质点的引力问题.设物体占有空间有界闭区域Ω, 它在点(x , y , z )处的密度为ρ(x , y , z ), 并假定ρ(x , y , z )在Ω上连续.在物体内任取一点(x , y , z )及包含该点的一直径很小的闭区域dv (其体积也记为dv ). 把这一小块物体的质量ρdv 近似地看作集中在点(x , y , z )处. 这一小块物体对位于P 0(x 0, y 0, z 0)处的单位质量的质点的引力近似地为 ),,(z y x dF dF dF d =F )))(,,(,))(,,(,))(,,((303030dv r z z z y x Gdv r y y z y x Gdv r x x z y x G---=ρρρ,其中d F x 、dF y 、dF z 为引力元素d F 在三个坐标轴上的分量, 202020)()()(z z y y x x r -+-+-=, G 为引力常数. 将d F x 、dF y 、dF z 在Ω上分别积分, 即可得F x 、F y 、F z , 从而得F =(F x 、F y 、F z ).例7设半径为R 的匀质球占有空间闭区域Ω={(x , y , z )|x 2+y 2+z 2≤R 2). 求它对于位于点M 0(0, 0, a ) (a >R )处的单位质量的质点的引力.解 设球的密度为ρ0, 由球体的对称性及质量分布的均匀性知F x =F y =0, 所求引力沿z 轴的分量为 dv a z y x a z G F z 2/32220])([-++-=⎰⎰⎰Ωρ ⎰⎰⎰--≤+-++-=R R z R y x a z y x dxdydza z G 22220])([)(ρ ⎰⎰⎰---+-=2202/322200])([)(z R RRa z d d dz a z G ρρρθρπ⎰-+----=R R dz aaz R z a a z G )211)((2220ρπ ]2)(12[2220⎰-+--+-=RRa az R d a z a R G ρπ)3222(2230aR R R G -+-=πρ2203134a M G a R G -=⋅⋅-=ρπ, 其中0334ρπR M =为球的质量. 上述结果表明: 匀质球对球外一质点的引力如同球的质量集中于球心时两质点间的引力.。

第九章 重积分 §1、二重积分的概念一．重积分的概念1．引例与定义 ⑴曲顶柱体的体积问题设函数(,)z f x y =，当(,)x y D ∈时，(,)0f x y ≥，且(,)f x y 在D 上连续。

由曲面(,)z f x y =、xoy 平面的区域D 、母线平行于z 轴的柱面所围成的空间区域称为曲顶柱体，或称为以曲面(,)z f x y =为顶，以平面区域D 为底，母线平行于z 轴的曲顶柱体。

已知：平顶柱体的体积=底面积ⅹ高 ①分割：用平面曲线网将区域D 分割为 1σ∆，2σ∆，...，i σ∆，...，n σ∆ 相应地将曲顶柱体分割为n 个小的曲顶柱体：1V ∆，2V ∆，... ，i V ∆，...，n V ∆其中i V ∆表示第i 个小曲顶柱体、也表示该柱体的体积，则：1ni i V V ==∆∑；②求V 的近似值：(,)i i i ξησ∀∈∆，(,)i i i i V f ξησ∆≈∆（1,2,,i n =L ）；故1ni i V V ==∆∑1(,)ni i i i f ξησ=≈∆∑③求V 的精确值：记max λ={所有i σ∆的直径}，则，01lim (,)ni i i i V f λξησ→==∆∑；⑵平面薄板的质量问题设平面薄板占有xoy 平面上的区域D ，密度函数为(,)x y ρρ=，当(,)x y D ∈时，(,)0x y ρ>且在D 上连续。

同理可得，质量计算公式：01lim (,)ni i i i m λρξησ→==∆∑；定义1、设函数(,)f x y 是有界闭域D 上的有界函数。

将D 任意分割成n 个小的区域：1σ∆、2σ∆、...、n σ∆，（i σ∆既表示第i 个小区域也表示小区域的面积）；任取(,)i i i ξησ∈∆，1,2,i n =L ，作和：1(,)niiii f ξησ=∆∑；记max λ={i σ∆的直径}，若极限,)x y i(,i ξ(,)i i f ξη=iσ(,i ξη1lim (,)ni i i i f λξησ→=∆∑存在，称极限值为函数(,)f x y 在区域D 上的二重积分，记作：1lim (,)ni i i i f λξησ→=∆∑(,)Df x y d σ=⎰⎰其中(,)f x y ~~被积函数，D ~~积分区域，d σ~~面积微元，,x y ~~积分变量，(,)f x y d σ~~被积表达式，1(,)ni i i i f ξησ=∆∑积分和。