m序列

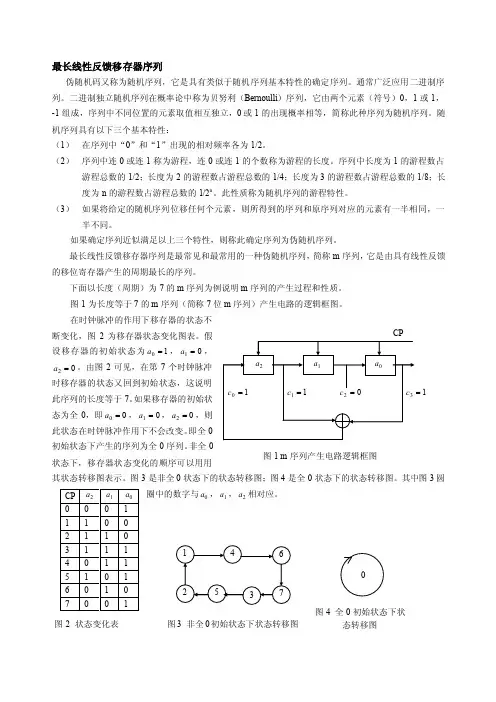
图4 全0初始状态下状态转移图 最长线性反馈移存器序列伪随机码又称为随机序列，它是具有类似于随机序列基本特性的确定序列。

通常广泛应用二进制序列。

二进制独立随机序列在概率论中称为贝努利（Bernoulli ）序列，它由两个元素（符号）0，1或1，-1组成，序列中不同位置的元素取值相互独立，0或1的出现概率相等，简称此种序列为随机序列。

随机序列具有以下三个基本特性：（1） 在序列中“0”和“1”出现的相对频率各为1/2。

（2） 序列中连0或连1称为游程，连0或连1的个数称为游程的长度。

序列中长度为1的游程数占游程总数的1/2；长度为2的游程数占游程总数的1/4；长度为3的游程数占游程总数的1/8；长度为n 的游程数占游程总数的1/2n 。

此性质称为随机序列的游程特性。

（3） 如果将给定的随机序列位移任何个元素，则所得到的序列和原序列对应的元素有一半相同，一半不同。

如果确定序列近似满足以上三个特性，则称此确定序列为伪随机序列。

最长线性反馈移存器序列是最常见和最常用的一种伪随机序列，简称m 序列，它是由具有线性反馈的移位寄存器产生的周期最长的序列。

下面以长度（周期）为7的m 序列为例说明m 序列的产生过程和性质。

图1为长度等于7的m 序列（简称7位m 序列）产生电路的逻辑框图。

在时钟脉冲的作用下移存器的状态不断变化，图2为移存器状态变化图表。

假设移存器的初始状态为10=a ，01=a ，02=a 。

由图2可见，在第7个时钟脉冲时移存器的状态又回到初始状态，这说明此序列的长度等于7。

如果移存器的初始状态为全0，即00=a ，01=a ，02=a ，则此状态在时钟脉冲作用下不会改变。

即全0初始状态下产生的序列为全0序列。

非全0状态下，移存器状态变化的顺序可以用用其状态转移图表示。

图3是非全0状态下的状态转移图；图4是全0状态下的状态转移图。

其中图3圆圈中的数字与0a ，1a ，2a 相对应。

图2 状态变化表 图3 非全0初始状态下状态转移图1=CP图1 m 序列产生电路逻辑框图CP上述7位吗m 序列产生器由三级移位寄存器组成，每一级移位寄存器有两个可能状态（0，1），三级移位寄存器的所有可能状态为23=8种：000，001，010，011，100，101，110，111，其中全0状态不能进入m 序列产生器的移存器，否则将出现全0序列。

M序列原理及代码1、m序列1.1概述1.1.1实验原理（1）m序列概念和⽤途①概念：m序列是由n级线性移位寄存器产⽣的周期为P=2^n-1的码序列，是最长线性移位寄存器序列的简称。

②⽤途：码分多址系统主要采⽤两种长度的m序列：⼀种是周期为P=2^15-1的m 序列，⼜称为短PN序列；另⼀种是周期为P=2^42-1的m序列，⼜称为长PN 序列。

（2）m序列的产⽣①4级m序列的码序列发⽣器假设初始状态为0001，在时钟作⽤下，产⽣的m序列的状态表。

4级m序列的周期P=24-1=15，相应的输出序列为：100010011010111。

②线性移位反馈移位寄存器反馈系数Ci③m序列特性均衡性：在⼀个周期中，m序列中“1”的个数⽐“0”的个数多1个。

游程特性：长度为k的游程数占游程总数的1/2^k移位相加特性：⼀个m序列与其循环移位逐位⽐较，相同码的位数与不同码的位数相差1位。

⾃相关特性：表征⼀个信号与延迟后⾃⾝信号的相似性。

④m序列的构造——反馈线性反馈移存器1.1.2实验意义m序列是⽬前⼴泛应⽤的⼀种伪随机序列，在所有的伪随机序列中，m序列是最重要、最基本的⼀种伪随机序列。

它容易产⽣，规律性强，有很好的⾃相关性和较好的互相关特性。

m序列的⽣成是接下来的实验的基础,具有指导性的意义。

1.1.3系统的主要功能设计本原多项式系数为13、23、103、203的m序列。

1.1.4使⽤⽅法输⼊m后，输出相应的m序列。

1.2程序设计1.2.1设计思想由m序列的产⽣过程，即通过带反馈的移位寄存器产⽣，容易想到EDA中的结构化的程序设计思想，即以DFF触发器作为底层⽂件，进⾏顶层⽂件设计，获得m序列。

此设计的优点是程序思路简单，结构清晰，只要做出⼀种反馈系数的m序列，容易得到其他反馈系数的m序列；但也存在缺点，那就是结构化的设计使得代码写的过长。

1.2.2软件设计流程及描述（1）流程图（2）描述clk上升沿触发程序，⽤case语句选择m为13,23,103,203中的哪种情况。

m序列的频谱摘要：一、M序列的概述二、M序列的频谱分析三、M序列的应用领域四、M序列的优缺点五、总结正文：一、M序列的概述M序列，又称为M-序列，是一种伪随机序列，具有周期性、非周期性和混沌特性。

它是由美国数学家克劳德·香农（Claude Shannon）在1948年提出的，主要用于数字通信系统和信号处理领域。

M序列具有良好的自相关性和互相关性，因此在通信系统中起到了重要作用。

二、M序列的频谱分析M序列的频谱分析主要包括功率谱密度（PSD）和傅里叶变换。

功率谱密度用于衡量M序列在频域上的能量分布，可以发现M序列具有较低的谱泄漏，从而降低干扰。

傅里叶变换则将时域信号转换为频域信号，便于分析M序列的频率特性。

三、M序列的应用领域1.通信领域：M序列在数字通信系统中作为扩频序列，可以提高通信系统的抗干扰性能。

2.密码学：M序列可以作为加密算法中的基本元素，提高密码系统的安全性。

3.信号处理：在信号处理领域，M序列可以作为信号调制和滤波器设计的基础。

4.控制工程：M序列在控制工程中可以用于模型验证和系统辨识。

5.生物学：M序列在生物信息学领域中具有潜在的应用价值，例如在基因序列比对和蛋白质结构预测中。

四、M序列的优缺点优点：1.良好的自相关性和互相关性。

2.较低的谱泄漏，抗干扰能力强。

3.周期性和非周期性特性，适用于多种应用场景。

缺点：1.序列长度较长，计算复杂度高。

2.与其他伪随机序列相比，线性复杂度较低。

五、总结M序列作为一种重要的伪随机序列，在通信、密码学、信号处理等领域具有广泛的应用。

通过对M序列的频谱分析，可以更好地了解其在频域上的特性，为实际应用提供理论依据。

m序列基本概念：M序列（即De Bruijn序列）又叫做伪随机序列、伪噪声(PN)码或伪随机码。

可以预先确定并且可以重复实现的序列称为确定序列；既不能预先确定又不能重复实现的序列称随机序列；不能预先确定但可以重复产生的序列称伪随机序列。

具体解释于一个n级反馈移位寄存器来说，最多可以有2^n 个状态，对于一个线性反馈移位寄存器来说，全“0”状态不会转入其他状态，所以线性移位寄存器的序列的最长周期为2^n-1。

当n级线性移位寄存器产生的序列{ai}的周期为T= 2^n-1时，称{ai}为n级m序列。

当反馈函数f（a1,a2,a3,…an）为非线性函数时，便构成非线性移位寄存器，其输出序列为非线性序列。

输出序列的周期最大可达2^n ，并称周期达到最大值的非线性移位寄存器序列为1.m序列的产生原理和结构m序列是n 级二进制线性反馈移位寄存器除去输出为0的状态外，产生的周期为2 n -1 的最大可能长度序列，又称为最大长度线性反馈移位序列。

其产生的原理如图1所示。

PN序列发生器由n级移位寄存器，模二加法器和反馈线三个部分组成。

图中，c i ( i =1…n ) 为反馈系数，若c i =1,表示有连接，有反馈，若c i =0则表示断开，无反馈。

c i 的取值决定了移位寄存器的反馈连接和序列的结构，故是一个很重要的参量。

2.m序列的基本性质(1) 移位相加特性。

一个m序列与其任意次延迟移位后产生的另一个不同序列模2相加，得到的仍是该m 序列的延迟移位序列。

如，0100111向右移1次产生另一个序列1010011 ，模2相加后的序列为1110100 ，相当于原序列右移3次后得到的序列。

(2) 平衡特性。

在m序列的每个2n－1周期中，"1"码元出现的数目为次，"0"码元出现的数目为2n －1－1 次，即"0"的个数总是比"1"的个数少一个，这表明，序列平均值很小。

m序列的原理及应用1. 什么是m序列？m序列，全名为最大长度线性反馈移位寄存器序列（Maximum Length Sequence），是一种特殊的二进制序列。

m序列的特点是具有最长的周期，并且波形均匀随机分布。

m序列可以通过一个线性反馈移位寄存器（LFSR）来生成。

2. m序列的生成原理m序列的生成原理基于线性反馈移位寄存器（LFSR）的运算。

LFSR是一种用于产生伪随机序列的硬件电路。

LFSR由寄存器和反馈函数组成。

寄存器是一组存储数据的单元，通常是一组触发器，每个触发器存储一个二进制位。

反馈函数根据寄存器的当前状态产生下一个状态。

反馈函数一般采用异或操作。

m序列的生成就是通过不断移位和反馈计算，使得LFSR的状态变化遍历所有可能的状态，从而生成了m序列。

3. m序列的应用m序列由于其随机性和均匀性，被广泛应用于通信、加密、导航等领域。

3.1 通信领域在通信领域中，m序列被用作伪随机序列发生器。

伪随机序列在信号传输、数据调制等方面起到关键作用。

m序列具有具有良好的互相关性和自相关性性质，能够提供伪随机的编码和解码功能。

3.2 加密领域m序列在加密领域中作为密钥序列广泛使用。

由于m序列的随机性和不可预测性，能有效地保护数据的安全性。

一种常见的应用是m序列与明文进行异或运算，生成密文，从而实现加密功能。

3.3 导航领域在导航领域中，m序列被用于全球卫星导航系统（GNSS）中的扩频码。

扩频码是通过将原始导航信号与m序列进行乘法运算而生成的。

m序列的均匀随机性使得扩频码具有良好的抗多径和抗干扰性能。

4. m序列的特点4.1 最长周期m序列具有最长的周期，周期长度为2^N-1，其中N为LFSR的位数。

这意味着m序列可以生成非常长的伪随机序列。

4.2 均匀随机性m序列的波形均匀分布，具有良好的随机性。

这个特性使得m序列在各个应用领域都能发挥重要作用。

4.3 线性可预测性m序列是由线性反馈移位寄存器生成的，其生成过程可以被完全预测。

m 序列互相关m序列是数字信号处理中常用的一种序列，也称为最大线性互相关序列。

它是一种具有良好互相关性质的二进制序列，主要用于通信系统中的伪随机码生成器、频谱分析以及信道估计等方面。

本文将从m序列的定义、性质和应用等方面进行介绍。

我们来了解一下m序列的定义。

m序列是一种由二进制数字组成的序列，具有2^m-1个元素，其中m为正整数。

m序列的生成是通过对一个初始序列进行递推生成的，每一次生成都基于前一次生成的结果。

具体而言，m序列的递推生成公式为：Sn = Sn-1 ^ Sm，其中^表示位异或运算，Sn表示第n个元素的值，Sm表示初始序列中的第m个元素。

通过这样的递推生成方式，m序列呈现出了良好的互相关性质。

接下来，我们来探讨一下m序列的性质。

首先，m序列具有最大线性互相关性，即任意两个不同的m序列的互相关函数为0，这使得m 序列在通信系统中的伪随机码生成具有很高的安全性和抗干扰性。

此外，m序列的自相关函数在非零偏移位置处为0，这说明m序列具有良好的自相关性质，可以减小码间干扰。

另外，m序列的频谱分布均匀，具有较低的谱峰，这使得m序列在频谱分析中具有较好的性能。

m序列在通信系统中有着广泛的应用。

首先，m序列可以用作伪随机码生成器，用于扩频通信系统中的码分多址技术。

通过与用户数据进行位异或运算，可以将用户数据扩展为具有良好互相关性质的信号，从而实现多用户之间的干扰隔离。

其次，m序列可以用于信道估计。

通过发送已知的m序列，接收端可以通过与接收到的序列进行互相关运算，从而得到信道的冲激响应，进而进行信号的均衡和解调。

此外，m序列还可以用于频谱分析和信号特征提取等方面。

总结起来，m序列是一种具有良好互相关性质的二进制序列，广泛应用于通信系统中的伪随机码生成、频谱分析和信道估计等方面。

通过对m序列的研究和应用，可以提高通信系统的性能和安全性。

在未来的发展中，我们可以进一步探索m序列的特性和应用，以满足不断变化的通信需求。

m序列信号
目录
1.m 序列信号的定义
2.m 序列信号的性质
3.m 序列信号的应用
正文
m 序列信号是一种在数字通信领域中广泛应用的信号类型。

它是由一系列数字构成的序列，这些数字按照一定的规律排列，具有确定的周期性。

m 序列信号有很多种，其中最常见的是 M 进制序列，即 M 个不同符号的序列。

例如，二进制序列（M=2）只有 0 和 1 两个符号，而三进制序列（M=3）则包括 0、1 和 2 三个符号。

m 序列信号具有很多重要的性质，这些性质在数字通信中具有重要的应用价值。

首先，m 序列信号具有较好的相关性和互相关性。

这意味着在接收端，通过一定的处理可以获得较好的信号质量。

其次，m 序列信号具有较低的峰均比。

峰均比是信号处理中的一个重要参数，它描述了信号峰值与均值之间的比值。

较低的峰均比可以提高信号的抗干扰性能，从而提高通信系统的稳定性。

m 序列信号在数字通信中有广泛的应用。

首先，它们可以用作数字调制信号的调制符号。

例如，在 QPSK（四相位偏移键控）调制中，正是利用了四进制序列作为调制符号，从而实现数字信号的调制与传输。

其次，m 序列信号还可以用作信道编码。

信道编码是一种重要的信道保护技术，它可以提高信号在信道中的传输可靠性。

m 序列信号由于其良好的相关性和互相关性，可以作为编码符号，实现高效的信道编码。

总之，m 序列信号作为一种重要的数字信号类型，具有很多优良的性质，并在数字通信领域发挥着重要作用。

m序列初始值
【原创版】
目录
1.M 序列的概述
2.M 序列的初始值
3.M 序列的性质
4.M 序列的应用
正文
1.M 序列的概述
M 序列，又称为 M 序列函数或 M 序列数列，是一种特殊的数列，具有很多独特的性质。

M 序列的研究起源于 20 世纪初，其名字来源于首次提出该概念的数学家 Merton。

M 序列在数学、统计学、信号处理等领域具有广泛的应用，如在信号处理中，M 序列可以用来生成伪随机数。

2.M 序列的初始值
M 序列的初始值通常表示为{a_n}，其中 a_1 是序列的第一个元素，称为初始值。

根据 M 序列的定义，我们可以得到如下递推关系式：a_n = a_{n-1} + r * a_{n-2}
其中，r 是递推常数，通常是一个非线性函数。

通过这个递推关系式，我们可以求解 M 序列的任意一项。

3.M 序列的性质
M 序列具有很多重要的性质，如：
(1) 恒非负性：M 序列的每一项都大于等于零。

(2) 齐次性：M 序列的任意一项都可以表示为其他项的线性组合。

(3) 稳定性：当 r 在特定区间内变化时，M 序列仍然保持其基本性质。

4.M 序列的应用
M 序列在各个领域都有广泛的应用，如：
(1) 在信号处理中，M 序列可以用来生成伪随机数，提高信号的抗干扰性能。

(2) 在通信系统中，M 序列可以用来设计同步码，实现数据的帧同步。

(3) 在密码学中，M 序列可以用来生成密钥，提高加密系统的安全性。

总之，M 序列作为一种特殊的数列，具有很多独特的性质，并在各个领域具有广泛的应用。

M序列什么是M序列？M序列是一种特殊的二进制序列，具有良好的相关性和平衡性。

它在通信系统、密码学和伪随机序列生成器等领域中被广泛应用。

M序列由线性移位寄存器（LSR）和反馈逻辑电路组合而成。

LSR是一种数字逻辑电路，可以实现数据在存储器中的循环移位。

反馈逻辑电路根据存储器中的数据决定输入数据的变化，从而形成M序列。

M序列的特点1.长度固定: M序列的长度是2的幂次方，通常为2^N-1。

例如，长度为7、15、31的M序列在实际应用中较为常见。

2.短周期：因为M序列的长度是有限的，所以它必定会在一定步数之后开始重复。

这使得M序列可以用于周期性信号的产生。

3.高相关性：M序列具有良好的自相关性和互相关性。

自相关性是指序列与其自身的相关性，互相关性是指序列与其他序列的相关性。

M序列在CDMA通信系统中的应用就是基于其高相关性的特点。

4.平衡性：M序列的各个周期内0和1的数量基本相等。

这一特点使得M序列在调制中不会有严重的低频分量和漂移。

M序列的应用1.伪随机序列生成器：M序列可以作为一种伪随机序列的生成器。

例如，可以用M序列生成随机的信道编码序列，用于提高通信系统的帧同步性能。

2.CDMA通信系统：CDMA是一种多用户通信技术，其中各个用户使用不同的码片（即M序列）进行编码。

接收端根据匹配滤波器对接收信号进行处理，从而实现对特定用户的信号的提取。

3.密码学：M序列可以用于加密和解密数据。

通过将明文与M序列进行异或操作，可以生成密文。

密文再与同样的M序列异或，即可还原成原始明文。

4.随机性检测：M序列可以用于随机性检测。

通过比较M序列与随机序列的相关性，可以得出序列的随机程度，从而判断其安全性。

M序列的生成算法M序列的生成算法基于反馈逻辑电路。

具体步骤如下： 1. 设置一个初始状态，初始状态可以是全0或全1。

2. 设定反馈逻辑电路，用来决定存储器中下一个数据的取值。

3. 将存储器中的数据进行移位，将最右边的数据移位到最左边，并根据反馈逻辑电路确定新的最右边的数据。