《理论力学》第十章--动量矩定理试题及答案
- 格式：pdf
- 大小：320.17 KB
- 文档页数：7
下载文档原格式
合集下载
理论力学试题含答案
精选文档理论力学试题及答案一、是非题（每题2分。
正确用√，错误用×，填入括号内。
）1、作用在一个物体上有三个力，当这三个力的作用线汇交于一点时，则此力系必定均衡。
2、力关于一点的矩不因力沿其作用线挪动而改变。
（）3、在自然坐标系中，假如速度υ=常数，则加快度α=0。
（）4、虚位移是偶想的，极细小的位移，它与时间，主动力以及运动的初始条件没关。
5、设一质点的质量为m，其速度与x轴的夹角为α，则其动量在x轴上的投影为mvx=mvcosa。
二、选择题（每题3分。
请将答案的序号填入划线内。
）1、正立方体的顶角上作用着六个大小相等的力，此力系向任一点简化的结果是。
①主矢等于零，主矩不等于零；②主矢不等于零，主矩也不等于零；③主矢不等于零，主矩等于零；④主矢等于零，主矩也等于零。
2、重P的均质圆柱放在V型槽里，考虑摩擦柱上作用一力偶，其矩为 M时（如图），圆柱处于极限均衡状态。
此时按触点处的法向反力N A与N B的关系为。
①N A=NB；②N A>NB；③N A<NB。
3、边长为L的均质正方形平板，位于铅垂平面内并置于圆滑水平面上，如图示，若给平板一细小扰动，使其从图示位置开始倾倒，平板在倾倒过程中，其质心C点的运动轨迹是。
①半径为L/2的圆弧；②抛物线；③椭圆曲线；④铅垂直线。
4、在图示机构中，A//O2B，杆O2C//O3D，且O1A=20cm，O2C=杆O140cm，CM=MD=30cm，若杆AO1以角速度ω=3rad/s匀速转动，则D点的速度的大小为cm/s，M点的加快度的大小为cm/s2。
①60；②120；③150；④360。
.精选文档5、曲柄OA以匀角速度转动，当系统运动到图示地点（OA//O1B。
AB |OA）时，有V A V B，A B，ωAB 0，AB 0。
①等于；②不等于。
三、填空题（每题5分。
请将简要答案填入划线内。
）1、已知A重100kN，B重25kN，A物与地面间摩擦系数为0.2。
理论力学10—动量定理
v A cost vc cos(90 2t )
p 2m1vC m1vC1 m2v A m2v B
B
m2 vB 2m1vC
C
C
C1 m1vC1 O t
m2 v A A
x
v A 2l sin t
vB cos(90 t ) vc cos(90 2t ) B c vB 2l cos t B
10.2
动量定理
F fN C f ( P sin 45 mg cos30 )
从而摩擦力为
0 0 tt 0 tt
动量定理积分形式应用时经常使用投影式：
tt
若作用于质点上的外力主矢恒等于零，则质点的动量守恒， 此即质点的动量守恒定律。 若作用于质点上的外力在某轴上投影的代数和恒等于零，则 质点的动量在该轴上的投影守恒，此即质点对轴的动量守恒 定律。
10.2
动量定理
y
例4 锤的质量m＝3000 kg，从高度h＝1.5 m 处自由下落到受锻压的工件上，工件发生变 形历时τ＝0.01s ；求锤对工件的平均压力。 解：以锤为研究对象，和工件接触后受力如图。 工件反力是变力，在短暂时间迅速变化，用 平均反力N*表示。 锤自由下落时间
d ri vi dt
代入式10—1，注意到质量mi是不变的，则有
d ri d p mi vi mi mi ri dt dt i 1 i 1
令
M mi
n
n
为质点系的总质量
10.1
动量与冲量
m r m r i i i i rC mi M
1 p mvC ml 2
10.1
动量与冲量
vC C
p 2m1vC m1vC1 m2v A m2v B
B
m2 vB 2m1vC
C
C
C1 m1vC1 O t
m2 v A A
x
v A 2l sin t
vB cos(90 t ) vc cos(90 2t ) B c vB 2l cos t B
10.2
动量定理
F fN C f ( P sin 45 mg cos30 )
从而摩擦力为
0 0 tt 0 tt
动量定理积分形式应用时经常使用投影式：
tt
若作用于质点上的外力主矢恒等于零，则质点的动量守恒， 此即质点的动量守恒定律。 若作用于质点上的外力在某轴上投影的代数和恒等于零，则 质点的动量在该轴上的投影守恒，此即质点对轴的动量守恒 定律。
10.2
动量定理
y
例4 锤的质量m＝3000 kg，从高度h＝1.5 m 处自由下落到受锻压的工件上，工件发生变 形历时τ＝0.01s ；求锤对工件的平均压力。 解：以锤为研究对象，和工件接触后受力如图。 工件反力是变力，在短暂时间迅速变化，用 平均反力N*表示。 锤自由下落时间
d ri vi dt
代入式10—1，注意到质量mi是不变的，则有
d ri d p mi vi mi mi ri dt dt i 1 i 1
令
M mi
n
n
为质点系的总质量
10.1
动量与冲量
m r m r i i i i rC mi M
1 p mvC ml 2
10.1
动量与冲量
vC C
动量矩定理
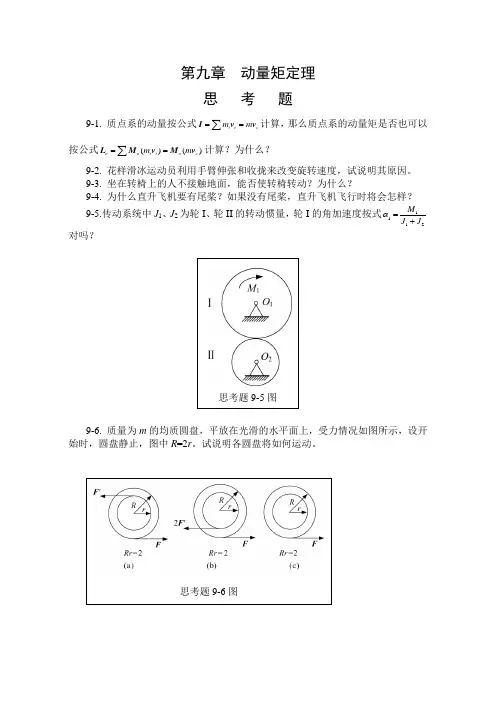
思 考 题9-1. 质点系的动量按公式i i c m m ==∑I v v 计算，那么质点系的动量矩是否也可以按公式()()o o i i o c m m ==∑L M v M v 计算？为什么？9-2. 花样滑冰运动员利用手臂伸张和收拢来改变旋转速度，试说明其原因。
9-3. 坐在转椅上的人不接触地面，能否使转椅转动？为什么？9-4. 为什么直升飞机要有尾桨？如果没有尾桨，直升飞机飞行时将会怎样？ 9-5.传动系统中J 1、J 2为轮I 、轮II 的转动惯量，轮I 的角加速度按式1112M J J α=+对吗？9-6. 质量为m 的均质圆盘，平放在光滑的水平面上，受力情况如图所示，设开始时，圆盘静止，图中R =2r 。
试说明各圆盘将如何运动。
思考题9-6图思考题9-5图习题9-4图习 题9-1 如图所示，已知均质杆的质量为M ，对1z 轴的转动惯量为1J ，求杆对2z 的转动惯量2J 。
9-2 均质直角折杆尺寸如图所示，其质量为3m ，求其对轴O 的转动惯量。
9-3 质量为m 的点在平面Oxy 内运动，其运动方程为：tb y ta x ωω2sin cos ==式中a 、b 和ω为常量。
求质点对原点O 的动量矩。
9-4 如图所示，质量为m 的偏心轮在水平面上作平面运动。
轮子轴心为A ，质心为C ，AC = e ；轮子半径为R ，对轴心A 的转动惯量为J A ；C 、A 、B 三点在同一铅直线上。
（1）当轮子只滚不滑时，若v A 已知，求轮子的动量和对地面上B 点的动量矩。
（2）当轮子又滚又滑时，若v A 、ω已知，求轮子的动量和对地面上B 点的动量矩。
习题9-2图习题9-1图习题9-5图习题9-7图9-5如图所示水平圆板可绕z 轴转动，在圆板上有一质点M 作圆周运动，已知其速度的大小为常量，等于v 0，质点M 的质量为m ，圆的半径为r ，圆心到z 轴的距离为l ，M 点在圆板的位置由ϕ角确定，如图所示。
理论力学第七版第十章 动量定理
第九章 质点动力学的基本方程 课程回顾 1、牛顿三定律适用于惯性参考系
(1) 质点具有惯性，其质量是惯性的度量 质点具有惯性， (2)作用于质点的力与其所产生的加速度成比例 (2)作用于质点的力与其所产生的加速度成比例 (3)作用力与反作用力等值、方向、共线， (3)作用力与反作用力等值、方向、共线，分别 作用力与反作用力等值 作用于两物体上。 作用于两物体上。
§10-1 动量与冲量 10一、冲 量
单位： N·s 1、常力的冲量 常力与作用时间t的乘积 F·t 称为常力的冲量。并用I表 常力与作用时间t 称为常力的冲量。并用I 冲量是矢量，方向与力相同。 示，冲量是矢量，方向与力相同。
I = F⋅ t
2、变力的冲量 若力F是变力， 若力 是变力，可将力的作用时间 t 分成无数的微小时间 是变力 dt，在每个 dt 内，力 F 可视为不变。 可视为不变。 ， 元冲量——力 元冲量——力F在微小时间段 dt 内的冲量称为力F 的元冲量。 内的冲量称为力F 元冲量。 变力 F 在 t1~t2 时间间隔内的冲量为： 时间间隔内的冲量为：
§10-2 动量定理 10二、冲量定理
p2 − p1 = ∑∫ F dt ≡ ∑I
t1
t2
t2
(e)
具体计算时，往往写成投影形式， 具体计算时，往往写成投影形式，即
p2x − p1x = ∑∫ Fx dt ≡ ∑Ix
t1
(e)
p2y − p1y = ∑∫ Fy dt ≡ ∑Iy
t2 t1
(e)
p2z − p1z = ∑∫ F dt ≡ ∑Iz z
I = ∫ Fdt
t1
t2
§10-1 动量与冲量 102、变力的冲量
t
I =∫ F dt
(1) 质点具有惯性，其质量是惯性的度量 质点具有惯性， (2)作用于质点的力与其所产生的加速度成比例 (2)作用于质点的力与其所产生的加速度成比例 (3)作用力与反作用力等值、方向、共线， (3)作用力与反作用力等值、方向、共线，分别 作用力与反作用力等值 作用于两物体上。 作用于两物体上。
§10-1 动量与冲量 10一、冲 量
单位： N·s 1、常力的冲量 常力与作用时间t的乘积 F·t 称为常力的冲量。并用I表 常力与作用时间t 称为常力的冲量。并用I 冲量是矢量，方向与力相同。 示，冲量是矢量，方向与力相同。
I = F⋅ t
2、变力的冲量 若力F是变力， 若力 是变力，可将力的作用时间 t 分成无数的微小时间 是变力 dt，在每个 dt 内，力 F 可视为不变。 可视为不变。 ， 元冲量——力 元冲量——力F在微小时间段 dt 内的冲量称为力F 的元冲量。 内的冲量称为力F 元冲量。 变力 F 在 t1~t2 时间间隔内的冲量为： 时间间隔内的冲量为：
§10-2 动量定理 10二、冲量定理
p2 − p1 = ∑∫ F dt ≡ ∑I
t1
t2
t2
(e)
具体计算时，往往写成投影形式， 具体计算时，往往写成投影形式，即
p2x − p1x = ∑∫ Fx dt ≡ ∑Ix
t1
(e)
p2y − p1y = ∑∫ Fy dt ≡ ∑Iy
t2 t1
(e)
p2z − p1z = ∑∫ F dt ≡ ∑Iz z
I = ∫ Fdt
t1
t2
§10-1 动量与冲量 102、变力的冲量
t
I =∫ F dt
理论力学：动量矩定理
பைடு நூலகம்
y’
2020/12/9
Fe maA aA mg
B
A
FN 1
F1
FN 2
x’
F2
10
理论力学
§6-2 动量矩定理
例：滑块A可在光滑水平面上滑动，为使AB杆以匀角速度 绕
铰链A转动，求作用在AB杆上的力偶M。设：m1 m2 m, AB L
y
FN
解：1、取滑块A和小球B为研究对象
2、受力分析与运动分析
m1 m2
2020/12/9
11
理论力学
§6-2 动量矩定理
y FAy
A
o
FAx aA xA x
3、研究AB杆和小球B，受力分析 4、应用相对动轴A的动量矩定理
dLrA
dt
n
M A (Fi(e) )
i1
rAC (maA )
A
M
杆相对A轴的动量矩
LrA m2L2
B m2xA 外力对A轴之矩
问题：若滑块不脱离地面，试确定AB杆的最大角速度。
2020/12/9
13
理论力学
§6-2 动量矩定理
2020/12/9
14
理论力学
§6-2 动量矩定理
思考题：图示系统中，系统结 构不同，求解方法是否相同？
m1 A
M
m1 A
M
m2
B
2020/12/9
m1 A
M
m2
R
m3 B
m2 B
15
理论力学
§6-2 动量矩定理
mg
B
AB L
2020/12/9
§6-2 动量矩定理
L
3(g 2
y’
2020/12/9
Fe maA aA mg
B
A
FN 1
F1
FN 2
x’
F2
10
理论力学
§6-2 动量矩定理
例：滑块A可在光滑水平面上滑动，为使AB杆以匀角速度 绕
铰链A转动，求作用在AB杆上的力偶M。设：m1 m2 m, AB L
y
FN
解：1、取滑块A和小球B为研究对象
2、受力分析与运动分析
m1 m2
2020/12/9
11
理论力学
§6-2 动量矩定理
y FAy
A
o
FAx aA xA x
3、研究AB杆和小球B，受力分析 4、应用相对动轴A的动量矩定理
dLrA
dt
n
M A (Fi(e) )
i1
rAC (maA )
A
M
杆相对A轴的动量矩
LrA m2L2
B m2xA 外力对A轴之矩
问题：若滑块不脱离地面，试确定AB杆的最大角速度。
2020/12/9
13
理论力学
§6-2 动量矩定理
2020/12/9
14
理论力学
§6-2 动量矩定理
思考题：图示系统中，系统结 构不同，求解方法是否相同？
m1 A
M
m1 A
M
m2
B
2020/12/9
m1 A
M
m2
R
m3 B
m2 B
15
理论力学
§6-2 动量矩定理
mg
B
AB L
2020/12/9
§6-2 动量矩定理
L
3(g 2
动量矩定理作业参考答案及解答
答案： α =
g (顺时针), 2r
FOx = 0,
1 FOy = mg (↑) 2
6．如题图所示，有一轮子，轴的直径为 50mm，无初速的沿倾角θ=20°的轨道
滚下，设只滚不滑，5s 内轮心滚过的距离为 s=3m。试求轮子对轮心的惯性半径。
s
提示：本题用刚体平面运动微分方程求解。注意到轮心加速度可由式 1 s = at 2 求得，且轮心加速度 a 与轮子角加速度α关系 a = rα ，其中 r 为轮轴的 2 半径。 解：
a mg
Ff × r = mρ α
2
由以上两式消去 Ff 得 ρ 2 =
r ( g sin θ − a )
α
=
r 2 t 2 g sin θ − r 2 = 8113(mm) 2 2s
ρ= & 90mm
r 2 t 2 g sin θ − r 2 = 8113(mm) 2 , ⇒ 2s
答案： ρ 2 =
整个系统对轴 O 的动量矩守恒
p 1 p LO = L1 + L2 = r 2 1 ω + 2 r (ωr − at ) = 0 2 g g
解得
ω=
2aP2 t , r (2 P2 + P1 )
α=
2aP2 dω = dt r (2 P2 + P1 )
答案： ω =
2aP2 t , r (2 P2 + P1 )
vB
A
ωB
B
D
1 1）对杆分析，杆对轴 A 的动量矩 L A1 = m2 R 2ω 3 2）对轮分析
ω B R = ωl
ωB =
齿轮对轮心 B 的动量矩为 齿轮对轴 A 的动量矩为
ωl
g (顺时针), 2r
FOx = 0,
1 FOy = mg (↑) 2
6．如题图所示，有一轮子，轴的直径为 50mm，无初速的沿倾角θ=20°的轨道
滚下，设只滚不滑，5s 内轮心滚过的距离为 s=3m。试求轮子对轮心的惯性半径。
s
提示：本题用刚体平面运动微分方程求解。注意到轮心加速度可由式 1 s = at 2 求得，且轮心加速度 a 与轮子角加速度α关系 a = rα ，其中 r 为轮轴的 2 半径。 解：
a mg
Ff × r = mρ α
2
由以上两式消去 Ff 得 ρ 2 =
r ( g sin θ − a )
α
=
r 2 t 2 g sin θ − r 2 = 8113(mm) 2 2s
ρ= & 90mm
r 2 t 2 g sin θ − r 2 = 8113(mm) 2 , ⇒ 2s
答案： ρ 2 =
整个系统对轴 O 的动量矩守恒
p 1 p LO = L1 + L2 = r 2 1 ω + 2 r (ωr − at ) = 0 2 g g
解得
ω=
2aP2 t , r (2 P2 + P1 )
α=
2aP2 dω = dt r (2 P2 + P1 )
答案： ω =
2aP2 t , r (2 P2 + P1 )
vB
A
ωB
B
D
1 1）对杆分析，杆对轴 A 的动量矩 L A1 = m2 R 2ω 3 2）对轮分析
ω B R = ωl
ωB =
齿轮对轮心 B 的动量矩为 齿轮对轴 A 的动量矩为
ωl
理论力学课后习题答案-第10章--动能定理及其应用-)
理论力学课后习题答案-第10章--动能定理及其应用-)(a)v ϕABC rv 1v 1v 1ωϕ(a)CCωCvωO第10章 动能定理及其应用10－1 计算图示各系统的动能：1．质量为m ，半径为r 的均质圆盘在其自身平面内作平面运动。
在图示位置时，若已知圆盘上A 、B 两点的速度方向如图示，B 点的速度为v B ，θ = 45º（图a ）。
2．图示质量为m 1的均质杆OA ，一端铰接在质量为m 2的均质圆盘中心，另一端放在水平面上，圆盘在地面上作纯滚动，圆心速度为v （图b ）。
3．质量为m 的均质细圆环半径为R ，其上固结一个质量也为m 的质点A 。
细圆环在水平面上作纯滚动，图示瞬时角速度为ω（图c ）。
解：1．222222163)2(2121)2(212121BBB CCCmv r v mr v m J mv T =⋅+=+=ω 2．222122222214321)(21212121v m v m r v r m v m vm T +=⋅++= 3．22222222)2(212121ωωωωmR R m mR mR T =++=10－2 图示滑块A 重力为1W ，可在滑道内滑动，与滑块A 用铰链连接的是重力为2W 、长为l 的匀质杆AB 。
现已知道滑块沿滑道的速度为1v ，杆AB 的角速度为1ω。
当杆与铅垂线的夹角为ϕ时，试求系统的动能。
解：图（a ） B AT T T +=)2121(21222211ωC CJ vgWv g W ++=21221121212211122]cos 22)2[(22ωϕωω⋅⋅+⋅++++=l gW l l v l v l g W v g W]cos 31)[(2111221222121ϕωωv l W l W v W W g +++=10－3 重力为P F 、半径为r 的齿轮II 与半径为r R 3=的固定内齿轮I 相啮合。
齿轮II 通过匀质的曲柄OC 带动而运动。
(完整版)动量定理精选习题+答案
小球由静止摆到最低点的过程中绳子的拉力不做功只有重力做功机械能守恒即可由机械能守恒定律求出小球与q碰撞前瞬间的速度?到达最低点时与q的碰撞时间极短且无能量损失满足动量守恒的条件且能量守恒由两大守恒定律结合可求出碰撞后小球与q在平板车p上滑动的过程中系统的合外力为零总动量守恒即可由动量守恒定律求出小物块q离开平板车时速度
三、计算题（本大题共 10 小题，共 100.0 分）
M 在水平轨道上向右移动了 0.54 m
11. 如图所示，质量为 5kg 的木板 B 静止于光滑水平面上，物块 A 质量为 5kg，停在 B 的左端 .质量为 1kg
的小球用长为 0.45??的轻绳悬挂在固定点 O 上，将轻绳拉直至水平位置后， 由静止释放小球， 小球在最
m 的静
止木块发生碰撞，碰撞的时间极短 .在此碰撞过程中，下列哪个或哪些说法是可
能发生的？ ( )
A. 在此过程中小车、木块、摆球的速度都发生变化，分别变为
??1、 ??2 、 ?3?，满足 (?? + ??0 )??= ???1? +
???2? + ??0 ??3
B. 在此碰撞过程中， 小球的速度不变， 小车和木块的速度分别为 ?1?和 ?2?，满足 (?? + ??0)??= ???1?+ ???2?
4
B. 5 ??0
1
C. 5 ??0
1
D. 25 ??0
2. 如图所示，小车静止在光滑水平面上， AB 是小车内半圆弧轨道的水平直径，现 将一小球从距 A 点正上方 h 高处由静止释放，小球由 A 点沿切线方向经半圆轨 道后从 B 点冲出，在空中能上升的最大高度为 0.8? ，不计空气阻力 .下列说法正 确的是 ( )
1
三、计算题（本大题共 10 小题，共 100.0 分）
M 在水平轨道上向右移动了 0.54 m
11. 如图所示，质量为 5kg 的木板 B 静止于光滑水平面上，物块 A 质量为 5kg，停在 B 的左端 .质量为 1kg
的小球用长为 0.45??的轻绳悬挂在固定点 O 上，将轻绳拉直至水平位置后， 由静止释放小球， 小球在最
m 的静
止木块发生碰撞，碰撞的时间极短 .在此碰撞过程中，下列哪个或哪些说法是可
能发生的？ ( )
A. 在此过程中小车、木块、摆球的速度都发生变化，分别变为
??1、 ??2 、 ?3?，满足 (?? + ??0 )??= ???1? +
???2? + ??0 ??3
B. 在此碰撞过程中， 小球的速度不变， 小车和木块的速度分别为 ?1?和 ?2?，满足 (?? + ??0)??= ???1?+ ???2?
4
B. 5 ??0
1
C. 5 ??0
1
D. 25 ??0
2. 如图所示，小车静止在光滑水平面上， AB 是小车内半圆弧轨道的水平直径，现 将一小球从距 A 点正上方 h 高处由静止释放，小球由 A 点沿切线方向经半圆轨 道后从 B 点冲出，在空中能上升的最大高度为 0.8? ，不计空气阻力 .下列说法正 确的是 ( )
1
理论力学答案完整版(清华大学出版社)10
两者总质量为 m2，对 O 轴的回转半径为 ρ 。当重物 A 下降时，滚
子 C 沿水平轨道滚动而不滑动，试求重物 A 的加速度。
解： 取整个系统为研究对象，自由度为 1。设重物速度为 vA ，则轮
题 10-9 图
的角速度 ω = vA ，轮心速度为 R−r
vO
=
R
r −
r
vA 。系统的动能为
( ) T
拉格朗日方程的普遍形式
d dt
∂L ∂q& j
− ∂L ∂q j
= Q′j
( j = 1,2,..., m)
式中 Q′j 为非有势力对应的广义力。
矢量方法
动量法：动量定理
动量矩定理 质心运动定理 定轴转动微分方程 平面运动微分方程
质点系统动力学
动静法
动能定理
能量方法
拉格朗日方程
3 保守系统拉格朗日方程的初积分
10-3 质量为 m1 的匀质杆，长为 l，一端放在水平面上， 另一端与质量为 m2、半径为 r 的匀质圆盘在圆盘中心 O 点 铰接。圆盘在地面上作纯滚动，圆心速度为 v。求系统在此
题 10-3 图
位置的动能。
解：杆作平移，动能为
T1
=
1 2
m1v2
；
圆盘作纯滚动，动能为
T2
=
1 2
m2v2
+
1 2
mivi
⋅ vi
，
其中 n 为系统中的质点数目，可以是有限或无穷，mi 和 vi 分别为各质点的质量和速度。 平
移刚体的动能 T = 1 mv2 ， 2
其中 m 为平移刚体的质量。
定轴转动刚体的动能
T
=
1 2
子 C 沿水平轨道滚动而不滑动，试求重物 A 的加速度。
解： 取整个系统为研究对象，自由度为 1。设重物速度为 vA ，则轮
题 10-9 图
的角速度 ω = vA ，轮心速度为 R−r
vO
=
R
r −
r
vA 。系统的动能为
( ) T
拉格朗日方程的普遍形式
d dt
∂L ∂q& j
− ∂L ∂q j
= Q′j
( j = 1,2,..., m)
式中 Q′j 为非有势力对应的广义力。
矢量方法
动量法：动量定理
动量矩定理 质心运动定理 定轴转动微分方程 平面运动微分方程
质点系统动力学
动静法
动能定理
能量方法
拉格朗日方程
3 保守系统拉格朗日方程的初积分
10-3 质量为 m1 的匀质杆，长为 l，一端放在水平面上， 另一端与质量为 m2、半径为 r 的匀质圆盘在圆盘中心 O 点 铰接。圆盘在地面上作纯滚动，圆心速度为 v。求系统在此
题 10-3 图
位置的动能。
解：杆作平移，动能为
T1
=
1 2
m1v2
；
圆盘作纯滚动，动能为
T2
=
1 2
m2v2
+
1 2
mivi
⋅ vi
，
其中 n 为系统中的质点数目，可以是有限或无穷，mi 和 vi 分别为各质点的质量和速度。 平
移刚体的动能 T = 1 mv2 ， 2
其中 m 为平移刚体的质量。
定轴转动刚体的动能
T
=
1 2
11 动量矩定理习题解答
R
O ve
r o B
vr
[解]
研究整体，由于∑Mz （F）= 0，且系统初始静止， 所以 Lz = 0，即 L z 盘+ L z 人 = 0 式中 Lz 盘= J z =
1P 2 R 2g
L z 人= 解得
ds Q (v －v )r， v = rω ， vr at e r e dt g
解：重物 A 和 B 速度 v A vB r ，
LO m1v A r m2 vB r J O 1 m1r r m2 r r m3r 2 2
A
B （c）
vA
vB
m1 g
m2 g
1 2 m1 m2 m3 r 2
…….. ①
对 B 轮，有
…….. ②
P aB P FT1 g
…….. ③
FT1 FT1
…….. ④
再以轮与绳相切点 D 为基点，则轮心 B 的加速度
v B v D v BD ，式中 v D r A ， v BD r B
∴ v B r A r B ， 对上式求导得轮心 B 的加速度为
Fx maCx , FNA maCx , Fy maCy , FNB mg maCy , M C ( F ) J C , FNB l cos FNA l sin 1 ml 2 2 2 12
l 2 FNA 2 ( sin cos )m, l 2 FNB mg ( cos sin )m, 2 l l 1 2 FNB 2 cos FNA 2 sin 12 ml
A
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
理论力学11章作业题解
11-3 已知均质圆盘的质量为m ，半径为R ，在图示位置时对O 1点的动量矩分别为多大？图中O 1C=l 。
解 (a) 2
1l m l mv L c O w == ，逆时针转动。
(b) w w 2
210||1mR J L v m r L c c c O =+=+´=r
r ，逆时针转动。
(c ) )2(2
2
212
2
212
1l R m ml mR ml J J c O +=+=+=
w w )2(2
22111l R m J L O O +==，逆时针转动。
(d)
w
w mR R l mv R l R v mR l mv J l mv L v m r L c c c c c c c O )5.0()5.0(/||2
2
11-=-=-=-=+´= r r
，顺时针转动
解毕。
v c
v c
v c
11-5 均质杆AB 长l 、重为G 1，B 端刚连一重G 2的小球，弹簧系数为k ，使杆在水平位置保持平衡。
设给小球B 一微小初位移0d 后无初速度释放，试求AB 杆的运动规律。
解 以平衡位置（水平）为0=j ，顺时针转为正。
平衡时弹簧受力为：
)5.0(312G G F s +=
弹簧初始变形量：
k G G k F s st /)5.0(3/12+==d
在j 角时弹簧的拉力为（小位移）：
3/)5.0(3)3/(12l k G G l k F st s j j d ++=+=¢
系统对A 点的动量矩：
j j j
&&&2
21233l g
G G l l g G J L A A +=×+= 对点的动量矩定理)(/å=E
i A A F M dt dL r ：
j j 9
3/5.0332
21221kl l F lG lG l g G G s -=¢-+=+&& 0)3(321=++j j
G G gk &&，令)
3(3212G G gk
p +=则有02=+j j
p &&，其解为： )cos()sin(pt B pt A +=j
由初始条件0| ,/|000====t t l j
d j &得l B A / ,00d ==。
故运动方程为： )cos(0
pt l
d j =
解毕。
G 1
G 2
F Ax F Ay
F s
11-10 一半径为r 、重为W 1的均质水平圆形转台，可绕通过中心Ｏ并垂直于台面的铅直轴转动。
重W 2的物块A ，按规律s =at /2 沿台的边缘运动。
开始时，圆台是静止的。
求物块运动以后，圆台在任一瞬时的角速度与角加速度。
解 （1）运动分析
物块A的相对速度: at dt ds v r ==/ （2）受力分析 （3）建立动力学方程
0)(==\=åconst L F M z i z Q
0)(2=-+=r m v r J L r z w w r
W W at
W )2(2212+=
w 求导得角加速度：
r
W W a
W )2(2212+=
a
解毕。
W 1
W 2
F x
F y
F z
m x m y
z
v r
11-17 均质圆柱体A 和B 的重量均为W ，半径均为r 。
一绳绕于可绕固定轴O 转动的圆柱A 上，绳的另一端绕在圆柱B 上。
求B 下落时质心的加速度。
摩擦不计。
解 (1) 运动分析
系统有2个独立的坐标参数，设两轮的角速度为ωA 和ωB 。
则有合成运动可得：r r v B A C w w +=
上式恒成立可求导得：r r a B A C a a += (2) 受力分析 (3) 建立动力学方程 对轮A:
r F J A O 1=a
对轮B:
1
1F mg ma r F J C B C -==a
3个方程求解3个未知量：1,,F B A a a
得：g a 54
=，
解毕。
C
v C
A
w
B
w
C mg
mg
F 1F R
11-19 半径为r 的均值圆轮在半径为R 的圆弧面上作纯滚动。
初瞬时0j j =（微小），00=j
&。
试求圆轮的运动方程。
解 圆轮由于受约束只有1个自由度，取广义坐标j 描述圆轮的运动。
（1）运动分析
r r R r R a r r R r R v t
C C /)( ),(/)( ),(-=-=-=-=j a j
j w j
&&&&&&
（2）受力分析，作示力图
（3）用刚体平运动微分方程建立圆轮的动力学方程
îíì-=--=-Fr r r R mr mg F r R m /)(sin )(2
2
1j j j
&&&& 解得：0sin )
(32=-+j j
r R g
&&
由于j 微小，故有j j »sin ，方程可简化为（另)
(322r R g
k -=
）
02=+j j
k && 其解为：)cos()sin(kt B kt A +=j 由初始条件得：0 ,0j ==B A 故运动方程为：) )
(32cos()cos(00t r R g
kt -==j j j
解毕。
W
F
F N
v C
w
11-23 长l 、质量为m 的均质杆AB 与BC 在B 点刚连成直角后置于光滑的水平面上。
试求在A 端作用一与AB 垂直的水平力F 后A 点的加速度。
解：首先求质心E 的加速度（E 在BD 的中点，D 在AC 的中点）。
根据质心运动定理可以判断初始质心在y 向无加速度。
设E 点的x 向加速度为a E ，杆的角加速为a 。
由质心运动定理得 îí
ì´==l F J F
ma E E 4
3
2a 式中2
1252
812
121
)(2ml l m ml J E =´+=，由方程可以解得
)2/(m F a E =，)5/(9ml F =a
基点法求A 点加速度
n
EA t EA E A a a a a ++=r
其中0=n
EA a EA a
t EA
´=a
m
F
l ml F m F a a a t EA
E Ax
203743592cos =´+=´+=q
m
F
l ml F a a t
EA Ay 209459sin -=´-
=´-=q
解毕。
11-25 两根质量m 、长度l 的均质杆构成的系统如图示(初始处于静止状态)。
如在B 端作用一个已知力F ，试求此时两根杆的角加速度。
解 (1) 运动分析
系统有2个独立的运动参数。
设OA 、AB 杆的角加速度为α1，α2。
OA 杆质心加速度（只有切向分量）：
2/1l a t D
a =
AB 杆质心加速度用基点法计算（只有水平分量）：
2/21l l a
a a t CA t A t C a a +=+=
(2) 受力分析 (3) 建立动力学方程 对OA 杆：l F J Ax O =1a
对AB 杆：mg
F m F F ma l F Fl J Ay Ax
t
C
Ax C -=×-=+=02
/2/2a
4个方程求解4个未知量：Ay Ax F F ,,,21a a 得：ml F 761=a ，ml
F
7302=a 。
解毕。
O
O B
C。