弹性势能的表达

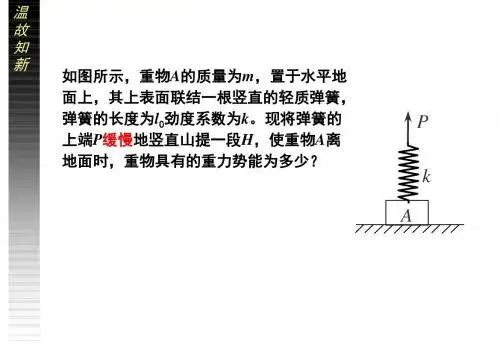
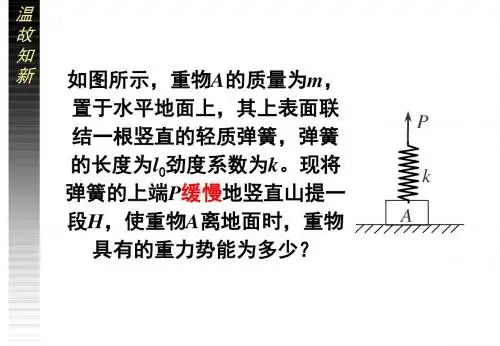
弹性势能知识点总结弹性势能是物体由于形变而储存的能量，当物体恢复原状时，这部分能量会释放出来。

这种能量转化的形式为弹性势能。

在自然界中，弹性势能的应用广泛，例如弹簧，弹簧的弹性势能会随着伸长或压缩而发生变化。

此外，橡胶、橡皮筋等也都具有弹性势能。

下面我们将详细介绍弹性势能的相关知识点。

一、弹性势能的定义弹性势能是指物体由于形变而储存的能量。

在物体恢复原状时，这部分能量会释放出来。

弹性势能的表示方式为U，其单位为焦耳(J)。

在物理学中，弹性势能的表达式为：U = 1/2kx²其中，U为弹性势能，k为弹簧的弹性系数，x为弹簧的伸长或压缩量。

二、弹性势能的计算1. 弹簧的弹性势能计算在弹簧的伸长或压缩过程中，其弹性势能的计算公式为：U = 1/2kx²其中，U为弹簧的弹性势能，k为弹簧的弹性系数，x为弹簧的伸长或压缩量。

弹簧的弹性系数可以通过实验进行测量。

2. 橡胶的弹性势能计算对于橡胶或橡皮等具有弹性的物体，其弹性势能的计算公式同样为U = 1/2kx²。

这也说明了弹性势能的计算公式是普适的，不同物体都可以用同一个公式来计算弹性势能。

三、弹性势能的应用1. 吊车的弹簧系统在吊车的弹簧系统中，弹簧经历了伸长或压缩，从而具有了弹性势能。

当吊车吊物体时，弹簧的弹性势能会转化为物体的动能，使得物体具有一定的速度。

2. 飞机起落架的弹性势能飞机的起落架采用弹簧系统，当飞机降落时，起落架会受到冲击，弹簧会发生压缩，从而具有了弹性势能。

起落架的弹性势能可以缓冲飞机的着陆过程，减少冲击力。

3. 弹簧振子系统在物理学中，弹簧振子系统经常被用来研究弹性势能。

在这个系统中，弹簧的弹性势能会随着振子的振动而发生变化，从而实现能量的转化。

4. 简谐振动简谐振动是弹簧振子系统的一种特殊情况，其弹性势能和动能之间存在周期性的转化，使得振子具有了周期性的振动。

四、弹性势能与动能弹性势能和动能是物体内能的两种形式。

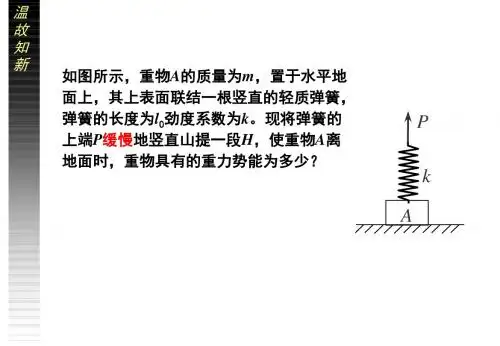
弹性势能的计算方法在物理学中，弹性势能是描述物体弹性变形能量的概念。

当物体受到外力作用发生形变时，它具有储存的能力，这种能量的大小可以通过计算弹性势能来确定。

本文将介绍几种常见的计算弹性势能的方法。

一、钢丝弹簧的弹性势能计算方法：钢丝弹簧是一种常见的弹性体，其弹性势能的计算可以通过胡克定律来实现。

胡克定律表明弹性体的形变与所施加的力成正比。

对于钢丝弹簧而言，弹性势能可以表示为：E = (1/2) kx^2其中，E代表弹性势能，k代表弹簧的劲度系数，x代表弹簧的形变长度。

通过测量弹簧的形变和知道劲度系数，即可计算出弹性势能的大小。

二、弹性体的弹性势能计算方法：对于一般的弹性体，弹性势能的计算方法可以采用应变能法。

弹性体的应变能可以表示为：E = (1/2) Vσε其中，E代表弹性势能，V代表弹性体的体积，σ代表应力，ε代表应变。

通过测量应力和应变，以及知道弹性体的体积，即可计算出弹性势能的大小。

三、四边形梁的弹性势能计算方法：对于四边形梁而言，弹性势能的计算方法可以采用弯曲能法。

四边形梁在受力作用下会产生弯曲变形，其弯曲能可以表示为：E = (1/2) EI(θ/L)^2其中，E代表弹性势能，I代表截面惯性矩，θ代表变形角度，L代表梁的长度。

通过测量梁的截面形状和尺寸，以及变形角度，即可计算出弹性势能的大小。

以上是几种常见的计算弹性势能的方法，在实际问题中可以根据具体情况选择适用的方法。

弹性势能的计算对于了解物体的弹性性质和变形情况具有重要意义，有助于优化设计和预测物体的行为。

因此，掌握这些计算方法对于物理学研究和工程应用都具有重要价值。

弹性势能的公式
根据胡克定律F=KX，在F-X图像中是过坐标原点的直线，图像和横轴x所围的面积为弹力做功，W=1/2KX^2弹性势能Ep=1/2kx^2k 弹簧劲度系数x弹簧形变量。

弹力做功的公式是E=1/2*k*x^2，即E=1/2*k*x*x
发生弹性形变的物体的各部分之间，由于有弹力的相互作用，也具有势能，这种势能叫做弹性势能。

同一弹性物体在一定范围内形变越大，具有的弹性势能就越多，反之，则越小。

弹性势能可与动能直接相互转化，但不能与重力势能直接转化。

核心或实质：（势能和动能间之间可直接转化，但势能不能与势能直接相互转化，就是说不可能在动能不变的情况下转化）。

弹性势能与弹力弹性势能和弹力是物体力学中重要的概念，它们描述了物体在受力作用下的行为和变形。

弹性势能是指物体存储在其内部的能量，而弹力则是指物体恢复原状的力量。

本文将介绍弹性势能和弹力的定义、计算方法和应用。

一、弹性势能的定义和计算方法弹性势能是物体由于形变而存储的能量。

当物体受到外力作用而发生形变时，其内部的弹性势能就会增加。

一般来说，弹性势能可以分为两种情况：弹簧的势能和弹性体的势能。

1. 弹簧的弹性势能当弹簧受力拉伸或压缩时，会发生形变。

假设弹簧的形变量为x，弹簧的弹性势能可以用下式计算：弹性势能 = 0.5kx²其中，k是弹簧的弹性系数，x是形变量。

这个公式表明，当形变量增加时，弹性势能也随之增加。

2. 弹性体的弹性势能弹性体也可以存储弹性势能。

当弹性体受到外力拉伸或压缩时，会发生形变。

弹性体的弹性势能可以通过以下公式计算：弹性势能= 0.5FΔL其中，F是作用力，ΔL是形变量。

这个公式表明，当作用力增加或形变量增加时，弹性势能也随之增加。

二、弹力的定义和计算方法弹力是物体恢复原状所产生的力量。

当物体发生形变后，弹力会使物体回复到原始状态。

根据胡克定律，弹力与形变量之间存在线性关系。

通常，弹性力可以通过以下公式计算：弹力 = kx其中，k是弹性系数，x是形变量。

这个公式表明，弹力与形变量成正比。

三、弹性势能和弹力的应用弹性势能和弹力在日常生活和工程领域中有广泛的应用。

1. 弹簧应用弹簧广泛应用于机械、电子和汽车工业中。

弹簧的弹性势能和弹力可以用来实现各种功能，如减震、保护和悬挂。

2. 弹簧秤应用弹簧秤是一种利用弹簧的弹性势能和弹力来测量物体重量的装置。

当物体放在弹簧秤上时，弹簧产生形变，根据形变量可以计算物体的重力。

3. 弹簧板应用弹簧板是一种弹性体，其弹性势能和弹力可以用来储存和释放能量。

它广泛应用于跳跃板、板簧箱和跷跷板等装置中。

4. 弹簧门应用弹簧门是一种利用弹簧的弹性势能和弹力来控制门的开关的装置。

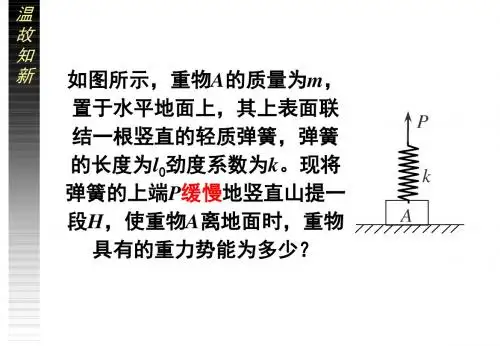
初中物理弹性势能解析弹性势能是物体因变形而具备的能量。

在弹簧、弓箭等物体中，我们常常遇到弹性势能的概念。

本文将对初中物理中的弹性势能进行解析，包括弹簧的弹性势能和弯曲物体的弹性势能。

1. 弹簧的弹性势能弹簧是一个常见的物体，它具备弹性特性。

当外力作用于弹簧时，它会发生形变，并具备弹性势能。

弹簧的弹性势能与其形变量有关。

假设弹簧的形变量为x，弹簧的弹性系数为k，则弹簧的弹性势能U可以表示为：U = (1/2)kx²其中，U代表弹性势能，k代表弹性系数，x代表形变量。

从公式可以看出，弹性势能与形变量的平方成正比，同时与弹性系数成正比。

形变量越大，弹性势能也越大。

2. 弯曲物体的弹性势能除了弹簧，弯曲物体也具备弹性特性，如弯曲的弹性杆、扁平弹簧等。

对于弯曲物体，其弹性势能与形变量以及材料的弹性模量有关。

假设弯曲物体的形变量为δ，物体的长度为L，横截面面积为A，材料的弹性模量为E，则弯曲物体的弹性势能U可以表示为：U = (1/2)(E × A × δ²) / L其中，U代表弹性势能，E代表弹性模量，A代表横截面面积，δ代表形变量，L代表长度。

从公式可以看出，弹性势能与形变量的平方成正比，与横截面面积和弹性模量成正比，与长度成反比。

形变量越大，弹性势能也越大。

3. 应用举例现在我们通过几个具体的例子来应用弹性势能的解析。

例一：弹簧挂重物假设一个弹簧挂着一个质量为m的重物。

重物下垂的距离为h，弹簧的劲度系数为k。

则重物的下垂过程中，弹簧的弹性势能可以表示为：U = (1/2)kx² = (1/2)k(h-L)²其中，x为形变量，等于h-L，L为弹簧的自然长度。

例二：悬挂弹簧球的下压量如果将一个弹性球吊挂在天花板上，并将其下压到最低点，球的下压量为d，球的质量为m，弹簧的劲度系数为k。

则球的下压过程中，弹簧的弹性势能可以表示为：U = (1/2)kx² = (1/2)kd²其中，x为形变量，等于d。

p
p 弹性势能
一、对弹性势能的理解
1.弹性势能是发生弹性形变的物体上所有质点因相对位置的改变而具有的能量，因而也是对系统而言。

2.弹性势能是相对的，其大小在选定了零势能点后才能确定，对于弹簧的零势能点一般在弹簧的自然长度处。

二、弹性势能的表达式
1.弹簧的弹性势能由弹簧本身的材料以及形变量所决定，其表达式为
E =1 2，其中k 为弹簧的劲度系数，l 为弹簧的形变量。

2
2.弹簧的弹性势能 E =1 2，是指弹簧的长度为原长时规定它的弹性势能
2
为零的表达式。

我们完全可以规定弹簧在某一任意长度时弹性势能为零，只不过这样在处理问题时不方便，因此在通常情况下我们规定弹簧在原长时弹性势能为零，那么弹性势能总为正值。

三、弹力做功与弹性势能变化的关系
1.弹力做负功，弹性势能增大，其他形式能转化为弹性势能；弹力做政工，弹性势能减小，弹性势能转化为其他形式能。

2.弹力做功与弹性势能的变化的关系，弹性势能的变化量总等于弹力对外做功的负值。

3.弹性势能具有相对性，但其变化量具有绝对性，因此在判断弹性势能的变化时不必考虑零势能点的位置。

弹性势能的公式范文
弹性势能是指弹性体在变形过程中因储存的形变能而具有的能量。

弹性势能可以用于描述许多物体的行为，如弹簧、橡胶等。

在本文中，我们将讨论弹性势能的公式以及其应用。

E=(F/A)/(ΔL/L)
其中E为弹性模量，F为应力，A为受力面积，ΔL为变形长度的改变量，L为原始长度。

根据胡克定律，应力与应变之间的关系可以表示为：
σ=Eε
其中σ为应力，ε为应变。

根据定义，应变为单位长度的改变量，可以表示为：
ε=ΔL/L
将上述公式代入胡克定律公式中，可得：
σ=(F/A)/(ΔL/L)
将上式两端的ΔL移项，并将F/A替换为σ，可得：
σ/ε=(F/A)/(ΔL/L)
由于F/A可以表示为力的大小，ΔL/L可以表示为位移的大小，因此σ/ε可以表示为单位体积内的能量。

定义单位体积内的能量为弹性势能U
U=(1/2)σε
将σ和ε的公式代入上式中，可得：
U=(1/2)σ^2/E
这就是弹性势能的公式。

另一个例子是弹性体的弹性变形。

当弹性体受到外力作用而发生变形时，其储存的能量可以通过弹性势能公式来计算。

这对于工程设计和力学分析非常重要。

此外，弹性势能的公式还可以用来计算弹性体的杨氏模量。

杨氏模量是弹性体特性的一个重要参数，可以用来比较不同材料的弹性性质。

通过测量弹性体的应力和应变，并将其代入弹性势能公式，可以计算出杨氏模量。

总结起来，弹性势能的公式是U=(1/2)σ^2/E，其中U为弹性势能，σ为应力，E为弹性模量。

这个公式可以用来计算弹簧和弹性体的弹性储能，并且可以应用于工程设计和力学分析中。

弹力和弹性势能弹力和弹性势能是物体力学中重要的概念，它们描述了物体在受力作用下发生形变和恢复的能力。

本文将深入探讨弹力和弹性势能的概念、公式以及应用。

一、弹力的概念和公式在物体受到外力作用时，会发生形变。

当外力作用消失后，物体通过恢复力恢复到原来的形状。

这种恢复力就是弹力。

弹力的大小与物体形变的程度成正比。

根据胡克定律，当物体的形变适用于弹性范围时，弹力与形变的关系可以表示为：F = -kx其中，F为弹力的大小，k为弹簧系数，x为物体的形变量，负号表示弹力方向与形变方向相反。

二、弹性势能的概念和公式弹性势能是物体在形变过程中储存的能量，也称为弹性势能。

当物体发生形变时，其具有了潜在能，这种能量称为弹性势能。

对于弹性形变，弹性势能可以用以下公式表示：Ee = 1/2 kx^2其中，Ee为弹性势能，k为弹簧系数，x为物体的形变量。

三、弹力和弹性势能的应用1. 弹簧弹簧是弹力和弹性势能应用最广泛的例子之一。

当外力作用于弹簧时，弹簧发生形变，形成弹力。

当外力消失时，弹簧通过弹性势能恢复到原来的形状。

弹簧的应用包括悬挂系统、减震器、测力仪等。

2. 弹簧板弹簧板是由弹力和弹性势能控制的机械系统。

它们可以用于调节机械设备的振动，实现机械部件的缓冲和减震。

3. 弹簧能量储存器弹簧能量储存器是一种将机械能转化为弹性势能的装置。

它们常用于循环能源系统或需要短期储能的应用，如锂电池、发动机启动器等。

4. 弹簧秤弹簧秤利用弹簧的弹力来测量物体的重力。

物体受到重力作用时，弹簧发生形变，形成弹力。

根据弹簧的弹性势能，我们可以推断出物体的重力大小。

结论弹力和弹性势能作为物体力学中的重要概念，描述了物体在受力作用下发生形变和恢复的能力。

弹力的大小与形变程度成正比，弹性势能是形变过程中储存的能量。

弹力和弹性势能的应用广泛，例如弹簧、弹簧板、弹簧能量储存器和弹簧秤等。

它们在工程、物理学和生活中都扮演着重要的角色。

通过深入理解和应用这些概念，我们可以更好地理解物体的形变和恢复过程。

熟悉弹性势能和动能弹性势能和动能是物体运动中的两个重要概念，它们在物理学领域中有着广泛的应用和意义。

本文将深入探讨弹性势能和动能的定义、特点以及它们在不同领域中的应用。

首先，我们来了解一下弹性势能和动能的定义。

弹性势能指的是物体由于形变而储存的能量，它与物体的形变程度成正比。

当物体发生形变时，它具有恢复原状的趋势，这种趋势就是弹性势能的来源。

一般来说，弹性势能可以通过以下公式进行计算: Ee = 1/2 k x^2，其中Ee代表弹性势能，k代表劲度系数，x代表形变量。

动能则是物体由于运动而具有的能量，包括物体的平动动能和转动动能。

平动动能的计算公式为: Ek = 1/2 mv^2，其中Ek代表平动动能，m代表物体的质量，v代表物体的速度。

转动动能的计算公式根据物体的形状不同而有所变化，比如对于旋转的刚体，转动动能的计算公式为: Er = 1/2 Iω^2，其中Er代表转动动能，I代表物体的转动惯量，ω代表物体的角速度。

弹性势能和动能有许多共同的特点。

首先，它们都是一种储存的能量，物体可以在需要时将这些能量转化为其他形式的能量。

其次，它们都是与物体的运动和形变相关的能量。

最后，它们都是以二次方方式与速度、形变量等变量相关联的。

弹性势能和动能在物理学领域中有着广泛的应用。

首先，在机械领域中，弹性势能和动能是弹簧、悬挂系统等设备设计中重要的考虑因素。

对于弹簧，根据胡克定律可以知道，弹簧的劲度系数k与形变量x成正比，根据弹性势能的定义可以知道，弹簧的弹性势能与形变量平方成正比。

因此，设计者可以通过合理选择弹簧的劲度系数和形变量，来满足设备的弹性势能需求。

对于悬挂系统，动能的大小与物体的质量和速度有关，设计者可以根据悬挂系统的需求来选择物体的质量和速度，以实现所需的动能。

其次，在工程领域中，弹性势能和动能在结构设计、材料选择等方面起着重要作用。

比如，在建筑结构中，设计者需要通过合理选择材料的劲度系数和形变量，来满足结构的强度和刚度需求。

弹力与弹性势能弹力和弹性势能是力学中重要的概念，它们描述了物体在受到外力作用时的变形和能量存储。

本文将介绍弹力和弹性势能的概念、公式及其在实际应用中的重要性。

一、弹力的概念与公式弹力是物体受到外力作用时发生的变形所产生的恢复力。

当物体受到外力作用时，其内部的原子和分子之间会产生相互作用力，使物体发生形变。

而弹力恢复力则代表了物体恢复原状的力量。

根据胡克定律，弹力与物体的形变是成正比的。

可用如下公式表示：F = -kx其中，F表示弹力的大小，k为弹簧系数或刚度系数，x为物体的形变量。

负号表示弹力的方向与形变方向相反。

二、弹性势能的概念与公式弹性势能是指在物体发生形变时，由于受力而储存的能量。

当物体受到外力作用发生形变时，弹性势能会由形变所导致的势场变化而存储。

物理学中常常用势能能量来描述物体的储能状态。

对于弹性势能，可以使用如下公式表示：U = (1/2) kx²其中，U表示弹性势能的大小，k为弹簧系数或刚度系数，x为物体的形变量。

这个公式表明，当物体形变量为x时，其弹性势能大小与形变量的平方成正比。

三、弹力和弹性势能的应用弹力和弹性势能在现实生活中有着广泛的应用。

下面将以弹簧作为例子进行说明。

1. 弹簧振子：在弹簧振子中，当弹簧拉伸或挤压时，弹力的作用会使弹簧回复到原来的形状，产生周期性的振动。

此时，弹性势能的储存与释放使得弹簧振动能够持续下去。

2. 弹簧秤：弹簧秤利用弹簧的弹力原理来测量物体的重量。

当物体悬挂在弹簧下方时，弹簧会发生形变，根据弹力的大小就可以推算出物体的重量。

3. 弹簧减震器：弹簧减震器常用于汽车等交通工具的悬挂系统中，通过弹簧的形变和弹力的作用来减缓和分散车辆行驶过程中产生的震动和冲击力，提高行驶的平稳性和舒适性。

综上所述，弹力和弹性势能在力学中起着重要的作用，它们描述了物体在受到外力作用时的变形和能量存储。

弹力和弹性势能的理论框架不仅适用于弹簧系统，也可以推广到其他具有弹性特性的材料和结构中。

2019年高考备考必考知识：弹性势能的表达式下面是编辑老师整理的2019高考备考必考知识弹性势能表达式，希望对您提高学习效率有所帮助.一、弹性势能：1、定义：发生弹性形变的物体的各部分之间，由于有弹力的相互作用，也具有势能，叫做弹性势能。

说明：1、弹性形变弹力的相互作用2、由于整个物体都发生了形变，各部分之间都有弹力3、这种能量归结为势能对比：重力势能是由于有重力的相互作用，具有对外做功本领而具有的一种能量引导：弹性势能和重力势能一样大小都和相对位置有关。

下面我们就来研究弹性势能的大小，我们研究最简单的，弹簧的弹性势能大小。

2、研究弹性势能的出发点弹性势能与重力势能都是物体凭借其位置而具有的能。

在讨论重力势能的时候，我们从重力做功的分析入手。

同样，在讨论弹性势能的时候，则要从弹力做功的分析入手。

弹力做功应是我们研究弹性势能的出发点。

二、探究弹簧弹性势能的大小1、猜想，并进行定性研究弹性势能表达式中相关物理量的猜测弹性势能的表达式可能与哪些物理量有关呢?①可能与弹簧被拉伸(或压缩)的长度有关。

这是因为，与重力势能相类比，重力势能与物体被举起(或下降)的高度有关，所以弹性势能很可能与弹簧被拉伸(或压缩)的长度有关。

重力势能与高度成正比，但是弹性势能与弹簧被拉伸(或压缩)的长度则不一定成正比，在地球表面附近可认为重力不随高度变化，而弹力在弹簧形变过程中则是变力。

②可能与弹簧的劲度系数有关。

这是因为，不同弹簧的软硬程度不同，即劲度系数不同，使弹簧发生相同长度的形变所需做的功也不相同。

2、探究弹性势能表达式1)弹性势能与拉力做功的关系当弹簧的长度为原长时，我们设它的弹性势能为0，弹簧被拉长或缩短后就具有了弹性势能。

我们研究弹簧被拉长的情况，那么弹簧的弹性势能应该与拉力所做的功相等。

可见，研究弹性势能的表达式，只需研究拉力做功的表达式。

2019高考备考必考知识弹性势能表达式已经呈现在各位考生面前，更多精彩尽在高考频道!。

弹性势能的概念
弹性势能是指弹性体在受到形变后，由于其具有弹性回复的能力而储存的能量。

在弹性体形变时，弹性体内部的原子或分子会发生相对位移，因此分子之间的相互作用力也会随之改变。

当形变结束后，这些作用力会重新恢复到原来的状态，而这个过程中所释放的能量就是弹性势能。

弹性势能通常用公式E_s=1/2kx^2来表示，其中E_s代表弹性势能，k代表恢复力常数，x代表形变量。

当形变量增大时，弹性势能也会增加，当形变量减小时，弹性势能也会减小。

当形变量为零时，弹性势能也为零。

弹性势能在物理学中有着广泛的应用，例如在弹簧、橡皮等弹性体的设计中，弹性势能的大小会影响其弹性性能和使用寿命。

此外，在物体碰撞或运动中，弹性势能也会发挥重要的作用。

因此，了解和掌握弹性势能的概念和计算方法是非常重要的。

- 1 -。

物理弹性势能弹性势能是物理学中的一个重要概念，它描述了物体在受力作用下发生形变后能够恢复原状的能力。

物体的弹性势能可以通过物体的形变程度和受力的大小来计算。

本文将从弹簧的弹性势能、材料的弹性势能和应用示例三个方面来介绍物理弹性势能。

一、弹簧的弹性势能弹簧是我们生活中常见的弹性体，它具有较好的弹性特性。

当一个弹簧受到外力拉伸或压缩时，会发生形变，但是当外力消失后，弹簧会恢复到原来的形状。

这种形变能够存储在弹簧中，并且能够通过弹性势能的计算来衡量。

弹簧的弹性势能计算公式为：E = 1/2kx²其中，E表示弹性势能，k表示弹簧的弹性系数，x表示弹簧的形变量。

弹性系数k越大，表示弹簧的刚度越大，形变量x一定的情况下，弹性势能E也越大，说明弹簧的弹性特性越显著。

二、材料的弹性势能除了弹簧，各种材料在受力作用下也会发生形变和恢复，具有弹性势能。

材料的弹性势能与物体的形变程度和材料的刚度有关。

对于拉伸或压缩杆件，材料的弹性势能可以通过下列公式计算：E = 1/2Fδ其中，E表示材料的弹性势能，F表示作用在杆件上的力，δ表示杆件的形变量。

材料的弹性势能可以用来衡量材料的弹性特性和储能能力。

不同材料的弹性势能计算方式不同，对于不同的应用和领域，要根据材料的特性来选择合适的计算方法。

三、应用示例物理弹性势能在日常生活和工程领域有着广泛的应用。

以下是几个典型的应用示例：1. 弹簧秤：弹簧秤是通过测量弹簧的形变量来推算物体的质量。

弹簧秤利用了弹簧的弹性势能原理，当物体悬挂在秤上时，弹簧会发生形变，形变量可以通过弹性势能的计算得到，从而推算出物体的质量。

2. 弹簧减震器：在汽车和建筑领域中常用的减震器就是利用了弹簧的弹性势能来减小震动的传播。

当汽车行驶或地震发生时，弹簧减震器能够吸收和释放弹性势能，使得震动能量得到减缓，从而减轻了对汽车或建筑物的损害。

3. 弹性储能器：弹性势能储存器是一种将机械能转化为弹性势能储存的装置，常用于一些机械系统的能量储备和传递。