九年级数学下册基础题测试.doc

2024年数学九年级下册指数基础练习题（含答案）试题部分一、选择题：1. 下列哪个数的指数是3？A. 2^3B. 3^2C. 2^2D. 3^32. 当a为正数时，下列哪个式子的值最小？A. a^0B. a^1C. a^2D. a^33. 若2^x = 32，则x的值为？A. 5B. 4C. 3D. 24. 下列哪个数的负整数指数幂等于1？A. 2B. 0C. 2D. 15. 下列哪个等式成立？A. 2^3 = 3^2B. 3^2 = 4^2C. 2^5 = 4^3D. 2^6 = 8^26. 当x为正数时，下列哪个式子的值最大？A. x^0B. x^1C. x^1D. x^27. 若3^(2x) = 9，则x的值为？A. 1B. 2C. 3D. 48. 下列哪个数的正整数指数幂等于它本身？A. 0B. 1C. 1D. 29. 下列哪个等式不成立？A. (2^3)^2 = 2^6B. (3^2)^3 = 3^6C. (4^2)^3 = 4^6D. (5^2)^3 = 5^610. 若a^2 = 25，则a的值为？A. 5B. 5C. 3D. 3二、判断题：1. 任何非零数的0次幂都等于1。

（）2. 负整数指数幂表示正整数指数幂的倒数。

（）3. 当底数大于1时，指数越大，结果越大。

（）4. 2^3 和 3^2 的值相等。

（）5. 任何正数的负整数指数幂都是正数。

（）6. 当指数为负数时，其值一定小于1。

（）7. (a^2)^3 = a^5。

（）8. 0的任何正整数指数幂都等于0。

（）9. 若a^3 = b^3，则a = b。

（）10. 指数函数的图像一定经过原点。

（）三、计算题：1. 计算：2^5 × 2^32. 计算：(1/2)^43. 计算：3^2 ÷ 3^34. 计算：5^0 + 3^05. 计算：(2/3)^26. 计算：4^(2)7. 计算：2^3 × 3^28. 计算：(1/5)^(1)9. 计算：2^2 ÷ 4^210. 计算：(3^2)^311. 计算：2^4 × 2^(3)12. 计算：(1/4)^(2)13. 计算：5^3 ÷ 5^214. 计算：3^0 2^015. 计算：(2/5)^(1)16. 计算：6^(2) × 6^317. 计算：(1/2)^(3)18. 计算：8^2 ÷ 4^319. 计算：10^0 + 10^(1)20. 计算：(3/4)^2四、应用题：1. 一个细菌每20分钟分裂一次，每次分裂成两个。

九年级下册数学基础训练答案人教版2022一、选择题（本题包括15小题，每小题5分，共75分。

每小题只有1个选项符合题意）1. 一元二次方程2x2－3x－4＝0的二次项系数是（） [单选题] *A. 2(正确答案)B. －3C. 4D. －42．抛物线y=2x2，y=﹣2x2，共有的性质是（） [单选题] *A．开口向下B．对称轴是y轴(正确答案)C．都有最高点D．y随x的增大而增大3．方程x2－2x-3＝0经过配方法化为(x＋a)2＝b的形式，正确的是（） [单选题] *A．(正确答案)B.C.D．4．下列说法中，正确的是（） [单选题] *A．不可能事件发生的概率为0(正确答案)B．随机事件发生的概率为0.5C．概率很小的事件不可能发生D．投掷一枚质地均匀的硬币100次，正面朝上的次数一定为50次5．方程的解是（） [单选题] *A．2B．3C．-1,2D．-1,3(正确答案)6.在平面直角坐标系中，将二次函数的图像向左平移2个单位长度，再向上平移1个单位长度，所得抛物线对应的函数表达式为（） [单选题] *A．B.(正确答案)C.D.7．有一个正方体，6个面上分别标有1～6这6个整数，投掷这个正方体一次，则出现向上一面的数字为偶数的概率是（） [单选题] *A．(正确答案)B.C.D．8．下列方程中，没有实数根的方程是（） [单选题] *A．B.(正确答案)C.D．(k属于任意实数）9．把方程x2+2x＝5（x﹣2）化成ax2+bx+c＝0的形式，则a，b，c的值分别为（） [单选题] *A．1，﹣3，2B．1，7，﹣10C．1，﹣5，12D．1，﹣3，10(正确答案)10．三张外观相同的卡片分别标有数字1、2、3，从中随机一次抽出两张，这张卡片上的数字恰好小于3的概率是（） [单选题] *A．B.(正确答案)C.D．11．抛物线的顶点坐标是（） [单选题] *A．B.(正确答案)C.D．12．某药品经过两次降价，每瓶零售价由168元降为128元．已知两次降价的百分率相同，每次降价的百分率为x，根据题意列方程得（） [单选题] *A.B.(正确答案)C.D.13．抛物线y=2（x﹣3）2+1的顶点坐标是（） [单选题] *A．（3，1）(正确答案)B．（3，﹣1）C．（﹣3，1）D．（﹣3，﹣1）14.对于二次函数y＝- x2+2，当x为x1和x2时，对应的函数值分别为y1和y2，若x1>x2>0，则y1与y2的大小关系是( ) [单选题] *A.B.(正确答案)CD.无法比较15在同一直角坐标系中，一次函数 y＝ax＋k 和二次函数 y＝ax2＋k的图象大致为() [单选题] *A.B.C.D.(正确答案)二、填空题（本题包括5小题，每小题5分，共25分）16．(2分)当k≠时，方程kx2-x=2+3x2是关于的一元二次方程． [填空题] *_________________________________(答案：3)17．（2分）不透明袋子中装有10个球，其中有2个红球、3个绿球和5个蓝球，这些球除颜色外无其他差别．从袋子中随机取出1个球，则它是红球的概率是．（小数表示） [填空题] *_________________________________(答案：0.5)18．（2分）一元二次方程x(x-6)=0的两个实数根中较大的为. [填空题] *_________________________________(答案：6)19．(2分)若关于的一元二次方程x2+(k-3)x+k=0的一个根是－2，则另一个根是______． [填空题] *空1答案：1020.抛物线y=7(x-3)2的开口______，对称轴是______，当x=_____时，取得最_______值，这个值等于________。

人教版九年级下册数学全册测试卷含答案 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】二次函数测试题一、填空题（每空2分，共32分）1.二次函数y=2x 2的顶点坐标是 ，对称轴是 .2.函数y=(x －2)2+1开口 ，顶点坐标为 ，当 时，y 随x 的增大而减小.3.若点（1，0），（3，0）是抛物线y=ax 2+bx+c 上的两点，则这条抛物线的对称轴是 .4.一个关于x 的二次函数，当x=－2时，有最小值－5，则这个二次函数图象开口一定 .5.二次函数y=3x 2－4x+1与x 轴交点坐标 ，当 时，y>0.6.已知二次函数y=x 2－mx+m －1，当m= 时，图象经过原点；当m= 时，图象顶点在y 轴上.7.正方形边长是2cm ，如果边长增加xcm ，面积就增大ycm 2，那么y 与x 的函数关系式是________________.8.函数y=2(x －3)2的图象，可以由抛物线y=2x 2向 平移 个单位得到.9.当m= 时，二次函数y=x 2－2x －m 有最小值5.10.若抛物线y=x 2－mx+m －2与x 轴的两个交点在原点两侧，则m 的取值范围是 .二、选择题（每小题3分，共30分）11.二次函数y=(x －3)(x+2)的图象的对称轴是（ ）=3 =－3 C. 12x =-D. 12x = 12.二次函数y=ax 2+bx+c 中，若a>0,b<0，c<0,则这个二次函数的顶点必在（ ）A.第一象限B.第二象限C.第三象限D.第四象限13.若抛物线y=+3x+m 与x 轴没有交点，则m 的取值范围是（ ）≤ ≥4.5 C.m> D.以上都不对14.二次函数y=ax 2+bx+c 的图如图所示，则下列结论不正确的是（ ）<0,b>0 －4ac<0 C.a －b+c<0 －b+c>015.函数是二次函数m x m y m +-=-22)2(，则它的图象（ ）A.开口向上，对称轴为y 轴B.开口向下，顶点在x 轴上方C.开口向上，与x 轴无交点D.开口向下，与x 轴无交点16.一学生推铅球，铅球行进高度y(m)与水平距离x(m)之间的关系是35321212++-=x x y ，则铅球落地水平距离为（ ） 53B.3mC.10mD.12m (第14题)17.抛物线y=ax 2+bx+c 与y 轴交于A 点，与x 轴的正半轴交于B 、C 两点，且BC=2，S ΔABC =4，则c 的值（ ）A.－5 或－4 C.4 D.－418.二次函数y=ax 2+bx+c 的图象如图所示，则此函数解析式为（ ）=－x 2+2x+3 =x 2－2x －3 C.y=－x 2－2x+3 = －x 2－2x －319.函数y=ax 2+bx+c 和y=ax+b 在同一坐标系中大致图象是（ ）20.若把抛物线y=x 2+bx+c 向左平移2个单位，再向上平移3个单位，得到抛物线y=x 2，则（ ）=－2,c=3 =2,c=－3 C.b=－4,c=1 =4,c=7三、计算题（共38分）21.已知抛物线y=ax 2+bx+c 与x 轴交点的横坐标分别为－1，2，且抛物线经过点（3，8），求这条抛物线的解析式。

【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

】第二十六章 反比例函数基础知识反馈卡·26.1.1时间：10分钟 满分：25分 一、选择题(每小题3分，共9分)1．下列函数中是反比例函数的是( ) A ．y ＝2x ＋1 B ．y ＝0.75x C ．x ∶y ＝18 D ．xy ＝12．若函数y ＝x 2m －1为反比例函数，则m 的值是( )A ．－1B ．0 C.12D ．13．反比例函数y ＝(m ＋1)x －1中m 的取值范围是( ) A ．m ≠1 B．m ≠－1 C ．m ≠±1 D ．全体实数 二、填空题(每小题4分，共8分)4．已知反比例函数y ＝k x的图象经过点(1，－2)，则k ＝________.5．老李家一块地收粮食1000 kg ，这块地的亩数s 与亩产量t kg/亩之间的关系是______________．三、解答题(共8分)6．已知y 与x 的反比例函数解析式为y ＝3，请完成下表：x －3 －1 1 3 y时间：10分钟 满分：25分一、选择题(每小题3分，共9分)1．已知反比例函数的图象经过点(－1,2)，则它的解析式是( )A ．y ＝－12xB ．y ＝－2xC ．y ＝2xD ．y ＝1x2．函数y ＝－1x的图象在( )A ．第一象限B ．第二象限C ．第一、三象限D ．第二、四象限3．若双曲线y ＝2k －1x的图象经过第二、四象限，则k 的取值范围是( )A ．k ＞12B ．k ＜12C ．k ＝12D ．不存在二、填空题(每小题4分，共8分)4．已知函数y ＝k x (k ≠0)，当x ＝－12时，y ＝6，则此函数的解析式为____________．5．试写出图象位于第二、四象限的一个反比例函数的解析式：___________. 三、解答题(共8分)6．己知反比例函数的图象经过点A (－2,3)．(1)函数的图象位于哪些象限内？y 随x 的增大如何变化？ (2)点B (1，－6)，C (－3，－2)是否在这个函数图象上？时间：10分钟 满分：25分一、选择题(每小题3分，共9分)1．某村的粮食总产量为a (a 为常数)吨，设该村的人均粮食产量为y 吨，人口数为x ，则y 与x 之间的函数关系式的大致图象应为( )2．已知反比例函数y ＝k x的图象经过点P (－3,5)，则这个函数的图象位于( ) A ．第二、三象限 B ．第一、三象限 C ．第三、四象限 D ．第二、四象限3．如图J26­2­1，点P 在反比例函数y ＝1x(x >0)的图象上，且横坐标为2.若将点P 先向右平移两个单位，再向上平移一个单位后所得的点为点P ′.则在第一象限内，经过点P ′的反比例函数图象的解析式是( )图J26­2­1A ．y ＝－5x (x >0)B ．y ＝5x (x >0)C ．y ＝－6x(x >0) D ．y ＝6x(x >0)二、填空题(每小题4分，共8分)4．计划修建水渠1000米，则修建天数y 和每日修建量x 之间的函数关系式为__________________．5．长方体的体积为103 m 3，底面积为S ，高度为d ，则S 与d 之间的函数关系式为 ____________；当S ＝500时，d ＝________________.三、解答题(共8分)6．某电厂有5000吨电煤．(1)求：这些电煤能够使用的天数x (单位：天)与该厂平均每天用煤吨数y (单位：吨)之间的函数关系；(2)若平均每天用煤200吨，则这批电煤能用多少天？(3)若该电厂前10天每天用200吨，后因各地用电紧张，每天用电煤300吨，则这批电煤共可用多少天？1．B 2.D3．B 解析：双曲线图象位于第二、四象限，则2k －1<0，所以k <12.4．y ＝－3x5．答案不唯一，如y ＝－2x6．解：设反比例函数的解析式为y ＝kx(k ≠0)， 把A (－2,3)点代入得 k ＝xy ＝－6.∴反比例函数的解析式为y ＝－6x.(1)函数位于第二、四象限内，在每个象限内y 随x 的增大而增大． (2)点B 满足函数关系式，点C 不满足函数关系式， ∴点B 在函数图象上，点C 不在函数图象上． 基础知识反馈卡·26.2 1．C 2.D 3.D4．y ＝1000x5．S ＝103d2 m6．解：(1)y ＝5000x.(2)把x ＝200代入y ＝5000x，得y ＝25.故这批电煤能用25天．(3)前10天后还剩下5000－10×200＝3000(吨)电煤，可以用3000300＝10(天)，故共可用20天．【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

陕西省九年级下学期数学基础试题姓名:________ 班级:________ 成绩:________一、单选题1 . 如图，小明为了测量河宽AB，先在BA延长线上取一点D，再在同岸取一点C，测得∠CAD=60°，∠BCA=30°，AC=15 m，那么河AB宽为（）A．15 m B． m C． m D． m2 . 如图，若，则下列结论中，与相等的是（）A．B．C．D．3 . AB是⊙O的直径，BD、CD分别是过⊙O上点B、C的切线，且∠BDC=100°，连接AC，则∠A的度数是（）A．15°B．30°C．40°D．45°4 . 如图所示的几何体的主视图为（）A．B．C．D．5 . 近视眼镜的度数y(度)与镜片焦距x(m)成反比例，已知400度近视眼镜镜片的焦距为0.25m，则y与x的函数关系式为（）A．B．C．D．6 . 下列计算结果正确的是（）A．B．C．D．7 . 以下说法正确的有（）①正八边形的每个内角都是135°;②反比例函数y=﹣，当x＜0时，y随x的增大而增大;③长度等于半径的弦所对的圆周角为30°;④分式方程的解为；A．1个B．2个C．3个D．4个8 . 在平面直角坐标系中，抛物线y＝x（x+2）经过平移变换后得到抛物线y＝（x﹣1）2，其变换是（）A．右移2个单位，下移1个单位B．右移2个单位，上移1个单位C．左移2个单位，上移1个单位D．左移2个单位，下移1个单位9 . 下面四个数中，属于负数的是（）A．-3B．0C．0.2D．310 . 下列所述图形中，是中心对称图形，但不是轴对称图形的是（）A．正三角形B．平行四边形C．正五边形D．圆二、填空题11 . 已知，如图，中，，，为形内一点，若，，则的度数为__________．12 . 不等式组：的解集在数轴上可表示为（）A．B．C．D．13 . 有六张正面分别标有数﹣1，0，1，2，3，4的不透明卡片，它除了数字不同外其余全部相同，现将它们背面朝上，洗匀后从中任取一张，将卡片上的数记为a，则使关于x的方程有正整数解的概率为_____．14 . 当x的取值为_____时，分式有意义．15 . 如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠D＝45°，则劣弧AC的长为_____．16 . 如图，在△ABC中，∠C=90°，AB=5，BC=4．点D是边AC的中点，点E在边AB上，将△ADE沿DE翻折，使点A落在点A′处，当线段AE的长为_______时，A′E∥BC．17 . 把多项式因式分解的结果是______.18 . 计算﹣的结果等于．19 . 点A（﹣3，y1），B（2，y2）在抛物线y＝﹣x2﹣3x+c上，则y1_____y2．（填“＞”，“＜”域或“＝”）20 . 若100粒大米的重量约为2.5克，请用科学记数法表示2吨大米约有______粒．三、解答题21 . （1）（问题发现）如图①，正方形AEFG的两边分别在正方形ABCD的边AB和AD上，连接CF．填空：①线段CF与DG的数量关系为；②直线CF与DG所夹锐角的度数为．（2）（拓展探究）如图②，将正方形AEFG绕点A逆时针旋转，在旋转的过程中，（1）中的结论是否仍然成立，请利用图②进行说明．（3（解决问题）如图③，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，AB＝AC＝4，O为AC的中点．若点D在直线BC上运动，连接OE，则在点D的运动过程中，线段OE长的最小值为（直接写出结果）．22 . 如图，平面直角坐标系中，矩形OABC的顶点B的坐标为（7，5），顶点A，C分别在x轴，y轴上，点D 的坐标为（0，1），过点D的直线与矩形OABC的边BC交于点G，且点G不与点C重合，以DG为一边作菱形DEFG，点E在矩形OABC的边OA上，设直线DG的函数表达式为y=kx+b（1）当CG=OD时，求直线DG的函数表达式；（2）当点E的坐标为（5，0）时，求直线DG的函数表达式；（3）连接BF，设△FBG的面积为S，CG的长为a，请直接写出S与a的函数表达式及自变量a的取值范围．23 . 好街坊橱具店购进电饭煲和电压锅两种电器进行销售，其进价与售价如表：进价（元/台）售价（元/台）电饭煲200250电压锅160200（1）一季度，橱具店购进这两种电器共 30 台，用去了 5520 元，并且全部售完，问橱具店在该买卖中赚了多少钱？（2）为了满足市场需求，二季度橱具店决定用不超过 8850 元的资金采购电饭煲和电压锅共 50 台，且电饭煲的利润不少于电压锅的利润的，问橱具店有哪几种进货方案？并说明理由；（3）在（2）的条件下，请你通过计算判断，哪种进货方案橱具店赚钱最多？24 . 如图，已知△ABC中，四边形DEGF为正方形，D、E在线段AC、BC上，F、G在AB上，如果S△ADF=S△CDE=1，S△BEG=3，求△ABC的面积．25 . 如图，O为∠MBN角平分线上一点，⊙O与BN相切于点C，连结CO并延长交BM于点A，过点A作AD⊥BO 于点D．（1）求证：AB为⊙O的切线；（2）若BC＝6，tan∠ABC＝，求AD的长．26 . 某班同学在一次综合实践活动中，对本县居民参加“全民医保”情况进行了调查，同学们利用节假日随机调查了3000人，对调查结果进行了统计分析，绘制出两幅不完整的统计图：[注：图中A表示城镇职工基本医疗保险；B表示城镇居民基本医疗保险；C表示“新型农村合作医疗”；D表示其他情况]（1）补全条形统计图；（2）在本次调查中，B类人数占被调查人数的百分比为；扇形统计图中D区域所对应的圆心角的大小为．（3）据了解，国家对B类人员每人每年补助210元．已知该县人口数约为100万，请估计该县B类人员每年享受国家补助共多少元？27 . （1）求不等式组的整数解；（2）化简参考答案一、单选题1、2、3、4、5、6、7、8、9、10、二、填空题1、2、3、4、5、6、7、8、9、10、三、解答题1、2、3、4、5、6、7、。

初中总复习基础测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷30分,第Ⅱ卷70分,共100分,考试时间100分钟.第Ⅰ卷(选择题共30分)一、选择题(每题3分,共30分)1.-3的相反数是( )A.3B.-3C.±3D.√32.已知☉O的半径是5,点A到圆心O的距离是7,则点A与☉O的位置关系是( )A.点A在☉O上B.点A在☉O内C.点A在☉O外D.点A与圆心O重合3.下列调查中,适宜采用普查方式的是( )A.了解一批圆珠笔的寿命B.了解全国九年级学生的身高现状C.检查一枚用于发射卫星的运载火箭的各零部件D.考察人们保护海洋的意识4.太阳的温度很高,其表面温度大约有6000 ℃,而太阳中心的温度达到了19200000 ℃,用科学记数法可将19200000表示为( )A.1.92×106B.1.92×107C.19.2×106D.0.192×1075.下列选项中不是图FX-1中正六棱柱三视图的是()图FX -1 图FX -26.下列运算正确的是 ( )A .a 2·a 3=a 6B .(13)-1=-3 C .√36=±6 D .a 6÷a 3=a 37.一个三角形的两边长分别为3和6,第三边的边长是方程(x-2)(x-4)=0的根,则这个三角形的周长是 ( )A .11B .11或13C .13D .以上选项都不正确8. 已知a ≠0,在同一平面直角坐标系中,函数y=ax 与y=ax 2的图象有可能是( )图FX -3图FX -49.如图FX -4所示,AB 是☉O 的直径,AD 是☉O 的切线,BC ∥OD 交☉O 于点C.若AB=2,OD=3,则BC 的长为 ( )A.32B.23C.√32D.√2210.如图FX-5(a)所示长方形纸带,∠DEF=20°,将纸带沿EF折叠成图(b),再沿BF折叠成图(c),则图(c)中∠CFE的度数是( )图FX-5A.110°B.120°C.140°D.150°请将选择题答案填入下表:题号 1 2 3 4 5 6 7 8 9 10 总分答案第Ⅱ卷(非选择题共70分)二、填空题(每题3分,共18分)11.函数y=√2−x的自变量x的取值范围是.12.因式分解:2x2-8=.13.如图FX-6,△ABC与△A'B'C'关于直线l对称,∠C'=30°,则∠A的度数为.14.从2,3,4这三个数字中,任意抽取两个不同数字组成一个两位数,则这个两位数能被3整除的概率是.15.如图FX-7,直线OA与反比例函数y=kx(k≠0)的图象在第一象限交于点A,AB⊥x轴于点B,△OAB的面积为2,则k=.图FX-6图FX-7图FX-816.如图FX-8所示,在△ABC中,BC=4,以点A为圆心,2为半径的☉A与BC相切于点D,交AB于点E,交AC于点F,且∠EAF=80°,则图中阴影部分的面积是.三、解答题(共52分)17.(5分)解不等式2(x+1)-1≥3x+2,并把它的解集表示在数轴上.图FX-918.(5分)先化简代数式(xx+3+3x-3)÷1x2-9,然后选取一个合适．．的x的值,代入求值.19.(6分)某班同学分三组进行数学活动,对七年级400名同学最喜欢喝的饮料种类情况、八年级300名同学零花钱的最主要用途情况、九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形统计图、条形统计图、统计表来描述整理得到的数据.图FX-10图FX-11九年级同学完成家庭作业时间情况统计表时间1小时 1.5小时2小时 2.5小时人数508012050根据以上信息,请回答下列问题:(1)七年级400名同学中最喜欢喝冰红茶的人数是多少?(2)补全八年级300名同学零花钱的最主要用途情况条形统计图;(3)九年级300名同学完成家庭作业的平均时间大约是多少小时(结果保留一位小数)?20.(6分)为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2014年市政府共投资3亿元人民币建设了廉租房12万平方米,2016年投资6.75亿元人民币建设廉租房,若在这两年内每年投资的增长率相同. (1)求每年市政府投资的增长率;(2)若这两年内的建设成本不变,则2016年建设了多少万平方米廉租房?20. (6分)如图FX -12,三楚第一山——东方山是黄石地区的佛教圣地,也是国家AAA 级游览景区.它的主峰海拔约为600米,主峰AB 上建有一座电信信号发射架BC ,在山脚P 处测得峰顶的仰角为α,发射架顶端的仰角为β,其中tan α=35,tan β=58,求发射架的高BC.图FX -1222.(6分)如图FX-13,在菱形ABCD中,对角线AC,BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.(1)证明:四边形ACDE是平行四边形;(2)若AC=8,BD=6,求△ADE的周长.图FX-1323.(8分)如图FX-14,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的☉O交BC于点G,交AB于点F,FB恰为☉O的直径.(1)求证:AE与☉O相切;(2)当BC=4,cos C=1时,求☉O的半径.3图FX-1424.(10分)某商场在销售旺季临近时,某品牌的童装销售价格呈上升趋势.假如这种童装开始时的售价为每件20元,并且每周(7天)涨价2元,从第6周开始,保持每件30元的稳定价格销售,直到第11周结束,该童装不再销售.(1)请写出销售价格y(元)与周次x之间的函数解析式;(2)如果该品牌童装于进货当周售完,且这种童装每件进价z(元)与周次x之间的关系为(x-8)2+12(1≤x≤11,且x为整数),那么该品牌童装在第几周售出后,每件获得的利润最大? z=-18最大利润是多少?初中总复习基础测试1.A2.C3.C4.B5.A6.D7.C8.C9.B10.B11.x≤212.2(x+2)(x-2)13.60°14.1315.416.4-89π17.解:去括号,得2x+2-1≥3x+2.移项,得2x-3x≥2-2+1.合并同类项,得-x≥1.系数化为1,得x≤-1.把这个不等式的解集表示在数轴上如图所示.18.解:解法一:原式=x(x -3)(x+3)(x -3)+3(x+3)(x -3)(x+3)÷1x 2-9=x 2+9(x+3)(x -3)·(x+3)(x-3)=x 2+9.取x=1,得原式=10. 解法二:原式=(x x+3+3x -3)·(x+3)(x-3)=x (x-3)+3(x+3)=x 2+9.取x=1,得原式=10. (注:只要x 的取值不是3或-3即可)19. 解:(1)七年级同学最喜欢喝冰红茶的人数是400×(1-25%-25%-10%)=160(人).(2)补全条形统计图如图所示.(3)1×50+1.5×80+2×120+2.5×5050+80+120+50≈1.8(时). 答:九年级300名同学完成家庭作业的平均时间大约是1.8小时. 20.解:(1)设每年市政府投资的增长率为x.根据题意,得3(1+x )2=6.75, 解得x 1=0.5,x=-2.5(不合题意,舍去).答:每年市政府投资的增长率为50%.(2)6.753×12=27(万平方米). 答:2016年建设了27万平方米廉租房.21.解:在Rt △PAB 中,tan α=AB PA ,∴PA=AB tanα=60035=1000(米).在Rt △PAC 中,tan β=AC PA ,∴AC=PA ·tan β=1000×58=625(米). ∴BC=AC -AB=625-600=25(米).22.解:(1)证明:∵四边形ABCD 是菱形,∴AB ∥CD ,AC ⊥BD ,∴AE ∥CD ,∠AOB=90°.∵DE ⊥BD ,即∠EDB=90°,∴∠AOB=∠EDB ,∴DE ∥AC ,∴四边形ACDE 是平行四边形.(2)∵四边形ABCD 是菱形,AC=8,BD=6,∴AO=4,DO=3,AD=CD=5.∵四边形ACDE 是平行四边形,∴AE=CD=5,DE=AC=8,∴△ADE 的周长为AD+AE+DE=5+5+8=18.23.[全品导学号:76132366]解:(1)证明:如图,连接OM ,则OM=OB ,∴∠1=∠2. ∵BM 平分∠ABC ,∴∠1=∠3,∴∠2=∠3,∴OM ∥BC ,∴∠AMO=∠AEB.∵在△ABC 中,AB=AC ,AE 是角平分线,∴AE ⊥BC ,∴∠AEB=90°,∴∠AMO=90°,即OM ⊥AE ,故AE 与☉O 相切.(2)∵在△ABC 中,AB=AC ,AE 是角平分线,∴BE=12BC ,∠ABC=∠C. ∵BC=4,cos C=13,∴BE=2,cos ∠ABC=13. ∵在△ABE 中,∠AEB=90°,∴AB=BE cos ∠ABC=6. 设☉O 的半径为r ,则AO=6-r.∵OM ∥BC ,∴△AOM ∽△ABE ,∴OM BE =AO AB ,即r 2=6−r 6,解得r=32,即☉O 的半径为32. 24.解:(1)y={20+2(x -1)=2x +18(1≤x <6,且x 为整数),30(6≤x ≤11,且x 为整数).(2)设利润为w 元,则w={y -z =2x +18+18(x -8)2-12=18x 2+14(1≤x <6,且x 为整数),y -z =30+18(x -8)2-12=18(x -8)2+18(6≤x ≤11,且x 为整数).对于w=18x 2+14(1≤x<6,且x 为整数),当x=5时,w 最大=1718. 对于w=18(x-8)2+18(6≤x ≤11,且x 为整数), 当x=11时,w 最大=18×9+18=1918. 综上可知,该品牌童装在第11周售出后,每件获得的利润最大,最大利润为1918元.。

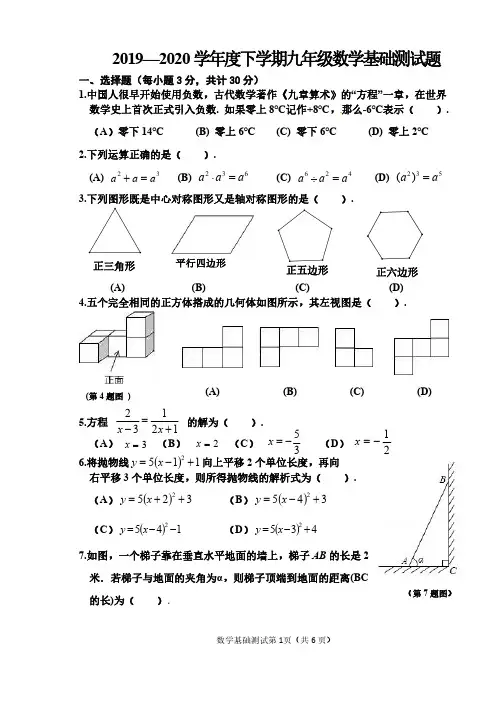
2019—2020 学年度下学期九年级数学基础测试题
一、选择题（每小题3 分，共计30 分）
1.中国人很早开始使用负数，古代数学著作《九章算术》的“方程”一章，在世界数学史上首次正式引入负数. 如果零上8℃记作+8℃，那么-6℃表示（）.
（A）零下14℃(B) 零上6℃(C) 零下6℃(D) 零上2℃
2.下列运算正确的是（）.
(A)a2 +a =a3(B)a2 ⋅a3 =a6(C)a6 ÷a2 =a4(D)(a2 )3 =a5
3.下列图形既是中心对称图形又是轴对称图形的是（）.
正三角形平行四边形正五边形
正六边形
(A) (B) (C) (D)
4.五个完全相同的正方体搭成的几何体如图所示，其左视图是（）.
(第4 题图)
2 1
(A) (B) (C) (D)
5.方程=
x - 3 2x+1
的解为（）.
x =-
5
x =-
1
（A）x = 3 （B）x = 2 （C）（D
3 2
6.将抛物线y =5(x-1)2 +1向上平移2 个单位长度，再向右
平移3 个单位长度，则所得抛物线的解析式为（）.
（A）y =5(x+2)2 +3
（C）y =5(x-4)2 -1
（B）y =5(x-4)2 +3
（D）y =5(x-3)2 +4
7.如图，一个梯子靠在垂直水平地面的墙上，梯子AB 的长是2
米．若梯子与地面的夹角为α，则梯子顶端到地面的距离(BC
的长)为（）．
（第7 题图）。

一、选择题（每题3分，共30分）1. 下列数中，绝对值最小的是（）A. -2B. 0C. 1D. -3答案：B解析：绝对值表示一个数到原点的距离，0的绝对值为0，其他数的绝对值都大于0，所以0的绝对值最小。

2. 如果a + b = 5，a - b = 1，那么a的值为（）A. 3B. 4C. 2D. 6答案：A解析：将两个等式相加得2a = 6，所以a = 3。

3. 下列图形中，是轴对称图形的是（）A. 矩形B. 正方形C. 圆D. 三角形答案：C解析：轴对称图形是指图形沿某条直线对折后，两边完全重合。

矩形、正方形和圆都是轴对称图形，但题目要求选择一个，故选C。

4. 如果x^2 - 4x + 3 = 0，那么x的值为（）A. 1，3B. -1，3C. 1，-3D. -1，-3答案：A解析：通过因式分解得(x - 1)(x - 3) = 0，所以x = 1或x = 3。

5. 下列函数中，是奇函数的是（）A. y = x^2B. y = x^3C. y = |x|D. y = 2x答案：B解析：奇函数满足f(-x) = -f(x)，只有y = x^3满足这个条件。

6. 下列方程中，有唯一解的是（）A. x + 1 = 0B. x^2 + 1 = 0C. x^2 - 4 = 0D. x^2 + 2x + 1 = 0答案：A解析：A选项的方程x + 1 = 0有唯一解x = -1；B、C选项的方程无实数解；D选项的方程x^2 + 2x + 1 = (x + 1)^2 = 0有两个解x = -1。

7. 下列命题中，正确的是（）A. 所有的偶数都是质数B. 所有的质数都是奇数C. 所有的奇数都是合数D. 所有的合数都是偶数答案：B解析：只有2是偶数同时也是质数，所以A错误；除了2以外的所有质数都是奇数，所以B正确；奇数中也有质数，如3，所以C错误；合数中也有偶数，如4，所以D错误。

8. 在△ABC中，若∠A = 30°，∠B = 60°，那么∠C的度数为（）A. 90°B. 120°C. 30°D. 60°答案：B解析：三角形内角和为180°，所以∠C = 180° - ∠A - ∠B = 180° - 30° - 60° = 90°。

专题27.13 黄金分割（基础篇）（专项练习）一、单选题1．大自然巧夺天工，一片树叶也蕴含着“黄金分割”．如图，P为AB的黄金分割点（AP>PB），如果AB的长度为8cm，那么BP的长度是（）A．12-B．9-C．4D．42．已知点C是线段AB的黄金分割点，且2<，则AC长是（）AB=，AC BCA B1C．3D3523．把2米的线段进行黄金分割，则分成的较短的线段长为（）A．3B1C．1D．34．已知2AB=，点P是线段AB上的黄金分割点，且AP BP>，则AP的长为（）A1B C35D．325．下列说法正确的是（）A．每条线段有且仅有一个黄金分割点B．黄金分割点分一条线段为两条线段，其中较长的线段约是这条线段的0.618倍C．若点C把线段AB黄金分割，则AC2＝AB•BCD．以上说法都不对6．下列说法正确的是（）A．每一条线段有且只有一个黄金分割点B．黄金分割点分一条线段为两段，其中较短的一段是这条线段的0.618倍C．若点C把线段AB黄金分割，则AC是AB和BC的比例中项D．黄金分割点分一条线段为两段，其中较短的一段与较长的一段的比值约为0.6187．下列命题正确的是（）A．任意两个等腰三角形一定相似B．任意两个正方形一定相似C ．如果C 点是线段AB 的黄金分割点，那么AC AB =D ．相似图形就是位似图形8．如图，线段1AB =，点1P 是线段AB 的黄金分割点(且11AP BP <)，点2P 是线段1AP 的黄金分割点（212AP PP <），点3P 是线段3AP 的黄金分割点()323,,AP P P <依此类推，则线段2020AP 的长度是（ ）A ．2020⎝⎭B ．2021⎝⎭C ．2020⎝⎭D ．2021⎝⎭9．已知点C 把线段AB 分成两条线段AC 、BC ，且AC BC >，下列说法错误的是（ ） A ．如果AC BCAB AC=，那么线段AB 被点C 黄金分割 B ．如果2AC AB BC =⋅，那么线段AB 被点C 黄金分割C ．如果线段AB 被点C 黄金分割，那么BC 与AB 的比叫做黄金比D ．0.618是黄金比的近似值10．等腰△ABC 中，AB=AC ，△A=36°，D 是AC 上的一点，AD=BD ，则以下结论中正确的有（ ）△△BCD 是等腰三角形；△点D 是线段AC 的黄金分割点；△△BCD△△ABC ；△BD 平分△ABC ． A ．1个B ．2个C ．3个D ．4个11．在△ABC 中，△A=36°，AB=AC ，BD 是△ABC 的角平分线，下列结论： △△ABD ，△BCD 都是等腰三角形； △AD=BD=BC ； △BC 2=CD•CA ； △D 是AC 的黄金分割点 其中正确的是（ ）A ．1个B ．2个C ．3个D ．4个二、填空题12．在线段AB 上，点C 把线AB 分成两条线段AC 和BC ，若AC BCAB AC=，则点C 叫做线段AB 的黄金分割点．若点P 是线段MN 的黄金分割点（PM PN >），当1MN =时，PM 的长是__________．13．勾股定理与黄金分割是几何中的双宝，前者好比黄金，后者堪称珠玉，生活中到处可见黄金分割的美．如图是一种贝壳的俯视图，点C分线段AB近似于黄金分割，已知AB=10 cm，AC＞BC，那么AC的长约为____________cm（结果精确到0.1 cm）．14．把2米长的线段进行黄金分割，则分成的较长的线段长为__________.15．古希腊时期，（称为黄金分割比例），著名的“断臂维纳斯” 2.236≈，则黄金分割比例约为______________．（精确到0.01）16．已知AB=2,点C是线段AB的黄金分割点（AC>BC），则AC= .17．把长度为4cm的线段进行黄金分割，则较长线段的长是__________cm．18．已知线段4AB=，点P是线段AB的黄金分割点（AP BP>），那么线段AP=______.（结果保留根号）19．已知线段AB长为2cm，P是AB的黄金分割点，则较长线段PA＝___；PB＝______．200.61803398=…，将这个分割比保留4个有效数字的近似数是．21．若点C为线段AB的黄金分割点，且AC＜BC，若AB＝10，则BC＝_____．22．若点P是线段AB的黄金分割点，AB=10cm，则较长线段AP的长是_____cm．三、解答题23．已知C、D是线段AB上的点，CD＝(√5﹣2)AB，AC＝BD，则C、D是黄金分割点吗？为什么？24．已知线段MN = 1，在MN 上有一点A ，如果AN =，求证：点A 是MN 的黄金分割点.25．（1）对于实数a 、b ，定义运算“⊕”如下：2a b a b ⊕=-．若(1)(2)8x x +⊕-=，求: 2(2)(23)x x x -⊕-的值；（2）已知点C 是线段AB 的黄金分割点（AC ＜BC ），若AB ＝4，求AC 的长．26．（1）我们知道，将一条线段AB 分割成大小两条线段AP 、PB ，使AP ＞PB ，点P 把线段AB 分成两条线段AP 和BP ，且=AP BP AB AP ，点P 就是线段AB 的黄金分割点，此时PAAB的值为 （填一个实数）：（2）如图，Rt△ABC 中，△B=90°，AB=2BC ，现以C 为圆心、CB 长为半径画弧交边AC 于D ，再以A 为圆心、AD 长为半径画弧交边AB 于E ． 求证：点E 是线段AB 的黄金分割点．27．某校要设计一座2m 高的雕像(如图)，使雕像的点C (肚脐)为线段AB (全身)的黄金分割点，上部AC (肚脐以上)与下部BC (肚脐以下)的高度比为黄金比．则雕像下部设计的高度应该为______(结果精确到0.001)米． 2. 236=，结果精确到0.001)．28．在等边三角形ABC中，点D，E分别在BC，AC上，且DC=AE，AD与BE交于点P，连接PC．(1)证明：ΔABE△ΔCAD．(2)若CE=CP，求证△CPD=△PBD．(3)在(2)的条件下，证明：点D是BC的黄金分割点.参考答案1．A【分析】根据黄金分割的定义得到AP AB，然后把AP的长度代入可求出AB的长．【详解】解：△P为AB的黄金分割点（AP＞PB），△AP AB，△AB的长度为8cm，△AP×8=4（cm），△BP=AB-AP=8-（4）=12-故选：A．【点拨】本题考查了黄金分割：把线段AB分成两条线段AC和BC（AC＞BC），且使AC 是AB和BC的比例中项（即AB：AC=AC：BC），叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点，其中AC AB．2．C【分析】利用黄金分割比的定义即可求解.【详解】由黄金分割比的定义可知BC AB===21△21)3=-=-=AC AB BC故选C【点拨】本题主要考查黄金分割比，掌握黄金分割比是解题的关键.3．A【分析】根据黄金分割的定义列式进行计算即可得解.【详解】解: 较短的线段长=2⨯(1=2故选A.【点拨】本题考查了黄金分割的概念, 熟记黄金分割的比值是解题的关键.4．A【分析】根据黄金分割点的定义和AP BP=，代入数据即可得出AP的长度．>得出AP AB【详解】解：由于P为线段AB＝2的黄金分割点，且AP BP>，则21==．ABAP=故选：A．35，2．5．B【分析】根据黄金分割的定义分别进行解答即可．【详解】A．每条线段有两个黄金分割点，故本选项错误；B．黄金分割点分一条线段为两条线段，其中较长的线段约是这条线段的0.618倍，正确；C．若点C把线段AB黄金分割，则AC2＝AB•BC，不正确，有可能BC2＝AB•AC．故选B．【点拨】本题考查了黄金分割，熟练掌握黄金分割的定义是解题的关键．6．D【分析】根据比例中项和黄金分割的概念分析各个说法.【详解】解：A、每一条线段有两个黄金分割点，错误；B、黄金分割点分一条线段为两段，其中较长的一段是这条线段的0.618倍，错误；C、若点C把线段AB黄金分割，则AC是AB和BC的比例中项，错误；D、黄金分割点分一条线段为两段，其中较长的一段与这条线段的比值约为0.618，正确；故选D．【点拨】此题考查黄金分割问题，理解比例中项、黄金分割的概念，是解题的关键． 7．B 【分析】根据相似多边形的概念、黄金分割点及位似可直接进行排除选项． 【详解】解：A 、任意两个等腰三角形的底角或顶角相等，则这两个等腰三角形相似，故原命题错误； B 、任意两个正方形一定相似，故原命题正确；C 、如果C 点是线段AB 的黄金分割点（AC ＞BC ），那么AC AB =D 、相似图形不一定是位似图形，故原命题错误； 故选B ．【点拨】本题主要考查相似多边形的概念、黄金分割点及位似，熟练掌握相似多边形的概念、黄金分割点及位似是解题的关键． 8．C 【分析】根据把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线叫做黄金比进行解答即可． 【详解】解：根据黄金比的比值，1BP =则11AP ==2323,,AP AP ==⎝⎭⎝⎭…依此类推，则线段20202020AP =⎝⎭，故选C ．【点拨】本题考查的是黄金分割的知识，理解黄金分割的概念，找出黄金分割中成比例的对应线段是解决问题的关键． 9．C 【解析】【分析】根据黄金分割的定义判断即可.【详解】根据黄金分割的定义可知A、B、D正确;C.如果线段AB被点C黄金分割（AC>BC）,那么AC与AB的比叫做黄金比,所以C错误.所以C选项是正确的.【点拨】本题考查了黄金分割的概念:把线段AB分成两条线段AC和BC（AC>BC）,且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB 的黄金分割点.注意线段AB的黄金分割点有两个.10．D【详解】△AB=AC，△△ABC=△C=12（180°-△A）=12（180°-36°）=72°，△AD=BD，△△DBA=△A=36°，△△BDC=2△A=72°，△△BDC=△C，△△BCD为等腰三角形，所以△正确；△△DBC=△ABC-△ABD=36°，△△ABD=△DBC，△BD平分△ABC，所以△正确；△△DBC=△A，△BCD=△ACB，△△BCD△△ABC，所以△正确；△BD：AC=CD：BD，而AD=BD，△AD：AC=CD：AD，△点D是线段AC的黄金分割点，所以△正确．故选D.11．D【解析】试题分析：在△ABC，AB=AC，△A=36°，BD平分△ABC交AC于点D，可推出△BCD，△ABD 为等腰三角形，可得AD=BD=BC，利用三角形相似解题．解：如图，△AB=AC，△A=36°，△△ABC=△C=72°，△BD平分△ABC交AC于点D，△△ABD=△CBD=△ABC=36°=△A，△AD=BD，△BDC=△ABD+△A=72°=△C ， △BC=BD ，△△ABD ，△BCD 都是等腰三角形，故△正确； △BC=BD=AD ，故△正确； △△A=△CBD ，△C=△C ， △△BCD△△ACB ， △，即BC 2=CD•AC ，故△正确； △AD=BD=BC ，△AD 2=AC•CD=（AD+CD ）•CD ， △AD=CD ，△D 是AC 的黄金分割点．故△正确， 故选D ．考点：相似三角形的判定与性质；黄金分割．12 【分析】根据若点P 是线段MN 的黄金分割点（PM PN >），则PM MN 计算即可． 【详解】当PM ＞PN 时，，．是解题的关键． 13．6.2 【分析】黄金分割又称黄金率，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值为1：0.618或1.618：1，即长段为全段的0.618，0.618被公认为最具有审美意义的比例数字．上述比例是最能引起人的美感的比例，因此被称为黄金分割．【详解】由题意知AC:AB=BC:AC，△AC:AB≈0.618，△AC=0.618×10cm≈6.2(结果精确到0.1cm)故答案为6.2.【点拨】本题考查黄金分割，解题关键是掌握黄金分割定理.14．米【解析】【分析】把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分叫做黄金比．【详解】解：△将长度为2米的线段进行黄金分割，△较长的线段=2⨯米.是解的关键．15．0.62【分析】把黄金分割比例按要求进行计算即可．【详解】解： 2.236≈，≈2.23612-≈0.62，故答案为：0.62．【点拨】本题考查了求一个数的近似值，有理数的除法，正确计算是解题的关键．161【解析】21AC==17．()2cm．【解析】根据黄金分割的定义得到较长线段的长=×4，然后进行二次根式的运算即可．解：较长线段的长=×4=（2）cm．故答案为（2）cm．18．2【分析】计算即可.【详解】解：△点P是线段AB的黄金分割点（AP>BP）△AP2AB==故答案为：2.【点拨】本题考查的知识点是黄金分割，熟记黄金分割点的比值是解题的关键.19．)1cm (3cm【分析】根据黄金分割的概念得到较长线段AB，则PB=AB-352AB，然后把AB=2cm代入计算即可．【详解】解：△P是AB的黄金分割点，△较长线段AB，△PB=AB-352AB，而AB=2cm，△PA=)1cm，PB=(3cm．故答案为：)1cm；(3cm．【点拨】本题考查了黄金分割的概念：一个点把一条线段分成两段，其中较长线段是较短线段与整个线段的比例中项，那么就说这条线段被这点黄金分割，这个点叫这条线段的黄金分倍．20．0.6180【解析】根据有效数字的定义，运用四舍五入法保留4个有效数字，需观察第五位有效数字，由于第五位有效数字是，不需往前面进一位．所以0.61803398…≈0.618021．5【分析】根据黄金分割点的定义，知BC为较长线段；则BC AB，代入数据即可得出AC的值．【详解】解：由于C为线段AB＝10的黄金分割点，且AC＜BC，BC为较长线段；则BC＝＝5．故答案为：5．【点拨】本题考查黄金分割：把线段AB分成两条线段AC和BC（AC＞BC），且使AC是AB和BC的比例中项（即AB：AC=AC：BC），叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点．其中AB≈0.618AB，并且线段AB的黄金分割点有两个．22．5【解析】△P是线段AB的黄金分割点，AP＞BP，AB，△AB=10cm，△AP=105=.故答案为5．点睛：若点P 是线段AB 的黄金分割点，且AP>BP ，则AP 2=BP·AB ，即AB. 23．C 、D 是黄金分割点.【解析】【分析】 根据题意求出AC 与AB 的关系，计算出AD 与AB 的关系，根据黄金比值进行判断即可．【详解】解：C 、D 是黄金分割点，△AC+CD+BD ＝AB ，CD ＝(√5﹣2)AB ，AC ＝BD ，△AC ＝3−√52AB ， AD ＝AC+CD ＝3−√52AB+(√5﹣2)AB ＝√5−12AB ， △D 是AB 的黄金分割点，同理C 也是AB 的黄金分割点．【点拨】本题考查黄金分割，关键是掌握黄金分割的概念和黄金比.24．见解析【解析】试题分析：先求得AM=√5−12，即可得到AM MN =AN AM =√5−12，结论得证。