六年级数学三角形

小学六年数学重要知识点归纳三角形的性质与分类在小学六年级的数学学习中，三角形是一个非常重要的几何形状。

学生们需要掌握三角形的性质与分类，以便更好地理解和解决与三角形相关的数学问题。

本文将对小学六年级数学中关于三角形的重要知识点进行归纳总结。

一、三角形的定义与性质1. 定义：三角形是由三条线段组成的闭合图形。

2. 三个顶点：三角形共有3个顶点，每个顶点由2条线段相交而成。

3. 三条边：三角形共有3条边，每条边是两个顶点之间的线段。

4. 三个角：三角形共有3个角，每个角是两条边之间的夹角。

5. 内角和：三角形的内角和等于180度。

二、三角形的分类根据三角形的边长和角度的大小，可以将三角形分为不同的类型。

1. 根据边长分类（1）等边三角形：三条边的长度相等。

（2）等腰三角形：两条边的长度相等。

（3）一般三角形：三条边的长度都不相等。

2. 根据角度大小分类（1）锐角三角形：三个角都是锐角，即小于90度。

（2）钝角三角形：三个角都是钝角，即大于90度。

（3）直角三角形：其中一个角是直角，即等于90度。

三、三角形的重要性质1. 外角和等于无关角的补角：三角形的任意一个外角与该外角相邻的两个内角的和等于180度。

2. 直角三角形的特性：直角三角形的两条直角边的平方和等于斜边的平方。

3. 等腰三角形的特性：等腰三角形的底边中线是高，两个底角相等，顶角的角平分线也是高和中线。

四、解决与三角形相关的数学问题1. 判断三角形类型：根据给定的边长和角度，判断三角形是等边、等腰还是一般三角形；判断三角形是锐角、钝角还是直角三角形。

2. 计算三角形的面积：根据给定的底边和高，应用三角形面积公式计算三角形的面积。

3. 判断三角形的相似性：根据给定的几何特征，判断两个三角形是否相似，并运用相似三角形的性质解决相关问题。

总结：小学六年级数学中，三角形的性质与分类是重要的知识点之一。

学生们需要掌握三角形的定义以及不同类型三角形的特点，同时要掌握三角形的重要性质和解决相关问题的方法。

六年级数学三角形试题答案及解析1.（2分）（2010•徐闻县）在三角形中，三个内角∠1，∠2，∠3，那么∠1=∠2﹣∠3，那么这个三角形一定是（）三角形．A.锐角B.直角C.钝角【答案】B【解析】根据三角形内角和等于180°，求出∠2=90°，从而判断这个三角形是直角三角形．解：∠1=∠2﹣∠3，即∠2=∠1+∠3，∠1+∠2+∠3=180°，2∠2=180°，∠2=90°；故这个三角形一定是直角三角形．故选：B．点评：本题主要考查三角形的分类、三角形内角和定理的运用，熟练掌握定理是解题的关键．2.图中阴影部分的面积是多少．(取)【答案】1.92【解析】如右上图，虚线将阴影部分分成两部分，分别计算这两部分的面积，再相加即可得到阴影部分的面积．所分成的弓形的面积为：；另一部分的面积为：；所以阴影部分面积为：．3.如图，长方形的面积是2平方厘米，，是的中点．阴影部分的面积是多少平方厘米？【答案】平方厘米【解析】如下图，连接，、的面积相等，设为平方厘米;、的面积相等，设为平方厘米，那么的面积为平方厘米．，．所以有．比较②、①式，②式左边比①式左边多，②式右边比①式右边大0.5，有，即,．而阴影部分面积为平方厘米．4.如图，已知，，，，线段将图形分成两部分，左边部分面积是38，右边部分面积是65，那么三角形的面积是多少？【答案】40【解析】连接，．根据题意可知，；；所以，，，，，于是：；；可得．故三角形的面积是40．5.如图，三角形中，是的5倍，是的3倍，如果三角形的面积等于1，那么三角形的面积是多少？【答案】15【解析】连接．∵∴又∵∴，∴．6.如图，与均为正方形，三角形的面积为6平方厘米，图中阴影部分的面积为多少？【答案】6【解析】如图，连接，比较与，由于，，即与的底与高分别相等，所以与的面积相等，那么阴影部分面积与的面积相等，为6平方厘米．7.图中三角形的面积是180平方厘米，是的中点，的长是长的3倍，的长是长的3倍．那么三角形的面积是多少平方厘米？【答案】22.5【解析】，等高，所以面积的比为底的比，有,所以=(平方厘米)．同理有(平方厘米)，(平方厘米)．即三角形的面积是22.5平方厘米．8.已知正方形边长为10，正方形边长为6，求阴影部分的面积．【答案】20【解析】如果注意到为一个正方形的对角线(或者说一个等腰直角三角形的斜边)，那么容易想到与是平行的．所以可以连接、，如上图．由于与平行，所以的面积与的面积相等．而的面积为，所以的面积也为20．9.右图中，和是两个正方形，和相交于，已知等于的三分之一，三角形的面积等于6平方厘米，求五边形的面积．【答案】49.5【解析】连接、，由于与平行，可知四边形构成一个梯形．由于面积为6平方厘米，且等于的三分之一，所以等于的，根据梯形蝴蝶定理或相似三角形性质，可知的面积为12平方厘米，的面积为6平方厘米，的面积为3平方厘米．那么正方形的面积为平方厘米，所以其边长为6厘米．又的面积为平方厘米，所以(厘米)，即正方形的边长为3厘米．那么，五边形的面积为：(平方厘米)．10.如图，已知长方形的面积，三角形的面积是，三角形的面积是，那么三角形的面积是多少？【答案】6.5【解析】方法一：连接对角线．∵是长方形∴∴，∴，∴∴．方法二：连接，由图知，所以，又由，恰好是面积的一半，所以是的中点，因此，所以11.是长方形内一点，已知的面积是，的面积是，求的面积是多少？【答案】3【解析】由于是长方形，所以，而，所以，则，所以．12.图中的、、分别是正方形三条边的三等分点，如果正方形的边长是，那么阴影部分的面积是多少？【答案】48【解析】把另外三个三等分点标出之后，正方形的个边就都被分成了相等的三段．把和这些分点以及正方形的顶点相连，把整个正方形分割成了个形状各不相同的三角形．这个三角形的底边分别是在正方形的个边上，它们的长度都是正方形边长的三分之一．阴影部分被分割成了个三角形，右边三角形的面积和第第个三角形相等：中间三角形的面积和第第个三角形相等；左边三角形的面积和第个第个三角形相等．因此这个阴影三角形的面积分别是、和的三分之一，因此全部阴影的总面积就等于正方形面积的三分之一．正方形的面积是，阴影部分的面积就是．13.如右图，三角形中，，且三角形的面积是，求三角形的面积．【答案】19【解析】连接BG，份根据燕尾定理，，得(份)，(份)，则(份)，因此,同理连接AI、CH得,,所以三角形GHI的面积是1，所以三角形ABC的面积是1914.如图，的面积为1，点、是边的三等分点，点、是边的三等分点，那么四边形的面积是多少？【答案】【解析】连接、、．根据燕尾定理，，，所以，那么，．类似分析可得．又，，可得．那么，．根据对称性，可知四边形的面积也为，那么四边形周围的图形的面积之和为，所以四边形的面积为．15.如图，面积为l的三角形ABC中，D、E、F、G、H、I分别是AB、BC、CA 的三等分点,求阴影部分面积.【答案】【解析】三角形在开会，那么就好好利用三角形中最好用的比例和燕尾定理吧！令BI与CD的交点为M，AF与CD的交点为N，BI与AF的交点为P,BI与CE的交点为Q,连接AM、BN、CP⑴求：在中，根据燕尾定理，设(份)，则(份),(份),(份),所以，所以,,所以,同理可得另外两个顶点的四边形面积也分别是面积的⑵求：在中，根据燕尾定理,所以,同理在中，根据燕尾定理,所以，所以同理另外两个五边形面积是面积的，所以16.如图，长方形被、分成四块，已知其中3块的面积分别为2、5、8平方厘米，那么余下的四边形的面积为多少平方厘米．【答案】9【解析】连接、．四边形为梯形，所以，又根据蝴蝶定理，，所以，所以(平方厘米)，(平方厘米)．那么长方形的面积为平方厘米，四边形的面积为(平方厘米)．17.如图，已知正方形的边长为，是边的中点，是边上的点，且，与相交于点，求【答案】32/11【解析】方法一：连接，延长，两条线交于点，构造出两个沙漏，所以有，因此，根据题意有，再根据另一个沙漏有，所以．方法二：连接，分别求，，根据蝴蝶定理，所以．18.如图在中，在的延长线上，在上，且，，平方厘米，求的面积．【答案】50【解析】连接，，所以，设份，则份，平方厘米，所以份是平方厘米，份就是平方厘米，的面积是平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比19.如图，在三角形中，已知三角形、三角形、三角形的面积分别是89，28，26．那么三角形的面积是多少？【答案】【解析】根据题意可知，，所以，那么，故．20.如图，长方形中，，．、分别是边上的两点，．那么，三角形面积的最小值是多少？【答案】717【解析】由于长方形的面积是一定的，要使三角形面积最小，就必须使、、的面积之和最大．由于、、都是直角三角形，可以分别过、作、的平行线，可构成三个矩形、和，如图所示．容易知道这三个矩形的面积之和等于、、的面积之和的2倍，而这三个矩形的面积之和又等于长方形的面积加上长方形的面积．所以为使、、的面积之和最大，只需使长方形的面积最大．长方形的面积等于其长与宽的积，而其长，宽，由题知，根据”两个数的和一定，差越小，积越大”，所以当与的差为0，即与相等时它们的积最大，此时长方形的面积也最大，所以此时三角形面积最小．当与相等时，，此时三角形的面积为：．(也可根据得到三角形的面积) 21.如图，,,则 .【答案】5：2【解析】根据燕尾定理有,,所以22.如图所示，平行四边形的面积是50平方厘米，则阴影部分的面积是多少平方厘米．【答案】25【解析】根据面积比例模型，可知图中空白三角形面积等于平行四边形面积的一半，所以阴影部分的面积也等于平行四边形面积的一半，为平方厘米．23.如图，三角形中，，，三角形ADE的面积是20平方厘米，三角形的面积是多少？【答案】120【解析】∵，∴，；又∵，∴，(平方厘米)．24.如图，三角形的面积是，是的中点，点在上，且，与交于点．则四边形的面积等于（）．【答案】【解析】方法一：连接，根据燕尾定理，，,设份，则份，份，份，如图所标所以方法二：连接，由题目条件可得到，，所以，，而．所以则四边形的面积等于．25.四边形的对角线与交于点(如图所示)．如果三角形的面积等于三角形的面积的，且，，那么的长度是的长度的多少倍．【答案】2【解析】在本题中，四边形为任意四边形，对于这种”不良四边形”，无外乎两种处理方法：⑴利用已知条件，向已有模型靠拢，从而快速解决；⑵通过画辅助线来改造不良四边形．看到题目中给出条件，这可以向模型一蝴蝶定理靠拢，于是得出一种解法．又观察题目中给出的已知条件是面积的关系，转化为边的关系，可以得到第二种解法，但是第二种解法需要一个中介来改造这个”不良四边形”，于是可以作垂直于，垂直于，面积比转化为高之比．再应用结论：三角形高相同，则面积之比等于底边之比，得出结果．请老师注意比较两种解法，使学生体会到蝴蝶定理的优势，从而主观上愿意掌握并使用蝴蝶定理解决问题．解法一：∵，∴，∴．解法二：作于，于．∵，∴，∴，∴，∴，∴．26.已知是平行四边形，，三角形的面积为6平方厘米．则阴影部分的面积是平方厘米．【答案】21【解析】连接．由于是平行四边形，，所以，根据梯形蝴蝶定理，，所以(平方厘米)，(平方厘米)，又(平方厘米)，阴影部分面积为(平方厘米)．27.如图，长方形被、分成四块，已知其中3块的面积分别为2、5、8平方厘米，那么余下的四边形的面积为多少平方厘米．【答案】9【解析】连接、．四边形为梯形，所以，又根据蝴蝶定理，，所以，所以(平方厘米)，(平方厘米)．那么长方形的面积为平方厘米，四边形的面积为(平方厘米)．28.如图，是等腰直角三角形，是正方形，线段与相交于点．已知正方形的面积48，，则的面积是多少？【答案】12【解析】由于是正方形，所以与平行，那么四边形是梯形．在梯形中，和的面积是相等的．而，所以的面积是面积的，那么的面积也是面积的．由于是等腰直角三角形，如果过作的垂线，为垂足，那么是的中点，而且，可见和的面积都等于正方形面积的一半，所以的面积与正方形的面积相等，为48．那么的面积为．29.如图，中，，，，，互相平行，，则．【答案】1：3：5：7：9【解析】设份，，因此份，进而有份，同理有份，份，份．所以有30.右图，中，是的中点，、、是边上的四等分点，与交于，与交于，已知的面积比四边形的面积大平方厘米，则的面积是多少平方厘米？【答案】336【解析】连接、．根据燕尾定理，，，所以；再根据燕尾定理，，所以，所以，那么，所以．根据题意，有，可得(平方厘米)。

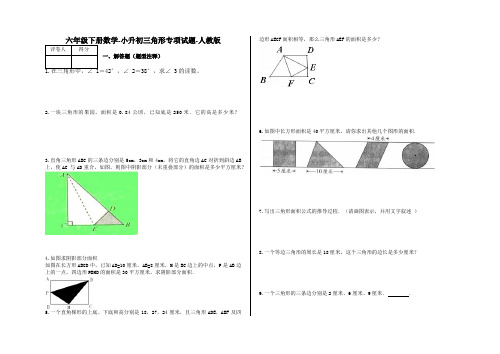
-小升初三角形专项试题-人教版一、解答题（题型注释）的读数。

2.一块三角形的果园，面积是0.84公顷，已知底是250米．它的高是多少米？3.直角三角形ABC的三条边分别是5cm，3cm和4cm，将它的直角边AC对折到斜边AB上，使AC 与AD重合，如图，则图中阴影部分（未重叠部分）的面积是多少平方厘米？4.如图求阴影部分面积如图在长方形ABCD中，已知AD=10厘米，AB=8厘米，M是BC边上的中点，P是AB边上的一点，四边形PBMD的面积是30平方厘米，求阴影部分面积．5.一个直角梯形的上底、下底和高分别是18，27，24厘米，且三角形ADE，ABF及四边形AECF面积相等，那么三角形AEF的面积是多少？6.如图中长方形面积是40平方厘米，请你求出其他几个图形的面积．7.写出三角形面积公式的推导过程．（请画图表示，并用文字叙述）8.一个等边三角形的周长是18厘米，这个三角形的边长是多少厘米？9.一个三角形的三条边分别是2厘米、6厘米、9厘米．．参数答案1.由三角形的内角和为180°，在三角形中，∠1＝42°，∠2＝38°，列式可得∠3＝180°－42°－38°＝100°答：∠3的读数为100°。

【解析】1.由三角形的内角和为180°，在三角形中，∠1＝42°，∠2＝38°，列式可得∠3＝180°－42°－38°＝100°答：∠3的读数为100°2.0.84公顷=8400平方米8400×2÷250=67.2（米）答：它的高是67.2米。

【解析】2.利用三角形的面积公式，即可以求出三角形的高。

3.1.5cm2或cm2【解析】3.试题分析：可设CE=DE=X，分两种情况：（1）AC=3，根据题意可以列出方程3X÷2×2+（5﹣3）X÷2=3×4÷2；（2）AC=4，根据题意可以列出方程4X÷2×2+（5﹣4）X÷2=3×4÷2；求解即可．解：设CE=DE=X，∠EDB=90，（1）AC=3，由题意有3X÷2×2+（5﹣3）X÷2=3×4÷2，4X=6，X=1.5，阴影部分（未重叠部分）的面积=1.5×2÷2=1.5（cm2）；（2）AC=4，由题意有4X÷2×2+（5﹣4）X÷2=3×4÷2，4.5X=6，X=；阴影部分（未重叠部分）的面积=×1÷2=（cm2）．4.25平方厘米【解析】4.试题分析：如图所示，连接DB，由“M是BC边上的中点”可知，S△DBM=S长方形ABCD，因长方形的长和宽已知，以及“四边形PBMD的面积是30平方厘米”，进而能求出三角形DPB的面积，于是三角形DPB的面积和高AD已知，就可以求出PB的长度，从而可以求三角形PBM的面积，所以阴影部分的面积=四边形PBMD的面积﹣三角形PBM的面积，问题得解．．解：S△DBM=×10×8=20（平方厘米），S△DPB=30﹣20=10（平方厘米），又因S△DPB=×PB×AD，所以PB=10×2÷10=2（厘米），则S△PBM=5×2÷2=5（平方厘米），阴影部分的面积=30﹣5=25（平方厘米）；答：阴影部分的面积是25平方厘米．5.156平方厘米【解析】5.试题分析：三角形ABF、三角形ADE和四边形AECF把梯形平均分成了3部分，根据梯形的面积求出求出四边形AECF面积，再根据三角形ABF、三角形ADE的面积求出EC 和CF的长度，进而求出三角形EFC的面积；用四边形AECF面积﹣三角形EFC的面积就是三角形AEF的面积．解：大梯形的面积是：（18+27）×24÷2=540（平方厘米）540÷3=180（平方厘米）DE=180×2÷18=20（厘米），EC=24﹣4=4（厘米），BF=180×2÷24=15（厘米），FC=12（厘米），S△AEF=SAECF﹣S△ECF=180﹣12×4÷2=180﹣24，=156（平方厘米）．答：三角形AEF 的面积是156平方厘米．6.40平方厘米，32平方厘米，50.24平方厘米【解析】6.试题分析：先依据长方形的面积公式求出长方形的长，也就等于知道了三角形的高、平行四边形的高和圆的直径，于是即可分别求出它们的面积．解：40÷5=8（厘米），10×8÷2=40（平方厘米）；4×8=32（平方厘米）；3.14×（8÷2）2=50.24（平方厘米）；答：三角形的面积是40平方厘米，平行四边形的面积是32平方厘米，圆的面积是50.24平方厘米．7.如图，将两个完全一样的三角形都可以拼成一个平行四边形，拼成的平行四边形的面积等于这两个三角形的面积，底等于三角形的底，高等于三角形的高，所以一个三角形的面积=这个平行四边形的面积的一半，因为平行四边形的面积=底×高，三角形的面积×2=底×高，则三角形的面积=底×高÷2，即S=ah÷2．【解析】7.试题分析：将两个完全一样的三角形都可以拼成一个平行四边形，计算这个平行四边形的面积的一半就可以推导出三角形面积的计算公式．解：如图，将两个完全一样的三角形都可以拼成一个平行四边形，拼成的平行四边形的面积等于这两个三角形的面积，底等于三角形的底，高等于三角形的高，所以一个三角形的面积=这个平行四边形的面积的一半，因为平行四边形的面积=底×高，三角形的面积×2=底×高，则三角形的面积=底×高÷2，即S=ah÷2．8.6厘米【解析】8.试题分析：等边三角形的三条边都是相等，用18除以3，就是这个三角形的边长．解：18÷3=6（厘米）．答：这个三角形的边长是6厘米．9.错误．【解析】9.试题分析：根据三角形的特性：两边之和大于第三边，三角形的两边的差一定小于第三边；进行解答即可．解：因为2+6＜9，所以三条分别是2厘米、6厘米、9厘米的边不能组成三角形；。

六年级数学上册教材重点剖析三角形的性质与计算在数学教育中，三角形是一个重要的基本概念。

它有许多特性和计算方法需要我们了解和掌握。

六年级数学上册教材中对三角形的性质和计算方法进行了详细的介绍和剖析。

本文将对教材中的重点内容进行梳理和总结。

1. 三角形的定义和分类三角形是由三条边和三个内角组成的多边形。

根据边长和角度的不同，三角形可以分为等边三角形、等腰三角形、直角三角形和一般三角形等不同的类型。

等边三角形的三条边相等，等腰三角形的两条边相等，直角三角形有一个内角为90度。

2. 三角形的性质教材中介绍了三角形的一些基本性质，需要我们掌握和理解。

其中包括：- 三角形内角的和为180度，即三个内角的度数之和等于180度。

- 等腰三角形的顶角和底角相等，等边三角形的三个内角均为60度。

- 直角三角形满足勾股定理，即直角三角形的两条直角边的平方和等于斜边的平方。

- 三角形的外角等于其与之相对的内角的补角。

即一个三角形的外角与相对的内角之和等于180度。

3. 三角形的计算方法除了了解三角形的性质外，我们还需要学习三角形的计算方法。

教材中提到了一些重要的计算方法，如：- 通过已知条件计算三角形的未知边长和角度。

根据三角形内角和的性质可以求解未知角度的数值，而利用三角形的边长比例关系可以计算未知边长的长度。

- 应用三角形的面积公式计算三角形的面积。

面积公式包括：面积=底边长×高/2、面积=1/2×边长1×边长2×sin(夹角)等。

- 利用勾股定理计算直角三角形的边长。

当已知一个直角三角形的两个边长时，可以通过勾股定理计算第三个边长的数值。

4. 解决实际问题我们学习三角形的性质和计算方法，目的是为了能够解决实际问题。

教材中提供了一些实际问题的解决方法，需要我们理解并运用所学的知识。

例如，通过计算三角形的面积可以求解一些与地理有关的问题，如测量一个不规则地形的面积。

通过计算三角形的边长和角度可以解决一些建筑和工程问题，如计算房屋的立面图尺寸等。

六年级数学复习理解三角形的角度与边长关系三角形是初中数学中的基础内容，也是数学中的重要概念之一。

在六年级数学的学习中，理解三角形的角度与边长关系对于解决相关问题非常重要。

本文将针对这一主题展开论述，帮助同学们更好地掌握三角形的相关知识。

一、三角形的定义与分类三角形是由三条线段组成的图形，在初中数学中我们通常将三个顶点记作A、B、C，对应的边分别为a、b、c。

在定义上，三角形的任意两边之和大于第三边，任意两角之和小于180度。

根据边长和角度的性质，我们可以将三角形分类为以下几种：1. 等边三角形：三条边长度相等的三角形，三个角也都相等；2. 等腰三角形：两边长度相等的三角形，两个底角也相等；3. 直角三角形：拥有一个直角（90度）的三角形，直角所对应的边称为斜边，其他两边称为腿；4. 钝角三角形：拥有一个钝角大于90度的三角形；5. 锐角三角形：三个角都小于90度的三角形。

二、三角形内角和在学习三角形的角度与边长关系时，我们首先要了解三角形内角和的性质。

无论是任意三角形还是特殊三角形，三个内角的和都是180度。

这一性质是解决三角形相关问题的基础。

三、角度与边长关系1. 直角三角形的边长关系直角三角形是最常见的三角形之一，它的边长关系可以由勾股定理得出。

设直角三角形的两条腿的长度分别为a和b，斜边的长度为c，则有勾股定理：a² + b² = c²利用这个关系，我们可以解决很多与直角三角形有关的问题。

2. 等边三角形的角度关系等边三角形是三边长度都相等的特殊三角形，它拥有以下角度关系：（1）三个角都相等，每个角均为60度；（2）每个角的补角均为120度。

3. 等腰三角形的角度关系等腰三角形是两个边相等的特殊三角形，它的角度关系包括以下几点：（1）等腰三角形的顶角（顶点对应的角）与底角（底边对应的角）相等，即∠A = ∠C；（2）顶角和底角的补角都相等，即∠A + ∠C = ∠B + ∠D = 180度。

六年级数学三角形试题1.一个三角形任意一条边上的高所在的直线，都是这个三角形的对称轴．这个三角形是（）。

A．等腰三角 B．等腰直角三角形 C．等边三角形【答案】C【解析】因为等边三角形的三条边上的高所在的直线，都是它的对称轴，所以“一个三角形任意一条边上的高所在的直线，都是这个三角形的对称轴”。

这个三角形是等边三角形。

故此题答案为：C。

2.如图中三角形的周长可能是（）厘米。

A．16B．18C．28D．36【答案】B【解析】根据三角形的特性：任意两边之和大于第三边，任意两边之差小于第三边；据此判断出三角形的第三条边的取值范围，然后结合选项中给出的周长，求出第三边，然后比较即可。

解：8-6＜第三边＜8＋6，2＜第三边＜14，所以第三条边可以是：2厘米～14厘米（不包括2厘米和14厘米）。

A、因为16-6-8=2（厘米），不合题意；B、18-6-8=4（厘米），符合题意；C、28-6-8=14（厘米），不合题意；D、36-6-8=22（厘米），不合题意；故选：B。

【考点】三角形的特性。

3.用3根等长的火柴可以摆成一个等边三角形．如图,用这样的等边三角形拼合成一个更大的等边三角形．如果这个大等边三角形昀每边由20根火柴组成，那么一共要用多少根火柴?【答案】630【解析】把大的等边三角形分为20“层”分别计算火柴的根数：最上一“层”只用了3根火柴；从上向下数第二层用了3×2＝6根火柴；从上向下数第三层用了3×3＝9根火柴；……从上向下数第20层用了3×20＝60根火柴．所以，总共要用火柴3×(1+2+3+…+20)＝630根．4.如图，用9枚钉子钉成水平和竖直间隔都为1厘米的正方阵．用一根橡皮筋将3枚不共线的钉子连结起来就形成一个三角形．在这样得到的三角形中，面积等于1平方厘米的三角形共有多少个?【答案】32【解析】我们分三种情况来找面积为1平方厘米的三角形，这些三角形的底与高分别为1厘米或2厘米，利用正方形的对称性：(1)等腰直角三角形，如下图a所示有△AOC，△COE，△EOG，△GOA，△BOH，△DFB，△FHD，△HBF，共计8个，其中以AC，CF，FG，GA为底的各一个，以BF，DH为底的各两个．(2)直角三角形，如图b所示有△ACH，△CHD，△ACD，△DHA，△BEF，△BCE，△CEF，△CFB，△DEG，△DGH，△EGH，△EHD，△GAB，△GBF，△FAB，△FGA，共计16个，其中以AD、CH、BE、CF、DG、EH、FA、GB为斜边的各两个．(3)钝角三角形，如图c所示有△ABE，△AHE，△ADE，△AFE，△CBG，△CFG，△CDG，△CHG共计8个，其中以AE、CG为边的各四个．于是，综上所述，共有面积为1平方厘米的三角形32个．5.如图，木板上钉着12枚钉子，排成三行四列的长方阵．那么用橡皮筋共可套出多少个不同的三角形?【答案】200【解析】我们先任意选取三个点，那么第1个点有12个位置可以选择，第2个点有11个位置可以选择，第3个点有10个位置可以选择，但是每6种选法对应的都是同一个图形，如下图，ABC，ACB，BAC，BCA，CAB，CBA均是同一个图形．所以有12×11×10÷6＝220种选法，但是如果这3点在同一条直线上就无法构成三角形，其中每行有4种情况，共3×4；每列有1种情况，共1×4；2个边长为2的正方形的4条对角线，共4种情况．所以，可以套出220－3×4－1×4－4＝200个不同的三角形．6.如下图中，数一数共有多少条线段？共有多少个三角形？【答案】60,30【解析】分析在数的过程中应充分利用上几例总结的规律，明确数什么？怎么数？这样两个问题.数：就是要数出图中基本线段（基本三角形）的条数，算：就是以基本线段（基本三角形）条数为最大加数的从1开始的连续几个自然数的和.①要数多少条线段：先看线段AB、AD、AE、AF、AC、上各有2个分点，各分成3条基本线段，再看BC、MN、GH这3条线段上各有3个分点，各分成4条基本线段.所以图中总共有线段是：（3+2+1）×5+（4+3+2+1）×3=30+30=60（条）.②要数有多少个三角形，先看在△AGH中，在GH上有3个分点，分成基本小三角形有4个.所以在△AGH中共有三角形4+3+2+1=10（个）.在△AMN与△ABC中，三角形有同样的个数，所以在△ABC中三角形个数总共：（4+3+2+1）×3=10×3=30（个）.解：①在△ABC中共有线段是：（3+2+1）×5+（4+3+2+1）×3=30+30=60（条）②在△ABC中共有三角形是：（4+3+2+1）×3=10×3=30（个）.7.图中共有多少个三角形？【答案】118【解析】显然三角形可分为尖向上与尖向下两大类，两类中三角形的个数相等．尖向上的三角形又可分为6类（1）最大的三角形1个(即△ABC)，（2）第二大的三角形有3个（3）第三大的三角形有6个（4）第四大的三角形有10个（5）第五大的三角形有15个（6）最小的三角形有24个所以尖向上的三角形共有1+3+6+10+15+24=59（个）图中共有三角形2×59=118（个）。

-小升初三角形专项试题-人教版一、解答题（题型注释）BC上的高AE长3.2厘米，现在底边增加20厘米，面积增加多少平方厘米？2.长方形ABCD被虚线分割成4个面积相等的部分（如下图，单位：厘米）．试求线段BE的长度3.在△ABC中，BD=DE=EC，CF：AC=1：3．若△ADH的面积比△HEF的面积多24平方厘米，求三角形ABC 的面积是多少平方厘米？4.有一个平行四边形面积是30.6平方厘米，与它面积相等的三角形的高是4.8厘米，求这个三角形的底是多少厘米？5.写出三角形面积公式的推导过程．（请画图表示，并用文字叙述）6.一块三角形地，底是20米，高是60米，如果每平方米可种植树苗4棵，最多可种多少棵树苗？7.有一个直角三角形，两条直角边是两个质数，和为12cm，这个直角三角形的面积是多少平方厘米？8.园林小路，曲径幽通．如图小路是由白色正方形石板和青、红两色的三角形石板铺成，问内圈三角形石板的总面积大还是外圈石板的总面积大？请说明理由．9.给下面三个三角形的底边画相应的高，并求三角形未知的角．图2和图3都是等腰三角形．10.根据三角形的内角和是180°，你能求出如图图形的内角和吗？参数答案1.解：20×3.2÷2=64÷2=32（平方厘米）答：面积增加32平方厘米．【解析】1.底边BC上的高AE长3.2厘米，现在底边增加20厘米，增加的就是一个底为20厘米，高为3.2厘米的三角形，根据三角形的面积公式：S=ah÷2可求出增加的面积，据此解答．2.线段BE的长是9厘米【解析】2.试题分析：如图，设FO=x厘米，CF=y厘米，根据长方形的面积公式S=ab，分别用x 与y的式子表示出长方形OPCF的面积长方形EBPO的面积，应用代换的方法，解方程即可．解答：解：设FO=x厘米，CF=y厘米，因为4个面积相等，所以CF×FO=3×8×2=48（平方厘米），即xy=48EO×EB=3×8=24（平方厘米）即（8﹣x）×y=3×8，8y﹣xy=24，8y=24+xy，8y=24+48，8y=72，y=9，即BE=9厘米；答：线段BE的长是9厘米．3.108平方厘米【解析】3.试题分析：由题意可知：△ADH的面积比△HEF的面积多24平方厘米，则三角形ADE 的面积比三角形FDE的面积多24平方厘米，又因三角形FDE和三角形FEC的面积相等，也就是说三角形AEC比三角形FEC的面积多24平方厘米，又因多出的24平方厘米，是三角形AEC的面积的，所以三角形AEC的面积是36平方厘米，从而求得三角形ABC的面积．解：△ADH的面积比△HEF的面积多24平方厘米，则三角形ADE的面积比三角形FDE的面积多24平方厘米，又因三角形FDE和三角形FEC的面积相等，也就是说三角形AEC比三角形FEC的面积多24平方厘米，又因多出的24平方厘米，是三角形AEC的面积的，所以三角形AEC的面积是24÷=36平方厘米，则三角形ABC的面积是36÷=108（平方厘米），答：三角形ABC的面积是108平方厘米．4.12.75厘米【解析】4.试题分析：由“三角形的面积=底×高÷2”可得“三角形的底=三角形的面积×2÷高”，据此即可求出这个三角形的底．解：30.6×2÷4.8，=61.2÷4.8，=12.75（厘米）；答：这个三角形的底是12.75厘米．5.如图，将两个完全一样的三角形都可以拼成一个平行四边形，拼成的平行四边形的面积等于这两个三角形的面积，底等于三角形的底，高等于三角形的高，所以一个三角形的面积=这个平行四边形的面积的一半，因为平行四边形的面积=底×高，三角形的面积×2=底×高，则三角形的面积=底×高÷2，即S=ah÷2．【解析】5.试题分析：将两个完全一样的三角形都可以拼成一个平行四边形，计算这个平行四边形的面积的一半就可以推导出三角形面积的计算公式．解：如图，将两个完全一样的三角形都可以拼成一个平行四边形，拼成的平行四边形的面积等于这两个三角形的面积，底等于三角形的底，高等于三角形的高，所以一个三角形的面积=这个平行四边形的面积的一半，因为平行四边形的面积=底×高，三角形的面积×2=底×高，则三角形的面积=底×高÷2，即S=ah÷2．6.2400棵【解析】6.试题分析：根据“三角形的面积=底×高÷2”计算出这块三角形土地的面积，然后用“每平方米种植树苗的棵数×土地的面积”进行解答即可．解：（20×60÷2）×4，=600×4，=2400（棵）；答：最多可种2400棵树苗．7.17.5平方厘米【解析】7.试题分析：根据一个直角三角形，两条直角边是两个质数，和为12cm，可以求出两条直角边的长，再根据直角三角形的面积公式求出直角三角形的面积．解：因为一个直角三角形，两条直角边是两个质数，和为12cm，所以两条直角边分别是5cm，7cm，所以这个直角三角形的面积是：×5×7=17.5（平方厘米）．答：这个直角三角形的面积是17.5平方厘米．8.外圈石板的总面积大于内圈三角形石板的总面积【解析】8.试题分析：如图所示，在小路中间作一辅助线，则三角形1、2、3、4、5、6、7、8的面积都等于正方形面积的一半，所以它们的面积都相等，但是10号平形四边形的面积大于9号三角形的面积，则外圈石板的总面积大于内圈三角形石板的总面积．．解：如图所示，在小路中间作一辅助线，则三角形1、2、3、4、5、6、7、8的面积都等于白色正方形面积的一半，所以它们的面积都相等，但是10号平形四边形的面积大于9号三角形的面积，则外圈石板的总面积大于内圈三角形石板的总面积．答：外圈石板的总面积大于内圈三角形石板的总面积．9.43度．45度．104度．【解析】9.试题分析：（1）依据过直线外一点作直线的垂线的方法即可做出三角形底边上的高；（2）根据三角形的内角和是180°即可求出第三个角的度数；（3）等腰直角三角形中，两个锐角相等，且两个锐角和是90度，由此即可解答；（4）等腰三角形的两个底角相等，所以顶角=180°﹣底角的度数×2．解：（1）如图所示，即为所作的三角形的高：（2）图1中：180﹣62﹣75=43（度），答：？处的度数是43度．（3）图2中：90÷2=45（度），答：等腰直角三角形中的一个底角是45度．（4）图3中：180﹣38×2=104（度），答：这个等腰三角形的顶角是104度．10.540°；720°．【解析】10.试题分析：（1）五边形由3个三角形组成，则五边形内角和=三角形内角和×3；（2）六边形由4个三角形组成，则五边形内角和=三角形内角和×4．解：（1）五边形：180°×3=540°；（2）六边形：180°×4=720°．。

小学六年级数学重要知识总结三角形的性质总结小学六年级数学重要知识总结：三角形的性质总结数学一直是小学六年级的重要学科之一，其中三角形作为数学中的重要概念之一，在数学学习中占据着重要的地位。

本文将从不同角度总结小学六年级数学中关于三角形的性质，帮助同学们更好地理解和掌握这一知识点。

一、三角形的定义三角形是由三条线段组成的图形，其中每个线段都是另外两个线段的共同端点，这个端点就是三角形的顶点。

三角形的三条线段称为三角形的边，而以边为边的两个角叫做三角形的角。

二、三角形的分类1. 根据三边的长短，三角形可以分为等边三角形、等腰三角形和普通三角形。

- 等边三角形：三条边的长都相等。

- 等腰三角形：至少有两条边的长相等。

- 普通三角形：三条边的长各不相等。

2. 根据角的大小，三角形可以分为直角三角形、钝角三角形和锐角三角形。

- 直角三角形：一个角为90度（右角）。

- 钝角三角形：一个角大于90度。

- 锐角三角形：三个角都小于90度。

三、三角形的性质1. 三角形的内角和等于180度（°）。

这是三角形最重要的性质之一，也是我们在解题过程中经常用到的性质。

通过这一性质，我们可以求解未知角度的大小。

2. 等腰三角形的特点：- 等腰三角形的底边上的两个角是相等的。

- 等腰三角形的两条腰线段长度相等。

3. 直角三角形的特点：- 直角三角形的两个锐角的两条直角边平方和等于斜边平方。

- 直角三角形的斜边是最长的一条边。

4. 等边三角形的特点：- 等边三角形的三个内角都是60度。

- 等边三角形的三条边长相等。

四、应用举例下面通过一些例题来应用以上所述的三角形性质：1. 若一个三角形的两个内角分别是60度和80度，那么第三个角的度数是多少？解析：根据三角形内角和等于180度的性质，我们可以用180度减去已知角的度数，得到未知角的度数。

即180度 - 60度 - 80度 = 40度。

所以第三个角的度数是40度。

2. 如果一个三角形的两边长度分别是5 cm 和 4 cm，那么第三边的长度范围是多少？解析：设第三边的长度为x，根据三角形两边之和大于第三边的性质，我们可以得到以下不等式：5 + 4 > x，即9 > x。