中考数学一轮专题复习测试题(15)及答案

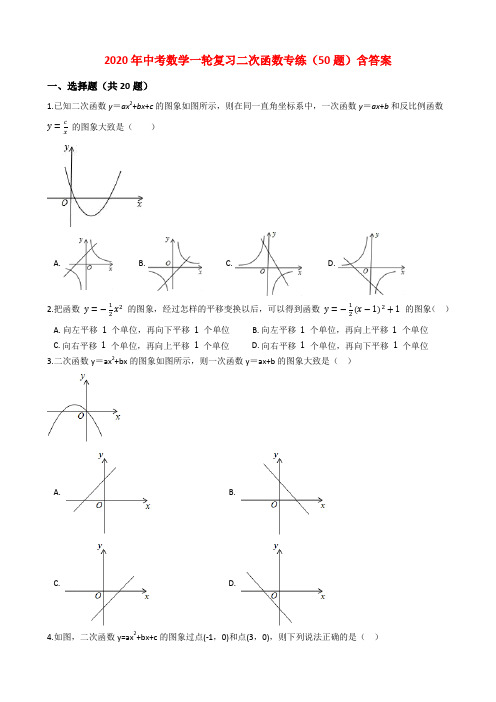
2020年中考数学一轮复习二次函数专练（50题）含答案一、选择题（共20题）1.已知二次函数y＝ax2+bx+c的图象如图所示，则在同一直角坐标系中，一次函数y＝ax+b和反比例函数的图象大致是（）A. B. C. D.2.把函数的图象，经过怎样的平移变换以后，可以得到函数的图象（）A. 向左平移个单位，再向下平移个单位B. 向左平移个单位，再向上平移个单位C. 向右平移个单位，再向上平移个单位D. 向右平移个单位，再向下平移个单位3.二次函数y＝ax2+bx的图象如图所示，则一次函数y＝ax+b的图象大致是（）A. B.C. D.4.如图，二次函数y=ax2+bx+c的图象过点(-1，0)和点(3，0)，则下列说法正确的是（）A. B. C. D.5.已知二次函数，关于该函数在﹣1≤x≤3的取值范围内，下列说法正确的是（）A. 有最大值﹣1，有最小值﹣2B. 有最大值0，有最小值﹣1C. 有最大值7，有最小值﹣1D. 有最大值7，有最小值﹣26.抛物线的对称轴是直线，且过点（1，0）.顶点位于第二象限，其部分图像如图所示，给出以下判断：① 且；② ；③ ；④ ；⑤直线与抛物线两个交点的横坐标分别为、，则.其中正确的个数有( )A. 5个B. 4个C. 3个D. 2个7.如图是二次函数y＝ax2+bx+c的图象，对于下列说法：①ac＞0，②2a+b＞0，③4ac＜b2，④a+b+c＜0，⑤当x＞0时，y随x的增大而减小，其中正确的是（）A. ①②③B. ①②④C. ②③④D. ③④⑤8.二次函数y=（x-1）2+3图象的顶点坐标是（）A. (1，3)B. （1，-3)C. （-1，3）D. （-1，-3）9.如图，二次函数y＝ax2+bx+c（a≠0）的图象过点（﹣2，0），对称轴为直线x＝1.有以下结论：①abc＞0；②8a+c＞0；③若A（x1，m），B（x2，m）是抛物线上的两点，当x＝x1+x2时，y＝c；④点M，N是抛物线与x轴的两个交点，若在x轴下方的抛物线上存在一点P，使得PM⊥PN，则a的取值范围为a≥1；⑤若方程a（x+2）（4﹣x）＝﹣2的两根为x1，x2，且x1＜x2，则﹣2≤x1＜x2＜4.其中结论正确的有（）A. 2个B. 3个C. 4个D. 5个10.已知m＞0，关于x的一元二次方程（x+1）（x﹣2）﹣m＝0的解为x1，x2（x1＜x2），则下列结论正确的是（）A. x1＜﹣1＜2＜x2B. ﹣1＜x1＜2＜x2C. ﹣1＜x1＜x2＜2D. x1＜﹣1＜x2＜211.如图是函数的图象，直线轴且过点，将该函数在直线l上方的图象沿直线l向下翻折，在直线1下方的图象保持不变，得到一个新图象．若新图象对应的函数的最大值与最小值之差不大于5，则m的取值范围是（）A. B. C. D. 或12.如图所示，已知二次函数的图象与轴交于两点，与轴交于点，，对称轴为直线，则下列结论：① ；② ；③ ；④ 是关于的一元二次方程的一个根.其中正确的有（）A. 1个B. 2个C. 3个D. 4个13.已知二次函数(其中是自变量)的图象与轴没有公共点，且当时，随的增大而减小，则实数的取值范围是( )A. B. C. D.14.从地面竖直向上抛出一小球，小球的高度ℎ(单位：)与小球运动时间(单位：)之间的函数关系如图所示．下列结论：①小球在空中经过的路程是；②小球抛出3秒后，速度越来越快；③小球抛出3秒时速度为0；④小球的高度ℎ时，．其中正确的是( )A. ①④B. ①②C. ②③④D. ②③15.北中环桥是省城太原的一座跨汾河大桥(如图1)，它由五个高度不同，跨径也不同的抛物线型钢拱通过吊桥，拉锁与主梁相连，最高的钢拱如图2所示，此钢拱(近似看成二次函数的图象-抛物线)在同一竖直平面内，与拱脚所在的水平面相交于A，B两点，拱高为78米(即最高点O到AB的距离为78米)，跨径为90米(即AB=90米)，以最高点O为坐标原点，以平行于AB的直线为轴建立平面直角坐标系，则此抛物线钢拱的函数表达式为( )A. B. C. D.16.如图，边长都为4的正方形ABCD和正三角形EFG如图放置，AB与EF在一条直线上，点A与点F重合．现将△EFG沿AB方向以每秒1个单位的速度匀速运动，当点F与B重合时停止．在这个运动过程中，正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是（）A. B. C. D.17.二次函数＝的部分图象如图所示，有以下结论：① ﹣＝；② ﹣；③ ﹣；④ ，其中错误结论的个数是（）A. 1B. 2C. 3D. 418.如图，正方形的边长为，动点，同时从点出发，在正方形的边上，分别按，的方向，都以的速度运动，到达点运动终止，连接，设运动时间为 ，的面积为 ，则下列图象中能大致表示与的函数关系的是（）A. B.C. D.19.如图，坐标平面上有一顶点为A的抛物线，此抛物线与方程式y=2的图形交于B、C两点，△ABC为正三角形.若A点坐标为（-3，0），则此抛物线与y轴的交点坐标为何？（）A. B. C. D.20.如图，二次函数y=ax2+bx+c的图象经过点A（﹣1，0）、点B（3，0）、点C（4，y1），若点D（x2，y2）是抛物线上任意一点，有下列结论：①二次函数y=ax2+bx+c的最小值为﹣4a；②若﹣1≤x2≤4，则0≤y2≤5a；③若y2＞y1，则x2＞4；④一元二次方程cx2+bx+a=0的两个根为﹣1和其中正确结论的个数是（）A. 1B. 2C. 3D. 4二、填空题（共15题）21.将抛物线的图象，向左平移1个单位，再向下平移2个单位，所得图象的解析式为________．22.已知抛物线y＝ax2+bx+c（a≠0）的对称轴是直线x＝1，其部分图象如图所示，下列说法中：①abc＜0；②a﹣b+c＜0；③3a+c＝0；④当﹣1＜x＜3时，y＞0，正确的是________（填写序号）.23.如图，若被击打的小球飞行高度ℎ（单位：）与飞行时间（单位：）之间具有的关系为ℎ，则小球从飞出到落地所用的时间为________ .24.已知抛物线过点，两点，若线段的长不大于，则代数式的最小值是________.25.二次函数的图象如图所示，若，﹣.则、的大小关系为________ .(填“ ”、“ ”或“ ”)26.如图，抛物线与x轴相交于两点，与轴相交于点，点在抛物线上，且. 与轴相交于点，过点的直线平行于轴，与拋物线相交于两点，则线段的长为________.27.二次函数的最大值是________.28.如图，在平面直角坐标系中，抛物线y=ax2-2ax+ (a>0)与y轴交于点A，过点A作x轴的平行线交抛物线于点M。

2021年中考数学一轮复习：轴对称与中心对称专项练习题一、选择题1. 如图所示电视台的台标中，是中心对称图形的是()2. 下列四个银行标志中，既是中心对称图形，又是轴对称图形的是()3. 如图，四边形ABCD与四边形FGHE关于一个点中心对称，则这个点是()A．O1B．O2C．O3D．O44. 如图，线段AB与A'B'(AB=A'B')不关于直线l成轴对称的是()5. 如图，在△ABC中，AC＝BC，点D和E分别在AB和AC上，且AD＝AE，连接DE，过点A的直线GH与DE平行．若∠C＝40°，则∠GAD的度数为()A．40°B．45°C．55°D．70°6. 如图，已知钝角三角形ABC，依下列步骤尺规作图，并保留作图痕迹.步骤1:以点C为圆心，CA长为半径画弧①;步骤2:以点B为圆心，BA长为半径画弧②，交弧①于点D;步骤3:连接AD，交BC的延长线于点H.则下列叙述正确的是()A.BH垂直平分线段ADB.AC平分∠BADC.S△ABC=BC·AHD.AB=AD7. 把一个图形先沿着一条直线进行轴对称变换，再沿着与这条直线平行的方向平移，我们把这样的图形变换叫做滑动对称变换.结合轴对称变换和平移变换的有关性质，你认为在滑动对称变换过程中，两个对应三角形(如图0)的对应点所具有的性质是()A.对应点所连线段与对称轴垂直B.对应点所连线段被对称轴平分C.对应点所连线段都相等D.对应点所连线段互相平行8. 如图，∠AOB=60°，点P是∠AOB内的定点且OP=，若点M，N分别是射线OA，OB上异于点O的动点，则△PMN周长的最小值是()A.B.C.6 D.3二、填空题9. 将一张矩形纸片折叠成如图所示的图形，若AB=10 cm ，则AC= cm .10. 等腰三角形的两边长分别为6 cm ，13 cm ，其周长为________ cm .11. 如图，四边形ABCD 是菱形，O 是两条对角线的交点，过O 点的三条直线将菱形分成阴影部分和空白部分.当菱形的两条对角线的长分别为6和8时，阴影部分的面积为 .12. 已知点P (x ，y )的坐标满足等式(x －2)2＋|y －1|＝0，且点P 与点P ′关于y 轴对称，则点P ′的坐标为________．13. 画图:试画出下列正多边形的所有对称轴，并完成表格.根据上表，猜想正n 边形有 条对称轴.14. (2019•黄冈)如图，AC BD ，在AB 的同侧，288AC BD AB ===，，，点M为AB 的中点，若120CMD ∠=︒，则CD 的最大值是__________．三、解答题15. 已知:如图，AB=AC，DB=DC，点E在直线AD上.求证:EB=EC.16. 如图，DF为△ABC的边BC的垂直平分线，F为垂足，DF交△ABC的外角平分线AD于点D，DE⊥AB于点E，且AB>AC，连接BD，CD.求证:(1)∠DBE=∠DCA;(2)BE=AC+AE.17. 如图，四边形OABC是矩形，点A、C的坐标分别为(3,0)，(0,1)．点D是线段BC上的动点（与端点B、C不重合），过点D作直线12y x b=-+交折线OAB于点E．（1）记△ODE的面积为S，求S与b的函数关系式；（2）当点E在线段OA上时，若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1，试探究四边形O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化？若不变，求出重叠部分的面积；若改变，请说明理由．18. 如图，已知一个直角三角形纸片ACB，其中∠ACB＝90°，AC＝4，BC＝3，E、F分别是AC、AB边上的点，连接EF.(1)如图①，若将纸片ACB的一角沿EF折叠，折叠后点A落在AB边上的点D处，且使S四边形ECBF ＝3S△EDF，求AE的长；(2)如图②，若将纸片ACB的一角沿EF折叠，折叠后点A落在BC边上的点M 处，且使MF∥CA.①试判断四边形AEMF的形状，并证明你的结论；②求EF的长．答案一、选择题1. 【答案】A2. 【答案】C3. 【答案】A[解析] 如图，连接HC和DE交于点O1.4. 【答案】A[解析] 选项A中，A'B'是由线段AB平移得到的，所以线段AB与A'B'不关于直线l成轴对称.5. 【答案】C[解析] ∵AC＝CB，∠C＝40°，∴∠BAC＝∠B＝12(180°－40°)＝70°.∵AD＝AE，∴∠ADE＝∠AED＝12(180°－70°)＝55°.∵GH∥DE，∴∠GAD＝∠ADE＝55°.6. 【答案】A[解析] 如图，连接CD，BD.∵CA=CD，BA=BD，∴点C，B都在线段AD的垂直平分线上.∴BH垂直平分线段AD.故选A.7. 【答案】B[解析] 连接BB'交对称轴于点O，过点B作BM⊥对称轴，垂足为M，过点B'作B'N⊥对称轴，垂足为N，由轴对称的性质及平移的性质可得BM=B'N.又因为∠BOM=∠B'ON，∠BMO=∠B'NO=90°，所以△BOM≌△B'ON.所以OB=OB'.同理其他对应点也有这样的结论.8. 【答案】D[解析]分别以OB，OA为对称轴作点P的对称点P1，P2，连接OP1，OP2，P1P2，P1P2交射线OA，OB于点M，N，则此时△PMN的周长有最小值，△PMN的周长=PN+PM+MN=P1N+P2M+MN=P1P2，根据轴对称的性质可知OP1=OP2=OP=，∠P1OP2=120°，∴∠OP1M=30°，过点O作MN的垂线段，垂足为Q，在Rt△OP1Q中，可知P1Q=，所以P1P2=2P1Q=3，故△PMN周长的最小值为3.二、填空题9. 【答案】10[解析]如图，∵矩形的对边平行，∴∠1=∠ACB，由翻折变换的性质，得∠1=∠ABC，∴∠ABC=∠ACB，∴AC=AB，∵AB=10 cm，∴AC=10 cm.故答案为10.10. 【答案】32[解析] 由题意知，应分两种情况：(1)当腰长为6 cm时，三角形的三边长为6 cm，6 cm，13 cm，6＋6＜13，不能构成三角形；(2)当腰长为13 cm时，三角形的三边长为6 cm，13 cm，13 cm，能构成三角形，周长＝2×13＋6＝32(cm)．11. 【答案】12[解析]∵菱形的两条对角线的长分别为6和8，∴菱形的面积=×6×8=24.∵点O是菱形两条对角线的交点，∴阴影部分的面积=×24=12.12. 【答案】(－2，1)[解析] ∵(x －2)2≥0，|y －1|≥0，又(x －2)2＋|y －1|＝0，∴x－2＝0且y －1＝0，即x ＝2，y ＝1.∴点P 的坐标为(2，1)．那么点P 关于y 轴的对称点P′的坐标为(－2，1)．13. 【答案】解:如图.故填3，4，5，6，n.14. 【答案】14【解析】如图，作点A 关于CM 的对称点A'，点B 关于DM 的对称点B'．∵120CMD ∠=︒，∴60AMC DMB ∠+∠=︒， ∴60CMA'DMB'∠+∠=︒， ∴60A'MB'∠=︒， ∵MA'MB'=，∴A'MB'△为等边三角形，∵14CD CA'A'B'B'D CA AM BD ≤++=++=， ∴CD 的最大值为14，故答案为：14．三、解答题15. 【答案】证明:连接BC.∵AB=AC ，DB=DC ，∴直线AD 是线段BC 的垂直平分线. 又∵点E 在直线AD 上，∴EB=EC.16. 【答案】证明:(1)如图，过点D 作DG ⊥CA 交CA 的延长线于点G .∵DF 是BC 的垂直平分线，∴BD=CD.∵AD 是△ABC 的外角平分线，DE ⊥AB ，DG ⊥CA ， ∴DE=DG ，∠DEB=∠DGC=90°. 在Rt △DBE 和Rt △DCG 中，∴Rt △DBE ≌Rt △DCG (HL). ∴∠DBE=∠DCA.(2)∵Rt △DBE ≌Rt △DCG ，∴BE=CG . 在Rt △DEA 和Rt △DGA 中，∴Rt △DEA ≌Rt △DGA (HL). ∴AE=AG .∴BE=CG=AC+AG=AC+AE ， 即BE=AC+AE.17. 【答案】(1)①如图2，当E 在OA 上时，由12y x b =-+可知，点E 的坐标为(2b ,0)，OE＝2b ．此时S ＝S △ODE ＝112122OE OC b b ⋅=⨯⨯=．②如图3，当E 在AB 上时，把y ＝1代入12y x b =-+可知，点D 的坐标为(2b －2,1)，CD ＝2b －2，BD ＝5－2b ．把x ＝3代入12y x b =-+可知，点E 的坐标为3(3,)2b -，AE ＝32b -，BE ＝52b -．此时S ＝S 矩形OABC －S △OAE － S △BDE －S △OCD＝1315133()()(52)1(22)22222b b b b -⨯-----⨯⨯-252b b =-+．(2)如图4，因为四边形O 1A 1B 1C 1与矩形OABC 关于直线DE 对称，因此DM ＝DN ，那么重叠部分是邻边相等的平行四边形，即四边形DMEN 是菱形．作DH⊥OA，垂足为H．由于CD＝2b－2，OE＝2b，所以EH＝2．设菱形DMEN的边长为m．在Rt△DEH中，DH＝1，NH＝2－m，DN＝m，所以12＋(2－m)2＝m2．解得54m ．所以重叠部分菱形DMEN的面积为54．图2 图3 图4考点伸展把本题中的矩形OABC绕着它的对称中心旋转，如果重叠部分的形状是菱形（如图5），那么这个菱形的最小面积为1，如图6所示；最大面积为53，如图7所示．图5 图6 图7 18. 【答案】(1)如解图①，∵折叠后点A落在AB边上的点D处，解图①∴EF⊥AB，△AEF≌△DEF，∴S △AEF ＝S △DEF ，∵S 四边形ECBF ＝3S △EDF ，∴S 四边形ECBF ＝3S △AEF ，∵S △ACB ＝S △AEF ＋S 四边形ECBF ，∴S △ACB ＝S △AEF ＋3S △AEF ＝4S △AEF ， ∴14△△AEF ACB S S =， ∵∠EAF ＝∠BAC ，∠AFE ＝∠ACB ＝90°，∴△AEF ∽△ABC ，∴2△△（）AEF ACB S AE ABS =， ∴214（）=，AE AB 在Rt △ACB 中，∠ACB ＝90°，AC ＝4，BC ＝3，∴AB 2＝AC 2＋BC 2，即AB ＝42＋32＝5，∴(AE 5)2＝14，∴AE ＝52；(2)①四边形AEMF 是菱形．证明：如解图②，∵折叠后点A 落在BC 边上的点M 处，∴∠CAB ＝∠EMF ，AE ＝ME ，又∵MF ∥CA ，∴∠CEM ＝∠EMF ，∴∠CAB ＝∠CEM ，∴EM ∥AF ，∴四边形AEMF 是平行四边形，而AE ＝ME ，∴四边形AEMF 是菱形，解图②②如解图②，连接AM ，与EF 交于点O ，设AE ＝x ，则AE ＝ME ＝x ，EC ＝4－x ， ∵∠CEM ＝∠CAB ，∠ECM ＝∠ACB ＝90°，∴Rt △ECM ∽Rt △ACB ，∴EC AC ＝EM AB ，∵AB ＝5，∴445-，x x =解得x ＝209， ∴AE ＝ME ＝209，EC ＝169，在Rt △ECM 中，∵∠ECM ＝90°，∴CM 2＝EM 2－EC 2，即CM ＝（209）2－（169）2＝43，∵四边形AEMF 是菱形，∴OE ＝OF ，OA ＝OM ，AM ⊥EF ， ∴S AEMF 菱形＝4S △AOE ＝2OE ·AO ， 在Rt △AOE 和Rt △ACM 中， ∵tan ∠EAO ＝tan ∠CAM ，∴OE AO ＝CM AC ，∵CM ＝43，AC ＝4，∴AO ＝3OE ，∴S AEMF 菱形＝6OE 2，又∵S AEMF 菱形＝AE ·CM ，∴6OE 2＝209×43，解得OE ＝2109，∴EF ＝2OE ＝4109.。

中考数学一轮复习考点知识专项训练一次函数命题点1一次函数的图象与性质1．(2020·浙江嘉兴)一次函数y＝2x－1的图象大致是( )2．(2020·湖南益阳)一次函数y＝kx＋b的图象如图所示，则下列结论正确的是( )A．k＜0B．b＝－1C．y随x的增大而减小D．当x＞2时，kx＋b＜03．(2019·山东临沂)下列关于一次函数y＝kx＋b(k<0，b>0)的说法，错误的是( ) A．图象经过第一、二、四象限B．y随x的增大而减小C．图象与y轴交于点(0，b)D．当x>－bk时，y>04．(2020·上海)已知正比例函数y＝kx(k是常数，k≠0)的图象经过第二、四象限，那么y的值随着x的增大而________(填“增大”或“减小”)．5．(2020·山东东营)已知一次函数y＝kx＋b(k≠0)的图象经过A(1，－1)，B(－1，3)两点，则k______0(填“＞”或“＜”)．命题点2一次函数表达式的确定6．(2019·山东枣庄)如图，一直线与两坐标轴的正半轴分别交于A，B两点，P是线段AB上任意一点(不包括端点)，过点P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8，则该直线的函数表达式是( )A．y＝－x＋4 B．y＝x＋4C．y＝x＋8 D．y＝－x＋87．(2020·贵州黔西南州)如图，正比例函数的图象与一次函数y＝－x＋1的图象相交于点P，点P到x轴的距离是2，则这个正比例函数的表达式是_______．8．(2020·江苏南通)如图，直线l1：y＝x＋3与过点A(3，0)的直线l2交于点C(1，m)，与x轴交于点B.(1)求直线l2的表达式；(2)点M在直线l1上，MN∥y轴，交直线l2于点N，若MN＝AB，求点M的坐标．9．(2019·江西)如图，在平面直角坐标系中，点A，B的坐标分别为(－32，0)，(32，1)，连接AB，以AB为边向上作等边三角形ABC.(1)求点C的坐标；(2)求线段BC所在直线的表达式．10．(2020·江苏南京)将一次函数y＝－2x＋4的图象绕原点O逆时针旋转90°，所得到的图象对应的函数表达式是________________．11．(2020·北京)在平面直角坐标系xOy中，一次函数y＝kx＋b(k≠0)的图象由函数y＝x 的图象平移得到，且经过点(1，2)．(1)求这个一次函数的表达式；(2)当x>1时，对于x的每一个值，函数y＝mx(m≠0)的值都大于一次函数y＝kx＋b的值，直接写出m的取值范围．能力点1 一次函数与方程(组)、不等式的关系12．(2018·辽宁辽阳)如图，直线y ＝ax ＋b (a ≠0)过点A (0，4)，B (－3，0)，则方程ax ＋b ＝0的解是( )A ．x ＝－3B ．x ＝4C ．x ＝－43D ．x ＝－3413．(2020·贵州遵义)如图，直线y ＝kx ＋b (k ，b 是常数，k ≠0)与直线y ＝2交于点A (4，2)，则关于x 的不等式kx ＋b ＜2的解集为______________．14．(2019·贵州贵阳)在平面直角坐标系内，一次函数y ＝k 1x ＋b 1与y ＝k 2x ＋b 2的图象如图所示，则关于x ，y 的方程组⎩⎨⎧y －k 1x ＝b 1，y －k 2x ＝b 2的解是____________．能力点2 一次函数的实际应用15．(2019·广东深圳)有A ，B 两个发电厂，每焚烧一吨垃圾，A 发电厂比B 发电厂多发40度电，A 焚烧20吨垃圾比B 焚烧30吨垃圾少发1 800度电．(1)求焚烧1吨垃圾A和B发电厂各发电多少度；(2)A，B两个发电厂共焚烧90吨的垃圾，A焚烧的垃圾不多于B焚烧的垃圾的两倍，求A发电厂和B发电厂总发电量的最大值．16．(2019·吉林)甲、乙两车分别从A，B两地同时出发，沿同一条公路相向行驶，相遇后，甲车继续以原速行驶到B地，乙车立即以原速原路返回到B地，甲、乙两车距B 地的路程y(km)与各自行驶的时间x(h)之间的关系如图所示．(1)m＝________，n＝________；(2)求乙车距B地的路程y关于x的函数表达式，并写出自变量x的取值范围；(3)当甲车到达B地时，求乙车距B地的路程．17．(2020·浙江衢州)2020年5月16日，“钱塘江诗路”航道全线开通．一艘游轮从杭州出发前往衢州，线路如图①所示．当游轮到达建德境内的“七里扬帆”景点时，一艘货轮沿着同样的线路从杭州出发前往衢州．已知游轮的速度为20 km/h，游轮行驶的时间记为t(h)，两艘轮船距离杭州的路程s(km)关于t(h)的图象如图②所示(游轮在停靠前后的行驶速度不变)．(1)写出图②中点C的横坐标的实际意义，并求出游轮在“七里扬帆”停靠的时长．(2)若货轮比游轮早36分钟到达衢州．问：①货轮出发后几小时追上游轮？②游轮与货轮何时相距12 km?图①图②18．(2020·湖北荆州)为了抗击新型冠状病毒肺炎疫情，我市甲、乙两厂积极生产了某种防疫物资共500吨，乙厂的生产量是甲厂的2倍少100吨．这批防疫物资将运往A地240吨，B地260吨，运费如下表(单位：元/吨)：(1)(2)设这批物资从乙厂运往A地x吨，全部运往A，B两地的总运费为y元，求y与x之间的函数关系式，并设计使总运费最少的调运方案；(3)当每吨的运费均降低m元(0＜m≤15且m为整数)时，按(2)中设计的调运方案运输，总运费不超过5 200元．求m的最小值．19．(2020·浙江绍兴)我国传统的计重工具——秤的应用，方便了人们的生活．如图①，可以用秤砣到秤纽的水平距离来得出秤钩上所挂物体的重量．称重时，若秤杆上秤砣到秤纽的水平距离为x(厘米)时，秤钩所挂物重为y(斤)，则y是x的一次函数．下表中为若干次称重时所记录的一些数据：(1)在上表哪一对是错误的；(2)根据(1)的发现，问秤杆上秤砣到秤纽的水平距离为16厘米时，秤钩所挂物重是多少？图①图②20．(2017·江西)如图所示的是一种斜挎包，其挎带由双层部分、单层部分和调节扣构成．小敏用后发现，通过调节扣加长或缩短单层部分的长度，可以使挎带的长度(单层部分与双层部分长度的和，其中调节扣所占的长度忽略不计)加长或缩短．设单层部分的长度为x cm，双层部分的长度为y cm，经测量，得到如下数据：(1)(2)根据小敏的身高和习惯，挎带的长度为120 cm时，背起来正合适，请求出此时单层部分的长度；(3)设挎带的长度为l cm，求l的取值范围．参考答案1．B 2.B 3.D4．减小 5.＜ 6.A 7.y ＝－2x8．解：(1)把x ＝1代入y ＝x ＋3中，得y ＝4， ∴C (1，4)．设直线l 2的表达式为y ＝kx ＋b ，将A ，C 两点的坐标分别代入， 得⎩⎨⎧k ＋b ＝4，3k ＋b ＝0，解得⎩⎨⎧k ＝－2，b ＝6， ∴直线l 2的表达式为y ＝－2x ＋6.(2)在y ＝x ＋3中，令y ＝0，解得x ＝－3，∴B (－3，0)． 设M (a ，a ＋3)，由MN ∥y 轴，得N (a ，－2a ＋6)， ∴MN ＝|a ＋3－(－2a ＋6)|＝AB ＝3－(－3)＝6， 解得a ＝3或a ＝－1， ∴M (3，6)或(－1，2)．9．解：(1)如图，过点B 作BD ⊥x 轴于点D ，∵点A 的坐标为(－32，0)，点B 的坐标为(32，1)，∴AD ＝3，BD ＝1，∴由勾股定理得AB ＝AD 2＋BD 2＝（3）2＋12＝2， ∴sin ∠BAD ＝BD AB ＝12，∴∠BAD ＝30°. 又∵△ABC 是等边三角形， ∴∠CAB ＝60°，AC ＝AB ＝2， ∴∠CAD ＝90°，∴点C 的坐标为(－32，2)．(2)设线段BC 所在直线的表达式为y ＝kx ＋b ，将点B (32，1)，C (－32，2)分别代入，得 ⎩⎪⎨⎪⎧32k ＋b ＝1，－32k ＋b ＝2，解得⎩⎪⎨⎪⎧k ＝－33，b ＝32， ∴线段BC 所在直线的表达式为y ＝－33x ＋32.10．y ＝12x ＋211．解：(1)∵一次函数y ＝kx ＋b (k ≠0)的图象由y ＝x 的图象平移得到， ∴k ＝1.将点(1，2)代入y ＝x ＋b ，可得2＝1＋b ，解得b ＝1， ∴这个一次函数的表达式为y ＝x ＋1.(2)当x >1时，对于x 的每一个值，函数y ＝mx (m ≠0)的值都大于一次函数y ＝x ＋1的值，即其图象在一次函数y ＝x ＋1图象的上方，由下图可知．临界值为当x ＝1时，两条直线都过点(1，2)，∴当x >1，m ≥2时，y ＝mx (m ≠0)的值都大于y ＝x ＋1的值， ∴m 的取值范围为m ≥2. 12．A 13.x ＜4 14.⎩⎨⎧x ＝2y ＝115．解：(1)设焚烧1吨垃圾A 发电厂发电a 度，B 发电厂发电b 度，根据题意，得⎩⎨⎧a －b ＝40，30b －20a ＝1 800，解得⎩⎨⎧a ＝300，b ＝260.答：焚烧1吨垃圾A 发电厂发电300度，B 发电厂发电260度．(2)设A 发电厂焚烧x 吨垃圾，则B 发电厂焚烧(90－x )吨垃圾．设两厂的总发电量为y 度，则y ＝300x ＋260(90－x )＝40x ＋23 400，∵⎩⎨⎧0≤x ，0≤90－x ，x≤2（90－x ），∴0≤x ≤60.∵y 随x 的增大而增大，∴当x ＝60时，y 有最大值，且最大值为40×60＋23 400＝25 800.答：A 发电厂和B 发电厂总发电量的最大值是25 800度．16．解：(1)4 120(2)当0≤x ≤2时，设乙车距离B 地的路程y 关于x 的函数表达式为y ＝kx ，∵图象过点(2，120)，∴2k ＝120，解得k ＝60，∴此时y 关于x 的函数表达式为y ＝60x (0≤x ≤2)；当2＜x ≤4时，设乙车距离B 地的路程y 关于x 的函数表达式为y ＝k 1x ＋b ，∵图象过(2，120)，(4，0)两点，∴⎩⎨⎧2k 1＋b ＝120，4k 1＋b ＝0，解得⎩⎨⎧k 1＝－60，b ＝240， ∴此时y 关于x 的函数表达式为y ＝－60x ＋240(2＜x ≤4)．综上所述，乙车距B 地的路程y 关于x 的函数表达式为y ＝⎩⎨⎧60x （0≤x≤2），－60x ＋240（2<x≤4）.(3)当x ＝3.5时，y ＝－60×3.5＋240＝30.∴当甲车到达B 地时，乙车距B 地的路程为30 km .17．解：(1)点C 横坐标的实际意义是游轮从杭州出发前往衢州共用了23 h ， ∴游轮在“七里扬帆”停靠的时长＝23－(420÷20)＝23－21＝2(h )．(2)①280÷20＝14(h )，14＋2＝16(h )，∴点A (14，280)，点B (16，280)，点D (14，0)．∵36÷60＝0.6(h )，23－0.6＝22.4(h )，∴点E (22.4，420)．设直线BC 的表达式为s ＝kt ＋b ，把B (16，280)，C (23，420)两点的坐标分别代入，得⎩⎨⎧280＝16k ＋b ，420＝23k ＋b ，解得⎩⎨⎧k ＝20，b ＝－40，∴线段BC 的表达式为s ＝20t －40(16≤t ≤23)．同理由D (14，0)，E (22.4，420)两点可得线段DE 的表达式为s ＝50t －700(14≤t ≤22.4)， 由题意，得20t －40＝50t －700，解得t ＝22.∵22－14＝8(h )，∴货轮出发后8 h 追上游轮．②当相遇之前相距12 km 时，20t －40－(50t －700)＝12，解得t ＝21.6；当相遇之后相距12 km 时，50t －700－(20t －40)＝12，解得t ＝22.4，∴游轮行驶21.6 h 或22.4 h 时游轮与货轮相距12 km .18．解：(1)设这批防疫物资甲厂生产了a 吨，乙厂生产了b 吨，则⎩⎨⎧a ＋b ＝500，2a －b ＝100，解得⎩⎨⎧a ＝200，b ＝300. ∴这批防疫物资甲厂生产了200吨，乙厂生产了300吨．(2)由题意，得y ＝20(240－x )＋25[260－(300－x )]＋15x ＋24(300－x )＝－4x ＋11 000，由题意，得⎩⎨⎧x≥0，240－x≥0，300－x≥0，260－（300－x ）≥0，解得40≤x ≤240， ∵－4＜0，∴y 随x 的增大而减小，∴当x ＝240时，y 有最小值，∴使总运费最少的调运方案为甲厂的200吨物资全部运往B 地，乙厂运往A 地240吨，运往B 地60吨．(3)由题意，得y ＝－4x ＋11 000－500m ，当x ＝240时，y 最小＝－4×240＋11 000－500m ＝10 040－500m ，由题意，得10 040－500m ≤5 200，解得m ≥9.68.又∵0＜m ≤15且m 为整数，∴m 的最小值为10.【核心素养提升】19．解：(1)描点连线如下图：观察图象可知，x ＝7，y ＝2.75这组数据错误．(2)设y 与x 之间的函数表达式为y ＝kx ＋b (x ＞0)，把x ＝1，y ＝0.75，x ＝2，y ＝1代入可得⎩⎨⎧k ＋b ＝0.75，2k ＋b ＝1，解得⎩⎪⎨⎪⎧k ＝14，b ＝12，∴y ＝14x ＋12.当x ＝16时，y ＝14×16＋12＝4.5，∴秤杆上秤砣到秤纽的水平距离为16厘米时，秤钩所挂物重是4.5斤．20．解：(1)70 0y 关于x 的函数表达式为y ＝－0.5x ＋75(0≤x ≤150)．(2)根据题意，得⎩⎨⎧x ＋y ＝120，y ＝－0.5x ＋75，解得⎩⎨⎧x ＝90，y ＝30.答：此时单层部分的长度为90 cm .(3)根据题意，得l ＝x ＋y ＝0.5x ＋75，∵0≤x ≤150，∴75≤l ≤150.答：l 的取值范围为75≤l ≤150.。

2023年中考数学一轮专题练习 ——正多边形和圆一、单选题（本大题共8小题）1. （上海市2022年）有一个正n 边形旋转90后与自身重合，则n 为（ ） A ．6B ．9C ．12D ．15 2. （湖南省邵阳市2022年）如图，⊙O 是等边△ABC 的外接圆，若AB =3，则⊙O 的半径是（ ）A．32 B ．C D ．523. （四川省雅安市2022年）如图，已知⊙O 的周长等于6π，则该圆内接正六边形ABCDEF 的边心距OG 为（ ）A ．3B ．32CD ．34. （四川省南充市2022年）如图，在正五边形ABCDE 中，以AB 为边向内作正ABF ，则下列结论错误的是（ ）A ．AE AF =B ．EAF CBF ∠=∠C ．F EAF ∠=∠D ．CE ∠=∠ 5. （四川省内江市2022年）如图，正六边形ABCDEF 内接于⊙O ，半径为6，则这个正六边形的边心距OM 和BC 的长分别为（ ）A ．4，3πB ．πC ．43πD ．32π6. （四川省成都市2022年）如图，正六边形ABCDEF 内接于⊙O ，若⊙O 的周长等于6π，则正六边形的边长为（ ）AB ．C ．3D ．7. （广西玉林市2022年）如图的电子装置中，红黑两枚跳棋开始放置在边长为2的正六边形ABCDEF 的顶点A 处．两枚跳棋跳动规则是：红跳棋按顺时针方向1秒钟跳1个顶点，黑跳棋按逆时针方向3秒钟跳1个顶点，两枚跳棋同时跳动，经过2022秒钟后，两枚跳棋之间的距离是( )A ．4B ．C ．2D ．08. （河南省2022年）如图，在平面直角坐标系中，边长为2的正六边形ABCDEF 的中心与原点O 重合，AB x ∥轴，交y 轴于点P ．将△OAP 绕点O 顺时针旋转，每次旋转90°，则第2022次旋转结束时，点A 的坐标为（ ）A ．)1-B ．(1,-C ．()1-D ．( 二、填空题（本大题共5小题）9. （辽宁省营口市2022年）如图，在正六边形ABCDEF 中，连接,AC CF ，则ACF ∠= 度．10. （江苏省宿迁市2022年）如图，在正六边形ABCDEF 中，AB =6，点M 在边AF 上，且AM =2．若经过点M 的直线l 将正六边形面积平分，则直线l 被正六边形所截的线段长是 ．11. （吉林省长春市2022年）跳棋是一项传统的智力游戏．如图是一副跳棋棋盘的示意图，它可以看作是由全等的等边三角形ABC 和等边三角形DEF 组合而成，它们重叠部分的图形为正六边形．若27AB =厘米，则这个正六边形的周长为 厘米．12. （吉林省2022年）第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素．如图，这个图案绕着它的中心旋转角()0360αα︒<<︒后能够与它本身重合，则角α可以为 度．（写出一个即可）13. （黑龙江省绥化市2022年）如图，正六边形ABCDEF 和正五边形AHIJK 内接于O ，且有公共顶点A ，则BOH ∠的度数为 度．三、解答题（本大题共1小题）14. （浙江省金华市2022年）如图1，正五边形ABCDE 内接于⊙O ，阅读以下作图过程，并回答下列问题，作法：如图2，①作直径AF ；②以F 为圆心，FO 为半径作圆弧，与⊙O 交于点M ，N ；③连接,,AM MN NA ．(1)求ABC ∠的度数．(2)AMN 是正三角形吗？请说明理由．(3)从点A 开始，以DN 长为半径，在⊙O 上依次截取点，再依次连接这些分点，得到正n 边形，求n 的值．参考答案1. 【答案】C【分析】根据选项求出每个选项对应的正多边形的中心角度数，与90一致或有倍数关系的则符合题意．【详解】如图所示，计算出每个正多边形的中心角，90是30的3倍，则可以旋转得到．A.B.C.D.观察四个正多边形的中心角，可以发现正12边形旋转90°后能与自身重合故选C．2. 【答案】C【分析】作直径AD，连接CD，如图，利用等边三角形的性质得到∠B=60°，关键圆周角定理得到∠ACD=90°，∠D=∠B=60°，然后利用含30度的直角三角形三边的关系求解．【详解】解：作直径AD，连接CD，如图，∵△ABC 为等边三角形，∴∠B =60°，∵AD 为直径，∴∠ACD =90°，∵∠D =∠B =60°，则∠DAC =30°，∴CD =12AD ， ∵AD 2=CD 2+AC 2，即AD 2=(12AD )2+32，∴AD∴OA =OB =12AD 故选：C ．3. 【答案】C【分析】 利用圆的周长先求出圆的半径，正六边形的边长等于圆的半径，正六边形一条边与圆心构成等边三角形，根据边心距即为等边三角形的高用勾股定理求出OG ．【详解】∵圆O 的周长为6π，设圆的半径为R ，∴26R ππ=∴R =3连接OC 和OD ，则OC=OD=3∵六边形ABCDEF 是正六边形，∴∠COD =360606︒=︒， ∴△OCD 是等边三角形，OG 垂直平分CD ， ∴OC =OD =CD ，1322CG CD ==∴OG =故选 C4. 【答案】C【分析】利用正多边形各边长度相等，各角度数相等，即可逐项判断．【详解】解：∵多边形ABCDE 是正五边形，∴该多边形内角和为：5218540(0)-⨯︒=︒，AB AE =， ∴5401085C E EAB ABC ︒∠=∠=∠=∠==︒，故D 选项正确； ∵ABF 是正三角形，∴60FAB FBA F ∠=∠=∠=︒，AB AF FB ==，∴1086048EAF EAB FAB ∠=∠-∠=︒-︒=︒，1086048CBF ABC FBA ∠=∠-∠=︒-︒=︒， ∴EAF CBF ∠=∠，故B 选项正确；∵AB AE =，AB AF FB ==，∴AE AF =，故A 选项正确；∵60F ∠=︒，48EAF ∠=︒，∴F EAF ∠≠∠，故C 选项错误，故选：C ．5. 【答案】D【分析】连接OC 、OB ，证出BOC ∆是等边三角形，根据勾股定理求出OM ，再由弧长公式求出弧BC 的长即可．【详解】解：连接OC 、OB ，六边形ABCDEF 为正六边形，360606BOC ︒∴∠==︒， OB OC =，BOC ∴∆为等边三角形，6BC OB ∴==，OM BC ⊥，132BM BC ∴==，OM ∴==BC 的长为6062180ππ⨯==． 故选：D ．6. 【答案】C【分析】连接OB ，OC ，由⊙O 的周长等于6π，可得⊙O 的半径，又由圆的内接多边形的性质，即可求得答案．【详解】解：连接OB ，OC ，∵⊙O 的周长等于6π，∴⊙O 的半径为：3，∵∠BOC 61=⨯360°＝60°， ∵OB ＝OC ，∴△OBC 是等边三角形，∴BC ＝OB ＝3，∴它的内接正六边形ABCDEF 的边长为3，故选：C ．7. 【答案】B【分析】由题意可分别求出经过2022秒后，红黑两枚跳棋的位置，然后根据正多边形的性质及含30度直角三角形的性质可进行求解．解：∵2022÷3=674，2022÷1=2022，∴67461122,20226337÷=⋅⋅⋅⋅⋅÷=，∴经过2022秒后，红跳棋落在点A 处，黑跳棋落在点E 处，连接AE ，过点F 作FG ⊥AE 于点G ，如图所示：在正六边形ABCDEF 中，2,120AF EF AFE ==∠=︒， ∴1,302AG AE FAE FEA =∠=∠=︒， ∴112FG AF ==，∴AG =∴AE =故选B ．8. 【答案】B【分析】首先确定点A 的坐标，再根据4次一个循环，推出经过第2022次旋转后，点A 的坐标即可．【详解】解：正六边形ABCDEF 边长为2，中心与原点O 重合，AB x ∥轴，∴AP ＝1， AO ＝2，∠OPA ＝90°，∴OP ＝∴A（1第1次旋转结束时，点A -1）；第2次旋转结束时，点A 的坐标为（-1，第3次旋转结束时，点A 的坐标为（1）；第4次旋转结束时，点A 的坐标为（1，∵将△OAP 绕点O 顺时针旋转，每次旋转90°，∴4次一个循环，∵2022÷4＝505……2，∴经过第2022次旋转后，点A 的坐标为（-1，9. 【答案】30【分析】连接BE ，交CF 与点O ，连接OA ，先求出360606AOF ︒∠==︒，再根据等腰三角形等边对等角的性质，三角形外角的性质求解即可．【详解】连接BE ，交CF 与点O ，连接OA ，在正六边形ABCDEF 中，360606AOF ︒∴∠==︒， OA OC =OAC OCA ∴∠=∠2AOF OAC ACF ACF ∠=∠+∠=∠30ACF =∴∠︒，故答案为：30．10. 【答案】【分析】如图，连接AD ，CF ，交于点O ，作直线MO 交CD 于H ，过O 作OP ⊥AF 于P ，由正六边形是轴对称图形可得：,ABCODEFO S S 四边形四边形 由正六边形是中心对称图形可得：,,AOM DOH MOF CHO S S S S ,OM OH = 可得直线MH 平分正六边形的面积，O 为正六边形的中心，再利用直角三角形的性质可得答案．【详解】解：如图，连接AD ，CF ，交于点O ，作直线MO 交CD 于H ，过O 作OP ⊥AF 于P ， 由正六边形是轴对称图形可得：,ABCODEFO S S 四边形四边形 由正六边形是中心对称图形可得：,,AOM DOH MOF CHO S S S S ,OM OH =∴直线MH 平分正六边形的面积，O 为正六边形的中心，由正六边形的性质可得：AOF 为等边三角形，60,AFO 而6,AB =6,3,ABAF OF OA AP FP 226333,OP2,AM 则1,MP22OM13327,MH OM247.故答案为：11. 【答案】54【分析】设AB交EF、FD与点M、N，AC交EF、ED于点G、H，BC交FD、ED于点O、P，再证明△FMN、△ANG、△BMO、△DOP、△CPH、△EGH是等边三角形即可求解．【详解】设AB交EF、FD与点M、N，AC交EF、ED于点G、H，BC交FD、ED于点O、P，如图，∵六边形MNGHPO是正六边形，∴∠GNM=∠NMO=120°，∴∠FNM=∠FNM=60°，∴△FMN是等边三角形，同理可证明△ANG、△BMO、△DOP、△CPH、△EGH是等边三角形，∴MO=BM，NG=AN，OP=PD，GH=HE，∴NG+MN+MO=AN+MN+BM=AB，GH+PH+OP=HE+PH+PD=DE，∵等边△ABC≌等边△DEF，∴AB=DE，∵AB=27cm，∴DE=27cm，∴正六边形MNGHPO的周长为：NG+MN+MO+GH+PH+OP=AB+DE=54cm，故答案为：54．12. 【答案】60或120或180或240或300（写出一个即可）【分析】如图（见解析），求出图中正六边形的中心角，再根据旋转的定义即可得．【详解】 解：这个图案对应着如图所示的一个正六边形，它的中心角3601606︒∠==︒， 0360α︒<<︒，∴角α可以为60︒或120︒或180︒或240︒或300︒，故答案为：60或120或180或240或300（写出一个即可）．13. 【答案】12【分析】连接AO ，求出正六边形和正五边形的中心角即可作答．【详解】连接AO ，如图，∵多边形ABCDEF 是正六边形，∴∠AOB =360°÷6=60°，∵多边形AHIJK 是正五边形，∴∠AOH =360°÷5=72°，∴∠BOH =∠AOH -∠AOB =72°-60°=12°，故答案为：12．14. 【答案】(1)108︒(2)是正三角形，理由见解析(3)15n =【分析】（1）根据正五边形的性质以及圆的性质可得BC CD DE AE AB ====，则AOC ∠(优弧所对圆心角)372216︒︒=⨯=，然后根据圆周角定理即可得出结论；（2）根据所作图形以及圆周角定理即可得出结论；（3）运用圆周角定理并结合（1）（2）中结论得出14412024NOD ∠=︒-︒=︒，即可得出结论．(1)解：∵正五边形ABCDE ．∴BC CD DE AE AB ====， ∴360725AOB BOC COD DOE EOA ︒∠=∠=∠=∠=∠==︒， ∵3AEC AE =，∴AOC ∠(优弧所对圆心角)372216︒︒=⨯=， ∴1121610822AOC ABC ∠=⨯︒=∠=︒； (2)解：AMN 是正三角形，理由如下：连接,ON FN ，由作图知：FN FO =,∵ON OF =，∴ON OF FN ==，∴OFN △是正三角形，∴60OFN ∠=︒，∴60AMN OFN ∠=∠=︒，同理60ANM ∠=︒，∴60MAN ∠=︒，即AMN ANM MAN ∠=∠=∠，∴AMN 是正三角形；(3)∵AMN 是正三角形，∴2120A N A N M O =∠=︒∠．∵2AD AE =，∴272144AOD ∠=⨯︒=︒，∵DN AD AN =-，∴14412024NOD ∠=︒-︒=︒， ∴3601524n ==．。

2022年中考数学一轮复习：方程和不等式 专项练习题一．选择题（共8小题）1．（2021•襄阳）随着生产技术的进步，某制药厂生产成本逐年下降．两年前生产一吨药的成本是5000元，现在生产一吨药的成本是4050元．设生产成本的年平均下降率为x ，下面所列方程正确的是（ ） A ．5000（1+x ）2＝4050 B ．4050（1+x ）2＝5000 C ．5000（1﹣x ）2＝4050D ．4050（1﹣x ）2＝50002．（2021•荆门）我国古代数学古典名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”其大意是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量，木条还剩余1尺；问长木多少尺？如果设木条长为x 尺，绳子长为y 尺，则下面所列方程组正确的是（ ） A ．{y =x +4.512y =x −1B ．{y =x −4.512y =x +1C ．{y =x +4.52y =x −1D ．{y =x −4.52y =x +13．（2021•荆州）定义新运算“※”：对于实数m ，n ，p ，q ．有[m ，p ]※[q ，n ]＝mn +pq ，其中等式右边是通常的加法和乘法运算，例如：[2，3]※[4，5]＝2×5+3×4＝22．若关于x 的方程[x 2+1，x ]※[5﹣2k ，k ]＝0有两个实数根，则k 的取值范围是（ ） A ．k ＜54且k ≠0B ．k ≤54C ．k ≤54且k ≠0D ．k ≥544．（2021•恩施州）分式方程x x−1+1=3x−1的解是（ ）A ．x ＝1B ．x ＝﹣2C ．x =34D ．x ＝25．（2021•十堰）某工厂现在平均每天比原计划多生产50台机器，现在生产400台机器所需时间比原计划生产450台机器所需时间少1天，设现在平均每天生产x 台机器，则下列方程正确的是（ ） A ．400x −450x−50=1 B ．450x−50−400x =1C ．400x−450x+1=50 D ．450x+1−400x=506．（2021•宜昌）我国古代数学经典著作《九章算术》中有这样一题，原文是：“今有共买物，人出八，盈三；人出七，不足四．问人数、物价各几何？”意思是：今有人合伙购物，每人出八钱，会多三钱；每人出七钱，又差四钱．问人数、物价各多少？设人数为x 人，物价为y 钱，下列方程组正确的是（ ）A ．{y =8x −3y =7x +4B ．{y =8x +3y =7x +4C ．{y =8x −3y =7x −4D ．{y =8x +3y =7x −47．（2021•武汉）已知a ，b 是方程x 2﹣3x ﹣5＝0的两根，则代数式2a 3﹣6a 2+b 2+7b +1的值是（ ） A ．﹣25B ．﹣24C ．35D ．368．（2021•武汉）我国古代数学名著《九章算术》中记载“今有共买物，人出八，盈三；人出七，不足四．问人数、物价各几何？”意思是：现有几个人共买一件物品，每人出8钱，多出3钱；每人出7钱，还差4钱．问人数，物价各是多少？若设共有x 人，物价是y 钱，则下列方程正确的是（ ） A ．8（x ﹣3）＝7（x +4） B ．8x +3＝7x ﹣4C ．y−38=y+47D ．y+38=y−47二．填空题（共9小题） 9．（2021•黄石）分式方程1x−2+1−x 2−x=3的解是 ．10．（2021•襄阳）不等式组{x +2≥4x −12x ＞1−x的解集是 ．11．（2021•湖北）我国明代数学读本《算法统宗》一书中有这样一道题：一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托．如果1托为5尺，那么索长为 尺．（其大意为：现有一根竿和一条绳索，如果用绳索去量竿，绳索比竿长5尺；如果将绳索对折后再去量竿，就比竿短5尺，则绳索长几尺．）12．（2021•湖北）关于x 的方程x 2﹣2mx +m 2﹣m ＝0有两个实数根α，β，且1α+1β=1，则m ＝ ．13．（2021•鄂州）已知实数a 、b 满足√a −2+|b +3|＝0，若关于x 的一元二次方程x 2﹣ax +b ＝0的两个实数根分别为x 1、x 2，则1x 1+1x 2= ．14．（2021•荆门）关于x 的不等式组{−(x −a)＜31+2x 3≥x −1恰有2个整数解，则a 的取值范围是 ．15．（2021•随州）已知关于x 的方程x 2﹣（k +4）x +4k ＝0（k ≠0）的两实数根为x 1，x 2，若2x 1+2x 2=3，则k ＝ ．16．（2021•荆州）若关于x 的方程2x+m x−2+x−12−x=3的解是正数，则m 的取值范围为．17．（2021•黄冈）若关于x的一元二次方程x2﹣2x+m＝0有两个不相等的实数根，则m的值可以是．（写出一个即可）三．解答题（共10小题）18．（2021•黄石）我国传统数学名著《九章算术》记载：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？”译文：有若干只鸡与兔在同一个笼子里，从上面数有35个头，从下面数有94只脚，问笼中各有几只鸡和兔？根据以上译文，回答以下问题：（1）笼中鸡、兔各有多少只？（2）若还是94只脚，但不知道头多少个，笼中鸡兔至少30只且不超过40只．鸡每只值80元，兔每只值60元，问这笼鸡兔最多值多少元？最少值多少元？19．（2021•湖北）（1）计算，（3−√2）0×4﹣（2√3−6）+√−83+√12；（2）解分式方程：22x−1+x1−2x=1．20．（2021•黄石）已知关于x的一元二次方程x2+2mx+m2+m＝0有实数根．（1）求m的取值范围；（2）若该方程的两个实数根分别为x1、x2，且x12+x22＝12，求m的值．21．（2021•十堰）已知关于x的一元二次方程x2﹣4x﹣2m+5＝0有两个不相等的实数根．（1）求实数m的取值范围；（2）若该方程的两个根都是符号相同的整数，求整数m的值．22．（2021•荆门）已知关于x的一元二次方程x2﹣6x+2m﹣1＝0有x1，x2两实数根．（1）若x1＝1，求x2及m的值；（2）是否存在实数m，满足（x1﹣1）（x2﹣1）=6m−5？若存在，求出实数m的值；若不存在，请说明理由．23．（2021•荆州）已知：a是不等式5（a﹣2）+8＜6（a﹣1）+7的最小整数解，请用配方法解关于x的方程x2+2ax+a+1＝0．24．（2021•宜昌）随着农业技术的现代化，节水型灌溉得到逐步推广．喷灌和滴灌是比漫灌更节水的灌溉方式，喷灌和滴灌时每亩用水量分别是漫灌时的30%和20%．去年，新丰收公司用各100亩的三块试验田分别采用喷灌、滴灌和漫灌的灌溉方式，共用水15000吨．（1）请问用漫灌方式每亩用水多少吨？去年每块试验田各用水多少吨？（2）今年该公司加大对农业灌溉的投入，喷灌和滴灌试验田的面积都增加了m%，漫灌试验田的面积减少了2m%．同时，该公司通过维修灌溉输水管道，使得三种灌溉方式下的每亩用水量都进一步减少了m%．经测算，今年的灌溉用水量比去年减少95m%，求m。

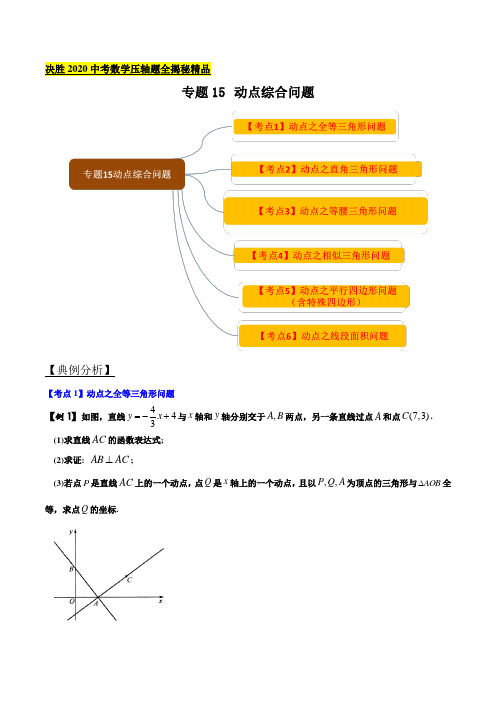
2024成都中考数学第一轮专题复习圆的有关概念及性质知识精练基础题1. (2023江西)如图，点A，B，C，D均在直线l上，点P在直线l外，则经过其中任意三个点，最多可画出圆的个数为()A. 3B. 4C. 5D. 6第1题图2. (2023广东省卷)如图，AB是⊙O的直径，∠BAC＝50°，则∠D＝()第2题图A. 20°B. 40°C. 50°D. 80°3. (2023广元)如图，AB是⊙O的直径，点C，D在⊙O上，连接CD，OD，A C.若∠BOD＝124°，则∠ACD的度数是()A. 56°B. 33°C. 28°D. 23°第3题图4. (2023山西)如图，四边形ABCD内接于⊙O，AC，BD为对角线，BD经过圆心O.若∠BAC ＝40°，则∠DBC的度数为()第4题图A. 40°B. 50°C. 60°D. 70°5. (2023安徽)如图，正五边形ABCDE内接于⊙O，连接OC，OD，则∠BAE－∠COD＝()A. 60°B. 54°C. 48°D. 36°第5题图6. (2023赤峰)如图，圆内接四边形ABCD中，∠BCD＝105°，连接OB，OC，OD，BD，∠BOC ＝2∠COD，则∠CBD的度数是()第6题图A. 25°B. 30°C. 35°D. 40°7. [新考法—数学文化](2023岳阳)我国古代数学名著《九章算术》中有这样一道题：“今有圆材，径二尺五寸．欲为方版，令厚七寸，问广几何？”结合下图，其大意是：今有圆形材质，直径BD为25寸，要做成方形板材，使其厚度CD达到7寸，则BC的长是() A. 674寸 B. 25寸C. 24寸D. 7寸第7题图8. (2023杭州)如图，在⊙O中，半径OA，OB互相垂直，点C在劣弧AB上．若∠ABC＝19°，则∠BAC＝()第8题图A. 23°B. 24°C. 25°D. 26°9. (2023广西)赵州桥是当今世界上建造最早，保存最完整的中国古代单孔敞肩石拱桥．如图，主桥拱呈圆弧形，跨度约为37 m，拱高约为7 m，则赵州桥主桥拱半径R约为()第9题图A. 20 mB. 28 mC. 35 mD. 40 m10. (2023凉山州)如图，在⊙O中，OA⊥BC，∠ADB＝30°，BC＝23，则OC＝()A. 1B. 2C. 2 3D. 4第10题图11. 如图，点A，B，D在⊙O上，CD垂直平分AB于点C.现测得AB＝CD＝16，则圆形宣传图标的半径为()第11题图A. 12B. 10C. 8D. 612. 如图，在平面直角坐标系中，⊙O的半径为4，弦AB的长为3，过O作OC⊥AB于点C，则OC的长度是________；⊙O内一点D的坐标为(－2，1)，当弦AB绕O点顺时针旋转时，点D到AB的距离的最小值是________．第12题图13. (2023武汉)如图，OA，OB，OC都是⊙O的半径，∠ACB＝2∠BA C.(1)求证：∠AOB＝2∠BOC；(2)若AB＝4，BC＝5，求⊙O的半径．第13题图拔高题14. (2023吉林省卷)如图，AB，AC是⊙O的弦，OB，OC是⊙O的半径，点P为OB上任意一点(点P不与点B重合)，连接CP.若∠BAC＝70°，则∠BPC的度数可能是()A. 70°B. 105°C. 125°D. 155°第14题图15. 如图，正方形ABCD 内接于⊙O ，点E 为弧AB 的中点，连接DE 与AB 交于点F .若AB＝1，记△ADF 的面积为S 1，△AEF 的面积为S 2，则S 1S 2的值为________．第15题图16. 如图，以原点O 为圆心的圆交x 轴于A ，B 两点，交y 轴的正半轴于点C ，且点A 的坐标为(－2，0)，D 为第一象限内⊙O 上的一点，若∠OCD ＝75°，则AD 的长为________．第16题图参考答案与解析1. D 【解析】本题考查了确定圆的条件及圆的有关定义及性质．∵过不在同一直线上的三个点一定能作一个圆，∴要经过题中所给的3个点画圆，除选定直线l 外的点P 外，再在直线l 上的A ，B ，C ，D 四个点中任选其中2个即可画圆．∵从A ，B ，C ，D 四个点中任选其中2个点的方法可以是AB ，AC ，AD ，BC ，BD ，CD ，共6种，∴最多可以画出圆的个数为6.2. B 【解析】∵AB 是⊙O 的直径，∠BAC ＝50°，∴∠ACB ＝90°，∠B ＝180°－50°－90°＝40°.∵AC ＝AC ，∴∠D ＝∠B ＝40°.3. C 【解析】∵∠BOD ＝124°，∴∠AOD ＝180°－124°＝56°，∴∠ACD ＝12∠AOD ＝28°. 4. B 【解析】∵BD 经过圆心O ，∴∠BCD ＝90°.∵∠BDC ＝∠BAC ＝40°，∴∠DBC ＝90°－∠BDC ＝50°.5. D 【解析】∵五边形ABCDE 是正五边形，∴∠BAE ＝（5－2）×180°5＝108°，∠COD ＝360°5＝72°，∴∠BAE －∠COD ＝108°－72°＝36°. 6. A 【解析】∵∠BCD ＝105°，∴∠BAD ＝180°－105°＝75°，∴∠BOD ＝150°.∵∠BOC＝2∠COD ，∴∠COD ＝13 ∠BOD ＝50°，∴∠CBD ＝12∠COD ＝25°. 7. C 【解析】∵BD 是圆的直径，∴∠BCD ＝90°.∵BD ＝25，CD ＝7，∴在Rt △BCD 中，由勾股定理得，BC ＝252－72 ＝24(寸).8. D 【解析】如解图，连接OC ，∵∠ABC ＝19°，∴∠AOC ＝2∠ABC ＝38°.∵半径OA ，OB 互相垂直，∴∠AOB ＝90°，∴∠BOC ＝90°－38°＝52°，∴∠BAC ＝12∠BOC ＝26°.第8题解图9. B 【解析】如解图，在Rt △OAB 中，由勾股定理，得AO 2＋AB 2＝OB 2，即(R －7)2＋(372)2＝R 2，解得R ≈28(m).第9题解图10. B 【解析】如解图，连接OB ，设OA 交BC 于点E ，∵∠ADB ＝30°，∴∠AOB ＝60°.∵OA ⊥BC ，BC ＝23 ，∴BE ＝12 BC ＝3 .在Rt △BOE 中，sin ∠AOB ＝BE OB，∴sin 60°＝3OB ＝32，∴OB ＝2，∴OC ＝2.第10题解图11. B 【解析】如解图，连接OA ，设圆形宣传图标的半径为R ，∵CD 垂直平分AB ，AB＝CD ＝16，∴CD 过点O ，AC ＝BC ＝12 AB ＝12×16＝8，∠DCA ＝90°.∵AO ＝OD ＝R ，∴在Rt △AOC 中，由勾股定理，得OC 2＋AC 2＝OA 2，即(16－R )2＋82＝R 2，解得R ＝10，即圆形宣传图标的半径为10.第11题解图 12. 552 ；552 －5 【解析】如解图，连接OB ，∵OC ⊥AB ，∴BC ＝12 AB ＝32.由勾股定理，得OC ＝OB 2－BC 2 ＝552.当OD ⊥AB 时，点D 到AB 的距离最小，由勾股定理，得OD ＝22＋12 ＝5 ，∴点D 到AB 的距离的最小值为552 －5 .第12题解图13. (1)证明：由圆周角定理，得∠ACB ＝12 ∠AOB ，∠BAC ＝12∠BOC . ∵∠ACB ＝2∠BAC ，∴∠AOB ＝2∠BOC ；(2)解：如解图，过点O 作半径OD ⊥AB 于点E ，连接BD .则∠DOB ＝12∠AOB ，AE ＝BE . ∵∠AOB ＝2∠BOC ，∴∠DOB ＝∠BOC .∴BD ＝BC .∵AB ＝4，BC ＝5 ，∴BE ＝2，DB ＝5 .在Rt △BDE 中，∵∠DEB ＝90°，∴DE ＝BD 2－BE 2 ＝1.在Rt △BOE 中，∵∠OEB ＝90°，∴OB 2＝(OB －1)2＋22，∴OB ＝52， 即⊙O 的半径是 52.第13题解图14. D 【解析】如解图，连接BC ，∵∠BAC ＝70°，∴∠BOC ＝2∠BAC ＝140°.∵OB ＝OC ，∴∠OBC ＝∠OCB ＝180°－140°2＝20°.∵点P 为OB 上任意一点(点P 不与点B 重合)，∴0°<∠OCP <20°.∵∠BPC ＝∠BOC ＋∠OCP ＝140°＋∠OCP ，∴140°<∠BPC <160°，故选D.第14题解图15. 2(2 ＋1) 【解析】如解图，连接OE 交AB 于点G ，连接AC .根据垂径定理的推论，得OE ⊥AB ，AG ＝BG .由题意可得，AC 为⊙O 的直径，AC ＝2 ，则圆的半径是22.根据正方形的性质，得∠OAF ＝45°，∴OG ＝12 ，EG ＝2－12.∵OE ∥AD ，∴△ADF ∽△GEF ，∴FE FD ＝EG DA ＝2－12 .∵△ADF 与△AEF 等高，∴S 1S 2 ＝S △ADF S △AEF＝DF EF ＝2(2 ＋1).第15题解图16. 23 【解析】如解图，连接OD ，BD .∵A (－2，0)，∴OA ＝OB ＝2，∴AB ＝4.∵OC ＝OD ，∴∠OCD ＝∠ODC ＝75°，∴∠DOC ＝180°－2×75°＝30°，∴∠DOB ＝90°－30°＝60°，∴∠DAB ＝12∠DOB ＝30°.∵AB 是⊙O 的直径，∴∠ADB ＝90°，∴AD ＝AB ·cos 30°＝23 .第16题解图。

2020 年中考数学一轮复习专题训练：一元一次方程一．选择题（共 8 小题）1．以下四个式子中，是方程的是（）A ．3+2＝5B ．x＝ 1C． 2x﹣ 3＜ 022 D． a +2ab+b2．若对于 x 的方程 2x﹣（ 2a﹣1） x+3＝0 的解是 x＝3，则 a＝（）A ．1B ．0C． 2D． 33．解是 x＝2 的方程是（）A ．2（ x﹣ 1）＝ 6B ．C．D．4．以下等式变形正确的选项是（）A ．若﹣ 3x＝ 5，则 x＝﹣B ．若，则2x+3（x﹣1）＝1C．若 5x﹣ 6＝2x+8，则 5x+2x＝ 8+6D ．若 3（ x+1）﹣ 2x＝ 1，则 3x+3 ﹣2x＝ 15．在解方程 3x+5＝﹣ 2x﹣ 1 的过程中，移项正确的选项是（）A ．3x﹣ 2x＝﹣ 1+5B．﹣ 3x﹣ 2x＝ 5﹣ 1C． 3x+2x＝﹣ 1﹣ 5D．﹣ 3x﹣ 2x＝﹣ 1﹣ 56．解方程： 2﹣＝﹣，去分母得（）A ．2﹣ 2 （2x﹣ 4）＝﹣（ x﹣ 7）B． 12﹣ 2 （ 2x﹣ 4）＝﹣ x﹣7C． 2﹣（ 2x﹣4）＝﹣（ x﹣ 7）D． 12﹣ 2 （ 2x﹣ 4）＝﹣（ x﹣ 7）7．有以下结论：①若 a+b+c＝ 0，则 abc≠ 0；②若 a（ x﹣ 1）＝ b（ x﹣ 1）有独一的解，则a≠b；③若 b＝2a，则对于 x 的方程 ax+b＝ 0（ a≠ 0）的解为 x＝﹣；④若 a+b+c＝ 1，且 a≠ 0，则 x＝ 1 必定是方程 ax+b+c＝ 1 的解；此中结论正确的个数有（）A．4 个B．3 个C．2 个D．1 个8．若对于x 的方程 |2x﹣3|+m＝ 0 无解， |3x﹣ 4|+n＝ 0 只有一个解， |4x﹣ 5|+k＝ 0 有两个解，A ．m ＞n ＞ kB ．n ＞ k ＞ mC ． k ＞ m ＞ nD ． m ＞ k ＞ n二．填空题（共8 小题）9．比 a 的 3 倍大 5 的数等于 a 的 4 倍用等式表示为． 10．已知等式 5x m+2m ＝．+3＝ 0 是对于 x 的一元一次方程，则11．在 ① 2x ﹣ 1； ② 2x+1＝ 3x ； ③ |π﹣ 3|＝ π﹣ 3 ； ④ t+1 ＝ 3 中，等式有，方程有．（填入式子的序号）12．已知 x ＝5 是方程 ax ﹣ 8＝ 20+a 的解，则 a ＝ ．13．小强在解方程时，不当心把一个数字用墨水污染成了x ＝1﹣ ，他翻阅了答案知道这个方程的解为 x ＝ 1，于是他判断●应当是．14．已知代数式 与 互为相反数，则 x 的值是 ．15．已知方程的解也是方程 |3x ﹣ 2|＝ b 的解，则b ＝ ．16．已知 x ﹣3y ＝ 3，则 7+6y ﹣ 2x ＝．三．解答题（共 6 小题）17．解方程：（ 1） 3x ﹣ 9＝ 6x ﹣1；（ 2） x ﹣＝ 1﹣．18．若方程 3（x+1 ）＝ 2+x 的解与对于 x 的方程 ＝ 2（ x+3）的解互为倒数，求 k 的值．19．已知对于 x 的方程（ m+5） x|m|﹣4+18＝ 0 是一元一次方程．试求：（ 1）m 的值；（ 2）代数式 的值．20．依据题意设未知数，并列出方程（不用求解）．（ 1）有两个工程队，甲队人数30 名，乙队人数10 名，问如何调整两队的人数，才能使甲队的人数是乙队人数的7 倍．（ 2）有一个班的同学准备去划船，租了若干条船，他们计算了一下，假如比原计划多租1 条船，那么正好每条船坐 6 人；假如比原计划少租 1 条船，那么正好每条船坐9 人．问这个班共有多少名同学？21．我们规定：若对于 x 的一元一次方程ax＝ b 的解为 b+a，则称该方程为“和解方程” ．比如：方程 2x＝﹣ 4 的解为 x＝﹣ 2，而﹣ 2＝﹣ 4+2，则方程 2x＝﹣ 4 为“和解方程”．请依据上述规定解答以下问题：（ 1）已知对于x 的一元一次方程3x＝ m 是“和解方程” ，求 m 的值；（ 2）已知对于x 的一元一次方程﹣2x＝ mn+n 是“和解方程” ，而且它的解是x＝n，求 m，n 的值．22．先阅读以下解题过程，而后解答问题（1）、（ 2）、（ 3）．例：解绝对值方程：|2x|＝ 1．解：议论：①当 x≥ 0 时，原方程可化为2x＝ 1，它的解是x＝．②当 x＜0 时，原方程可化为﹣2x＝ 1，它的解是x＝﹣．∴原方程的解为x＝和﹣．问题（ 1）：依例题的解法，方程|的解是；问题（ 2）：试试解绝对值方程：2|x﹣2|＝ 6；问题（ 3）：在理解绝对值方程解法的基础上，解方程：|x﹣ 2|+|x﹣ 1|＝ 5．参照答案一．选择题（共8 小题）1．【解答】解：A、不是方程，由于不含有未知数，故本选项错误；B、是方程， x 是未知数，式子又是等式，故本选项正确；C、不是方程，由于它是不等式而非等式，故本选项错误；D、不是方程，由于它不是等式，故本选项错误；应选： B．2．【解答】解：把x＝3 代入方程获得：6﹣ 3（ 2a﹣ 1） +3＝ 0解得： a＝ 2．应选： C．3．【解答】解：将x＝2 分别代入题目中的四个选项得：A、 2（ x﹣ 1）＝ 2（ 2﹣ 1）＝ 2≠ 6，因此， A 错误；B.＝ +1＝2＝ X＝2，因此， B 正确；C.＝＝，因此，C错误；D .＝＝≠1﹣x＝1﹣2＝﹣1，因此D错误；应选： B．4．【解答】解： A、若﹣ 3x＝5，则 x＝﹣，错误，故本选项不切合题意；B、若，则2x+3（x﹣1）＝6，错误，故本选项不切合题意；C、若 5x﹣ 6＝2x+8，则 5x﹣ 2x＝ 8+6，错误，故本选项不切合题意；D 、若 3（ x+1）﹣ 2x＝ 1，则 3x+3 ﹣2x＝ 1，正确，故本选项切合题意；应选： D．5．【解答】解：方程3x+5＝﹣ 2x﹣ 1 移项得： 3x+2 x＝﹣ 1﹣ 5．应选： C．6．【解答】解：去分母得：12﹣2（ 2x﹣ 4）＝﹣（ x﹣ 7），应选： D．7．【解答】解：① 错误，当a＝0， b＝ 1， c＝﹣ 1 时， a+b+c＝0+1 ﹣ 1＝0，可是 abc＝ 0；②正确，方程整理得：（ a﹣ b） x＝ a﹣b，③ 错误，由 a ≠ 0， b ＝ 2a ，方程解得： x ＝﹣ ＝﹣ 2；④ 正确，把 x ＝ 1，a+b+c ＝ 1 代入方程左侧得： a+b+c ＝ 1，右侧＝ 1，故若 a+b+c ＝ 1，且 a ≠ 0，则 x ＝ 1 必定是方程 ax+b+c ＝ 1 的解，应选： C ．8．【解答】解： （ 1）∵ |2x ﹣ 3|+m ＝ 0 无解，∴ m ＞ 0．（ 2）∵ |3x ﹣ 4|+n ＝ 0 有一个解，∴ n ＝ 0．（ 3）∵ |4x ﹣ 5|+k ＝ 0 有两个解，∴ k ＜ 0．∴ m ＞ n ＞ k ．应选： A ．二．填空题（共 8 小题）9．【解答】解：依据题意得： 3a+5 ＝ 4a ．故答案为： 3a+5＝ 4．10．【解答】解：由于 5x m+2+3＝ 0 是对于 x 的一元一次方程，因此 m+2＝ 1，解得 m ＝﹣ 1．故填：﹣ 1．11．【解答】解：等式有 ②③④ ，方程有 ②④ ．故答案为： ②③④ ，②④ ．12．【解答】解：把 x ＝ 5 代入方程 ax ﹣ 8＝ 20+a得： 5a ﹣ 8＝ 20+a ，解得： a ＝ 7．故答案为： 7．13．【解答】解：●用 a 表示，把 x ＝ 1 代入方程得 1＝ 1﹣，解得： a ＝ 1．故答案是： 1．514．【解答】解：∵代数式与x﹣3 互为相反数，∴﹣＝x﹣3，解得 x＝．故答案为：．15．【解答】解：2（x﹣ 2）＝ 20﹣ 5（ x+3），2x﹣ 4＝20﹣ 5x﹣ 15，7x＝ 9，解得： x＝．把 x＝代入方程|3x﹣2|＝b得：|3×﹣2|＝b，解得： b＝．故答案为：．16．【解答】解：x﹣ 3y＝ 3，方程两边都乘以﹣2，得6y﹣ 2x＝﹣ 6，方程两边都加7，得7+6y﹣ 2x＝﹣ 6+7＝ 1，故答案为： 1．三．解答题（共 6 小题）17．【解答】解：（ 1）移项归并得：3x＝﹣ 8，解得： x＝﹣；（2）去分母得： 4x﹣ x+1＝4﹣ 6+2x，移项归并得： x＝﹣ 3．18．【解答】解：解3（ x+1）＝ 2+x，得 x＝﹣，∵双方程的解互为倒数，∴将 x＝﹣ 2 代入＝2（x+3）得＝2，解得 k＝0．19．【解答】解：（ 1）由题意得，|m|﹣ 4＝ 1， m+5≠ 0，解得， m＝ 5；（2）当 m＝5 时，原方程化为 10x+18 ＝0，解得， x＝﹣，∴＝＝﹣．20．【解答】解：（1）设从乙队调x 人去甲队，则乙队此刻有10﹣ x 人，甲队有30+x 人，由题意得30+x＝ 7（ 10﹣ x）；（2）设这个班共有 x 名同学，由题意得﹣1＝ +1．21．【解答】解：（ 1）∵方程3x＝ m 是和解方程，∴＝ m+3，解得： m＝﹣．（2）∵对于 x 的一元一次方程﹣ 2x＝ mn+n 是“和解方程” ，而且它的解是 x＝ n，∴﹣ 2n＝ mn+n，且 mn+n﹣2＝ n，解得 m＝﹣ 3， n＝﹣．22．【解答】解：（ 1） |x|＝ 2，①当 x≥0 时，原方程可化为x＝ 2，它的解是x＝ 4；②当 x＜0 时，原方程可化为﹣x＝2，它的解是x＝﹣ 4；∴原方程的解为x＝ 4 和﹣ 4，故答案为： x＝ 4 和﹣ 4．（2） 2|x﹣ 2|＝ 6，①当 x﹣ 2≥ 0 时，原方程可化为2（x﹣ 2）＝ 6，它的解是x＝ 5；②当 x﹣ 2＜ 0 时，原方程可化为﹣2（x﹣ 2）＝ 6，它的解是x＝﹣ 1；∴原方程的解为x＝ 5 和﹣ 1．（ 3） |x﹣ 2|+|x﹣ 1|＝ 5，①当 x﹣ 2≥ 0，即 x≥ 2 时，原方程可化为x﹣ 2+x﹣ 1＝ 5，它的解是x＝ 4；②当 x﹣ 1≤ 0，即 x≤ 1 时，原方程可化为2﹣ x+1﹣ x＝ 5，它的解是x＝﹣ 1；③当 1＜ x＜ 2 时，原方程可化为2﹣x+x﹣ 1＝ 5，此时方程无解；∴原方程的解为x＝ 4 和﹣ 1．。

第3讲分式及二次根式 2023年中考数学一轮复习专题训练（浙江专用）一、单选题1．（2022·江北模拟）无论x取什么数，总有意义的代数式是（）A．√x2B．4xx3+1C．1(x−2)2D．√x+32．（2022·浦江模拟）若分式1x−1有意义，则x的取值范围是（）A．x>1B．x>2C．x≠0D．x≠13．（2022·平阳模拟）若分式x−2x−3的值为0，则x的值为（）A．-3B．-2C．0D．2 4．（2022·慈溪模拟）若二次根式√1−x在实数范围内有意义，则下列各数中，x 可取的值是()A．4B．πC．√2D．1 5．（2022·北仑模拟）若二次根式√3−x在实数范围内有意义，则x的取值范围是（）A．x≠3B．x≥3C．x≤3D．x<3 6．（2022·慈溪模拟）下列计算正确的是()A．22+23=25B．23−22=2C．23⋅22=25D．2−1=−27．（2022·定海模拟）对于以下四个命题：①若直角三角形的两条边长与3与4，则第三边的长是5；②(√a)2=a；③若点P(a，b)在第三象限，则点Q(−a，−b)在第一象限；④两边及其第三边上的中线对应相等的两个三角形全等，正确的说法是（）A．只有①错误，其他正确B．①②错误，③④正确C．①④错误，②③正确D．只有④错误，其他正确8．（2022·宁波模拟）二次根式√x−3中字母x的取值范围是（）A．x＞3B．x≠3C．x≥3D．x≤39．（2022·洞头模拟）计算2aa+2−a−22+a的结果为（）A．a+2B．a−2C．1D．a−2a+210．（2021·北仑模拟）要使代数式√x−1有意义，x的取值应满足() A．x≥1B．x>1C．x≠1D．x≠0二、填空题11．（2022·台州）如图的解题过程中，第①步出现错误，但最后所求的值是正确的，则图中被污染的x的值是．先化简，再求值：3−xx−4+1，其中x=解：原式=3−xx−4⋅(x−4)+(x−4)…①=3−x+x−4=−112．（2022·丽水）如图，标号为①，②，③，④的矩形不重叠地围成矩形PQMN.已知①和②能够重合，③和④能够重合，这四个矩形的面积都是5，AE=a，DE=b，且a>b.（1）若a，b是整数，则PQ的长是；（2）若代数式a2﹣2ab﹣b2的值为零，则S四边形ABCDS矩形PQMN的值是．13．（2022·宁波模拟）若二次根式√3+x在实数范围内有意义，则x的取值范围是.14．（2022·衢江模拟）二次根式√x−4中字母x的取值范围是.15．（2022·温州）计算：x 2+xyxy+xy−x2xy=．16．（2022·金华）若分式2x−3的值为2，则x的值是.17．（2022·永康模拟）若分式1x−3有意义，则x的取值范围为．18．（2022·湖州）当a=1时，分式 a+1a 的值是 . 19．（2022·萧山模拟）计算：√3×√2= .20．（2022·宁波模拟）分式 2x−6x+1有意义的条件是 .三、计算题21．（2022·北仑模拟）先化简，直求值：(2a −1)⋅aa 2−4，共中a ＝√2−2.22．（2022·温州模拟）（1）计算：6÷(−3)+√4−8×2−2.（2）化简：2x x 2−4−1x−2.23．（2022·衢州模拟）计算：（1）−12+20180−(12)−1+√83； （2）a 2−b 2a−b ÷a+b 2a−2b.24．（2022·龙湾模拟）（1）计算： 2−1−(√5−1)0+|−32|−√273 ． （2）化简： a 2+3a 2−a +3a−a2 ．25．（2022·瓯海模拟）（1）计算：（﹣2）2×32+|﹣5|﹣√9．（2）化简：a 2a 2−2a +42a−a 2． 四、解答题26．（2022·衢州模拟）先化简，再求值：（1x−1−1x+1）÷x+2x 2−1，然后从﹣1，1，3中选择适当的数代入求值.27．（2022·台州模拟）先化简，再求值：（1﹣1a ）÷a 2−1a，其中a ＝2020.28．（2022·衢州模拟）先化简4m 2−4−1m−2，从-2，-1，0，2四个数中选取一个合适的数代入求值.29．（2022·余杭模拟）化简： 3x−1+x−31−x 2小明的解答如下： 原式= 3x−1−x−3x 2−1=（x2-1）3x−1-（x 2-1）x−3x2−1=3（x+1）-（x-3）=2x+6小明的解答正确吗？如果不正确，请写出正确的解答过程．30．（2022·江干模拟）化简：xx−1−1x+1−1.小马的解答如下，小马的解答正确吗？如果不正确，写出正确的解答.解：xx−1−1x+1−1=x(x+1)−(x−1)−1=x2+x−x+1−1=x2答案解析部分1．【答案】A【解析】【解答】解：A 、无论x 取任何数，√x 2有意义，A 选项符合题意； B 、x≠-1时，4xx 3+1有意义，B 选项不符合题意；C 、x≠2时，1（x−2）2有意义，C 选项不符合题意； D 、x≥-3时，√x +3有意义，D 选项不符合题意. 故答案为：A.【分析】根据二次根式有意义的条件，即被开方数为非负数，及分式有意义的条件，即分母不为零，逐项进行判断即可.2．【答案】D【解析】【解答】解：∵分式1x−1有意义，∴x −1≠0，解得x ≠1， 故答案为：D.【分析】分式有意义的条件：分母不为0，据此解答即可.3．【答案】D【解析】【解答】解：∵分式x−2x−3的值为0∴x ﹣2＝0，x ﹣3≠0， ∴x ＝2. 故答案为：D.【分析】根据分式值为0的条件可得x-2＝0，x-3≠0，求解即可.4．【答案】D【解析】【解答】解：由题意得1-x≥0 解之：x≤1. ∴x 可以为1. 故答案为：D.【分析】利用二次根式有意义的条件：被开方数是非负数，可求出x 的取值范围，即可求解.5．【答案】C【解析】【解答】解：要使二次根式√3−x在实数范围内有意义，必须3−x≥0，解得：x≤3.故答案为：C.【分析】根据二次根式有意义的条件是被开方数不为负数，据此可得3−x≥0，求解即可.6．【答案】C【解析】【解答】解：22+23≠25，故A不符合题意；B、23-22≠2，故B不符合题意；C、22·23=25，故C符合题意；D、2−1=12，故D不符合题意；故答案为：C.【分析】同底数幂相加减，要先算乘方，再算加法或减法，可对A，B作出判断；利用同底数幂相乘，底数不变，指数相加，可对C作出判断；利用负整数指数幂的性质，可对D作出判断.7．【答案】A【解析】【解答】解：①错误，应强调为直角三角形的两条直角边长为3与4，则第三边的长是5；②正确，隐含条件a≥0，根据二次根式的意义，等式成立；③正确，若点P（a，b）在第三象限，则a＜0，b＜0；则-a＞0，-b＞0，点Q（-a，-b）在第一象限；④正确，已知：如图，AB=A'B'，AC=A'C'，AD=A'D'，BD=CD，B'D'=C'D'，求证：△ABC≌△A'B'C'；证明：过点C作CE∥AB交AD的延长线于E，∵∠BAD=∠E，∠ABD=∠ECD，∵BD=CD，∴△ABD≌△ECD（AAS），∴AB=CE，AD=DE，过点C'作C'E'∥A'B'交A'D'的延长线于E'，同理：A'B'=C'E'，A'D'=D'E'，∵AD=A'D'，AB=A'B'，∴AE=A'E'，CE=C'E'，∵AC=A'C'，∴△ACE≌△A'C'E'（SSS），∴∠CAE=∠C'A'E'，∠E=∠E'=∠BAD=∠B'A'D'，∴∠BAC=∠B'A'C'，∴△ABC≌△A'B'C'（SAS），即：两边及第三边上的中线对应相等的两个三角形全等，正确.故答案为：A.【分析】根据勾股定理可判断①；根据二次根式有意义的条件可得a≥0，据此判断②；根据点的坐标与象限的关系可判断③；画出示意图，已知AB=A'B'，AC=A'C'，AD=A'D'，BD=CD，B'D'=C'D'，过点C作CE∥AB交AD的延长线于E，证明△ABD ≌△ECD，得到AB=CE，AD=DE，过点C'作C'E'∥A'B'交A'D'的延长线于E'，证明△ACE≌△A'C'E'（SSS），得到∠CAE=∠C'A'E'，∠E=∠E'=∠BAD=∠B'A'D'，推出∠BAC=∠B'A'C'，据此判断④.8．【答案】C【解析】【解答】解：∵√x −3，∴x-3≥0， ∴x≥3. 故答案为：C.【分析】根据二次根式被开方数为非负数，即x-3≥0，求解不等式即可得x 的取值范围.9．【答案】C【解析】【解答】解：原式=2a−a+2a+2=a+2a+2 =1.故答案为：C.【分析】直接根据同分母分式减法法则进行计算即可.10．【答案】B【解析】【解答】解：由题意得：{x −1≥0x −1≠0，解得x ＞1.故答案为：B.【分析】依据被开方数大于等于0及分母不为零，列出不等式组，求解即可.11．【答案】5【解析】【解答】解：原式=3−x x−4+x−4x−4=−1x−4∵最后所求的值是正确的∴−1x−4=-1 解之：x=5经检验：x=5是方程的解. 故答案为：5.【分析】先通分计算，再由题意可得到−1x−4=-1；然后解方程求出x 的值. 12．【答案】（1）a-b（2）3+2√2【解析】【解答】解：(1)∵①和②能够重合，③和④能够重合，AE=a ，DE=b ，∴PQ=AE+DE-2ED=a+b-2b=b ，故答案为：a-b ； (2)∵a 2- 2ab- b 2=0， ∴a 2-b 2=2ab ， 则(a-b)2=2b 2，∴a=(√2+1)b 或(1-√2)b(舍去)，∵四个矩形的面积都是5，AE=a ，DE=b ， ∴EP=5a ，EN=5b，∴S四边形ABCD S矩形PQMN=(a+b )(5a +5b )(a−b )(5b −5a)=a 2+2ab+b2a 2−2ab+b 2=a 2b2=(√2+1)2b2b2=3+2√2.故答案为：3+2√2.【分析】(1)直接根据线段和差关系，结合两组全等矩形的边相等，列式计算可得结论；(2)解关于a 的二元一次方程：a 2-2ab-b 2=0， 得到a=(√2+1)b ，根据四个矩形的面积都是5分别表示小矩形的宽，再利用含a 、b 的代数式表示S四边形ABCDS 矩形PQMN，化简后，再代入a=(√2+1)b ，即可解答.13．【答案】x≥-3【解析】【解答】解：由题意得： 3+x ≥0，解得： x ≥−3， 故答案为： x ≥−3.【分析】根据二次根式的被开方数不能为负数可得3+x≥0，求解即可.14．【答案】x≥4【解析】【解答】解：由题意，得x-4≥0， 解得：x≥4. 故答案为：x≥4.【分析】根据二次根式有意义的条件是被开方数不能为负数，可得x-4≥0，求解即可.15．【答案】2【解析】【解答】解：原式=x 2+xy+xy−x 2xy=2..故答案为：2.【分析】利用同分母分式相加，分母不变，把分子相加，然后化简即可.16．【答案】4【解析】【解答】解：∵分式2x−3的值为2，∴2x−3=2， ∴2=2x-6， ∴x=4. 故答案为：4.【分析】由分式2x−3的值为2，得2x−3=2，再解分式方程即可求出x 的值.17．【答案】x≠3【解析】【解答】解：由题意得x-3≠0 解之：x≠3. 故答案为：x≠3.【分析】利用分式有意义的条件：分母不等于0，可得到关于x 的不等式，然后求出不等式的解集.18．【答案】2【解析】【解答】解：把a=1代入分式中， ∴a+1a =1+11=2.故答案为：2.【分析】把a=1代入分式中，化简求值即可求解.19．【答案】√6【解析】【解答】解：√3×√2，=√3×2， =√6； 故答案为：√6.【分析】直接根据二次根式的乘法法则进行计算.20．【答案】x≠-1【解析】【解答】解：要使分式有意义，则x+1≠0，∴x≠-1.故答案为：x≠-1.【分析】分式有意义的条件是分母不等于零，依此列式求解，即可解答.21．【答案】解：(2a −1)⋅a a 2−4=2−a a ⋅a (a+2)(a−2)=−1a+2 当a =√2−2时，原式=1√2−2+2=1√2=−√22 【解析】【分析】对括号中的式子进行通分，对括号外分式的分母进行分解，然后约分即可对原式进行化简，接下来将a 的值代入计算即可.22．【答案】（1）解：6÷(−3)+√4−8×2−2=−2+2−8×14=−2+2−2=−2（2）解：2x x 2−4−1x−2 =2x −(x +2)(x +2)(x −2)=x −2(x +2)(x −2)=1x +2 【解析】【分析】（1）根据算术平方根的概念、负整数指数幂的运算性质及有理数的除法法则分别计算，然后计算乘法，再计算加减法即可；（2）对第一个分式的分母进行分解，然后通分，再约分即可.23．【答案】（1）解：−12+20180−(12)−1+√83 =﹣1+1﹣2+2=0；（2）解：a 2−b 2a−b ÷a+b 2a−2b=(a+b)(a−b)a−b ÷a+b 2(a−b) =(a+b)(a−b)a−b×2(a−b)a+b =2(a −b)=2a ﹣2b.【解析】【分析】（1）根据乘方、开方、零指数幂及负整数幂的性质分别h 进行计算，然后根据有理数的加减法法则算出答案即可；（2）先将分子、分母进行因式分解，再将除法转化为乘法，然后约分即可.24．【答案】（1）解：原式=12-1+32-3=-2. （2）解：原式=a 2+3a 2−a −3a 2−a=a 2a (a−1)=a a−1. 【解析】【分析】（1）根据负整数指数幂的性质、零指数幂的性质、立方根的定义进行化简，再计算加减法，即可得出答案；（2）先通分，再计算分式的减法，即可得出答案.25．【答案】（1）解：（﹣2）2×32+|﹣5|﹣√9 =4×32+5﹣3 =6+5-3=8（2）解：a 2a 2−2a +42a−a 2=a 2a(a−2)+4a(2−a)=a 2a(a −2)−4a(a −2)=a 2−4a(a −2)=(a +2)(a −2)a(a −2)=a+2a ．【解析】【分析】（1）根据有理数的乘方法则、绝对值的性质以及算术平方根的概念可得原式=4×32+5-3，然后计算乘法，再计算加减法即可； （2）对两个分式的分母进行分解，然后结合同分母分式减法法则进行计算.26．【答案】解：(1x−1−1x+1)÷x+2x 2−1=x+1−x+1(x−1)(x+1)÷x+2(x−1)(x+1)=2(x−1)(x+1)×(x−1)(x+1)x+2 =2x+2； ∵x −1≠0，x +1≠0，x +2≠0，∴x ≠±1，x ≠−2，当x =3时，2x+2=23+2=25【解析】【分析】对括号中的式子进行通分，对括号外分式的分母进行分解，然后将除法化为乘法，再约分即可对原式进行化简，接下来选择一个使分式有意义的x 的值代入计算即可.27．【答案】解：原式=a−1a ·a (a+1)(a−1)=1a+1当a=2020时，原式=12021【解析】【分析】对括号中的式子进行通分，将第二个分式的分子分解因式，同时除法化为乘法，再进行约分即可对原式进行化简，接下来将a 的值代入计算即可.28．【答案】解：原式=4(m+2)(m−2)−1m−2=4−(m +2)(m +2)(m −2)=2−m (m +2)(m −2)=−1m +2要使分式有意义，则m 2−4≠0且m −2≠0解得m≠±2，∴只能选择-1或0当m=-1时，原式=−1当m=0时，原式=−1 2【解析】【分析】对第一个分式的分母进行分解，再通分后按同分母分式的加减法进行计算，并进行约分即可对原式进行化简，然后选取一个使分式有意义的m的值代入进行计算.29．【答案】解：不正确原式＝－＝－＝＝【解析】【分析】根据分式加法法则，先通分，化为同分母的分式相加减，再进行计算，即可得出答案.30．【答案】解：不正确，正确解答如下：xx−1−1x+1−1=x(x+1)x2−1−x−1x2−1−x2−1x2−1=x2+x−x+1−x2+1x2−1=2x2−1.【解析】【分析】首先第一项的分子、分母都乘以（x+1），第二项的分子、分母都乘以（x-1），第三项的分析分母都乘以（x+1）（x-1）进行通分，然后根据同分母分式减法法则进行计算。

2021中考数学一轮专题训练：一次方程（组）及其应用一、选择题（本大题共10道小题）1. 充若关于x的一元一次方程2x a－2＋m＝4的解为x＝1，则a＋m的值为() A．9 B．8 C．5 D．42. 如果x＝y，那么根据等式的性质，下列变形不正确的是()A．x＋2＝y＋2 B．3x＝3yC．5－x＝y－5 D．－x3＝－y33. 学校组织知识竞赛，共设20道选择题，各题分值相同．下表记录了3名参赛学生的得分情况，若参赛学生小亮只答对了16道选择题，则小亮的得分是()参赛学生答对题数答错或不答题数得分A200100B18288C101040A.80分B．76分C．75分D．70分4. 若a－2与1－2a的值相等，则a等于()A．0 B．1 C．2 D．35. 《孙子算经》中有一道题，原文是:“今有木，不知长短.引绳度之，余绳四尺五寸;屈绳开始度之，不足一尺.木长几何?”意思是:用一根绳子去量一根木条，绳子剩余4.5尺.将绳子对折再量木条，木条剩余1尺，问木条长多少尺?现设绳长x 尺，木条长y尺，则可列二元一次方程组为 ()A.B.C.D.6. 2019·荆门欣欣服装店某天用相同的价格a (a ＞0)元卖出了两件服装，其中一件盈利20%，另一件亏损20%，那么该服装店卖出这两件服装的盈利情况是( ) A ．盈利 B ．亏损C ．不盈不亏D ．与售价a 有关7. 若关于x ，y 的二元一次方程组的解也是二元一次方程2x ＋3y ＝6的解，则k 的值为( )A ．－34 B.34 C.43 D ．－438. 已知⎪⎪⎪⎪⎪⎪2－23x ＝4，则x 的值是( ) A ．－3 B ．9C ．－3或9D ．以上结果都不对9. 《算法统宗》记载：“有个学生资性好，一部孟子三日了，每日增添一倍多，问君每日读多少．”其大意是：有个学生天资聪慧，三天读完一部《孟子》，每天阅读的字数是前一天的两倍，问他每天各读多少个字．已知《孟子》一书共有34685个字，设他第一天读x 个字，则下面所列方程正确的是( ) A ．x ＋2x ＋4x ＝34685 B ．x ＋2x ＋3x ＝34685C ．x ＋2x ＋2x ＝34685D ．x ＋12x ＋14x ＝3468510. 甲、乙两名运动员在长为100 m 的直道AB (A ，B 为直道两端点)上进行匀速往返跑训练，两人同时从A 点起跑，到达B 点后，立即转身跑向A 点，到达A 点后，又立即转身跑向B 点……若甲跑步的速度为5 m/s ，乙跑步的速度为4 m/s ，则起跑后100 s 内，两人相遇的次数为( ) A ．5B ．4C ．3D ．2二、填空题（本大题共10道小题）11. 下列方程中，解是x ＝5的是________．(填序号)① x ＋2015＝2020；②x ＋63＝3；③x ＋1＝2(8－x )；④x 2－x 3＝56.12. 用适当的数或式子填空，使所得结果仍是等式，并说明变形的依据以及是如何变形的．(1)如果3x ＋5＝8，那么3x ＝8－________， 根据________________________________________________________________________；(2)如果－4x ＝14，那么x ＝________，根据____________________________________； (3)如果3x ＝x ＋4，那么x ＝________， 根据________________________________________________________________________；(4)如果7y ＝－7x ，那么y ＝________(用含x 的式子表示)， 根据________________________________________________________________________；(5)如果3x ＝2－4y ，那么y ＝________(用含x 的式子表示)， 根据________________________________________________________________________．13. 不论x 取何值，等式ax －b －4x ＝3永远成立，则12ab ＝________．14. 已知a ，b ，c ，d 为有理数，现规定一种新的运算：⎪⎪⎪⎪⎪⎪ab c d ＝ad －bc .则满足等式⎪⎪⎪⎪⎪⎪⎪⎪x 2 x ＋13 2 1＝1的x 的值为________．15. 若m ＋1与－2互为相反数，则m 的值为________．16. 若13a ＋1与2a －73的值互为相反数，则a 的值为________．17.如果方程(m －1)x |m |＋2＝0是关于x 的一元一次方程，那么m 的值是__________．18. 一只蜘蛛有8条腿，一只蜻蜓有6条腿，现有蜘蛛、蜻蜓若干只，它们共有120条腿，且蜻蜓的只数是蜘蛛的2倍，那么蜘蛛有________只．19. 我国古代数学著作《九章算术》中有一道阐述“盈不足术”的问题，译文为：“现有几个人共同购买一个物品，每人出8元，则多3元；每人出7元，则差4元．问这个物品的价格是多少元．”该物品的价格是________元．20. 一个两位数，十位上的数字比个位上的数字的3倍大1，若将个位上的数字与十位上的数字对调，则所得新两位数比原两位数小45，则原来的两位数是________．三、解答题（本大题共6道小题）21. 某商店的老板销售一种商品，他要以不低于进价120%的价格出售，但为了获得更多的利润，他以高出进价80%的价格标价，若你想买标价为360元的这种商品，老板最多降价多少元？22. 某校长暑假将带领该校市级“三好学生”去北京旅游，甲旅行社说：“如果校长买全票一张，那么其余学生票价可享受半价优惠．”乙旅行社说：“包括校长在内全部按全票价的六折付款．”若甲、乙两家旅行社的全票价均为240元，设学生人数为x .(1)分别计算两家旅行社的收费(用含x 的式子表示)； (2)当学生人数是多少时，两家旅行社的收费一样？23. 某车间共有28名工人生产螺栓和螺母，每人每天平均生产螺栓12个或螺母18个．如果每天生产的螺栓和螺母要按1∶2配套，那么应分别安排多少工人生产螺栓，多少工人生产螺母？24. 若关于x的方程(m－2)x2＋3mx－(5－2m)＝0是一元一次方程，求方程的解．25. 互逆思维能不能由(a＋3)x＝b－1得到等式x＝b－1a＋3，为什么？反之，能不能由x＝b－1a＋3得到(a＋3)x＝b－1，为什么？26. 根据下表中的两种移动电话计费方式，解决下列问题：方式一方式二月租费50元/月10元/月本地通话费0.3元/分0.5元/分(1)一个月本地通话时间为150分钟和300分钟，计算按两种移动电话计费方式各需要交话费多少元；(2)会出现两种移动电话计费方式收费一样的情况吗？请你说明在怎样的选择下较省钱．2021中考数学一轮专题训练：一次方程（组）及其应用-答案一、选择题（本大题共10道小题）1. 【答案】C[解析] 因为关于x 的一元一次方程2x a －2＋m ＝4的解为x ＝1，所以a －2＝1，2＋m ＝4，解得a ＝3，m ＝2.所以a ＋m ＝3＋2＝5.故选C.2. 【答案】C3. 【答案】B[解析] 根据表格数据，A 学生答对20道题得100分，可知答对一题得100÷20＝5(分)．设答错或不答一道题得x 分，由B 学生答对18道题，答错2道题得88分，可得18×5＋2x ＝88，解得x ＝－1，故答错或不答一题扣1分．小亮答对16道题，则有16×5＋(－1)×(20－16)＝76(分)．故选B.4. 【答案】B5. 【答案】B[解析]本题等量关系是:绳长-木条长=4.5;木条长-×绳长=1，据此可列方程组.依题意，得故选B .6. 【答案】B[解析] 设第一件服装的进价为x 元，依题意得x(1＋20%)＝a.设第二件服装的进价为y 元，依题意得y(1－20%)＝a ，所以x(1＋20%)＝y(1－20%)，整理得3x ＝2y.该服装店卖出这两件服装的盈利情况为0.2x －0.2y ＝0.2x －0.3x ＝－0.1x(元)，即赔了0.1x 元．7. 【答案】B 解析：关于x ，y 的二元一次方程组⎩⎨⎧ x ＋y ＝5k ，x －y ＝9k ，得⎩⎨⎧x ＝7k ，y ＝－2k .将之代人方程2x ＋3y ＝6，得k ＝34.8. 【答案】C [解析] 由⎪⎪⎪⎪⎪⎪2－23x ＝4，得2－23x ＝4或2－23x ＝－4，解得x ＝－3或x ＝9.故选C.9. 【答案】A10. 【答案】B[解析] 设两人相遇的次数为x ，依题意有100×25＋4x ＝100，解得x ＝4.5，因为x 为整数，所以x 取4.故选B.二、填空题（本大题共10道小题）11. 【答案】①③④12. 【答案】(1)5等式的性质1，等式两边同时减去5(2)－116 等式的性质2，等式两边同时除以－4(3)2 等式的性质1，等式两边同时减去x ，得2x ＝4；再根据等式的性质2，等式两边同时除以2，得 x ＝2(4)－x 等式的性质2，等式两边同时除以7(5)－3x －24 等式的性质1，等式两边同时减去2，得3x －2＝－4y ；再根据等式的性质2，等式两边同时除以－4，得－3x －24＝y ，由等式的对称性，得y ＝－3x －24 13. 【答案】－6[解析] 将等式转化为(a －4)x ＝3＋b ，根据题意，等式成立的条件与x 的值无关，则a －4＝0，解得a ＝4，此时，3＋b ＝0，解得b ＝－3，于是12ab ＝12×4×(－3)＝－6.14. 【答案】－10[解析] 依据运算程序构造一元一次方程，然后解方程即可．根据题意得x 2－2（x ＋1）3＝1.去分母，得3x －4(x ＋1)＝6.去括号，得3x －4x －4＝6.移项，得3x －4x ＝6＋4.合并同类项，得－x ＝10.系数化为1，得x ＝－10.15. 【答案】116. 【答案】43 [解析] 根据题意，得13a ＋1＋2a －73＝0，解得a ＝43.17. 【答案】－1[解析] 由一元一次方程的定义得|m|＝1且m －1≠0，解得m ＝－1.故填：－1.18. 【答案】6[解析] 设蜘蛛有x 只，则蜻蜓有2x 只，由题意，得8x ＋2x·6＝120，解得x ＝6.19. 【答案】53[解析] 设有x 个人共同购买该物品，依题意，得8x －3＝7x ＋4，解得x＝7.8x－3＝8×7－3＝53.故答案为53.20. 【答案】72[解析] 设原来的两位数个位上的数字为x，则十位上的数字为3x ＋1，根据题意，得10(3x＋1)＋x－45＝10x＋(3x＋1)，解得x＝2.所以3x＋1＝7，10×7＋2＝72.故原来的两位数为72.三、解答题（本大题共6道小题）21. 【答案】解：设商品的进价为x元，则有(1＋80%)x＝360，解得x＝200.120%×200＝240(元)，360－240＝120(元)．答：老板最多降价120元．22. 【答案】解：(1)甲旅行社的收费为12·240x＋240＝(120x＋240)元；乙旅行社的收费为610×240(x＋1)＝(144x＋144)元．(2)解方程120x＋240＝144x＋144，得x＝4.故当学生人数为4时，两家旅行社的收费一样．23. 【答案】[解析] 由题意可找出两个相等关系：(1)生产螺栓工人数＋生产螺母工人数＝28.(2)螺栓总数∶螺母总数＝1∶2.题目要求的是生产螺栓、螺母的工人数，因此表示这两者关系的(1)用来设未知数，而关系(2)用来列方程．对于(2)还可用“螺母总数＝螺栓总数×2”来表示，更易列方程．解：设安排x名工人生产螺栓，则安排(28－x)名工人生产螺母．根据题意，得12x×2＝18(28－x)， 解得x ＝12，28－x ＝16.答：应安排12名工人生产螺栓，16名工人生产螺母．24. 【答案】解：因为方程是关于x 的一元一次方程，所以含x 2项的系数为0. 所以m －2＝0.所以m ＝2. 当m ＝2时，原方程为6x －1＝0.当x ＝16时，6x 的值是1，这时方程6x －1＝0等号左右两边相等，故方程6x －1＝0的解为x ＝16.25. 【答案】解：不能由(a ＋3)x ＝b －1得到x ＝b －1a ＋3，因为当a ＝－3时，a ＋3＝0，而0不能作除数，即不符合等式的性质2的规定． 能由x ＝b －1a ＋3得到(a ＋3)x ＝b －1，因为x ＝b －1a ＋3是已知条件，已知条件中已经隐含着a ＋3≠0，等式两边同乘一个数，等式仍成立．26. 【答案】解：(1)150×0.3＋50＝95(元)； 150×0.5＋10＝85(元)； 300×0.3＋50＝140(元)； 300×0.5＋10＝160(元)．所以一个月本地通话150分钟时，按方式一需要交话费95元，按方式二需要交话费85元；一个月本地通话300分钟时，按方式一需要交话费140元，按方式二需要交话费160元．(2)会．设通话时间为t 分钟时两种移动电话计费方式收费一样，则50＋0.3t ＝10＋0.5t ，解得t＝200，所以当t＝200时，两种移动电话计费方式收费一样；当t＞200时，选方式一较省钱；当0<t＜200时，选方式二较省钱．。