河南省商丘市永城市龙岗镇2017_2018学年八年级数学上学期四分之一考试试题扫描版无答案新人教版2

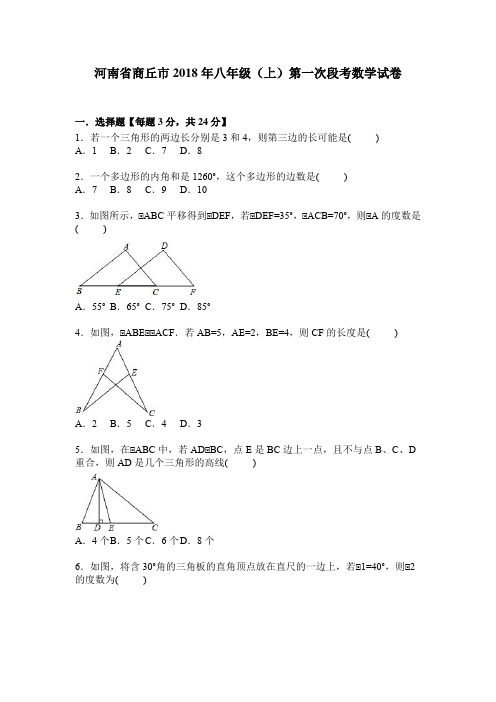
河南省商丘市2018年八年级（上）第一次段考数学试卷一．选择题【每题3分，共24分】1．若一个三角形的两边长分别是3和4，则第三边的长可能是( )A．1 B．2 C．7 D．82．一个多边形的内角和是1260°，这个多边形的边数是( )A．7 B．8 C．9 D．103．如图所示，△ABC平移得到△DEF，若∠DEF=35°，∠ACB=70°，则∠A的度数是( )A．55°B．65°C．75°D．85°4．如图，△ABE≌△ACF．若AB=5，AE=2，BE=4，则CF的长度是( )A．2 B．5 C．4 D．35．如图，在△ABC中，若AD⊥BC，点E是BC边上一点，且不与点B、C、D 重合，则AD是几个三角形的高线( )A．4个B．5个C．6个D．8个6．如图，将含30°角的三角板的直角顶点放在直尺的一边上，若∠1=40°，则∠2的度数为( )A．90°B．80°C．75°D．70°7．如图，EA∥DF，AE=DF，要使△ACE≌△DBF，则只要（）A．AB=CD B．EC=BF C．∠A=∠D D．AB=BC8．如图：在不等边△ABC中，PM⊥AB，垂足为M，PN⊥AC，垂足为N，且PM=PN，Q在AC上，PQ=QA，下列结论：①AN=AM，②QP∥AM，③△BMP ≌△QNP，其中正确的是（）A．①②③B．①②C．②③D．①二.填空【每题3分，共24分】9．如图，D是AB边上的中点，将△ABC沿过D的直线折叠，使点A落在BC 上F处，若∠B=50°，则∠BDF=度．10．如图，△ABC的周长为32，且AB=AC，AD⊥BC于D，△ACD的周长为24，那么AD的长为．11．如图，等边△ABC的边长为1cm，D、E分别是AB、AC上的点，将△ADE 沿直线DE折叠，点A落在点A′处，且点A′在△ABC外部，则阴影部分图形的周长为cm．12．纸片△ABC中，∠A=65°，∠B=75°，将纸片的一角折叠，使点C落在△ABC 内（如图），若∠1=20°，则∠2的度数为．13．如图，△ABC中，∠A=100°，BI、CI分别平分∠ABC，∠ACB，则∠BIC=，若BM、CM分别平分∠ABC，∠ACB的外角平分线，则∠M=．14．如图，在∠AOB的两边截取OA=OB，OC=OD，连接AD，BC交于点P，则下列结论中①△AOD≌△BOC，②△APC≌△BPD，③点P在∠AOB的平分线上．正确的是；（填序号）15．如图，△ABC中，∠C=90°，AD平分∠BAC，AB=5，CD=2，则△ABD的面积是．16．已知如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC，∠CED=35°，则∠EAB是度．三.解答题17．（7分）如图，AC=DF，AD=BE，BC=EF．求证：∠C=∠F．18．（7分）如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个可以直接到达A和B的点C，连结AC并延长到D，使CD=CA．连结BC并延长到E，使EC=CB，连结DE，量出DE的长，就是A、B的距离．写出你的证明．19．（8分）如图，AD为△ABC的高，E为AC上一点，BE交AD于F，且有BF=AC，FD=CD，那么BE⊥AC吗？为什么？20．（8分）如图：E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足为C，D．求证：（1）OC=OD；（2）DF=CF．21．（10分）如图，△ABC中，∠ACB=90°，AC=BC，AE是BC边上的中线，过C作CF⊥AE，垂足为F，过B作BD⊥BC交CF的延长线于D．（1）求证：AE=CD；（2）若AC=12cm，求BD的长．22．（12分）如图a，△ABC和△CEF是两个大小不等的等边三角形，且有一个公共顶点C，连接AF和BE（1）线段AF和BE有怎样的大小关系？请证明你的结论；（2）将图a中的△CEF绕点C旋转一定的角度，得到图b，（1）中的结论还成立吗？作出判断并说明理由．2018年河南省商丘市八年级（上）第一次段考数学试卷参考答案与试题解析一．选择题【每题3分，共24分】1．若一个三角形的两边长分别是3和4，则第三边的长可能是( )A．1 B．2 C．7 D．8【考点】三角形三边关系．【分析】根据三角形的三边关系求得第三边的取值范围解答即可．【解答】解：设第三边长x．根据三角形的三边关系，得1＜x＜7．故选B．【点评】本题主要考查三角形三边关系的知识点，此题比较简单，注意三角形的三边关系．2．一个多边形的内角和是1260°，这个多边形的边数是( )A．7 B．8 C．9 D．10【考点】多边形内角与外角．【专题】常规题型．【分析】根据多边形的内角和公式列式求解即可．【解答】解：设这个多边形的边数是n，则（n﹣2）•180°=1260°，解得n=9．故选C．【点评】本题考查了多边形的内角和公式，熟记公式是解题的关键，是基础题，比较简单．3．如图所示，△ABC平移得到△DEF，若∠DEF=35°，∠ACB=70°，则∠A的度数是( )A．55°B．65°C．75°D．85°【考点】平移的性质．【分析】根据平移变换只改变图形的位置不改变图形的形状可得∠B=∠DEF，然后根据三角形的内角和定理列式计算即可得解．【解答】解：∵△ABC平移得到△DEF，∴∠B=∠DEF=35°，在△ABC中，∠A=180°﹣∠B﹣∠ACB=180°﹣35°﹣70°=75°．故选C．【点评】本题考查了平移的性质，熟记平移变换只改变图形的位置不改变图形的形状是解题的关键．4．如图，△ABE≌△ACF．若AB=5，AE=2，BE=4，则CF的长度是( )A．2 B．5 C．4 D．3【考点】全等三角形的性质．【分析】根据全等三角形的性质解答即可．【解答】解：∵△ABE≌△ACF，∴CF=BE=4，故选：C．【点评】本题考查的是全等三角形的性质，掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键．5．如图，在△ABC中，若AD⊥BC，点E是BC边上一点，且不与点B、C、D 重合，则AD是几个三角形的高线( )A．4个B．5个C．6个D．8个【考点】三角形的角平分线、中线和高．【分析】根据三角形高的定义可知，三角形的高可以在三角形内部，可以是三角形的边，还可以在三角形外部，结合图形即可求解．【解答】解：∵在△ABC中，AD⊥BC，点E是BC边上一点，且不与点B、C、D重合，∴AD是△ABD，△ABE，△ABC，△ADE，△ADC，△AEC的高．故选C．【点评】本题考查了三角形的高的定义：从三角形的一个顶点向它的对边作垂线，垂足与顶点之间的线段叫做三角形的高．注意：锐角三角形的三条高在三角形内部，相交于三角形内一点；直角三角形有两条高与直角边重合，另一条高在三角形内部，它们的交点是直角顶点；钝角三角形有两条高在三角形外部，一条高在三角形内部，三条高所在直线相交于三角形外一点．6．如图，将含30°角的三角板的直角顶点放在直尺的一边上，若∠1=40°，则∠2的度数为( )A．90°B．80°C．75°D．70°【考点】平行线的性质．【分析】根据平行线的性质求出∠3=∠1=40°，根据三角形的外角性质求出∠2=∠3+∠A，代入求出即可．【解答】解：∵EF∥MN，∠1=40°，∴∠1=∠3=40°，∵∠A=30°，∴∠2=∠A+∠3=70°，故选D．【点评】本题考查了平行线的性质，三角形外角性质的应用，能求出∠3的度数是解此题的关键，注意：两直线平行，内错角相等．7．如图，EA∥DF，AE=DF，要使△ACE≌△DBF，则只要（）A．AB=CD B．EC=BF C．∠A=∠D D．AB=BC【考点】全等三角形的判定．【分析】根据AB=CD求出AC=DB，根据平行线的性质得出∠A=∠D，根据SAS 推出两三角形全等即可．【解答】解：∵EA∥DF，∴∠A=∠D，∵AB=CD，∴AB+BC=CD+BC，∴AC=DB，在△ACE和△DBF中，，∴△ACE≌△DBF（SAS），即只有选项A正确，选项B、C、D都不能推出两三角形全等，故选：A．【点评】本题考查了全等三角形的性质和判定的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，全等三角形的对应边相等，对应角相等．8．如图：在不等边△ABC中，PM⊥AB，垂足为M，PN⊥AC，垂足为N，且PM=PN，Q在AC上，PQ=QA，下列结论：①AN=AM，②QP∥AM，③△BMP ≌△QNP，其中正确的是（）A．①②③B．①②C．②③D．①【考点】角平分线的性质；平行线的判定；全等三角形的判定．【分析】利用“HL”证明△APM和△APN全等，根据全等三角形对应边相等可得AN=AM；全等三角形对应角相等可得∠PAM=∠PAN，再根据等边对等角可得∠PAN=∠APQ，从而得到∠PAM=∠APQ，然后根据内错角相等，两直线平行可得QP∥AM；欲证△BMP和△QNP全等，须得BP=PQ=AQ，从而得到AC=BC，而此条件无法得到，所以，两三角形不一定全等．【解答】解：∵PM⊥AB，PN⊥AC，∴∠AMP=∠ANP=90°，在Rt△APM和Rt△APN中，∵，∴Rt△APM≌Rt△APN（HL），∴AN=AM，故①正确；∠PAM=∠PAN，∵PQ=QA，∴∠PAN=∠APQ，∴∠PAM=∠APQ，∴QP∥AM，故②正确；假设△BMP≌△QNP，则BP=PQ，∵PQ=QA，∴BP=PQ=AQ，又∵QP∥AM，∴AC=BC，此条件无法从题目得到，所以，假设不成立，故③错误．综上所述，正确的是①②．故选B．【点评】本题考查了角平分线的性质，全等三角形的判定与性质，平行线的判定，等边对等角的性质，比较复杂，熟记性质并准确识图是解题的关键．二.填空【每题3分，共24分】9．如图，D是AB边上的中点，将△ABC沿过D的直线折叠，使点A落在BC 上F处，若∠B=50°，则∠BDF=80度．【考点】翻折变换（折叠问题）．【分析】由折叠的性质，即可求得AD=DF，又由D是AB边上的中点，即可得DB=DF，根据等边对等角的性质，即可求得∠DFB=∠B=50°，又由三角形的内角和定理，即可求得∠BDF的度数．【解答】解：根据折叠的性质，可得：AD=DF，∵D是AB边上的中点，即AD=BD，∴BD=DF，∵∠B=50°，∴∠DFB=∠B=50°，∴∠BDF=180°﹣∠B﹣∠DFB=80°．故答案为：80．【点评】此题考查了折叠的性质，等腰三角形的判定与性质，以及三角形内角和定理．此题难度不大，解题的关键是注意数形结合思想的应用．10．如图，△ABC的周长为32，且AB=AC，AD⊥BC于D，△ACD的周长为24，那么AD的长为8．【考点】等腰三角形的性质．【分析】由已知条件根据等腰三角形三线合一的性质可得到BD=DC，再根据三角形的周长定义求解．【解答】解：∵AB=AC，AD⊥BC，∴BD=DC．∵AB+AC+BC=32，即AB+BD+CD+AC=32，∴AC+DC=16∴AC+DC+AD=24∴AD=8．故填8．【点评】本题考查等腰三角形的性质；由已知条件结合图形发现并利用AC+CD 是△ABC的周长的一半是正确解答本题的关键．11．如图，等边△ABC的边长为1cm，D、E分别是AB、AC上的点，将△ADE 沿直线DE折叠，点A落在点A′处，且点A′在△ABC外部，则阴影部分图形的周长为3cm．【考点】翻折变换（折叠问题）；轴对称的性质．【分析】由题意得AE=A′E，AD=A′D，故阴影部分的周长可以转化为三角形ABC 的周长．【解答】解：将△ADE沿直线DE折叠，点A落在点A′处，所以AD=A′D，AE=A′E．则阴影部分图形的周长等于BC+BD+CE+A′D+A′E，=BC+BD+CE+AD+AE，=BC+AB+AC，=3cm．故答案为：3．【点评】折叠问题的实质是“轴对称”，解题关键是找出经轴对称变换所得的等量关系．12．纸片△ABC中，∠A=65°，∠B=75°，将纸片的一角折叠，使点C落在△ABC 内（如图），若∠1=20°，则∠2的度数为60°．【考点】三角形内角和定理．【分析】先根据∠A=65°，∠B=75°，求出∠C的度数．再由∠1=20°可求出∠CED 的度数，由三角形内角和定理及平角的性质即可求解．【解答】解：∵△ABC中，∠A=65°，∠B=75°，∴∠C=180°﹣∠A﹣∠B=180°﹣65°﹣75°=40°，∵∠1=20°，∴∠CED==80°，在△CDE中，∠CDE=180°﹣∠C﹣∠CED=180°﹣40°﹣80°=60°，∴∠2=180°﹣2∠CDE=180°﹣2×60°=60°，故答案为60°．【点评】本题考查的是三角形内角和定理及平角的性质，解答此题的关键是熟知三角形的内角和是180°．13．如图，△ABC中，∠A=100°，BI、CI分别平分∠ABC，∠ACB，则∠BIC= 140°，若BM、CM分别平分∠ABC，∠ACB的外角平分线，则∠M=40°．【考点】三角形内角和定理；三角形的外角性质．【分析】首先根据三角形内角和求出∠ABC+∠ACB的度数，再根据角平分线的性质得到∠IBC=∠ABC，∠ICB=∠ACB，求出∠IBC+∠ICB的度数，再次根据三角形内角和求出∠I的度数即可；根据∠ABC+∠ACB的度数，算出∠DBC+∠ECB的度数，然后再利用角平分线的性质得到∠1=∠DBC，∠2=ECB，可得到∠1+∠2的度数，最后再利用三角形内角和定理计算出∠M的度数．【解答】解：∵∠A=100°，∵∠ABC+∠ACB=180°﹣100°=80°，∵BI、CI分别平分∠ABC，∠ACB，∴∠IBC=∠ABC，∠ICB=∠ACB，∴∠IBC+∠ICB=∠ABC+∠ACB=（∠ABC+∠ACB）=×80°=40°，∴∠I=180°﹣（∠IBC+∠ICB）=180°﹣40°=140°；∵∠ABC+∠ACB=80°，∴∠DBC+∠ECB=180°﹣∠ABC+180°﹣∠ACB=360°﹣（∠ABC+∠ACB）=360°﹣80°=280°，∵BM、CM分别平分∠ABC，∠ACB的外角平分线，∴∠1=∠DBC，∠2=ECB，∴∠1+∠2=×280°=140°，∴∠M=180°﹣∠1﹣∠2=40°．故答案为：140°；40°．【点评】此题主要考查了三角形内角和定理，以及角平分线的性质，关键是根据三角形内角和定理计算出∠ABC+∠ACB的度数．14．如图，在∠AOB的两边截取OA=OB，OC=OD，连接AD，BC交于点P，则下列结论中①△AOD≌△BOC，②△APC≌△BPD，③点P在∠AOB的平分线上．正确的是①②③；（填序号）【考点】全等三角形的判定与性质．【分析】根据题中条件，由两边夹一角可得△AOD≌△BOC，得出对应角相等，又由已知得出AC=BD，可得△APC≌△BPD，同理连接OP，可证△AOP≌△BOP，进而可得出结论．【解答】解：∵OA=OB，OC=OD，∠O为公共角，∴△AOD≌△BOC，∴∠A=∠B，又∠APC=∠BPD，∴∠ACP=∠BDP，OA﹣OC=OB﹣OD，即AC=BD，∴△APC≌△BPD，∴AP=BP，连接OP，即可得△AOP≌△BOP，得出∠AOP=∠BOP，∴点P在∠AOB的平分线上．故题中结论都正确．故答案为：①②③．【点评】本题主要考查了全等三角形的判定及性质问题，能够熟练掌握．15．如图，△ABC中，∠C=90°，AD平分∠BAC，AB=5，CD=2，则△ABD的面积是5．【考点】角平分线的性质．【分析】要求△ABD的面积，有AB=5，可为三角形的底，只求出底边上的高即可，利用角的平分线上的点到角的两边的距离相等可知△ABD的高就是CD的长度，所以高是2，则可求得面积．【解答】解：∵∠C=90°，AD平分∠BAC，∴点D到AB的距离=CD=2，∴△ABD的面积是5×2÷2=5．故答案为：5．【点评】本题主要考查了角平分线上的一点到两边的距离相等的性质．注意分析思路，培养自己的分析能力．16．已知如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC，∠CED=35°，则∠EAB是35度．【考点】角平分线的性质．【分析】过点E作EF⊥AD，证明△ABE≌△AFE，再求得∠CDE=90°﹣35°=55°，进而得到∠CDA和∠DAB的度数，即可求得∠EAB的度数．【解答】解：过点E作EF⊥AD，∵DE平分∠ADC，且E是BC的中点，∴CE=EB=EF，又∵∠B=90°，且AE=AE，∴△ABE≌△AFE，∴∠EAB=∠EAF．又∵∠CED=35°，∠C=90°，∴∠CDE=90°﹣35°=55°，∴∠CDA=110°，∵∠B=∠C=90°，∴DC∥AB，∴∠CDA+∠DAB=180°，∴∠DAB=70°，∴∠EAB=35°．故答案为：35．【点评】本题考查了角平分线的性质，解答此题的关键是根据题意作出辅助线EF⊥AD，构造出全等三角形，再由全等三角形的性质解答．三.解答题17．如图，AC=DF，AD=BE，BC=EF．求证：∠C=∠F．【考点】全等三角形的判定与性质．【分析】由AD=BE，可得AB=DE，则由三边相等，进而可得三角形全等，即可得出结论．【解答】证明：∵AD=BE∴AD+BD=BE+BD，即AB=DE，又∵AC=DF，BC=EF，∴△ABC≌△DEF，∴∠C=∠F．【点评】本题主要考查了全等三角形的判定及性质问题，能够熟练掌握并运用．18．如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个可以直接到达A和B的点C，连结AC并延长到D，使CD=CA．连结BC并延长到E，使EC=CB，连结DE，量出DE的长，就是A、B的距离．写出你的证明．【考点】全等三角形的应用．【分析】连接AB，由题意知AC=DC，BD=EC，根据∠ACB=∠DCE即可证明△ABC≌△DEC，即可得AB=DE，即可解题．【解答】解：连接AB，由题意知：AC=DC，BC=EC，在△ABC和△DEC中∵，∴△ABC≌△DEC（SAS），∴DE=AB故量出DE的长，就是A，B两点间的距离．答：量出DE的长，就是A，B两点间的距离．【点评】本题考查了全等三角形在实际生活中的应用，考查了全等三角形对应边相等的性质，本题中求证△ABC≌△DEC是解题的关键．19．如图，AD为△ABC的高，E为AC上一点，BE交AD于F，且有BF=AC，FD=CD，那么BE⊥AC吗？为什么？【考点】全等三角形的判定与性质．【分析】由于∠BFD、∠FBD互余，若证BE⊥AC，就必须证得∠BFD=∠C，观察图形后可得：结合已知条件证Rt△BDF≌Rt△ADC即可．【解答】解：BE⊥AC．理由是：由∠ADB=∠ADC=90°，得到△BDF和△ADC都为直角三角形，在Rt△BDF和Rt△ADC中，，∴Rt△BDF≌Rt△ADC（HL），∴∠CAD=∠DBF，∵∠AFE=∠BFD，∠CBF+∠BFD=90°，∴∠CAD+∠AFE=90°，∴∠AEF=90°，∴BE⊥AC．【点评】此题主要考查的是全等三角形的判定和性质，难度不大，找准全等的三角形是正确解决本题的关键．20．如图：E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足为C，D．求证：（1）OC=OD；（2）DF=CF．【考点】角平分线的性质；全等三角形的判定与性质；等腰三角形的判定与性质．【分析】（1）首先根据角平分线的性质可得EC=DE，∠ECO=∠EDO=90°，然后证明Rt△COE≌Rt△DOE可得CO=DO；（2）证明COF≌△DOF可根据全等三角形的性质可得FC=FD．【解答】证明：（1）∵E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，∴EC=DE，∠ECO=∠EDO=90°，在Rt△COE和Rt△DOE中，，∴Rt△COE≌Rt△DOE（HL），∴CO=DO；（2）∵EO平分∠AOB，∴∠AOE=∠BOE，在△COF和△DOF中，，∴△COF≌△DOF（SAS），∴FC=FD．【点评】此题主要考查了角平分线的性质，以及全等三角形的判定与性质，关键是掌握角平分线的性质：角的平分线上的点到角的两边的距离相等．21．（10分）（2002•呼和浩特）如图，△ABC中，∠ACB=90°，AC=BC，AE 是BC边上的中线，过C作CF⊥AE，垂足为F，过B作BD⊥BC交CF的延长线于D．（1）求证：AE=CD；（2）若AC=12cm，求BD的长．【考点】直角三角形全等的判定；全等三角形的性质．【分析】（1）证两条线段相等，通常用全等，本题中的AE和CD分别在三角形AEC和三角形CDB中，在这两个三角形中，已经有一组边相等，一组角相等了，因此只需再找一组角即可利用角角边进行解答．（2）由（1）得BD=EC=BC=AC，且AC=12，即可求出BD的长．【解答】（1）证明：∵DB⊥BC，CF⊥AE，∴∠DCB+∠D=∠DCB+∠AEC=90°．∴∠D=∠AEC．又∵∠DBC=∠ECA=90°，且BC=CA，在△DBC和△ECA中，∵∴△DBC≌△ECA（AAS）．∴AE=CD．（2）解：由（1）得AE=CD，AC=BC，在Rt△CDB和Rt△AEC中，∴Rt△CDB≌Rt△AEC（HL），∴BD=CE，∵AE是BC边上的中线，∴BD=EC=BC=AC，且AC=12cm．∴BD=6cm．【点评】三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．22．（12分）（2013•荆州模拟）如图a，△ABC和△CEF是两个大小不等的等边三角形，且有一个公共顶点C，连接AF和BE（1）线段AF和BE有怎样的大小关系？请证明你的结论；（2）将图a中的△CEF绕点C旋转一定的角度，得到图b，（1）中的结论还成立吗？作出判断并说明理由．【考点】旋转的性质；全等三角形的判定与性质；等边三角形的性质．【分析】（1）根据题中所给的等边三角形的条件，两对边对应相等，有一个角都等于60°，变换这个60°的对应角，利用SAS证AF和BE所在的三角形全等；（2）利用了等边三角形的性质，根据特殊角和旋转不变性确定两线段相等．【解答】解：（1）AF=BE．证明：在△AFC和△BEC中，∵△ABC和△CEF是等边三角形，∴AC=BC，CF=CE，∠ACF=∠BCE=60°，在△AFC与△BEC中，，∴△AFC≌△BEC（SAS），∴AF=BE．（2）成立．理由：在△AFC和△BEC中，∵△ABC和△CEF是等边三角形，∴AC=BC，CF=CE，∠ACB=∠FCE=60度，∴∠ACB﹣∠FCB=∠FCE﹣∠FCB，即∠ACF=∠BCE，在△AFC与△BEC中，，∴△AFC≌△BEC（SAS），∴AF=BE．【点评】本题主要考查旋转的性质：旋转前后图形的大小和形状不变，只是位置发生了变化．证两条线段相等，通常是证这两条线段所在的两个三角形全等，类似的题，证明方法基本不变．。

2017-2018学年度第一学期期末教学质量检测八年级数学试题（时间：120分钟）友情提示：亲爱的同学，你好！今天是你展示才能的时候，只要你仔细审题，认真答题，你就会有出色的表现！1.考生务必将姓名、班级、座号、准考证号填写在答题卡规定的位置上。

2.本试题分第Ⅰ卷和第Ⅱ卷，共25道小题。

3.第Ⅰ卷是选择题，共8道小题，每小题选出的答案后，用2B铅笔把答题卡上对应的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其它答案标号，答案不能答在试卷上。

4.第Ⅱ卷是填空题和解答题，共17小题，答案必须用0.5毫米黑色签字笔写在答题卡题目指定区域内相应的位置，不能写在试题上；如需改动，先划掉原来的答案，然后再写上新的答案。

不按以上要求作答的答案无效。

5.考试结束只上交答题卡。

第Ⅰ卷一、选择题：下列每小题都给出标号为A、B、C、D的四个结论，其中只有一个是正确的，请将所选答案的字母标号涂在答题卡的相应位置。

1.3的相反数是（）A、3B、-3C、3D、-32.在平面直角坐标系中，点P（-2,3）关于x轴的对称点坐标为（）A、（-2,3）B、（2，-3）C、（-2，-3）D、（3，-2）3.下列语句：①三角形的内角和是180°；②作为一个角等于一个已知角；③两条直线被第三条直线所截，同位角相等；④延长线段AB到C，使BC=AB，其中是命题的有（）A、①②B、②③C、①④D、①③4.方程组的解是（）A、 B、 C、 D 、5.若一次函数y=kx+b，（k，b为常熟，且k≠0）的图像经过点（1,2）且y随x的增大而减小，则这个函数的表达式可能是（）A、y=2x+4B、y=3x-1C、y=-3x-1D、y=-2x+46.如图，∠AOB的边OA为平面反光镜，一束光线从OB上的C点射出，经OA上的D点反射后，反射光线DE恰好与OB平行，若∠AOB=40°，则∠BCD的度数是（）A、60°B、80°C、100°D、120°x +|y-2|=0，则（x+y）2017的值为（）7.若3A、-1B、1C、±1D、08.若一组数据10,9.a，12,9的平均数是10，则这组数的方差是（）A、0.9B、1C、1.2D、1.4第Ⅱ卷二、填空题：请把正确答案填写在答题卡的相应位置9.实数7的整数部分是_______10.命题“对顶角相等”的条件是_______________ ，结论是___________ 。

2017～2018学年度第一学期八年级期末调研考试数 学注意事项考生在答题前请认真阅读本注意事项1．本试卷共6页，满分为100分，考试时间为100分钟．考试结束后，请将本试卷和答题纸一并交回． 2．答题前，请务必将自己的姓名、考试证号用0.5毫米黑色字迹的签字笔填写在试卷及答题纸指定的位置． 3．答案必须按要求填涂、书写在答题纸上，在试卷、草稿纸上答题一律无效．一、选择题（本大题共10小题，每小题2分，共20分．在每小题给出的四个选项中,恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题纸相应位置上)1．下面四个图形分别是绿色食品、节水、低碳和节能标志，是轴对称图形的是2．若式子4xx -有意义,则x 的取值范围是 A ．x ＝0B ．x ＝4C ．x ≠0D ．x ≠43．计算(－a 3)2的结果是A ．a 6B ．－a 6C ．－a 5D ．a 54．下列根式是最简二次根式的是A ．13B ．3C ．0.3D ．205．如图，∠ABC ＝∠BAD ，添加下列条件还不能判定△ABC ≌△BAD 的是A ．∠CAB ＝∠DBA B ．∠C ＝∠D C ．AC ＝BD D ．BC ＝AD6．若a ＋b ＝3,则代数式(a b 2－a ）÷ab a -的值为A ．－13B ．－3C ．13D ．3C ．A ．B ．D ．ABCD （第5题）7．直角三角形有一条直角边为6，另两条边长是连续偶数,则该三角形周长为A ．20B ．22C ．24D ．268．如图，小莹和小华在棋盘中练习摆图案，小莹执圆子，小华执星子．棋盘中心圆子的位置用(－1，0)表示，右下角圆子的位置用(0，－1）表示．若小华将第4枚星子放入棋盘后，所有棋子构成一个轴对称图形,则他放的位置是A ．（－2，1）B ．(0，－2）C ．(1，－2）D ．（－1，1）9．如图是5×5的正方形网格中，以D ,E 为顶点作位置不同的格点的三角形与△ABC 全等，这样格点三角形最多可以画出A ．2个B ．3个C ．4个D ．5个10．如图，在长方形ABCD 中,AB ＝10，BC ＝30．E ，F ,G ，H 分别是AB ，BC ,CD ,DA 上的点，且∠1＝∠2＝∠3＝∠4，则四边形EFGH 的周长为 A ．3010 B ．2010C ．64D ．60二、填空题(本大题共8小题，每小题2分，共16分．不需写出解答过程,请把答案直接填写在答题纸相应位置上）11．肥皂泡沫的泡壁厚度约是0.0007mm ，则0。

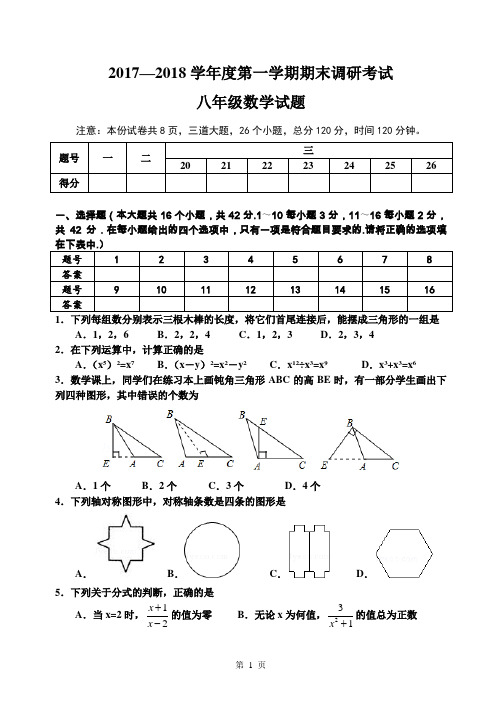
2017—2018学年度第一学期期末调研考试八年级数学试题注意：本份试卷共8页，三道大题，26个小题，总分120分，时间120分钟。

一、选择题（本大题共16个小题，共42分.1～10每小题3分，11～16每小题2分，共42分．在每小题给出的四个选项中，只有一项是符合题目要求的.请将正确的选项填在A．1，2，6 B．2，2，4 C．1，2，3 D．2，3，42．在下列运算中，计算正确的是A．（x5）2=x7B．（x－y）2=x2－y2C．x12÷x3=x9D．x3+x3=x63．数学课上，同学们在练习本上画钝角三角形ABC的高BE时，有一部分学生画出下列四种图形，其中错误的个数为A．1个B．2个C．3个D．4个4．下列轴对称图形中，对称轴条数是四条的图形是A．B．C．D．5．下列关于分式的判断，正确的是A．当x=2时，12xx+-的值为零B．无论x为何值，231x+的值总为正数C ．无论x 为何值，31x +不可能得整数值 D ．当x≠3时，3x x -有意义6．如图，已知AB=AC ，AD=AE ，若要得到“△ABD ≌△ACE”，必须添加一个条件，则下列所添条件不恰当的是A ．BD=CEB ．∠ABD=∠ACEC ．∠BAD=∠CAED ．∠BAC=∠DAE 7．若把分式2x yxy+中的x 和y 都扩大3倍，且x+y≠0，那么分式的值 A ．扩大3倍 B ．不变 C ．缩小3倍 D ．缩小6倍 8．若x=－2，y=12，则y （x+y ）+（x+y ）（x －y ）－x 2的值等于 A ．－2 B ．12C ．1D ．－19．如图，在△ABC 中，DE 是AC 的垂直平分线，AC=6cm ，且△ABD 的周长为13cm ，则△ABC 的周长为A ．13cmB ．19cmC ．10cmD ．16cm10.观察等式（2a ﹣1）a+2=1，其中a 的取值可能是A ．﹣2B ．1或﹣2C ．0或1D ．1或﹣2或0 11．下列计算中正确的是A ．22155b a a b ab -⨯=-- B ．32x y x y ya b a b a b+--=+++ C ．m m n m n n m n ÷⨯= D ．1224171649xy xy a xy a -⎛⎫⎛⎫÷=⎪ ⎪⎝⎭⎝⎭12．如图，C 在AB 的延长线上，CE ⊥AF 于E ，交FB 于D ，若∠F=40°，∠C=20°，则∠FBA 的度数为A ．50°B ．60°C ．70°D ．80°13．若y －x=－1，xy=2，则代数式－12x 3y+x 2y 2－12xy 3的值是 A ．2 B ．－2 C ．1 D ．－114．图1是一个长为 2a ，宽为2b （a ＞b ）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图2那样拼成一个正方形，则中间空的部分的面积是A ．a 2－b 2B ．（a －b ）2C ．（a+b ）2D ．ab15．如图，△ABC的顶点坐标分别为A（4，4）、B（2，1）、C（5，2），沿某一直线作△ABC的对称图形，得到△A′B′C′，若点A的对应点A′的坐标是（3，5），那么点B的对应点B′的坐标是A．（0，3）B．（1，2）C．（0，2）D．（4，1）16．如图，点E是BC的中点，AB⊥BC，DC⊥BC，AE平分∠BAD，下列结论：①∠AED=90°②∠ADE=∠CDE ③DE=BE ④AD=AB+CD，四个结论中成立的是A．①②④B．①②③C．②③④D．①②二、填空题（本大题共3小题，共10分.17～18小题各3分；19小题有2个空，每空2分.把答案写在题中横线上）17．一个多边形的每一个外角都为36°，则这个多边形是边形．18．若x2+2（m－3）x+16是一个完全平方式，那么m应为．19．对于实数a、，b，定义运算⊗如下：a⊗b=()(),0,0bba ab aa ab a-⎧>≠⎪⎨≤≠⎪⎩，例如：2⊗4=2－4=116，计算[4⊗2] =，[2⊗2]×[3⊗2]=．三、解答题（本大题共7小题，共68分．解答应写出文字说明、证明过程或演算步骤）20．计算（本题满分8分）如图，在平面直角坐标中，△ABC各顶点都在小方格的顶点上．（1）画出△ABC关于x轴对称的图形△A1B1C1；（2）在y轴上找一点P，使PA+PB1最短，画出图形并写出P点的坐标．21．（本题满分9分）先化简，再求值：2214411a aa a a-+⎛⎫-÷⎪--⎝⎭，其中－2＜a≤2，请选择一个a的合适整数代入求值．22．（本题满分9分）两个大小不同的等腰直角三角形三角板如图①所示放置，图②是由它抽象出的几何图形，B，C，E在同一条直线上，连接DC，（1）请找出图②中的全等三角形，并给予证明（结论中不得含有未标识的字母）；（2）求证：DC⊥BE．23．（本题满分9分）先阅读以下材料，然后解答问题．将一个多项式分组后，可提公因式或运用公式继续分解的方法是因式分解中的分组分解法，一般的分组分解法有四种形式，即“2+2”分法、“3+1”分法、“3+2”分法及“3+3”分法等．如“2+2”分法：ax+ay+bx+by=（ax+ay）+（bx+by）=a（x+y）+b（x+y）=（x+y）（a+b）请你仿照以上方法，探索并解决下列问题：（1）分解因式：x2－y2－x－y；（2）分解因式：9m2－4x2+4xy－y2；24．（本题满分10分）如图，已知BD平分∠ABC，AB=AD，DE⊥AB，垂足为E．（1）求证：AD∥BC；（2）若DE=6cm，求点D到BC的距离；（3）当∠ABD=35°，∠DAC=2∠ABD时，①求∠BAC的度数；②证明：AC=AD．25．（本题满分11分)随着城际铁路的正式开通，从甲市经丙市到乙市的高铁里程比普快里程缩短了90km，运行时间减少了8h，已知甲市到乙市的普快列车里程为1220km．高铁平均时速是普快平均时速的2.5倍．（1）求高铁列车的平均时速；（2）某日王先生要从甲市去距离大约780km的丙市参加14：00召开的会议，如果他买到当日9：20从甲市到丙市的高铁票，而且从丙市火车站到会议地点最多需要1小时．试问在高铁列车准点到达的情况下，它能否在开会之前20分钟赶到会议地点？26．(本题满分12分)如图1，△ABC是边长为5cm的等边三角形，点P，Q分别从顶点A，B同时出发，沿线段AB，BC运动，且它们的是速度都为1厘米/秒．当点P到达点B时，P、Q两点停止运动．设点P的运动时间为t（秒）．（1）当运动时间为t秒时，BQ的长为厘米，BP的长为厘米；（用含t 的式子表示）（2）当t为何值时，△PBQ是直角三角形；（3）如图2，连接AQ、CP，相交于点M，则点P，Q在运动的过程中，∠CMQ会变化吗？若变化，则说明理由；若不变，请求出它的度数．参考答案及评分标准说明：1.在阅卷过程中，如果考生还有其它正确解法，可参照评分参考酌情给分；2.填空题缺少必有的单位或答案不完整不得分；3.坚持每题评阅到底的原则,当考生的解答在某一步出现错误,影响了后继部分时,如果该步以后的解答未改变这一题的内容和难度,可视影响的程度决定后面部分的给分,但不得超过后继部分应给分数的一半;如果这一步后面的解答有较严重的错误，就不给分；4.解答右端所注分数，表示正确做到这一步应得的累积分数.一、(本大题有16小题，共43分.1~10每小题各3分，11~16每小题各2分)二、(本大题有3个小题，共10分.17~18小题个3分；19小题有2个空，每空2分) 17．十；18．－1或7；19．16，．三、（本大题有7小题，共68分）20.解：（1）如图所示：△A1B1C1为所求作的三角形；……………………….……4分（2）如图，……………………………………………………………………..…..……7分点P的坐标为：（0，1）．………………………………………………………...………8分21．解：原式=……………………………………………………….2分=……………………………………………………………………………4分=，………………………………………………………………………………………6分当a=－1时，…………………………………………………………………….…………8分原式=．……………………………………………..……………………………9分22．（1）解：△BAE≌△CAD，证明如下：……………………………………………1分∵△ABC，△DAE是等腰直角三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=90°．……………………………..……………2分∠BAE=∠DAC=90°+∠CAE，………………………………………………………...…4分在△BAE和△DAC中∴△BAE≌△CAD（SAS）．………………………………………………………………6分（2）证明：∵△ABC，△DAE是等腰直角三角形，∴∠B=45°，∠BCA=45°，……………………………………………………………..…7分∵△BAE≌△CAD．∴∠DCA=∠B=45°．………………………………………………………………………8分∴∠BCD=∠BCA+∠DCA=90°，∴DC⊥BE．…………………………………………………………………………………9分23．解：（1）原式=（x2－y2）－（x+y）…………………………………………………2分=（x+y）（x－y）－（x+y）…………………………….……………………………….…3分=（x+y）（x－y－1）；……………………………………………….………………………4分（2）原式=9m2－（4x2－4xy+y2）……………………………………………………….6分=（3m）2－（2x－y）2…………………………………………………………………….8分=（3m+2x－y）（3m－2x+y）. ……………………………………………………….……9分24．（1）证明：∵AB=AD，∴∠ADB=∠ABD…………………………………………………….………..……………1分又∵BD平分∠ABC，即∠ABD=∠DBC，∴∠ADB =∠DBC，…………………………………………………………..……………2分∴AD∥BC；…………………………………………………………………………………3分（2）解：作DF⊥BC交BC的延长线于F．∵BD平分∠ABC，DE⊥AB，DF⊥BC，∴DF=DE=6cm；即点D到BC的距离为6cm. ……………………………………………………..……5分（3）①解：∵BD平分∠ABC，∴∠ABC=2∠ABD=70°，…………………………………………………………..….…6分∵AD∥BC，∴∠ACB=∠DAC=70°，……………………………………………………………….…7分∴∠BAC=180°－∠ABC－∠ACB=180°－70°－70°=40°．……………………………8分②证明：∵∠ABC=70°，∠ACB=70°，∴∠ABC=∠ACB，∴AB=AC，…………………………………………………………………………………9分又∵AB=AD，∴AC=AD．………………………………………………………………………………..10分25．解：（1）设普快的平均时速为x千米/小时，高铁列车的平均时速为2.5x千米/小时，根据题意得，……………..……………………………………………………..…………1分－=8，…………………………………………..………………….……4分解得：x=96，……………..………………5分经检验，x=96是原分式方程的解，且符合题意，……………..………………………6分则2.5x=240，答：高铁列车的平均时速为240千米/小时；………………………………..…………7分（2）780÷240=3.25，则坐车共需要3.25+1=4.25（小时），……………………………………..…………..…9分从9：20到13：40，共计4小时，………………………………...…………………10分因为4小时＞4.25小时，所以王先生能在开会之前到达．………………………………………………..………11分26．解：（1）t；（5－t）；………………………..………………….…………..………2分（2）∵△ABC是等边三角形，∴∠B=60°．①当∠PQB=90°时，∵∠B=60°，∴∠BPQ=30°，∴PB=2BQ，得5－t=2t，解得，t=，………………………………………………………………………………4分②当∠BPQ=90°时，∵∠B=60°，∴∠BQP=30°，∴BQ=2BP，得t=2（5－t），解得，t=，………………………………………………………………...…………6分∴当t的值为或时，△PBQ为直角三角形；…………………………..………7分（3）∠CMQ不变，∠CMQ=60°理由如下：………………………………….……8分∵△ABC是等边三角形，∴AB=AC，∠B=∠BAC=60°，由题意可知：AP=BQ，在△ABQ与△CAP中，，∴△ABQ≌△CAP（SAS），…………………………………………………..………10分∴∠BAQ=∠ACP，∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°，∴∠CMQ不会变化，总为60°．………………………..……………………………12分。

2017-2018学年人教版八年级上册期末数学试卷1一、选择题(共10小题，每小题3分,共30分)下列名题中均有四个备选答案，其中有且只有一个正确，请在答卷上将正确答案的代号涂黑．1．（3分）计算：a2•a的结果是（）A．a B．a2C．a3D．2a22．（3分）如图,图形中x的值为（）A．65B．75C．85D．953．（3分）使分式有意义，则x满足条件( ）A．x＞0B．x≠0C．x＞1D．x≠14．（3分）如图，△OCA≌△OBD，∠1=40°，∠C=110°，则∠D=（）A．30°B．40°C．50°D．无法确定5．(3分）在Rt△ABC中，∠C=90°，∠B=2∠A，则边AB与BC的关系（）A．AB=BC B．AB=2BC C．AB=BC D．AB＜BC6．(3分）把8m2n﹣2mn分解因式（）A．2mn（4m+1）B．2m（4m﹣1)C．mn（8m﹣2）D．2mn（4m﹣1）7．(3分)如图的三角形纸片中，AB=8,BC=6，AC=5,沿过点B的直线折叠这个三角形，使点C 落在AB边上的点E处，折痕为BD,则△AED的周长是（）A．7B．8C．11D．148．（3分）计算的结果是( ）A．B．0C．D．9．（3分）如图,△ABC中,AC=BC，∠ACB=90°,AE平分∠BAC交BC于E，BD⊥AE于D，连CD，下列结论：①AB﹣AC=CE;②∠CDB=135°；③S△ACE=2S△CDB;④AB=3CD,其中正确的有（）A．4个B．3个C．2个D．1个10．(3分）若等式恒成立，则（a2+b2﹣2ab）﹣8a+8b+17的值是（) A．50B．37C．29D．26二、填空题（共6小题,每小题3分,共18分)11．(3分）如图，在等腰三角形中，它的一个底角的度数是度．12．（3分）已知△ABC≌△DEF，若△ABC的三边长分别为6cm、8cm、10cm，则△DEF的周长是cm．13．（3分）计算：(x﹣4）(x+1）= ．14．（3分）如图，在△ABC中,AD是高，AE是角平分线，若∠B=72°，∠DAE=16°，则∠C= 度．15．（3分）若,则= ．16．（3分)如图，在平面直角坐标系中，点B、A分别在x轴、y轴上,∠BAO=60°，在坐标轴上找一点C,使得△ABC是等腰三角形,则符合条件的等腰三角形ABC有个．三、解答题（共8小题，共72分）17．（8分）解下列方程:（1）（2）18．（8分）计算：（1）（2a)3•b4÷12a3b2（2)（x﹣3y）（﹣6x）19．(8分）如图，CD⊥AB,BE⊥AC，垂足分别为D、E，BE、CD相交于点O，OB=OC，连AO，求证:∠1=∠2．20．（8分）（1）如图1，在△ABC中，点D、E分别是AB、AC的中点，请你在BC边上确定一点P，使△PDE的周长最小．(要求：保留作图痕迹，不写作法，但要说明点P是如何确定的．）（2)如图2，∠AOB内有一定点P，试在OA、OB上各找一点D、E,使△PDE的周长最小．（要求:保留作图痕迹，不写作法，但要说明点D、E是如何确定的．）21．（8分)先化简，再求值．[（x+3y）(x﹣3y）+（2y﹣x)2+5y2（1﹣x）﹣（2x2﹣x2y）]÷（﹣xy），其中x=95，y=220．22．（10分）如图,“主收1号”小麦的试验田是边长为am（a＞1)的正方形去掉一个边长为1m 的正方形蓄水池后余下的部分，“丰收2号”小麦的试验田是边长为（a﹣1）m的正方形，两块试验田的小麦都收获了500kg．（1)哪种小麦的单位面积产量高？（2）若高的单位面积产量是低的单位面积产量的(kg）倍，求a的值（3）利用（2）中所求的a的值，分解因式x2﹣ax﹣108= ．23．（10分）已知:△ABC中，∠ACB=90°，AC=BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD=BF；（2）如图2，点D在线段BC上,连AD，过A作AE⊥AD,且AE=AD，连BE交AC于F,连DE，问BD与CF有何数量关系,并加以证明；（3）如图3，点D在CB延长线上，AE=AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC=3MC,请直接写出的值．24．（12分）如图，在平面直角坐标系中，A（x，0)，B（0，y),其中x与y互为相反数,且x 满足：x2﹣14ax+49a2=0（a＞0），点C为x轴负半轴上一点，AD⊥AB，垂足为A，∠DCA=∠CBO．(1)求∠ABC+∠D的度数；（2）如图1，若点C的坐标为（﹣3a,0）,求点D的坐标．(用含a的式子表示）（3)如图2，在（2）的条件下，若a=1，过点D作DE⊥y轴于E,DF⊥x轴于F，点M为线段DF上一点．若第一象限内存在点N（n，2n﹣3)，使△EMN为等腰直角三角形，请直接写出符合条件的N点的坐标．参考答案与试题解析一、选择题（共10小题,每小题3分，共30分）下列名题中均有四个备选答案,其中有且只有一个正确,请在答卷上将正确答案的代号涂黑．1．【分析】直接利用同底数幂的乘法运算法则计算得出答案．【解答】解：a2•a=a3．故选:C．【点评】此题主要考查了同底数幂的乘法运算,正确掌握运算法则是解题关键．2．【分析】根据四边形的内角和等于360°,列方程即可得到结果．【解答】解：∵四边形的内角和为（4﹣2)×180°=360°,∴x°+x°+140°+90°=360°，解得：x=65．故选:A．【点评】本题考查了四边形的内角和，熟记四边形的内角和定理是解题的关键．3．【分析】分式有意义时,分母x﹣1≠0．【解答】解：依题意得：x﹣1≠0．解得x≠1．故选：D．【点评】本题考查了分式有意义的条件．（1）分式有意义的条件是分母不等于零．（2）分式无意义的条件是分母等于零．4．【分析】根据全等三角形对应角相等解答即可．【解答】解:∵△OCA≌△OBD，∠1=40°，∠C=110°,∴∠D=∠A=180°﹣40°﹣110°=30°,故选：A．【点评】本题考查了全等三角形的性质，根据全等三角形对应顶点的字母写在对应位置上是解题的关键．5．【分析】根据题意得到∠A=30°，根据直角三角形的性质解答即可．【解答】解：∵∠C=90°，∠B=2∠A，∴∠A=30°，∴AB=2BC，故选：B．【点评】本题考查的是直角三角形的性质，掌握在直角三角形中,30°所对的直角边等于斜边的一半是解题的关键．6．【分析】直接找出公因式进而提取得出答案．【解答】解：8m2n﹣2mn=2mn(4m﹣1）．故选：D．【点评】此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．7．【分析】根据翻折变换的性质得到DC=DE，BE=BC，根据已知求出AE的长，根据三角形周长公式计算即可．【解答】解：由折叠的性质可知，DC=DE，BE=BC=6，∵AB=8，∴AE=AB﹣BE=2，△AED的周长为:AD+AE+DE=AC+AE=7,答：△AED的周长为7．故选：A．【点评】本题考查的是翻折变换的知识，掌握翻折变换的性质、找准对应关系是解题的关键．8．【分析】根据分式的混合运算顺序和运算法则计算可得．【解答】解：原式=•﹣•+=﹣﹣==0，故选：B．【点评】本题主要考查分式的混合运算,分式的混合运算，一般按常规运算顺序，但有时应先根据题目的特点，运用乘法的运算律进行灵活运算．9．【分析】①作高线EH，先根据角平分线定理得：CE=EH,再证明△ACE≌△AHE（AAS）可得：AH=AC，根据线段的和可得结论;②先证明点A，B,D，C在以AB为直径的圆上，得∠ADC=∠ABC=45°，所以可得∠BDC=135°;③作辅助线,构建全等三角形，证明△ACE≌△BCG,根据等腰三角形三线合一得BD=DG，知道:△BDC和△CDG的面积相等，由此可得：S△ACE=S△BCG=2S△BDC；④根据③知：AB=AG=AC+CG,在△CDG中，可知CD＞CG，从而得结论．【解答】解：①过点E作EH⊥AB于H,如图1，∵∠ABC=45°，∴△BHE是等腰直角三角形，∴EH=BH，∵AE平分∠CAB，∴EH=CE，∴CE=BH,在△ACE和△AHE中，∵，∴△ACE≌△AHE（AAS），∴AH=AC,∴AB﹣AC=AB﹣AH=BH=CE,故①正确；②∵∠ACB=90°，BD⊥AE于D，∴∠ACB=∠ADB=90°，∴点A，B，D，C在以AB为直径的圆上,∴∠ADC=∠ABC=45°，∴∠BDC=∠ADB+∠ADC=90°+45°=135°故②正确；③如图2,延长BD、AC交于点G,∵AD平分∠BAG，AD⊥BG，∴BD=DG，∴CD是Rt△BCG的斜边的中线,∴CD=BD，S△BCD=S△CDG，∴∠DBC=∠DCB=22。

2017-2018学年第一学期期末测试卷初二数学一、选择题（每小题2分，本题共16分）1．剪纸是古老的汉族民间艺术,剪纸的工具材料简便普及，技法易于掌握，有着其他艺术门类 不可替代的特性，因而，这一艺术形式从古到今，几乎遍及我国的城镇乡村，深得人民群 众的喜爱.请你认真观察下列四幅剪纸图案, 其中不是．．轴对称图形的是A ．B ．C ．D ．2. 若代数式4xx -有意义，则实数x 的取值范围是 A ．0x = B ．4x = C ．0x ≠ D ．4x ≠3. 实数9的平方根是A ．3B ．±3C．3± D ．814. 在下列事件中，是必然事件的是A ．买一张电影票，座位号一定是偶数B ．随时打开电视机，正在播新闻C ．通常情况下，抛出的篮球会下落D ．阴天就一定会下雨5. 下列变形中，正确的是A. (23)2＝2×3＝6B.2)52(-＝－52C.169+＝169+ D. )4()9(-⨯-＝49⨯6. 如果把yx y322-中的x 和y 都扩大5倍，那么分式的值A ．扩大5倍B ．不变C ．缩小5倍D ．扩大4倍7. 如图，将ABC △放在正方形网格图中（图中每个小正方形的边长均为1），点A ，B ，C 恰好在网格图中的格点上，那么ABC △中BC 边上的高是A. B. C. D.8. 如图所示，将矩形纸片先沿虚线按箭头方向向右对折，对折后的纸片沿虚线向下对折，然后剪下一个小三角形，再将纸片打开，则打开后的展开图是A. B. C. D.二、填空题（每小题2分,本题共16分）9. 写出一个比3大且比4小的无理数：______________．10. 如图，AE ＝DF ，∠A ＝∠D ，欲证ΔACE ≌ΔDBF ，需要添加条件 ____________,证明全等的理由是________________________；AE P BCD11. 一个不透明的盒子中装有6张生肖邮票，其中有3张“猴票”，2张“鸡票”和1张“狗票”，这些邮票除了画面内容外其他都相同，从中随机摸出一张邮票，恰好是“鸡票”的可能性为 .12. 已知等腰三角形的两条边长分别为2和5，则它的周长为______________． 13.mn ＝______________． 14. 小明编写了一个如下程序：输入x →2x →立方根→倒数→算术平方根→21， 则x 为 .15. 如图，等边△ABC 的边长为6，AD 是BC 边上的中线，点E 是AC 边上的中点. 如果点P 是AD 上的动点，那么EP+CP 的最小值 为______________．16. 如图，OP =1，过P 作OP PP ⊥1且11=PP ，根据勾股定理，得21=OP ；再过1P 作121OP P P ⊥且21P P =1，得32=OP ；又过2P 作232OP P P ⊥且132=P P ，得 =3OP 2；…依此继续，得=2018OP ， =n OP （n 为自然数，且n ＞0）三、解答题（本大题共9小题，17—25小题，每小题5分，共45分） 17．计算：238)3(1230-+----π18. 计算：1)P 4P 3P 2PP 1O19. 如图，点A 、F 、C 、D 在同一条直线上. AB ∥DE ，∠B =∠E ，AF=DC. 求证：BC =EF .20. 解分式方程：3x 3x 211x x +=-+21. 李老师在黑板上写了一道题目，计算：23311x x x---- .小宇做得最快，立刻拿给李老 师看，李老师看完摇了摇头，让小宇回去认真检查. 请你仔细阅读小宇的计算过程，帮 助小宇改正错误．23311x x x ----=()()33111x x x x --+-- （A ） =()()()()()3131111x x x x x x +--+-+- （B ） = 33(1)x x --+ （C ） = 26x -- （D ）（1） 上述计算过程中， 哪一步开始．．出现错误？ ；(用字母表示) （2） 从（B ）到（C ）是否正确？ ；若不正确，错误的原因是 ； （3） 请你写出此题完整正确的解答过程．D22.如图：在△ABC 中，作AB 边的垂直平分线，交AB 于点E ，交BC 于点F ，连结AF （1（2）你的作图依据是 .（3）若AC=3，BC=5，则△ACF 的周长是23. 先化简，再求值：121112++÷⎪⎭⎫ ⎝⎛+-a a aa ，其中13-=a ．24. 如图，在△ABC 中，∠C=90°，AD 平分∠BAC 交BC 于 DE ⊥AB 于E, 当时，求DE 的长。

2017-2018 学年初二数学第一学期第一次阶段性测试本次100 分，分100 分一、细心选一选：（本大共8 小，每小 3 分，共24 分）1、下列法正确的是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯A.形状相同的两个三角形全等B.面相等的两个三角形全等C. 完全重合的两个三角形全等D.所有的等三角形全等2、下列交通志案是称形的是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（（））．3．如所示：ABC 和DEF中① AB DE，BC EF，AC DF；② AB DE，B E，BC EF ；③B E， BC EF ，C F ；④ AB DE，AC DF， BE ．第 3其中，能使△ ABC ≌△ DEF 的条件共有⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（）A． 1B． 2C． 3D． 44、如，△ ABC中，∠ C=90°， AD平分∠ BAC，点 D作 DE⊥ AB于 E，得 BC=9， BE=3，△ BDE的周是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯() A． 6B． 9C． 12D． 15A1 号袋2 号袋EBD C第 7第 4 3 号袋 4 号袋第 6第55．如是一个改造的3×5 的台球桌面示意，中四个角上的阴影部分分表示四个入球孔，如果一个球按中所示的方向被出（球可以台球多次反）那么球最后将落入的球袋是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（，）A.1 号袋B.2 号袋C.3 号袋D. 4 号袋6．如，把方形 ABCD 沿 EF 折后使两部分重合，若∠ 1=50°，∠ AEF=A ．110°B ．115°C． 120°D． 130°7、如，在 CD上求一点 P，使它到 OA，OB的距离相等，P 点是⋯⋯⋯⋯⋯A. 段 CD的中点B.OA与OB的中垂的交点C.OA与 CD的中垂的交点D.CD与∠ AOB的平分的交点(（)）8．如图，过边长为 1 的等边△ ABC 的边 AB 上一点 P，作 PE⊥ AC 于 E， Q 为 BC 延长线上一点，当 PA=CQ 时，连 PQ 交 AC 边于 D，则 DE 的长为 ()A．B．C． D ．不能确定CDA 50oB第 8 题图 .1-15第 12 题第 13 题第 10 题二、精心填一填：空，每空 2 分，共 20 分．）（本大题共有 109．角的对称轴是．10．小新是一位不错的足球运动员，他衣服上的号码在镜子里如图，他是号运动员．11．如果等腰三角形的两边长分别是4、 8，那么它的周长是 ____________ ．12、如图， AC、BD 相交于点 O，∠ A=∠D，请补充一个条件，使△AOB≌△ DOC，你补充的条件是（填出一个即可）．BAFAEDC lB C第 14 题第 15 题第 16 题第 17题13．如图所示，ADC°．14．如图，已知AB∥CF，E为DF的中点，若AB=9 cm ，CF=5 cm ，则BD=cm．15、如图，在△ ABC 中，AB＝ AC＝ 32cm，DE 是 AB 的垂直平分线，分别交 AB、AC 于 D、E 两点． (1) 若∠ C ＝ 700，则∠ CBE ＝ ______(2)若 BC ＝ 21cm ，则△ BCE 的周长是______cm．16．已知：∠ BAC 的平分线与 BC 的垂直平分线相交于点 D ， DE ⊥AB ， DF ⊥ AC ，垂足分别为 E、 F，AB =6 ， AC =3 ，则 BE= ___________．17．如图，△ ABC 中，∠ ACB ＝ 90°，AC ＝6cm， BC＝ 8cm．点 P 从 A 点出发沿 A→ C→ B终点为 B 点；点Q 从 B 点出发沿B→C→ A 路径向终点运动，终点为 A 点．点 P 和 Q 分别以1cm/ 秒和 3cm/ 秒的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过 P 和 Q 作 PE⊥ l 于 E，QF⊥ l 于 F．设运动时间为（t秒），当t＝________秒时，△ PEC 与△ QFC 全等．三、认真答一答（本大题八题，共56 分）18.（本题满分 7 分）如图，点 B、 F、 C、E 在一条直线上， FB=CE， AC=DF ，请从下列三个条件：①AB=DE ；②∠ A=∠ D；③∠ ACB=∠ DFE 中选择一个合适的条件，使．．AAB∥ ED 成立，并给出证明．(1) 选择的条件是(填序号 )CE(2) 证明：B FD19．（本题满分 6 分）如图，阴影部分是由5 个小正方形组成的一个直角图形，请用3 种方法分别在下图方格内添涂黑二个小正方形，使它们成为轴对称图形．20、（本题满分6 分）如图，在所给网格图（每小格均为边长是 1 的正方形）中完成下列各题： (1) 画出格点△ ABC（顶点均在格点上）关于直线DE对称的△ A1B1C1；(2)在直线 DE上画出点 Q，使QA QC最小．C DA B21、（本题满分 6 分）如图，校园有两条路OA、OB，在交叉口附近有两块宣传牌C、D，学校准备E在这里安装一盏路灯，要求灯柱的位置 P 离两块宣传牌一样远，并且到两条路的距离也一样远，请你用尺规作出灯柱的位置点 P。

2017—2018学年度第一学期期末检测试卷八年级数学A 卷 B 卷题号一二三2324252627总 分得分A 卷（100分）一、选择题（每小题4分，共40分）1、-8的立方根为 （ ）A ．2B ．-2C ．±2D ．±42、实数, -π, , , 0, 3 , 0.1010010001……中，无理数的71132-4个数是 （ ）A ．2B ．3C ．4D ．53、下列图形中是中心对称图形的为 （ ）4、下列运算正确的是 （ ）A. B. C. D.623a a a =⨯633x x =）（1055x x x =+3325b a ab ab -=-÷-）（）（5、分解因式结果正确的是 （ ）32b b a -A 、B 、C 、D 、)(22b a b -2)(b a b -))((b a b ab -+))((b a b a b -+6、通过估算，估计 76 的大小应在 （ ）A ．7～8之间B ．8.0～8.5之间C ．8.5～9.0之间D ．9～10之间7、下列图形中是旋转对称图形有 （ ）①正三角形 ②正方形 ③三角形 ④圆 ⑤线段A.个B.个C.个D.个54328、已知a 、b 、c 是三角形的三边长，如果满足，则0108)6(2=-+-+-c b a 三角形的形状是 （ ）A ．底与边不相等的等腰三角形B ．等边三角形C ．钝角三角形D ．直角三角形9、如图：在菱形ABCD 中，AC=6，BD=8，则菱形的边长为 （ ）A ．5B ．10C ．6D ．810、如图，□ABCD 中，对角线AC 和BD 交于O ，若AC =8，BD =6，则AB 长的取值范围是 （ ）A ．B ．71<<AB 42<<AB C ．D ．86<<AB 43<<AB 二、填空题（每小题4分，共32分）11、的算术平方根是________;3612、.计算： .()[]=+-222322221n m mn n m 13、多项式是完全平方式，则m = .6422++mx x 14、如图,在平行四边形ABCD 中,EF∥AD,GH∥AB,EF 、GH10题图9题图相交于点O,则图中共有____ 个平行四边形.15、已知，如图，网格中每个小正方形的边长为1，则四边形ABCD 的面积为 .16、已知：等腰梯形的两底分别为和，一腰长为，则它的对cm 10cm 20cm 89角线的长为 ．cm 17、□中，是对角线，且，，则ABCD BD BD BC =︒=∠70CBD =∠ADC 度．三、解答题（共28分）19、（每小题4分，共8分）因式分解（1） （2）22916y x -22242y xy x +-20、(本题8分) 先化简，再求值:，其中()()()()224171131x x x x +--++-12x =-15题图18题图A B CD 14题H G F EO21、（每小题3分，共6分）在如图的方格中，作出△ABC 经过平移和旋转后的图形：（1）将△ABC 向下平移4个单位得△；C B A '''（2）再将平移后的三角形绕点顺时针方向旋转90度。

2017—2018学年度上学期第一次质量监测八 年 数 学（时间：90分钟 满分： 100分） 一. 选择题（本大题共10小题，每小题2分，共20分）. 1. 下列实数中，是无理数的是A. 0 B .2 C .-2 D.72 2. 在平面直角坐标系中，一次函数y=kx ＋b示，观察图像可得A. 0>k ，0>b B. 0>k ，0<b C. 0<k ，0>b D. 0<k ，0<b 3. 9的算数平方根是A. 3B. -3C. ±3D. 3 第2题图 4.“赵爽炫图”巧妙地利用面积关系证明了勾股定理，是 我国古代数学的骄傲，如图所示的“赵爽炫图”是由四个 全等直角三角形和一个小正方形拼成的一个大正方形， 设直角三角形较长直角边长为a ,较短直角边长为b ，若21)(2=+b a ，大正方形的面积为13，则小正方形的边长为 第4题图A. 3B. 2C. 5D. 6 5. 估计41的值在A. 4和5之间B. 5和6之间C. 6和7之间D.7和8之间 6. 如图，等腰直角OAB ∆的斜边OA 在x 轴上，且2=OA ,则点B 坐标为 A. (1， 1) B. (2, 1) C.(2, 2) D. (1，2) 7. 已知一次函数2+=kx y 的图象经过点（3，-3），则k 值为A.35 B. 35- C. 53 D.53- 8. 小学我们就知道：四边形具有不稳定性，如图，在平面直角坐标系中，边长为2的正方形ABCD 的边长AB 在x 轴上，AB 的中点是坐标原点O ,固定点A 、B ，把正方形沿箭头方向推，使点D 落在y 轴正率轴上点D 处，则点C 的对应点C 的坐标为 A. (3, 1) B. (2， 1) C. (1， 3) D.(2，3)9. 已知一次函数x m kx y 2--=的图象与y 轴的负半 第8题图 轴相交，且函数值y 随自变量x 的增大而减小，则下列 结论正确的是A. 2<k ,0>mB. 2<k ,0<mC. 2>k ,0>mD. 0<k ,0<m 10. 如图是边长为10cm 的正方形铁片，过两个顶点减掉一个三角形，以下四种剪法中，裁剪线长度所标的数据（单位：cm)不正确的是A B C D 第10题图 二、填空题（本大题共6小题，每小题2分，共12分） 11. 若正比例函数kx y =(k 是常数，0≠k ）的图像经过第二、四象限，则k 的值可以是____▲____.(写出一个即可）. 12. =-++3131______▲___.13. 在平面直角坐标系xOy 中，点A 的坐标为（3,4）， 第14题图则OA 长为____▲_____.14. 如图，已知圆柱的底面直径π6=BC ,高3=AB ,小虫在圆柱表面爬行，从点C 爬到点A ，然后在沿另一面爬回点C ，则小虫爬行的最短路程为______▲_____. 第15题图 15. 如图，在长方形ABCD 中，8=BC ,6=CD .、点E 在边AD 上，将△ABE 沿着BE 折叠，使点A 恰好落在对角线BD 上点F 处，则DE 的长是____▲_______. 16. 如图，在平面直角坐标系中，直线I 与x 轴交于点1B ,与y 轴交点于D ,且11=OB ,601=∠ODB °,以 1OB 为边长作等边三角形11OB A ,过点1A 作21B A 平行于x 轴，交直线I 于点2B ,以21B A 为边长作等边三角 第16题图 行212B A A ,过点2A 作32B A 平行于x 轴，交直线I 于 点3B ,以2A 3B 为边长坐等三角形323B A A ,…，则点10A 的横坐标是_____▲______.三、解答题（每题6分，共18分） 17. 计算：22)2(8)12(-+-+，（将答案写在答题卡上，不要在此处答题） 18. 如图，ABC ∆的边2=AC ,22=BC ,60=∠C °,求边AB 的长.（将答案写在答题卡上，不要在此处答题） 第18题图19.一次函数m x y +-=2的图像经过点)3,2(-P ,且与x 轴、y 轴分别交与点A 、B ,求 △AOB 的面积.（将答案写在答题卡上，不要在此处答题） 四、（每题6分，共12分）20. 如图，在平面直角坐标系xOy 中，ABC ∆的 顶点,A ,B C 均在正方形网格的格点上， （1）画出ABC ∆关于y 轴的对称图形111C B A ∆: （2）画出111C B A ∆关于x 轴的对称图形222C B A ∆,并直接写出222C B A ∆的顶点2A ,2B ,2C 的坐标. 第20题图 （将答案写在答题卡上，不要在此处答题）21. 如图，已知ABC ∆≌C B A '''∆, 其中点A '与点A 重合， 点C 落在边AB 上，连接C B '.若90=''∠=∠B C A ACB °3==BC AC ,求C B '的长.（将答案写在答题卡上，不要在此处答题）（本题8分）22. 某数学兴趣小组根据学习函数的经验，对函数 第21题图1-=x y 的图象与性质进行了探究，下面是该小组的探究过程，请补充完整：ABC∙)(A '(1)函数1-=x y 的自变量x 的取值范围是____▲____: (2)列表，找出y 与x 的几组对应值：其中，=b ___▲____:(3)在平面直角坐标系xOy 中，描出以上表中对应值为坐标的点，并画出该函数的图像. 第22题图 （将答案写在答题卡上，不要在此处答题） 六、（本题8分）23. 对于实数p ，q ，我们用符号{}q p ,max 表示q p ,两数中较大的数，如{}22,1max =，（1）请直接写出{}3,2max --的值： （2）我们知道，当12=m 时，=m ±1，利用这种方法解决下面问题：若{}4,)1(max 22=-x x ，求x 的值.（将答案写在答题卡上，不要在此处答题） 七、（本题10分）24. 一辆轿车从甲城驶往乙城，同时一辆卡车从乙城驶往甲城，两车沿相同路线匀速行使，轿车到达乙城停留一段时间后，按原路原速 返回甲城：卡车到达甲城比轿车返回甲城早 0.5小时，轿车比卡车每小时多行使60千米， 两车到达甲城后均停止行使，两车之间的路程为y （千米）与轿车行使时间t （小时）的函 第24题图 数图象如图所示，请结合图象提供的信息解答下列问题：（1）甲城 和乙城之间的路程为_____▲_____千米，并求出轿车和卡车的速度： （2）轿车在乙城停留的时间为____▲____小时，点D 的坐标为_____▲_____,:（3）请直接写出轿车从乙城返回甲城过程中离甲城的路程s （千米）与轿车行使时间t （小时）之间的函数关系式（不要求写出自变量的取值范围）. （将答案写在答题卡上，不要在此处答题） 八、（本题12分）25.阅读理解：在以后你的学习中，我们会学习一个定理：直角三角形斜边上的中线等于斜边的一半，即：如图1， 在ACB Rt ∆中，90=∠ACB °,若点D 是斜边AB 的中点， 则AB CD 21=. 第25题图1 灵活应用：如图2，ABC ∆中，90=∠BAC °,3=AB ,4=AC ,点D 是BC 的中点， 将ABD ∆沿AD 翻折得到AED ∆,连接BE ,CE . （1）求AD 的长： （2）判断BCE ∆的形状： （3）请直接写出CE 的长.（将答案写在答题卡上，不要在此处答题） 第25题图2一、选这题（本大题共10小题，每小题2分，共20分）二、填空题（本大题共6小题，每小题2分，共12分）11. ____________ 12. ____________ 13. ___________14. ____________ 15. ____________ 16. ___________三、解答题（每题6分，共18分） 17.()()222812-+-+4221222+-++= 7=322102355262-18. 作 223=-=∴CD BC BD 90=∠ADC ° ,60=∠C ° =在ABD Rt ∆中90=∠ADB °30=∠∴CAD ° 由勾股定理得22221==∴CD 222AB BD AD =+∴在ACD Rt ∆中，90-∠ADC ° 6=∴AB 由勾股定理得26222=∴=-∴AD AD CD AC19.把,2(-p )3带入 当0=x 时 1-=y143)2(23-=+=+--=m mmBOAO AOB S .21=∆ 12--=x y当0=y 时21120-=--=x x四、（每题6分，共12分）20. （1）如图111C B A ∆即为所求. （2）如图222C B A ∆即为所求.)2,1()2,4()3,2(222-----C B A 第20题图21. 90=∠ACB °,3==BC AC 在B C A Rt ''∆中，90='∠B CA ° ACB ∆∴为等腰直角三角形 由勾股定理得45=∠=∠∴CAB CAB ° 222C B B A AC '=''+∴ABC ∆ ≌C B A '''∆ 33='∴C B4114112121=⨯=⨯⨯=BCAD ⊥3=''=''∴C B C AB C A '''∆∴为等腰直角三角形 45='''∠='''∠∴C B A B A C ° B A C B A C B CA '''∠+'∠='∠ 90='∠∴B CA °在C B A Rt '''∆中，90='''∠B C A ° 由勾股定理得222B A C B C A ''='+'∴ 23=''∴B A 五、（本题8分） 22. （1）任意实数（2）2（3）如图即为所求第22题图六、（本题8分）（1）{}3,2max --的值为2-。