确定摆动从动件盘形凸轮基圆半径的一种简易方法
- 格式:doc
- 大小:26.50 KB
- 文档页数:2

机械原理课程设计目录1.设计题目及要求--------------------------------------------------------------------P32.设计目的------------------------------------------------------------------------------P33.设计过程与思路----------------------------------------------------------------------P44.从动件运动规律设计--------------------------------------------------------------P55.凸轮基本尺寸设计-------------------------------------------------------------------P86.凸轮廓线设计------------------------------------------------------------------------P97.校核压力角和凸轮廓线是否出现运动失真现象------------------------P108.改进设计------------------------------------------------------------------------------P119.绘制机构工作图-------------------------------------------------------------------P1110.结束语--------------------------------------------------------------------------------P12 附录及参考文献:机械原理课本机械原理课程ppt,pdf1. 设计题目及要求某技术人员欲设计一台打包机,其推送包装物品的机构如图所示。

机械原理课程教案一凸轮机构及其设计一、教学目标及基本要求1了解凸轮机构的基本结构特点、类型及应用,学会根据工作要求和使用场合选择凸轮机构。
2.了解凸轮机构的设计过程,对凸轮机构的运动学、动力学参数有明确的概念。
3.掌握从动件常用运动规律的特点及适用场合,了解不同运动规律位移曲线的拼接原则与方法。
4.掌握凸轮机构基本尺寸设计的原则,学会根据这些原则确定移动滚子从动件盘形凸轮机构的基圆半径、滚子半径和偏置方向,摆动从动件盘形凸轮机构的摆杆长、中心距以及移动平底从动件平底宽度。
5.熟练掌握应用反转法原理设计平面凸轮廓线,学会凸轮机构的计算机辅助设计方法。
二、教学内容及学时分配第一节概述第二节凸轮机构基本运动参数设计第三节凸轮机构基本尺寸设计(第一、二、三节共2学时)第四节凸轮轮廓曲线设计(15学时)第五节凸轮机构从动件设计(1学时)第六节凸轮机构的计算机辅助设计(0.5学时)三、教学内容的重点和难点重点:1.凸轮机构的型式选择。
2.从动件运动规律的选择及设计。
3.盘形凸轮机构基本尺寸的设计,凸轮轮廓曲线设计的图解法和解析法。
4.从动件的设计,包括高副元素形状选择,滚子半径和平底宽度的确定。
难点:凸轮轮廓曲线设计的图解法四、教学内容的深化与拓宽空间凸轮机构与高速凸轮机构简介。
五、教学方式与手段及教学过程中应注意的问题充分利用多媒体教学手段,围绕教学基本要求进行教学。
在教学过程中应强调凸轮机构的运动学参数与结构参数的概念及其选用设计;应用反转法原理进行凸轮轮廓曲线的图解法设计时凸轮转角的分度,要注意从动件反转方向;正确确定偏置移动从动件凸轮机构在反转过程中从动件所依次占据的位置线;滚子从动件凸轮机构理论轮廓曲线与实际轮廓曲线的联系和区别等。
要注意突出重点,多采用启发式教学以及教师和学生的互动。
六、主要参考书目1黄茂林,秦伟主编.机械原理.北京:机械工业出版社,2010 2申永胜主编.机械原理教程(第2版).北京:清华大学出版社,20053孙桓,陈作模、葛文杰主编.机械原理(第七版).北京:高等教育出版社,20064石永刚,徐振华.凸轮机构设计.上海:上海科学技术出版社,1995七、相关的实践性环节凸轮机构运动参数测试实验。


第三节 盘形凸轮廓线的设计当根据工作要求和结构条件选定了凸轮机构的类型、从动件的运动规律和凸轮的基圆半径(其确定将在下节中介绍)等结构参数后,就可以设计凸轮的轮廓曲线。
凸轮廓线的设计方法有图解法和解析法,其设计原理基本相同。
本节先简要介绍图解法,后重点介绍解析法设计凸轮廓线。
一、凸轮廓线设计的基本原理图4-13 反转法设计凸轮廓线基本原理图4-13所示为一尖顶对心盘形凸轮机构,设凸轮以等角速度ω逆时针转动,推动从动件2在导路中上、下往复移动。
当从动件处于最低位置时,凸轮轮廓曲线与从动件在A 点接触,当凸轮转过1ϕ角时,凸轮的向径A A 0将转到A A '0位置,而凸轮轮廓将转到图中虚线所示的位置。
从动件尖端从最低位置A 上升至B ',上升的位移为B A S '=1,这是从动件的运动位移。
若设凸轮不动,从动件及其运动的导路一起绕A 0点以等角速度-ω转过1ϕ角,从动件将随导路一起以角速度-ω转动,同时又在导路中作相对导路的移动,如图中的虚线位置,此时从动件向上移动的位移为B A 1。
而且,11S B A B A ='=,即在上述两种情况下,从动件移动的距离不变。
由于从动件尖端在运动过程中始终与凸轮轮廓曲线保持接触,所以从动件尖端的运动轨迹即为凸轮轮廓。
设计凸轮廓线时,可由从动件运动位移先定出一系列的B 点,将其连接成光滑曲线,即为凸轮廓线。
由于这种方法是假设凸轮固定不动而使从动件连同导路一起反转,故称为反转法。
对其它类型的凸轮机构,也可利用反转法进行分析和凸轮廓线设计。
二、图解法设计凸轮廓线1. 移动从动件盘形凸轮廓线的设计(1)尖端从动件 图4-14a 所示为一偏置移动尖端从动件盘形凸轮机构。
设已知凸轮的基圆半径为b r ,从动件导路偏于凸轮轴心A 0的左侧,偏距为e ,凸轮以等角速度ω顺时针方向转动。
从动件的位移曲线如图4-14b 所示,试设计凸轮的轮廓曲线。
图4-14 尖端从动件盘形凸轮廓线设计依据反转法原理,具体设计步骤如下。

所属标签:产品外观设计根据使用要求确定了凸轮机构的类型、基本参数以及从动件运动规律后,即可进行凸轮轮廓曲线的设计。
设计方法有几何法和解析法,两者所依据的设计原理基本相同。
几何法简便、直观,但作图误差较大,难以获得凸轮轮廓曲线上各点的精确坐标,所以按几何法所得轮廓数据加工的凸轮只能应用于低速或不重要的场合。
对于高速凸轮或精确度要求较高的凸轮,必须建立凸轮理论轮廓曲线、实际轮廓曲线以及加工刀具中心轨迹的坐标方程,并精确地计算出凸轮轮廓曲线或刀具运动轨迹上各点的坐标值,以适合在数控机床上加工。
圆柱凸轮的廓线虽属空间曲线,但由于圆柱面可展成平面,所以也可以借用平面盘形凸轮轮廓曲线的设计方法设计圆柱凸轮的展开轮廓。
下面时间财富网的小编分别介绍用几何法和解析法设计凸轮轮廓曲线的原理和步骤。
1 几何法反转法设计原理:以尖底偏置直动从动件盘形凸轮机构为例:凸轮机构工作时,凸轮和从动件都在运动。
为了在图纸上画出凸轮轮廓曲线,应当使凸轮与图纸平面相对静止,为此,可采用如下的反转法:使整个机构以角速度(-w)绕O转动,其结果是从动件与凸轮的相对运动并不改变,但凸轮固定不动,机架和从动件一方面以角速度(-w)绕O转动,同时从动件又以原有运动规律相对机架往复运动。
根据这种关系,不难求出一系列从动件尖底的位置。
由于尖底始终与凸轮轮廓接触,所以反转后尖底的运动轨迹就是凸轮轮廓曲线。
1). 直动从动件盘形凸轮机构尖底偏置直动从动件盘形凸轮机构:已知从动件位移线图,凸轮以等角速w顺时针回转,其基圆半径为r0,从动件导路偏距为e,要求绘出此凸轮的轮廓曲线。
运用反转法绘制尖底直动从动件盘形凸轮机构凸轮轮廓曲线的方法和步骤如下:1) 以r0为半径作基圆,以e为半径作偏距圆,点K为从动件导路线与偏距圆的切点,导路线与基圆的交点B0(C0)便是从动件尖底的初始位置。
2) 将位移线图s-f的推程运动角和回程运动角分别作若干等分(图中各为四等分)。
授课教案No任务3.1 凸轮机构的认识一、复习10分钟复习上次课学习内容二、教师导课与课程学习:(1)学习提示,教师介绍本任务的学习内容。
15分钟本项目以直动从动件的盘形凸轮机构为例,在从动件等速运动、等加速等减速运动、余弦加速度运动(简谐运动)规律条件下,分析了凸轮机构中存在的柔性冲击与刚性冲击。
教师介绍本任务的学习内容:凸轮机构的分类;常用术语;从动件的运动规律;凸轮机构的结构形式;常用材料及热处理(2)分小组学习: 40分钟3.1.1常用设备中的凸轮机构1. 凸轮机构的组成如图所示的凸轮机构是由凸轮、从动件和机架等三个基本构件组成的机构。
2.凸轮机构应用实例自动钻床进给机构、冲床凸轮机构等。
3.1.2凸轮机构的分类凸轮机构的类型很多,按凸轮和从动件的形状及其运动形式的不同,凸轮机构的分类方法有以下几种:1.按凸轮形状分类(1)盘形凸轮(2)移动凸轮。
(3)圆柱凸轮2.按从动件形式分类(1)尖顶从动件(2)滚子从动件(3)平底从动件从动件的结构形式3.按从动件的运动形式分类学生发言汇报、记录学习笔记学生发言汇报并记录学习笔记阅读教材和PPT、分组讨论、撰写发言提纲、学生发言汇报,课,记录学习笔记No(1)直动从动件直动从动件指相对于机架作直线往复移动的从动件,如图3.1.1中所示。
直动从动件又分为对心直动从动件和偏置直动从动件。
(2)摆动从动件:绕某一固定转动中心摆动的从动件。
4.按凸轮与从动件的锁合方式分类 (1)力锁合利用从动件的重力、弹簧力或其他外力使从动件与凸轮轮廓保持接触,(2)形锁合利用从动件和凸轮特殊的几何形状来维持接触,例如圆柱凸轮机构是利用滚子与凸轮凹槽两侧面的配合来实现形锁合。
3.1.3凸轮机构的常用术语如下:1.凸轮基圆与基圆半径b r2.凸轮的转角δ凸轮相对于某一位置转过的角度,称为凸轮转角δ。
具体包括推程运动角0δ、远停程运动角S δ回程运动角0′δ和近停程运动角Sδ'。


摆动滚子从动件盘形凸轮机构设计的解析法①0前言摆动滚子从动件盘形凸轮机构的设计主要包括基本尺寸的确定[ 1 ]和凸轮轮廓的设计. 基本尺寸主要是根据压力角确定的, 凸轮轮廓是根据基本尺寸和从动件的运动规律设计的. 过去这两部分的设计常常采用图解法, 虽然图解法简单、直观, 但精度低, 随着计算机技术的发展和数控机床的普及, 凸轮机构设计的解析法[ 2 ]正逐步取代传统的图解法.图1摆动从动件盘形凸轮机构的压力角1机构压力角的计算如图1 所示, 为摆动从动件盘形凸轮机构的压力角示意图. 摆杆长度O 2A = l, 机架长O 1O 2 = a.过瞬心P 作摆杆O 2A 的垂直线, 交O 2A延长线于B 点. 则有:tan A= BAPB=O 2P cos (W0 + W) - lO 2P sin (W0 + W)P 点为机构的瞬心, 则有: X1O 1P = X2O 2PX2X1=O 1PO 2P=d Wd U=O 1PO 1P + a∴O 1P =d Wd U a1 -d Wd UO 2P = O 1P + a = a1 -d Wd U∴tan A=a cos (W0 + W) - l (1 -d Wd U)a sin (W0 + W)上式是按X1 和X2 同向推出的, 否则tan A=a cos(W0 + W) - l (1 +d Wd U)a sin (W0 + W)工程设计中, 必须对凸轮机构的最大压力角加以限制, 凸轮机构的最大压力角应小于许用压力角.2机构基本尺寸的确定图2确定基本尺寸示意图2. 1基本尺寸确定的方法图2 中O 2 为摆杆的回转中心,A 为滚子摆杆的滚子中心. A 0 到A 6 为按给定运动规律W= f (U) 作出的摆杆各个位置, 位置个数可任选. 在摆杆的每位置上截取长为ld Wd U,其中l 为摆杆长, W为摆杆摆角, U为凸轮转角.截取方法为: 若摆杆与凸轮转向相同, 由A 点向着回转中心O 2 取; 若摆杆与凸轮转向相反, 由A 点背着回转中心O 2 取.图2 中凸轮与摆杆的相对转动关系为: 凸轮逆时针转,摆杆推程逆时针转, 回程顺时针转. 若推程许用压力角为[A], 回程许用压力角为[A′], 线段A 1a1,A 2a2, ⋯为对应推程截取的; 线段A 1a′1,A 2a′2, ⋯为对应回程截取的. 过端点a1, A2, ⋯和a′1 , a′2, ⋯作与相应的摆杆成(90°- [A]) 或(90°- [A]) 的直线, 简称a 斜线和a′斜线. 这些线的包络线É , Ê , Ë 所包围的阴影区域为满足许用压力角的前提下, 凸轮回转中心的可选区域. O ′1A 0 为最小基圆半径,O ′1O 2 为对应的中心距.以O 2 为原点,O 2A 0 为x 轴, 使A 1,A 2, ⋯各点y 坐标为正值的方向为y 轴, 建立直角坐标系. 若已知包络线É , Ê , Ë 的方程, 则可知凸轮回转中心O 1 的许用区域.2. 2包络线方程的求法及基本尺寸的确定在图2 中, 任意a 斜线的斜率为k = tan A= cot (- [A] - W) , 各a 点的坐标为:x = l (1 -d Wd U cos W) , y = l (1 -d Wd U) sin W, 由点斜式可写出任意a 斜线的方程. 同理, 对任意a′斜线, 斜率为k′= cot ( [A] - W) , 各a′点的坐标为: x ′= l (1 +d Wd U) cos W, y ′= l (1 +d Wd U) sin W, 同样可写出任意a′斜线的方程.由以上包络线方程相交, 可求出凸轮回转中心O 1 的许用区域, 此过程较繁, 可上机求解. 在O 1 的取值范围内任取一点(x , y ) 作为凸轮的回转中心, 则凸轮的基圆半径可确定:图3反转法设计凸轮的轮廓r0 = ( l - x ) 2 + y 2.3凸轮轮廓的设计图3 中, 直角坐标系的原点位于凸轮的回转中心O 1 点. 机架长为a, 摆杆长为l. 摆动滚子从动件的初始位置在行程起始位置1 时的O 20A 0. 反转U角后, 到达位置2 的O 2A. 凸轮与从动件的接触点A 0 到达A 点,A ′A为对应的弧位移s, 对应从动件的摆角W.从动件O 2A的运动可以看作O 20A 0 绕O 1 点反转U角, 到达O 2A ′位置,O 2A ′再摆动W角到达O 2A 位置. 从动件O 2A 的运动还可以看作O 20A 0 绕O 20 点反转(U+ W) 角, 到达O 20A ″点,O 20A ″再平移到O 2A 位置. 设A 0 点的坐标为(x A 0,第1 期毕艳丽等: 摆动滚子从动件盘形凸轮机构设计的解析法37y A 0) ,A 点的坐标为(x , y ) ,O 2A 的复合运动可用下述的坐标旋转和平移变换来实现.y=cos(U+ W) sin (U+ W)- sin (U+ W) cos (U+ W)x A 0 - x O20y A 0 - y O20+x O2y O2(1)式中: x O 2 = a sin U, y O 2 = a co s U, x O20 = 0, y O20 = a, x A 0 = - l sin W 0, y A 0 = a - l co s WW0 为摆杆的初始位置角, 其值为W0 = arccosa2 + l2 - r202al将其代入方程(1) 并整理, 可得理论廓线方程:x = a sin U- l sin (U+ W+ W0) ; y = a cos U- l cos (U+ W+ W0)则其实际廓线方程[ 2 ] 为:x A= x ±r rd yd Ud xd U2+d yd U2, y A= y ºr rd xd Ud xd U2d yd U2其中r r 为滚子半径; 滚子圆的包络线有两条, 上面一组符号用于求解外凸轮的包络线方程, 下面一组符号用于求解内凸轮的包络线方程.4结束语本文利用解析法设计摆动滚子从动件盘形凸轮机构, 适用于用计算机辅助运算设计凸轮机构, 其精度高, 使用方便, 特别适合高精度凸轮机构的设计.参考文献:[ 1 ]尚锐等. 摆动从动件盘形凸轮机构基本尺寸确定的解析法[J ]. 辽宁工学院学报, 1999, (6) : 29- 32.[ 2 ]邹慧君等. 机械原理[M ]. 北京: 高等教育出版社, 1999, 117- 132.。


《南昌工程学院机械设计基础》习题与解答一、选择题1. 曲柄摇杆机构中,摇杆为主动件时,B 死点位置。
(A)不存在(B)曲柄与连杆共线时为(C)摇杆与连杆共线时为2. 曲柄摇杆机构中,曲柄为主动件时,C 死点位置。
(A)曲柄与连杆共线时(B)摇杆与连杆共线时(C)不存在3. 为保证四杆机构良好的机械性能,B不应小于最小许用值。
(A)压力角;(B)传动角(C)极位夹角4. 平面四杆机构无急回特性时的行程速比系数C。
(A)K>1 (B)K<1 (C)K=15. 在双曲柄机构中,已知三杆长度为a=80mm,b=150mm,c=120mm,则d杆长度为B 。
(A)<110mm (B)110mm≤d≤190mm (C)≥190mm6. 凸轮机构中的压力角是指A 间的夹角。
(A)凸轮上接触点的法线与从动件的运动方向(B)凸轮上接触点的法线与该点线速度(C)凸轮上接触点的切线与从动件的运动方向7. B 决定了从动杆的运动规律。
(A)凸轮转速(B)凸轮轮廓曲线(C)凸轮形状8. 凸轮机构中,基圆半径是指凸轮转动中心至_C_向径。
(A)理论轮廓线上的最大(B)实际轮廓线上的最大(C)理论轮廓线上的最小(D)实际轮廓线上的最小9. 在曲柄滑块机构中,当取滑块为原动件时,_C_死点位置。
(A)有一个(B)没有(C)有两个(D)有三个10.对于铰链四杆机构,当满足杆长之和的条件时,若取__C_为机架,将得到双曲柄机构。
(A)最长杆(B)与最短杆相邻的构件(C)最短杆(D)与最短杆相对的构件11.曲柄摇杆机构中,曲柄为主动件,则传动角是_B_。
(A)摇杆两个极限位置之间的夹角(B)连杆与摇杆之间所夹锐角(C)连杆与曲柄之间所夹锐角(D)摇杆与机架之间所夹锐角15.拧紧螺母时的功率主要与螺纹的D有关。
(A)升角(B)线数(C)螺距和牙型角(D)升角和牙型角16.螺纹联接是一种A。
(A)可拆联接(B)不可拆联接(C)具有防松装置的为不可拆联接,否则为可拆联接(D)具有自锁性能的为不可拆联接,否则可拆17.被联接件受横向外力时,如采用普通螺纹联接,则螺栓可能失效的形式为B 。
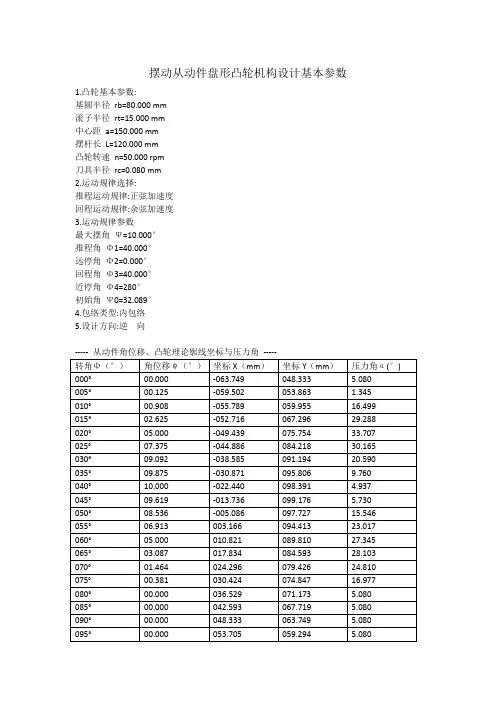
摆动从动件盘形凸轮机构设计基本参数
1.凸轮基本参数:
基圆半径rb=80.000 mm
滚子半径rt=15.000 mm
中心距a=150.000 mm
摆杆长L=120.000 mm
凸轮转速n=50.000 rpm
刀具半径rc=0.080 mm
2.运动规律选择:
推程运动规律:正弦加速度
回程运动规律:余弦加速度
3.运动规律参数
最大摆角Ψ=10.000°
推程角Φ1=40.000°
远停角Φ2=0.000°
回程角Φ3=40.000°
近停角Φ4=280°
初始角Ψ0=32.089°
4.包络类型:内包络
5.设计方向:逆向
推程最大压力角: 033.707 回程最大压力角: 028.257
-----参数说明-----
Φ-凸轮转角(°)
Xa、Ya-实际廓线坐标(mm)
ρb-理论廓线曲率半径(mm)
ρa-实际廓线曲率半径(mm)
曲率半径:“-”曲线外凸,“+”曲线内凹Xc、Yc-刀具中心轨迹坐标(mm)。
第03章 凸轮机构及其设计一、填空题1.凸轮机构中的压力角是 和 所夹的锐角。
2.凸轮机构中,使凸轮与从动件保持接触的方法有 和 两种。
3.在回程过程中,对凸轮机构的压力角加以限制的原因是 。
4.在推程过程中,对凸轮机构的压力角加以限制的原因是 。
5.在直动滚子从动件盘形凸轮机构中,凸轮的理论廓线与实际廓线间的关系是 。
6.凸轮机构中,从动件根据其端部结构型式,一般有 、 、 等三种型式。
7.设计滚子从动件盘形凸轮机构时,滚子中心的轨迹称为凸轮的 廓线;与滚子相包络的凸轮廓线称为 廓线。
8.盘形凸轮的基圆半径是 上距凸轮转动中心的最小向径。
9.根据图示的ϕϕ-22d d s 运动线图,可判断从动件的推程运动是_____________,从动件的回程运动是______________。
题9图10.从动件作等速运动的凸轮机构中,其位移线图是 线,速度线图是 线。
11.当初步设计直动尖顶从动件盘形凸轮机构中发现有自锁现象时,可采用 、 、 等办法来解决。
12.在设计滚子从动件盘形凸轮轮廓曲线中,若出现 时,会发生从动件运动失真现象。
此时,可采用 方法避免从动件的运动失真。
13.用图解法设计滚子从动件盘形凸轮轮廓时,在由理论轮廓曲线求实际轮廓曲线的过程中,若实际轮廓曲线出现尖点或交叉现象,则与 的选择有关。
14.在设计滚子从动件盘形凸轮机构时,选择滚子半径的条件是 。
15.平底从动件盘形凸轮机构中,凸轮基圆半径应由 来决定。
16.凸轮的基圆半径越小,则凸轮机构的压力角越 ,而凸轮机构的尺寸越 。
17.凸轮基圆半径的选择,需考虑到、,以及凸轮的实际廓线是否出现变尖和失真等因素。
18.在许用压力角相同的条件下,从动件可以得到比从动件更小的凸轮基圆半径。
或者说,当基圆半径相同时,从动件正确偏置可以凸轮机构的推程压力角。
19.直动尖顶从动件盘形凸轮机构的压力角是指;直动滚子从动件盘形凸轮机构的压力角是指;而直动平底从动件盘形凸轮机构的压力角等于。
1-1.图题1-1是由点(线)接触所构成的运动副。
试分析计算它们的自由度数量和性质,并从封闭形式和受力状况与相对应的面接触低副进行比较1-2.观察分析工作原理,绘制机构运动简图,计算机构自由度。
题图1-2a为一夹持自由度。
实线位置为从上输送带取出工件(夹头处于夹紧状态);虚线位置为将工件放到下输送带上(夹头松开)。
该机构是由行星轮系、凸轮机构及连杆机构组合而成。
题图1-2b是为了减小活塞与汽缸盖之间的摩擦而设计的一种结构形式的内燃机,画出它们的机构运动简图、计算其自由度。
分析结构中存在的虚约束和它们是如何来实现减小摩擦这一目的的。
题图1-2c为一种型式的偏心油泵,画出其机构运动简图,计算其自由度,并分析它们是如何由运动简图演化得到的。
题图1-2d为针织机的针杆驱动装置的结构示意图,绘制其机构运动简图及运动链图。
1-3.用公式推导法,求出F=1、N=10的单铰运动链的基本结构方案以及它们的单铰数和所形成的闭环数k,并从中找出图1-17所示的双柱压力机构简图所对应的运动链。
1-4.计算下列各机构的自由度。
注意分析其中的虚约束、局部自由度合复合铰链等。
题图1-4a为使5、6构件能在相互垂直方向上作直线移动的机构,其中AB=BC=CD=AD题图1-4b 为凸轮式4缸活塞气压机的结构简图,在水平和垂直方向上作直线运动,其中仍满足AB=BC=CD=AD。
题图1-4c 所示机构,导路AD⊥AC、BC=CD/2=AB。
该机构可有多种实际用途,可用于椭圆仪,准确的直线轨迹产生器,或作为压缩机或机动马达等。
题图1-4d 为一大功率液压动力机。
其中AB=A`B`,BC=B`C`,CD=C`D`,CE=C`E`,且E、E`处于滑块移动轴线的对称位置。
1-5.采用基本杆组法综合运动链和机构。
1)试用Ⅱ级和Ⅲ级基本杆组,综合出如下的瓦特杆链和斯蒂芬逊6杆链。
2)取题图1-5b、stephenson 6杆链中的不同构件为机架和原动件,得出不同级别、不同组合方式得机构。
3-1试分别标出四种凸轮机构在图示位置的压力角α。
a)b)c)d)a)b)c)d)3-2图示尖底直动从动件盘形凸轮机构,C 点为从动件推程的起始点。
完成下列各题:(1)在图上标出凸轮的合理转向;(2)试在图上作出凸轮的基圆与偏心圆,并标注其半径r b 与e ;(3)在图上作出轮廓上D 点与从动杆尖顶接触时的位移s 和压力角α;(4)在原图上画出凸轮机构的推程运动角Φ。
题3-2图3-3由图所示直动盘形凸轮的轮廓曲线,在图上画出此凸轮的基圆半径r b、各运动角即推程运动角Φ、远休止角ΦS、回程运动角Φ′和近休止角Φ′S及从动件升程h。
题3-3图3-4图示的对心滚子从动件盘形凸轮机构中,凸轮的实际轮廓为一圆,圆心在A 点,半径R=40mm,凸轮转动方向如图所示,l OA=25mm,滚子半径r r=10mm,试问:(1)凸轮的理论曲线为何种曲线?(2)凸轮的基圆半径r b=?(3)在图上标出图示位置从动件的位移S,并计算从动件的升距h?(4)用反转法作出当凸轮沿ω方向从图示位置转过90°时凸轮机构的压力角。
题3-4图解:(1)理论轮廓曲线为:以A点为圆心,半径为R+r r的圆。
(2)此时所求的基圆半径为理论轮廓曲线的r b.r b=R-OA+r r=40-25+10=25mm(3)从动件的位移S如图所示。
升程h=R+OA+r r-r b=40+25+10-25=50mm(4)从动件导路沿-ω方向转过90°到B,压力角α'如图中所示。
3-5如图所示偏置移动滚子从动件盘形凸轮机构。
已知凸轮实际轮廓线为一圆心在O 点的偏心圆,其半径为R ,从动件的偏距为e ,试用图解法:(1)确定凸轮的合理转向;(2)画出凸轮的基圆;(3)标出当从动件从图示位置上升到位移s 时,对应凸轮机构的压力角α;(要求量出具体的数值)题3-5图3-8试以作图法设计一偏置直动滚子推杆盘形凸轮机构。
已知凸轮以等角速度逆时针回转,正偏距e =10mm ,基圆半径r 0=30mm ,滚子半径r r =10mm 。
本文作者将确定直动从动件盘形凸轮基圆半径的简易方法推广至摆动从动件凸轮。
根据机械原理,摆动从动件盘形凸轮的压力角满足:
式中:ψ为摆动从动件摆角,ψ。
为初始最小摆角,ψ为凸轮转角,α为压轮中心与摆杆摆动中心的距离,l为摆杆器,α为压力角,[α]为许用压力角。
由于在设计凸轮之前基圆半径还未知,且工程中广泛采用改进型运动规律,一个行程中包含几种曲线,很难由上式求最大压力角。
我们将式(1)整理成:
设函数
显然,当α=[α]时,E(φ)=E max。
仿照E建立另一函数:
因为
故
因此,只要求E1(φ)的最大值E1max:
和基圆半径
新方法的巧妙之处在于事先不知r b即可确定max及其对应转角,不需要反复试算。