图形与几何复习
- 格式:ppt
- 大小:7.50 MB
- 文档页数:12

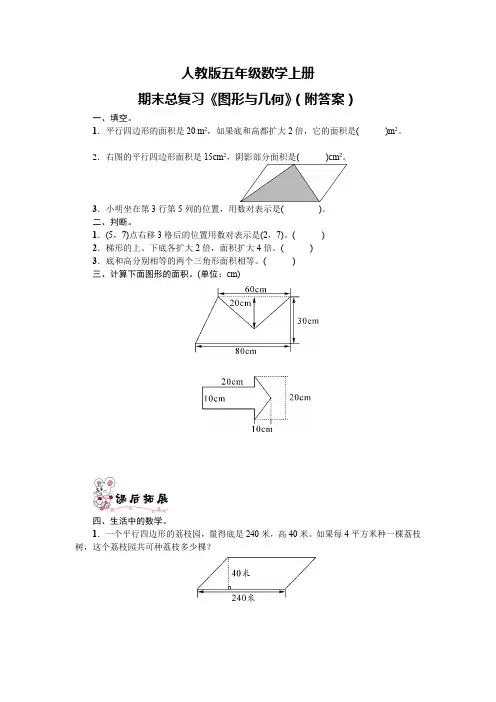
人教版五年级数学上册
期末总复习《图形与几何》(附答案)
一、填空。
1.平行四边形的面积是20 m2,如果底和高都扩大2倍,它的面积是()m2。
2.右图的平行四边形面积是15cm2,阴影部分面积是()cm2。
3.小明坐在第3行第5列的位置,用数对表示是()。
二、判断。
1.(5,7)点右移3格后的位置用数对表示是(2,7)。
()
2.梯形的上、下底各扩大2倍,面积扩大4倍。
()
3.底和高分别相等的两个三角形面积相等。
()
三、计算下面图形的面积。
(单位:cm)
四、生活中的数学。
1.一个平行四边形的荔枝园,量得底是240米,高40米。
如果每4平方米种一棵荔枝树,这个荔枝园共可种荔枝多少棵?
2.一间房子的侧面如下图,如果每平方米用砖190块,砌这堵墙大约需要多少块砖?
五、求下图阴影部分的面积。
(单位:dm)
参考答案
一、1.80 2.7.5 3.5,3
二、1.× 2.× 3.√
三、1500(cm2)300(cm2)
四、1.240×40÷4=2400(棵)答:荔枝园共可种荔枝2400棵。
2.(8×1.5÷2+
3.2×8)×190=(6+25.6)×190=31.6×190=6004(块)答:砌这堵墙大约需要6004块砖。
五、4×7-4×(7-5)÷2=24(dm2)
答:阴影部分的面积是24 dm2。

图形与几何知识点整理图形与几何复习知识点1.点、线、面:点是几何学的基本要素,没有大小和形状;线由无数个点组成,具有长度但没有宽度;面由无数个线组成,具有宽度和长度。
2.基本图形:包括三角形、四边形、多边形、圆、椭圆等。
三角形是由三条边和三个顶点组成的图形;四边形是由四条边和四个顶点组成的图形;多边形是由多条边和多个顶点组成的图形;圆是由一个圆心和等长的半径组成的图形;椭圆是由两个焦点和到焦点的距离之和等于常数的点组成的图形。
3.直线和曲线:直线是由无数个连续的点组成,其上的任意两点可以确定一条直线;曲线是由无数个连续的点组成,其上的任意两点不能确定一条直线。
4.角:角是由两条射线共同的一个端点组成,分为锐角、直角、钝角和平角。
锐角的度数小于90°,直角的度数等于90°,钝角的度数大于90°,平角的度数等于180°。
5.同位角和内错角:同位角是指两条平行线被一条交叉线所切割所形成的一对相对的角;内错角是指两条平行线被一条交叉线所切割所形成的一对非相对的角。
6.相似与全等:两个图形如果形状和大小完全相同,则它们全等;如果形状相同但大小不同,则它们相似。
7.平行四边形性质:平行四边形的对边平行且相等,对角线互相平分。
8.直角三角形性质:直角三角形的两条直角边的平方和等于斜边的平方(勾股定理)。
9.圆的性质:圆的任意一条弦都可以确定一个圆心角,相交的两条弦所对应的圆心角相等,半径相等的两个圆是全等的。
10.平行线和垂直线:平行线是指在同一个平面上永远不相交的线;垂直线是指两条线相交而且相交的角为直角。
11.多边形的内角和:多边形的内角和等于180°乘以(边数-2)。
12.正多边形性质:正n边形的外角和等于360°,内角和等于180°乘以(n-2)。
13.多面体:多面体是指由有一定数量的面、边和顶点构成的立体图形,包括三棱柱、正四棱锥、正八面体、正十二面体等。

图形与几何知识点整理图形与几何复习知识点在数学中,图形和几何是非常重要的部分。
图形是由线条、点和面组成的实体,而几何则是研究这些实体的形状、大小、位置等性质的学科。
掌握图形和几何知识对于解决各种数学问题和生活中的实际问题都非常重要。
在本文中,我们将一些常见的图形和几何知识点整理,希望能够对读者有所帮助。
矩形的定义、性质及判定1.定义:有一个角是直角的平行四边形叫做矩形2.性质:矩形的四个角都是直角,矩形的对角线相等3.判定:(1)有一个角是直角的平行四边形叫做矩形(2)有三个角是直角的四边形是矩形(3)两条对角线相等的平行四边形是矩形4.对称性:矩形是轴对称图形也是中心对称图形。
几何平均数的定义几何平均数是对各变量值的连乘积开项数次方根。
求几何平均数的方法叫做几何平均法。
如果总水平、总成果等于所有阶段、所有环节水平、成果的连乘积总和时,求各阶段、各环节的一般水平、一般成果,要使用几何平均法计算几何平均数,而不能使用算术平均法计算算术平均数。
根据所拿握资料的形式不同,其分为简单几何平均数和加权几何平均数两种形式。
几何平均数的公式几何平均值是n个变量值连乘积的n次方根。
根据所拿握资料的形式不同,其分为简单几何平均数和加权几何平均数两种形式。
简单的几何平均值的计算公式为G=n√X1·X2·…·Xn。
1.几何平均数受极端值的影响较算术平均数小。
2.如果变量值有负值,计算出的几何平均数就会成为负数或虚数。
3.它仅适用于具有等比或近似等比关系的数据。
4.几何平均数的对数是各变量值对数的算术平均数。
菱形的定义、性质及判定1.定义:有一组邻边相等的平行四边形叫做菱形(1)菱形的四条边都相等(2)菱形的对角线互相垂直,并且每一条对角线平分一组对角(3)菱形被两条对角线分成四个全等的直角三角形(4)菱形的面积等于两条对角线长的积的一半2.s菱=争6(n、6分别为对角线长)3.判定:(1)有一组邻边相等的平行四边形叫做菱形(2)四条边都相等的四边形是菱形(3)对角线互相垂直的平行四边形是菱形4.对称性:菱形是轴对称图形也是中心对称图形几何图形,即从实物中抽象出的各种图形,可帮助人们有效的刻画错综复杂的世界。


图形几何练习4:一、填空(24分)1、用圆规画一个周长是9.42厘米的圆,圆规两脚间的距离是()。
2、一个三角形的底边长6厘米,面积是15平方厘米,这个三角形底边上的高是()厘米。
3、用三根小棒围成一个三角形,其中两根小棒的长度分别是5厘米,9厘米,另一根小棒的长度应该大于()厘米,而且小于()厘米。
4、一个圆形花坛,它的直径是3米,这个花坛的周长是()米,面积是()平方米。
5、把一个圆平均分成若干份后,正好可以拼成宽为4厘米的长方形,这个长方形的长是()厘米,原来圆的面积是()平方厘米。
6、一个梯形,如果上底增加了2.5厘米,就变成一个平行四边形;如果上底减少4厘米,就成了一个三角形,这时面积比原梯形减少了12平方厘米,原梯形的面积是()平方厘米。
7、如果一个等腰三角形的顶角和一个底角的和是130°,那么这个等腰三角形的顶角是()。
8、在一个边长是6厘米的正方形中画一个最大的圆。
画出的圆的周长()厘米,面积是()平方厘米。
9、5.03立方分米=()立方厘米 3平方分米=()立方厘米0.08立方米=()升 35分=()时10.一个长方体的棱长总和是48分米,它的长是3分米,宽是2分米,高是()分米。
11.一个棱长2厘米的正方体,表面积是()平方厘米,再增加()个同样的正方体就可以拼成棱长4厘米的正方体。
12.把一个圆柱削成一个与它等底等高的圆锥,削去的体积是36立方厘米,削成的圆锥是()立方厘米。
13.一个直角三角形的两条直角边长分别是3厘米和4厘米,斜边长5厘米,如果以4厘米长的直角边为轴把三角形旋转一周,得到一个圆锥体,这个圆锥体的高是()厘米,底面半径是()厘米,体积是()立方厘米。
14.把3个棱长是3厘米的正方体拼成一个长方体,拼成的长方体的表面积是()平方厘米。
15.一个圆柱的侧面展开后是一个正方形,这个圆柱的()和()相等。
16、把一根长5米的圆柱体的木料截成3段,表面积增加了3.14平方米,原来这根木料的体积是()立方米。

小升初数学《图形与几何》专题复习讲义(含答案)一、填空题1、如图所示,有一个五边形ABCDE,其中M、N、P分别为边AE、BC、DE的中点,每块图形中的数表示该图形的面积(单位:平方厘米),则图中阴影部分的面积是()平方厘米2、如图所示,长方形ABCD的面积是56cm²。
BE=3cm,DF=2cm。
请你回答:三角形AEF的面积是()3、如图所示,一个正六边形分成6个相同的三角形,每个三角形又可以分成三个相同的小三角形,已知阴影部分的面积是18平方厘米,那么正六边形的面积是()平方厘米4、如图所示,在平行四边形ABCD中,点E是BC的中点,DF=2FC。
若的面积是10,则平行四边形的面积是()5、如图所示,正方形ABCD中,点E在边AD上,点F在边DC上,AE=2ED,DF=3FC,则△BFE的面积与正方形ABCD的面积的比值是()6、有一块长50.24厘米、宽18.84厘米的长方形硬纸板,横着可以卷成一个圆柱,竖着可以卷成一个圆柱,两种卷法表面积相差( )平方厘米(接头处忽略不计)7、一个半圆的周长是257厘米,它的面积是( )平方厘米8、一个圆柱的底面周长和一个圆锥的底面周长的比是3:4,它们的体积之比是9:7,那么圆柱和圆锥的高之比是( )9、如图所示,有3个圆从小到大的半径分别为1厘米,2厘米,3厘米。
阴影部分和非阴影部分面积之比是( )10、如图,圆的半径是1厘米,阴影部分的周长是( )厘米11、把一根长1米的圆柱铁棒锯成三段(每段仍然是圆柱体),表面积增加了0.36平方分米,这跟铁棒原来的体积是( )立方分米12、一个圆柱形水桶的侧面积是它的底面积的6倍,水桶的底面半径为1分米,这个水桶的容积是( )立方分米13、一个圆柱体,侧面积是37.68平方分米,高是2分米,它的表面积是( )平方分米14、一根横截面为正方形的方木长2.4米,锯下一个最大的正方体后,表面积减少了36平方分米,这跟方木原来的体积是( )立方分米15、一个长方体木块,长、宽、高分别是8分米、4分米、2分米,把它锯成若干个小正方体,然后拼成一个大正方体,那么拼成的大正方体的表面积是( )平方分米 二、解答题1、如图所示,梯形ABCD 的面积为45平方厘米,三角形AED 的面积是三角形ABE 面积的2倍,BE =4厘米,EC =9厘米,求三角形DEC 的面积。


图形与几何复习题答案【图形与几何复习题答案】一、选择题1. 下列哪个选项不是平面图形?A. 三角形B. 圆C. 立方体D. 椭圆答案:C2. 一个正方形的对角线长度是边长的多少倍?A. 1倍B. √2倍C. 2倍D. √3倍答案:B3. 一个圆的半径是5厘米,那么它的周长是多少?A. 10π厘米B. 15π厘米C. 20π厘米D. 25π厘米答案:C二、填空题4. 一个长方形的长是10厘米,宽是5厘米,它的面积是________厘米²。
答案:505. 如果一个三角形的底是8厘米,高是6厘米,那么它的面积是________厘米²。
答案:246. 一个圆的直径是14厘米,那么它的半径是________厘米。
答案:7三、计算题7. 一个正六边形的边长是3厘米,求它的周长和面积。
答案:周长 = 18厘米;面积= 27√3平方厘米8. 已知一个梯形的上底是5厘米,下底是10厘米,高是4厘米,求它的面积。
答案:面积= (5 + 10) × 4 ÷ 2 = 30平方厘米四、简答题9. 解释什么是相似图形,并给出两个相似图形的例子。
答案:相似图形是指两个图形的对应角相等,对应边成比例的图形。
例如,两个等边三角形或两个矩形,如果它们的边长成比例,它们就是相似的。
10. 描述如何使用勾股定理计算直角三角形的斜边长度。
答案:勾股定理指出,在直角三角形中,直角的两条边(直角边)的平方和等于斜边的平方。
如果直角边的长度分别为a和b,斜边的长度为c,那么根据勾股定理,a² + b² = c²。
通过这个公式,我们可以计算出斜边的长度。
【结束语】以上是图形与几何的复习题答案,希望这些答案能帮助你更好地理解和掌握图形与几何的相关知识。
如果你有任何疑问或需要进一步的解释,请随时提问。
祝你学习进步!。

小学数学《图形与几何》毕业复习指南一、知识网络:二、知识要点及考点:1.线段、直线、射线的之间关系:线段和射线都是直线的一部分射线线段射线直线2.垂线、平行线的画法。
(二)角1.角的概念:从一点引出两条射线所组成的图形叫做角。
这个点叫做角的顶点,这两条射线叫做角的边。
角的大小与两边张开的的大小有关,与两边的长短无关。
考点:▲ 线段、射线、直线的特征▲ 垂线和平行线的特点及画法 ▲角的意义 ▲角的分类 ▲角的度量测试练习题: 一、填空:1.通过一点可以画( )条直线。
2. 线段有( )个端点,射线有( )个端点,直线 ( )端点。
3.通过一张纸上一点,能画( )条直线;通过一张纸上两点,可以画( )条直线。
此图中有( )条线段,( )条射线。
5. 在同一平面内,不相交的两条直线叫做( )。
6.从一点引出两条( )就组成一个角。
7.平角的一半是( )角 1周角=( )直角 二、判断:1.直线都比射线长。
( )2.永不相交的两条直线叫做平行线。
( )3.一条射线长10分米。
( )4.一个角的两条边越长,这个角就越大。
( )5.大于90°的角叫做钝角。
( )6.平角就是一条直线,周角就是射线。
( ) 三、选择题:1.垂直的两条线( )交点。
A.没有B.有一个C. 有两个D. 有无数个2. 在纸上画一条长15cm的( )。
A.直线 B.射线 C.线段3. 两直线相交成(),这两条直线互相垂直。
A.平角 B.锐角 C.直角 D.任意角4.用一个5倍的放大镜看一个20°的角,这个角是()。
A.20°B.40°C.100°四、操作题:1.过B点作直线a的垂线,过C点作直线a的平行线。
B ·C ·a2.用量角器分别画出35°、145°的角。
(三)三角形1.三角形的定义:由三条线段首尾顺次相接围成的封闭图形叫做三角形。

图形与几何知识点整理图形与几何复习知识点一、平面几何知识点:1.点、直线、线段、射线的基本定义和性质:点是没有大小和形状的,直线是由无数个点组成的,线段是由两个端点和这两个端点之间的所有点组成的,射线是由一个端点和这个端点到无限远方的所有点组成的。
2.角的基本概念和性质:角是由两条边和它们的公共端点组成的,以顺时针或逆时针方向为正方向。
角的度量是以度为单位,一个圆周角等于360度。
3.三角形的性质:三角形是由三条边和三个顶点组成的,根据边长和角度可以分为等边三角形、等腰三角形、直角三角形等,根据角度可以分为锐角三角形、钝角三角形、直角三角形等,根据边的关系可以分为全等三角形、相似三角形等。
4.四边形的性质:四边形是由四条边和四个顶点组成的,根据边的关系可以分为平行四边形、矩形、正方形、菱形等。
5.圆的性质:圆是由一个固定点和到这个点距离相等的所有点组成的,圆的中心到圆上任意一点的距离称为半径,关于半径的线称为半径。
6.整除性质:整除指的是一个数能够被另一个数整除,可以整除的数称为约数,而可以被整除的数称为倍数。
7.直角三角形的勾股定理:直角三角形中,两直角边的平方和等于斜边的平方。
8.相似三角形的性质:两个三角形对应的角相等,对应边的比值相等。
二、立体几何知识点:1.立体图形的基本概念:包括点、线、面、体的概念。
2.立体图形的展开与视图:通过展开立体图形可以得到平面的投影视图,包括正交投影和斜投影。
3.三棱柱、四棱柱、五棱柱等的性质:包括底面类型、侧面类型、轴线类型、全等类型等。
4.三棱锥、四棱锥、五棱锥等的性质:包括底面类型、侧面类型、轴线类型、全等类型等。
5.正多面体的性质:包括正方体、正六面体、正八面体、正十二面体等的性质。
三、向量几何知识点:1.向量的基本概念和性质:向量是有大小和方向的,用箭头表示。
2.向量的加减法:向量的加法是对应分量相加,向量的减法是对应分量相减。
3.向量的数量积和向量积:数量积是两个向量的乘积,向量积是两个向量的叉乘。
第四节:图形与几何专项复习四边形的初步认识【例1】下列说法不正确的是()。
A.正方形是特殊的长方形B.长方形是特殊的平行四边形C.正方形是特殊的平行四边形D.四边形是特殊的平行四边形思路引导长方形和正方形是四个角都为直角的特殊的平行四边形。
正确解答:D四边形的特点:有4条边、4个角的封闭图形。
各类图形的包含关系是常考点且是易错点,主要明确四边形包含平行四边形、梯形、长方形、正方形等等;长方形和正方形是特殊的平行四边形;正方形是特殊的长方形。
【变式1】1.把各个图形的编号填在合适的圈里。
周长的认识【例2】小明和晓东周末参加骑行比赛,下面是比赛场地平面图。
比赛规则:从起点(★)出发,绕A区或B区边线骑行一周,先回到起点者胜。
小明对晓东说:“你个子小,我让你绕A区骑,近一些,我绕B区骑。
”小明真的让了吗?请说明理由。
我认为小明()。
(填“让了”或“没让”)我的理由:思路引导观察上图可知,中间曲线是A、B的公共边,长方形的对边相等,所以A区、B区的周长相等,据此即可解答。
正确解答:小明没有让。
因为中间曲线是A、B的公共边,长方形的对边相等,A区、B区的周长相等,说明无论是绕A区还是B区,他们骑行的距离相等。
本题主要考查周长定义的应用,是周长比较大小的易错点,注意周长是指图形一周的长度,并非指图形的大小。
本题可用笔描绘一下两个区域的外轮廓,即可发现周长是相等的。
【变式2】2.下图中,甲的周长()乙的周长。
A.大于B.等于C.小于【例3】解答下列各题。
(1)一块长方形菜地长50米,宽32米,沿这块菜地走一周,可以走多少米?(2)一块正方形花坛的边长是25米,在它的四周围上铁栏杆,这些铁栏杆至少需要围多少米?思路引导由题意可知,两道题均求的是图形的周长,根据长方形的周长=(长+宽)×2,正方形的周长=边长×4,代入数据计算即可。
正确解答:(1)(50+32)×2=82×2=164(米)答:可以走164米。
小学数学图形与几何一、图形的认识和测量1、图形知识大盘点(1)点、线、角○1从一点出发可以画无数条射线,过一点可以画无数条直线,过两点只能画一条直线○2直线没有端点,可以向两端无限延伸,所以直线长度无法测量。
射线有一个端点,可以向一端无限延伸,所以直线长度无法测量。
线段有两个端点,长度可以测量。
○3从一点引出两条射线,就组成了一个角。
角的大小和角两边的长短无关。
(2)平面图形○1三角形三角形具有稳定性三角形任意两条边之和大于第三条边。
任意两条边之差都小于第三条边。
三条线段,如果两条短的线段长度之和小于第三条,则一定能围城三角形。
三角形的内角和是180度。
一个三角形,至少有2个锐角。
三角形的三个内角中,有一个角是直角的三角形叫做直角三角形;有一个角是钝角的三角形叫做钝角三角形。
三个角都是锐角的三角形叫做锐角三角形。
○2四边形两组对边分别平行四边形叫做平行四边形。
平行四边形具有不稳定性,容易变形。
只有一组对边平行的四边形叫做梯形。
两组对边分别平行且相等,四个角都是直角的四边形是长方形。
有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
四条边都相等的长方形是正方型。
长方形是特殊的平行四边形正方形是特殊的长方形、平行四边形。
○3圆圆是曲线图形在同一个圆内,所有的半径都相等,所有的直径都相等。
○4平面图形的面积和周长计算公式(3)立体图形○1长方体和正方体长方体是由6个长方形围成的立体图形。
在一个长方体中,相对的面完全相等。
(特殊情况是有两个相对的面是正方形,其它四个面都是长方形,且完全相等)长方体有12条棱,相对的棱长度相等。
可分为三组,每一组有4条棱。
长方体有8个顶点。
每个顶点连接三条棱。
长方体相邻的两条棱互相(相互)垂直。
正方体是由6个完全相同的正方形围成的立体图形。
在一个正方体中,6个面完全相等。
○2圆柱和圆锥圆柱的两个圆面叫做地面,周围的面叫做侧面;两个底面之间的距离叫做高。
圆柱的侧面是曲面,展开后可能是长方形,也可能是正方形,还可能是平行四边形。
数学图形与几何复习资料数学是一门抽象而精确的学科,而几何则是数学中的一个重要分支。
在学习几何的过程中,我们需要掌握各种数学图形的性质和计算方法。
为了帮助大家复习几何知识,我整理了一些几何复习资料,希望对大家有所帮助。
一、基本概念几何学的基础是一些基本概念,如点、线、面等。
点是几何学中最基本的概念,它没有大小和形状,只有位置。
线是由无数个点组成的,它有长度但没有宽度。
面是由无数个线组成的,它有长度和宽度。
这些基本概念是我们理解几何学的基础,也是解决几何问题的前提。
二、平面几何平面几何是几何学的重要分支,它研究的是在平面上的图形和性质。
在平面几何中,我们需要掌握各种图形的定义和性质,如三角形、四边形、圆等。
三角形是平面几何中最基本的图形之一,它由三条线段组成。
我们需要了解三角形的各种分类和性质,如等腰三角形、直角三角形等。
四边形是由四条线段组成的图形,它有矩形、正方形、菱形等不同的分类。
圆是由一条曲线组成的图形,它的性质包括圆心、半径、直径等。
三、立体几何立体几何是几何学中另一个重要的分支,它研究的是在空间中的图形和性质。
在立体几何中,我们需要掌握各种立体图形的定义和性质,如球体、长方体、正方体等。
球体是由一条曲线旋转而成的图形,它有半径、直径等性质。
长方体是由六个矩形组成的图形,它有长、宽、高等性质。
正方体是一种特殊的长方体,它的六个面都是正方形。
我们需要了解这些立体图形的性质,以便在解决几何问题时能够灵活运用。
四、几何计算在解决几何问题时,我们经常需要进行一些计算。
几何计算包括计算图形的面积、周长、体积等。
计算图形的面积需要掌握各种图形的计算公式,如三角形的面积公式、矩形的面积公式等。
计算图形的周长需要了解各种图形的周长公式,如圆的周长公式、正方形的周长公式等。
计算图形的体积需要了解各种立体图形的体积公式,如长方体的体积公式、球体的体积公式等。
掌握这些计算方法可以帮助我们更好地解决几何问题。
五、几何证明几何证明是几何学中的重要内容,它要求我们用严密的推理和论证方法证明几何命题。
“空间与图形”复习资料一、填空题。
1. 用圆规画一个周长是 15.7 厘米的圆, 圆规两脚间的距离是( )厘米。
2.一个长方体的棱长总和是 144 厘米,长 20 厘米,宽 8 厘米,高是( )厘米。
3. 三角形三个内角度数的比是 2∶3∶4,其中最大内角是( )度,这是( )三角形。
4. 两个等腰三角形和一个正方形拼成一个梯形(如右图)。
如果梯形的上底长 5 厘米, 面积是( )平方厘米;如果把这个梯形改拼成长方形,且长方形的长是 10 厘米,则宽是( )厘米。
5. 将 2 升水倒入右图(单位:厘米)中的两个长方体水槽中,使它们水面的高度相等,这个高度是( )厘米。
6. 用一根 36 厘米长的铁丝折成一个最大的正方形,正方形的面积是( )平方厘米,如果用它围成一个正方体框架,这个正方体的体积是( )立方厘米。
7. 一幢高 50 米 、长 30 米 、宽 25 米的住宅楼 ,我们说这幢楼的占地面积是( )平方米。
8. 一个圆柱形水桶 ,里面盛 48 升的水,正好盛满。
如果把一块与水桶等底等高的圆锥体完全浸入水中,桶内还有( )升水。
9. 用 3 块相同的长方体木料拼成一个大长方体 ,每块的长是 5 厘米,宽是 4 厘米,高是 3 厘米。
拼成的长方体的表面积最大是( )平方厘米。
10. 用一根 12 厘米长的铁丝围成长方形或正方形(接头处忽略不计 ),有 ( )种不同的围法 (边长取整厘米数)。
其中最大的面积是( )平方厘米。
11. 下图 (单位 :厘米 )中 ,平行四边形的面积是 72平方厘米, 图中丙三角形的面积是甲三角形的( ),阴影部分的面积是( )平方厘米。
12. 有一个长方体木块 (如下图 ),如果把它的高锯掉 3 厘米,就变成一个正方体,这样正方体木块的表面积比原来长方体的表面积少 96 平方厘米。
原来长方体木块的表面积是 ( ) 平方厘米,体积是( )立方厘米。
13. 如下图,AB 的长为 20 厘米,一只蚂蚁从 A 到 B 沿着四个半圆爬行,蚂蚁的行程是( )厘米。