卷积码的编解码仿真与研究

【报告】卷积码实验报告一、实验目的本次卷积码实验的主要目的是深入理解卷积码的编码与译码原理，掌握其在数字通信系统中的应用，并通过实际实验操作和结果分析，评估卷积码的纠错性能和对通信质量的改善效果。

二、实验原理（一）卷积码的基本概念卷积码是一种有记忆的非分组码，它将输入的信息序列经过特定的编码器生成输出的码序列。

卷积码的编码过程不仅取决于当前输入的信息位，还与之前的若干个信息位有关。

（二）编码原理卷积码的编码器通常由若干个移位寄存器和模 2 加法器组成。

输入的信息位在时钟的控制下依次进入移位寄存器，同时与寄存器中的内容进行模 2 加法运算，生成输出的编码位。

（三）译码原理卷积码的译码方法有多种，常见的有维特比译码算法。

维特比译码算法基于最大似然准则，通过在码的网格图上寻找最有可能的路径来实现译码。

三、实验环境与设备本次实验在计算机上进行，使用了以下软件和工具：1、 MATLAB 编程环境，用于实现卷积码的编码、传输和译码过程，并进行性能分析。

2、通信系统仿真工具，用于构建通信系统模型，模拟信号的传输和接收。

四、实验步骤（一）编码实现1、在 MATLAB 中定义卷积码的编码器结构，包括移位寄存器的数量和连接方式，以及模 2 加法器的位置。

2、编写编码函数，输入信息序列，按照编码器的工作原理生成编码后的序列。

（二）信道传输1、模拟加性高斯白噪声信道，设置不同的信噪比条件。

2、将编码后的序列通过信道传输，引入噪声干扰。

（三）译码实现1、使用维特比译码算法对接收序列进行译码。

2、编写译码函数，输入接收序列和信道参数，输出译码后的信息序列。

（四）性能评估1、计算误码率，即错误译码的比特数与总传输比特数的比值。

2、绘制误码率曲线，分析卷积码在不同信噪比条件下的纠错性能。

五、实验结果与分析（一）不同卷积码参数对性能的影响1、改变卷积码的约束长度，观察其对纠错性能的影响。

结果表明，约束长度越长，卷积码的纠错能力越强，但编码效率会有所降低。

文章标题：深度解析通信综合课程设计中卷积码的实现与仿真引言：通信综合课程设计是通信工程领域的重要教育环节，而卷积码作为其中的重要内容之一，其实现与仿真更是学生们需要深入了解和掌握的技能。

本文将从简到繁地讨论通信综合课程设计中卷积码的实现与仿真，帮助读者更好地理解和掌握这一重要内容。

第一部分：通信综合课程设计概述1.1 通信综合课程设计的重要性在通信工程领域，通信综合课程设计是学生将在实际工作中常常用到的实践环节，通过这一环节，学生们可以将所学的理论知识应用到实际项目中，提高实践能力和解决问题的能力。

1.2 通信综合课程设计的内容概述通信综合课程设计内容丰富多样，包括调制解调、信道编码、卷积码、纠错码等多个主题，而卷积码的实现与仿真是其中的重要部分之一。

第二部分：卷积码的基本原理2.1 卷积码的定义卷积码是一种线性时不变系统（LTI）编码器，在通信系统中起到纠错码的作用。

2.2 卷积码的编码和解码原理通过引入时延、存储元素和加法器，实现对输入序列进行编码；而解码过程则是通过译码器进行，根据输入序列和已知的编码规则进行解码。

第三部分：通信综合课程设计中卷积码的实现3.1 卷积码的软件实现在通信综合课程设计中，学生们可以利用MATLAB等软件工具，编写程序实现卷积码的编码和解码过程，从而加深对卷积码原理的理解。

3.2 卷积码的硬件实现除了软件实现，通信综合课程设计中也常常涉及到卷积码的硬件实现，学生们可以通过FPGA等硬件开发评台，实现卷积码的编码和解码过程。

第四部分：通信综合课程设计中卷积码的仿真4.1 仿真环境的建立在通信综合课程设计中，学生们需要建立仿真环境，包括信道模型、信号源、噪声源等，以便对卷积码的性能进行评估。

4.2 仿真结果的分析通过仿真实验，学生们可以得到卷积码在不同信噪比下的误码率曲线等性能参数，从而对卷积码的性能有更深入的了解。

结论：通过本文的深入讨论，相信读者已经对通信综合课程设计中卷积码的实现与仿真有了更深入的理解。

卷积码（或者Turbo码）的交织与解交织的仿真编程和仿真实验一、实验目的实现卷积码（或者Turbo码）的交织与解交织的仿真编程和仿真实验，观察交织编码分别在白噪声信道和衰落信道下系统误码率的影响，分析原因。

二、实验原理信道编码中采用交织技术，可打乱码字比特之间的相关性，将信道中传输过程中的成群突发错误转换为随机错误，从而提高整个通信系统的可靠性。

交织编码根据交织方式的不同，可分为线性交织、卷积交织和伪随机交织。

其中线性交织编码是一种比较常见的形式。

所谓线性交织编码器，是指把纠错编码器输出信号均匀分成m个码组，每个码组由n段数据构成，这样就构成一个n×m的矩阵。

这里把这个矩阵称为交织矩阵。

如图1所示，数据以a11，a12，…，a1n，a21，a22，…，a2n，…，aij，…，am1，am2，…，amn(i=1，2，…，m;j=1，2，…，n)的顺序进入交织矩阵，交织处理后以a11，n21，…，am1，a12，a22，…，am2，…，a1n，a2n，…，amn的顺序从交织矩阵中送出，这样就完成对数据的交织编码，如图1所示。

还可以按照其他顺序从交织矩阵中读出数据，不管采用哪种方式，其最终目的都是把输入数据的次序打乱。

如果aij只包含1个数据比特，称为按比特交织;如果aij包含多个数据比特，则称为按字交织。

接收端的交织译码同交织编码过程相类似。

图 1 交织编码矩阵一般来说，如果有n个(m，k)码，排成，n×m矩阵，按列交织后存储或传送，读出或接收时恢复原来的排列，若(m，k)码能纠t个错误，那么交织后就可纠m个错误。

对纠正信道传输过程中出现的突发错误效果明显，如图2所示。

图2 交织编码示例GSM中使用这种比特交织器。

其交织方式为将信道编码后的每20ms的数据块m=456b拆分到8组中，每组57b，然后这每组57 b分配到不同的Burst中三、实验流程卷积交织解卷积交织四、源程序1、交织程序1）卷积交织function [aa]=jiaozhi(bb,n)%jiaozhi.m 卷积交织函数n=28; %分组长度%bb 卷积交织前原分组序列%aa 卷积交织后分组序列%序号重排方式：cc=[ 1 23 17 11 5 17 21; 8 2 24 18 12 6 28; 15 9 3 25 19 13 7; 22 16 10 4 26 20 14 ];%交织矩阵bb=[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28];for i=1:naa(i)=bb(cc(i));end（2）循环等差交织function [aa]=jiaozhi_nocnv(bb,n)%jiaozhi_nocnv.m 循环等差交织函数n=28; %分组长度%bb 循环等差交织前原分组序列%aa 循环等差交织后还原分组序列%序号重排方式：bb=[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 ]; j=1;for i=1:nj=rem(j+5-1,n)+1; %序号重排方式迭代算法aa(n+1-i)=bb(j);end2、解交织程序（1）解卷积交织function [bb]=jiejiaozhi(aa,n)%jiejiaozhi.m 解卷积交织函数n=28;% 分组长度%aa 解卷积交织前原分组序列%bb 解卷积交织后分组序列%序号重排方式：cc=[ 1 23 17 11 5 27 21; 8 2 24 18 12 6 28; 15 9 3 25 19 13 7 ;22 16 10 4 26 20 14 ]; aa=[ 1 8 15 22 23 2 9 16 17 24 3 10 11 18 25 4 5 12 19 26 27 6 13 20 21 28 7 14 ]; for i=1:nbb(cc(i))=aa(i);end（2）解循环等差交织function [bb]=jiejiaozhi_nocnv(aa,n)%jiaozhi_nocnv.m 解循环等差交织函数n=28;% 分组长度%aa 解循环等差交织前原分组序列%bb 解循环等差交织后还原分组序列%序号重排方式：aa=[ 1 24 19 14 9 4 27 22 17 12 7 2 25 20 15 10 5 28 23 18 13 8 3 26 21 16 11 6];j=1;for i=1:nj=rem(j+5-1,n)+1; %序号重排方式迭代算法bb(j)=aa(n+1-i);End交织码通常表示为（M，N），分组长度L=MN，交织方式用M行N列的交织矩阵表示。

卷积码编码和维特比译码的原理、性能与仿真分析1.引言卷积码的编码器是由一个有k位输入、n位输出，且具有m位移位寄存器构成的有限状态的有记忆系统，通常称它为时序网络。

编码器的整体约束长度为v,是所有k个移位寄存器的长度之和。

具有这样的编码器的卷积码称作[n,k,v]卷积码。

对于一个（n,1,v）编码器，约束长度v等于存储级数m.卷积码是由k个信息比特编码成n（n>k）比特的码组，编码出的n比特码组值不仅与当前码字中的k个信息比特值有关，而且与其前面v个码组中的v*k个信息比特值有关。

卷积码有三种译码方式：序列译码、门限译码和概率译码。

其中，概率译码根据最大似然译码原理在所有可能路径中求取与接收路径最相似的一条路径，具有最佳的纠错性能，维特比译码是概率译码中极重要的一种方式。

序列译码和门限译码则不一定能找出与接收路径最相似的一条路径。

不同于维特比译码，门限译码与序列译码所需的计算量是可变的且对于给定信息分组的最终判决仅仅基于（m+1）个接收分组，而不是基于整个接收序列。

与维特比译码所使用的对数似然量度不同，序列译码所使用的量度为Fano量度。

在接收序列受扰严重的情况下，序列译码的计算量大于维特比译码所需的固定计算量，虽然序列译码要求的平均计算次数通常小于维特比译码。

在采用并行处理的情况下，维特比译码的速度会优于序列译码。

在同样码率和存储级数的条件下，门限译码的性能比维特比译码低大约3dB.维特比译码的数据输出方式有硬判决及软判决两种方式，本文选取生成多项式为561,753的（2,1,8）卷积码对硬判决的性能进行分析，并依据维特比译码的原理以及卷积码的特性，对卷积码编码和维特比译码过程在加性高斯白噪声（AWGN）信道下进行仿真，并且根据仿真结果对维特比译码（硬判决）的结果进行分析。

由于卷积码的生成可以看做一个马尔科夫过程，因此，不同状态间的转移概率对描述这个过程有极关键的作用。

本文则基于MATLAB对不同状态间的转移概率进行求解，从而更准确地分析维特比译码的性能。

实验四 卷积码的编解码一、实验目的1、掌握卷积码的编解码原理。

2、掌握卷积码的软件仿真方法。

3、掌握卷积码的硬件仿真方法。

4、掌握卷积码的硬件设计方法。

二、预习要求1、掌握卷积码的编解码原理和方法。

2、熟悉matlab 的应用和仿真方法。

3、熟悉Quatus 的应用和FPGA 的开发方法。

三、实验原理1、卷积码编码原理在编码器复杂度相同的情况下，卷积码的性能优于分组码，因此卷积码几乎被应用在所有无线通信的标准之中，如GSM ， IS95和CDMA 2000 的标准中。

卷积码通常记作( n0 ， k0 ， m) ，它将k 0 个信息比特编为n 0 个比特， 其编码效率为k0/ n0 ， m 为约束长度。

( n0 ， k0 ， m ) 卷积码可用k0 个输入、n0 个输出、输入存储为m 的线性有限状态移位寄存器及模2 加法计数器来实现。

本实验以（2，1，3）卷积码为例加以说明。

图1就是卷积码编码器的结构。

图1 （2，1，3）卷积码编码器其生成多项式为：21()1G D D D =++； 22()1G D D =+；如图1 所示的(2，1，3)卷积码编码器中，输入移位寄存器用转换开关代替，每输入一个信息比特经编码产生二个输出比特。

假设移位寄存器的初始状态为全0，当第一个输入比特为0时，输出比特为00；若输入比特为１，则输出比特为11。

随着第二个比特输入，第一个比特右移一位，此时输出比特同时受到当前输入比特和前一个输入比特的影响。

第三个比特输入时，第一、二个比特分别右移一位，同时输出二个由这三位移位寄存器存储内容所共同决定的比特。

依次下去就完成了编码过程。

下面是卷积码的网格图表示。

他是比较清楚而又紧凑的描述卷积码的一种方式，它是最常用的描述方式之一。

图2(2，1，3)卷积码的网格图表示2、Viterbi译码原理2k N-种状态，每个节点（即每个状态）有2k条支路引入也有2k条如图2所示，卷积码网格图中共有(1)支路引出。

卷积编码设计与仿真实验报告一、实验目的了解卷积码对信号的纠错性能，掌握维特比译码算法，分析卷积码不同码率下纠错能力的强弱，深刻理解CCSDS标准、信道编译码等相关概念和算法。

二、实验内容1、自己编码实现（2,1,3）卷积码的编译码，对比不同信噪比条件下，是否采用编码对于误码率性能的影响；2、基于MATLAB自带的vitdec函数实现对（2,1,7）卷积码以及2/3、3/4码率删除码的编译码，并对于不同码率抗噪声能力的强弱；3、构造BPSK调制、加性高斯白噪声的传输环境。

三、实验原理卷积码一般表示为(n,k,N)的形式，即将k个信息比特编码为n个比特的码组，N为编码约束长度，说明编码过程中相互约束的码段个数。

卷积码编码后的n个码元不仅与当前组的k个信息比特有关，还与前N-1个输入组的信息比特有关。

编码过程中相互关联的码元有N*n个。

R=k/n是编码效率。

编码效率和约束长度是衡量卷积码的两个重要参数。

典型的卷积码一般选n,k较小，但N值可取较大(>10)，以获得简单而高性能的卷积码。

1、卷积码的编码原理卷积码的编码器一般比较简单，为一个具有k个输入端，n个输出端，m 级移位寄存器的有限状态有记忆系统。

下图所示为(2,1,7)卷积码的编码器。

图1 （2,1,7）卷积码编码器若输入序列为u=(u0u1u2u3……),则对应两个码字序列 C1=(ca0ca1ca2ca3……)和C2=(cb0cb1cb2cb3……)，相应的编码方程可写为 P1=u*C1，P2=u*C2，P=(P1,P2)。

“*”符号表示卷积运算，P1，P2表示编码器的两个冲激响应，即编码器的输出可以由输入序列和编码器的两个冲击响应卷积而得到，故称为卷积码。

这里的冲激响应指：当输入为[1 0 0 0 0 … … ]序列时，所观察到的两个输出序列值。

由于上图N 值为7，故冲激响应至多可持续到第7位，可写为P1=[1 1 1 1 0 0 1]，P2=[1 0 1 1 0 1 1]然后将两个输出端的码字序列合并为一个码字序列为C=(ca0cb0ca1cb1ca2cb2……)。

实验名称：___ 卷积编码_______1、使用MATLAB进行卷积编码的代码编写、运行、仿真等操作；2、熟练掌握MATLAB软件语句；3、理解并掌握卷积编码的原理知识。

二、实验原理卷积码是由Elias于1955 年提出的，是一种非分组码，通常它更适用于前向纠错法，因为其性能对于许多实际情况常优于分组码，而且设备较简单。

卷积码的结构与分组码的结构有很大的不同。

具体地说，卷积码并不是将信息序列分成不同的分组后进行编码，而是将连续的信息比特序列映射为连续的编码器输出符号。

卷积码在编码过程中，将一个码组中r 个监督码与信息码元的相关性从本码组扩展到以前若干段时刻的码组，在译码时不仅从此时刻收到的码组中提取译码信息，而且还可从与监督码相关的各码组中提取有用的译码信息。

这种映射是高度结构化的，使得卷积码的译码方法与分组译码所采用的方法完全不同。

可以验证的是在同样复杂度情况下，卷积码的编码增益要大于分组码的编码增益。

对于某个特定的应用，采用分组码还是卷积码哪一种更好则取决于这一应用的具体情况和进行比较时可用的技术。

（一）卷积编码的图形表示卷积码的编码器是由一个有k 个输人位，n 个输出位，且有m 个移位寄存器构成的有限状态的有记忆系统，其原理如图1所示。

图1 卷积码编码器的原理图描述这类时序网络的方法很多，它大致可分为两大类型：解析表示法与图形表示法。

在解析法中又可分为离散卷积法、生成矩阵法、码多项式法等；在图形表示法中也可分为状态图法、树图法和网络图法等。

图2给出的是一个生成编码速率为1／2 卷积码的移位寄存器电路。

输人比特在时钟触发下从左边移人到电路中，每输入一位，分别去两个模2加法器的输出值并复用就得到编码器的输出。

对这一编码，每输入一比特就产生两个输出符号，故编码效率为1／2。

可以看出，每个特定的输入比特不仅影响本时间间隔内的编码器输出，同时还影响紧接着的下两个输入比特时间间隔的编码器输出。

卷积编码由移位寄存器的阶数、输出的数量（即模2加法器的个数）和移位寄存器与模2 加法器间的连接所决定。

一、概述卷积码是一种常用的编码技术，用于提高数字通信系统的可靠性和抗干扰能力。

而编码的解码过程则需要运用编译码技术，以恢复原始数据。

Matlab作为一种强大的工程仿真软件，可以用来对卷积码编译码进行仿真分析，帮助工程师们更好地理解和优化卷积码系统，提高通信系统的性能。

二、卷积码原理1. 卷积码的概念卷积码是一种线性块码，它采用移位寄存器和模2加法器进行编码，通过引入冗余比特来提高信号的可靠性。

卷积码的编码过程可以简单描述为：将输入信息数据与特定的生成多项式进行卷积运算，得到编码后的输出数据。

2. 卷积码的特点卷积码具有较高的编码效率和能够很好地控制码长、纠错能力等特性，因此在实际通信系统中得到广泛应用。

三、编译码原理1. Viterbi算法卷积码的译码过程通常采用Viterbi算法，它是一种最大似然译码算法，通过计算最小距离路径的方式来进行译码。

Viterbi算法能够有效地对卷积码进行解码，提高译码的准确性。

2. 编译码的实现在Matlab中，编译码的实现通常是通过编写一定的程序来模拟Viterbi算法的译码过程。

通过仿真分析，可以评估不同的编码方案对通信系统性能的影响。

四、Matlab仿真环境1. Matlab的特点Matlab作为一种强大的仿真软件，具有丰富的工具和函数库，能够方便地进行数字通信系统设计与仿真分析。

Matlab提供了直观的图形界面和强大的数据处理能力，可用于展示仿真结果和进行数据分析。

2. 使用Matlab进行卷积码编译码仿真在Matlab环境中，可以编写程序来实现卷积码的编码和Viterbi算法的译码过程。

通过调用Matlab中的工具函数和绘图函数，可以直观地展示通信系统的性能指标，并对比不同编码方式的性能差异。

五、仿真实例分析1. 卷积码编码仿真我们可以编写Matlab程序，实现对卷积码的编码过程。

通过模拟不同的编码率和约束长度，可以观察到编码后的效果，并评估编码的性能。

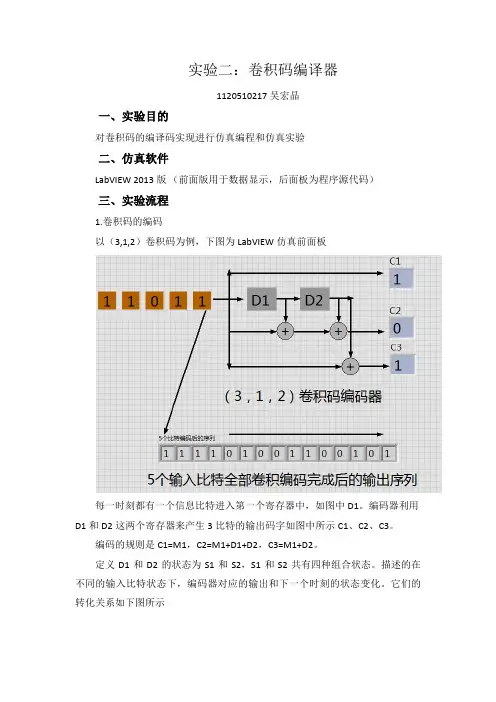
实验二：卷积码编译器1120510217 吴宏晶一、实验目的对卷积码的编译码实现进行仿真编程和仿真实验二、仿真软件LabVIEW 2013版（前面版用于数据显示，后面板为程序源代码）三、实验流程1.卷积码的编码以（3,1,2）卷积码为例，下图为LabVIEW仿真前面板每一时刻都有一个信息比特进入第一个寄存器中，如图中D1。

编码器利用D1和D2这两个寄存器来产生3比特的输出码字如图中所示C1、C2、C3。

编码的规则是C1=M1，C2=M1+D1+D2，C3=M1+D2。

定义D1和D2的状态为S1和S2，S1和S2共有四种组合状态。

描述的在不同的输入比特状态下，编码器对应的输出和下一个时刻的状态变化。

它们的转化关系如下图所示2.卷积码的译码卷积码的译码采用维特比译码法。

维特比算法的思路：在每个节点处，留下到达该节点处局部度量最大的路径，丢弃其余的局部路径，这条留下来的路径叫做幸存路径。

如果所有幸存路径在某个支路处是重合的，就可以输出这个支路上数据的译码结果。

为了避免延时，在当前局部路径中，找出局部累积量最大的，沿着这个路径回退N步会有一个分支，输出这个分支的数据。

（3,1,2）卷积码t0~t5六个时刻，第一次选取幸存路径发生在从t2到t3转移时刻。

四、实验源程序说明1.卷积码的编码程序源代码如下图所示1.坐标1处是输入码元数组，它经过一个FOR循环依次进入循环中。

2.坐标2处是D1和D2两个移位寄存器，D1的结果在一次循环过后移入D2中。

3.坐标3处表示C1的值为每次直接进来的码元值。

4.坐标4处为C2的计算值，对局部进行放大，有如下图说明：C2=D1+D2+M1（模2加法），M1为码元值。

因为没有模2加法的函数，故调用除2函数，再对余数与0进行比较是否相等，若结果为TRUE，则表明C2为2的倍数，即为0，故将0送入C2中，否则将1送入C2中。

5.坐标5处为C3的计算值，对局部进行放大，有如下图说明：C3=M1+C2，故将两数相加，再对结果与1比较，因为只有01或10相加才为1，其他值为0或者2，故若判断结果为TRUE,则将1的值赋值给C3，如上图所示。

卷积编码与解码的M A T L A B实现及能分析长沙理工大学《通信原理》课程设计报告王情学院城南学院专业通信工程班级通信1102 学号 201185250230 学生姓名王情指导教师曹敦课程成绩完成日期 2014年1月9日课程设计成绩评定学院城南学院专业通信工程班级通信1102 学号 201185250230 学生姓名王情指导教师曹敦课程成绩完成日期 2014年1月9日指导教师对学生在课程设计中的评价指导教师对课程设计的评定意见卷积编码与解码的MATLAB实现及性能分析学生姓名：王情指导老师：曹敦摘要本课程设计主要解决通信系统中卷积编码与解码技术在Matlab中实现以及对其性能进行分析。

用贝努利二进制序列产生器作为信号源，产生基带信号，对其中的卷积进行编码，调制解调，然后采用Viterbi译码输出，最后计算误码率，对其性能进行分析。

关键词卷积码；卷积编码器；Viterbi译码器；BSK调制与解调；约束长度。

目录1引言 (4)1.1课程设计的目的 (4)1.2 课程设计的基本任务和要求 (4)1.2.1本次课程设计的基本任务 (4)1.2.2课程设计中的要求 (5)1.3设计平台 (5)2设计原理 (5)2.1卷积码的基本概念 (5)2.2卷积码的编码 (5)2.2.1卷积编码 (5)2.2.2卷积码的树状图 (6)2.2.3卷积码的网格图 (7)2.2.4卷积码的状态图 (8)2.3卷积码的解码 (8)3卷积码的仿真与性能分析 (9)3.1 卷积码的仿真 (9)3.1.1卷积码的设计框图 (9)3.1.2Simulink仿真模块的参数设置 (9)3.2 卷积码的波形输出 (15)3.2.1输入信号波形 (15)3.2.2输入信号与解码输出波形 (16)3.3卷积码的性能分析 (17)4出现的问题及解决方法 (19)5 结束语 (19)6参考文献 (20)1 引言本课程设计主要解决基于Matlab的Simulink下的模块对卷积编码与解码进行仿。

厦门理工学院实验报告书课程名称：信息论与编码实验实验名称：卷积码编译码m•个有效的寄存器单元，而输出移位寄存器仅中输入移位寄存器最多只有k起一个并串转换作用。

因此称参量m为卷积吗的记忆长度（段）2、维比特译码原理它的基本思想是把接收到的矢量，和网格图上诸种可能的路径比较，删去距离大的路径，保留距离小的路径，以距离最小路径作为发码的估值五、实验内容在MATLAB环境下卷积码编/解码器的实现。

1、主函数main.mclear;clc;msg = randint(1,20,[0,1])word = encode_conv213(msg)word(1) =~word(1); %信道中存在污染，人为的模拟传输过word(10) =~word(10); %程中的出错码字word(15) =~word(15);word1=wordmsg_1 = decode_conv213(word1)msg-msg_12 、状态积state_machine.mfunction [output,nextState] = state_machine(input,current_state)output(1) = mod(current_state(1)+current_state(3),2);output(2) = mod(input+current_state(2)+current_state(1),2);nextState(1) = current_state(2);nextState(2) = current_state(3);nextState(3) = input;3、汉明距离hamming_distance.mfunction distance = hamming_distance(a,b)temp = a+b;temp = mod(temp,2);distance = sum(temp);4 、213编码程序encode_conv213.mfunction word = encode_conv213(msg)word = zeros(1,length(msg)*2);current = [0 0 0];for i = 1:length(msg)[out,next] = state_machine(msg(i),current);current = next;word(2*i-1) = out(1);word(2*i) = out(2);End5、213维比特译码decode_conv213.mfunction msg = decode_conv213(word)chip = 10; %初始状态选十个信息for i = 1:2^chipM(i,:) = de2bi(i-1,chip); %把所有可能性按二进制输出W(i,:) = encode_conv213(M(i,:));%得到相应的二进制编译后的码字D(i) = hamming_distance(W(i,:),word(1:chip*2));%与出错码字对比得到汉明距end[val,index] = sort(D);%val中存汉明距从小到大排列，index中存对应val数据所在位置ret_msg = zeros(1,length(word)/2); %开辟译出码字的存放空间for i = 1:6%1024种选择6种最小距离，并输出在ret_msg中，最小汉明距存于ret_dis ret_msg(i,1:chip) = M(index(i),:);ret_dis(i) = D(index(i));enditer = (length(word)-chip*2)/2; %剩余要译出的码字个数for i=1:iter %迭代过程for j=1:6msg_temp1 = [ret_msg(j,1:chip+i-1) 0]; %下一状态出“0”msg_temp2 = [ret_msg(j,1:chip+i-1) 1]; %下一状态出“1”word_temp1 = encode_conv213(msg_temp1);%下一状态为“0”时的编码word_temp2 = encode_conv213(msg_temp2);%下一状态为“1”时的编码dis_temp1 = hamming_distance(word_temp1,word(1:chip*2+2*i));dis_temp2 = hamming_distance(word_temp2,word(1:chip*2+2*i)); %算两种汉明距if (dis_temp1<dis_temp2)ret_msg(j,1:chip+i) = msg_temp1;ret_dis(j) = dis_temp1;elseret_msg(j,1:chip+i) = msg_temp2;ret_dis(j) = dis_temp2;%选择较小汉明距的状态储存并输出在ret_msg中，最小汉明距存于ret_disendendend[val,index] = sort(ret_dis); %把最终选择的6种最小汉明距按从小到大排列msg =ret_msg(index(1),:); %选出维特比译码最小的距离所译出的信息六、实验数据记录及分析（包括源程序清单及运行结果）：。

实验十九卷积码的编解码实验实验内容1. 熟悉卷积码编码实验2．熟悉卷积码译码实验一、实验目的1．了解卷积码的基本概念和原理2．加深对卷积码的编解码过程的理解3. 学习通过CPLD编程实现卷积码编译码实验二、实验电路工作原理卷积码又称连环码，是1955年提出来的一种纠错码，它和分组码有明显的区别，但在编码器复杂度相同的情况下, 卷积码的性能优于分组码,因此卷积码几乎被应用在所有无线通信的标准之中, 如GSM, IS95和CDMA 2000 的标准中。

1．卷积码编码方法：卷积码通常记作( n0 , k0 , m) ,它将k0 个信息比特编为n0 个比特, 其编码效率为k0/ n0 , m为约束长度。

( n0 , k0 , m )卷积码可用k0 个输入、n0 个输出、输入存储为m的线性有限状态移位寄存器及模2 加法计数器来实现。

实验中所选(2 ,1 ,6) 卷积编码器上图所示,其子生成元为: g(1 ,1) ( D) = 1 , g(1 ,2) ( D) = 1 + D2 + D5 +D6 ,生成矩阵G( D) = (1 ,1 + D2 + D5 + D6) 。

设输入信息序列M = (1111) ,即M( D) = 1 + D + D2 + D3 ,则编码器的输出C( D) = M( D) ·G( D) ,即:C( D) = (1+D+D2+D3)·(1,1+D2+D5+D6)= (1+D+D2+D3 ,1+D+D2+D3+D2+D3+D4+D5+D5+D6+D7+D8+D6+D7+D8+D9)= (1+D+D2+D3 ,1+D+D4+D9)= (11)+(11)D+(10)D2+(10)D3+(01)D4+(00)D5+(00)D6+(00)D7+(00)D8+(01)D9+⋯因此,编码器输出序列为11111010010000000001。

2．卷积码编码算法process(clk,clr)beginif(clr='1')thenif(clk'event and clk='1')thentemp(0)<=datain;temp(1)<=temp(0);temp(2)<=temp(1);temp(3)<=temp(2);temp(4)<=temp(3);end if;else temp<="00000";end if;end process;y2j<= (datain xor temp(2) xor temp(3) xor temp(4));y1j<=datain;3．大数逻辑解码器大数逻辑解码器是卷积码代数解码最主要的解码方法, 既可用于纠随机错误, 又可用于纠突发错误,但要求卷积码是自正交码或可正交码。

卷积编译码实验
卷积编码是一种在通信系统中广泛应用的误码控制编码方式,通常用于提高数字信号的抗噪性能。

卷积编码可以降低误码率,保证数据的传输质量。

需要进行卷积编译码实验的话,可以按照以下步骤进行：
1. 选择一个适合的卷积码：可以从已经定义好的标准卷积码中进行选择,也可以根据应用需要自行设计卷积码。

常用的卷积码如（3,1,2）,（4,1,3）、（4,2,3）等。

2. 编写卷积编码器程序：利用 MATLAB 或者 Python 等编程语言编写程序实现卷积编码,对输入的二进制数据进行编码处理,并输出编码后的信号。

3. 模拟信道传输：利用模拟信道对编码后的信号进行传输模拟,模拟信道可以包括加性高斯噪声信道、多径衰落信道等,可以根据实际需求进行设置。

4. 编写卷积解码器程序：利用 MATLAB 或者 Python 等编程语言编写卷积解码器程序,对模拟信道传输后的信号进行卷积解码处理,输出解码后的二进制数据流。

5. 分析误码率：对比编码前后的误码率,分析卷积编译码在特定的信道条件下的性能表现及其变化规律,可以进行多次实验,比较不同卷积码的误码率性能。

需要注意的是,在进行实验的过程中,需要注意数据随机性,以及卷积码的参数选择等方面的合理性。

现代编码理论基于MATLAB的卷积码编码及译码仿真姓姓名名：闫嘉川学学号号：1433170所在院系：电子与信息工程学院实验名称：基于MAATLAB的卷积码编码及译码仿真实验目的：卷积码是一种性能优越的信道编码。

它的编码器和译码器都比较容易实现，同时它具有较强的纠错能力。

随着纠错编码理论研究的不断深入，卷积码的实际应用越来越广泛。

本实验简明地介绍了卷积码的编码原理和Viterbi译码原理。

并在SIMULINK模块设计中，完成了对卷积码的编码和译码以及误比特统计整个过程的模块仿真。

最后，通过在仿真过程中分别改变卷积码的重要参数来加深理解卷积码的这些参数对卷积码的误码性能的影响。

经过仿真和实测，并对测试结果作了分析。

实验原理：1、卷积码编码原理卷积码是一种性能优越的信道编码，它的编码器和解码器都比较易于实现，同时还具有较强的纠错能力，这使得它的使用越来越广泛。

卷积码一般表示为(n,k,K)的形式，即将 k个信息比特编码为 n 个比特的码组，K 为编码约束长度，说明编码过程中相互约束的码段个数。

卷积码编码后的 n 各码元不经与当前组的 k 个信息比特有关，还与前 K-1 个输入组的信息比特有关。

编码过程中相互关联的码元有 K*n 个。

R=k/n 是编码效率。

编码效率和约束长度是衡量卷积码的两个重要参数。

典型的卷积码一般选 n,k 较小，K 值可取较大(>10)，但以获得简单而高性能的卷积码。

卷积码的编码描述方式有很多种：冲激响应描述法、生成矩阵描述法、多项式乘积描述法、状态图描述，树图描述，网格图描述等。

2、卷积码Viterbi译码原理卷积码概率译码的基本思路是:以接收码流为基础，逐个计算它与其他所有可能出现的、连续的网格图路径的距离，选出其中可能性最大的一条作为译码估值输出。

概率最大在大多数场合可解释为距离最小，这种最小距离译码体现的正是最大似然的准则。

卷积码的最大似然译码与分组码的最大似然译码在原理上是一样的，但实现方法上略有不同。

三级项目报告课程名称：信息论与编码___________ 课程设计题目：卷积码的仿真与分析_______指导教师：______________系别：专业：学号：姓名： _____合作者完成时间： 2012 年 6 月 10 日至 6 月 14 日成绩：评阅人：1. 卷积码及其编译码原理概述非分组码的卷积码的编码器是在任一段规定时间内产生n 个码元，但它不仅取决于这段时间中的k 个信息位，还取决于前(K -1)段规定时间内的信息位，这K 段时间内的码元数目为K ·k ，称参数K 为卷积码的约束长度，每k 个比特输入，得到n 比特输出，编码效率为k /n ，约束长度为K 。

在k =1的条件下，移位寄存器级数m =K -1。

卷积码一般可用(n ，k ，K )来表示，其中k 为输入码元数，n 为输出码元数，而K 则为编码器的约束长度。

典型的卷积码一般选n 和k ( k < n ) 值较小，但约束长度K 可取较大值(K <10)，以获得既简单又高性能的信道编码[6]。

卷积码是1955年Elias 最早提出，1957年Wozencraft 提出了序列译码。

1963年Massey 提出了一种性能稍差，但比较实用的门限译码方法。

1967年维特比(Viterbi)提出了最大似然译码。

它对存储器级数较小的卷积码的译码很容易实现，称为维特比算法或维特比译码。

图1、二进制卷积码的编码器图2给出了（3，1，2）二进制卷积码编码器。

在每一时间单位，输入一个比特信息i m，同时存贮器内的数据向右移一位，产生3个比特的输出i c ，其中一个是输入比特i m，两个是校验比特,1i p ，,2i p 。

图2由图可知： ,12,212i i i i i i i p m m p m m m ---=⊕=⊕⊕因为校验比特是输入信息元i m的模2和，它们是线性关系，所以这类卷积码是线性码。

称i c为卷积码的一个子码或码段，它不仅与当前输入信息有关，还与前2个（m ）时间单位的输入信息有关，即和前2个子码有关；而且i m要经过2个时间单位才能移出存贮器，所以i c 也参与了后2个子码中的校验运算，称1N m =+为编码约束度，说明编码过程中互相约束的码段个数。

【实验名称】卷积码的编码与译码【实验内容】写一份程序实现卷积码的编码和译码。

【实验原理】卷积码的编码方法是对输入的数据流每次1比特或K比特进行编码，输出N 个编码符号。

但输出的码字的每个码元不仅和当前时刻输入的K个信息有关，也和之前的M个连续输入的信息元有关，因此卷积编码是有记忆的。

而译码则是通过一串码字通过状态流程图或网格图找出唯一的最佳路径进行逆推而得到码元信息。

（这里不再赘述，下面有例子说明）。

【实验流程】（举例说明如下）1、编码过程：本次设计以（2，1，2）卷积码为例。

图1为这种卷积编码器的结构，它的编码方法是：序列依此移入一个两级移位寄存器，编码器每次输入一位信息b，输出端的开关就在c1和c2之间来回切换一次，输出为c1c2，其中c1=b1+b2+b3c2=b1+b3图1（2，1，2）卷积编码器假设寄存器m1、m2的起始状态为全零，则编码器的输入输出时序关系图可用图2来表示。

图2 （2，1，2）卷积编码器输入输出时序如果输入的数据流是101011，则根据上面编码器我们可以得到输出的编码数据流为11 10 00 10 00 01。

.2、解码过程解码是编码的逆过程，了解了编码过程后，理解解码过程的操作就相对容易了。

首先我们根据卷积码的特点，我们采用了两种图解对卷积码进行研究，一种是状态转移图，另一种是网格图。

其状态转移图如图3所示，椭圆里面的数据代表当前状态，箭头方向代表转移的方向，0/11代表输入的码元为0，输出11。

.图3 （2，1，2）卷积编码器状态转移图另一种更为常用的是网格图，横坐标表示时间轴，每一次状态转移利用连接相邻的时间点上的两个状态的有向线段来表示。

图4便是对应的网格图。

图4 （2，1，2）卷积编码器网格图我们解码的思路是由于信息序列和编码序列有着一一对应的关系，而这种关系又唯一对应网格图的一条路径，因此译码就是根据接收序列在网格图上的路径逆推出源码码元信息序列。

但是这样的最大似然译码在现实编码难以实现，因为找出最佳路径用的是逐步比较，把接收序列的第j个分支码字和网格图上相应的两个时刻t1和t2之间进行比较，计算和记录他们的汉明距离等，这样比较分支较多不易实现。

毕业设计（论文）开题报告题目名称:卷积码编码与译码算法的仿真研究院系名称: 电子信息学院班级:学号:学生姓名:指导教师:2010年4月1课题背景及意义通信的目的是要把对方不知道的消息及时可靠地传送给对方。

这就要求一个通信系统传输消息必须可靠和快速。

在数字通信系统中可靠与快速往往是一对矛盾, 若要求快速,则必然使得每个数据码元所占的时间缩短、波形变窄、能量减少, 从而在受到干扰后产生错误的可能性增加, 传送消息的可靠性减低。

若要求可靠, 则使得传送消息的速率变慢。

因此, 如何合理地解决可靠性与速度这一对矛盾, 是正确设计一个通信系统的关键问题之一。

随着现代通信的发展, 在高速信息传输和高可靠性传输成为信息传输的两个主要方面中, 可靠性尤其重要.因为信道状况的恶劣, 信号不可避免会受到干扰而出错.为实现可靠性通信, 主要有两种途径: 一种是增加发送信号的功率, 提高接收端的信号噪声比；另一种是采用编码的方法对信道差错进行控制。

前者常常受条件限制, 不是所有情况都能采用。

例如卫星通信系统以很远的距离传送数据, 由于衰落、噪声和干扰等的影响,信号在传输过程中将产生严重的畸变。

如果要求信号具有尽可能大的能量, 卫星体积和载重就大大增加, 会使成本相对于原来大大增加, 所以不可能给信号提供太大的能量, 建立在香浓基础上的编码理论正可以解决这个问题, 使得成本降低, 实用性增强。

1948年，美国贝尔实验室的Claude E。

Shannon在贝尔技术杂志上发表了题为《通信的数学理论》的论文,这是一篇关于现代信息理论的奠基性论文，它的发表标志着信息与编码理论这一学科的创立。

Claude E.Shannon在该文中指出，任一通信信道都有一个参数,称之为信道容量C，如果通信系统所要求的传输速率R小于C，则存在一种编码方法,当码长n充分长并应用最大似然译码时,系统的错误概率可以达到任意的小.这就是著名的信道编码理论。