最新人教版小学四年级下册数学总复习资料
- 格式:doc
- 大小:207.00 KB
- 文档页数:13

人教版最新最全四年级数学下册知识点总结(总复习)第一单元四则运算1.加减法的意义和各部分间的关系。
(1)把两个数合并成一个数的运算,叫做加法。
加法各部分间的关系:和=加数+加数加数=和-另一个数(2)已知两个数的和与其中一个加数,求另一个数的运算,叫做减法。
减法各部分间的关系:差=被减数-减数减数=被减数-差被减数=差+减数(3)加法和减法是互逆运算。
2.乘除法的意义和各部分间的关系。
(1)求几个相同加数的和的简便运算,叫做乘法。
乘法各部分间的关系:积=因数×因数因数=积÷另一个因数(2)已知两个因数的积与其中一个因数,求另一个因数的运算,叫做除法。
除法各部分间的关系:商=被除数÷除数除数=被除数÷商被除数=商×除数(3)乘法和除法是互逆运算。
3.关于“0”的运算(1)“0”不能做除数;字母表示:a÷0是错误的(2)一个数加上0还得原数;字母表示:a+0=a (3)一个数减去0还得原数;字母表示:a-0=a (4)被减数等于减数,差是0;字母表示:a-a=0 (5)任何数和0相乘,仍得0;字母表示:a×0=0(6)0除以任何非0的数,还得0;字母表示:0÷a(a≠0)=0 (7)0÷0得不到固定的商;5÷0得不到商. (8)被减数等于减数,差是0;a-a=0(9)被除数等于除数,商是1;a÷a=1(a不为0)4.在没有括号的算式里,如果只有加.减法或者只有乘.除法,都要从左往右按顺序计算。
5.在没有括号的算式里,有乘.除法和加.减法.要先算乘除法,再算加减法。
6.一个算式里既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算括号外面的有括号,要先算括号里面的,再算括号外面的;括号里面的算式计算顺序遵循以上的计算顺序。
第二单元观察物体1.从不同的位置观察同一物体,看到的形状一般是不一样的。

总复习总复习——四则运算本学期内容总结:{四则运算观察物体(二)运算定律小数的意义和性质三角形小数的加法和减法图形的运动(二)平均数与条形统计图数学广角——鸡兔同笼四则运算即加、减、乘、除,计算的话相信大家都会,但它们表示的意义以及什么时候使用哪种运算呢?我们就来复习一下例1、加、减、乘、除的概念(1)(),叫做加法。
相加的两个数叫做(),加得的数叫做()。
(2)(),叫做减法。
在减法中,已知的和叫做(),已知的加数叫做(),未知的加数叫做()。
(3)()叫做乘法。
相乘的两个数叫做(),乘得的数叫做()。
(4)()叫做除法。
例2、四则运算中,各部分的关系。
(1)加法各部分的关系:(2)减法各部分的关系:①()①()②()②()③()(3)乘法各部分的关系:(4)除法各部分的关系:①()①()②()②()③()(5)加法与减法互为逆运算,乘法与除法互为逆运算。
例3、四则运算的运算顺序:从()往()运算,先算()法,再算加减法()。
例4、括号有()括号、()括号、()括号,分别写作()、()、()。
例5、四则混合运算的顺序:步骤①:有括号,要先算()里面的式子。
从()往()运算,先算()括号的,再算()括号的,最后算()括号的。
步骤②:没有括号,也要从()往()运算。
先算()法,后算()法。
例6、在计算(200-36×47)÷44时,先算(),再算(),最后算()法,结果是()。
例7、650-320÷80,如果要改变运算顺序,先算减法,那么必须使用括号,算式是()。
例8、根据500÷125=4,4+404=408,804-408=396组成一个综合算式是()。
例9、与0相关的性质(1)一个数加上0,得()。
例如:5+0=5,9+0=9 。
(2)一个数减去0,得()。
例如:5-0=5,9-0=9 。
(3)当被减数等于减数,它们的差等于()。
例如:5-5=(),9-9=()。

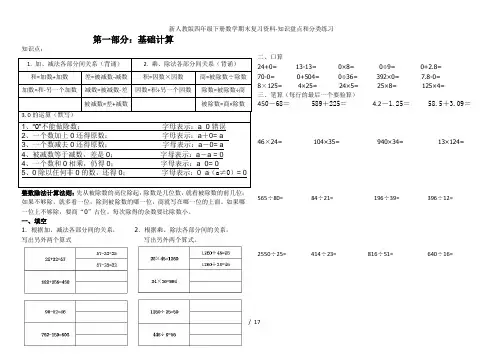
第一部分:基础计算知识点:1. 加、减法各部分间关系(背诵)2. 乘、除法各部分间关系(背诵)和=加数+加数差=被减数-减数积=因数×因数商=被除数÷除数加数=和-另一个加数减数=被减数-差因数=积÷另一个因数除数=被除数÷商被减数=差+减数被除数=商×除数3. 0的运算(默写)1、“0”不能做除数;字母表示:a÷0错误2、一个数加上0还得原数;字母表示:a+0= a3、一个数减去0还得原数;字母表示:a-0= a4、被减数等于减数,差是0;字母表示:a-a = 04、一个数和0相乘,仍得0;字母表示:a×0= 05、0除以任何非0的数,还得0;字母表示:0÷a(a≠0)= 0整数除法计算法则:先从被除数的高位除起,除数是几位数,就看被除数的前几位;如果不够除,就多看一位,除到被除数的哪一位,商就写在哪一位的上面。
如果哪一位上不够除,要商“0”占位。
每次除得的余数要比除数小。
一、填空1.根据加、减法各部分间的关系,2.根据乘、除法各部分间的关系,写出另外两个算式写出另外两个算式。
二、口算24+0= 13-13= 0×8= 0÷9= 0+2.8=70-0= 0+504= 0÷36= 392×0= 7.8-0=8×125= 4×25= 24×5= 25×8= 125×4=三、笔算(每行的最后一个要验算)450-68= 589+225= 4.2-1.25= 58.5+3.09=46×24= 104×35= 940×34= 13×124= 565÷80= 84÷21= 196÷39= 396÷12= 2550÷25= 414÷23= 816÷51= 640÷16=1 / 172 /四、思考题14 + 82 - =87 ×6+10 = 58 = = 计算过关检测 一、填空。

四年级下册知识点汇总一、四则运算:1、加法、减法、乘法和除法统称为四则运算。
2、四则运算的意义(什么叫加减乘除法)3、四则运算各部分之间的关系(见课本,共10条)补充:在有余数的除法里被除数=商×除数+余数除数=(被除数–余数)÷商商=(被除数–余数)÷除数余数=被除数–商×除数4、四则运算运算顺序:(1)、在没有括号的算式里,如果只有加减法或只有乘除法,都要从左往右按顺序(依次)计算。
(2)、在没有括号的算式里,有加减法又有乘除法,要先算乘除法,后算加减法。
(3)、算式里有括号时,要先算括号里面的,再算括号外面的。
(小括号起到改变运算顺序的作用)。
(4)既有小括号,又有中括号的,要先算小括号里面的。
5、有关0的运算:(1)一个数加上0得原数。
a+0=a(2)一个数减去零还得原数。
a-0=a(3)任何一个数乘0得0。
a×0=0(4)0除以一个非0的数等于0。
0÷a=0(a≠0).0不能做除数,0作除数没有意义。
(5)被减数等于减数,差是0. a-b=0→a=b6、※:除和除以不同。
A除以B,写成A÷B。
A除B,写成B÷A。
二、观察物体:从不同位置观察不同形状的物体,得到的视图形状可能是相同的,也可能是不同的三、运算定律及简便运算:1、加法运算定律:(1)、加法交换律:a+b=b+a(2)、加法结合律:(a+b)+c=a+(b+c)※:交换律改变的是数的位置,结合律改变的是运算顺序。
结合律的标志是小括号的应用。
2、乘法运算定律:(1)、乘法交换律: a × b = b × a (2)、乘法结合律:(a×b)×c = a × ( b ×c )※:特殊数的乘积:5×2=10 25×4=100125×8=1000 25×8=200 75×4=300※:在乘法中,如果一个因数是25或125,另一个因数正好是4或8的倍数,就将另一个因数分解成4或8与其他数乘积的形式,再利用乘法结合律先算25×4或125×8.(3)、乘法分配律:(a+b )×c=a ×c+b ×c ※:注意如果乘法算式,可以找出相同的因数时,逆用乘法分配律。

最新新人教版四年级下册数学总复习资料(精华版)-人教版四下数学总复习研究——好资料总复一:数与代数第一单元:四则运算一、加减法的意义和各部分间的关系。
加法是把两个数合并成一个数的运算。
和等于两个加数的和,加数等于和减去另一个加数。
减法是已知两个数的和与其中一个加数,求另一个加数的运算。
差等于被减数减去减数,减数等于被减数减去差。
二、乘除法的意义和各部分间的关系。
乘法是求几个相同加数的和的简便运算。
积等于两个因数相乘,因数等于积除以另一个因数。
除法是已知两个因数的积与其中一个因数,求另一个因数的运算。
商等于被除数除以除数,除数等于被除数除以商。
注意:减法是加法的逆运算,除法是乘法的逆运算。
有余数的除法的关系式为被除数等于除数乘商加余数。
三、有关的运算1、不能作除数,可以作被除数。
A÷÷错误。
2、一个数加上0,还是原数。
A+0=A。
3、一个数减去0,还是原数。
A-0=A。
4、一个数和0相乘,得0.A×0=0.5、除以一个非零数,得0.A÷A=1(A≠0)。
6、被减数等于减数,差是0.A-A=0.7、被除数等于除数(除外),商是1.A÷A=1(A≠0)。
四、四则运算顺序四则运算包括加、减、乘、除四种运算。
加法和减法称为第一级运算,乘法和除法称为第二级运算。
在没有括号的算式里,如果只有加、减法或者只有乘、除法,都要从左往右按顺序计算。
在没有括号的算式里,有加减法,又有乘除法,要先算乘除法,后算加减法。
如果一个算式里既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算括号外面的。
五、租船问题解决租船问题时,尽量乘坐人均租金便宜的船,大小船搭配正好满员,没有空余座位时最省钱。
例题:老师和同学们一起去划船,一共有30人,大船每条限乘6人,租金35元。
小船每条限乘4人,租金20元。
怎样租船最省钱?第三单元:运算定律与简便计算一、加法运算定律加法交换律:两个数相加,交换加数的位置,和不变。



第一单元四则运算一、加、减法的意义和各部分间的关系1、加法的意义:把两个数合并成一个数的运算,叫做加法。
相加的两个数叫做加数,加得的数叫做和。
2、加法各部分间的关系:和=加数+加数加数=和-另一个加数3、减法的意义:已知两个数的和与其中一个加数,求另一个加数的运算,叫做减法。
在减法中,已知的和叫做被减数,减号后面的数叫做减数,等号后面的数叫做差。
4、减法各部分间的关系:差=被减数-减数减数=被减数-差被减数=减数+差5、加法与减法的关系:减法是加法的逆运算。
二、乘、除法的意义和各部分间的关系1、乘法的意义:求几个相同加数的和的简便运算,叫做乘法。
相乘的两个数叫做因数,乘得的数叫做积。
2、乘法各部分间的关系:积=因数X因数因数=积÷另一个因数3、除法的意义:已知两个因数的积与其中一个因数,求另一个因数的运算,叫做除法。
已知的积叫做被除数,已知的因数叫做除数,求得的另一个因数叫做商。
4、除法各部分间的关系:①、在没有余数的除法中:商=被除数÷除数除数=被除数÷商被除数=商X除数②、在有余数的除法中:被除数=商X除数+余数商=(被除数-余数)÷除数除数=(被除数-余数)÷商三、有关0的运算①、一个数加上或减去0还得原数②、任何数减去自身都得0③、0除以任何非0的数还得0④、任何数乘0都得0⑤、0不能作除数四、四则混合运算的运算顺序1、在没有括号的算式里,只有乘除法或只有加减法,要按从左到右的顺序计算,有乘除法和加减法的,要先算乘除法,后算加减法。
2、有小括号的算式里,要先算小括号里面的,再算小括号外面的。
3、一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
第二单元观察物体1、从不同位置观察由小正方体拼摆的物体,辨认观察到的物体的形状的方法:在哪一位置观察物体,就从哪一面数出小正方形的数量,并确定摆出的形状。

人教版四年级数学下册知识点归纳一、四则运算1. 加法的意义和各部分间的关系- 意义:把两个数合并成一个数的运算,叫做加法。
- 各部分间的关系:和 = 加数+加数;加数 = 和 - 另一个加数。
2. 减法的意义和各部分间的关系- 意义:已知两个数的和与其中的一个加数,求另一个加数的运算,叫做减法。
- 各部分间的关系:差=被减数 - 减数;减数 = 被减数 - 差;被减数 = 差+减数。
- 减法是加法的逆运算。
3. 乘法的意义和各部分间的关系- 意义:求几个相同加数的和的简便运算,叫做乘法。
- 各部分间的关系:积 = 因数×因数;因数 = 积÷另一个因数。
4. 除法的意义和各部分间的关系- 意义:已知两个因数的积与其中一个因数,求另一个因数的运算,叫做除法。
- 各部分间的关系:商 = 被除数÷除数;除数 = 被除数÷商;被除数 = 商×除数。
- 除法是乘法的逆运算。
5. 四则混合运算的顺序- 在没有括号的算式里,如果只有加、减法或者只有乘、除法,都要从左往右按顺序计算。
- 在没有括号的算式里,如果既有乘、除法又有加、减法,要先算乘、除法,后算加、减法。
- 一个算式里有括号,要先算括号里面的,再算括号外面的;如果既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算括号外面的。
二、观察物体(二)1. 从不同位置观察物体- 从不同的位置观察同一物体,所看到的形状一般是不同的。
- 从同一位置观察不同的物体,所看到的形状可能相同,也可能不同。
2. 根据视图摆物体- 根据从一个方向看到的图形摆立体图形,有多种摆法。
- 根据从三个方向看到的图形摆立体图形,一般可以确定立体图形的形状。
三、运算定律1. 加法运算定律- 加法交换律:两个数相加,交换加数的位置,和不变。
用字母表示为a +b=b + a。
- 加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。

人教版最新最全四年级数学下册知识点总结(总复习)2.加法结合律:三个数相加,先把前两个数相加,再把和与第三个数相加,结果不变。
a+(b+c)=(a+b)+c。
二.乘法运算定律:1.乘法交换律:两个数相乘,交换因数的位置,积不变。
a×b=b×a。
2.乘法结合律:三个数相乘,先把前两个数相乘,再把积与第三个数相乘,结果不变。
a×(b×c)=(a×b)×c。
三.分配律:乘法分配律和加法分配律。
1.乘法分配律:一个数乘以两个数的和,等于这个数分别乘以这两个数的和的积。
a×(b+c)=a×b+a×c。
2.加法分配律:两个数相加,再乘以一个数,等于这两个数分别乘以这个数的和再相加。
a+b×c=(a×c)+(b×c)。
四.乘方:1.一个数的平方是这个数自己乘以自己。
a²=a×a。
2.一个数的立方是这个数自己乘以自己再乘以自己。
a³=a×a×a。
3.一个数的n次方是这个数自己连乘n个自己。
aⁿ=a×a×a×。
×a(n个a)。
五.简便运算:1.末尾是0的数,可以先把0去掉再计算。
例如:30+50=3×10+5×10=8×10=80.2.相邻的数相减,可以把相同的数去掉,例如:9876-9870=6.3.乘法口诀表:用来快速计算两个数的积。
例如:7×8=56,可以在口诀表中找到7所在的行和8所在的列,交叉处的数就是积。
加法结合律指出,三个数相加时,可以先把前两个数相加,再加上第三个数,或者先把后两个数相加,再加上第一个数,和不变。
例如,165+93+35=93+(165+35)。
这个定律通常与加法交换律一起使用。
连减的性质是指,一个数连续减去两个数,等于这个数减去那两个数的和。
人教版数学四年级下册《总复习》(四则运算、运算定律与简便计算)教案一. 教材分析人教版数学四年级下册《总复习》主要涉及四则运算、运算定律与简便计算。
这一部分内容是小学数学的基础,对于培养学生的逻辑思维和数学素养具有重要意义。
教材通过复习和总结,帮助学生巩固已学的知识,提高解决问题的能力。
二. 学情分析四年级的学生已经掌握了基本的四则运算和运算定律,但对于一些复杂的简便计算方法可能还不够熟练。
学生的学习兴趣较高,但部分学生可能对一些概念和运算方法的理解不够深入,需要通过教学加以引导和巩固。
三. 教学目标1.使学生掌握四则运算的基本方法和运算定律。
2.培养学生运用运算定律进行简便计算的能力。
3.提高学生的逻辑思维和解决问题的能力。
四. 教学重难点1.重点:掌握四则运算的基本方法,熟练运用运算定律进行简便计算。
2.难点:理解并运用一些特殊的简便计算方法。
五. 教学方法采用问题驱动、案例教学、合作学习等方法,引导学生通过自主学习、讨论交流,掌握四则运算和运算定律,提高简便计算能力。
六. 教学准备1.教材和人教版数学四年级下册《总复习》相关资料。
2.教学PPT或其他辅助教学材料。
3.练习题和答案。
七. 教学过程1.导入(5分钟)通过一个实际问题,引出四则运算和运算定律的重要性,激发学生的学习兴趣。
示例问题:小明有12个苹果,他想把它们平均分给4个朋友,每个朋友能得到多少个苹果?2.呈现(10分钟)呈现四则运算和运算定律的相关知识,引导学生回顾和总结已学的知识。
四则运算:加法、减法、乘法、除法运算定律:交换律、结合律、分配律3.操练(10分钟)通过一些具体的例子,让学生运用四则运算和运算定律进行计算,巩固所学知识。
1.23 + 17 = ?2.35 - 18 = ?3.42 × 5 = ?4.63 ÷ 9 = ?5.巩固(10分钟)让学生分成小组,互相讨论和解答一些有关四则运算和运算定律的问题,提高合作学习能力。
人教版四年级下册数学知识点总结
人教版四年级下册数学知识点总结:
1. 四角形:包括矩形、正方形、菱形、平行四边形等。
掌握它们的性质和特点。
2. 平行线与垂直线:学会通过直角获得垂直线、平行线的定义与判断。
3. 分数:认识分数的概念,能够用图形模型表示分数。
4. 单位换算:掌握厘米、分米、米之间的换算关系,用计量器具进行测量。
5. 三角形:学会认识、分类和计数三角形。
6. 读表:掌握读取时、分、秒的常用表述和指示钟表的读法。
7. 数据统计和图表:学会读懂数据表和直方图,进行简单的数据统计和比较。
8. 三位数相减:用在三位数相加的基础上,进一步掌握三位数相减的方法。
9. 数量的估计:学会用精确的数值估算数量,掌握近似估算的方法。
10. 钱的计算:学习变换货币单位和精确计算的方法。
11. 二位数乘一位数:学习二位数和一位数的乘法运算。
12. 长方体的表面积:计算并解决长方体表面积的问题。
13. 二位数除一位数:学习二位数和一位数的除法运算。
14. 图形的位置关系:学会在平面上描述、比较、判定图形的位置关系。
这些是人教版四年级下册数学的主要知识点,通过学习这些知识点,能够提高数学能力,培养逻辑思维和解决问题的能力。
四年级数学下册复习资料第1单元四则运算1、运算顺序P5:在没有括号的算式里,如果只有加、减法或者只有乘、除法,都要按从左往右的顺序计算。
P6:在没有括号的算式里,有乘、除法和加、减法,要先算乘除法,再算加减法。
P11:算式里有括号的,要先算括号里面的,再算括号外面的。
2、P12:加、减、乘和除统称四则运算。
3、P13:有关0的运算一个数与0相加,还得这个数。
一个数减去0,还得这个数。
一个数与0相乘,得0。
0除以一个数,得0。
0不能做除数,例如5÷0 是不存在,没有意义的。
4、四则混合运算方法一看(看数字,运算符号,想想运算顺序是什么。
)二画(画线,哪一步先算,就在哪一步的下面画一条横线,没有计算的要照抄下来。
)三算(按照运算顺序计算)四检验(检验运算顺序是否错误,计算是否算错。
)第2单元位置与方向1、确定物体的位置(1)找参照物:以谁为参照物,就以谁为观测点。
如:“在XXX的东偏南”就是以“XXX”为观测点(2)找出较小的夹角,从箭头方向开始写出方向。
(3)确定物体位置的条件:方向和距离这两个条件缺一不可。
2、在平面图上标出物体位置的方法(1)确定观测点,建立方向标。
(2)用量角器确定建筑物的方向。
(3)用直尺确定建筑物的距离。
(4)画出建筑物具体位置,标出名称。
3、位置关系的相对性4、描述并绘制简单的路线图第3单元运算定律与简便计算1、运算定律与算式特点P28:加法交换律a+b=b+a 34+89+66=34+66+89 26+47-6=26-6+471、只有加法,减法。
2、注意减法时要将前面的“一”号一起交换。
3、在简便计算时,一般将加法交换律和加法结合律同时运用。
P29:加法结合律a+b+c=a+(b+c) 88+104+96=88+(104+96) 79+26-9=26+(79-9)P34:乘法交换律a × b=b× a 4×58×25=4×25×581、只有乘法。
第一部分:基础计算知识点:写出另外两个算式。
二、口算24+0= 13-13= 0×8= 0÷9= 0+2.8=70-0= 0+504= 0÷36= 392×0= 7.8-0=8×125= 4×25= 24×5= 25×8= 125×4=三、笔算(每行的最后一个要验算)450-68= 589+225= 4.2-1.25= 58.5+3.09=46×24= 104×35= 940×34= 13×124=565÷80= 84÷21= 196÷39= 396÷12=2550÷25= 414÷23= 816÷51= 640÷16=四、思考题14 + 82 - =87 ×6+10 = 58= =计算过关检测一、填空。
(7分)1、一个数和0相乘,得()。
2、被减数等于减数,差是()。
除以任何非零的数都得( )。
700-169= 511+479= 4.2-0.359= 738+1.17=36×27= 108×25= 124×31= 18×930=88÷14= 119÷15 = 2134÷24= 396÷12=364÷70= 64÷22 = 952÷28= 3276÷84=三、解决问题(29分)1.蜗牛每天可爬行120m ,21天能爬行多少米?2.120支铅笔,每12支装一盒,可以装几盒?3.蜗牛每天爬120m ,平均每小时爬多少米?(1天=24小时)4.一头大象的体中是5600kg ,正好是一头牛的体重的8倍,这头牛有多重?思考题1. ( ) — ( )2.把下面一组用图形表示的算是改写成一个综合算式 — =×列式为:第二部分四则运算一、填空。
四年级数学下册知识点重点难点考点汇总复习建议第一单元:四则运算1. 重点知识点-四则运算的意义和各部分间的关系:加法是把两个数合并成一个数的运算,减法是已知两个数的和与其中一个加数,求另一个加数的运算,乘法是求几个相同加数和的简便运算,除法是已知两个因数的积与其中一个因数,求另一个因数的运算。
如加法中,和=加数+ 加数,加数= 和-另一个加数;乘法中,积= 因数×因数,因数= 积÷另一个因数。
-四则混合运算的顺序:在没有括号的算式里,如果只有加、减法或者只有乘、除法,都要从左往右按顺序计算;如果既有乘、除法又有加、减法,要先算乘、除法,后算加、减法。
有括号的算式,要先算括号里面的,再算括号外面的。
2. 难点-理解减法是加法的逆运算、除法是乘法的逆运算的含义,尤其是在解决复杂问题中运用这种关系。
-正确处理含有括号的四则混合运算,特别是多层括号的情况,容易出现运算顺序错误。
3. 考点-根据四则运算各部分间的关系填空或解决简单问题,如已知和与一个加数求另一个加数。
-四则混合运算的计算,常以脱式计算的形式考查,要求准确遵循运算顺序。
第二单元:观察物体(二)1. 重点知识点-从不同方向观察物体:能正确辨认从前面、上面、左面观察到的简单物体或由几个正方体组成的几何体的形状。
例如,通过观察一个由多个正方体搭建的立体图形,描述从不同方向看到的平面图形。
-根据视图还原物体:根据从不同方向观察到的图形,想象和还原出物体的形状,培养空间观念。
2. 难点-从斜方向观察物体的视图判断,以及根据给出的三个方向视图准确还原立体图形,需要较强的空间想象能力。
-对于复杂的组合几何体,准确分析从各个方向看到的形状,尤其是有遮挡情况的判断。
3. 考点-给出立体图形,选择从不同方向看到的视图,以选择题或判断题形式出现。
-根据给定的几个方向视图,画出或选择正确的立体图形,多为操作题或选择题。
第三单元:运算定律1. 重点知识点-加法运算定律:加法交换律(a + b = b + a)和加法结合律((a + b)+ c = a +(b + c)),能运用这些定律进行简便计算,如计算25 + 36 + 75,可以利用加法交换律和结合律得到(25 + 75)+ 36 = 136。
第一单元:四则运算【知识要点1】:加减法的意义和各部分间的关系【重点内容】:★把两个数合并成一个数的运算,叫做加法。
★相加的两个数叫做加数,加得的数叫做和。
★已知两个数的和与其中一个加数,求另一个加数的运算叫做减法。
★在减法中,已知的和叫做被减数,减得的数叫做差。
★加法和减法互为逆运算。
和=加数+加数加数=和-另一个加数差=被减数-减数减数=被减数-差被减数=加数+差【例题】:根据864+325=1189直接写出下面两道题的得数。
1189-864= 1189-325=【知识要点2】:乘除法的意义和各部分间的关系【重点内容】:★求几个相同加数的和的简便运算,叫做乘法。
★相乘的两个数叫做因数,乘得的数叫做积。
★在乘法算式中,0乘以任何数都得0;1乘以任何数都是任何数。
★已知两个因数的积与其中一个因数,求另一个因数的运算叫做除法。
★在除法中,已知的积叫做被除数,除得的数叫做商。
★在除法算式中,0除以任何数都得0;0不能作除数;任何数除以1都是任何数。
★除法和乘法互为逆运算。
积=因数×因数因数=积÷另一个因数商=被除数÷除数除数=被除数÷商被减数=商×除数有余数的除法各部分间的关系:被除数÷除数=商……余数被除数=商×除数+余数除数=(被除数-余数)÷商商=(被除数-余数)÷除数余数=被除数-除数×商【例题】根据36×14=504直接写出下面两道题的得数。
504÷14= 504÷36=【知识要点3】:有关0的运算【重点内容】:★一个数加上0,还得原数。
字母表示:a + 0 = a★被减数等于减数,差是0。
字母表示:a - a = 0★一个数减去0,还得原数。
字母表示:a - 0 = a★一个数和0相乘,仍得0。
字母表示:a X 0 = 0★ 0除以一个非0的数,得0。
字母表示:0 ÷ a = 0 (a ≠ 0)★两个不等于0的相同数相除,商一定是1。
字母表示:a ÷ a = 1 (a ≠ 0)★ 0不能作除数,0可以作被除数。
字母表示:a ÷ 0 此式错误,不成立【例题】:计算: 0÷27+5×0+4【知识要点4】:四则运算顺序【重点内容】:★加、减、乘、除四种运算统称四则运算。
★在没有括号的算式里,如果只有加、减法或者只有乘、除法,都要从左往右按顺序计算。
★在没有括号的算式里,有加减法,又有乘除法,要先算乘除法,后算加减法。
★算式里有括号的,要先算括号里面的。
既有小括号,又有中括号和大括号时,要先算小括号里面的,再算中括号里面的,后算大括号里的,最后再按照同级运算规则来算括号外面的。
【例题】计算(34×2+92)÷16-7【知识要点5】:租船问题【重点内容】:★解决租船问题时,尽量乘坐人均租金便宜的船,大小船搭配正好满员,没有空余座位时最省钱。
【例题】:老师和同学们一起去划船,一共有30人,大船每条限乘6人,租金35元。
小船每条限乘4人,租金20元。
怎样租船最省钱?第二单元:观察物体(二)【知识要点1】:从不同位置观察物体【重点内容】:★从不同位置观察不同的物体,所看到的形状可能相同,也可能不相同。
★观察时,先确定看到的图形有几层(列),每层(列)的小正方体有几列(层)。
★只有从正面、左面、上面观察小正方体组成的几何图形时才可以确定其形状。
【例题】:1、连线题:2、画出从前面、上面、左面看到的图形。
从前面看:从上面看:从左面看:第三单元:运算定律与简便计算【知识要点6】:加法运算定律【重点内容】:★加法交换律:两个数相加,交换加数的位置,和不变。
字母表示:a + b = b + a★加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
字母表示;(a+b)+ c = a +(b+c)。
【例题】计算: 26+37+74 46+28+54+72【知识要点7】:连减的简便计算【重点内容】:★一个数连续减去两个数,等于这个数减去这两个数的和。
字母表示:a-b-c = a-(b+c)★在减法计算中,交换减数的位置,差不变。
字母表示:a-b-c = a-c-b【例题】计算: 356—27—73 545—167—145【知识要点8】:乘法运算定律【重点内容】:★乘法交换律:两个数相乘,交换两个因数的位置,积不变。
字母表示为:a×b = b×a。
★乘法结合律: 三个数相乘,先乘前两个数,或者先乘后两个数,积不变。
字母表示为:(a×b)×c = a×(b×c)★乘法分配律:两个数的和与一个数相乘,可以把它们与这个数分别相乘,再相加。
字母表示为:(a+b)× c = a×c+b×c a×(b+c) = a×b + a×c逆运算:a×b + a×c = a×(b+c)★结合律是一种运算,分配律是两种运算。
乘法分配律也适用于减法。
【例题】1、图书馆新进一批图书共12包,每包25本,每本4元。
这批图书一共多少元?2、计算(21+25)×4 64×64+36×64 265×105—265×5【知识要点9】:除法的运算定律【重点内容】:★一个数连续除以两个数,等于这个数除以两个除数的积。
字母表示为:a÷b÷c=a÷(b×c)★在除法中,交换除数的位置,商不变。
字母表示为:a÷b÷c=a÷c÷b 【例题】计算:①3200÷4÷25 ②88×125 ③99×38+38【使用简便方法的例子】:敏感数字:25×4=100; 125×8=10001、加法交换律简算例子2、加法结合律简算例子75+98+25 488+40+60=75+25+98 =488+(40+60)=100+98 =488+100=198 =5883、乘法交换律简算例子4、乘法结合律简算例子25×56×4 99×125×8=25×4×56 =99×(125×8)=100×56 =99×1000=5600 =990005、含有加法交换律与结合律简算例子6、含有乘法交换律与结合律简算例子 65+28+35+72 25×125×4×8=(65+35)+(28+72) =(25×4)×(125×8)=100+100 =100×1000=200 =1000007、乘法分配律简算例子:分解式例子合并式例子特殊1(添项)25×(40+4) 135×12-135×2 99×256+256=25×40+25×4 =135×(12-2) =99×256+256×1=1000+100 =135×10 =(99+1)×256=1100 =1350 =100×256=25600特殊2 特殊3 特殊445×102 99×26 35×8-4×35 =45×(100+2) =(100-1)×26 =35×(8-4)=4500+90 =100×26-1×26 =35×4=4590 =2600-26 =140=25748、连续减法简算例子528-65-35 528-89-128528-(150+128)=528-(65+35) =528-128-89 =528-150-128=528-100 =400-89 =528-128-150=428 =311 =400-150=2509、连续除法简算例子 10、其他简算例子(带着符号搬家)3200÷4÷25 256-58+44250÷8×4=3200÷(4×25) =256+44-58 =250×4÷8=3200÷100 =300-58 =1000÷8=32 =242 =125第四单元:小数的意义和性质【知识要点10】:小数的产生和意义【重点内容】:★小数是由整数部分、小数点、小数部分组成的。
★在进行测量和计算时,往往不能正好得到整数的结果,这时常用小数来表示。
★分母是10、100、1000……的分数可以用小数来表示。
小数的计数单位是十分之一、百分之一、千分之一……分别写作0.1、0.01、0.001…每相邻两个计数单位之间的进率是10。
【例题】0.7里面有()个0.1。
0.42里面有()个0.01。
0.736里面有()个0.001。
2.83是由()个一、()个十分之一和()个百分之一组成的。
【知识要点11】:小数的读法和写法【重点内容】:★小数是由整数部分、小数点、小数部分组成的。
★小数的数位顺序如下表:★整数部分的最低位是个位,没有最高位。
小数部分的最高位是十分位,没有最低位。
因此,没有最大的小数,也没有最小的小数。
★小数的读法:第一种读法:先读整数部分,整数部分按整数的读法来读,再读小数点,最后读小数部分,小数部分要依次读出每个数字,有几个0就读出几个0。
例:0.45读作“零点四五”;1.0002读作“一点零零零二”。
另一种读法:按照分数的读法来读,整数部分按整数的读法来读,小数部分按分数的法来读。
例如:0.38读作百分之三十八;14.25读作十四又百分之二十五。
★小数的写法:先写整数部分,整数部分按整数的写法写,如果整数部分是零就直接写0,在个位的右下角点上小数点,小数部分依次写出每个数字。
【例题】1、读数:6.8 () 0.05() 320.08()2、写数:三百点八五()九点零七()零点零四二()3、写出下面各数中的“2”表示的意思。
20.04() 5.42 () 0.25() 0.672()【知识要点12】:小数的性质【重点内容】:★小数的末尾添上0或去掉0,小数的大小不变。
★应用小数的性质,可以根据需要改写小数。
★注意:只能在小数的末尾添上0或者去掉0,其他数位上的0不能动。
将整数改写成小数时,要先点上小数点,再在末尾添上0。
【例题】1、化简小数:0.80=() 105.0400=()2、不改变小数的大小爱,把下面小数改写成三位小数。