最优控制习题及参考答案[1]
- 格式:pdf
- 大小:185.82 KB
- 文档页数:12

2-5 求通过(0)1x =,(1)2x =,使下列性能泛函为极值的极值曲线*()x t :2(1)ft t J x dt =+⎰解:由题可知,始端和终端均固定被积函数21L x =+,0L x ∂=∂,2L x x ∂=∂, 2d L x dt x∂⋅=∂ 代入欧拉方程0L d L x dt x∂∂-⋅=∂∂,可得20x =,即0x = 故1x c = 其通解为:12x c t c =+代入边界条件(0)1x =,(1)2x =,求出11c =,21c = 极值曲线为*()1x t t =+2-6 已知状态的初值和终值为(1)4x =,()4f x t =式中f t 自由且f t >1,试求使下列性能泛函达到极小值的极值轨线*()x t :211[2()()]2ft J x t x t dt =+⎰ 解:由题可知,2122L x x =+,()4f t ψ=,()14x =,()4f x t = 欧拉方程:L 0d L x dt x∂∂-=∂∂ 横截条件:()00t x =x ,()()f f x t t ψ=,()0fTt L L x x ψ∂⎛⎫+-= ⎪∂⎝⎭易得到2dxdt= 故12x t c =+ 其通解为:()212x t t c t c =++根据横截条件可得:()()()122121114424f f f f f x c c x t t c t c x t t c ⎧=++=⎪⎪=++=⎨⎪=+=⎪⎩解以上方程组得:12569f t c c =⎧⎪=-⎨⎪=⎩将f t ,1c ,2c 代入J 可得5*201500502150233J x x dt =+=-=⎰ 极值轨线为()*269x t t t =-+2-7 设性能泛函为120(1)J x dt =+⎰求在边界条件(0)0x =,(1)x 自由情况下,使性能泛函取极值的极值轨线*()x t 。
解:由题可知,21L x =+,()00x =,()1x 自由欧拉方程:L 0d L x dt x∂∂-=∂∂ 横截条件:()00t x =x ,L 0ft x∂=∂,0fTt L L x x ∂⎛⎫+= ⎪∂⎝⎭易得到()x t a =其通解为:()x t at b =+代入边界条件()f x t a =,()00x =,1f t =,求出0a =,0b = 将f t ,a ,b 代入J 可得()1*211J x dt =+=⎰极值轨线为()*0x t = 2-9 求使泛函22211220(2)J x x x x dt π=++⎰为极值并满足边界条件1(0)0x =,2(0)0x =1()12x π=,2()12x π=- 的极值轨线*1()x t 和*2()x t 。


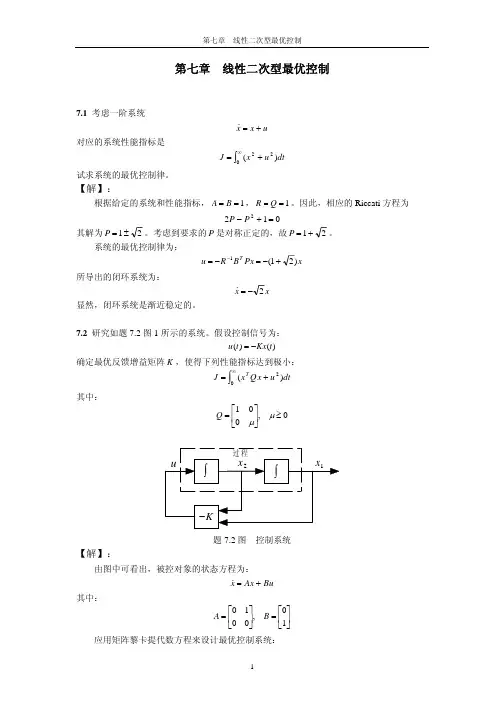
1. ·2.已知二阶系统的状态方程122()(),()()x t x t x t u t ==性能泛函3222221212120111[(3)2(3)][2()4()2()()()]222J x x x t x t x t x t u t dt =+++++⎰求最优控制。
解:把状态方程和性能指标与标准状态方程和标准性能指标比较,可得0,101,02,11,,,,0,010,21,42A B P Q R ⎡⎤⎡⎤⎡⎤⎡⎤=====⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦考虑到()K t 是对称阵,设11121222,(),k k K t k k ⎡⎤=⎢⎥⎣⎦代入黎卡提方程1()()()()()()()()()()()T T K t K t A t A t K t K t B t R t B t K t Q t -=--+-即1112111211121112111212221222122212221222,,,,,0,10,002,12[0,1],0,01,0,,1,1,4,k k k k k k k k k k k k k k k k k k k k ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=--+-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦令上式等号左右端的对应元相等,得211121211122222212222221224k k k k k k k k k =-=-+-=-+-这是一组非线性微分方程。
由边界条件(3)K P =即11121222(3),(3)1,0(3),(3)0,2k k k k ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ 最优控制为11112112122212222()()(),()2*[0,1]2()2(),()T u t R B K t X t k k x t k x t k x t k k x t -=-⎡⎤⎡⎤=-=--⎢⎥⎢⎥⎣⎦⎣⎦3. )4.能控的系统状态方程为122()(),()()x t x t x t u t ==这是一种双积分系统,其输出为1()x t ,其输入为()u t ,其传递函数为12()1()()x s G s u s s==其性能泛函为222112201[()2()()()()]2J x t bx t x t ax t u t dt ∞=+++⎰其中220a b ->求最优控制。


最优控制习题答案1.设系统方程及初始条件为⎩⎨⎧=+-=)()()(2)()(1211t x t x t u t x t x,⎩⎨⎧==0)0(1)(21x t x 。
约束5.1)(≤t u 。
若系统终态)(f t x 自由,利用连续系统极大值原理求)(*t u 性能指标,)3(2x J =取最小值。
解:2.设一阶离散时间系统为)()()1(k u k x k x +=+,初值2)0(=x ,性能指标为∑=+=2022)(21)2(k k u x J ,试用离散系统最小值原理求解最优控制序列:)2(),1(),0(u u u ,使J 取极小值。
解:3.软着落、空对空导弹的拦截问题、防空拦截问题。
解答:4.设离散系统状态方程为)(2.00)(101.01)1(k u k x k x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=+,已知边界条件⎥⎦⎤⎢⎣⎡=01)0(x ,⎥⎦⎤⎢⎣⎡=00)1(x 。
试用离散系统最小值原理求最优控制序列,使性能指标∑==102)(03.0k k u J 取极小值,并求出最优的曲线序列。
解:属于控制无约束,N 不变,终端固定的离散最优控制问题,构造离散哈密尔顿函数)](2.0)()[1()](1.0)()[1()(03.0)(222112k u k x k k x k x k k u k H ++++++=λλ其中)1(),1(21++k k λλ为给定拉个朗日乘子序列,由伴随方程:)1()()(111+=∂∂=k k x H k λλ,)1()1(1.0)()(2122+++=∂∂=k k k x Hk λλλ得出 ⎩⎨⎧+==+==)2()2(1.0)1(),2()1()1()1(1.0)0(),1()0(2121121211λλλλλλλλλλ,由极值条件⎪⎪⎩⎪⎪⎨⎧>=∂∂=++=∂∂006.0)(0)1(2.0)(06.0)(222k u H k k u k u Hλ极小)1(310)(2+-=k k u λ可使min )(=k H ,令k=0和k=1的⎪⎩⎪⎨⎧-=-=)2(310)1(*)1(310)0(*22λλu u ,)(k u 带入状态方程并令k=0和1得到: 5.求泛函dtx x x x J ⎰++=102221211],[ 满足边界条件π===-=)3(,0)0(,0)3(,3)0(2211x x x x 和约束条件36221=+t x 的极值曲线。


1. 已知二阶系统的状态方程122()(),()()x t x t x t u t ==性能泛函3222221212120111[(3)2(3)][2()4()2()()()]222J x x x t x t x t x t u t dt =+++++⎰求最优控制。
解:把状态方程和性能指标与标准状态方程和标准性能指标比较,可得0,101,02,11,,,,0,010,21,42A B P Q R ⎡⎤⎡⎤⎡⎤⎡⎤=====⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦考虑到()K t 是对称阵,设11121222,(),k k K t k k ⎡⎤=⎢⎥⎣⎦代入黎卡提方程1()()()()()()()()()()()T T K t K t A t A t K t K t B t R t B t K t Q t -=--+-即1112111211121112111212221222122212221222,,,,,0,10,002,12[0,1],0,01,0,,1,1,4,k k k k k k k k k k k k k k k k k k k k ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=--+-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦令上式等号左右端的对应元相等,得211121211122222212222221224k k k k k k k k k =-=-+-=-+-这是一组非线性微分方程。
由边界条件(3)K P =即11121222(3),(3)1,0(3),(3)0,2k k k k ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ 最优控制为11112112122212222()()(),()2*[0,1]2()2(),()T u t R B K t X t k k x t k x t k x t k k x t -=-⎡⎤⎡⎤=-=--⎢⎥⎢⎥⎣⎦⎣⎦2. 能控的系统状态方程为122()(),()()x t x t x t u t ==这是一种双积分系统,其输出为1()x t ,其输入为()u t ,其传递函数为12()1()()x s G s u s s==其性能泛函为222112201[()2()()()()]2J x t bx t x t ax t u t dt ∞=+++⎰其中220a b ->求最优控制。

最优控制习题及参考答案6212最优控制习题及参考答案习题 1求通过 x (0) = 1 , x (1) = 2 ,使下列性能指标为极值的曲线:t f J = ∫(x2 +1)dt t 0解: 由已知条件知: t 0=0 , t f= 1d由欧拉方程得:(2x ) = 0dtx = C 1x = C 1t + C 2将 x (0) = 1,x (1) = 2 代入,有:C 2 = 1,C 1 = 1得极值轨线: x *(t ) = t +1习题 2求性能指标:J = ∫ 1(x 2 +1)dt在边界条件 x (0) = 0 , x (1) 是自由情况下的极值曲线。
解: 由上题得:x * (t ) = C t + Cx * (t )63x f由 x (0) = 0 得: C 2= 0∂L由 ∂xt =tf= 2x (t f ) = 2C 1 t =t = 0t0 1于是: x *(t ) = 0【分析讨论】对于任意的 x (0) = x,x (1)自由。
6421∫ ⎩λ =有: C = x , C = 0 ,即: x *(t ) = x其几何意义: x (1) 自由意味着终点在虚线上任意点。
习题 3已知系统的状态方程为:x 1 (t ) = x 2 (t ), x 2 (t ) = u (t )边界条件为: x 1(0) = x 2(0) = 1 , x 1(3)= x 2(3) = 0 ,31 试求使性能指标 J =u 2(t )dt 2取极小值的最优控制 u *(t ) 以及最优轨线 x *(t ) 。
⎡ x ⎤解: 由已知条件知: f = ⎢ 2⎥⎢⎣ u ⎥⎦Hamiton 函数: H = L + λTfH = 1u 2+ λ x + λ u⎧λ = 0由协态方程: ⎨12121 2 2⎧λ = C① 得: ⎨1 1⎩λ2 = −C 1t + C2 ② ∂H由控制方程:∂u= u + λ2 = 0 得: u = −λ2= C 1t − C 2③由状态方程:x2 = u = C1t −C2得:x (t) = 1 C t2 −C t + C ④2 2由状态方程:x1 = x21 2 3得:x (t) = 1 C t3 −1 C t 2 + C t + C ⑤1 6 12 23 465661⎪⎩=− ∫⎡1⎤ ⎡0⎤将x (0) = ⎢ ⎢,x (3) = ⎢0⎢代入④,⑤, ⎣1⎦⎣ ⎦ 10联立解得: C 1 =由③、④、⑤式得:u * (t ) = 10t − 29,C 2 = 2 , C3=C 4 =1 9x * (t ) = 5 t 3 −t 2+ t +1 27 x *(t ) = 5 t 2 − 2t +1 29习题 4已知系统状态方程及初始条件为x =u , x (0) = 1试确定最优控制使下列性能指标取极小值。

最优控制理论与系统胡寿松版课后习题答案(总32页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2-5 求通过(0)1x =,(1)2x =,使下列性能泛函为极值的极值曲线*()x t :2(1)ft t J x dt =+⎰解:由题可知,始端和终端均固定,被积函数21L x =+,0L x ∂=∂,2L x x ∂=∂, 2d L x dt x ∂⋅=∂ 代入欧拉方程0L d Lx dt x∂∂-⋅=∂∂,可得20x =,即0x =故1x c = 其通解为:12x c t c =+代入边界条件(0)1x =,(1)2x =,求出11c =,21c = 极值曲线为*()1x t t =+2-6 已知状态的初值和终值为(1)4x =,()4f x t =式中f t 自由且f t >1,试求使下列性能泛函达到极小值的极值轨线*()x t :211[2()()]2ft J x t x t dt =+⎰ 解:由题可知,2122L x x =+,()4f t ψ=,()14x =,()4f x t = 欧拉方程:L 0d Lx dt x∂∂-=∂∂ 横截条件:()00t x =x ,()()f f x t t ψ=,()0fTt L L x x ψ∂⎛⎫+-= ⎪∂⎝⎭易得到2dxdt= 故12x t c =+ 其通解为:()212x t t c t c =++根据横截条件可得:()()()122121114424f f f f f x c c x t t c t c x t t c ⎧=++=⎪⎪=++=⎨⎪=+=⎪⎩解以上方程组得:12569f t c c =⎧⎪=-⎨⎪=⎩ 还有一组解⎪⎩⎪⎨⎧===12121c c t f (舍去,不符合题意f t >1)将f t ,1c ,2c 代入J 可得3140)3(4)212(50250.2*=-=+=⎰⎰•t dt x x J . 极值轨线为()*269x t t t =-+2-7 设性能泛函为120(1)J x dt =+⎰求在边界条件(0)0x =,(1)x 自由情况下,使性能泛函取极值的极值轨线*()x t 。

考试题一、简答题:(25分)1、最优控制的三要素是什么?答:优化目标,优化参数,约束条件。
2、如何才能够将有约束优化问题转化为无约束优化问题?答:可以利用惩罚函数将有约束优化问题转化为无约束优化问题。
3、简述遗传算法的计算过程。
答:先确定种群个数,交叉率,变异率,编码方式和适应度函数,已完成初始化后产生第一代种群,然后进行交换,由交换概率挑选的每两个父代通过将相异的部分基因进行交换(如果交换全部相异的就变成了对方而没什么意义),从而产生新的个体。
再进行适应度值评估检测,计算交换产生的新个体的适应度。
接着进行选择,选择的目的是为了从交换后的群体中选出优良的个体,使它们有机会作为父代为下一代繁殖子孙。
变异,变异首先在群体中随机选择一定数量个体,对于选中的个体以一定的概率随机地改变串结构数据中某个基因的值,变异为新个体的产生提供了机会。
4、什么是泛函。
答:泛函是一种映射,是一个由向量空间到标量空间的映射。
泛函是一种变换,它把向量空间N R 的一个子集投影到R 标量空间中的一个元素。
泛函是函数的函数。
5、什么是鲁棒控制。
答:由于工作状况变动、外部干扰以及建模误差的缘故,实际工业过程的精确模型很难得到,而系统的各种故障也将导致模型的不确定性,因此可以说模型的不确定性在控制系统中广泛存在。
如何设计一个固定的控制器,使具有不确定性的对象满足控制品质,也就是鲁棒控制。
二、问答题(20分)1、试述最优控制在控制领域中所处的位置。
答:最优控制理论是50年代中期在空间技术的推动下开始形成和发展起来的 ,由贝尔曼提出的动态规划和庞特里亚金等人提出的最大值原理对最优控制理论的形成和发展起了重要的作用。
最优控制是现代控制理论的核心,着重于研究使控制系统的性能指标实现最优化的基本条件和综合方法。
2、试述菌群优化算法的工作原理。
答:菌群优化算法主要通过趋向性操作、复制操作和迁徙操作这三种操作迭代计算来求解问题。
大肠杆菌的整个生命周期就是在游动和旋转这两种基本运动之间进行变换(鞭毛几乎不会停止摆动),游动和旋转的目的是寻找食物并避开有毒物质。
标准文档1 2f最优控制习题及参考答案习题 1 求通过 x (0) = 1 , x (1) = 2 ,使下列性能指标为极值的曲线:t f J = ∫(x2 +1)dt t 0解: 由已知条件知: t 0 = 0 , t f = 1d由欧拉方程得: (2x ) = 0dtx = C 1x = C 1t + C 2将 x (0) = 1,x (1) = 2 代入,有:C 2 = 1,C 1 = 1得极值轨线: x *(t ) = t +1习题 2 求性能指标: J = ∫ 1(x 2 +1)dt在边界条件 x (0) = 0 , x (1) 是自由情况下的极值曲线。
解:由上题得: x *(t ) = C t + C由 x (0) = 0 得: C 2 = 0∂L由∂xt =t f= 2x (t f ) = 2C 1 t =t = 0 t于是: x *(t ) = 0【分析讨论】对于任意的 x (0) = x 0 ,x (1) 自由。
2 0 1∫⎩ λ = −λ有: C = x , C = 0 ,即: x *(t ) = x 其几何意义: x (1) 自由意味着终点在虚线上任意点。
习题 3 已知系统的状态方程为: x1 (t ) = x2 (t ) , x 2 (t ) = u (t )边界条件为: x 1 (0) = x 2 (0) = 1 , x 1 (3) = x 2 (3) = 0 ,31 试求使性能指标 J =u 2(t )dt 2取极小值的最优控制 u *(t ) 以及最优轨线 x *(t ) 。
⎡ x ⎤解:由已知条件知: f = ⎢ 2⎥⎢⎣ u ⎥⎦Hamiton 函数: H = L + λT f H = 1u 2 + λ x + λ u⎧λ = 0由协态方程: ⎨ 12 121 22⎧λ = C① 得: ⎨11⎩λ2 = −C 1t + C 2②∂H由控制方程: ∂u= u + λ2 = 0得: u = −λ2 = C 1t − C 2 ③由状态方程: x 2 = u = C 1t − C 2得: x (t ) = 1C t 2− C t + C④22 由状态方程: x 1 = x 21 2 3得: x (t ) = 1C t 3− 1C t 2+ C t + C⑤16 122 3 41 ∫⎪⎩=−=−⎡1⎤ ⎡0⎤将 x (0) = ⎪ ⎪ , x (3) = ⎪0⎪ 代入④,⑤,⎣1⎦ ⎣ ⎦10联立解得: C 1 =由③、④、⑤式得:u * (t ) = 10t − 29 , C 2 = 2 , C 3 = C 4 = 1 9x *(t ) = 5 t 3 −t 2 + t +127 x *(t ) = 5 t 2 − 2t +1 29习题 4 已知系统状态方程及初始条件为x =u , x (0) = 1试确定最优控制使下列性能指标取极小值。
1. 2**'2**'*'*01min ()2y J y y y y y y dx ⎡⎤=+++⎢⎥⎣⎦⎰,若(0)y 与(2)y 任意,求*y 及(*)J y 。
解:这是端点自由问题,相应的欧拉—拉格朗日方程为:()0f d f y dt y∂∂-=∂∂即''1(1)0d y y y dt +-++=得''1y =则'1y x c =+,21212y x c x c =++由横截条件:0f y∂=∂得'1y y ++=0即21121(1)102x c x c c +++++=0x =,1210c c ++=;2x =,12350c c ++=。
联立得122,1c c =-=所以*21212y x x =-+,*'2y x =-代入得2**'2**'*'*02321()21(221)243J y y y y y y dxx x x dx⎡⎤=+++⎢⎥⎣⎦=-+-=-⎰⎰2.电枢控制的直流电动机忽略阻尼时的运动方程:()u t θ=式中,θ为转轴的角位移,()u t 为输入。
目标函数为221min ()2u J dt θ=⎰,使初态(0)1θ=及(0)1θ=转移到终态(2)0θ=及(2)0θ=,求最优控制*()u t 及最优角位移*()t θ,最优角速度*()t θ。
解: 设12,x x θθ==则122,x x x u ==。
哈密顿函数:212212H u x u λλ=++ 协态方程: 121120,0H Hx x λλλ∂∂=-==-=-=∂∂ 控制方程:20Hu uλ∂=+=∂即*2()()u t t λ=-将*()u t 代入状态方程,可得 1222121(),(),0,()x x t x t t λλλλ==-==-边界条件为1212(0)1,(0)1,(2)0,(2)0x x x x ==== 可见这是两点边值问题,对正则方程进行拉氏变换,可得11222211221()(0)()()(0)()()(0)0()(0)()sX s x X s sX s x s s s s s s λλλλλλ-=-=--=-=-联立以上四式,可解出43211221()(0)(0)(0)(0)s X s s x s x s λλ=+-+代入初始条件12(0)1,(0)1x x ==,可得1212341111()(0)(0)X s s s s sλλ=+-+ 故 2312111()1(0)(0)26x t t t t λλ=+-+同样可解得 22212322221111()(0)(0)(0)1()(0)(0)(0)2X s x s s sx t x t t λλλλ=-+=-+利用终端条件12(2)0,(2)0x x ==可得2121432(0)(0)0312(0)2(0)0λλλλ-+=-+=解得127(0)3,(0)2λλ== 1111(0)(),()(0)s t s λλλλ==;221221211()(0)(0),()(0)(0)s t t s sλλλλλλ=-=-即 127()3,()32t t t λλ==-所以:最优控制*27()()32u t t t λ=-=-+最优角位移*23171()142x t t t t θ==+-+最优角速度*2273()122x t t t θ==-+3. 222201min (2)()22.,(),(0) 1.()u s J x u t dt s t x u t x s =+==⎰为常量试求出最优控制*u ()t 及相应的轨线*()x t 。
最优控制最优控制——————最小值原理最小值原理七 几种典型的几种典型的工程工程工程应用应用 1.时间最优控制时间最优控制问题,是可以运用极小值原理求解的一个常见的工程实际问题。
如果性能指标是系统有初态转移到目标集的运动时间,则使转移时间为最短的控制称为时间最优控制,或称最速控制。
本节主要介绍线形定常系统的时间最优控制分析法及其应用。
1.1 一类非线性系统的时间最优控制先把需要解决的问题叙述如下:[问题3-1] 移动目标集的一类非线性系统的时间最优控制问题为()1min ,1,2,,fj t u t t J dt j m ≤==∫⋯..s t ① [][]00()(),(),(),()xt f x t t B x t t u t x t x =+=ɺ ② (),0f f x t t ψ =式中()n x t R ∈,()m u t R ∈;()f •和()B •维数适当,其各元对()x t 和t 连续可微;移动目标集()r R ψ•∈,其各元对()f x t 和f t 连续可微,f t 是状态轨线与移动目标集相遇的末端时刻。
显然,问题3-1属于时变条件、积分型性能指标、f t 自由和末端约束的最优控制问题。
根据极小值原理,令哈密顿函数[][]{}(,,,)1()(),(),()T H x u t t f x t t B x t t u t λλ=++ (3-136)正则方程为:[][]()(),(),()Hxt f x t t B x t t u t λ∂==+∂ɺ (3-137) [](),()()()()()TTB x t t u t H ft t t x xx t λλλ ∂∂∂=−=−−∂∂∂ɺ (3-138)边界条件及横截条件为00()x t x = (3-139)(),0f f x t t ψ = (3-140)()()T f f t x t ψλγ∂=∂ (3-141)极小值条件:***1()(),()(),()T T t f x t t t B x t t u t λλ ++{}**1min 1()(),()(),()j T T u t f x t t t B x t t u t λλ≤ =++ 或者[]{}*1()(),()min ()(),()j T T u t B x t t u t t B x t t u t λλ≤ = (3-142)因而得:**()sgn (,)()T u t B x t t λ =− (3-143)式中sgn()•为符号函数。
2-5 求通过(0)1x =,(1)2x =,使下列性能泛函为极值的极值曲线*()x t :解:由题可知,始端和终端均固定,被积函数21L x =+,0L x ∂=∂,2L x x ∂=∂, 2d L x dt x∂⋅=∂ 代入欧拉方程0L d Lx dt x∂∂-⋅=∂∂,可得20x =,即0x =故1x c = 其通解为:12x c t c =+代入边界条件(0)1x =,(1)2x =,求出11c =,21c = 极值曲线为*()1x t t =+2-6 已知状态的初值和终值为(1)4x =,()4f x t =式中f t 自由且f t >1,试求使下列性能泛函达到极小值的极值轨线*()x t :解:由题可知,2122L x x =+,()4f t ψ=,()14x =,()4f x t = 欧拉方程:L 0d L x dt x∂∂-=∂∂ 横截条件:()00t x =x ,()()f f x t t ψ=,()0fTt L L xx ψ∂⎛⎫+-= ⎪∂⎝⎭易得到2dxdt= 故12x t c =+ 其通解为:()212x t t c t c =++根据横截条件可得:()()()122121114424f f f f f x c c x t t c t c x t t c ⎧=++=⎪⎪=++=⎨⎪=+=⎪⎩解以上方程组得:12569f t c c =⎧⎪=-⎨⎪=⎩ 还有一组解⎪⎩⎪⎨⎧===12121c c t f (舍去,不符合题意f t >1)将f t ,1c ,2c 代入J 可得3140)3(4)212(5025.2*=-=+=⎰⎰∙t dt x x J .极值轨线为()*269x t t t =-+2-7 设性能泛函为求在边界条件(0)0x =,(1)x 自由情况下,使性能泛函取极值的极值轨线*()x t 。
解:由题可知,21L x =+,()00x =,()1x 自由欧拉方程:L 0d L x dt x∂∂-=∂∂ 横截条件:()00t x =x ,L 0ft x∂=∂,0fT t L L x x ∂⎛⎫+= ⎪∂⎝⎭易得到()x t a =其通解为:()x t at b =+代入边界条件()f x t a =,()00x =,1f t =,求出0a =,0b =将f t ,a ,b 代入J 可得()1*2011J x dt =+=⎰极值轨线为()*0x t =2-8 设泛函端点),,(02010t x x A 固定,端点)),(),((21t t x t x B f f 可沿空间曲线 移动。