当前位置：文档之家 › 最优控制胡寿松版部分习题答案

最优控制胡寿松版部分习题答案

  • 格式：doc
  • 大小：783.37 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

(完整word版)最优控制理论与系统胡寿松版部分习题答案

(完整word版)最优控制理论与系统胡寿松版部分习题答案

2-5 求通过(0)1x =，(1)2x =，使下列性能泛函为极值的极值曲线*()x t ：2(1)ft t J x dt =+⎰解：由题可知，始端和终端均固定被积函数21L x =+,0L x ∂=∂，2L x x ∂=∂， 2d Lx dt x ∂⋅=∂代入欧拉方程0L d Lx dt x ∂∂-⋅=∂∂,可得20x =，即0x =故1x c = 其通解为：12x c t c =+代入边界条件(0)1x =，(1)2x =，求出11c =，21c = 极值曲线为*()1x t t =+2-6 已知状态的初值和终值为(1)4x =，()4f x t =式中f t 自由且f t 〉1，试求使下列性能泛函达到极小值的极值轨线*()x t ：211[2()()]2ft J x t x t dt =+⎰ 解：由题可知，2122L x x =+，()4f t ψ=，()14x =,()4f x t = 欧拉方程：L 0d Lx dt x ∂∂-=∂∂横截条件：()00t x =x ，()()f f x t t ψ=，()0fT t L L x x ψ∂⎛⎫+-= ⎪∂⎝⎭易得到2dxdt= 故12x t c =+ 其通解为:()212x t t c t c =++根据横截条件可得：()()()122121114424f f f f f x c c x t t c t c x t t c ⎧=++=⎪⎪=++=⎨⎪=+=⎪⎩解以上方程组得：12569f t c c =⎧⎪=-⎨⎪=⎩将f t ,1c ,2c 代入J 可得5*201500502150233J x x dt =+=-=⎰ 极值轨线为()*269x t t t =-+2-7 设性能泛函为120(1)J x dt =+⎰求在边界条件(0)0x =，(1)x 自由情况下,使性能泛函取极值的极值轨线*()x t 。

解：由题可知，21L x =+，()00x =，()1x 自由欧拉方程：L 0d L x dt x∂∂-=∂∂ 横截条件:()00t x =x ，L 0ft x∂=∂，0fT t L L x x ∂⎛⎫+= ⎪∂⎝⎭易得到()x t a =其通解为：()x t at b =+代入边界条件()f x t a =，()00x =，1f t =，求出0a =,0b = 将f t ，a ,b 代入J 可得()1*2011J x dt =+=⎰极值轨线为()*0x t = 2-9 求使泛函22211220(2)J x x x x dt π=++⎰为极值并满足边界条件1(0)0x =，2(0)0x =1()12x π=，2()12x π=- 的极值轨线*1()x t 和*2()x t 。

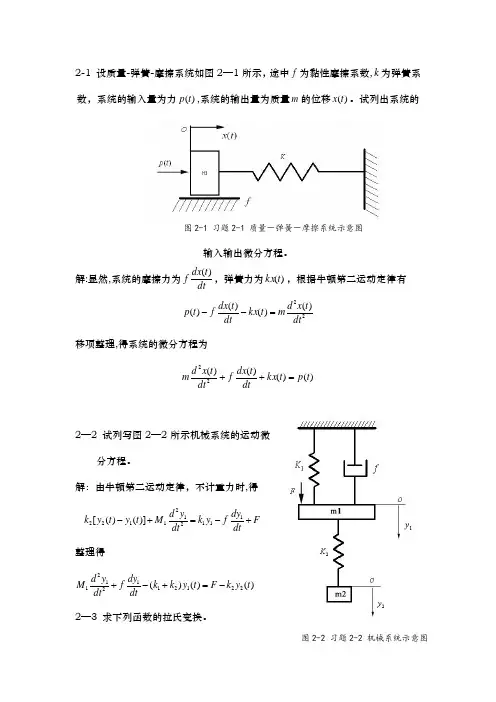
胡寿松版完整答案自动控制原理第五版课后习题答案

胡寿松版完整答案自动控制原理第五版课后习题答案

2-1 设质量-弹簧-摩擦系统如图2—1所示，途中f 为黏性摩擦系数,k 为弹簧系数，系统的输入量为力()p t ,系统的输出量为质量m 的位移()x t 。

试列出系统的输入输出微分方程。

解:显然,系统的摩擦力为dtt dx f)(，弹簧力为)(t kx ，根据牛顿第二运动定律有 22)()()()(dtt x d m t kx dt t dx f t p =-- 移项整理,得系统的微分方程为)()()()(22t p t kx dtt dx f dt t x d m =++2—2 试列写图2—2所示机械系统的运动微分方程。

解：由牛顿第二运动定律，不计重力时,得2112211112[()()]d y dyk y t y t M k y f F dt dt-+=-+整理得2111121222()()()d y dyM f k k y t F k y t dt dt+-+=-2—3 求下列函数的拉氏变换。

图2-1 习题2-1 质量－弹簧－摩擦系统示意图图2-2 习题2-2 机械系统示意图（1))sin 1(3)(t t f -= （2）at te t f =)( (3）)43cos()(π-=t t f解：（1）[()][3(1sin )]L f t L t =-2223([1][sin ])113()13(1)(1)L L t s s s s s s =-=-+-+=+ (2)at te t f =)(21[]L t s=21[()][]()at L f t L te s a ==-(3）()cos(3))cos(3)]42f t t t t π=-=+[()])cos(3)]2L f t t t =+222[sin(3)][cos(3)])3)29939L t L t s s s s s =+=++++=+2—4 求下列函数的拉氏反变换 （1）)5)(2(1)(++-=s s s s F(2）)3(6)(2+-=s s s s F（3）)1(152)(22++-=s s s s s F解：(1)112()(2)(5)25s F s s s s s --==+++++1112[()][]25L F s L s s ---=+++ 112512[]2[]252ttL L s s e e ----=-+++=-+ (2)226211()(3)3s F s s s s s s --==++++ 112211[()][]3L F s L s s s ---=+++ 111231112[][][]321t L L L s s s t e ----=+-+=+- （3)22225115()(1)1s s s F s s s s s -+-==+++ 11215[()][]1s L F s L s s ---=++11215[][]11cos 5sin s L L s s t t ---=++=+-2—5 试分别列写图2—3中各无源网络的微分方程（设电容C 上的电压为)(t u c ，电容1C 上的电压为)(1t u c ，以此类推）。

《自动控制原理》 胡寿松第五章习题解答

《自动控制原理》 胡寿松第五章习题解答

= 0.447 sin(t + 3.4 0 ) − 0.354 cos(2t − 90 0 )
e ss (t ) = c ss (t ) − r (t ) = 0.447 sin(t + 3.4 0 ) − 0.354 cos(2t − 90 0 ) − sin(t + 30 0 ) + cos(2t − 45 0 )
5-4 典型二阶系统的开环传递函数
2 ωn s( s + 2ζω n )
G( s) =
当取 r (t ) = 2 sin t 时，系统的稳态输出
css (t ) = 2 sin(t − 450 )
试确定系统参数 ω n , ζ 。 解：根据公式（5-16）和公式（5-17） 得到： c ss (t ) = A G B ( jω ) sin(ωt + ϕ + ∠G B ( jω ))
ξ = 0.6532
G( s) H ( s) =
K (τs + 1) ; s 2 (Ts + 1)
K ,τ , T > 0
试分析并绘制 τ > T 和 T > τ 情况下的概略开环幅相曲线。 解：相频特性为
ϕ (ω ) = −180 0 + arctan τω − arctan Tω
(1)
τ > T 时， ϕ (ω ) > −180 0 概略开环幅相曲线如下
胡寿松自动控制原理习题解答第五章
5-2 若系统单位阶跃响应为
h(t ) = 1 − 1.8e −4t + 0.8e −9t (t ≥ 0)
试确定系统的频率特性。 解：对单位阶跃响应取拉氏变换得：
1 1.8 0.8 36 − + = s s + 4 s + 9 s ( s + 4)( s + 9)

胡寿松自动控制原理课后习题答案

胡寿松自动控制原理课后习题答案

1 请解释下列名字术语：自动控制系统、受控对象、扰动、给定值、参考输入、反馈。

解：自动控制系统：能够实现自动控制任务的系统，由控制装置与被控对象组成；受控对象：要求实现自动控制的机器、设备或生产过程扰动：扰动是一种对系统的输出产生不利影响的信号。

如果扰动产生在系统内部称为内扰；扰动产生在系统外部，则称为外扰。

外扰是系统的输入量。

给定值：受控对象的物理量在控制系统中应保持的期望值参考输入即为给定值。

反馈：将系统的输出量馈送到参考输入端，并与参考输入进行比较的过程。

2 请说明自动控制系统的基本组成部分。

解：作为一个完整的控制系统，应该由如下几个部分组成：①被控对象：所谓被控对象就是整个控制系统的控制对象；②执行部件：根据所接收到的相关信号，使得被控对象产生相应的动作；常用的执行元件有阀、电动机、液压马达等。

③给定元件：给定元件的职能就是给出与期望的被控量相对应的系统输入量（即参考量）；④比较元件：把测量元件检测到的被控量的实际值与给定元件给出的参考值进行比较，求出它们之间的偏差。

常用的比较元件有差动放大器、机械差动装置和电桥等。

⑤测量反馈元件：该元部件的职能就是测量被控制的物理量，如果这个物理量是非电量，一般需要将其转换成为电量。

常用的测量元部件有测速发电机、热电偶、各种传感器等；⑥放大元件：将比较元件给出的偏差进行放大，用来推动执行元件去控制被控对象。

如电压偏差信号，可用电子管、晶体管、集成电路、晶闸管等组成的电压放大器和功率放大级加以放大。

⑦校正元件：亦称补偿元件，它是结构或参数便于调整的元件，用串联或反馈的方式连接在系统中，用以改善系统的性能。

常用的校正元件有电阻、电容组成的无源或有源网络，它们与原系统串联或与原系统构成一个内反馈系统。

3 请说出什么是反馈控制系统，开环控制系统和闭环控制系统各有什么优缺点？解：反馈控制系统即闭环控制系统，在一个控制系统，将系统的输出量通过某测量机构对其进行实时测量，并将该测量值与输入量进行比较，形成一个反馈通道，从而形成一个封闭的控制系统；开环系统优点：结构简单，缺点：控制的精度较差；闭环控制系统优点：控制精度高，缺点：结构复杂、设计分析麻烦，制造成本高。

胡寿松《自动控制原理》笔记和课后习题(含考研真题)详解(动态系统的最优控制方法)【圣才出品】

胡寿松《自动控制原理》笔记和课后习题(含考研真题)详解(动态系统的最优控制方法)【圣才出品】
二、最优控制中的变分法 （1）泛函 如果变量 J 对于某一类函数{x（t）}中的每一个函数 x（t），都有一个确定的值与之对 应，那么就称变量 J 为依赖于函数 x（t）的泛函，记为：J[x（t）]。
1 / 32
圣才电子书

（2）变分和变分法
十万种考研考证电子书、题库视频学习平台
t
tx t dt
试求：
（1）δJ 的表达式；
（2）当 x（t）＝t2，δx＝0.1t 和 δx＝0.2t 时的变分 δJ 的值。
解：（1）由泛函变分规则可知：
4 / 32
圣才电子书 十万种考研考证电子书、题库视频学习平台

（2）由（1）可知，δx＝0.1t 时：
δx＝0.2t 时：
10-6 试求下列性能指标的变分 δJ。
J tf t2 x2 x&2 dt t0
解：由泛函变分规则，求得：
10-7 已知性能指标为： 求 J 在约束条件 t2＋x12＝R2 和边界条件 x1（0）＝－R，x2（0）＝0，x1（R）＝0，x2 （R）＝π 下的极值。 解：构造广义泛函为：
5 / 32
圣才电子书 十万种考研考证电子书、题库视频学习平台

第 10 章 动态系统的最优控制方法
10.1 复习笔记
考研初试一般不考查本章内容，下文为最优控制问题的基础理论部分。
一、最优控制的基本概念 （1）最优控制 概念：在系统状态方程和约束条件给定的情况下，寻找最优控制律，使衡量系统的某一 性能指标达到最优（最小或最大）。 （2）最优控制问题 任何一个最优控制问题均应包含四方面内容：①系统数学模型；②边界条件与目标集； ③容许控制；④性能指标。 （3）最优控制的研究方法 包括：解析法；数值计算法；梯度型法。

胡寿松自控课后课后答案-12345章

胡寿松自控课后课后答案-12345章


lim
s0
s • En2 (s)

lim
s0
s • en2(s) • N2 (s)

0
根据叠加原理：ess(n1n2) essn1 essn2 0
[3-20]*设随动系统的微分方程为
T1
d2c(t) dt2

dc(t) dt

K2u(t)
u(t) K1[r(t) b(t)]
差动电位器
最大工作角度330o
30k Ω
20k Ω
+15v
ui
-15v10k
uo 10k
10k
u1 –
-K1Biblioteka 10k + ut-K2
u2
功放 K3
ua SM
TG
运放
+15v -15v
K0=30v/330o=1/11(v/o)=5.21(v/rad)
K1=3 K2=2
i K0 ui u K3 u1 K2
z

1
1（0 附加了零点）
（ 由P.97式（3 - 45）至（3 - 50）
1
开系环统增型益别K2
10 1
由静态误差系数法：ess2
r(t)t
1 K
1 K2
0.1
[3-18]控制系统如图所示，其中
G(s)

KP

K s
,
F(s)

1 Js
输入r(t)、扰动n1(t)和n2(t)均为单位阶跃函数，求： （1）在r(t)作用下系统的稳态误差；

(s
Ka (s 4) 12)(s 2)
闭环系统特征方程：

自动控制原理胡寿松第四版课后题答案

自动控制原理胡寿松第四版课后题答案
整理得：
C1C 2 R
d 2u0 du 0 u 0 d 2ui ui du C C C C R + ( + 2 ) + = + + 2C1 i 2 1 1 2 2 2 dt R R dt dt dt
2-5
设初始条件均为零，试用拉氏变换法求解下列微分方程式，并概略绘制x(t)曲线，指出各方程式的模态。
试通过结构图等效变换求系统传递函数c14胡寿松自动控制原理习题解答第二章15胡寿松自动控制原理习题解答第二章16胡寿松自动控制原理习题解答第二章17胡寿松自动控制原理习题解答第二章18试简化图266中的系统结构图并求传递函数c18胡寿松自动控制原理习题解答第二章进一步化简得19胡寿松自动控制原理习题解答第二章再进一步化简得
2-7 设弹簧特性由下式描述：
F = 12.65 y 1.1
其中，是弹簧力；是变形位移。若弹簧在变形位移附近作微小变化，试推导的线性化方程。
解： 设正常工作点为 A，这时 F0 = 12.65 y 0 在该点附近用泰勒级数展开近似为：
1.1
df ( x) y = f ( x0 ) + ( x − x0 ) dx x0
整理上式得
&0 + f1 K 2 x & 0 + K1 f1 x & 0 + K1 f 2 x & 0 + K1 K 2 x0 f1 f 2 & x &i + f1 K 2 x &i + K1 f 2 x & i + K 1 K 2 xi = f1 f 2 & x
对上式去拉氏变换得
3
胡寿松自动控制原理习题解答第二章

胡寿松自动控制原理习题解答第三章

胡寿松自动控制原理习题解答第三章

1=3-1 设随动系统的微分方程为：T &x &0 + x &0 = K 2 uu = K 1 [r (t ) x f ]T f x& f + x f = x 0其中 T,T f, K 2 为正常数。

如果在外作用 r(t)=1+t 的情况下，使 x 0 对 r(t)的稳态误差不大于正 常数∑ 0 ,试问 k1 应满足什么条件？ 见习题 3-20 解答3-2 设系统的微分方程式如下：（1） 0.2c&(t ) = 2r (t )（2） 0.04c& (t ) + 0.24c &(t ) + c (t ) = r (t )试求系统的单位脉冲响应 k(t)和单位阶跃响应 h(t)。

已知全部初始条件为零。

解：（1） 因为 0.2sC (s ) = 2R (s )单位脉冲响应： C (s ) = 10 / s k (t ) = 10 t ε 0单位阶跃响应 h(t) C (s ) = 10 / s 2（2） (0.04s 2 + 0.24s + 1)C (s ) = R (s )h (t ) = 10tC (s ) =t ε 0R (s )0.04s 2 + 0.24s + 1单位脉冲响应： C (s ) = 0.04s 21 + 0.24s + 1 k (t ) = 25 e 33tsin 4t单位阶跃响应 h(t)C (s ) =25 12s + 6 2s [( s + 3)h (t ) = 1 e 3tcos 4t 3 e 3t sin 4t4+ 16] s (s + 3) + 163-3 已知系统脉冲响应如下，试求系统闭环传递函数Φ（ｓ）。

（1） k (t ) = 0.0125e1.25t（2） k (t ) = 5t + 10 sin(4t + 450)（3） k (t ) = 0.1(1 e t / 3)解：（1）√(s) =0.0125s +1.2523n2 n = （2） k (t ) = 5t + 10 sin 4t cos 450 + 10 cos 4t sin 450√(s ) = 5 + 5 s 2 2 4 + 5 s 2 + 162s= 5 + 5s 2 + 16 s 22 s + 4s 2+ 16（3） √(s ) = 0.1 s 0.1s + 1 / 33-4 已知二阶系统的单位阶跃响应为h (t ) = 10 12.5e 1.2tsin(1.6t + 53.1o )试求系统的超调量σ％、峰值时间ｔp 和调节时间ｔs 。

胡寿松自控习题答案 第二章习题解答

胡寿松自控习题答案 第二章习题解答
Z 2 = R2 + 1 1 (R2 C 2 s + 1) = 1 (T2 s + 1) = C2 s C2 s C2 s
1 (T2 s + 1) U 0 ( s) Z2 C2 s (T1 s + 1)(T2 s + 1) = = = 所以： R1 1 U i ( s) Z1 + Z 2 R1C 2 s + (T1 s + 1)(T2 s + 1) + (T2 s + 1) T1 s + 1 C 2 s
即 F − F0 = K 1 ( y − y 0 )
其中 K 1 = = 12.65 × 1.1y 0 dy y= y
0
dF
0.1
0.1 = 13.915 × 1.1y 0
2-8 设晶闸管三相桥式全控整流电路的输入量为控制角，输出量为空载整流电压，它们之间的关系为：
ed = E d 0 cos α
xi (0) = x0 (0) = 0
则系统传递函数为
X 0 (s) fs + K 1 = X i ( s ) fs + ( K 1 + K 2 )
2-3 试证明图2-58(ａ)的电网络与(b)的机械系统有相同的数学模型。
2
胡寿松自动控制原理习题解答第二章
图 2-58
电网络与机械系统
1 C1 s R1 R1 1 解：（a）：利用运算阻抗法得： Z 1 = R1 // = = = 1 C1 s R1C1 s + 1 T1 s + 1 R1 + C1 s R1
& (t ) + x(t ) = t ; (1) 2 x
解：对上式两边去拉氏变换得： （2s+1）X（s）=1/s2→ X ( s ) =

自动控制原理(胡寿松)课后习题答案详解

自动控制原理(胡寿松)课后习题答案详解

=
0.04 s 2
1 + 0.24s
+1
C (s)
=
0.04 s 2
10 6s + 10
R(s) 1 + G(s)H (s) 1 + 20 10
6s + 10 20s + 5
E(s) =
10
=
10
R(s) 1 + G(s)H (s) 1 + 20 10
6s + 10 20s + 5
=
(6s
200(20s + 5) + 10)(20s + 5) +
200
=
200(20s + 5) 120s 2 + 230s + 250
U 0 (s) + U i (s) R0
U1 (s) R0
U 2 (s) R0
式（1）（2）（3）左右两边分别相乘得
9
胡寿松自动控制原理习题解答第二章
U0 (s)
= − Z1 Z 2 R2 即
U 0 (s) + U i (s) R0 R0 R0
U 0 (s) + U i (s) = − R03
U0 (s)
正比，此时有
F
d(H − dt
H0)
=
(Q1
−
Q0 )
−
(Q2
−
Q0 )
于是得水箱的微分方程为
F
dH dt
= Q1 − Q2
胡寿松自动控制原理习题解答第二章
图 2-58 电网络与机械系统
1
解：（a）：利用运算阻抗法得： Z1
=
R1

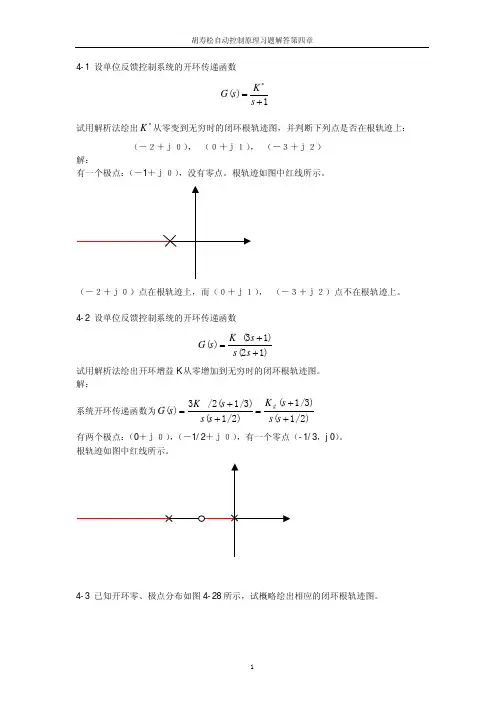
胡寿松自动控制原理习题解答第四章

胡寿松自动控制原理习题解答第四章

4-1 设单位反馈控制系统的开环传递函数 1)(+=∗s K s G试用解析法绘出∗K 从零变到无穷时的闭环根轨迹图，并判断下列点是否在根轨迹上： （－２＋ｊ０）， （０＋ｊ１）， （－３＋ｊ２） 解：有一个极点：（－1＋ｊ０），没有零点。

根轨迹如图中红线所示。

（－２＋ｊ０）点在根轨迹上，而（０＋ｊ１）， （－３＋ｊ２）点不在根轨迹上。

4-2 设单位反馈控制系统的开环传递函数 )12()13()(++=s s s K s G 试用解析法绘出开环增益K 从零增加到无穷时的闭环根轨迹图。

解：系统开环传递函数为)2/1()3/1()2/1()3/1(2/3)(++=++=s s s K s s s K s g G 有两个极点：（0＋ｊ０），（－1/2＋ｊ０），有一个零点（-1/3，j0）。

根轨迹如图中红线所示。

4-3 已知开环零、极点分布如图4-28所示，试概略绘出相应的闭环根轨迹图。

图4-28 开环零、极点分布图4-4 设单位反馈控制系统开环传递函数如下，试概略绘出相应的闭环根轨迹图(要求确定分离点坐标d)：　 (1) )15.0)(12.0()(++=s s s Ks G解：系统开环传递函数为)2)(5()2)(5(10)(++=++=s s s K s s s Ks g G 有三个极点：（0＋ｊ０），（－2＋ｊ０），（－5＋ｊ０）没有零点。

分离点坐标计算如下：051211=++++d d d 3解方程的010142=++d d 7863.31−=d ，d 88.02−=取分离点为88.0−=d根轨迹如图中红线所示。

（2） )12()1()(++=s s s K s G解：系统开环传递函数为)5.0()1()5.0()1(2/)(++=++=s s s K s s s K s g G有两个极点：（0＋ｊ０），（－0.5＋ｊ０），有一个零点（－1＋ｊ０）。

分离点坐标计算如下：115.011+=++d d d 解方程的05.022=++d d 7.11−=d ，d 29.02−=取分离点为7.11−=d ，29.02−=d 根轨迹如图中红线所示。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2-5 求通过(0)1x =，(1)2x =，使下列性能泛函为极值的极值曲线*()x t ：2(1)ft t J x dt =+⎰解：由题可知，始端和终端均固定被积函数21L x =+，0L x ∂=∂，2L x x ∂=∂， 2d L x dt x∂⋅=∂ 代入欧拉方程0L d L x dt x∂∂-⋅=∂∂，可得20x =，即0x = 故1x c = 其通解为：12x c t c =+代入边界条件(0)1x =，(1)2x =，求出11c =，21c = 极值曲线为*()1x t t =+2-6 已知状态的初值和终值为(1)4x =，()4f x t =式中f t 自由且f t >1，试求使下列性能泛函达到极小值的极值轨线*()x t ：211[2()()]2ft J x t x t dt =+⎰ 解：由题可知，2122L x x =+，()4f t ψ=，()14x =，()4f x t = 欧拉方程：L 0d L x dt x∂∂-=∂∂ 横截条件：()00t x =x ，()()f f x t t ψ=，()0fTt L L x x ψ∂⎛⎫+-= ⎪∂⎝⎭易得到2dxdt= 故12x t c =+ 其通解为：()212x t t c t c =++根据横截条件可得：()()()122121114424f f f f f x c c x t t c t c x t t c ⎧=++=⎪⎪=++=⎨⎪=+=⎪⎩解以上方程组得：12569f t c c =⎧⎪=-⎨⎪=⎩将f t ，1c ，2c 代入J 可得5*201500502150233J x x dt =+=-=⎰ 极值轨线为()*269x t t t =-+2-7 设性能泛函为120(1)J x dt =+⎰求在边界条件(0)0x =，(1)x 自由情况下，使性能泛函取极值的极值轨线*()x t 。

解：由题可知，21L x =+，()00x =，()1x 自由欧拉方程：L 0d L x dt x∂∂-=∂∂ 横截条件：()00t x =x ，L 0ft x∂=∂，0fTt L L x x ∂⎛⎫+= ⎪∂⎝⎭易得到()x t a =其通解为：()x t at b =+代入边界条件()f x t a =，()00x =，1f t =，求出0a =，0b = 将f t ，a ，b 代入J 可得()1*211J x dt =+=⎰极值轨线为()*0x t = 2-9 求使泛函22211220(2)J x x x x dt π=++⎰为极值并满足边界条件1(0)0x =，2(0)0x =1()12x π=，2()12x π=- 的极值轨线*1()x t 和*2()x t 。

解：由题可知，2211222L x x x x =++，1(0)0x =，2(0)0x =，1()12x π=，2()12x π=-欧拉方程：1122L 0L 0d Lx dt x d L x dt x ∂∂⎧-=⎪∂∂⎪⎨∂∂⎪-=⎪∂∂⎩可得：21L 2x x ∂=∂，11L 2x x ∂=∂，112d L x dt x ∂=∂ 12L 2x x ∂=∂，22L 2x x ∂=∂，222d L x dt x ∂=∂ 所以这时的欧拉方程为12210x x x x -=⎧⎨-=⎩对上述第一个方程求导两次，再由第二个方程，可以将2x 消去，得(4)110x x -=不难求出此方程的解11234cos sin t t x c e c e c t c t -=+++对此式求导两次，得21234cos cos t t x c e c e c t c t -=+--利用给定的端点条件，可求出1230c c c ===，41c =因此，极值轨线为*1*2()sin ()sin x t tx t t⎧=⎪⎨=-⎪⎩2-12 设二次积分模型为()()t t θω=，()()t u t ω=性能指标1201()2J u t dt =⎰ 已知初态(0)(0)1θω==，末态(1)0θ=，(1)ω自由，试求最优控制*()u t 和最优轨迹*()t θ与*()t ω。

解：由题可知构造H ：21212TH L f u u λλωλ=+=++ 正则方程：1210H H λθλλω∂⎧=-=⎪⎪∂⎨∂⎪=-=-⎪∂⎩由上式可得 11212()()t c t c t c λλ=⎧⎨=-+⎩ 控制方程：20Hu u λ∂=+=∂ 由上式可得 212()u t c t c λ=-=-由状态方程()()t t θω=，()()t u t ω=可得321234212311()621()2t c t c t c t c t c t c t cθω⎧=-++⎪⎪⎨⎪=-+⎪⎩横截条件2(1)0(1)ϕλω∂==∂ 有12c c = 由边界条件(0)(0)1θω==，(1)1θ=可求43123412111162c c c c c c c c =⎧⎪=⎪⎪⎨-++=⎪⎪=⎪⎩ 即12346611c c c c =⎧⎪=⎪⎨=⎪⎪=⎩ 所以 最优控制为*()66u t t =-最优轨线*32*2()31()361t t t t t t t θω⎧=-++⎪⎨=-+⎪⎩ 2-13 设系统状态方程12()()x t x t =，1(0)2x = 2()()x t u t =，2(0)1x =性能指标如下：21()2f t J u t dt =⎰ 要求达到()0f x t =，试求（1）5f t =时的最优控制*()u t 。

（2）f t 自由时的最优控制*()u t 。

解：由题可知构造H ：212212TH L f u x u λλλ=+=++ 正则方程：11212()0()H t x H t x λλλ∂⎧=-=⎪∂⎪⎨∂⎪=-=-⎪∂⎩ 可求得 11212()()t c t c t c λλ=⎧⎨=-+⎩控制方程：20Hu uλ∂=+=∂ 由上式可得 212()u t c t c λ=-=- 由状态方程12()()x t x t =，2()()x t u t =可得32112342212311()621()2x t c t c t c t c x t c t c t c ⎧=-++⎪⎪⎨⎪=-+⎪⎩（1）5f t =时由边界条件1(0)2x =，2(0)1x =，1()0f x t =，2()0f x t =可得343212342123121155506215502c c c c c c c c c =⎧⎪=⎪⎪⎨*-*+*+=⎪⎪*-*+=⎪⎩ 得123454125322512c c c c ⎧=⎪⎪⎪=⎨⎪=⎪⎪=⎩ 故32122916()2125252732()112525x t t t t x t t t ⎧=-++⎪⎪⎨⎪=-+⎪⎩有 25432()12525x t t =-有最优控制*5432()12525u t t =- （2）若5f t =自由由哈密顿函数在最优轨线末端应满足的条件21221()()()()()()02f f f f f f fH t u t t x t t u t t ϕλλ∂=++=-=∂即2()0f t λ=，从而21f c c t =，代入32122121120621102f f f f f c t c t t c t c t ⎧-++=⎪⎪⎨⎪-+=⎪⎩可得6f t =-因为时间总为正值，所以此题无解。

2-14 设一阶系统()()x t u t =，(0)1x =性能指标12201()2J x u dt =+⎰已知(1)0x =。

某工程师认为，从工程观点出发可取最优控制函数*()1u t =-。

试分析他的意见是否正确，并说明理由。

解：由题可知将()()u t x t =代入性能泛函，得1221()2J x x dt =+⎰ 于是，性能泛函中只含有一个宗量()x t 。

以上问题就变成了求性能泛函为极值的极值曲线问题 令22L x x =+ 则欧拉方程为：220L d L x x x dt x∂∂-⋅=-=∂∂ 解得：12()t t x t c e c e -=+根据横截条件(0)1x =，(1)0x =可得211212(1)(1)c e c e ---⎧=-⎪⎨=-⎪⎩ 因此，使给定性能泛函取极值的最优解为*2121()(1)(1)t t x t e e e e ----=-+- *2121()(1)(1)t t u t e e e e ----=-+-由此知该工程师的意见不正确3-4 给定一阶系统方程()()()x t x t u t =-+，(0)1x =控制约束为()1u t ≤，试求使下列性能指标：101[()()]2J x t u t dt =-⎰为极小值的最优控制*()u t 及相应的最优轨线*()x t 。

解：由题可知构造H ：1()()(1)()22uH x x u x u λλλ=-+-+=-+-哈密顿函数达到极小值就相当于使性能指标极小，因此要求1()2u λ-极小。

且取其约束条件的边界值，即()1u t =时，使哈密顿函数H 达到最小值。

所以，最优控制应取*11,2()112u t λλ⎧->⎪⎪=⎨⎪<⎪⎩，由协态方程 ()1Ht xλλ∂=-=-∂可得 ()1t t ce λ=- 由横截条件 (1)0λ=求得 1c e -=，于是有1()1t t e λ-=-显然，当()0.5s t λ=时，*()u t 产生切换，其中s t 为切换时间。

不难求得ln2s et =，故最优控制为 *1,0ln 2()1,ln 12e t u t e t ⎧-≤<⎪⎪=⎨⎪≤≤⎪⎩将*()u t 代入状态方程，得1,0ln 2()1,ln 12e x t x t e x t ⎧--≤<⎪⎪=⎨⎪-+≤≤⎪⎩解得121,0ln 2()1,ln 12tt e c e t x t e c e t --⎧-≤<⎪⎪=⎨⎪+≤≤⎪⎩代入初始条件(0)1x =，可得 12c =，因而()21t x t e -=-，0ln2et ≤< 在上式中，令ln2e t =，可求出ln 12et ≤≤时()x t 的初始条件ln 24(ln )2112e e x e e-=-=-从而求得22c e =-。

因而()(2)1t x t e e -=-+，ln12et ≤≤ 于是，最优轨线为21,0ln 2()(2)1,ln 12tt e e t x t e e e t --⎧-≤<⎪⎪=⎨⎪-+≤≤⎪⎩将求得的*()u t 和*()x t 代入式J ，得最优性能指标1ln 1*200ln 211132[()()](2)[(2)]ln 0.4522222e t t e eJ x t u t dt e dt e e dt e --=-=-++-=--≈⎰⎰⎰3-7 已知二阶系统方程121()()4x t x t =+，11(0)4x =- 2()()x t u t =，21(0)4x =-式中控制约束为1()2u t ≤试确定最优控制*()u t 。