级数理方程试题+答案

数理方程习题答案数理方程习题答案数理方程是数学中一门重要的学科，它研究的是各种各样的方程。

在学习数理方程的过程中，习题是不可或缺的一部分。

通过解习题，我们可以加深对数理方程的理解，掌握解题的方法和技巧。

在这篇文章中，我将为大家提供一些数理方程习题的答案，希望能对大家的学习有所帮助。

1. 求解方程：2x + 5 = 17。

解：将方程化简，得到2x = 17 - 5，即2x = 12。

再将等式两边同时除以2，得到x = 6。

所以方程的解为x = 6。

2. 求解方程组：2x + y = 73x - 2y = 4解：可以使用消元法来求解这个方程组。

首先，将第一个方程乘以2，得到4x + 2y = 14。

然后将第二个方程与这个结果相加，得到7x = 18。

再将等式两边同时除以7，得到x = 18/7。

将x的值代入第一个方程，可以求得y的值为y = 7 - 2x = 7 - 2(18/7) = 7 - 36/7 = 7/7 - 36/7 = -29/7。

所以方程组的解为x = 18/7，y = -29/7。

3. 求解二次方程：x^2 - 5x + 6 = 0。

解：可以使用因式分解法来求解这个二次方程。

首先，将方程化简，得到(x - 2)(x - 3) = 0。

根据乘积为零的性质，可以得到x - 2 = 0或者x - 3 = 0。

解这两个方程，可以得到x = 2或者x = 3。

所以方程的解为x = 2或者x = 3。

4. 求解三次方程：x^3 - 3x^2 + 2x - 4 = 0。

解：可以使用综合除法来求解这个三次方程。

首先，将方程按照降幂排列，得到x^3 - 3x^2 + 2x - 4 = 0。

然后，尝试将方程的第一项x^3除以x的最高次数x^3，得到商为1。

将这个商乘以方程的所有项，得到x^3 - 3x^2 + 2x - 4 - (x^3 - 3x^2 + 2x - 4) = 0。

化简这个等式，可以得到0 = 0。

（2） z 4 4 0 ； 解 z 4 4 2 4 1 2 4 cos j sin
93


2k 1 j sin 2k 1 = 2 cos 4 4
k 0,1,2,3
1 1 k 0 ： z1 2 cos j sin 2 j 1 j 4 4 2 2 3 3 1 1 k 1 ： z2 2 cos j sin 2 j 1 j 4 4 2 2 5 5 1 1 k 2 ： z3 2 cos j sin 2 j 1 j 4 4 2 2 7 7 1 1 k 3 ： z4 2 cos j sin 2 j 1 j 4 4 2 2
3 8
k k 2 8 cos j sin 2 16 2 16
3 3 8 3
k 0,1,2,3
7 7 2 cos j sin ， 2 8 cos j sin ， 16 16 16 16 9 15 15 9 2 cos j sin ， 2 8 cos j sin ； 16 16 16 16
1 3 5 5 （2） j sin cos j sin 2 2 j cos 3 3 3 3 1 3 j 2 2
4
cos j sin 4 4
4
2
cos j sin 1 j 3 5 5 cos j sin 3 3

+
α
2 2
=
α32
+
α
2 4
，取单位特征方向，
α12
+
α
2 2
+ α32
+
α
2 4
= 1。所以，α12
+
α
2 2
= α32
+
α
2 4
=
1 2
。记
α1
=
1 2
cosθ ,
α2
=
1 2
sinθ ,α3
=
1 2
cosϑ,
α4
=
1 2
sinϑ
，则
α
=
⎛ ⎜⎝
1 2
cosθ ,
1 sinθ , 2
1 2
cosϑ,
则杆上各点 在时刻 的位移是
。
在杆上任取一段，其两端点静止时的坐标为
,此小杆段在时刻 的相对伸长
为： 律知张力为
，令
得 点在时刻 的相对伸长为ux (x, t) ，由 Hooke 定
，再此小杆段上用 Newton 第二定律得
两边同除 并令
得：
若杨氏模量为 为常数则得：
。
1 牛顿(Newton)第二定律与动量守恒定律等价，也可以用动量守恒定律来见方程，见《数学物理方程 讲义》 （姜礼尚、陈亚浙）P1
=
1 2
sinθ ,α3
=
±
1 sinθ ，则 2
α
=
⎛ ⎜⎝
cosθ
,
1 sinθ , ± 2
1 2
sin
θ
⎞ ⎟⎠
。
( ) 2 对波动方程utt − a2 uxx + uyy = 0 过直线l : t = 0, y = 2x 的特征平面。

d dx
k
(x)
dy dx
q(x)
y
(x)
y
0
在第一类齐次边界条件及自然条件下
特征函数系
Pm (r)
J
n
(
(n m R
)
r)
m 1, 2,...
R 0
rJ
n
(
(n) m R
r
)J
n
(
(n) k R
r)dr
0 mk
R2 2
J
2 n1
(m(n)
)
R2 2
J
2 n1
(
(n m
)
)
mk
设
① ② ①-②
J0 ( x)
贝塞尔函数的图象
J1(x)
J 2 ( x)
J3 ( x)
贝塞尔方程在第一 类边界条件下的 特征值和特征函数
r2P(r) rP(r) (r2 n2 )P(r) 0
P(r) rR 0
P(r) r0
Jn ( R) 0
R
(n) m
(m 1, 2,...)
(n) m
(
(n) m
贝塞尔函数的性质（4）
二维热传导物理问题
u
t
a2
2u x2
2u y 2
u t0 (x, y)
,
x2 y2 R2
u 0 x2 y2 R2
u(x, y,t) V (x, y)T (t)
T (t) a2T (y 2
V
0
V 0 x2 y2 R2
贝塞尔函数的性质（1）
第一类贝赛尔函数：
在整个数轴上收敛，在每个指定的点都
取有限值 第二类贝赛尔函数：

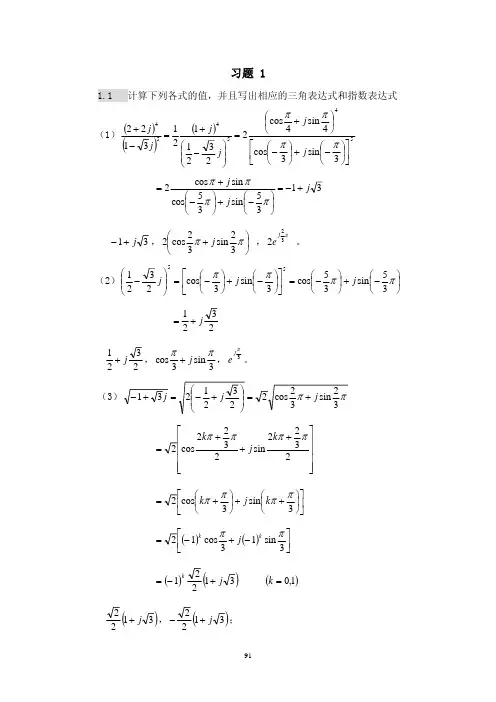
长沙理工大学考试试卷…………………………………………………………………………………………………………………试卷编号 拟题教研室（或教师）签名 教研室主任签名…………………………………………………………………………………………………………………课程名称（含档次） 数学物理方程与特殊函数 课程代号专 业 层次（本、专） 本 科 考试方式（开、闭卷） 闭卷一．判断题：（本题总分25分，每小题5分）1．二阶线性偏微分方程062242=+++-y x yy xy xx u u u u u 属于椭圆型； （ ）2．定解问题的适定性包括解的稳定性、解的唯一性和解的存在性； （ ）3．如果格林函数),(0M M G 已知，且它在Γ+Ω上具有一阶连续偏导数，又若狄利克雷问题⎩⎨⎧=Ω∈=∆Γ ).,,(|,),,(0z y x f u z y x u 在Γ+Ω上具有一阶连续偏导数的解存在，那么其解可表示为=)(0M u dS nG z y x f ⎰⎰Γ∂∂-),,(； （ ） 4．设)(x P n 为n 次Legendre 多项式，则0)()(111050358⎰-=dx x P x P ； （ ）5．设)(x J n 为n 阶Bessel 函数，则[])()(021ax xJ a ax xJ dxd =． （ ） 二．解答题：（本题总分65分） 1．（本小题15分）设有一根长为l 的均匀细杆，它的表面是绝热的，如果它的端点温度为1),0(u t u =，2),(u t l u =，而初始温度为0T ，写出此定解问题．2．（本小题20分）利用固有函数法求解下面的定解问题⎪⎪⎩⎪⎪⎨⎧====><<+=.0),(,0),0(,0)0,(,0)0,(),0,0(cos sin 2t l u t u x u x u t l x l x t A u a u x x t xx tt πω 其中ω,A 是常数．3．（本小题15分）求出方程xy u u yy xx =+的一个特解．第 1 页（共 2 页）4．（本小题15分）用试探法求解拉普拉斯方程狄氏问题：⎩⎨⎧+=≤≤<=∆ .sin cos ),()20,(,0),(22θθθπθθB A R u R r r u 三．证明题：（本题总分10分） 证明：函数⎰+-+++-=atx at x ds s a at x at x t x u )(212)()(),(ψϕϕ是下面的齐次方程的初值问题 ⎪⎩⎪⎨⎧==>+∞<<-∞=).()0,(),()0,(),0,(2x x u x x u t x u a u txx tt ψϕ 的解．第 2 页（共 2 页）长沙理工大学试卷标准答案课程名称： 数学物理方程与特殊函数(B) 试卷编号：03一．判断题：（本题总分25分，每小题5分）1．×； 2．√； 3．√； 4．√； 5．×．二．解答题：（本题总分65分）1．（本小题15分）泛定方程：xx t u a u 2=，)0,0(><<t l x ； …………………5分 边界条件：1),0(u t u =，2),(u t l u =； …………………10分 初始条件：0)0,(T x u =． …………………15分2．（本小题20分） 泛定方程相应的齐次方程满足齐次边界条件的固有函数系为⎭⎬⎫⎩⎨⎧l x n πcos ，故可设方程的解为∑∞==0cos)(),(n n lx n t u t x u π， ……………5分 将它代入泛定方程，得l x t A l x n t u l a n t u n n n πωππcos sin cos )()(02=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+''∑∞=， ……………10分 于是),1(0)()(2≠=⎪⎭⎫ ⎝⎛+''n t u l a n t u n n π .s i n )()(121t A t u l a t u ωπ=⎪⎭⎫ ⎝⎛+'' ……………12分 由初始条件，得 ),2,1(0)0()0( =='=n u u n n …………14分显然，当1≠n 时，0)(=t u n ；当1=n 时，解上面的微分方程得ττπωτπd t l a A a l t u t)(sin sin )(01-=⎰第1页（共3页）⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⋅=t l a l at l a a Al ωππωπωπsin sin 122， ……………18分 故所求的解为 l x t l a l at l a a Al t x u πωππωπωπcos sin sin 1),(22⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⋅=。

u = f( − 3 ) + g(x + y) (−3 ) + ( ) = 3 代入边界条件得： (−3 ) + ( ) = 0 (2)式积分得： (−3 ) + ( ) = 3 −
(−3 ) + ( ) = 0 (3)
求得： 所以：
( )= ( )= u= ( + ) + ( −3 )
14.解下列定解问题. = , > 0, − ∞ < x < +∞ (2). (0, ) = 特征方程： 特征线 f(x + at) f(x) = u=( + )
∫ ( )
[∫ ( ) +
∫ ( )
+ ]
( ) ( )
( )]
+ ( )+
(2).
+ ( , ) = ( , ) ,u = u(x, y)
直接套用公式 6. 推导杆的微小纵振动方程 解： 设细杆截面积 S，密度 ，杨氏模量 E 取一小段 dx, 用牛顿第二定律得：
E S u ( x dx, t ) u ( x, t ) 2u ES Sdx 2 x x t
数理方程 A 参考答案 中国科学技术大学
代入原方程得：
u 1, u f ( )
u xy f ( x 2 y 2 ) 15.一端固定的半无界弦的定解问题. = , > 0, >0 ( , 0) = 0 (0, ) = sin , (0, ) =
若为cos ,则 =? 解： 为满足边界条件作以下延拓： φ(x) = sin , 由达朗贝尔公式得： u(t, x) = [sin( +
d 2 R 2 dR )0 dr 2 r dr

参考答案与试题解析A组一．（共30小题）1．在方程、、、中，无理方程共有（）、2．三角形的三条边长分别为2、k、4，若k满足方程k2﹣6k+12﹣=0，则k的值（）﹣3．已知，则x等于（），先化简再求值即可得出答案．解：已知∴原式可化简为：+34．若，则x+y的值为（）=a不能为负，5．方程的所有解的和为（）解：方程时，时，6．已知四个方程①；②；③；④，其中有实数解的方C D原方程可化为8．已知下列关于x的方程：①；②+1=0；③+2x=7；④﹣7=0；⑤+=2；⑥﹣=．C±或是二元二次方程是分式方程是无理方程D．先移项得到=C DC D、∵、∵，∴、∵14．方程的解的情况是（）此题需将方程变形为，再分三种情况讨论，即可得出方程解的解：将方程变形为，即，即成为B组15．如果满足=a的实数x恰有6个值，那么a的取值范围是（）C D=|﹣）|时，=a=，；）|时，=a=，≥﹣）|时，=a=，；时，16．方程+=12的实数解个数为（）时，=8+17．已知a为非负实数，若关于x的方程至少有一个整数根，则a可能取值的个数为（）=ya=，18．方程的根为（）C D==020．在方程、、、中，无理方程的个数有（）、C D=，去掉分母后、因为22．下列方程中，无实根的方程是（）C D24．（2006•闸北区一模）下列方程中有实数解的方程是（）+1=0 =x﹣2 C++1=0 D=、由于≥+1C DCC D 、∵，而C DC D。

第一章曲线论§ 1 向量函数1.证明本节命题3、命题5 中未加证明的结论略2.求证常向量的微商等于零向量。

证：设，为常向量，因为所以。

证毕3.证明证：证毕4.利用向量函数的泰勒公式证明：如果向量在某一区间所有的点其微商为零，则此向量在该区间上是常向量。

证：设，为定义在区间上的向量函数，因为在区间上可导当且仅当数量函数，和在区间上可导。

所以，，根据数量函数的Lagrange 中值定理，有其中，，介于与之间。

从而上式为向量函数的0 阶Taylor 公式，其中。

如果在区间上处处有，则在区间上处处有，从而，于是。

证毕5.证明具有固定方向的充要条件是证：必要性：设具有固定方向，则可表示为，其中为某个数量函数，为单位常向量，于是。

充分性：如果，可设，令，其中为某个数量函数，为单位向量，因为，于是为常向量，于是，，即具有固定方向证毕因为，故，从而6.证明平行于固定平面的充要条件是。

证：必要性：设平行于固定平面，则存在一个常向量，使得，对此式连续求导，依次可得和，从而，，和共面，因此充分性：设，即，其中，如果，根据第5 题的结论知， 具有固定方向， 则某个数量函数， 为单位常向量，任取一个与 垂直的单位常向量 ，于是作以 为法向量过原点的平面 ，则 平行于 。

如果 ，则 与 不共线， 又由 可知， ， ，和 共面，于是 ，，那么 ，这说明 与共线，从而，根据第 5 题的结论知， 具有固定方向，则 可表 示为，其中 为某个数量函数， 为单位常向量，作以为法向 量，过原点的平面 ，则 平行于 §2 曲线的概念1. 求圆柱螺线 在点 的切线与法平面的方程。

解： ，点 对应于参数 ，于是当 时， ，，于是切线的方程为：法平面的方程为2. 求三次曲线 在点 处的切线和法平面的方程。

解： ，当 时， ， ， 于是切线的方程为：法平面的方程为3. 证明圆柱螺线 的切线和 轴成固定角 证：可表示为 ，其中 为其中 ， 为数量函数， 令 证毕令为切线与轴之间的夹角，因为切线的方向向量为，轴的方向向量为，则证毕4.求悬链线从起计算的弧长解：5.求抛物线对应于的一段的弧长解：6. 求星形线，的全弧长。

化简之后，可以得到定解问题为
utt (Y / )uxx a2uxx u |x0 0,ux |xL 0

u
|t 0
0, ut
|t 0
I
(x
L)
5.高频传输线，原点端施以电动势 E，另一端接地，初始电流为(x) ，电压为 (x) 。
试建立电压的定解问题。（忽略电阻和介质的电导）
Q3 c 4 r2drdu
Q3 Q1 Q2
c 4 r2drdu kur (r dr,t)4 (r dr)2 dt kur (r,t)4 r2dt
4
k
r
(r
2ur
)drdt

即
ut
k c
1 r2
r
(r2ur )

3.设物体表面的绝对温度为 u ，它向外辐射出去的热量，按斯特凡-波尔兹曼定 律正比于 u4 ，即 dQ ku4dSdt ，设物体与周围介质之间，只有热辐射而无热传
习题 2.4 1.判断下列方程的类型 (1) auxx 4auxy auyy bux cuy u 0 4a2 a2 0 ,双曲型 (2) auxx 2auxy auyy bux cuy u 0 a2 a2 0 ,抛物型 (3) 2auxx 2auxy auyy 2bux 2auy u 0 a2 2a2 0 ,椭圆型 (4) uxx xuxy 0
ut
k c
ux
2k1 cr
(u
u1 )
0

2.导出匀质且在每一个同心球上等温的孤立球体的热传导方程。
S1
S2
r r+dr
解： dt 时间内通过 S1 流入壳层的能量 Q1 kur (r,t)4 r2dt dt 时间内通过 S2 流入壳层的能量 Q2 kur (r dr,t)4 (r dr)2 dt dt 时间内壳层升高 du 所需的能量

作业参考答案3、在（,ππ-）这个周期上，2()f x x x =+，试将它展开为傅立叶级数，又在本题所得展开式中置x π=，由此验证222211112346π++++=解：因为2()f x x x =+在（,ππ-）上满足狄氏定理，可以展开为傅立叶级数 又 l π=所以()0101()cos sincos sin k k k k k k k k f x a a x b x l l a a kx b kx ππ∞=∞=⎛⎫=++ ⎪⎝⎭=++∑∑23201111()d 2233a x x x x πππππππ--=+==⎰ 21()cos d k a x x kx xπππ-=+⎰()()22312sin cos sin 2cos sin xkx kx kx kx kx kx kx k k k πππππππππ---=+++-()241k k =- 21()sin d k b x x kx xπππ-=+⎰()()22312sin cos 2sin cos cos xkx kx kx kx kx kx kx k k k πππππππππ---=-+--()121k k +=- 所以 ()()1221142()1cos 1sin 3k k k f x kx kx kk π∞+=⎛⎫=+-+- ⎪⎝⎭∑222,,,x x x x x ππππππ⎧+-<<⎪==-⎨⎪=⎩令x π=代入上式得:()()()()122222211142141cos 1sin 1133k k k k k k kx kx k k kπππ∞∞+==⎛⎫⎛⎫+-+-=+-⨯-= ⎪ ⎪⎝⎭⎝⎭∑∑ 所以有222211112346π++++=得证5．（1）()cos ,(0,),(0)0,()0f x x x f f αππ=∈==作奇延拓，展为奇函数（sin 函数）1()sin k k f x b kx ∞==∑2cos sin d k b x kx x παπ=⎰2sin()sin()d 2k x k xx πααπ-++=⎰0111cos()cos()k x k x k k ππααπαα--⎡⎤=-++⎢⎥-+⎣⎦()()111cos cos 1cos cos 1k k k k παππαππαα--⎡⎤=-+-⎢⎥-+⎣⎦12221(1)cos ()k k k αππα+⎡⎤=+-⎣⎦- 12212()1(1)cos sin ,0()k k kf x kx x k απππα∞+=⎡⎤∴=+-<<⎣⎦-∑6． （1）2cos(/),(0,/2)(),(0)0,()00,(,)lx l x l f x f f l x l π∈⎧''===⎨ ∈⎩ 作偶延拓，展为偶函数（cos 函数）01()cos k k k x f x a a l π∞=⎛⎫=+ ⎪⎝⎭∑/2/200002111cos d cos d sin 2l l l x x x a x x l l l l l πππππ⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎰⎰ /202cos cos d l k x k x a x l l l ππ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭⎰所以要讨论k ＝1的情况/221021cos d 2l x a x l l π⎛⎫== ⎪⎝⎭⎰ /202cos cos d l k x k x a x l l l ππ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭⎰/202111cos cos d 2l k k x x x l l l ππ⎡+-⎤⎛⎫⎛⎫= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎰ /211111sin sin 11l k k x x k l k l πππ⎡+-⎤⎛⎫⎛⎫=+ ⎪ ⎪⎢⎥+-⎝⎭⎝⎭⎣⎦11111sin sin 1212k k k k πππ⎡+-⎤⎛⎫⎛⎫=+ ⎪ ⎪⎢⎥+-⎝⎭⎝⎭⎣⎦120,212(1),2(41)m k m k m m π+ =+⎧⎪=-⎨ =⎪-⎩121112(1)2()cos cos ,02(41)m m x mf x x x l l m l ππππ+∞=-∴=++<<-∑ （2）()(1/),(0,),(0)0,()0f x a x l x l f f l ''=-∈==作偶延拓，展为偶函数（cos 函数）01()cos k k k x f x a a l π∞=⎛⎫=+ ⎪⎝⎭∑002(1/)d 22l aa a x l x l =-=⎰ 02(1)cos d l k x k x a a x l l l π⎛⎫=- ⎪⎝⎭⎰ 202221sin cos l a l k k k x x x l l k l l l ππππ-⎛⎫=+ ⎪⎝⎭()222202211421(21)k k n a a k n k n ππ=⎧⎪⎡⎤=--=⎨⎣⎦=+⎪+⎩220421()cos ,02(21)n a a n f x x x l n lππ∞=+∴=+<<+∑8．矩形波()f x 在(/2,/2)T T -这个周期上可以表示为0,/2/2(),/2/20,/2/2T x f x H x x T ττττ-<<-⎧⎪=<<-⎨⎪<<⎩试将它展为复数形式的傅立叶级数解：因为()f x 在(/2,/2)T T -上满足狄氏定理，可以展开为复数形式的傅立叶级数 又 2l T =2()k k ix ix lTkkk k f x c ec eππ∞∞=-∞=-∞==∑∑22/2/2/2/211()d d k k T i x i x T Tk T c f x e x He x T T ππττ--==⎰⎰ 2/2/22k ixTH T e T i k πττπ-⎛⎫=⎪-⎝⎭sin 2k k i i TT H e e H k k i k T πτπτπτππ-⎛⎫- ⎪== ⎪ ⎪⎝⎭当k ＝0时，/2/2/2/211()d d T k T H c f x x H x T T Tτττ--===⎰⎰ 2211()sin sin k k i x i x T Tk k H H k H k f x e e T k T k T ππτπτπτππ-∞=-∞=∴=++∑∑*****************************************************************3．把下列脉冲()f t 展开为傅立叶积分0,(),0,00,t T f t h T t h t T t T⎧⎪<-⎪⎪=--<<⎨⎪<<⎪>⎪⎩解：在(,)t ∈-∞∞，()f t 满足狄氏条件，且绝对可积，所以()f t 可以展开为付氏积分。

u0 X0T0 B0A0 C0
0
Tn
a2n22
l2
Tn
0
a2n22 t
Tn Ane l2
un XnTn
ABea2nl222t nn
cons l
xCea2nl222t n
cosn
l
x
un 0unC 0n 1Cnea2n l2 22tconlsx
数学物理方程与特殊函数
第2章习题选讲
u(uutx(,0x0,)at)2xx,20u2,,u(lx,t) 0,
由此可得：w (x)1
xt
dt
f()dC xA ,
a2 0 0
其中
C1 l(BAa 1 2 0 ldt0 tf()d),
数学物理方程与特殊函数
第2章习题选讲
然后用分离变量解
v(vt0,t)a2
2v x2 , 0, v(l,
t)
0,
0 x l,t 0 t 0
v(x,0) g(x) w(x), 0 x l
0xl1,0yl2 0yl2
u(x,0)0,u(x,l2)(x), 0xl1
uXY
XX0,
X(0)X(l1)0
0xl1
YY0
n n2 nl1 2,n1,2,3,L
n
Xn An sin l1 x
Yn
n2 2
l12
Yn
0
ny
ny
Yn Cnel1 Dne l1
数学物理方程与特殊函数
第2章习题选讲
un 1unn 1Cnenl1 yD nenl1 ysinnl1 x u(x,0)n 1CnDnsinnl1x0 u(x,l2)(x)n 1 C nenl1l2D nenl1l2 sinn l1x

数理方程第二版课后习题答案第一章曲线论§1 向量函数1. 证明本节命题3、命题5中未加证明的结论。

略2. 求证常向量的微商等于零向量。

证：设，为常向量，因为所以。

证毕3. 证明证：证毕4. 利用向量函数的泰勒公式证明：如果向量在某一区间内所有的点其微商为零，则此向量在该区间上是常向量。

证：设，为定义在区间上的向量函数，因为在区间上可导当且仅当数量函数，和在区间上可导。

所以，，根据数量函数的Lagrange中值定理，有其中，，介于与之间。

从而上式为向量函数的0阶Taylor公式，其中。

如果在区间上处处有，则在区间上处处有，从而，于是。

证毕5. 证明具有固定方向的充要条件是。

证：必要性：设具有固定方向，则可表示为，其中为某个数量函数，为单位常向量，于是。

充分性：如果，可设，令，其中为某个数量函数，为单位向量，因为，于是因为，故，从而为常向量，于是，，即具有固定方向。

证毕6. 证明平行于固定平面的充要条件是。

证：必要性：设平行于固定平面，则存在一个常向量，使得，对此式连续求导，依次可得和，从而，，和共面，因此。

充分性：设，即，其中，如果，根据第5题的结论知，具有固定方向，则可表示为，其中为某个数量函数，为单位常向量，任取一个与垂直的单位常向量，于是作以为法向量过原点的平面，则平行于。

如果，则与不共线，又由可知，，，和共面，于是，其中，为数量函数，令，那么，这说明与共线，从而，根据第5题的结论知，具有固定方向，则可表示为，其中为某个数量函数，为单位常向量，作以为法向量，过原点的平面，则平行于。

证毕§2曲线的概念1. 求圆柱螺线在点的切线与法平面的方程。

解：，点对应于参数，于是当时，，，于是切线的方程为：法平面的方程为2. 求三次曲线在点处的切线和法平面的方程。

解：，当时，，，于是切线的方程为：法平面的方程为3. 证明圆柱螺线的切线和轴成固定角。

证：令为切线与轴之间的夹角，因为切线的方向向量为，轴的方向向量为，则证毕4. 求悬链线从起计算的弧长。

若 在 点连续，则
1
定义
设函数 f ( x) 在 (−∞, +∞) 上的任意有限区间上满足狄利克雷条件，在 (−∞, +∞) 上绝
对可积，则称广义积分
为
的傅里叶变换，或者称为 定义 称
的像函数。通常记为
，或
。
为
的傅里叶逆变换，或者称为 傅里叶变换及其逆变换的基本性质
的像原函数。记为
.
性质 1（线性性质） 傅里叶变换及其逆变换都是线性变换，即
其中 ， 是任意常数。 性质 2（相似性质） 对于任意实常数 ，有 . 性质 3（位移性质）对于任意实常数 ，有 , 性质 4（微分性质）设 ， 的傅里叶变换存在，则 . 一般地，若 , ,…, 的傅里叶变换存在，则 . 性质 5（乘多项式性质）设 的傅里叶变换存在，则
2
.
. 性质 6 (积分性质) . 性质 7 (对称性质) . 定义 于所有的 设函数 和 是 上定义的函数。 如果广义积分 对
2 ∂ 2u 2 ∂ u a − = 0 (−∞ < x < +∞, t > 0), ∂t 2 ∂x 2 ∂u u| ψ ( x). ( x), = = t =0 ϕ ∂t t =0
的解为
二维拉普拉斯方程的边值问题
∂ 2u ∂ 2u = 0 ( −∞ < x < +∞, y > 0), ∂x 2 + ∂ y2 u | = f ( x ), x =0 u = 0. |xlim |→+∞ 的解为
2
s2
例3 解
求函数 F ( p ) = 因为
p 的拉普拉斯逆变换 p − 2 p +5

第一章曲线论§ 1向量函数1 .证明本节命题3、命题5中未加证明的结论略2 .求证常向量的微商等于零向量。

证：设31,回为常向量，因为r(t4- At) -r(t) c-c 11m = lim = 0it —AtAt —At所以E33 .证明⑹ p 2(t)则此向量在该区间上是常向量 证：设［=«r)=)⑴ 返 ［回 回1为定义在区间口上的向量函数，因为 回在区间口上可导当且仅当数量函数 晅］,EH3和EH3在区间 口上可导。

所 以，।° I ,根据数量函数的Lagrange 中值定理，有证毕4.利用向量函数的泰勒公式证明：如果向量在某一区间内所有的点其微商为零,x(t) - X(t o ) 4- %)y(t) =y(S)+ y r (日”(t -力式 t) = z(M)+ /(%)《一其中 51,囹，因介于口与口之间。

从而* =3(口 =比⑷ y(t) 4 t)} =+ £(%)(「-1) y(j) + 4(%)«-咐 《%) +={刀(珀 “幻)+ X(sp 4电)/(%)}("明=『口 +年一%)上式为向量函数的 0阶 Taylor 公式，其中 :—卜("'_‘(")_一 ⑻):。

如果在 区间口上处处有F ⑴=口⑷ *)曰!,则在区间口上处处有适三从而F = (，©) y'(%) ，(1)] = o]于是E3。

证毕5 .证明左逗1具有固定方向的充要条件是F 黑亍二°1证：必要性：设F=1a)l 具有固定方向,则F =直力1可表示为F =, 其中四为某个数量函数，目为单位常向量，于是f"=。

⑴P 住"X" Q] 充分性：如果区三可，可设[_叫,令巨运三叵画,其中四为某个 数量函数，回为单位向量，因为F=p 岸前⑴+。

("'⑴]于是r x ? = O-*p(t)2(t) x [p'(t)?(t) + p(t)e (t) - O^*p 2(f)[e(t) x e (t) - 0 因为回，故国亘1,从而F⑷x.(t)=。

u( 0 , t) = u( l, t) = 0 现考虑初始条件,当冲量 k 作用于 x = c处时, 就相当于在这点 给出了一个初速度 , 我们考虑以 c点为中心 , 长为 2δ的一小段弦 ( c δ, c + δ) , 设弦是均匀的 , 其线密度为 ρ, 则这 一小段 弦的质量 为 2δρ, 受冲击时速度为 ut ( x, 0) , 由动量定理得
h c
x
l
h -
c(
l
-
x)
(0 ≤ x ≤ c) ( c < x ≤ l)
ut ( x, 0) = ψ( x ) = 0
则 u( x, t) 是下列定解问题的解 :
utt - a2 uxx = 0
( 0 < x < l, t > 0)
u( x, 0) = φ( x ) , ut ( x, 0 ) = ψ( x )
2 .4 习题全解
1. 设弦的两端固定于 x = 0 及 x = l, 弦的初始位称如图 2 2 所 示,初速度为零, 又设有外力作用, 求弦作横向振动时的位移函数 u( x, t) 。
解 如图 2 2 所示, 弦作横向振动时初始条件为
62
数学物理方程与特殊函数导教·导学·导考
图2 2
u( x, 0) = φ( x ) =
5. 若 F( z) , G( z) 是任意两个二次连续可微函数 , 验证
u = F( x + at ) + G( x - at )
满足方程
2u t2
=
a2
2x2u。
解 作自变量代换ξ= x + at,η= x - at, 由复合函数求导法则
有
所以 于是
u t

1．细杆（或弹簧）受某种外界原因而产生纵向振动，以u(x,t)表示静止时在x 点处的点在时刻t 离开原来位置的偏移，假设振动过程发生的张力服从虎克定律，试证明),(t x u 满足方程()⎪⎭⎫ ⎝⎛∂∂∂∂=⎪⎭⎫ ⎝⎛∂∂∂∂x u E x t u x t ρ 其中ρ为杆的密度，E 为杨氏模量。

证：在杆上任取一段，其中两端于静止时的坐标分别为 x 与+x x ∆。

现在计算这段杆在时刻t 的相对伸长。

在时刻t 这段杆两端的坐标分别为：),();,(t x x u x x t x u x ∆++∆++其相对伸长等于 ),()],([)],([t x x u xxt x u x t x x u x x x ∆+=∆∆-+-∆++∆+θ令0→∆x ，取极限得在点x 的相对伸长为x u ),(t x 。

由虎克定律，张力),(t x T 等于),()(),(t x u x E t x T x =其中)(x E 是在点x 的杨氏模量。

设杆的横截面面积为),(x S 则作用在杆段),(x x x ∆+两端的力分别为x u x S x E )()(x u x x S x x E t x )()();,(∆+∆+).,(t x x ∆+于是得运动方程 tt u x x s x ⋅∆⋅)()(ρx ESu t x =),(x x x x x ESu x x |)(|)(-∆+∆+ 利用微分中值定理，消去x ∆，再令0→∆x 得tt u x s x )()(ρx∂∂=x ESu () 若=)(x s 常量，则得22)(tu x ∂∂ρ=))((x u x E x ∂∂∂∂即得所证。

4. 绝对柔软逐条而均匀的弦线有一端固定，在它本身重力作用下，此线处于铅垂平衡位置，试导出此线的微小横振动方程。

解：如图2，设弦长为l ，弦的线密度为ρ，则x 点处的张力)(x T 为)()(x l g x T -=ρ且)(x T 的方向总是沿着弦在x 点处的切线方向。

数理方程课后习题答案数理方程课后习题答案数理方程是数学中的一个重要分支，它研究的是各种数学模型中的方程。

在学习数理方程的过程中，课后习题是巩固知识、提高能力的重要途径之一。

本文将为大家提供一些数理方程课后习题的答案，希望能对大家的学习有所帮助。

1. 解方程：2x + 5 = 13解答：将方程中的常数项5移到等号右边，得到2x = 13 - 5，即2x = 8。

然后将2移到等号右边，得到x = 8/2，即x = 4。

所以方程的解为x = 4。

2. 解方程组：{2x + y = 7，x - y = 1}解答：可以使用消元法来解决这个方程组。

首先将第二个方程的系数取负，得到{-x + y = -1}。

然后将第二个方程乘以2，得到{-2x + 2y = -2}。

将这两个方程相加，得到{0x + 3y = -3}，即3y = -3。

解得y = -1。

将y的值代入第一个方程，得到2x - 1 = 7，即2x = 8。

解得x = 4。

所以方程组的解为x = 4，y = -1。

3. 解二次方程：x^2 - 5x + 6 = 0解答：可以使用因式分解法来解决这个二次方程。

将方程因式分解为(x - 2)(x - 3) = 0。

根据乘积为零的性质，得到x - 2 = 0或x - 3 = 0。

解得x = 2或x = 3。

所以方程的解为x = 2或x = 3。

4. 解三次方程：x^3 - 6x^2 + 11x - 6 = 0解答：可以使用因式分解法来解决这个三次方程。

观察方程，可以发现x = 1是一个解。

通过除以x - 1，得到(x - 1)(x^2 - 5x + 6) = 0。

将x^2 - 5x + 6进行因式分解，得到(x - 1)(x - 2)(x - 3) = 0。

根据乘积为零的性质，得到x - 1 = 0或x - 2 = 0或x - 3 = 0。

解得x = 1或x = 2或x = 3。

所以方程的解为x = 1或x = 2或x = 3。