信息光学复习考点.doc
- 格式:doc
- 大小:104.40 KB
- 文档页数:4

光信息处理(信息光学)复习提纲第一章线性系统分析1.空间频率的定义是什么?如何理解空间频率的标量性和矢量性?2.空间频率分量的定义及表达式?3.平面波的表达式和球面波的表达式?4.相干照明下物函数复振幅的表示式及物理意义?5.非相干照明下物光强分布的表示式及物理意义?6.线性系统的定义7.线性系统的脉冲响应的表示式及其作用8.何谓线性不变系统9.卷积的物理意义10.线性不变系统的传递函数及其意义11.线性不变系统的本征函数第二章标量衍射理论1.衍射的定义2.惠更斯-菲涅耳原理3.衍射的基尔霍夫公式及其线性表示4.菲涅耳衍射公式及其近似条件5.菲涅耳衍射与傅立叶变换的关系6.会聚球面波照明下的菲涅耳衍射7.夫琅和费衍射公式8.夫琅和费衍射的条件及范围9.夫琅和费衍射与傅立叶变换的关系10.矩形孔的夫琅和费衍射11.圆孔的夫琅和费衍射(贝塞尔函数的计算方面不做要求)12.透镜的位相变换函数13.透镜焦距的判别14.物体位于透镜各个部位的变换作用15.几种典型的傅立叶变换光路第三章光学成象系统的传递函数1.透镜的脉冲响应2.相干传递函数与光瞳函数的关系3.会求几种光瞳的截止频率4.强度脉冲响应的定义5.非相干照明系统的物象关系6.光学传递函数的公式及求解方法7.会求几种情况的光学传递函数及截止频率第五章光学全息1.试列出全息照相与普通照相的区别2.简述全息照相的基本原理3.试画出拍摄三维全息的光路图4.基元全息图的分类5.结合试验谈谈做全息实验应注意什么(没做过实验,只谈一些理论性的注意方面)6.全息照相为什么要防震,有那些防震措施,其依据是什么7.如何检测全息系统是否合格8.全息照相的基本公式9.全息中的物像公式及解题(重点)复 习第一章 线性系统分析1.空间频率的定义是什么?如何理解空间频率的标量性和矢量性?时间量 空间量22v T πωπ==22K f ππλ== 时间角频率 空间角频率其中:v ----时间频率 其中:f ---空间频率T----时间周期 λ-----空间周期 物理意义:由图1.7.3知:(设光在z x ,平面内传播,0=y )cos xd λα=, 又 ∵ 1x xf d =联立得:cos x f αλ=讨论:① 当090,,<γβα时0,,>z y x f f f ,表示k沿正方向传播;②标量性,当α↗时,αcos ↘→x f ↘→x d ↗当α↘时,αcos ↗→x f ↗→x d ↘ ③标量性与矢量性的联系条纹密x d ↘→x f ↗→α↘→θ↗x x f d 1=λαcos =x f 条纹疏x d ↗→x f ↘→α↗→θ↘2.空间频率分量的定义及表达式?{}γβαcos ,cos ,cos k k ={}z y x r ,,=)cos cos cos (γβαz y x k r k ++=⋅代入复振幅表达式:()()()[]γβαμcos cos cos ex p ,,,,0z y x jk z y x z y x U ++=()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++=z y x j z y x λγλβλαπμcos cos cos 2exp ,,0 ()()[]z f y f x f j z y x z y ++=λπμ2ex p ,,0式中:λαcos =x f ,λβcos =yf ,λγcos =z f3.平面波的表达式和球面波的表达式?平面波()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++=z y x j z y x U λγλβλαπμcos cos cos 2exp ,,0 ()()[]z f y f x f j z y x U z y x ++=πμ2ex p ,,0球面波()1,,jkr a U x y z e γ=()21212212121221⎪⎪⎭⎫ ⎝⎛++=++=z y x z z y x r近轴时()1,,U x y z ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛++=1221021exp z y x jkz r a()⎪⎪⎭⎫ ⎝⎛+⋅≈1221102exp exp z y x jkjkz z a ⎪⎪⎭⎫ ⎝⎛+=12202exp z y x jkU若球面波中心不在坐标原点,上式改为:()1,,U x y z ()()⎥⎥⎦⎤⎢⎢⎣⎡++-=1202002exp z y y x x jk U4.相干照明下物函数复振幅的表示式及物理意义?设()y x f ,为一物函数的复振幅,其傅氏变换对为 ()()(),exp 2x y x y F f f f x y j f x f y dxdyπ∞-∞⎡⎤=-+⎣⎦⎰⎰ ()()(),exp 2x yxyxyf x y F f f j f x f y df dfπ∞-∞⎡⎤=+⎣⎦⎰⎰可见:物函数()y x f ,可以看作由无数振幅不同()x y x y F f f df df 方向不同()cos ,cos xyf f αλβλ==的平面波相干迭加而成。


1、 线性系统、平移不变系统的定义线性系统:若一个系统同时具有叠加性和均匀性,即:{(,)(,)}{(,)}{(,)}L a f x y a f x y a L f x y a L f x y +=+(,)a g x y a g=+则称此系统为线性系统.平移不变性:若{}1122(,)(,)L f x y g x y =,则}1122(,)(,)L f x x y y g x Mx y My --=--则称该系统具有平移不变性线性平移不变系统:既具有线性又具有平移不变性的系统称为线性平移不变系统. 2、惠更斯-菲涅耳原理光场中任一给定曲面上的诸面可以看做是子波源,如果这些子波源是相干的,则在波继续传播的空间上任一点处的光振动,都可以看做是这些子波源各自发出的子波在该点相干叠加的结果。
3、对衍射受限系统传递函数的表达式i 、相干传递函数:=),(y x c f f H (){}{}y d x d P i i ~,~λλF F ),(y i x i f d f d P λλ--=①这说明,相干传递函数),(y x c f f H 等于光瞳函数,仅在空域坐标xy 和频域坐标y x f f 之间存在着一定的坐标缩放关系。
如果在一个反射坐标中来定义P ,则可以去掉负号的累赘,把式①改写为 ),(),(y i x i y x c f d f d P f f H λλ= ,尤其是一般光瞳函数都是对光轴呈中心对称的,这样处理的结果不会产生任何实值性的影响。
对于直径为D 的圆形光瞳,其孔径函数()y x P ,可表为 ⎪⎪⎭⎫⎝⎛+=2/),(22D y x circ y x P 其相干传递函数为 ⎪⎪⎪⎭⎫⎝⎛+==iy x y i x i y x c d D f f circ f d f d P f f H λλλ2/),(),(22由圆柱函数的定义可知,在()i d D λ2区域内1=),(y x c f f H ,在)i d D λ2之外0=),(y x c f f H 。

第二章:2.7互相关定义:互相关的意义:自相关定义:自相关意义:自相关的作用:归一化互相关的定义及范围:归一化自相关的定义:功率函数定义:功率函数积分的意义:有限功率函数定义:有限功率函数的互相关定义式:3.3解析信号的定义:单色光场的定义:解析信号频谱和实信号频谱的关系:3.4定态光场定义:复振幅的定义:球面波的复振幅:球面波的旁轴近似复振幅:(为什么相位项不能近似)中心离轴的球面波波函数,相当于中心在轴上的球面波函数与一个倾斜平面波函数的乘积3.5空间频率定义:平面波的复振幅:平面波的复振幅(空间频率形式):为什么球面波没有空间频率:角谱定义:平面波基元分析法和余弦基元分析法:简单波和复杂波定义:3.6空间带宽积的定义及意义:分辨率:4.2惠更斯-菲涅尔原理:根据惠更斯-菲涅尔原理的得到的衍射公式(为什么不能用来处理复杂的衍射): 菲涅尔-基尔霍夫衍射公式及其物理意义:球面波的衍射理论:4.3角谱在空间中的传递函数:衍射孔径对光波的作用:4.4衍射的菲涅尔近似和夫琅禾费近似菲涅尔衍射的卷积积分表达式及其条件:夫琅禾费衍射的卷积积分表达式及其条件:用汇聚球面波照明衍射屏时:互补屏定义:互补屏透射函数关系:4.5菲涅尔衍射的计算塔尔伯特效应:塔尔伯特距离定义:傅里叶成像意义:一维余弦光栅的菲涅尔衍射:正弦光栅的振幅透过率函数为:‘代况)= - + ycos(2^0x o)用单位单色平面波垂直照射该光栅时:矩形孔的菲涅尔衍射:设平面衍射孔径为矩形,其透射率函数可由二维矩形函数来描述,取坐标原点位于矩形孔的中心,由式(L1.5),有矩形孔的透射率函4.6夫琅禾费衍射的计算夫琅禾费衍射公式:矩形孔的夫琅禾费衍射:设平面衍射孔径为矩形,其透射率函数可由二维矩形函数来描述,取坐标原点位于矩形孔的中心,由式(1.1.5),有矩形孔的透射率函单狭缝的夫琅禾费衍射:当矩形中的一边很长,另一边很短,矩形孔就变成了狭缝,如下图所示。
1、电子与光子有哪些差别?光子有哪些显著的特征?光子具冇极高的信息容最和效率,极快的响应能力,极强的互联能力与并行能力,极人的存储能力。
光了静止质量为零,但是可以传输电磁能和动能,也可以传输偏振特性。
光了在真空中以光速传播,在其他介质中速度会有所减小。
光子没冇自旋,电了冇自旋•电了是费米了,带基本电荷,具冇空间局域性。
它可以是信息的载体, 也可以是能最的载体。
作为信息载体时,可以通过金局导线或无线电波在白由空间进行传递。
电载信息的主要储存方式为磁储存。
光子是玻色子,电中性,没有空间局域性而具有时间可逆性。
它可以是信息的载体,也可以是能量的载体。
作为信息载体时,可以通过光纤(光缆)或口由空间进行传递,光载信息的主要存储方式为光储存。
光子具有的优异特性:光子具有极高的信息容量和效率,光子具有极快的响应能力,具有极强的互连能力与并行能力,光子具有极人的存储能力。
2、为什么说光波是理想的信息载体,光纤是理想光信息传输介质?・>发送信号的频率越高(波长越短),可载送的信息量就越多.光波范围包括红外线、可见光、紫外线,波长范围为300um^6*10-3um,光波的波长远远比无线电波波长短,所以目前可以认为光波是理想的信息载体。
・>光纤是理想的光信息传输介质:1.传输频带宽,通信容量大。
2.信息传输的损耗小,容易实现长中继距离的传输。
3.可用光纤作为传输,介质损耗小(可达到0.2dB/km),传输速率大(50Tbit/s)o3、描述半导体激光器激光产生的过程。
半导体激光器的材料应如何选择?首先,由外界的泵浦作用使增益介质处于激发态;然后,白发辐射开始发生,产生一系列具冇不同波长的光了源;冇些光了经过频率选择并获得了反馈,重新进入增益介质;这些被反馈会凹来的光子会使处于激发态的增益介质受激跃迁,并发生受激辐射,产生更多与Z相同的光子;上述过程反复发工,直到激光器中只有经过选频的频率和增益大于损耗的光频率存在。
这吋输出的激光实际上是从半导体激光器谐振腔中泄漏出來的激光,谐振腔小的激光强度要远大于输出的激光强度。

信息光学复习提纲Ch1. 线性系统分析1.矩形函数:①定义②图像③作用④傅里叶变换谱函数2.sinc函数:①定义②图像③作用④不要求求其傅里叶变换谱函数3.三角函数:①定义②图像③作用④傅里叶变换谱函数4.符号函数:①定义②图像③作用④傅里叶变换谱函数5.阶跃函数:①定义②图像③作用④傅里叶变换谱函数6.圆柱函数:①定义②图像③作用④傅里叶变换谱函数7. 函数:①三种定义②四大性质③作用8.梳状函数:①定义②图像③作用④傅里叶变换谱函数9.高斯函数:①定义②图像③作用④傅里叶变换谱函数10.傅里叶变换(常用傅里叶变换对)11.卷积:四大步骤,两大效应12.互相关、自相关的定义、物理意义13.傅里叶变换的基本性质和有关定理14.线性平移不变系统的传递函数Ch2. 标量衍射理论1. 标量衍射理论成立的两大条件2. 平面波及球面波表达式:)]cos cos (exp[βαy x ik A +)](2exp[]exp[22y x zik ikz z A + 3.惠更斯——菲涅耳原理:()⎰⎰∑=ds rikr K P U cQ U )exp()()(0θ 4.基尔霍夫衍射理论: ⎰⎰∑-=dsrikr r n r n r ikr a j Q U )exp(]2),cos(2),cos([)exp(1)(0000λ令()()θλK rikr j Q P h )exp(1,=所以()⎰⎰∑=ds Q P h P U Q U ,)()(0当光源足够远,且入射光在孔径平面上各点的入射角都不大时,(),1,cos 0≈r n(),1,cos ≈r n ().1≈∴θK故()zikr j Q P h )exp(1,λ=,]})()[(211{20020z y y z x x z r -+-+≈ 5. 菲涅耳衍射——近场衍射:0000202000022)](2exp[)](2exp[),()](2exp[)exp(),(dy dx yy xx zj y x z jk y x U y x zjkz j jkz y x U +-++=⎰⎰∞∞-λπλ6. 夫琅禾费衍射——远场衍射:000000022)](2exp[),()](2exp[)exp(),(dy dx yy xx zj y x U y x zjkz j jkz y x U +-+=⎰⎰∞∞-λπλ 7. 夫琅禾费衍射的条件及与菲涅耳衍射之比较(TBP46)8.衍射的角谱理论:(TBP41) 9.透镜的傅里叶变换性质:①相位变换作用:)](2exp[),(),(22y x f jky x p y x t +-=②透镜的傅里叶变换特性:a. 物在透镜前b.物在透镜后(二次位相因子)Ch.3 光学成像系统的传递函数1. 绪论部分:几何光学:空域成像规律,有星点法和分辨率法(像质评价) 信息光学:频域成像规律,光学传递函数(全面、科学像质评价) 2. 衍射受限系统的点扩散函数:⎰⎰∞∞--+--=--yd x d y y y x x x j y d x d P d K y y x x h i i i i ii i ~~]}~)~(~)~[(2exp{)~,~()~,~(002200πλλλ 光瞳相对于i d λ足够大时,)~,~()~,~(22o i o i i o i o i y y x x d K y y x x h --≅--δλ理想情况:点物成点像3. 相干照明下衍射受限系统的成像规律:),(),(~),(i i g i i i i i y x U y x h y x U *=其中,)]~,~([),(~y d x d P F y x h i i i i λλ=,),(1),(0My M x U M y x U i i i i g = 4.衍射受限系统的相干传递函数:()()ηλξληξi i d d P H ,,=(坐标轴反演)5. 菲涅耳衍射——近场衍射:0000202000022)](2exp[)](2exp[),()](2exp[)exp(),(dy dx yy xx zj y x z jk y x U y x zjkz j jkz y x U +-++=⎰⎰∞∞-λπλ6. 截止频率:圆形光瞳:oc oc i cd DM d D λρρλρ2,2=== 正方形光瞳不同方向的截止频率不同,45度时最大)22max ic d aλρ=Ch.4 光学全息1. 普通照相与全息照相的比较(定义)2. 全息照相的核心:波前记录和再现①方法:干涉法(标准方法,即将空间相位调制→空间强度调制) ②特点:全息图实际上就是一幅干涉图 ③分类:a 物、参位置:同轴全息+离轴全息b 物、图位置:菲涅耳全息图+像面全息图+傅里叶变换全息图c 介质厚度:平面全息图+体积全息图3. 全息基本公式:()()C r O C r O C i i i b ORCe ORCe Ce O t δδδδδδδβ---+-++'+)(2 0级(背景光) -1级(实像) +1级(虚像) 4. 菲涅耳全息图 像位置坐标:112121-⎪⎪⎭⎫ ⎝⎛±=o r p i z z z z λλλλp pir r i o o i i x z z x z z x z z x +±=1212λλλλp pi r r i o o i i y z zy z z y z z y +±=1212λλλλ横向放大率:1120121--====p or o i o i o i z z z z z z dy dy dx dx M λλλλ纵向放大率:221M dz dz M o i z λλ==5. 傅里叶变换全息图①定义②特点③照明与再现的两种方式,相互是独立的6. 位相全息图①定义②两种制作方法③性质7. 平面全息图的衍射效率①定义②振幅全息图的衍射效率:正弦型(6.25%),矩形(10.13%)③位相全息图的衍射效率:正弦型(33.9%),矩形(40.4%)结论:无论振幅型还是位相型,矩形波衍射效率均大于正弦波8. 全息干涉计量Ch.5 空间滤波1. 阿贝成像理论第1步:物体(P1)经L在透镜后焦面P2成各级衍射斑第2步:各级衍射斑在P3面相互干涉成像2. 空间滤波的傅里叶分析:透镜作频谱分析器;空间滤波器改变物体光的频谱3. 空间滤波系统:典型的4f系统4. 空间滤波器:位于空间频谱平面上的一种模片,它改变输入信息的空间频谱,从而实现对输入信息的某种变换。

信息光学复习题信息光学复习题一、光的本质和特性1. 什么是光的本质?光是由电磁波组成的,具有粒子和波动性质的物质。
2. 光的波长和频率之间有什么关系?光的波长和频率之间成反比关系,即波长越长,频率越低;波长越短,频率越高。
3. 什么是光的干涉?光的干涉是指两束或多束光波相互叠加而产生的干涉现象。
4. 什么是光的衍射?光的衍射是指光通过一个孔或绕过一个障碍物后,光波的传播方向发生了改变。
5. 什么是光的偏振?光的偏振是指光波中的电矢量在特定方向上振动的现象。
二、光的传播和折射1. 光在真空中的传播速度是多少?光在真空中的传播速度是每秒约300,000公里。
2. 什么是光的折射?光的折射是指光从一种介质传播到另一种介质时,光线的传播方向发生改变的现象。
3. 什么是折射定律?折射定律是描述光在两种介质间折射规律的定律,即入射角、折射角和两种介质的折射率之间满足的关系。
4. 什么是全反射?全反射是指光从光密介质射向光疏介质时,入射角大于临界角时,光线完全被反射回原介质内的现象。
5. 什么是光纤?光纤是一种能够将光信号传输的细长光导纤维,通常由光纤芯和包层组成。
三、光的色散和光谱1. 什么是光的色散?光的色散是指光通过某些介质或物体时,不同波长的光被分散成不同的角度或位置的现象。
2. 什么是光的光谱?光的光谱是指将光按照波长或频率进行排序后的光线分布图。
3. 什么是连续光谱?连续光谱是指包含了所有波长的光谱,如太阳光。
4. 什么是线状光谱?线状光谱是指只包含特定波长的光谱,如氢光谱。
5. 什么是衍射光谱?衍射光谱是指通过衍射现象产生的光谱,如菲涅尔衍射光谱。
四、光的偏振和偏振光器件1. 什么是偏振光?偏振光是指只在一个特定方向上振动的光波。
2. 什么是偏振片?偏振片是一种能够选择性地通过特定方向偏振光的光学器件。
3. 什么是偏振器?偏振器是一种能够将非偏振光转化为偏振光的光学器件。
4. 什么是偏振旋转?偏振旋转是指光在通过某些物质时,其偏振方向发生旋转的现象。

信息光学复习提纲信息光学的特点Ch1. 线性系统分析1.矩形函数:①定义②图像③作用④傅里叶变换谱函数2.sinc函数:①定义②图像③作用④傅里叶变换谱函数3.三角函数:①定义②图像③作用④傅里叶变换谱函数4.符号函数:①定义②图像③作用④傅里叶变换谱函数5.阶跃函数:①定义②图像③作用④傅里叶变换谱函数6.余弦函数:①定义②图像③作用④傅里叶变换谱函数7. 函数:①三种定义②四大性质③作用8.梳状函数:①定义②图像③作用④傅里叶变换谱函数9.高斯函数:①定义②图像③作用④傅里叶变换谱函数10.傅里叶变换(常用傅里叶变换对)11.卷积:四大步骤,两大效应12.互相关、自相关的定义、物理意义13.傅里叶变换的基本性质和有关定理14.线性系统理论15.线性不变系统的输入输出关系,脉冲响应函数,传递函数16.抽样定理求抽样间隔Ch2. 标量衍射理论1. 标量衍射理论成立的两大条件2.平面波及球面波表达式:exp[(cos cos cos )]A ik x y z αβγ++(求平面波的空间频率))](2exp[]exp[22y x zik ikz z A + 3.惠更斯——菲涅耳原理:()⎰⎰∑=dsrikr K P U cQ U )exp()()(0θ 4.基尔霍夫衍射理论: ⎰⎰∑-=dsrikr r n r n r ikr a j Q U )exp(]2),cos(2),cos([)exp(1)(0000λ令()()θλK rikr j Q P h )exp(1,=所以()⎰⎰∑=ds Q P hP UQ U ,)()(0当光源足够远,且入射光在孔径平面上各点的入射角都不大时,(),1,cos 0≈r n(),1,cos ≈r n ().1≈∴θK故()z ikr j Q P h )exp(1,λ=,]})()[(211{20020zy y z x x z r -+-+≈ 5. 菲涅耳衍射——近场衍射:0000202000022)](2exp[)](2exp[),()](2exp[)exp(),(dy dx yy xx zj y x z jk y x U y x zjkz j jkz y x U +-++=⎰⎰∞∞-λπλ6. 夫琅禾费衍射——远场衍射:(根据屏函数求衍射光强分布)000000022)](2exp[),()](2exp[)exp(),(dy dx yy xx zj y x U y x zjkz j jkz y x U +-+=⎰⎰∞∞-λπλ 7.衍射的角谱理论:(角谱的传播,求角谱分布)Ch.3 光学成像系统的频率特性1.透镜的傅里叶变换性质: ①相位变换作用:)](2exp[),(),(22y x f jky x p y x t +-=(二次位相因子)②透镜的傅里叶变换特性:(满足条件?什么情况下实现准确傅立叶变换) a. 物在透镜前b.物在透镜后 2. 衍射受限系统的点扩散函数:⎰⎰∞∞--+--=--yd x d y y y x x x j y d x d P d K y y x x h i i i i ii i ~~]}~)~(~)~[(2exp{)~,~()~,~(002200πλλλ 光瞳相对于i d λ足够大时,理想情况:点物成点像)~,~()~,~(22o i o i i o i o i y y x x d K y y x x h --≅--δλ3. 相干照明下衍射受限系统的成像规律:),(),(~),(i i g i i i i i y x U y x h y x U *=其中,)]~,~([),(~y d x d P F y x h i i i i λλ=,),(1),(0My M x U M y x U i i i i g =4.衍射受限系统的相干传递函数(CTF ):()()ηλξληξi i d d P H ,,=(坐标轴反演)5. 截止频率:圆形光瞳:o c oc i c d DM d D λρρλρ2,2=== 正方形光瞳:不同方向的截止频率不同,45度时最大)22max ic d aλρ= 6. 衍射受限系统的非相干传递函数(OTF ) 7. OTF 与CTF 的关系Ch.4 光学全息1. 普通照相与全息照相的比较2. 全息照相的核心:波前记录和再现①方法:干涉法(标准方法,即将空间相位调制→空间强度调制) ②特点:全息图实际上就是一幅干涉图 ③全息图的分类:a 。


一、选择题(每题2分,共40分)1.三角函数可以用来表示光瞳为________________的非相干成像系统的光学传递函数。
A 、矩形B 、圆孔C 、其它形状2.Sinc 函数常用来描述________________的夫琅和费衍射图样A 、圆孔B 、矩形和狭缝C 、其它形状3.高斯函数)](exp[22y x +-π常用来描述激光器发出的________________A 、平行光束B 、高斯光束C 、其它光束4.圆域函数Circ(r)常用来表示________________的透过率A 、圆孔B 、矩孔C 、方孔5.卷积运算是描述线性空间不变系统________________的基本运算A 、输出-输入关系B 、输入-输出关系C 、其它关系6.相关(包括自相关和互相关)常用来比较两个物理信号的________________A 、相似程度B 、不同程度C 、其它关系7.卷积运算有两种效应,一种是展宽,还有一种就是被卷函数经过卷积运算,其细微结构在一定程度上被消除,函数本身的起伏振荡变得平缓圆滑,这种效应是________________A 、锐化B 、平滑化C 、其它8互相关是两个信号之间存在多少相似性的量度。
两个完全不同的,毫无关系的信号,对所有位置,它们互相关的结果应该为________________A 、0B 、无穷大C 、其它9.周期函数随着其周期逐渐增大,频率(即谱线间隔)________________。
当函数周期变为无穷大,实质上变为非周期函数,基频趋于零A .愈来愈小B 、愈来愈大C 、不变14.函数rect(x)rect(y)的傅立叶变换为________________A 、),(y x f f δB 、1C 、)(sin )(sin y x f c f c16.一个 空间 脉冲 在输入平面位移,线性系统的响应函数形式不变 ,只产生相应的位移,这样的系统称为________________A、时不变系统B、空间不变系统或位移不变系统C、其它系统17.线性空间不变系统的脉冲响应的傅立叶变换称为系统的________________。
1.常用的非初等函数:矩形函数、Sinc函数、三角形函数、符号函数、阶跃函数、圆柱函数。
2.δ函数的定义:a.类似普通函数定义b.序列极限形式定义c.广义函数形式定义δ函数的性质:a.筛选性质 b.坐标缩放性质 c.可分离变量性d.与普通函数乘积性质4.卷积,性质:线性性质、交换律、平移不变性、结合律、坐标缩放性质5.互相关,两个函数f(x,y)和g(x,y)的互相关定义为含参变量的无穷积分6.惠更斯-菲涅尔原理:光场中任意给定曲面上的诸面元可以看作是子波源,如果这些子波源是相干的,则在波继续传播的空间上任意一点处的光振动都可看作是子波源各自发出的子波在该点相干叠加的结果。
7.基尔霍夫理论:在空域中光的传播,把孔径平面上的光场看作点源的集合,观察平面上的场分布则等于他们所发出的带有不同权重的因子的球面子波的相干叠加。
8.角谱理论:孔径平面和观察平面上的光场分布都可以分别看成是许多不同方向传播的单色平面波分量的线性组合。
9.点扩散函数:面元的光振动为单位脉冲即δ函数时,这个像场分布函数叫做~。
10.菲涅尔衍射成立的充分条件:传递函数:11.泰伯效应:当用单色平面波垂直照明一个具有周期性透过率函数的图片时,发现在该透明片后的某些距离上出现该周期函数的现象,这种不用透镜就可以对周期物体成像的现象称为~。
12.夫琅禾费衍射:13.衍射受限系统:不考虑系统的几何像差,仅仅考虑系统的衍射限制。
14.单色信号的复表示:去掉实信号的负频成分,加倍实信号的正频成分。
多色信号的复表示:16.如果两点处的光扰动相同,两点间的互相干函数将变成自相干函数。
18.光学全息:利用干涉原理,将物体发出的特定光波以干涉条纹的形式记录下来,使物光波前的全部信息都储存在记录介质中,做记录的干涉条纹图样被称为“全息图”,当用光波照射全息图时,由于衍射原理能能重现出原始物光波,从而形成与原物体逼真的三维像,这个波前记录和重现的过程成为~19.+1级波(虚像),-1级波(实像),±1级波(赝像)20.从物光与参考光的位置是否同轴考虑:同轴全息、离轴全息。
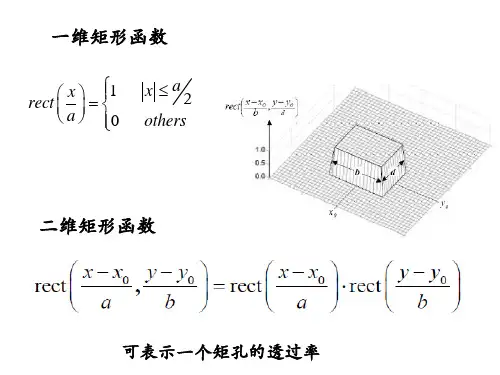
[]{}{}{}{}{}{}),(),(),(),(),(),(),(),()2()()]()([212sin )](exp[)](exp[)]()([212cos )()()()(),()](2exp[)(sin )(sin )()(1),()(sin )(sin )()()](2exp[),()()(),()()(11)()(),(),(),(),()(),(1),(),(),(),(1),(000),(1)2(),()(),(01)(exp ),(exp 01)()(),()()(sin sin Sinc )()(),(021)(11110002222000220000000000222212222212222222222000200ηεηεηεηερπρδδπππδδπδπδπδτδτδτττδδδδδδδδδδδππππππG b F a bG aF y x g b y x f a y x bg y x af J r circ f f f f jx f f f y x f f f f xf f comb f comb y comb x comb f f f f y f x f j f c f c y tri x tri y x f c f c y rect x rect b f a f j b y a x y Comb x Comb y x Comb n x n x x Comb y x y x y y x x y x f y y x x xy f y x abby ax y x f dxdy y y x x y x f dxdy y x y x y x y x y x N J N y x f y x N Circ N y x f a y x a y x Circ y x N N y x f a x a x Gaus ax a x a x a x Tir Ny Sinc Nx Sinc N y x f a x x ax x a x x c Ny rect Nx rect N y x f a x x a x x rect x x y x x x y x b y a x b a y x y x y x n n N NN N N ---∞-∞=∞-∞=∞+∞-∞+∞-+=++=+---+-+--+---++---=-=-=⎪⎭⎫ ⎝⎛=--=--==--⎪⎩⎪⎨⎧=≠≠=++=+=⎪⎩⎪⎨⎧≤+=++-=⎥⎦⎤⎢⎣⎡-=⎪⎩⎪⎨⎧≤-=∧==--=-=⎪⎩⎪⎨⎧≤-=-∑∑⎰⎰⎰⎰F F FF F F 频谱函数原函数频谱函数原函数,梳状函数:分离性质:相乘性质:比例性质:筛选性质:函数的定义及性质:贝塞尔函数:,其它)()(圆域函数:,)()(高斯函数:其它)()(三角函数:,)(函数:,其它矩形函数:线性关系。
信息光学复习要点1 (5.1&5.2)全息概述&波前记录与再现/所有的感光材料只能记录光强信息,全息记录的关键是必须冻住位相信息,要想实现全息记录必须使位相信息转化为光强信息,转化途径是光的干涉.2 (波面形状与干涉场分布的关系)平面波与平面波相干,干涉场:平面族;平面波与球面波相干,干涉场:旋转双曲面;球面波与球面波相干,干涉场:双叶旋转双曲面;复杂波面与平(球)面波相干,干涉场:复杂的曲面分布.(对应关系)干涉场曲面的形状、间隔与相干波面一一对应;一种干涉场分布只对应一种干涉特征包括:波面形状和相干“姿态”——全息记录的依据3 全息记录的基本光路4 (全息记录的数学描述)单色光波 , 振幅,位相,“+”号表示正向传播,“-”号表示反向传播.5 (全息定义)将物体发出的特定光波以干涉条纹的形式记录下来,使物体波前的全部信息都贮存在记录介质中,故所记录的干涉条纹图样被称为“全息图”.当用光波照射全息图时,由于衍射原理能重现出原始物光波,从而形成与原物体逼真的三维像,这个波前记录和重现的过程称为全息术或全息照相.6 (依据全息原理解释全息照片的三大特点:三维立体性,可分割性,白光不能再现)每一个物点的信息覆盖干板表面所有点,干板表面上每一点接收到所有物点的信息.普通照片不可分割的原因是物点与像点是一一对应关系.7 (全息图的分类)物参光主光轴:同轴全息和立轴全息;记录介质相对物体的位置:菲涅耳全息图、夫琅和费全息图和傅里叶变换全息图;记录介质的厚度:平面全息图和体积全息图;记录和再现的光路配置:透射型和反射型;透射率函数的性质:振幅型、位相型和混合型;再现照明条件:激光再现和白光再现(像面全息图、彩虹全息图、360°全彩色全息和真彩色全息)8 其他的全息图只能用激光重现.为什么像全息图和彩虹全息图却能用白光重现呢?普通的全息图是薄全息图,它的记录介质的感光层非常薄,以致全系记录的干涉条纹只分布在表面层,它只能在单色光照射下清晰地再现物光波,如果采用白光即连续非单色光,照射薄全息图,则由于再现物的纵向位置、横向位置和放大率因波长而异,以致各色光的+1级衍射波混杂一起,而模糊一片,不能再现物体形貌,如果,记录介质的感光层足够厚,以致全息记录时的干涉强度沿纵向Z 也被记录下来,便形成一个三维周期分布的光驻波场,经线性冲洗后,就获得一张体全息图.像全息图和彩虹全息图是体全息图,可以用白光重现9 全息图记录到的实际上是一些纵横分布的干涉条纹,这些干涉条纹的形状、疏密、强度分布取决于物光波和参考光波的波前特性,以及两者之间的相互位置关系.干涉条纹是两光位相差为常量的点的轨迹.10 (5.3)同轴全息图和离轴全息图(P117)11 (5.4)基元全息图:由单一物点构成的物光波与点源构成的参考光波所形成的最基本、最简单的全息图.其他复杂的结构则可看成是这些简单结构的组合.(空域:基元波带片;频域:基元光栅)12 (P122例题)13 (5.5)菲涅尔全息图:记录平面位于衍射光场的菲涅尔衍射区,物光由物体直接照在底片上.物体特征:二维或三维漫射体,透射型或反射型;物光波特征:是物体的菲涅耳衍射波,物与干板距离满足菲涅耳近似条件;记录与再现:激光记录,激光再现.14 菲涅耳全息图在什么条件下能再现出原始像来?请用数学描述,并说明其虚、实.P126(1)菲涅耳全息图在什么条件下能再现出共轭像来?请用数学描述,并说明其虚、实,有何特点?P127(2)15 *夫琅和费全息图,近似条件:)(20200y x z +>>λπ(特点)物体特征:二维透射型物体,即平面漫射体;物光波特征:是物体的夫琅和费衍射波物与干板距离满足夫琅和费近似条件;记录与再现:激光记录,激光再现;参考波特征:平面波16 (5.6)傅立叶全息图凸透镜的傅里叶变换功能表述为:当目标物置于透镜前焦面上时,透镜的后焦面上得到物的傅里叶变换.结论:利用凸透镜可以实现光学傅里叶变换.17 全息方法既可以在空域中记录物光波,也可以在频域中记录物频谱.物体或图像频谱的全息图,称为傅立叶变换全息图.实现方法:物置于透镜前→在照明光的共轭位置得到物光波的傅立叶频谱+参考光波→傅立叶变换全息图.18准傅立叶变换全息图: 凡是采用带有二次位相因子的傅立叶变换系统记录的关系图.无透镜傅立叶变换全息:参考光是从和物体共面点发出的一个球面波,用这种特殊光路记录的全息图.19傅里叶变换全息技术用于特征识别第一步:制作待识别物的傅里叶变换全息图(匹配滤波器)第二步:将该物的匹配滤波器置于4f 系统的(x2,y2)平面上(频谱平面)第三步:将比对物置于4f 系统的(x1,y1)平面上(输入平面)第四步:在4f 系统的(x3,y3)平面上进行判别(输出平面)指纹识别全息锁** 机器人视觉…20傅里叶变换全息图的特点与应用1)全息图上记录的干涉条纹排列有序→适用于计算全息术2)全息图记录的是目标物的频谱分布集中,面积小→适用于大容量、高密度全息存储3)全息图记录的是干涉条纹,即使用高倍显微镜也看不到内容保密性好→适用于存储高密级资料21(5.7)像面全息定义:物体靠近记录介质,或利用成像系统使物成像在记录介质附近,或者使一个全息图再现的实像靠近记录介质,都可以得到像面全息图特点:可以用扩展的白光光源照明再现.1)物体靠近记录介质,或利用成像系统使物体成像在记录介质附近,就可以拍摄像全息图;2)当物体的像位于记录介质面上时,称为像面全息.这时对于记录介质来讲,物体的像就是被记录的物,物距为零.再现的像距也相应为零;3)这时线模糊与色模糊也为零,可以用宽光源和白光照明再现出清晰的像;4)对于物体靠近记录介质的像全息图,线模糊与色模糊也非常小.显然这个特性对于全息的实际应用有极重要的意义.因此像全息图是一类极重要的全息图;5)像全息图的数学模型和菲涅耳全息相同,只是物、像距为零.221)怎样得到“物光波”——成像光波?2)记录像面全息图的光路有何特殊性?3)像面全息图可否用白光再现?23透镜成像法(一步法)——透射型,采用原光路白光再现,反射型像面全息图如何记录?无透镜法(二部法) 记录:1)记录菲涅耳全息图用平行参考光;2)共轭再现干板记录像面全息图,为什么要用共轭再现?景深反演→赝像两种方法的优缺点:1方法简便;视场角小(受透镜孔径限制);可用于多重像的多角度存储;噪声小/2方法较一步法复杂;噪声大;视场角大;可通过增大干板1相对干板2的张角实现241)为什么像面全息图用白光再现时不会出现像模糊?2)要想使再现像处于干板后(或干板前)是否可能?记录光路应怎样改变?25(5.8)彩虹全息定义:彩虹全息是利用记录时在光路的适当位置加狭缝,再现时同时再现狭缝像,观察再现像时将受到狭缝再现像的限制.当用白光照明时,对不同颜色的光,狭缝和物体的再现像位置都不同,在不同位置将看到不向颜色的像,颜色的排列顺序与波长顺序,犹如彩虹一样.彩虹全息图的特点:1)可以用白光再现;2)再现像呈现彩虹状的彩色,但再现像的色彩与原物体的色彩无关,而仅与再现照明光包含的波长组分有关.例如:用白炽灯照明和用日光灯照明,得到的彩虹效果有很大差异.3)彩虹全息属于假彩色全息.26扩大视场角、降低噪声的方法:条形散斑屏法;移动法;零光程差法;像散彩虹全息法;与计算机技术相结合的更先进的方法.27彩虹全息的发明思路1)普通全息图为什么不能用白光再现?/是由于不同波长的再现像错位重叠,发生色模糊和像模糊所致.2)能否设法把再现光波压缩在空间很窄的一个条形区域里,不同的波长占据空间不同的区域.3)当用白光照明时眼睛处在空间某一个位置,只能看到一种波长的再现像.4)移动观察位置,依次看到不同波长的像,不再会出现色模糊,于是达到了白光再现的目的.28一步彩虹全息和二步彩虹全息的比较:1)一步彩虹全息制作简单,噪声小,但视场较小;2)二步彩虹全息制作复杂,噪声较大,但视场大.29记录彩虹全息图需注意的问题:1)狭缝的宽度应选择适当:狭缝过宽,再现时各波长对应的衍射区展宽,引起“混频”,像的单色性差;狭缝过窄,像的单色性好,色彩鲜艳,但光能量损失较大,增加曝光时间,对系统的稳定度要求提高.2)注意狭缝的放置方位:狭缝应垂直于光路平面.3)注意物体的放置方位:为了保证再现像是正立的,记录时,物体应“卧”在光路平面内,即与狭缝相垂直.30 1.记录彩虹全息图时1)为什么狭缝应垂直于光路平面放置?2)为什么物体应“卧”在光路平面内?2.彩虹全息图和像面全息图的区别是什么?3.一步彩虹全息图可以用原光路再现,为什么二步彩虹全息图需要用共轭光再现?31全视场彩虹全息特点:1)可以用白光再现,出现彩虹像;2)可以用二步彩虹全息方法制作;3)满足共轭再现条件时,可在一张全息图的正、反两面分别观察到物体的正面和背面,更加逼真.32记录体视对彩虹全息注意事项1)第一步用普通照相记录时,必须根据与目标的距离以及人眼的平均间距,精确计算两架相机的间距,以及对准角度,包括水平方位和俯仰角度,保证符合人眼观察大景物的视差值;2)两架照相机曝光必须严格同步,尤其是拍摄动态实景时更为重要;3)第二步用全息照相记录时,OL、OR必须精确对准,否则将得不到预期的观察效果. 33 体视对彩虹全息特点:1)体视对彩虹全息图“牺牲”了再现像的三维特性,立体感的产生,是靠两眼分别接收了左视图和右视图,继而产生了视差;2)观察再现像时,仅当双眼处于双孔像位置时,才能看到三维立体像;离开该位置则看不到预期的效果;3)体视对彩虹全息由于引入了普通照相技术,因而不必要求目标物体完全静止,可用于实时记录动态大场景.34 (5.9)相位全息图:衍射效应起因于位相调制,而不是振幅调制相位全息图的特点:相位全息图对光是透明的;光束通过时,相位分布发生变化而导致衍射作用的发生,从而使记录在上面的物信息得以恢复.相位全息图的优点:相位全息图的衍射效率相当高;重铬酸盐明胶、光致聚合物的衍射效率可高达100%在全息技术中占有相当重要的地位.35 相位全息图的类型 1)折射率型:如全息图的位相分布是由折射率变化引起的,称为折射率型全息图.如将银盐干板漂白,后可得到折射率全息图.再如用重铬酸盐明胶或光致聚合物制成的全息图,也属折射率型.(2)表面浮雕型:若位相分布是由记录介质表面厚度变化而引起的,则称为表面浮雕型.如将银盐干板制成的全息图置于鞣化漂白液中,经干燥便可制得浮雕型全息图;再如用光致抗蚀剂(光刻胶)作记录介质,得到的全息图也是浮雕型.36 模压全息图:模压方法复制全息图的一项新技术.与凸版印刷术类似,称为全息印刷术.优点:解决了复制问题,可大规模生产;商品化,走进社会、家庭.制作技术分三个阶段:1)白光再现浮雕全息图的制作;2)电铸金属模板;3)模压复制.需要在白光下再现观察,所以母版的全息图多采用彩虹全息图,为了制作电铸金属板的母版,彩虹全息图还必须记录成相位浮雕型全息图.模压(P147):也称印压,即在一定压力和温度下,利用专门模压机将镍板上的全息干涉条纹印刷到聚氯乙烯等热塑料薄膜上以制成模压全息图,再将模压全息图表面镀铝,使之成为反射再现全息图,便于观察.37 电铸金属模板(P146)38 (5.11)体积全息(P147)当用白光照明体积全息图时,会发生什么?1)布喇格条件保证了体积全息图的角度或波长选择性;2)尽管记录过程必须用单色光完成,再现却可以用白光实现;3)白光中只有一个很窄的光谱成分能够满足布喇格条件, 得到有效的衍射,不会产生其它颜色的干扰.这在全息术的许多应用中是明显的优点.按衍射条件:所有波长的光波都可能得到再现,但各自的衍射角不同: 按反射条件:反射角=入射角= 结果:只可能有一个波长,其出射方向同时满足两个条件如图中的4 ,其它波长的衍射光被抑制,不能得到再现39 1)“谁”能满足布喇格条件?只有波长等于记录光波长的衍射光才能满足布喇格条件,得到物光的再现,即当的单波长光能得以再现.2)再现像有何特点? 形象与物相同,单色.40 透射型体积全息图特点:1)记录/物光和参考光在全息干板同侧;2)再现/照明光与观察者在全息图两侧;3)干涉条纹趋向/垂直于全息图表面;4)敏感点/对角度特别敏感.反射型体积全息图特点:1)记录/物光和参考光在全息干板两侧;2)再现/照明光与观察者在全息图同侧;3)干涉条纹趋向/平行于全息图表面;4)敏感点/对波长特别敏.(比较)透射体全息对角度敏感 时,有再现像; 时,无再现像.(实现多重像的存储)记录时对不同的目标物采用不同角度入射的参考光,白光再现时改变照明光入射的角度,得到多重像的再现反射体全息对波长敏感 时,有再现像, 时,无再现像.用白光再现时,得到单色像不会出现色混淆“蓝移”现象:再现单色像的波长通常并不与 相同原因是全息图在化学处理过程中发生了乳胶收缩41 1)体积全息图在化学处理过程中发生了乳胶收缩,再现像为什么会发生“蓝移”现象而不是“红移”呢?满足什么条件有可能发生“红移”现象?2)什么叫体积全息图?它和平面全息图的主要区别是什么?3)什么是布喇格条件?4)透射体全息和反射体全息有何区别?记录光路;干涉条纹趋向;再现特点.42 (5.12)平面全息图的衍射效率(P150)43*真彩色全息术一般原理:任何颜色都由三原色按比例合成三原色:红绿蓝(R G B );人眼辨别颜色靠视网膜上三种感色的锥体细胞,分别对红绿蓝三种颜色敏感;三原色波长的国际标准(由国际照明委员会规定):1964年CIE —RGB 系统的标准.红He-Ne Laser(632.8 nm);绿Ar + Laser(514.5 nm);蓝Ar + Lase(488.0nm).若用 R 、G 、B三种波长记录三套全息图,将再现出十二项,相互干扰白光再现时造成严重的,用哪一种类型的全息技术有望消除?色串扰44(5.13)全息干涉计量(P152)§6计算全息1计算全息1)计算全息将计算机技术与光全息术结合起来,可以实现光学全息术无法实现或难以实现的某些特殊功能.2)光全息术是利用光的干涉原理,借助于参考光将物光波的复振幅记录在感光材料上,能够实现这种记录的必要条件是物体的真实存在3)很多实际应用中理想的“物体”是很难制作,例如,用于检测光学元件加工质量的标准件,用于光学信息处理的空间滤波器,用于数据存储系统的相移器4)计算全息发展极其迅速,已成功地应用在三维显示、空间滤波、光学信息存储和激光扫描等诸多方面2计算全息图的制作计算全息图的计算机制作分为五步:对物光信息的采集:对于实际存在的物体,可用扫描仪或数字摄像机进行数据采集.而对于那些实际不存在的物体,可将其函数直接输入计算机抽样:用抽样定理将物函数离散化,得到物体或者波面再离散样点上的值,取抽样单元数不超过物的空间带宽积计算:计算物函数在全息平面上的光场分布编码:(两种途径)干涉的计算机仿真和迂回位相法存储:用计算机绘图仪直接画在纸上,然后用精密照相翻拍在照相底片上,适当放大或缩小到合适的尺寸3物信息的采集物光信息的采集是指确定物光信息的函数形式,一般表现为复振幅透射率函数(或反射率函数)对于实际存在的物体,可利用扫描仪或数字摄像机进行数据采集对于那些实际不存在的物体,可将其函数形式直接从键盘输入计算机物函数需要离散化,一般取抽样单元数不超过物的空间带宽积,即满足关系式式中M、N分别为X方向和Y方向的抽样单元数,Δx和Δy为物体的空间宽度,Δfx和Δfy为物的频带宽度4物信息的处理计算傅里叶变换全息图:被记录的复数波面是物波函数的傅立叶变换.必须使用计算机完成物函数的傅里叶变换(借助快速傅立叶变换算法完成),得到全息图平面的光场复振幅函数.计算全息多采用傅里叶变换全息图.计算菲涅耳全息图:被记录的复数波面是物体发出的菲涅耳衍射波.须计算物函数经菲涅耳衍射到达全息图的复振幅分布,再将该复振幅分布编码成全息图的透过率变化.计算像全息:被记录的复数波面是物波函数本身或者其几何像.只需由计算机完成物函数的坐标缩放变换与抽样.全息图平面上函数的抽样数不得少于物函数的抽样数5信息的编码到达全息图的物光波通常呈现为复数形式,包括振幅信息和位相信息;将二维光场复振幅分布变换为全息图的二维透过率函数分布的过程,称为计算全息的编码.计算全息的编码主要为如下两大类:一种途径是对光全息术的计算机仿真,用计算机算出全息图上参考光波与物光波的干涉条纹分布函数,这种编码方式称为干涉型编码方式,用这种方法制作的全息图称为干涉型计算全息图.(缺点:参考光波的加入增加了空间带宽积,因此全息图上的抽样点数必须增加)分别对振幅和相位编码(计算全息所特有的:迂回位相法)6信息的存储计算全息图通常都用光学方法实现波前重现,因而存储手段必须与此相适应信息存储的方法有多种,最普遍的一种是用计算机绘图仪将计算机处理的结果直接画在纸上,然后用精密照相拍制在照相底片上,适当放大或缩小到合适的尺寸,制成实用的全息图还可用图形发生器、光绘仪、显微密度仪、激光光束扫描记录装置等来制作振幅型计算全息图对于浮雕型位相计算全息图(如相息图),由于只记录物的位相信息,因此还必须用光刻机、离子束刻蚀机或电子束刻蚀机等制作7计算全息图的再现计算全息图的再现方法是根据全息图类型来确定的用干涉编码法制作的傅里叶变换全息图,可以用下图所示的光学系统来再现.用置于R处的点光源通过透镜L1生成平行光,照明透镜L2前焦面上的计算全息图H,在透镜L2后焦面处光轴上观察再现像8迂回位相编码计算全息图的再现对于用迂回编码法制作的全息图,再现时,用衍射角度保证在一个抽样单元内获得从0到2π变化的位相差.因为透镜前后焦面是傅里叶变换关系,前焦面上对中心的偏离在后焦面上表现为波面位相的变化.这就是迂回位相编码的物理基础.9计算全息术的应用(1)三维图象显示:计算全息可对那些能方便地用数字描述但却难以实际制作的物体进行三维显示计算全息元件:用于校正普通全息元件像差用的像差校正器用于激光扫描器,可实现多束光同时高速扫描用于数据存储中进行编码的相移器功能特殊的全息透镜10计算全息术的应用(2)光学检测:计算全息制作标准波面精度很高光学信息处理中的各种空间滤波器:用于图象消模糊的逆滤波器用于像边缘增强或图象加减的微分滤波器图象处理的各种带通滤波器等等11全息记录介质全息记录介质是记录光全息图的载体,因而要求记录材料有较高的分辨率,较强的衍射效率,较大的动态范围和较高的感光灵敏度.目前用于全息记录的材料种类繁多:卤化银乳胶;重铬酸明胶;光致抗蚀剂;光导热塑;光致变色材料;液晶;光致聚合物;光折变晶体;小杆细菌视紫红质(BR)12卤化银乳胶胶片(或干板)的结构如下图示,卤化银乳胶均匀涂布在片基上,构成软片或干板记录的物理过程曝光:卤化银盐在光的作用下先是分解再还原成单个金属银原子,以微粒的形式散布在乳胶内部,形成潜像.这样析出的银粒子密度很小,只是形成了进一步显影的中心显影:还原剂作用下,显影中心周围的卤化银大量地被还原成金属银定影:使未反应的卤化银晶粒溶于定影液中,保持影像的稳定性.漂白:利用漂白剂的氧化作用,使底板上黑色的金属银变成近乎透明的卤化银盐,使全息图由振幅型转化为位相型,以提高衍射效率13卤化银乳胶的特性几个物理量的定义:曝光量E:定义为入射到感光表面上每单位面积的光能量,单位常用毫焦耳/厘米2(mJ/cm2)或微焦耳/厘米2(μJ/cm2)入射光强度I :定义为单位时间里通过单位面积的光能量,单位常用毫瓦/ 厘米2(mW/cm2)或微瓦/厘米2(μW/cm2)曝光时间T:定义为记录介质受光照射的时间,用分或秒为单位上述三个物理量的关系为:E = I·T透射率:定义为透射光强和入射光强之比,即强度透射率E = I透射/ I入射光密度D也称黑度:定义为透射率倒数的对数:D = lg(1/τ)14卤化银乳胶的感光特性照片的光密度D与曝光量的对数lgE之间的关系曲线,简称H-D曲线可大致分为五段:灰雾区;趾部;线性区;饱和区;过饱和区照相多用线性区.设CD段的斜率为,常用胶片的值表示之:也常称为反差系数,值越高说明反差越大.值的大小除与胶片型号有关外,还与曝光量和显影条件有关.选择合适的参数,可获得预期的值.15卤化银乳胶的分辨率和信噪比分辨率:乳胶能记录的空间光强度变化的最小周期,单位通常用“线对/mm”.分辨率的高低取决于卤化银颗粒的大小外,还与曝光量和显影条件等有关.用稀释显影法可以提高乳化银乳胶的分辨率信噪比:通常表示为“S/N”,S和N分别表示信号和噪声的光强度形成噪声的因素很多:有光散射;显影液选择不当;显影速度过快;漂白处理不当提高信噪比的途径:尽可能减小颗粒尺寸;选择适当的显影液和显影速度16卤化银乳胶的常规处理方法卤化银乳胶板曝光后的化学处理是很重要的环节,其过程为:显影—水洗—停显—定影—水洗—干燥.(1)显影:D-19是最常用的高反差显影剂,显影时间2-5分钟. D-76是一种低调显影剂,适用于曝光量范围很宽的傅里叶变换全息图.(2)停显:一般用水冲洗即可达停显效果,但用停显液效果更好.(3)定影:常规的定影液是F-5,时间在5分钟以上.(4)水洗:目的是清除底片上的定影液和其他物质,必须充分(5)干燥:可用自然干燥,为缩短时间也可浸入无水乙醇后吹干(6)漂白:有时为了提高衍射效率,可将全息图进行漂白处理,使其转化为位相型.还有一种方法是显影后先漂白后定影,有利于长期保存17重铬酸盐明胶(DCG)重铬酸盐明胶是一种很重要的全息记录材料,它几乎具有相位全息图的理想特性可产生很大的折射率变化,衍射效率最高可达100%,分辨率可高达5000线对/mm以上,噪声低再现像显得很“干净”重铬酸盐明胶的曝光机理十分复杂,处理过程与卤化银明胶不同,DCG的缺点:灵敏度低,稳定度差,在高温高湿度环境下容易消象.在实际应用中需经封胶处理,才能长期保存.18光致抗蚀剂(Photoresist)光致抗蚀剂能形成浮雕型相位全息图,常用于全息压印复制工艺光致抗蚀剂即光刻胶.其曝光机理是:曝光部分比未曝光部分溶解速率快200倍,置于稀碱溶液中显影曝光区便迅速溶解,使表面形成凹凸不平的浮雕状条纹光刻胶对紫外光灵敏度较高,曝光时间可达秒量级,而对于全息照相常用的可见光波段,灵敏度要低得多.常用的显影液是NaOH溶液,浓度0.7-1.2%,显影温度20+10C,显影时间在10秒内为宜.光刻胶板在显影液中若浸泡时间过长,会使表面粗糙而影响表面质量;显影短则衍射效率低光刻胶的分辨率较卤化银乳胶低,一。
湖北第二师范学院信息光学复习要点整理者:李方圆1、用宽度为a 的狭缝,对平面上光强分布 扫描,在狭缝后用光电探测器,求输出强度分布。
2 、已知某一平面波的复振幅表达式试计算其波长以及沿x,y,z 方向的空间频率。
3、什么是泰伯效应,从理论上证明之。
4 、菲涅耳衍射公式以及如何求透镜焦点处的强度。
5、正方形出瞳的衍射受限系统的成像研究6、MTF 的物理意义,P73,3.4.11,7、无透镜傅里叶变换全息图的制作及有关应用。
8、什么是散射物体的菲涅耳全息图的冗余性,碎片的尺寸对再现像的质量有哪些影响?9、彩虹全息照相中使用狭缝的作用是什么?10、对比光学离轴全息函数和修正型离轴全息函数,说明如何选择载频和制作计算全息图的抽样频率,如何求空间带宽积。
11、画图说明策尼克相衬显微镜的原理及其有关应用。
12、如何去掉一幅图上的离散扫描点?13、什么是图像识别,如何用匹配滤波器识别某一特征信息(比如指纹)?14、如何用逆滤波消模糊?15、什么是切趾术?16、什么是假彩色编码,举例说明(等密度编码、等频率编码和θ调制和相位调制假彩色编码)原理。
17、相干光学处理、非相干光学处理和白光光学处理的特点和局限性。
18、用矩形函数表示狭缝的透过率h (x ), 并对光强的空间分布f (x )扫描,在狭缝后面用光电探测器记录光强分布g(x).这一扫描记录过程的特点,狭缝宽度对信息的影响。
19.、互相关、自相关的定义和相应的意义?20、什么叫基元函数?在线性分析系统中,常用的基元函数有哪些?21、对线性平移不变系统,可以采用两种研究方法是什么?22、标量衍射理论的条件是什么?23、称为单色光场中P 点的复振幅是如何表示的?单色光场为什么能用复振幅描述?24、透镜孔径对于参与变换的有效物体的各种频率成分的影响?25、成像系统的普遍模型由哪三个部分组成?26、什么叫衍射受限系统?27、相干照明和非相干照明光场的特点?如何实现两种照明?28、什么叫OTF 和CTF ?两者的联系,像差对OTF 以及像的影响。
Rect函数物理意义:用来描述无限大不透明屏上矩形孔的透过率。
Sine函数:与矩形函数(单缝、矩孔的透过率)之间的这种紧密联系,致使他们在傅里叶光学中经常被用到。
阶跃函数:描述光学直边(或刀口)的透过率。
符号函数:描述孔径的复振幅透过率。
三角形函数:表示一个光瞳为矩形的非相干成像系统的光学传递函数。
高斯函数:在统计学领域内经常遇到。
在光学领域小,描述激光器发出的高斯光束,有时也用于光学信息处理中的“切趾术”。
圆域函数:描述无限大不透明屏上圆孔的透过率。
§函数:在物理学和工程技术中常用来描述一个极限状态,描述脉冲状态这一类的物理现象。
互相关是两个信号间存在多少相似性或关联性的量度。
自相关是两个相同函数图像重叠程度的量度。
位相调制作用:不改变振幅,只改变位相。
相干、非相干成像系统是广场复振幅变换的线性空间不变系统。
F(/v , f y ) = F{/(x, y)} = J L /(x, y)e~l27r(flX+f )y)dxdy
基尔霍夫积分定理:
X ))= 士"咕云仏 +九).才{“ 3,x )}
5诂你唱-嚎心已 cos(n, &)
一 cos(〃, ©)
菲涅尔衍射积分公式:
夫琅禾费衍射公式:
卷积物理意义:光学系统像平面上的光强分布是物的光强分布与单位强度点光源对应的
像强度分布的卷积。
几何意义:1、置换变量:将f(X)与h (x) >p的自变量X换成积分
变量;
2、折叠:将h ()绕轴旋转180度,构成对称于纵轴的镜像h (-);
3、位移:将曲线h (-) 移动距离x,得到h(X-);
4、相乘:将位移后的函数h (x-)乘以f (),得到f ()h(x-);
5、积分:f () h (x-)曲线下的面积即为给定于x值得卷积值。
线性系统:设函数于= 代表对系统的激励,函数
/=!
果在激励与响应之间成立关系匕(兀2,丿2)=必(坷」)}'
&(%2,)‘2)= £纟心2』2)代表系统相应的响应,勺是任意复常数,(p{ }表示系统算符。
如 /=! Y 4 gi (兀2,旳)=0{工a i fi (X1,X )卜则称此系统为线性系统o
/=1 I Z=1 J
线性空间不变系统(LSI):
设线性系统对输入信号f^y )和f2(x)分别产生输出信号g低」)=0”;(无』)}
和g2& *)=0也(兀* )},若输入函数在空间发生了平移,切对任意复常数务和色,有
(p\ciJ x{x-x^.y-y^ + a2f2{x-x Q Xy-y^} = ci x g^-^y-y^^此系统为线性空间不变系统。
线性空间不变系统的特性:1、脉冲响应具有比较简单的形式2、叠加积分式具有特别形式,即g (兀,丁)=(匸/(&%(>2 -&丁2 -处切〃=/(兀2,丁2)*加>2,歹2)3、傅里叶变换形式特别简单。
基尔霍夫积分定理意义:衍射光场中任意点P0的复振幅分布U (p0)可以用包围p0点的任意封闭曲而S上的各点的波动边界值U和du/dn求得。
两个衍射的联系:夫琅禾费衍射范围包含在菲涅尔衍射范围Z内,所以凡能用计算菲涅尔衍射的公式都能用来计算夫琅禾费衍射。
但是夫琅禾费近似从形式上破坏了卷积关系,破坏了衍射过程“系统”的空间不变特性。
傅里叶成像:当用单色平面光波照明一个具有周期性透过率函数的透明物体(例如透射光栅) 时,将会在该物体后面某些特定距离上重现此周期结构物体的像。
这种不用透镜而仅靠光的衍射就可以对周期性物体成像的方法.
薄透镜:是指透镜的最大厚度和透镜的表面曲率半径相比可以忽略的透镜•在傍轴条件下薄透镜的变换函数是纯相位的。
通过透镜的相位变换作用,把一个发散球面波变成了会聚球面波。
用透镜来实现傅里叶变换的途径:1、采用平行光照明,在透镜的后焦面上观察到物的频谱。
2、点光源照明衍射屏时,在点光源的像平面上将得到衍射屏函数的傅里叶变换谱,且频谱的零频位置就在点光源的像点处。
相干成像与非相干成像系统的比较:截止频率、两个点物间的分辨、像强度的频谱、对锐边相应迥然不同。
第五章
全息照相:以干涉、衍射为基础的无透镜摄影,记录物体所发光波的振幅(频率)和位相(全部光信息)。
优点:可以再现物体的立体形象。
全息底片:没有物体的影像,而是记录了物体所发光波的全部信息的干涉条纹。
全息图的记录和重现:全息记录:在物波场引入一个参考光波,使其在物光波住纪录平面上发生
干涉,从而将物光波的位相分布频率换成记录在照相底片上的光强分布。
振幅不同使条纹变黑程度不同,相位不同则使条纹的密度、形状各异。
产生及精密的干涉条纹,被记录在全息干板上,形成一张全息图底片。
全息图的重现:全息图底片经过显影、定影后,当用参考光照明时,光通过全息图后的衍射和衍射光Z间的干涉,形成与物体光波完全相同的光波,从而得到原物的清晰的像。
全息照相的基本特点:1、全息照相最突出的特点是由它所形成的三位形象。
2、全息图具有弥漫性。
3、全息照相可进行多重记录。
4、全息图可同时得到虚像和实像。
全息图的类型:1、按照参考光波与物光波主光线是否同轴,同轴全息图、离轴全息图。
2、按全息图的结构与观察方式分类,投射全息图、反射全息图。
3、按全息图的复振幅透过率分类,振幅型全息图、位相型全息图。
4、按全息底片与物的远近关系分类,菲涅尔全息图、像面全息图和傅里叶变换全息图。
5、按所用重新光源,激光重新、白光重现。
6、按记录介质乳胶的厚度分类,平面全息图、体枳全息图。
傅里叶变换全息图的记录和重现:记录:在物波场引入一个参考光波,使其在物光波在纪录平而上发生干涉,物光波的傅里叶频谱被记录在全息干板上,形成一张全息图底片。
全息图的重现:全息图底片经过显影、定影后,当用参考光照明时,光通过全息图后的衍射和衍射光之间的干涉,形成与物体光波完全相同的光波,从而得到原物的清晰的像。
像全息图:将物体靠近介质,或利用成像透镜使物体成像在记录介质附近,或是一个全息图重现的像靠近记录介质,都可以得到像全息图。
彩虹全息图:是像全息图和狭缝技术相结合的产物。
分为一步法彩虹全息二步法彩虹全息4f系统:由相干点光源S发出单色球面波经透镜Lc准直为平面波,垂直入射到平面P1上。
P2为频谱平面,P3为输出平面。
Lk L2为一对傅里叶透镜,用来在P1血至P2面之间进行两次傅立叶变换。
P1、【」、P2、L2、P3之间距离依次为f简称为4f系统。
阿贝成像理论:第一步:物光波通过透镜在其后焦平而上产生夫琅禾费衍射时,汇聚成衍射iki,形成频谱。
第二步:焦平面上的衍射iki作为相干的点光源发岀的次波在像平面上想干叠加形成物的像。
空间滤波在光学系统的傅立叶频谱而放置适当的;滤波器,以改变光波的频谱结构,使其按照人们的要求得到预期的改善。
空间滤波系统:利用透镜的傅立叶变换特性,把透镜作为一个频谱分析仪,并在其频谱分析面上通过插入适当的滤波器,谱仪改变物的频谱,从而使物象得到改善。
图像相减的两种方法:正弦光栅法、全息照相法。
图像相减两种方法步骤:
t
想实现图像相减,% =三光栅G置于频谱面,原点在光栅1/4周期处
g(%3,必)二寸⑺-厶仗3,丫3)] +其余四项
________ _________________ 位相相反图像相减丨
全息照相法:利用二次曝光法记录两幅全息图。
通过引入p相位板,使得A与B反相,实现相减。