《傅里叶光学》试题A

《傅里叶光学导论》历年考题2002/2003(开卷)1.(24分) 一个衍射屏的振幅透射率函数为)()cos 2121()(2lr circ r r t β+=。

(1)这个屏的作用在什么方面像透镜？(2)给出此屏焦距的表达式。

(3)当用波长为m μλ6.0=的单色平面波垂直照明时，若23.0mm =β，mm l 20=，在其中的会聚焦点处的艾里斑半径0r 为多大（略去其他两项光束背景影响）？2.(20分) 某周期性物体的振幅透过率)()(nd x x t n -∑=∞-∞=δ，假定用均匀的平面波垂直照明，试证明这个物体是“自成像”的，意即物体后面周期性距离上能成自身的理想像，而不需要透镜。

3.(24分) 一成像系统光瞳函数为)2/()2/()()(),(l y rect l x rect l y rect l x rect y x P -=，mm l 20=，成像透镜焦距mm f 200'=，物像距mm d d o i 400==，照明波长m μλ5.0=。

(1)用非相干光照明时，求)2(2000ix d l f f f f λ=≤≤，这一区间的光学传递函数)0,(x f ℘，画出截面图（请注明标度尺）。

(2)用非相干光照明强度透射率)2cos 1(21)(02x f m x I π+=的物体，其中mm f 周252=，试求出其像的强度分布。

(3)用相干光照明时，求其频率传递函数)0,(x f H ，画出)0,(x f H 的截面图（请注明横纵坐标的标度尺）。

(4)用相干平面波垂直照明振幅透射率为)2cos 1(21)(01x f m x t π+=的物体，其中mm f 周5.371=，试求出其像的强度分布。

4.(20分) (1)波长m μλ5.0=的单色平面波。

（cm x 1043⨯=，cm y 1041⨯=，cm z 1023⨯=）。

试求光场x 轴和y 轴的空间频率。

(2)已知一个相干成像系统的截止频率cm c f 5000=，像面大小为cm cm 11⨯，最少可用多少个抽样点取值来表示。

傅立叶光学期末试题及答案一、选择题（每题4分，共40分）1. 在傅立叶光学中，下列哪个定理描述了一个三维函数在频域中的傅立叶变换与该函数在空域中的傅立叶变换之间的关系？A. 傅立叶变换定理B. 空域传递函数定理C. 空域采样定理D. 空域衍射定理2. 对于一个透镜，在使用傅立叶光学方法进行分析时，下列哪个参数描述了透镜的厚度？A. 光程差B. 折射率C. 焦距D. 相位延迟3. 傅立叶光学中的角谱表达了光波通过一个系统时的哪个参数？A. 相位B. 振幅C. 空间频率D. 时间频率4. 下列哪个方法可以用来获取光波的角谱？A. 干涉仪B. 衍射仪C. 透镜组合D. 聚焦光束5. 在傅立叶变换光谱学中，通过对透镜进行不同衍射角度的空间频率编码，可以实现哪项功能？A. 相位重建B. 滤波C. 聚焦D. 强度调制6. 傅立叶光学中的矢量衍射理论考虑了光波的哪些性质？A. 偏振B. 相位C. 振幅D. 空间频率7. 对于一个平面波，其在通过一个傅立叶光学系统后，下列哪个效应不会改变？A. 振幅B. 相位C. 波长D. 入射角度8. 在傅立叶光学中，下列哪个方法可以用来恢复被透镜组合模糊化的图像？A. 相衬显微镜B. 斑点衍射模糊理论C. 叠加投影法D. 透镜阵列9. 傅立叶光学中的反射与传输不完全衍射补偿方法的基本思想是什么？A. 利用傅立叶变换来补偿光波的相位失真B. 利用远场衍射方法来补偿光波的振幅丧失C. 利用多物体干涉的通道选择性来补偿光波传播的路径差D. 利用时频域变换来补偿光波的波长丢失10. 傅立叶光学中的相移干涉方法可以用来实现下列哪个功能？A. 相位测量B. 聚焦控制C. 衍射成像D. 滤波操作二、简答题（每题10分，共60分）1. 请简述傅立叶光学的基本原理及其在实际应用中的意义。

傅立叶光学基于傅立叶变换理论，将光波的传输、衍射与成像等现象用数学方法进行分析和处理。

其基本原理是将光波通过光学系统时的传递函数进行傅立叶变换，从而可以得到频域上的光波信息。

第一章 傅里叶分析部份习题解答及参考答案[1-1] 试分别写出图X1－1中所示图形的函数表达式。

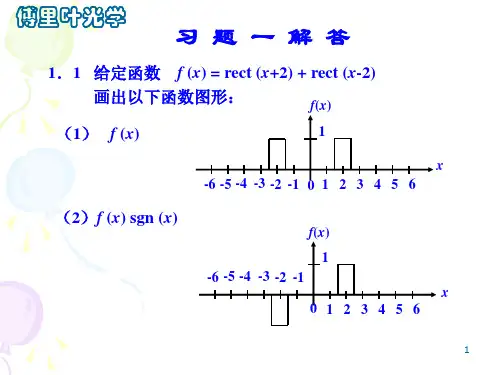
图X1-1 习题[1-1]各函数图形解：(a)−∧L x x a 0 (b) () ∧−−L x b a L x a 2rect(c) ()x L x a sgn 2rect (d) x L x cos 2rect[1-2] 试证明下列各式。

(1) += 21comb 21comb x x- (2) ()()x i e x x x πcomb comb 2comb +=(3)()()()x x N x N ππsin sin lim comb ∞→= (4) ()()xx x πωδωsin lim ∞→=(5)()()∫∞∞−=ωωπδd cos 21x x (6)()ωπδωd 21∫∞∞−±=x i e x解：(1)原式左端∑∑∞−∞=∞−∞=+−−=−−=m n m x n x 12121δδ 令()1−=m n=−+=∑∞−∞=m m x 21δ右端 (2)()∑∑∞−∞=∞−∞=−=−= n n n x n x x 2222comb δδ n 2只取偶数()()∑∞−∞=−=m m x x δcomb()()πδδππm m x e m x e x m im m x i cos 2comb ∑∑∞−∞=∞−∞=−=−=当=m 奇数时，()()0comb comb =+xi ex x π；当=m 偶数时，令n m 2=，则12 cos =x π，并且有： ()()()∑∞−∞=−=+n n x x x 22e comb comb xi δπ 得证。

(3)由公式(1-8-7)知：()∑∞−∞=−=n nxex π2i comb上式可视为等比级数求和，其前N 项之和为：()()()()()x Nx e e e e e e e e q q a S x i x i x i Nx i Nx i Nx i x i Nx i N N ππππππππππsin sin 1111221=−−=−−=−−=−−−−−− 所以 ()()()x Nx S x N N N ππsin sin limlim comb ∞→∞→==得证。

信息光学复习第一部分基本概念第二部分基本技能简单和复合孔径的数学描述矩孔、圆孔、单缝、位相板等；它们的中心位置、缩放比例及其它参数多孔、多缝、线光栅、余弦光栅等；它们的各种参数线光栅的线间距余弦光栅的空间频率、调制度、尺寸会用单个孔径函数与δ函数或梳状函数的卷积表示重复性孔径多缝和矩形光栅的缝宽、缝间距、缝数卷积和相关的运算)()( ) () ()(x h x f d x h f x g ∗=−=∫+∞∞−ξξξ有限宽度的两个函数，卷积后的宽度通常是两函数宽度的和卷积的位移不变性： 若f (x )*h (x ) = g (x ), 则f (x- x 0) * h (x ) =g (x - x 0) 或 f (x ) *h (x - x 0) = g (x - x 0) f (x )*δ(x - x 0) = f (x - x 0) 包含脉冲函数的卷积:基本卷积：rect(x )*rect(x )=tri(x )相关运算主要化为卷积进行，并结合OTF 性质常用基本函数的傅里叶变换和逆变换要求会利用傅里叶变换的性质和卷积定理，借助图解，计算较复杂函数的卷积和傅里叶变换利用傅里叶变换的性质和定理求较复杂函数的傅里叶变换和卷积会用图解表示卷积定理第三部分综合能力用解析法和图解法处理衍射受限系统的成像问题注意区分相干照明和非相干照明给出物函数（复振幅或光强透射率），会写出其频谱函数；给出光学系统参数，会写出其相干传递函数或光学传递函数，画出草图，算出相应的截止频率；计算像（复振幅或强度）的频谱，再反算出相应的空间分布，或用图表示；相干照明下，由像的复振幅分布再求像强度.。

第一章光场的表示和Fourier分析1.1 Maxwell方程与标量波1.2 平面波和球面波1.3 二维Fourier变换的定义和物理意义1.4 卷积和相关1.5 Fourier变换的基本性质1.6 可分离变量的Fourier变换1.7 一些常用函数和它们的Fourier变换17空间频率概念的引入f (2j eU )y ,x (U π=/1/1==f f y x λcos =X9112. ( f x , f y )的物理意义方向余弦为(cos α, cos β) 的单色平面波在xoy平面上的复振幅分布是以2π为周期的分布，该复振幅分布可用沿x，y 方向的空间频率( f x , f y ) 来描述3.根据波叠加原理，任何复杂的光场分布可以分解为许多不同方向传播的平面波的叠加，或分解为许多不同空间频率的波的叠加.此式表示一个在xy 平面上沿x方向的空间频率为f x ，沿y方向的空间频率为f y 作周期的复振幅函数，它代表一个传播方向为( cos α＝λf x ，cos β＝λf y )的平面波.)(20),(y f x f j y x eU y x U +=π)cos cos (0),(βαy x jk e U y x U +=四、球面波的复振幅1、定义：点光源发出的单色光波等相位面是球面波1215近轴条件：只考虑xoy 平面上与S 点张角不大的范围.3、近轴条件下球面波的复振幅(1)171.3 Fourier变换的定义和物理意义一、广义变换∫∞∞−=dxx k x f I f ),()()(αα把函数f (x)在x 空间变换成α空间的I f (α)的函数，I f (α) 叫函数f (x) 的以k (α,x) 为核的积分变换.变换Fourier e x k x j −−=−παα2),(拉普拉斯变换−−−x e α梅林变换−−−1αx 阶汉克尔变换n xJ n −−)(α18二、一维Fourier变换1、定义t j eπν2基元函数代表频率为ν的简谐振荡.F (ν)= F {f ( t )}=∫∞∞−−dte tf t j πν2)({}dve v F v F tf vt j π21)()()(∫∞∞−−==F 2、物理意义：1) f (t)可分解为许多基元函数的线性组合;2) F (ν)权重因子.1921四、存在条件(函数g(x,y)存在FT的条件)1、g(x,y)在整个xy平面绝对可积∫∫∞<dxdy y x g |),(|五、广义Fourier变换g (x ,y)＝),(lim y x g n n ∞→G (f x ,f y )＝),(lim y x n n f f G ∞→2、在任一有限区域里，g(x,y) 必须只有有限个间断点和有限个极大和（或）极小点;3、g(x,y)必须没有无限大间断点.23若g(x,y) 为实函数，G( f x , f y ) 是厄米函数，则G (-f x ,-f y ) = ( f x , f y )即振幅|G (-f x ,-f y ) | = |G( f x , f y )|幅角φ(-f x ,-f y ) = -φ( f x , f y )其中( f x , f y )是G( f x , f y )的共轭复数，G ( f x , f y )是中心对称的函数.傅立叶变换并不改变函数的奇偶性,通常该性质称为傅立叶变换的对称性.∗G ∗G24一、卷积（Convolution）1. 定义：αααd x h f x h x f x g )()()()()(−∫=∗=∞∞−展宽：卷积运算的宽度是原来两个函数宽度之和.设f (x) 宽度为b 1, h (x) 的宽度为b 2,则g (x) 的宽度是：b = b 1＋b 2 .1.4 卷积和相关卷积运算的几何解释：先反转h (α)，每平移一个距离x，计算f (α)h (x -α)相乘，∫∞∞−−da a x h a f )()(求面积；再绘成g(x) 随x 变化的图形；积分252627)}()({)}()({)()}()({x h x v b x h x u a x h x bv x au ∗+∗=∗+4)结合性：)()()()()()()()}()({x v x h x u x h x v x u x h x v x u ∗∗=∗∗=∗∗)()()(x u x v x h ∗∗=卷积的次序是无关紧要的.2. 性质：1)平滑性：g (x)的变化率<< f (x)、h (x)的最大变化率；2)对易性：f (x) * h (x)= h (x) * f(x)；3)线性性质：30二、相关（correlation）1. 定义：αααd x h f x h x f x g )()()()()(*−∫==∞∞−★令：x −=αβ得：βββd h x f )()(*∫∞∞−+ηξηξηξd d y x h f y x h y x f y x g ),(),(),(),(),(*−−∫∫=∞∞−＝★ηξηξηξ′′′′∫∫+′+′∞∞−d d h y x f ),(),(*＝与卷积运算的区别：没有反转，只有平移.)(αh )(α−h31相关运算示意图322.性质：1)尖峰化：相关运算是两个信号之间存在相似性的量度.34若f (x) = h (x),则：αααd x f f x f x f x g )()()()()(*−∫==∞∞−★ηξηξηξ∫∫−−=∞∞−d d y x f f y x f y x f ),(),(),(),(*★ηξηξηξ′∫∫′′′+′+′=∞∞−d d f y x f ),(),(*3. 自相关函数：1)定义：3538六、自相关定理七、Fourier积分定理对函数相继进行正FT变换和逆FT，得到原函数.八、FT的FT对函数相继进行FT，所得的函数形式不变，仅将坐标反向.F {g (x,y )☆g (x,y )}=|G (f x , f y )|2F {|G (f x , f y )|2}= g (x,y )☆g (x,y )F –1{F {g (x,y )}}= F {F –1{g (x,y )}}=g (x,y )F {F {g (x,y )}}=g (-x,-y )自相关函数的FT是原函数的功率谱，信号的自相关和功率谱之间存在FT关系.F {g (x,y )☆h (x,y )}= (f x , f y )·H (f x , f y )——互相关定理∗G 两函数的互相关与其互谱密度之间存在FT关系.41结论：在极坐标中可分离变量函数g (r ,θ)=g r (r )g θ(θ)它的频谱在极坐标中也是可分离变量函数，关于φ的函数是exp(j k φ)，关于ρ的函数是G k (ρ) 它为g r (r ) 的k 阶汉克尔变换.=ρ45464748491.7、一些常用函数和它们的FT50。

傅⽴叶光学习题与答案云南师范⼤学2005-2006学年上学期统⼀考试学院物理与电⼦学院专业光学⼯程年级 2005级班级学号姓名⼀、⼀个正复振幅光栅，振幅透过率为：0002cos 22),(fx ll y x t π+=放在⼀个直径为的圆形会聚透镜(焦距为f )之前,并且⽤平⾯单⾊波倾斜照射,平⾯波的传播⽅向在z x 0平⾯内，与轴夹⾓为θ，如图1所⽰。

(1) < (2) 求通过物投射的光振幅分布的频谱。

(3) 假定f d d i 20==，问像平⾯上会出现强度变化的⾓θ是多少(4) 假定⽤的倾斜⾓就是这个最⼤值，求像平⾯上的强度分布。

它与0=θ时相应的强度分布⽐较,情况如何(5) 假定照明倾⾓θ采⽤上述极⼤值，问使得像平⾯上出现强度变化的最⼤光栅频率是多少这个频率与0=θ时的截⽌频率⽐较，结论如何(40%)(1) 解：倾斜单⾊平⾯波⼊射，在物平⾯上产⽣的⼊射光为)sin ex p(0θjRx A ，则物平⾯的投射光场为：=)sin ex p(),(0000θjRx A y x U )2cos 1(21)sin exp(,(00)00fx jRx A y x t πθ+?= <)]}sin (2exp[21)sin (2exp[21)sin 2{exp(2000λθπλθπλθπ--+++=f x j f x j x j A 它的频谱为：)},({),({),(00000y x U F y x U F f f A y x ==)};sin ([21]),sin ([21),sin ({2λθδλθδλθδ+-++-+-=f f f f f f f A x y x x x (2) 解: 在相⼲光照明下，系统的截⽌频率为id lf λ20=，为了取到尽可能⼤的θ，即取最低的两个频率分量)0,sin (),0,sin (λθλθ+-f于是要求;2sin i d l λλθ≤及 ii d l f d l λλθλ2sin 2≤+-≤- 将f d i 2=代⼊上述两个不等式,得到满⾜两个频率分量通过系统的条件,4sin 4f l f l f ≤≤-θλ最⼤值为)4(sin 1max fl-=θ；（3）解：直径为的圆形透镜相⼲传递函数为)2(),(322d l f f circ f f H y x y x λ+=，;当θ取最⼤值，fl4sin =θ；此时物场的三个频率分量中只有⼀个较⾼频率分量超出系统的截⽌频率，因⽽()=y x f f H ,{,sin 0,sin 0,sin 1=+==+-===y x y x y x f f f f f f f f λθλθλθ当以及当像的频谱为：()()()()???+--+??? ??-=??+--+??? ??+-+??? ??-==],sin [21,sin 2,],sin [21],sin [21,sin 2,,,03y x y x y x y x y x y x y x y x y x f f f f f A f f H f f f f f f f f A f f H f f A f f A λθσλθσλθσλθσλθσ像平⾯复振幅分布为：()(){}()]2exp 211[42exp 2]sin 2exp[21sin 2exp 2,,33333133f x j f l x j A f x j x j A f fA f y x u y xsi πλπλθπλθπ-+????? ?=??+-+??? ??==- 光强分布为：()()()()]2cos 45[4]2ex p 211[]2ex p 211[4,,23322333333fx A f x j f x j A y x u y x I πππ+=+?-+== …………………………①当 0=θ时；设0f f ≤ ，则()()33332cos 12,fx Ay x u π+=相应光强分布为：()??++=332334cos 212cos 2234,fx fx A y x I i ππ…………………②通过①②两式⽐较，可看出max θθ=时，条纹对⽐度较差，且没有倍频成分。