下载文档原格式
逻辑三段论口诀
逻辑三段论是一种经典的逻辑推理方式，它可以很好地帮助我们分析问题和推理结论。
在逻辑三段论中，我们需要通过两个前提来推导出一个结论。
下面介绍逻辑三段论的口诀：
“凡A皆B，凡B皆C，故凡A皆C。
”
这是逻辑三段论的口诀，也是它的基本形式。
其中，“凡A皆B”和“凡B皆C”分别是两个前提，“故凡A皆C”是结论。
这个口诀的意思是，如果A都有B，B都有C，那么就可以得出A都有C的结论。
举个例子，如果我们知道“凡人都会死”，“凡动物都是有生命的”，那么我们就可以得出结论“凡人都是有生命的”。
这个结论是符合逻
辑的，因为它符合逻辑三段论的基本形式。
逻辑三段论的口诀看起来很简单，但是它实际上有很多变化形式。
比如，有时候我们只知道“凡A皆B”，没有“凡B皆C”，但是我们
仍然可以推导出结论。
这时候我们需要用到逆否命题、转化命题等方法来转换前提，使得符合逻辑三段论的基本形式。
逻辑三段论在日常生活中也有很多应用。
比如，我们可以用逻辑三段论来分析新闻报道和社交媒体上的言论，看看它们是否符合逻辑。
同时，我们也可以用逻辑三段论来判断一些事情的真伪，比如说谣言、八卦等。
总之，逻辑三段论是很实用的逻辑推理方式，它可以帮助我们更好地分析问题和推导结论。
我们需要掌握逻辑三段论的基本形式和变化形式，才能更好地应用它。
第十一讲三段论格的规则、式、省略式关系推理四、三段论的格及其规则前面在讲三段论推理的结构时，已讲到按照中项所处的4种不同位置，我们可以把三段论推理分成四种，这四种就是4个格。
M—P P—M M—P P—MS—M S—M M—S M—SS—P S—P S—P S—P(第一格) （第二格）（第三格）（第四格）由于中项所处的特殊位置，运用三段论的一般规则，可以推出不同的格的特殊规则，这些同时规则的好处是更为简便直观。
第一格规则p165M—PS—MS—P1、小前提必须肯定。
2、大前提必须全称。
证明1：设小前提否定，则结论否定（前提之一否定结论否定）；结论否定，P一定周延（因其处在否定判断的谓项）；P周延，则前提必须否定（P在前提种处于谓项位置，而只有否定判断的谓项才周延）；小前提否定，大前提也否定，推不出结论（两个否定的前提推不出结论）；所以，小前提必须肯定。
证明2：因为小前提必须是肯定的，处于谓项的中项必不周延（肯定判断的谓项不周延）；根据“中项至少在前提种周延一次”的规则，中项只能在大前提中周延，而中项在大前提中处主项位置；所以，大前提必须全称。
第一格的特点是根据一般的原理推出特殊的和个别的结论。
由于前提是全称的，推出的又是特殊和个别的结论，最能体现“遍有遍无”的公理，所以可以把它称为“典型格”。
第二格规则p166P—MS—MS---P第二格中项都处于谓项位置上，要保证其至少周延一次，就要使它至少有一次处于否定判断的谓项上。
1、前提之一必须否定。
2、大前提必须全称。
证明1：因为在第二格中，中项都处于谓项位置，而只有在否定判断中谓项才周延；又由于两个否定的判断推不出结论，所以只能有一个前提是否定的。
所以，前提之一必须否定。
证明2：因为前提之一是否定的，所以结论是否定的（前提之一否定，结论是否定的）；结论否定，则大项周延（否定判断的谓项周延）；大项在第二格中处于前提的主项，只有全称时主项周延；所以，大前提必须全称。
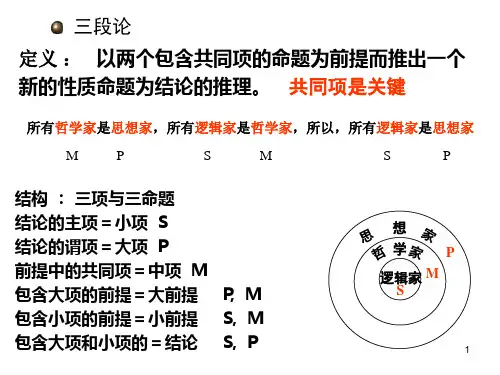
三段论三段论是由包含着一个共同项的两个性质判断为前提，推出一个新的性质判断为结论的推理形式。
例如:所有的律师都必须有律师资格证书；某甲是律师；——————————————所以，某甲有律师资格证书。
开展公共关系活动是对本公司有利的，举行产品信息发布会是公共关系活动中的一种重要形式；—————————————————所以，举行产品发布会对本公司是有利的。
三段论的结构（1）任何一个三段论都包含并且只能包含三个不同的概念。
小项：结论中的主项。
用“S”表示。
中项：前提中的共同项，用“ M ”表示。
大项：结论中的谓项。
用“P”表示。
（2）任何一个三段论都是由三个性质判断组成的。
大前提：包含着大项“P”和中项“M”的前提判断。
小前提：包含着小项“S”和中项“M”的前提判断。
结论：包含着大项“P”和小项“S”，由两个前提推出的新判断。
典型的三段论结构式：所有M都是P MAPS是M 或SAM—————————所以，S是P ∴SAP四、三段论的格与式1．三段论的格三段论的格是由于中项在前提中的位置不同而形成的各种三段论形式，三段论共有四个格：第一格：中项在大前提中处于主项的位置，在小前提中处于谓项的位置。
例如：所有科学(M)都是有用的(P)；逻辑学(S)是科学(M) ；所以，逻辑学(S)是有用的(P )。
M—PS—MS—P第一格的特殊规则(1) 小前提必须是肯定判断；(2)大前提必须是全称判断。
所有科学(M)都是有用的(P)；逻辑学(S)是科学(M) ；所以，逻辑学(S)是有用的(P )。
三段论推理的第一格主要是用来证明某一命题的真实性。
第一格典型地表现了由一般到特殊的演绎过程。
它是三段论推理的标准格或典型格。
第一格在司法审判工作中有很重要的意义，法庭是根据有关法律条款，结合具体案情，作出判决时，就是使用第一格，因此，在普通逻辑里，人们把第一格又叫做审判格。
例如：凡过失杀人的应处以五年以下有期徒刑；某甲是过失杀人的；所以，某甲应处以五年以下有期徒刑。
三段论各个格的例子(一)三段论各个格的例子与讲解引言三段论是一种基本的逻辑推理形式，由前提和结论组成。
它主要包含三个格：主题格、一格和中枢格。
在本文中，我将针对每个格列举一些例子并详细讲解。
主题格主题格是三段论中的前提，它是一个普遍性的前提。
以下是几个常见的主题格的例子：•所有人类都会呼吸。
•所有哺乳动物都有乳房。
•所有正方形都具有四个相等的角。
主题格中的前提是一个普遍性的陈述，它适用于所有的案例。
在这些例子中，我们可以看到主题格提供了一个普遍性的声明，为后续的推理提供基础。
一格一格是三段论中的第二个格，它是一个特殊性的前提。
以下是一些常见的一格的例子：•许多人都喜欢巧克力。
•已知有些哺乳动物会下蛋。
•有些正方形具有相等的边长。
一格中的前提是一个特殊性的陈述，它不适用于所有的案例，只适用于部分案例。
在这些例子中，我们可以看到一格提供了一个特殊性的声明，限制了主题格中的普遍性声明。
中枢格中枢格是三段论中的结论，它是根据主题格和一格的前提推导出的结论。
以下是一些常见的中枢格的例子：•所以，所有的人类都会喜欢巧克力。
•所以，所有下蛋的动物都是哺乳动物。
•所以，所有具有相等边长的正方形都具有四个相等的角。
中枢格中的结论是基于主题格和一格的前提推理而来的。
在这些例子中，我们可以看到中枢格提供了一个结论，通过对主题格和一格的前提进行推理和综合。
结论三段论是一种基本的逻辑推理形式，它由主题格、一格和中枢格组成。
本文通过列举了几个例子，并对每个格进行详细讲解，展示了三段论在不同场景下的应用。
了解三段论的各个格有助于我们进行逻辑推理和思考。
三段论的格及其规则第一格：中项位于大前提的主项和小前提的谓项。
规则1：大前提必须是全称的。
证明：①如果大前提是特称的，那么特称命题的主项即中项M则是不周延的。
②根据三段论一般规则二（中项在前提中至少周延一次）可知中项M在小前提中周延。
又已知M在小前提中是谓项，则小前提是否定的。
③根据三段论一般规则五（前提中有一个是否定的，当且仅当，结论是否定的）可知结论是否定的，那么否定命题的谓项即大项P 是周延的。
④根据三段论一般规则三（如果项在前提中不周延，则在结论中不得周延），又因为P在结论中周延，所以P在大前提中周延。
⑤又因为P是大前提中的谓项，又具有周延性质，根据否定命题的谓项是周延的可知大前提是否定的。
⑥至此，大前提、小前提均为否定命题，由三段论一般规规则四（两个否定的前提不能推出结论）可知假设不成立。
所以大前提必须全称的。
规则2：小前提必须是肯定的。
证明：①如果小前提是否定的，根据三段论一般规则五（前提中有一个是否定的，当且仅当，结论是否定的）可知结论是否定的。
②结论为否定命题，那么否定命题的谓项即大项P是周延的。
③根据三段论一般规则三（如果项在前提中不周延，则在结论中不得周延）可知P在大前提中是周延的。
④又因为P是周延的，是大前提中的谓项，根据否定命题的谓项是周延的，所以大前提是否定的。
⑤至此，大前提、小前提均为否定命题，由三段论一般规则四（两个否定的命题不能推出结论）可知假设不成立，所以小前提必须是肯定的。
第二格：中项位于两个前提的谓项位置。
规则1 ：两个前提必须有一个是否定的。
证明：①如果两个前提都是否定的，根据三段论一般规则四（两个都否定的命题不能推出结论）可知不成立。
②如果两个结论都是肯定的，肯定命题的谓项即两个中项M都是不周延的。
③根据三段论一般规则二（中项在前提中至少周延一次）可知假设不成立，两个前提必须有一个是否定的。
规则2：大前提必须是全称的。
证明：①如果大前提是特称的，那么特称命题的主项即大项P是不周延的。
