数分试卷

北京航空航天大学2011-2012学年第一学期期中考试工科数学分析试卷（2011.12.25）一、计算(5’*8=40’)1) 用Stolz 定理计算极限41233122123lim n n n nn +→∞++++L .2) 设32()(1)x f x x x x =++,求()f x '.3) 求极限10(1)e lim xx x x→+-. 4)求函数2()(4)f x x x =-的拐点。

5) 设(cos sin )()=(sin cos )x a t t f x y a t t t =+⎧⎨=-⎩,求d d y x. 6) 求函数()ln f x x x =在(0,)+∞上的最值.7) 判断函数211()=e x n f x x-⋅间断点的类型. 8) 求函数2()=ln(1)f x x x ++在0x =处直到四阶的Taylor 展开（Peano 余项形式）.二、证明(15’) 1) 3sin (0)6x x x x >-> 2) 设函数1()=ln ()n f x xx n -+∈¢,证明()(1)!n n y x -=. 三、(10’) 设1110,0,(2),1,2,n n n A x x x Ax n A +><<=-=L ,证明不等式11n n x x A+<<对任意n +∈¢成立，并求出极限lim n n x →∞. 四、(10’)用Cauchy 收敛原理证明数列2sin (sin )n n k kx x k k kx ==+∑收敛. 五、(15’)设()f x 在0x 处二次可导，且()0f x ''≠，由Lagrange 中值定理知存在0()1h θ<<,使得式子000(+)()(())f x h f x f x h h h θ'=++成立，计算或者证明下列结论：1) 写出()f x 和()f x '在0x x =处的Taylor 公式；2) 证明01lim ()2h h θ→=. 六、(10’)设()f x '在(0,]a连续，且极限lim()x x →'存在，证明()f x 在(0,]a 上一致连续.[附加题]七、(10’)以下题目任选其一： 1) 设()[01]f x ∈£，，且()0f x >,令0()max (),[0,1]t x M x f t x ≤≤=∈, 证明：函数()()lim ()n n f x Q x M x →∞⎡⎤=⎢⎥⎣⎦连续的充要条件是()f x 单调递增. 2) 证明开区间套定理1. 设开区间序列(,),n n n I a b n +=∈¥ 满足12121n n n a a a b b b b -<<<<<<<<L L L .2. 区间长度0()n n n I b a n =-→→∞,则存在唯一1(,)n i i i a b ξ==I 满足lim lim n n n n a b ξ→∞→∞==.。

《数学分析（二）》试卷（A ）一、 写出以下定义1、函数f(x)在[a,b]上可积；（5分）2、函数序列f n (x)在(0,1)上内闭一致收敛于f(x)；（5分)二、求不定积分∫x 2+1x +1dx （5分）三、令I n =∫(sin x)n dx π0，求I n 与I n−2之间的递推公式。

（10分）四、 平面上的心脏线参数表达式为r (θ)=a (1+cos (θ))，(0≤θ≤2π)，求该曲线所谓区域面积。

（10分）五、 旋轮线的参数表达式由x (t )=r (t −sin (t ))，y (t )=r (1−cos (t ))，(0≤t ≤2π)给出，把该曲线绕x 轴旋转一周，求所得旋转体体积。

（10分）六、 对不同的值a ，判断反常积分∫ln(1+x)x +∞0dx 的收敛性（条件收敛、绝对收敛）。

（10分）七、 令S =∑k 2+12∞k=11、判断该数项级数收敛性（条件收敛、绝对收敛）；（10分）2、求幂级数∑n 2x n ∞k=1的收敛区域；（10分）3、求S 的值；（5分）八、周期函数f(x)={1，(x∈(2kπ,2kπ+π])−1，(x∈(2kπ−π,2kπ])1.求f(x)的傅里叶级数展开a02+∑[a k cos(kx)∞k=1+b k sin(kx)]；（10分）2.求部分和函数a02+∑[a k cos(kx)∞k=1+b k sin(kx)]的极限函数f̃(x)；（5分）3.判断函数序列{f n(x)}是否一致收敛于f̃(x)，并说明理由。

（5分）《数学分析（二）》试卷（B）一、写出以下定义1、函数序列f n(x)一致收敛于函数f(x)；（5分）2、数列{a n}的上极限为A；（5分）二、求不定积分∫ln(x 2+1)xdx。

（10分）三、计算定积分∫x sin x1+(cos x)2dxπ。

（5分）四、求椭圆x 24+y2=1内部区域面积。

（10分）五、平面上的心脏线参数表达式为r(θ)=a(1+cos(θ))，(0≤θ≤2π)，ba该曲线在x轴以上的部分绕x轴旋转一周，求所得旋转体的体积（5分）六、对反常积分∫[ln(x)]8x a dx+∞1，1、在a取不同的值时判断它的收敛性（条件收敛、绝对收敛）；（10分）2、在a=2时计算该反常积分的值（5分）七、令S=1−12+13−14+⋯+(−1)n−11n+⋯=∑[∞n=1(−1)n−11n]，1、判断该数项级数收敛性（条件收敛、绝对收敛）；（10分）2、写出函数ln(1+x)及11+x在x=0处的幂级数展开，并判断收敛性；（10分）3、求S的值；（5分）八、定义在全部实数上的周期函数f(x)=x，x∈[2kπ−π,2kπ+π)，1、求f(x)的傅里叶级数展开a02+∑[a k cos(kx)∞k=1+b k sin(kx)]；（10分）2、求部分和函数a02+∑[a k cos(kx)∞k=1+b k sin(kx)]的极限函数f̃(x)；（5分）3、判断函数序列{f n(x)}是否一致收敛于f̃(x)，并说明理由。

第二学期数学分析期末考试题一、选择题：1、 函数)(x f 在 [a,b ] 上可积，那么（ ）A )(x f 在[a,b ]上有界B )(x f 在[a,b ]上连续C )(x f 在[a,b ]上单调D )(x f 在[a,b ]上只有一个间断点 2、函数)(x f 在 [a,b ] 上连续，则在[a,b ]上有（ ）A)()(x f dx x f dx d b a =⎰ B )()(x f dt t f dx d xa =⎰ C )()(x f dt t f dx db x -=⎰ D )()(x f dt t f dxd bx =⎰ 3、 在[a ，+∞]上恒有)()(x g x f ≥，则（ ） A ⎰+∞a dx x f )(收敛⎰+∞adx x g )(也收敛 B ⎰+∞adx x g )(发散⎰+∞adx x f )(也发散C⎰+∞adx x f )(和⎰+∞adx x g )(同敛散 D 无法判断4、级数∑∞=1n na收敛是（ ）对p =1,2…，0)(lim 21=++++++∞→p n n n n a a aA 充分条件B 必要条件C 充分必要条件D 无关条件 5、若级数∑∞=+111n n α收敛，则必有（ ）A 0≤αB 0≥αC 0<αD 0>α 6、)()(1x ax f n n∑∞==在[a ，b ]一致收敛，且a n (x )可导（n =1,2…），那么（ ） A f （x ）在[a ，b ]可导，且∑∞==1'')()(n nx ax fB f （x ）在[a ，b ]可导，但)('x f 不一定等于∑∞=1')(n nx aC∑∞=1')(n nx a点点收敛，但不一定一致收敛1D∑∞=1')(n nx a不一定点点收敛7、下列命题正确的是（ ） A)(1x an n∑∞=在[a ，b ]绝对收敛必一致收敛B)(1x an n∑∞=在[a ，b ] 一致收敛必绝对收敛C)(1x an n∑∞=在[a ，b ] 条件收敛必收敛D 若0|)(|lim =∞→x a n n ，则)(1x an n∑∞=在[a ，b ]必绝对收敛8、∑∞=--1)11()1(n n nx n 的收敛域为（ ） A (-1,1) B (-1,1] C [-1,1] D [-1,1）二、计算题：（每小题6分，共30分）1、)0(21lim1>++++∞→p n n p pp p n 2、计算由曲线2x y =和2y x =围成的面积 3、求极限)1sin 11(lim 2222)0,0(),(x y y x y x y x +-+++→4， 计算nn n n x n ∑∞=--112)1(的收敛半径和收敛域三、讨论判断题：1、讨论dx x x qp p⎰∞++--01|1|的敛散性 2、 判断∑∞=--+122)11(n n n 的敛散性3、 判断∑∞=+-121sin )1(n n n nx的一致收敛性 四、证明题：1、设f (x )是以T 为周期的函数，且在[0，T ]上可积，证明⎰⎰=+TTa adx x f dx x f 0)()(2、设级数∑∞=10n n n x α收敛，则当0αα>时，级数∑∞=1n nnx α也收敛参考答案一、1A ；2B ；3D ；4A ；5D ；6D ；7C ；8A.二、1、由于p x 在[0，1]可积，由定积分的定义知（2分）=++++∞→121lim p p p p n n n 11)21(1lim 10+==++⎰∞→p dx x nn n n n pp p p p p p n （4分） 2、 、两曲线的交点为（0，0），（1，1）（2分）所求的面积为：31)(12=-⎰dx x x （4分） 3、解：由于x 1sin 有界，01sin lim )0,0(),(=→xy y x （2分）)1sin 11(lim 2222)0,0(),(x y y x y x y x +-+++→=)11)(11()11)((lim22222222)0,0(),(+++-++++++→y x y x y x y x y x （3分）=111lim22)0,0(),(+++→y x y x =2（1分）4、解：212)1(lim 1=--∞→n nn n n ，r =2（3分） 由于x =-2，x =2时，级数均不收敛，所以收敛域为（-2，2）（3分）三、1、解、因为被积函数可能在x =0和x =1处无界，所以将其分为dx x x q p p ⎰∞++--01|1|=dx x x p q p ⎰-+-101|1|14+dx x x q p p ⎰∞++--11|1|（2分）考虑奇点x =0应要求p-1<1；奇点x =1应要求p+q<1；（4分）当+∞→x 时，由于1211~)1(1-++--q p q p p x x x ，知2p+q -1>1时积分收敛（2分） 所以反常积分满足p <2且2(1-p)<q<1-p 收敛，其余发散（2分）2、解：由于nn n n n 1~112112222-++=--+（6分），又∑∞=11n n 发散（2分）所以原级数发散（2分）3、解：2211sin )1(nn nx n ≤+-（6分），由weierstrass 判别法原级数一致收敛性（4分）四、证明题（每小题10分，共20分） 1、证明：⎰⎰⎰⎰++++=Ta TT aTa adx x f dx x f dx x f dx x f )()()()(00（1）（4分） ⎰⎰⎰=+++=+aaTa Tdt t f T t d T t f t T x dx x f 0)()()()(（2）（4分） 将式（2）代入（1）得证（2分）2、证明：∑∑∞=-∞==11)1)((00n n n n n nx n x αααα（4分）01αα-n 单调下降有界（3分）由Abel 定理知原级数收敛（3分）数学分析期末考试题一、选择题：1， 函数)(x f 在 [a,b ] 上可积的充要条件是（ ）A ∀ε>0,∃ σ>0和δ>0使得对任一分法∆，当λ（∆）<δ时，对应于ωi ≥ε的那些区间∆x i长度之和∑∆x i < σB ∀ε>0,σ>0, δ>0使得对某一分法∆，当λ（∆）<δ时，对应于ωi ≥ε的那些区间∆x i 长度之和∑∆x i < σC ∀ε>0,∃δ>0使得对任一分法∆，当λ（∆）<δ时，对应于ωi ≥ε的那些区间∆x i 长度之和∑∆x i < εD ∀ε>0, σ>0，∃ δ>0使得对任一分法∆，当λ（∆）<δ时，对应于ωi ≥ε的那些区间∆x i 长度之和∑∆x i < σ2、函数)(x f 连续，则在[a,b ]上⎰xdt t f dxd 21)(=（ ） A )2(x f B )2(2x f C )(2x f D )()2(2x f x f -,3，=⎰-1121dx x （ ） A -2 B 2 C 0 D 发散54、0lim ≠∞→n n a ，则∑∞=1n na( )A 必收敛B 必发散C 必条件收敛D 敛散性不定 5、若级数∑∞=1n nb是∑∞=1n na更序级数，则（ ）A∑∞=1n na和∑∞=1n nb同敛散 B∑∞=1n nb可以发散到+∞C 若∑∞=1n na绝对收敛，∑∞=1n nb也收敛 D 若∑∞=1n na条件收敛，∑∞=1n nb也条件收敛6、)(1x an n∑∞=在[a ，b ]一致收敛，且a n (x )可导（n =1,2…），那么( ) A f （x ）在[a ，b ]可导，且∑∞==1'')()(n nx ax fB f （x ）在[a ，b ]可导，但)('x f 不一定等于∑∞=1')(n nx aC∑∞=1')(n nx a点点收敛，但不一定一致收敛D∑∞=1')(n nx a不一定点点收敛7、函数项级数)(1x an n∑∞=在D 上一致收敛的充要条件是（ ）A ∀ε>0,∃ N （ε）>0，使∀m >n> N 有ε<++)()(1x a x a m nB ∀ε>0, N >0，使∀m >n> N 有ε<++)()(1x a x a m nC ∃ε>0, ∀ N （ε）>0，使∀m >n> N 有ε<++)()(1x a x a m nD ∀ε>0,∃ N （ε）>0，使∃m >n> N 有ε<++)()(1x a x a m n 8、∑∞=-1)1(1n n x n的收敛域为（ ） A (-1,1) B (0,2] C [0,2） D [-1,1）6 9、=∂∂),(00|),(y x xy x f （ ） A x y x f y y x x f x ∆-∆+∆+→∆),(),(lim00000B x y x f y x x f x ∆-∆+→∆),(),(lim 00000C x y x x f y y x x f x ∆∆+-∆+∆+→∆),(),(lim00000D xy x x f x ∆∆+→∆),(lim 000二、计算题：1、dx x x x ⎰-++11211cos sin2、计算由曲线2,0,1==+=xy y x y 和2e x =围成的面3、 求2xe -的幂级数展开式三、判断题： 1、 讨论∑∞=3cosln n nπ的敛散性2、 判断∑∞=+121n nnx x 的绝对和条件收敛性 三、 证明题：71、设f (x )是[-a ，a ]上的奇函数，证明0)(=⎰-aadx x f2、证明级数∑∞==04)!4(n nn x y 满足方程y y =)4(参考答案一、1D ； 2B ；3D ；4B ；5C ；6D ；7A ；8C ；9B.二、1、解：dx x x x ⎰-++11211cos sin =++⎰-dx x x x 1121cos sin dx x ⎰-+11211（2分）由于21cos sin x x x +为奇函数dx xx x ⎰-+1121cos sin =0（2分）dx x ⎰-+11211=2|arctan 11π=-x （2分）所以积分值为2π（1分）2，解：两曲线的交点为（1，2）（2分）所求的面积为：1/2⨯2⨯2+6221=⎰e dx x（4分） 3、解：由于 ++++=!!212n x x x e n x（3分）， +-++-=-!)1(!212422n x x x e n n x （3分） 三、1、解：由于222~cosln n nππ（6分），又∑∞=121n n收敛（2分） 所以原级数收敛（2分）2、解：当1||<x 时，有n x nx x x ||12≤+，所以级数绝对收敛（4分）， 当1||=x 时，2112=+xn x x ，原级数发散（2分）当1||>x 时，有∑∑∞=∞=+=+1122)1(1)1(1n n nn nnxx xx ，由上讨论知级数绝对收敛（4分） 四、证明题：1、证明：⎰⎰⎰+=--aaa adx x f dx x f dx x f 00)()()(（1）（4分） 8⎰⎰⎰-=---=-aaadt t f t d t f t x dx x f 0)()()()(（2）（4分） 将式（2）代入（1）得证（2分）2、证明：所给级数的收敛域为),(+∞-∞，在收敛域内逐项微分之，得∑∞=--=114')!14(n n n x y ∑∞=--=124'')!24(n n n x y ∑∞=--=134''')!34(n n n x y ∑∞=--=144)4()!44(n n n x y （8分）代入得证（2分）。

案(word版可编辑修改)的全部内容。

数学分析(3）期末试卷2005年1月13日班级_______ 学号_________ 姓名__________ 考试注意事项：2. 试卷含三大题，共100分。

3. 试卷空白页为草稿纸，请勿撕下！散卷作废！4. 遵守考试纪律。

一、填空题（每空3分,共24分)1、 设z x u ytan =，则全微分=u d __________________________。

2、 设32z xy u =，其中),(y x f z =是由xyz z y x 3333=++所确定的隐函数，则=x u _________________________。

3、 椭球面14222=-+z y x 在点)1,1,2(M 处的法线方程是__________________.4、 设,d ),()(sin 2y y x f x F xx⎰=),(y x f 有连续偏导数，则=')(x F __________________. 5、 设L 是从点（0，0)到点(1,1)的直线段，则第一型曲线积分⎰=Ls x yd _____________。

6、 在xy 面上，若圆{}122≤+=y x y x D |),(的密度函数为1),(=y x ρ，则该圆关于原点的转动惯量的二重积分表达式为_______________，其值为_____________.7、 设S 是球面1222=++z y x 的外侧，则第二型曲面积分=⎰⎰dxdy z S2_______。

二、计算题(每题8分,共56分)1、 讨论yx y x y x f 1sin 1sin )(),(-=在原点的累次极限、重极限及在R 2上的连续性。

2、 设),(2xy y x f u =具有连续的二阶偏导数，求二阶偏导数xx u 和xy u .3、 求22333),(y x x y x f --=在}16|),{(22≤+=y x y x D 上的最大值和最小值。

数学分析试卷及答案6套第一套试卷一、选择题（共20题，每题4分，共80分）1. 若函数f(x) = 3x^2 + 2x - 1，求f(-1)的值是多少？A. -4B. 4C. 0D. 12. 函数f(x) = ln(x^2 + 1)在区间(-∞, 0)上的最小值是多少？A. ln(1)B. ln(0)C. ln(-1)D. 不存在最小值3. 已知函数f(x)在区间[0, 5]上连续，且f(0) = 2, f(5) = 1，证明在该区间上存在一个点c，使得f(c) = 3.（请写出证明过程）4. 求不等式2x - 5 < 3x + 2的解集。

A. x < -7B. x > -7C. x > -3D. x < -35. 设函数f(x)在区间[a, b]上连续，且f(a) = f(b)，证明在该区间上至少存在两个不同的点c和d，使得f(c) = f(d).（请写出证明过程）..................第一套答案一、选择题1. B2. A3. (证明过程略)4. A5. (证明过程略)二、填空题（共5题，每题4分，共20分）1. 若e^x = 2，则x = ln(2)；2. 设a, b为实数，若a^2 + 2ab + b^2 = 0，则a = -b；3. lim(x→∞) (x^2 - 2x - 3)/(3x + 1) = 1；4. 若函数f(x) = x^2 + 3x - 2，则f(-1) = -6；5. 若f(x) = √(2x + 1)，则f'(x) = 1/√(2x + 1)。

三、解答题（共3题，每题20分，共60分）1. 设函数f(x) = x^3 - 2x + 1在区间[-2, 2]上的一个驻点为c，请求该驻点c的值以及f(c)的极值。

（请写出解题过程）2. 求函数f(x) = x^3 - 3x + 1的所有零点。

（请写出解题过程）3. 若函数f(x) = 3x^4 + 4x^3 - 12x^2 + 4在区间[0, 3]上的导函数f'(x)恰有一个零点c，并且f(c) = 2，求函数f(x)在该区间上的最大值。

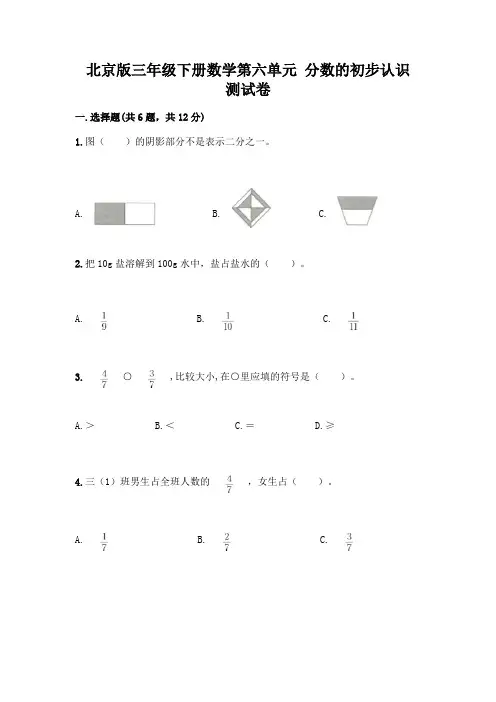
北京版三年级下册数学第六单元分数的初步认识测试卷一.选择题(共6题，共12分)1.图（）的阴影部分不是表示二分之一。

A. B. C.2.把10g盐溶解到100g水中，盐占盐水的（）。

A. B. C.3.○,比较大小,在○里应填的符号是（）。

A.＞B.＜C.＝D.≥4.三（1）班男生占全班人数的，女生占（）。

A. B. C.5.在爱心捐款活动中，淘气捐了自己零花钱的，笑笑也捐了自己零花钱的，（）。

A.一样多B.淘气多C.无法比较6.两袋大米同样重，第一袋用去，第二袋用去千克，剩下的（）。

A.第一袋重B.第二袋重C.同样重D.无法确定二.判断题(共6题，共12分)1.在中，8表示其中的8份，3表示平均分成了3份。

（）2.表示8个。

（）3.分数的分母越小，它的分数单位越大。

（）4.两根同样长的彩带，一根用去米，另一根用去，则剩下的一样长。

（）5.把一个圆分成4份，每份就是这个圆的。

（）6.既可以表示一个分数，也可以表示一个比。

（）三.填空题(共5题，共10分)1.一卷胶卷，照相时已经用去了，剩下的比用去的多（）。

2.一个西瓜平均分成8块，每块占这个西瓜的（），小刚吃了2块，吃了这个西瓜的（）。

3.将米长的绳子平均分成7段，每段长________米，每段占全长的________。

4.1元的是（）角，10千克的是（）千克。

5.比多（）个，比1少（）个。

四.解答题(共5题，共27分)1.老鼠家买回了一块千克的饼，鼠妈妈吃了千克，鼠爸爸比鼠妈妈多吃了千克，剩下的被鼠宝宝全吃光了。

鼠宝宝吃了多少千克的饼？2.一本连环画封面的宽是米，长比宽多米，这本连环画封面的长是多少米？3.学校篮球队有36名队员，其中是女队员，是男队员。

（1）男队员比女队员多几分之几？（2）男队员比女队员多几人？4.阳光小学今年春季植树72棵，其中杨树占总数的，柿子树占总数的，剩余的是山楂树，今年春季阳光小学种植的杨树、柿子树、山植树各有多少棵？5.一块菜地，其中的种西红柿，种茄子，其余的种黄瓜。

数分习题⼗六章练习题1.叙述⼆元函数⼀致连续的定义; 2．判断题1）两个累次极限存在但不相等，则重极限⼀定不存在. 2）函数)0,0(1sin),(在yx y x f =点的重极限与两个累次极限均为0.3）设函数),(y x f 在集合2R D ?上对x 连续，对y 满⾜利普希茨条件y y L y x f y x f ''-'≤''-'),(),(，其中L D y x y x ,),(),,(∈'''为常数，则),(y x f在D 上处处连续.4）两个累次极限存在且相等，则重极限⼀定存在 5）重极限存在，两个累次极限则存在 6）重极限与累次极限不可相等7）重极限不存在，则累次极限有可能存在 8）重极限不存在，则累次极限也不存在 9）内点和⾮孤⽴的界点⼀定是聚点10）任意)(0A U 内都含有E 中的点，则称A 为E 的聚点 11）若平⾯点集E 的所有聚点都属于E ，则E 为闭集 12）平⾯点集E 的聚点⼀定属于E 13）闭集⼀定是闭域14）没有聚点的点集也是闭集15）闭域⼀定是闭集16）平⾯点集的聚点都属于它本⾝，则该点集为闭集 17）两个累次极限不存在，则重极限⼀定不存在. 18）函数)0,0(1sin ), (在xy y x f =点的重极限不存在.3．依定义证明：.7)(lim22)1,2(),(=++→y xy x y x4．证明若函数f 在有界闭域2R D ?上连续，则f 在D 上能取得最⼤值.5. 求极限yx xy x x++∞→+2)11(lim )(),(22222在y x y x yx y x f -+=点的重极限与累次极限.7．讨论函数)0,0()0(,0,0,0,)(),(222222在>??=+≠++=p y x y x y x x y x f p点的连续性.9．说明函数=+≠++=,0,0,0,)(),(22223122y x y x y x x y x f 在)0,0(点连续. 10．函数242),(yx y x y x f +=在)0,0(点的重极限与累次极限的值，下列说法正确的是( ).A .两个累次极限为0,重极限也为0B . 两个累次极限为0,重极限不存在C . 两个累次极限不存在,重极限也为0D . 两个累次极限不存在，重极限也不存在.11．若在点A 的任何空⼼邻域内都含有点集E 中的点，则称A 是E 的 ; 13．若函数),(y x f 在有界闭区域2R D ?上连续，则),(y x f 在D 上能取得最⼤值. 14．函数22),(yx xy y x f +=在)0,0(点的重极限与累次极限的值，下列说法正确的是( ).C. 两个累次极限不存在,重极限也为0D. 两个累次极限不存在，重极限也不存在 15．下列说法中, 不正确的是( ).A. 平⾯点集的聚点都属于它本⾝，则该点集为闭集B. 没有聚点的点集也是闭集C. 闭域⼀定是闭集D. 闭集⼀定是闭域 17．下列说法中, 正确的是( ).A. 平⾯点集的聚点都属于该点集B.没有聚点的点集是开集C. 闭域⼀定是闭集D. 闭集⼀定是闭域. 18．函数yx y x y x f 1sin1sin)(),(+=在)0,0(的重极限与累次极限的值，下列说法正确的是( ).A. 两个累次极限为0,重极限也为0;B. 两个累次极限为0,重极限不存在;C. 两个累次极限不存在,重极限也为0;D. 两个累次极限不存在，重极限也不存在 19．求)0,0(),(22在yx yx y x y x f +++-=点的重极限与累次极限.20．举例说明两个累次极限存在且相等，但重极限可能不存在 21求极限y x y x xysin ),(),()11(lim ++∞+∞→⼗七章练习题1、设)ln(22v u z +=，⽽y x v e,2，求yz ??.2、求函数)0(>=x x z y 的偏导数.3、证明函数=+≠++=0,00,),(2222222y x y x yx y x y x f 在原点连续且偏导数存在，但在此点不可微. 4、设n 为正整数，0,>y x ，⽤条件极值⽅法证明：.)2(2nnn y x y x +≥+5、判断题（1）设),(y x f 为区域D 内的可微函数,则),(y x f 在D 内任⼀点0P 存在连续的偏导数.( )（2）设32),,(yz xy z y x f +=，则)1,1,2(),,(0-P z y x f 在点处的梯度为)3,31(--.( )（3）设),(y x f 为区域D 内的可微函数,则),(y x f 在D 内连续. ( ) （4）设32),,(yz xy z y x f +=，则)1,1,2(),,(0-P z y x f 在点处的梯度为)3,3,1(-. ( ) 6、填空题（1）函数)0,0(22在y x z +=连续，偏导数 ,⽅向导数等于 ;（2）函数)0,0(22在y x z +=偏导数不存在，但沿任意⽅向的⽅向导数存在，都等于 ; （3）设),,(2yx x f z =则=??xz .7、计算函数z++-+=y x y x y x f 的极值. 9、计算函数y xz u )(=的偏导数.10、若函数f 在点),(0000z y x P 可微，则f 在点0P 处沿任⼀⽅向l 的⽅向导数都存在，且γβαcos )(cos )(cos )()(0000P f P f P f P f z y x l ++=，其中γβαcos ,cos ,cos 为⽅向l 的⽅向余弦.11、选择题（1）下列说法不正确的是（）A ⼆元函数的偏导数不存在，则它不可微B ⼆元函数的偏导数连续，则它可微C ⼆元函数可微的充要条件是⽅向导数存在D ⼆元函数存在偏导数不⼀定连续 12、设),(y x u u =可微，在极坐标变换θθsin ,cos r y r x ==，证明 .)()()(1)(2222 2yu xu u rru ??+??=??+??θ13、设)ln(22v u z +=，⽽y x v e u y x +==+2,2，求yz ??.14、设)sin (sin sin y x f y z -+=，其中f 为可微函数，试计算.sec sec y yz x xz ??+15、若⼆元函数f 在点),(00y x P 的某邻域)(P U 内的偏导函数x f 与y f 有界，则f 在)(P U 内连续.16、证明函数??=+≠+++=0,00,1sin )(),(222222x y x yx y x y x f 在原点)0,0(连续且偏导数存在，但偏导数在原点)0,0(不连续，⽽),(y x f 在原点)0,0(可微.17．(,)x z f x y=，求22z x18.设()f u 可微，()'00f =，()()(),232F x t f x t f x t =++-，求()()0,0,0,0x t F F第⼗⼋章1、求⽅程0),,(323=-++=z y x xyzz y x F 在原点附近所确定的⼆元隐函数及其偏导数.2、求椭球⾯632222=++z y x 在)1,1,1(处的切平⾯⽅程与法线⽅程. 3、求体积⼀定⽽表⾯积最⼩的长⽅体. 4、判断题（1）平⾯曲线09)(233=-+xy y x 在点)1,2(处的切线⽅程为01354=-+y x . ( )（2）平⾯曲线09)(233=-+xy y x 在点)1,2(处的法线⽅程为01354=-+y x . ( ) 5、填空题（1）椭球⾯)1,1,1(632222在=++z y x 处的切平⾯⽅程为（2）椭球⾯632222=++z y x 在)1,1,1(处的法线⽅程为 ;（3）曲⾯),(y x f z =在点)),(,,(0000y x f y x P 存在不平⾏于z 轴的切平⾯的充要条件是 ; （4）⽅程0sin 21),(=--=y x y y x F 所确定的隐函数的导数等于 .（5）6、设n 为正整数，0,>y x ，⽤条件极值⽅法证明：.)2(nny x y x +≥+7、证明曲⾯)0(3>=a a xyz 上任意⼀点的切平⾯与三个坐标⾯围成的四⾯体体积是常数.8、验证⽅程组?=++=-++006222z y x z y x 在点)1,2,1(-的邻域满⾜隐函数组存在定理的条件，在10=x 的邻域存在唯⼀⼀组有连续导数的函数组)(),(21x f z x f y ==，并求.dxdz dxdy 与10、求⽅程0),,(323=-++=z y x xyzz y x F 在原点附近所确定的⼆元隐函数及其偏导数.11、将正数a 分为三个正数之和，使它们乘积为最⼤，求这三个数.。

数分成练习题在学习数学分析课程中，掌握解决各种数分题目的方法是非常关键的。

通过练习题的完成，可以提高对于数分知识的理解，增强解题能力。

本文将介绍一些常见的数分练习题，并提供详细的解答和思路，帮助读者更好地应对这些题目。

一、求导与积分题目1. 求函数$f(x) = 3x^2 - 2x + 1$的导函数。

解答：首先，我们可以使用幂函数的求导法则来求解。

根据幂函数求导法则，对于函数$f(x) = ax^n$，其导函数为$f'(x) = anx^{n-1}$。

因此，对于给定的函数$f(x) = 3x^2 - 2x + 1$，我们可以按照此法则进行求导。

根据导函数的线性运算法则，导函数的求导操作可以分别应用到多个项上。

因此，我们可以得到导函数$f'(x) = 6x - 2$。

2. 求函数$g(x) = \int_0^x (2t + 1)dt$。

解答：此题要求我们求函数$g(x)$的原函数。

对于函数积分，我们可以按照常数倍法则和积分基本法则进行求解。

对于形如$\int_a^b (tx^n)dt$的积分问题，可以使用幂函数的积分法则进行求解。

根据积分的线性运算法则，积分的操作可以分别应用到多个项上。

因此，我们可以得到函数的原函数$g(x) = x^2 + x$。

二、极限与连续题目1. 求极限$\lim_{x \to 0}\frac{\sin x}{x}$。

解答：此题要求我们计算一个极限值。

根据极限的定义，我们可以通过直接计算来求解。

首先，我们可以将式子$\frac{\sin x}{x}$展开成幂函数的形式。

通过泰勒级数的展开，我们可以得到$\sin x = x -\frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + ...$。

将展开公式代入原式中，得到$\lim_{x \to 0}\frac{x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + ...}{x}$。

工科数学分析(1)期中考试试题 答案2007年11月25日一、填空题 (每小题4分,共20分) 。

得分[ ]1、 ；=--+∞→)17(lim n n n n 4解： ；=--+∞→)17(lim n n n n =-++∞→178lim n n nn 411718lim=-++∞→nn n 2、设数列，（），则有 ；!)!2(n n n x n n ⋅= ,3,2,1=n =+→∞nn n x x 1lim e 4解 ；n nn nn n n n n n n n x x )1()1)(1()22)(12(lim lim 1+++++=∞→+∞→e nn n n n nn 4)11(1)11)(11()22)(12(lim =+++++=∞→3、 ；=-→22sin 0)31(lim xx x x32-e解 ；=-→22sin 0)31(lim xx x x3222sin )3231031(lim ---→=-exx x x x 4、设，， 则有x x f arccos )(=1||<x ='')(x f 32232)1()1(x x x x --=--- ；解，；2122)1(11)(---=--='x xx f 32232)1()1()(x xx x x f --=--=''-5、；=-+∞→)1(lim 1xx x x ∞+解 =-+∞→)1(lim 1xx x x =-+∞→x x xx 11lim1xe x xx 11lim ln 1-+∞→ 。

=--=+∞→22ln 11ln 1limxx xe x xx +∞=-+∞→)1(ln lim 1x x xx二、选择题(每小题4分,共20分)将代表答案的字母填入右边括号内。

得分[ ]1、设数列，与不是基列不等价的一个命题是 【 D 】}{n x }{n x （A ），对任意大的正整数，总存在正整数，使得0>∃εN Nn m N N>, ；02||ε≥-NNn m x x （B ），无论正整数多么大，总存在正整数和正整数，使得00>∃εN N n N>N p ；03||ε≥-+N N N n p n x x （C ），存在两个子列和，满足，；0>∃ε}{kn x}{k m x 0||ε≥-k k m n x x ,2,1=k （D ），，对于所有满足的，都有00>∃ε*N ∈∀N N n m >,*N ,∈n m 0||ε≥-n m x x 。

好的开始，是成功的一半，祝您天天进步！发明在于发现，发现在于实践分一分(一)①1．填一填。

(1)把一块蛋糕平均分成6份，其中的一份为( )。

(2)九分之四写作( )，它的分子是( )，分母是( )。

(3)是4个( )，( )个是。

645153 (4)1里面有( )个。

412．用分数表示图中的阴影部分和空白部分。

阴影部分 阴影部分 阴影部分 阴影部分 空白部分 空白部分 空白部分 空白部分3．用分数表示下面各图中的涂色部分。

( ) ( ) ( ) ( )4．选择题。

（1)在下图中，阴影部分占图形的的图形是( )。

31A B C(2)下面几个分数，不能表示图中阴影部分的是( )。

A ．B ．C ． 41164124(3)把一个圆平均分成5份，其中的3份是( )。

A ．B ．C ． 513153(4)八分之六写作( )。

A ．B ．C ． 6886865．下图中阴影部分的表示法对吗？对的打“√”，错的打“×”。

( ) ( ) ( ) ( ) ( ) ( ) 2132418461416．按分数把下面各图形涂上颜色。

参考答案1. 略2. 略3. 略4．(1)B (2)C (3)C (4)B5．√ × × × × √6．略相信自己，就能走向成功的第一步教师不光要传授知识，还要告诉学生学会生活。

数学思维可以让他们更理性地看待人生。

#### 一、选择题（每题3分，共30分）1. 下列各数中，不是有理数的是（）A. 0.5B. -3/4C. √2D. 1/22. 下列各数中，绝对值最小的是（）A. -2B. 0C. 1/2D. -1/23. 如果a > b，那么下列不等式中一定成立的是（）A. a + 2 > b + 2B. a - 2 > b - 2C. a + 2 < b + 2D. a - 2 < b - 24. 已知x + y = 5，x - y = 1，那么x的值是（）A. 3B. 4C. 2D. 55. 一个长方形的面积是18平方厘米，如果长是6厘米，那么宽是（）A. 3厘米B. 2厘米C. 1厘米D. 0.5厘米6. 一个数的平方是25，那么这个数可能是（）A. 5B. -5C. 25D. -257. 下列各式中，不是同类项的是（）A. 3a^2B. 2a^2C. 5a^3D. 4a^28. 如果a^2 = 4，那么a的值是（）A. 2B. -2C. 4D. -49. 下列各数中，无理数是（）A. √4B. √9C. √16D. √2510. 一个等腰三角形的底是8厘米，腰是10厘米，那么这个三角形的面积是（）A. 40平方厘米B. 32平方厘米C. 48平方厘米D. 36平方厘米#### 二、填空题（每题5分，共25分）11. 3/4的倒数是__________。

12. |5 - 3|的值是__________。

13. 如果a = 3，那么a^2 + a的值是__________。

14. 下列数中，最小的有理数是__________。

15. 一个数的平方根是-3，那么这个数是__________。

#### 三、解答题（每题10分，共40分）16. 解方程：2x - 3 = 7。

17. 已知a - b = 5，a + b = 3，求a和b的值。

18. 一个等边三角形的边长是10厘米，求这个三角形的面积。

一、选择题（每题2分，共20分）1. 下列各数中，既是质数又是合数的是（）A. 2B. 4C. 6D. 92. 一个长方形的长是10厘米，宽是5厘米，它的周长是（）A. 15厘米B. 20厘米C. 25厘米D. 30厘米3. 小华有8个苹果，小红比小华少2个苹果，小红有多少个苹果？（）A. 6B. 7C. 8D. 94. 一个数既是2的倍数又是3的倍数，那么这个数最小是（）A. 6B. 8C. 10D. 125. 一个三角形的三边长分别是3厘米、4厘米、5厘米，这个三角形是（）A. 直角三角形B. 钝角三角形C. 锐角三角形D. 等腰三角形6. 一个正方形的边长是4厘米，它的面积是（）A. 8平方厘米B. 12平方厘米C. 16平方厘米D. 20平方厘米7. 下列各数中，最小的负数是（）A. -1B. -2C. -3D. -48. 下列各图形中，不是轴对称图形的是（）A. 正方形B. 等腰三角形C. 长方形D. 梯形9. 小明从家出发去学校，向东走了500米，又向北走了300米，最后又向东走了400米，此时他距离家的距离是（）A. 800米B. 1000米C. 1200米D. 1400米10. 下列各数中，最大的两位数是（）A. 98B. 99C. 100D. 101二、填空题（每题2分，共20分）1. 0的相反数是______，0的倒数是______。

2. 5个3相加的和是______。

3. 24除以6的商是______。

4. 6米等于______分米。

5. 0.25的小数点向右移动两位后变成______。

6. 下列各数中，最小的数是______。

7. 一个正方形的边长是6厘米，它的周长是______厘米。

8. 下列各图形中，最大的面积是______。

9. 小明有5本书，小红比小明多2本书，小红有______本书。

10. 下列各数中，最小的三位数是______。

三、计算题（每题5分，共20分）1. 计算：324 ÷ 3 + 12 × 52. 计算：7.8 - 2.3 + 5.23. 计算：6 × 8 ÷ 24. 计算：36.5 + 0.3 - 2.45. 计算下列各图形的面积：（1）一个长方形的长是8厘米，宽是4厘米。

华东师范大学数分期末试卷（A 卷）2009-2010年第一学期一．（20分）判断下列结论是否成立（若成立，说明理由；若不成立，举出反例）1．设()f x 在（a,b ）连续，()f x 在0(,)x a b ∈取极值，则0'()0f x =；2．设()f x 在点0x 可导，则存在0δ>，使得()f x 在00(,)x x δδ-+上连续；3．设数列{}n a ，{}n b 满足1(1,2,)n n a b n ≤≤=…，lim()0n n n b a →∞-=，则极限lim ,lim n n n n a b →∞→∞ 都存在；4．设()f x 是区间（-a,a ）上的可导偶函数，则()f x 在x=0取极值。

二．（16分）计算下列极限；1．20arctan limtan x x x x x→-； 2．20ln(1)sin lim x x x x →+-； 三．（16分）计算下列函数的导函数dy dx： 1．1,0,()1,0;x x e x y x e x -⎧≥⎪=⎨⎪+<⎩ 2．()y y x =由极坐标方程2(1cos )(0)a a ρθ=+>所确定。

四．（14分）讨论2x y x e -=的单调性区间，凹凸性区间，极值与拐点。

五．（14分）证明不等式：1．2arctan (0,);12, x x x x π+<∈+∞+ 2．过研究ln ()x f x x =的单调性，证明：e e ππ>. 六．（8分）设()f x 在区间I 上连续但不一致连续，()g x 在(,)-∞+∞上可导且'()0g x k ≥>.证明：复合函数(())g f x 在I 上不一致连续。

七．（12分）设()f x ，()g x 在[,)a +∞上连续可微，且极限()lim ()x f f x →+∞+∞=，()lim ()x g g x →+∞+∞= 存在，证明：1． 若()()f a f =+∞，则：(,)a ξ∃∈+∞，使得'()0f ξ=；2． 若对[,),'()0,x a g x ∈+∞≠则：(,)a ξ∃∈+∞，使得'()()()'()()()f f f ag g g a ξξ+∞-=+∞- 八．（附加题10分）设()f x 在[,)a +∞上二阶可导且''()1f x ≤，又极限lim ()x f x A →+∞=存在。

一、选择题（每题2分，共20分）1. 下列哪个数字比5大？A. 3B. 4C. 6D. 72. 下列哪个图形是圆形？A. 正方形B. 三角形C. 圆形D. 长方形3. 下列哪个物品可以用“个”来计数？A. 钱币B. 电脑C. 橡皮D. 汽车4. 下列哪个句子是正确的？A. 2加3等于5B. 2减3等于5C. 3乘2等于5D. 5除以2等于35. 下列哪个物品需要用“千克”来计量？A. 一本书B. 一根铅笔C. 一块橡皮D. 一袋米6. 下列哪个数字是奇数？A. 2B. 3C. 4D. 57. 下列哪个图形是平行四边形？A. 正方形B. 三角形C. 平行四边形D. 梯形8. 下列哪个物品可以用“厘米”来计量？A. 一本书B. 一根铅笔C. 一块橡皮D. 一袋米9. 下列哪个句子是错误的？A. 4减2等于2B. 3加3等于6C. 5乘1等于5D. 2除以1等于310. 下列哪个物品需要用“平方米”来计量？A. 一本书B. 一根铅笔C. 一块橡皮D. 一张桌子二、填空题（每题2分，共20分）11. 3加2等于______。

12. 5减3等于______。

13. 4乘2等于______。

14. 6除以2等于______。

15. 一根铅笔长______厘米。

16. 一个苹果重______克。

17. 一本书有______页。

18. 一个苹果比一个橘子______。

19. 三个苹果比两个橘子______。

20. 两个苹果加一个橘子等于______。

三、判断题（每题2分，共10分）21. 3加3等于6。

（）22. 4减1等于5。

（）23. 6乘2等于10。

（）24. 8除以4等于2。

（）25. 一个正方形有四个角。

（）四、应用题（每题5分，共20分）26. 小明有5个苹果，小华有7个苹果，他们一共有多少个苹果？27. 小红有3个铅笔，小明给她2个铅笔，小红现在有多少个铅笔？28. 一盒铅笔有12支，小明每天用3支，几天后铅笔会用完？29. 小华有10个橡皮，小明借走5个，小华还剩多少个橡皮？30. 一辆汽车有4个轮子，一辆自行车有2个轮子，一辆汽车和一辆自行车一共有多少个轮子？答案：一、选择题1. C2. C3. A4. A5. D6. B7. C8. A9. D10. D二、填空题11. 512. 213. 814. 315. 1516. 20017. 3018. 多19. 多20. 5三、判断题21. √22. ×23. √24. √25. √四、应用题26. 12个27. 5个28. 4天29. 5个30. 6个。

数分基础试题及答案一、单项选择题（每题2分，共10分）1. 函数f(x)=x^2在区间(-∞, +∞)上是：A. 增函数B. 减函数C. 常数函数D. 非单调函数答案：A2. 以下哪个选项是闭区间[a, b]上的连续函数？A. f(x) = x^2, x ∈ [0, 1]B. f(x) = 1/x, x ∈ (0, 1]C. f(x) = |x|, x ∈ [-1, 1]D. f(x) = sin(1/x), x ∈ (0, 1]答案：C3. 函数f(x) = x^3 - 3x在R上的零点个数为：A. 0B. 1C. 2D. 3答案：D4. 函数f(x) = e^x的导数为：A. e^xB. -e^xC. e^(-x)D. -e^(-x)答案：A5. 以下哪个函数在R上是周期函数？A. f(x) = x^2B. f(x) = sin(x)C. f(x) = e^xD. f(x) = ln(x)答案：B二、填空题（每题3分，共15分）6. 若函数f(x)在x=a处可导，则f'(a)等于________。

答案：f(x)在x=a处的导数7. 函数f(x) = x^2 + 3x + 2的极小值点为________。

答案：x = -18. 函数f(x) = x^3的不定积分为________。

答案：1/4 * x^4 + C9. 若f(x)在[a, b]上连续，则f(x)在[a, b]上________。

答案：有界10. 函数f(x) = sin(x) + cos(x)的周期为________。

答案：2π三、解答题（每题10分，共20分）11. 求函数f(x) = x^2 - 4x + 4在区间[1, 3]上的最小值。

答案：函数f(x) = (x-2)^2，其在区间[1, 3]上的最小值出现在x=2处，此时f(2) = 0。

12. 证明函数f(x) = x^3在R上是增函数。

答案：对于任意x1, x2 ∈ R，且x1 < x2，有f(x1) - f(x2) = x1^3 - x2^3 = (x1 - x2)(x1^2 + x1x2 + x2^2)。

一、选择题（每题4分，共20分）1. 下列哪个数是整数？（）A. 3.14B. 2.5C. 2D. 1.5答案：C解析：整数是指没有小数部分的数，所以选项C是整数。

2. 下列哪个数是正数？（）A. -5B. 0C. 3D. -3答案：C解析：正数是指大于0的数，所以选项C是正数。

3. 下列哪个数是偶数？（）A. 5B. 8C. 10D. 15答案：C解析：偶数是指能被2整除的数，所以选项C是偶数。

4. 下列哪个数是质数？（）A. 4B. 6C. 7D. 9答案：C解析：质数是指只能被1和它本身整除的数，所以选项C是质数。

5. 下列哪个数是立方数？（）A. 4B. 8C. 27D. 32答案：C解析：立方数是指一个数的三次方，所以选项C是立方数。

二、填空题（每题4分，共20分）1. 3的平方根是______。

答案：√3解析：平方根是指一个数的平方等于另一个数，所以3的平方根是√3。

2. 5的立方根是______。

答案：∛5解析：立方根是指一个数的立方等于另一个数，所以5的立方根是∛5。

3. 下列数中，既是偶数又是质数的是______。

答案：2解析：偶数是指能被2整除的数，质数是指只能被1和它本身整除的数，所以2既是偶数又是质数。

4. 下列数中，既是正数又是整数的是______。

答案：5解析：正数是指大于0的数，整数是指没有小数部分的数，所以5既是正数又是整数。

5. 下列数中，既是负数又是偶数的是______。

答案：-4解析：负数是指小于0的数，偶数是指能被2整除的数，所以-4既是负数又是偶数。

三、解答题（每题10分，共30分）1. 简化下列各式：（1）5√2 + 3√2答案：8√2解析：同类项相加，系数相加，所以5√2 + 3√2 = 8√2。

（2）2x^2 - 3x^2 + 4x^2答案：3x^2解析：同类项相加，系数相加，所以2x^2 - 3x^2 + 4x^2 = 3x^2。

2. 求下列方程的解：（1）2x - 3 = 7答案：x = 5解析：将方程两边同时加3，得到2x = 10，再将方程两边同时除以2，得到x = 5。

习 题 1-11．计算下列极限（1）limx ax aa x x a→--, 0;a >解：原式lim []xaa ax aa a x a x ax a→--=---=()|()|xax a x aa x ==''-=1ln a a a a a a --⋅=(ln 1)a a a - （2）sin sin lim sin()x ax a x a →--；解：原式sin sin limx ax ax a→-=-(sin )'cos x a x a===（3）2lim 2), 0;n n a →∞>解：原式2lim1/n n→∞=20[()']xx a ==2ln a=（4）1lim [(1)1]pn n n→∞+-，0;p >解：原式111(1)1lim()|p pp x n n nx =→∞+-'===11p x pxp -==（5）1010(1tan )(1sin )lim;sin x x x x →+-- 解：原式101000(1tan )1(1sin )1limlimtan sin x x x x xx→→+---=--=990010(1)|10(1)|20t t t t ==+++=（6）1limx →，,m n 为正整数；解：原式11lim1x x →=-1111()'()'m x n x x x ===n m=2．设()f x 在0x 处二阶可导，计算0002()2()()lim h f x h f x f x h h→+-+-.解：原式000()()lim 2h f x h f x h h→''+--=00000()()()()lim2h f x h f x f x f x h h→''''+-+--=00000()()()()limlim22h h f x h f x f x h f x hh→→''''+---=+-00011()()()22f x f x f x ''''''=+=3．设0a >，()0f a >，()f a '存在，计算1ln ln ()lim[]()x ax af x f a -→.解：1ln ln ()lim[]()x a x a f x f a -→ln ()ln ()lim f x f a x a e -→=ln ()ln ()limln ln x af x f a x ae→--=ln ()ln ()limln ln x a f x f a x ax a x a e→----='()()f a af a e=习 题 1-21.求下列极限（1）lim (sin sin x →+∞;解：原式lim cos 1)(1)]0x x x →+∞=+--= ，其中ξ在1x -与1x +之间（2）4cos(sin )cos limsin x x xx→-;解：原式=4sin (sin )limx x x xξ→--=3sin sin lim ()()()x x x xxξξξ→--⋅=16，其中ξ在x 与sin x之间（3）lim x →+∞解：原式116611lim [(1)(1)]x x xx→+∞=+--56111lim (1)[(1)(1)]6x x xxξ-→+∞=⋅+⋅+--5611lim(1)33x ξ-→+∞=+=，其中ξ在11x-与11x+之间（4） 211lim(arctanarctan);1n n n n →+∞-+解：原式22111lim ()11n n n n ξ→+∞=-++ 1=，其中其中ξ在11n +与1n之间2．设()f x 在a 处可导，()0f a >，计算11()lim ()nn n n f a f a →∞⎡⎤+⎢⎥-⎣⎦.解：原式1111(ln ()ln ())lim (ln ()ln ())lim n n f a f a n f a f a nn nn n e e→∞+--+--→∞==11ln ()ln ()ln ()ln ()[limlim]11n n f a f a f a f a nn nne→∞→∞+---+-=()()2()()()()f a f a f a f a f a f a ee'''+==习 题 1-31．求下列极限 （1）0(1)1lim(1)1x x x λμ→+-+-,0;μ≠解：原式0lim x xxλλμμ→==（2）0lim x →;解：02ln cos cos 2cos lim12x x x nxIx→-⋅⋅⋅=2ln cos ln cos 2ln cos 2limx x x nxx→++⋅⋅⋅+=-2cos 1cos 21cos 12limx x x nx x→-+-+⋅⋅⋅+-=-2222(2)()limx x x nx x→++⋅⋅⋅+=21ni i ==∑（3）011lim )1xx x e →--（;解：原式01lim(1)x xx e x x e →--=-201limxx e xx→--=01lim2xx e x→-=01lim22x x x→==（4）112lim[(1)]xx x x x x →+∞+-;解：原式11ln(1)ln 2lim ()x xxxx x ee+→+∞=-21lim (ln(1)ln )x x x x x →+∞=+- 1lim ln(1)x x x→+∞=+ 1lim 1x xx→+∞==2. 求下列极限 （1）2221cos ln cos limsin xxx x x eex -→----;解：原式222201122lim 12x x x x x→+==- （2）0ln()2sin limsin(2tan 2)sin(tan 2)tan xx x e xx x x→++--;解：原式ln(11)2sin limsin(2tan 2)sin(tan 2)tan xx x e x x x x→++-+=--012sin limsin(2tan 2)sin(tan 2)tan xx x e xx x x→+-+=--2lim442x x x x x x x→++==--习 题 1-41．求下列极限 （1）21lim (1sin)n nn n→∞-；解：原式2331111lim [1(())]3!n nn o n nn→∞=--+11lim ((1))3!6n o →∞=+=（2）求3361limsin xx exx→--；解：原式3636336600()112limlim2xx x xx o x x e x xx→→++---===（3）21lim[ln(1)]x x xx →∞-+；解：原式222111lim [(())]2x x xo x xx→∞=--+12=（4）21lim (1)xxx ex-→+∞+；解：原式211[ln(1)]2lim x x x x ee+--→∞==此题已换3．设()f x 在0x =处可导，(0)0f ≠，(0)0f '≠.若()(2)(0)af h bf h f +-在0h →时是比h 高阶的无穷小，试确定,a b 的值.解：因为 ()(0)(0)()f h f f h o h '=++，(2)(0)2(0)()f h f f h o h '=++所以0()(2)2(0)(1)(0)(2)(0)()0lim limh h af h bf h f a b f a b f o h hh→→'+-+-+++==从而10a b +-= 20a b += 解得：2,1a b ==-3．设()f x 在x 处二阶可导，用泰勒公式求0002()2()()limh f x h f x f x h h→+-+-解：原式22220000100022''()''()()'()()2()()'()()2!2!limh f x f x f x f x h h o h f x f x f x h h o h h→+++-+-++=2220122''()()()limh f x h o h o h h→++=0''()f x =4. 设()f x 在x =处可导，且2sin ()lim () 2.x x f x xx→+=求(0),(0)f f '和1()limx f x x→+.解 因为22sin ()sin ()2lim ()limx x x f x x xf x xxx→→+=+=[]22()(0)(0)()limx x o x x f f x o x x→'++++=222(1(0))(0)()limx f x f x o x x→'+++=所以 1(0)0,(0)2f f '+==,即(0)1,(0)2f f '=-=所以01()l i m x f x x →+01(0)(0)()l i m x f f x o x x →'+++=02()l i m 2x x o x x→+==习 题 1-51. 计算下列极限(1)limn →∞解：原式lim n →∞=lim2n →∞==(2)2212lim(1)nn n a a naa na+→∞+++⋅⋅⋅+>解：原式21lim(1)nn n n nanan a++→∞=--2lim(1)n n na n a→∞=--21a a=-2． 设lim n n a a→∞=，求 (1)1222limnn a a na n→∞+++ ；解：原式22lim(1)nn na n n →∞=--lim212n n na a n →∞==-(2)12lim111n nna a a →∞+++，0,1,2,,.ia i n ≠=解：由于1211111lim limnn n na a a na a→∞→∞+++==，所以12lim111n nnaa a a →∞=+++3．设2lim ()0n n n x x -→∞-=，求limn n x n→∞和1limn n n x x n-→∞-.解：因为2lim ()0n n n x x -→∞-=，所以222lim ()0n n n x x -→∞-= 且2121lim ()0n n n x x +-→∞-= 从而有stolz 定理2222lim lim22n n n n n x x x n-→∞→∞-==，且212121limlim0212n n n n n x x x n ++-→∞→∞-==+所以lim0n n x n →∞=，111lim lim lim 01n n n n n n n x x x x n n n n n --→∞→∞→∞--=-=- 4．设110x q <<，其中01q <≤，并且1(1)n n n x x qx +=-，证明：1lim nn nx q→∞=.证明：因110x q<<，所以211211(1)111(1)()24qx qx x x qx q q q+-=-≤=<，所以210x q<<，用数学归纳法易证，10nx q<<。

数分考试试题一、选择题1. 极限的定义中，ε的取值范围是：A. ε > 0B. ε ≤ 0C. ε ≥ 0D. ε < 02. 若函数f(x)在点x=a处连续，那么以下哪个条件一定成立？A. f(a)存在B. f(a-0)存在C. f(a+0)存在D. f(a-0)和f(a+0)都存在3. 函数f(x)=x^2在x=0处的导数为：A. 0B. 1C. 2D. 不存在4. 以下哪个级数是收敛的？A. 1 + 1/2 + 1/3 + ...B. (1 + 1/2) + (1/4 + 1/8) + ...C. 1 - 1/2 + 1/4 - 1/8 + ...D. 1/1 + 1/√2 + 1/√3 + ...5. 以下哪个积分是发散的？A. ∫(1/x)dx (从1到∞)B. ∫(e^(-x^2))dx (从-∞到∞)C. ∫(sin(x))/x dx (从0到∞)D. ∫(x^2)dx (从0到1)二、填空题1. 极限lim(x→0) (sin(x)/x) = ____。

2. 函数f(x)=x^3在x=1处的导数为 ____。

3. 定积分∫(2x+1)dx (从0到2) = ____。

4. 级数∑(n=1到∞) (1/n^2) 是 ____（收敛或发散）。

5. 曲线y=x^3在x=2处的切线斜率为 ____。

三、计算题1. 求函数f(x)=1/(x^2+1)在区间[-1, 1]上的定积分值。

2. 计算极限lim(n→∞) (1 + 1/2 + 1/3 + ... + 1/n)。

3. 证明级数∑(n=1到∞) 1/n 收敛，并求其和。

4. 求函数g(x)=x^4 - 4x^3 + 6x^2 - 4x + 1在区间[0, 2]上的最大值和最小值。

5. 求曲线y=cos(x)在点x=π/4处的法线方程。

四、应用题1. 一个物体从高处自由落下，不考虑空气阻力，求其在前2秒内下落的距离。

2. 某公司的年利润增长率逐年递减，第一年增长率为20%，且之后每年的增长率是前一年的一半，问第五年的年利润增长率是多少？3. 一个水池可以用一根水管在8小时内灌满，现有另一根水管，其灌水速度是第一根水管的两倍，两根水管同时使用，问需要多少时间能灌满水池？4. 某人以固定速度v沿直线行走，他发现在t小时内他走过的距离是s，求他的速度v。