计量经济学异方差性参考答案讲解
- 格式:doc
- 大小:509.50 KB
- 文档页数:14

第五章 异方差二、简答题1.异方差的存在对下面各项有何影响? (1)OLS 估计量及其方差; (2)置信区间;(3)显著性t 检验和F 检验的使用。
2.产生异方差的经济背景是什么?检验异方差的方法思路是什么?3.从直观上解释,当存在异方差时,加权最小二乘法(WLS )优于OLS 法。
4.下列异方差检查方法的逻辑关系是什么? (1)图示法 (2)Park 检验 (3)White 检验5.在一元线性回归函数中,假设误差方差有如下结构:()i i i x E 22σε=如何变换模型以达到同方差的目的?我们将如何估计变换后的模型?请列出估计步骤。
三、计算题1.考虑如下两个回归方程(根据1946—1975年美国数据)(括号中给出的是标准差):t t t D GNP C 4398.0624.019.26-+=e s :(2.73)(0.0060) (0.0736)R ²=0.999t t t GNP D GNP GNP C ⎥⎦⎤⎢⎣⎡-+=⎥⎦⎤⎢⎣⎡4315.06246.0192.25 e s : (2.22) (0.0068)(0.0597)R ²=0.875式中,C 为总私人消费支出;GNP 为国民生产总值;D 为国防支出;t 为时间。
研究的目的是确定国防支出对经济中其他支出的影响。
(1)将第一个方程变换为第二个方程的原因是什么?(2)如果变换的目的是为了消除或者减弱异方差,那么我们对误差项要做哪些假设? (3)如果存在异方差,是否已成功地消除异方差?请说明原因。
(4)变换后的回归方程是否一定要通过原点?为什么? (5)能否将两个回归方程中的R ²加以比较?为什么?2.1964年,对9966名经济学家的调查数据如下:资料来源:“The Structure of Economists’ Employment and Salaries”, Committee on the National Science Foundation Report on the Economics Profession, American Economics Review, vol.55, No.4, December 1965.(1)建立适当的模型解释平均工资与年龄间的关系。

计量经济学试题异方差性与加权最小二乘法计量经济学试题:异方差性与加权最小二乘法一、引言计量经济学作为经济学的一个重要分支,通过运用数理统计和经济理论的方法,旨在分析经济现象并进行经济政策的评估。
在实证分析中,经常会遇到异方差性的问题,而加权最小二乘法是处理异方差性的一种重要方法。
本文将探讨异方差性的来源、加权最小二乘法的原理与应用。
二、异方差性的来源异方差性是指随着自变量的变化,随机误差的方差也会发生变化。
异方差性可能会导致经验结果不准确、偏离真实情况,并影响对经济现象的解释和预测。
以下是可能导致异方差性的原因:1. 条件异方差性:数据的方差可能与自变量之间的关系存在相关性。
例如,在研究家庭收入对教育支出的影响时,高收入家庭的支出方差可能比低收入家庭更大。
2. 记忆效应:在纵向数据分析中,随着时间的推移,个体经济行为可能受到过去观测结果的影响,进而导致异方差性的存在。
3. 测量误差:数据收集中的测量误差可能会导致异方差性。
例如,对于某些变量,测量误差可能更大,从而导致随机误差的方差不一致。
三、加权最小二乘法的原理加权最小二乘法(Weighted Least Squares, WLS)是一种用于处理异方差性的回归方法,其原理是通过给不同观测值分配不同的权重,以减小异方差的影响。
具体来说,加权最小二乘法的目标是最小化加权残差平方和。
在加权最小二乘法中,权重的选择是关键。
常见的权重选择方法包括:1. 方差稳定化权重:根据方差与自变量的关系,将观测值的权重设置为方差的倒数,以减小方差变化带来的影响。
2. 广义最小方差法权重:将权重设置为具有稳定方差的函数形式,例如Huber权重函数、Andrews权重函数等。
3. 经验权重:根据经验判断,给不同观测值分配权重,以反映其重要性。
四、加权最小二乘法的应用加权最小二乘法在计量经济学中有广泛的应用。
以下是一些常见的应用领域:1. 金融经济学:在金融领域中,异方差性往往普遍存在。



第五章课后答案5.1(1)因为22()i i f X X =,所以取221iiW X =,用2i W 乘给定模型两端,得 312322221i i ii i i i Y X u X X X X βββ=+++ 上述模型的随机误差项的方差为一固定常数,即22221()()i i i iu Var Var u X X σ==(2)根据加权最小二乘法,可得修正异方差后的参数估计式为***12233ˆˆˆY X X βββ=-- ()()()()()()()***2****22232322322*2*2**2223223ˆi i i i i i i i i i i i i i i i i iW y x W x W y x W x x W x W x W x x β-=-∑∑∑∑∑∑∑()()()()()()()***2****23222222332*2*2**2223223ˆii ii i i iii i i ii i i i i iW y x W x W y x W x x Wx W x W x x β-=-∑∑∑∑∑∑∑其中22232***23222,,iii i i i iiiW XW X W Y X X Y WWW ===∑∑∑∑∑∑******222333i i i i i x X X x X X y Y Y=-=-=- 5.2(1)2222211111 ln()ln()ln(1)1 u ln()1Y X Y X Yu u X X X u ββββββββββ--==+≈=-∴=+[ln()]0()[ln()1][ln()]11E u E E u E u μ=∴=+=+=又(2)[ln()]ln ln 0 1 ()11i i iiP P i i i i P P i i E P E μμμμμμμ===⇒====∑∏∏∑∏∏不能推导出所以E 1μ()=时,不一定有E 0μ(ln )= (3) 对方程进行差分得:1)i i βμμ--i i-12i i-1lnY -lnY =(lnX -X )+(ln ln 则有:1)]0i i μμ--=E[(ln ln5.3(1)该模型样本回归估计式的书写形式为:Y = 11.44213599 + 0.6267829962*X (3.629253) (0.019872)t= 3.152752 31.5409720.944911R =20.943961R = S.E.=9.158900 DW=1.597946 F=994.8326(2)首先,用Goldfeld-Quandt 法进行检验。

第五章-异方差性-答案第五章 异方差性一、判断题1. 在异方差的情况下,通常预测失效。
( T )2. 当模型存在异方差时,普通最小二乘法是有偏的。
( F )3. 存在异方差时,可以用广义差分法进行补救。
(F )4. 存在异方差时,普通最小二乘法会低估参数估计量的方差。
(F )5. 如果回归模型遗漏一个重要变量,则OLS 残差必定表现出明显的趋势。
( T )二、单项选择题1.Goldfeld-Quandt 方法用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性2.在异方差性情况下,常用的估计方法是( D )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法3.White 检验方法主要用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性4.下列哪种方法不是检验异方差的方法( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即( B )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用6.如果戈里瑟检验表明,普通最小二乘估计结果的残差与有显著的形式的相关关系(满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为( B )A. B. C. D. 7.设回归模型为,其中()2i2i x u Var σ=,则b 的最有效估计量为( D )i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=A. B. C. D. ∑=i i x y n 1b ˆ 8.容易产生异方差的数据是( C )A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=,则使用加权最小二乘法估计模型时,应将模型变换为( C )。

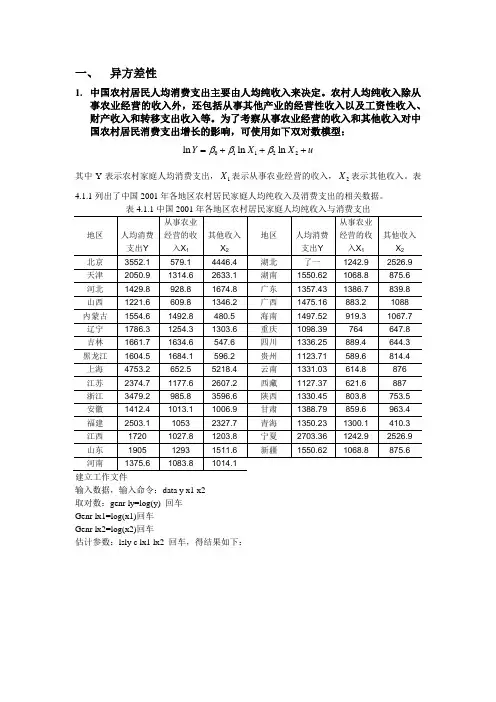
一、 异方差性1. 中国农村居民人均消费支出主要由人均纯收入来决定。
农村人均纯收入除从事农业经营的收入外,还包括从事其他产业的经营性收入以及工资性收入、财产收入和转移支出收入等。
为了考察从事农业经营的收入和其他收入对中国农村居民消费支出增长的影响,可使用如下双对数模型:01122ln ln ln Y X X u βββ=+++其中Y 表示农村家庭人均消费支出,1X 表示从事农业经营的收入,2X 表示其他收入。
表4.1.1列出了中国2001年各地区农村居民家庭人均纯收入及消费支出的相关数据。
表4.1.1中国2001年各地区农村居民家庭人均纯收入与消费支出建立工作文件输入数据,输入命令:data y x1 x2 取对数:genr ly=log(y) 回车 Genr lx1=log(x1)回车Genr lx2=log(x2)回车估计参数:lsly c lx1 lx2 回车,得结果如下:用OLS 法进行估计,结果如下:对应的表达式为:12ln 1.6030.325ln 0.507ln Y X X =++(1.86) (3.14) (10.43)20.7965,0.78,0.8117R R RSS ===不同地区农村人均消费支出的差别主要来源于非农经营收入及其他收入的差别,因此,如果存在异方差性,则可能是2X 引起的。
对异方差性的检验:做OLS 回归得到的残差平方项与ln 2X 的散点图:从散点图可以看出,两者存在异方差性。
下面进行统计检验。
采用White异方差检验:EViews提供了包含交叉项和没有交叉项两个选择。
本例选择没有包含交叉项。
得到如下结果:所以辅助回归结果为:2221122ˆ 3.9820.579ln 0.042(ln )0.563ln 0.04(ln )eX X X X =-+-+ (1.38) (-0.63) (0.63) (-2.77) (2.9)其他收入2X 与2X 的平方项的参数的t 检验是显著的,且White 统计量为13.36,在5%的显著性水平下,拒绝同方差性这一原假设,方程确实存在异方差性。

第8章异方差性8.1复习笔记一、异方差性对OLS 所造成的影响1.异方差性对无偏性的影响多元线性回归模型表达式为:01122k k y x x x uββββ=+++⋅⋅⋅+异方差性并不会导致j β的OLS 估计量出现偏误或产生不一致性,但诸如省略一个重要变量之类的情况出现则具有这种影响。
2.异方差性对拟合优度的影响对拟合优度指标R 2和2R 的解释不受异方差性的影响。
通常的R 2和调整2R 都是估计总体R 2的不同方法,而总体R 2无非就是221/u y σσ-(因为2/11/SSR SSR n R SST SST n=-=-),其中2u σ是总体误差方差,2y σ是y 的总体方差。
关键是,由于总体R 2中这两个方差都是无条件方差,所以总体R 2不受()1Var | k u x x ⋅⋅⋅,,中出现异方差性的影响。
无论()1Var | k u x x ⋅⋅⋅,,是否为常数,SSR/n 都一致地估计了2u σ,SSR/n 也一致地估计了2y σ。
当使用自由度调整时,依然如此。
因此,无论同方差假定是否成立,R 2和2R 都一致地估计了总体R 2。
3.估计量的方差()ˆVar jβ在没有同方差假定的情况下,估计量的方差ˆ()jVar β是有偏的。
由于OLS 标准误直接以这些方差为基础,所以它们都不能用来构造置信区间和t 统计量。
4.对统计检验的影响在出现异方差性的情况下,在高斯-马尔可夫假定下用来检验假设的统计量都不再成立。
(1)在出现异方差性时,通常普通最小二乘法的t 统计量就不具有t 分布,使用大样本容量也不能解决这个问题。
(2)F 统计量也不再是F 分布。
(3)LM 统计量也不服从渐近2χ分布。
二、OLS 估计后的异方差—稳健推断1.单个自变量模型01i i iy x u ββ=++假定前4个高斯-马尔可夫假定成立。
如果误差包含异方差性,那么()2Var |i i iu x σ=其中,给2σ加上下标i,表示误差方差2i σ不再是固定的值,而是随着x i 的不同而不同。

第五章 异方差性思考题5.1 简述什么是异方差?为什么异方差的出现总是与模型中某个解释变量的变化有关?答 :设模型为),....,,(....n 21i X X Y i i 33i 221i =μ+β++β+β=,如果其他假定均不变,但模型中随机误差项的方差为),...,,()(n 21i Var 2i i =σ=μ,则称i μ具有异方差性。
由于异方差性指的是被解释变量观测值的分散程度是随解释变量的变化而变化的,所以异方差的出现总是与模型中某个解释变量的变化有关。
5.2 试归纳检验异方差方法的基本思想,并指出这些方法的异同。
答:各种异方差检验的共同思想是,基于不同的假定,分析随机误差项的方差与解释变量之间的相关性,以判断随机误差项的方差是否随解释变量变化而变化。
其中,戈德菲尔德-跨特检验、怀特检验、ARCH 检验和Glejser 检验都要求大样本,其中戈德菲尔德-跨特检验、怀特检验和Glejser 检验对时间序列和截面数据模型都可以检验,ARCH 检验只适用于时间序列数据模型中。
戈德菲尔德-跨特检验和ARCH 检验只能判断是否存在异方差,怀特检验在判断基础上还可以判断出是哪一个变量引起的异方差。
Glejser 检验不仅能对异方差的存在进行判断,而且还能对异方差随某个解释变量变化的函数形式进行诊断。
5.3 什么是加权最小二乘法?它的基本思想是什么?答:以一元线性回归模型为例:12i i i Y X u ββ=++经检验i μ存在异方差,公式可以表示为22var()()i i i u f X σσ==。
选取权数 i w ,当2i σ 越小 时,权数i w 越大。
当 2i σ越大时,权数i w 越小。
将权数与 残差平方相乘以后再求和,得到加权的残差平方和:2i 21i 2i i X Y w e w )(**β-β-=∑∑,求使加权残差平方和最小的参数估计值**ˆˆ21ββ和。
这种求解参数估计式的方法为加权最小二乘法。
第五章 异方差性一、判断题1. 在异方差的情况下,通常预测失效。
( T )2. 当模型存在异方差时,普通最小二乘法是有偏的。
( F )3. 存在异方差时,可以用广义差分法进行补救。
(F )4. 存在异方差时,普通最小二乘法会低估参数估计量的方差。
(F )5. 如果回归模型遗漏一个重要变量,则OLS 残差必定表现出明显的趋势。
( T ) 二、单项选择题1.Goldfeld-Quandt 方法用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 2.在异方差性情况下,常用的估计方法是( D )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法 3.White 检验方法主要用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 4.下列哪种方法不是检验异方差的方法( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验 5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即( B )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用 6.如果戈里瑟检验表明,普通最小二乘估计结果的残差与有显著的形式的相关关系(满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为( B ) A. B.C. D.7.设回归模型为,其中()2i2i x u Var σ=,则b 的最有效估计量为( D )A. B.C. D. ∑=ii x y n 1b ˆ8.容易产生异方差的数据是( C )A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=,则使用加权最小二乘法估计模i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=∑∑=2ˆxxy b 22)(ˆ∑∑∑∑∑--=x x n y x xy n b xyb=ˆ型时,应将模型变换为( C )。
计量经济学第五章异⽅差性参考答案讲解第五章异⽅差性课后题参考答案 5.1(1)因为22()i i f X X =,所以取221iiW X =,⽤2i W 乘给定模型两端,得 312322221i i ii i i i Y X u X X X X βββ=+++ 上述模型的随机误差项的⽅差为⼀固定常数,即22221()()i i i iu Var Var u X X σ==(2)根据加权最⼩⼆乘法,可得修正异⽅差后的参数估计式为***12233Y X X βββ=-- ()()()()()()()***2****22232322322*2*2**2223223?i i i i i i i i i i i i i i i i i iW y x W x W y x W x x W x W x W x x β-=-∑∑∑∑∑∑∑()()()()()()()***2****23222222332*2*2**2223223?ii ii i i iii i i ii i i i i iW y x W x W y x W x x Wx W x W x x β-=-∑∑∑∑∑∑∑其中22232***23222,,iii i i i iiiW XW X W Y X X Y WWW ===∑∑∑∑∑∑******222333i i i i i x X X x X X y Y Y=-=-=- 5.2 (1)2222211111 ln()ln()ln(1)1 u ln()1Y X Y X Yu u X X X u ββββββββββ--==+≈=-∴=+ [ln()]0 ()[ln()1][ln()]11E u E E u E u µ=∴=+=+=⼜(2)[ln()]ln ln 0 1 ()11i i iiP P i i i i P P i i E P E µµµµµµµ===?====∑∏∏∑∏∏不能推导出所以E 1µ()=时,不⼀定有E 0µ(ln )= (3)对⽅程进⾏差分得:1)i i βµµ--i i-12i i-1lnY -lnY =(lnX -X )+(ln ln则有:1)]0i i µµ--=E[(ln ln5.3(1)该模型样本回归估计式的书写形式为:Y = 11.44213599 + 0.6267829962*X (3.629253) (0.019872)t= 3.152752 31.5409720.944911R =20.943961R = S.E.=9.158900 DW=1.597946 F=994.8326(2)⾸先,⽤Goldfeld-Quandt 法进⾏检验。
计量经济学练习题第一章导论一、单项选择题⒈计量经济研究中常用的数据主要有两类:一类是时间序列数据,另一类是【 B 】A 总量数据B 横截面数据C平均数据 D 相对数据⒉横截面数据是指【A 】A 同一时点上不同统计单位相同统计指标组成的数据B 同一时点上相同统计单位相同统计指标组成的数据C 同一时点上相同统计单位不同统计指标组成的数据D 同一时点上不同统计单位不同统计指标组成的数据⒊下面属于截面数据的是【D 】A 1991-2003年各年某地区20个乡镇的平均工业产值B 1991-2003年各年某地区20个乡镇的各镇工业产值C 某年某地区20个乡镇工业产值的合计数D 某年某地区20个乡镇各镇工业产值⒋同一统计指标按时间顺序记录的数据列称为【B 】A 横截面数据B 时间序列数据C 修匀数据D原始数据⒌回归分析中定义【 B 】A 解释变量和被解释变量都是随机变量B 解释变量为非随机变量,被解释变量为随机变量C 解释变量和被解释变量都是非随机变量D 解释变量为随机变量,被解释变量为非随机变量二、填空题⒈计量经济学是经济学的一个分支学科,是对经济问题进行定量实证研究的技术、方法和相关理论,可以理解为数学、统计学和_经济学_三者的结合。
⒉⒊现代计量经济学已经形成了包括单方程回归分析,联立方程组模型,时间序列分析三大支柱。
⒋⒌经典计量经济学的最基本方法是回归分析。
计量经济分析的基本步骤是:理论(或假说)陈述、建立计量经济模型、收集数据、计量经济模型参数的估计、检验和模型修正、预测和政策分析。
⒍⒎常用的三类样本数据是截面数据、时间序列数据和面板数据。
⒏⒐经济变量间的关系有不相关关系、相关关系、因果关系、相互影响关系和恒等关系。
三、简答题⒈什么是计量经济学?它与统计学的关系是怎样的?计量经济学就是对经济规律进行数量实证研究,包括预测、检验等多方面的工作。
计量经济学是一种定量分析,是以解释经济活动中客观存在的数量关系为内容的一门经济学学科。
课后习题参考答案第二章教材习题与解析1、 判断下列表达式是否正确:y i =β0+β1x i ,i =1,2,⋯ny ̂i =β̂0+β̂1x i ,i =1,2,⋯nE(y i |x i )=β0+β1x i +u i ,i =1,2,⋯n E(y i |x i )=β0+β1x i ,i =1,2,⋯nE(y i |x i )=β̂0+β̂1x i ,i =1,2,⋯ny i =β0+β1x i +u i ,i =1,2,⋯ny ̂i =β̂0+β̂1x i +u i ,i =1,2,⋯n y i =β̂0+β̂1x i +u i ,i =1,2,⋯n y i =β̂0+β̂1x i +u ̂i ,i =1,2,⋯n y ̂i =β̂0+β̂1x i +u ̂i ,i =1,2,⋯n答案:对于计量经济学模型有两种类型,一是总体回归模型,另一是样本回归模型。
两类回归模型都具有确定形式与随机形式两种表达方式:总体回归模型的确定形式:X X Y E 10)|(ββ+= 总体回归模型的随机形式:μββ++=X Y 10样本回归模型的确定形式:X Y 10ˆˆˆββ+= 样本回归模型的随机形式:e X Y ++=10ˆˆββ 除此之外,其他的表达形式均是错误的2、给定一元线性回归模型:y =β0+β1x +u (1)叙述模型的基本假定;(2)写出参数β0和β1的最小二乘估计公式;(3)说明满足基本假定的最小二乘估计量的统计性质; (4)写出随机扰动项方差的无偏估计公式。
答案:(1)线性回归模型的基本假设有两大类,一类是关于随机误差项的,包括零均值、同方差、不序列相关、满足正态分布等假设;另一类是关于解释变量的,主要是解释变量是非随机的,如果是随机变量,则与随机误差项不相关。
(2)12ˆi iix yxβ=∑∑,01ˆˆY X ββ=- (3)考察总体的估计量,可从如下几个方面考察其优劣性:1)线性性,即它是否是另一个随机变量的线性函数; 2)无偏性,即它的均值或期望是否等于总体的真实值;3)有效值,即它是否在所有线性无偏估计量中具有最小方差;4)渐进无偏性,即样本容量趋于无穷大时,它的均值序列是否趋于总体真值; 5)一致性,即样本容量趋于无穷大时,它是否依概率收敛于总体的真值;6)渐进有效性,即样本容量趋于无穷大时,它在所有的一致估计量中是否具有最小的渐进方差。
第12章时间序列回归中的序列相关和异方差性12.1复习笔记考点一:含序列相关误差时OLS 的性质★★★1.无偏性和一致性当时间序列回归的前3个高斯-马尔可夫假定成立时,OLS 的估计值是无偏的。
把严格外生性假定放松到E(u t |X t )=0,可以证明当数据是弱相关时,∧βj 仍然是一致的,但不一定是无偏的。
2.有效性和推断假定误差存在序列相关,即满足u t =ρu t-1+e t ,t=1,2,…,n,|ρ|<1。
其中,e t 是均值为0方差为σe 2满足经典假定的误差。
对于简单回归模型:y t =β0+β1x t +u t 。
假定x t 的样本均值为零,因此有:1111ˆn x t tt SST x u -==+∑ββ其中:21nx t t SST x ==∑∧β1的方差为:()()122221111ˆ/2/n n n t j xt t x x t t j t t j Var SST Var x u SST SST x x ---+===⎛⎫==+ ⎪⎝⎭∑∑∑βσσρ其中:σ2=Var(u t )。
根据∧β1的方差表达式可知,第一项为经典假定条件下的简单回归模型中参数的方差。
因此,当模型中的误差项存在序列相关时,OLS 估计的方差是有偏的,假设检验的统计量也会出现偏差。
3.拟合优度当时间序列回归模型中的误差存在序列相关时,通常的拟合优度指标R 2和调整R 2便会失效;但只要数据是平稳和弱相关的,拟合优度指标就仍然有效。
4.出现滞后因变量时的序列相关(1)在出现滞后因变量和序列相关的误差时,OLS 不一定是不一致的假设E(y t |y t-1)=β0+β1y t-1。
其中,|β1|<1。
加上误差项把上式写为:y t =β0+β1y t-1+u t ,E(u t |y t-1)=0。
模型满足零条件均值假定,因此OLS 估计量∧β0和∧β1是一致的。
误差{u t }可能序列相关。
虽然E(u t |y t-1)=0保证了u t 与y t-1不相关,但u t-1=y t -1-β0-β1y t-2,u t 和y t-2却可能相关。
第五章 异方差性课后题参考答案 5.1(1)因为22()i i f X X =,所以取221iiW X =,用2i W 乘给定模型两端,得 312322221i i ii i i i Y X u X X X X βββ=+++ 上述模型的随机误差项的方差为一固定常数,即22221()()i i i iu Var Var u X X σ==(2)根据加权最小二乘法,可得修正异方差后的参数估计式为***12233ˆˆˆY X X βββ=--()()()()()()()***2****22232322322*2*2**2223223ˆii ii i i i i i i i i i i i i i iW y x W x W y x W x x W x W x W x x β-=-∑∑∑∑∑∑∑()()()()()()()***2****23222222332*2*2**2223223ˆii ii i i iii i i ii i i i i iW y x W x W y x W x x Wx W x W x x β-=-∑∑∑∑∑∑∑其中22232***23222,,iii i i i iiiW XW X W YX X Y WWW===∑∑∑∑∑∑******222333i i i i i x X X x X X y Y Y=-=-=- 5.2 (1)2222211111 ln()ln()ln(1)1 u ln()1Y X Y X Yu u X X X u ββββββββββ--==+≈=-∴=+ [ln()]0()[ln()1][ln()]11E u E E u E u μ=∴=+=+=又(2)[ln()]ln ln 0 1 ()11i i iiP P i i i i P P i i E P E μμμμμμμ===⇒====∑∏∏∑∏∏不能推导出所以E 1μ()=时,不一定有E 0μ(ln )= (3)对方程进行差分得:1)i i βμμ--i i-12i i-1lnY -lnY =(lnX -X )+(ln ln则有:1)]0i i μμ--=E[(ln ln5.3(1)该模型样本回归估计式的书写形式为:Y = 11.44213599 + 0.6267829962*X (3.629253) (0.019872)t= 3.152752 31.5409720.944911R = 20.943961R = S.E.=9.158900 DW=1.597946F=994.8326(2)首先,用Goldfeld-Quandt 法进行检验。
a.将样本X 按递增顺序排序,去掉中间1/4的样本,再分为两个部分的样本,即1222n n ==。
b.分别对两个部分的样本求最小二乘估计,得到两个部分的残差平方和,即21624.3004e =∑ ,222495.840e =∑求F 统计量为F= 2221ee ∑∑=2495.840624.3004=3.9978给定0.05α=,查F 分布表,得临界值为0.05(20,20) 2.12F =。
c.比较临界值与F 统计量值,有F =4.1390>0.05(20,20) 2.12F =,说明该模型的随机误差项存在异方差。
其次,用White 法进行检验。
具体结果见下表 White Heteroskedasticity Test: Obs*R-squared10.58597 Probability0.005027给定0.05α=,在自由度为2下查卡方分布表,得25.9915χ=。
比较临界值与卡方统计量值,即2210.8640 5.9915nR χ=>=,同样说明模型中的随机误差项存在异方差。
(2)用权数1/|e|W =,作加权最小二乘估计,得如下结果 Dependent Variable: YMethod: Least SquaresDate: 05/28/07 Time: 00:20Sample: 1 60Included observations: 60var 4Adjusted R-squared 1.000000 S.D. dependentvar379.8909S.E. of regression 8.44E-10 Akaike infocriterion -38.91622Sum squared resid 4.13E-17 Schwarz criterion -38.84641Log likelihood 1169.487 F-statistic 4.88E+17 Durbin-Watson 0.786091 Prob(F-statistic) 0.00000var 7Adjusted R-squared 0.881117 S.D. dependentvar38.68984S.E. of regression 13.34005 Sum squaredresid 10321.5Durbin-Watson 0.3778042 Obs*R-squared 4.584017 Probability 0.10106 Test Equation:Dependent Variable: STD_RESID^2Method: Least SquaresDate: 05/28/07 Time: 00:27 Sample: 1 60X 3.21E-21 2.16E-21 1.489532 0.1419 X^2 -7.59E-2 6.18E-24 -1.229641 0.2239var 9Adjusted R-squared 0.043993 S.D. dependent var 1.56E-19 S.E. of regression 1.52E-19 Sum squared resid 1.32E-36F-statistic 2.357523 Durbin-Watson stat 1.1915315.4令Y 表示农业总产值,X1-X5分别表示农业劳动力、灌溉面积、化肥用量、户均固定资产和农机动力。
建立模型:01122334455Y X X X X X ββββββ=+++++回归结果如下:1234522ˆ 4.7171980.039615-0.0368950.2632560.0134630.025469(0.516910) (1.452697) ( -0.474813) (0.479104) (2.712997) (1.625993)R 0.974539 R =0.953321 DW=1.969898 F=45.93047Y X X X X X t =++++== 从回归结果可以看出,模型的2R 和2R 值都较高,F 统计量也显著。
但是除4X 的系数显著之外,其他系数均不显著,模型可能存在多重共线性。
计算各解释变量的相关系数。
相关系数矩阵X1 X2 X3 X4 X5 X1 1.000000 0.851867 0.963173 0.456913 0.892506 X2 0.851867 1.000000 0.843541 0.549390 0.856933 X3 0.963173 0.843541 1.000000 0.583048 0.924806 X4 0.456913 0.549390 0.583048 1.000000 0.543765 X5 0.892506 0.856933 0.924806 0.543765 1.000000由相关系数矩阵可以看出,解释变量之间的相关系数较高,存在多重共线性。
采用逐步回归的办法,来解决多重共线性问题。
分别做Y 对X1、X2、X3、X4、X5的一元回归,结果如下表所示:一元回归结果 其中加入X3的方程2R 最大,以X3为基础,顺次加入其他变量逐步回归,结果如下:加入新变量的回归结果(一)变量X1 X2 X3 X4 X5 2R X3, X10.002636 (0.089770) 1.481909 (2.8792930.915816 X3, X2 0.066909 0.789958 1.360291 5.4565840.921204X3, X4 1.352291 9.776764 0.009691 2.1590710.944492X3, X51.115680 (3.355936) 0.023552 (1.335921)0.929684经比较,新加入X4的方程2R 0.944492 ,改进最大。
且从经济意义来看,户均固定资产对农业总产值有影响,因此保留X4,再加入其他变量逐步回归,结果如下:加入新变量的回归结果(二)变量 X1 X2 X3 X4 X5 2R X3,X4 X1 0.035438 (1.365712) 0.696651 (1.399128) 0.012887 (2.638461)0.949360X3,X4 X2 0.047486 (1.487193) 1.241502 (5.528062) 0.009296 (1.984375)0.940595X3, X4 ,X5 0.951924 (3.375236) 0.009594 (2.312344) 0.023059 (1.592574) 0.952585加入X1后方程的2R 增大,但是t 值不显著;加入X2后2R 降低,且系数不显著;假如X5后方程的2R 增大,但是t 值不显著。
修正多重共线性影响的回归结果为:变量 X1 X2 X3 X4 X5 参数估计值 0.084078 0.456767 1.526410 0.035277 0.078269 t 统计量 8.097651 5.099371 11.62132 2.991326 8.197929 2R 0.867676 0.722250 0.931061 0.472241 0.870476 2R0.8544430.6944750.9241670.4194650.8575243422ˆ14.74802 1.3522910.0096911.835441 9.776764 2.159071R =0.954584 R 0.944492 DW=2.482223 F=94.58409i Y X X t =++==White 检验:220.054.132927(5)11.0705nR χ=<=接受原假设,模型不存在异方差。
5.5(1)建立样本回归模型。
2ˆ192.99440.0319(0.1948)(3.83)0.4783,..2759.15,14.6692YX R s e F =+=== (2)利用White 检验判断模型是否存在异方差。
White Heteroskedasticity Test: 给定0.05α=和自由度为2下,查卡方分布表,得临界值25.9915χ=,而White 统计量25.2125nR =,有220.05(2)nR χ<,则不拒绝原假设,说明模型中不存在异方差。