塔器现代工程设计的流体力学计算方案
- 格式:pdf
- 大小:1.26 MB
- 文档页数:39


塔的水力学计算手册1.目的与适用范围................................................. 错误!未定义书签。
2.塔设备特性..................................................... 错误!未定义书签。
3.名词术语和定义................................................. 错误!未定义书签。
4.浮阀/筛孔板式塔盘的设计........................................ 错误!未定义书签。
5.填料塔的设计................................................... 错误!未定义书签。
1.目的与适用范围为提高工艺工程师的设计质量,推广计算机应用而编写本手册。
本手册是针对气液传质塔设备中的普遍性问题而编写。
对于某些具体塔设备的数据(比如:某生产流程中针对某塔设备的板效率而采用的计算关联式,或者对于某吸收填料塔的传质单元高度或等板高度而采用的具体计算公式)则未予收入。
本设计手册以应用为主,主要是指导性的计算方法和步骤,并配合相应的计算程序,具体公式及理论推阐可参考有关文献。
2.塔设备特性作为气(汽)、液两相传质用的塔设备,首先必须能使气(汽)、液两相得到充分的接触,以得到较高的传质分离效率。
此外,塔设备还应具有以下一些特点:(1)当气(汽)、液处理量过大(超过设计值)时,仍不致于发生大量的雾沫挟带或液泛等影响正常操作的现象。
(2)当操作波动(设计值的50%~120%)较大时,仍能维持在较高的传质效率下稳定操作,并具有长期连续操作所必须具备的可靠性。
(3)塔压力降尽量小。
(4)结构简单、耗材少、制造和安装容易。
(5)耐腐蚀、不易堵塞。
(6)塔内的滞留液量要小。
3.名词术语和定义塔径(tower diameter),DT塔筒体内壁直径,见图(a)。


塔的水力学计算手册1.目的与适用范围 (1)2.塔设备特性 (1)3.名词术语和定义 (1)4.浮阀/筛孔板式塔盘的设计 (1)5.填料塔的设计 (1)1.目的与适用范围为提高工艺工程师的设计质量,推广计算机应用而编写本手册。
本手册是针对气液传质塔设备中的普遍性问题而编写。
对于某些具体塔设备的数据(比如:某生产流程中针对某塔设备的板效率而采用的计算关联式,或者对于某吸收填料塔的传质单元高度或等板高度而采用的具体计算公式)则未予收入。
本设计手册以应用为主,主要是指导性的计算方法和步骤,并配合相应的计算程序,具体公式及理论推阐可参考有关文献。
2.塔设备特性作为气(汽)、液两相传质用的塔设备,首先必须能使气(汽)、液两相得到充分的接触,以得到较高的传质分离效率。
此外,塔设备还应具有以下一些特点:(1)当气(汽)、液处理量过大(超过设计值)时,仍不致于发生大量的雾沫挟带或液泛等影响正常操作的现象。
(2)当操作波动(设计值的50%~120%)较大时,仍能维持在较高的传质效率下稳定操作,并具有长期连续操作所必须具备的可靠性。
(3)塔压力降尽量小。
(4)结构简单、耗材少、制造和安装容易。
(5)耐腐蚀、不易堵塞。
(6)塔内的滞留液量要小。
3.名词术语和定义3.1 塔径(tower diameter),DT塔筒体内壁直径,见图3.1-(a)。
3.2 板间距(tray spacing),HT塔内相邻两层塔盘间的距离,见图3.1-(a)。
3.3 降液管(downcomer),DC各层塔盘之间专供液相流体通过的组件,单溢流型塔盘为侧降液管,双溢流型塔盘有侧降液管和中央降液管,三或多溢流型塔盘有侧降液管、偏侧降液管、偏中央降液管及中央降液管。
3.4 降液管顶部宽度(DC top width),Wd弓形降液管面积的弦高。
掠堰另有算法,见图3.1-(a),-(b)。
3.5 降液管底间隙(DC clearance),ho降液管底部边缘至塔盘(或受液盘)之间的距离,见图3.1-(a)。
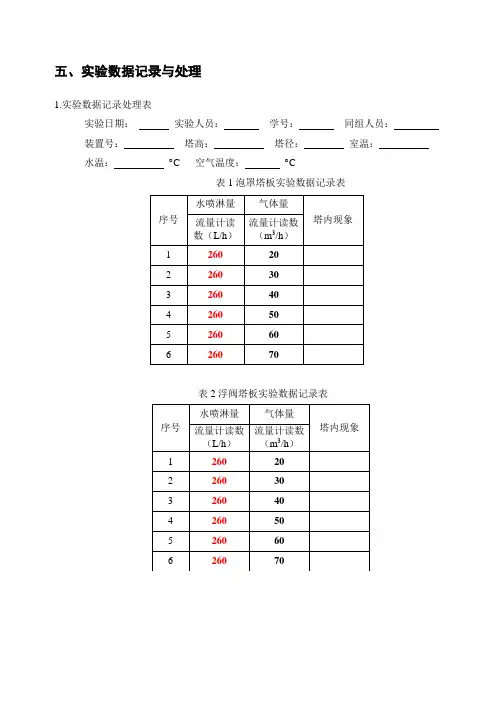
五、实验数据记录与处理1.实验数据记录处理表实验日期:实验人员:学号:同组人员:装置号:塔高:塔径:室温:水温:︒C 空气温度:︒C表1泡罩塔板实验数据记录表表2浮阀塔板实验数据记录表表3有降液管的筛孔板实验数据记录表表4无降液管的筛孔板实验数据记录表塔内现象:指漏液、鼓泡、泡沫、雾沫夹带、淹塔;六、实验结果根据实验结果,观察实验临界气速:1.确定操作下限的“漏液点”(漏液)和操作上限的“液泛点”(淹塔);表5塔板临界气速实验数据结果表2.计算塔板弹性:VV操作上限操作下限操作弹性3.分别比较:泡罩塔板、浮阀塔板、有降液管的筛孔板和无降液管的筛孔板的区别;七、思考题:1、2、3板式塔流体力学实验实验指导书板式塔流体力学实验一.实验目的1.观察板式塔各类型塔板的结构,比较各塔板上的气液接触状况。
2.实验研究板式塔的极限操作状态,确定各塔板的漏液点和液泛点。
二.实验原理板式塔是一种应用广泛的气液两相接触并进行传热、传质的塔设备,可用于吸收(解吸)、精馏和萃取等化工单元操作。
与填料塔不同,板式塔属于分段接触式气液传质设备,塔板上气液接触的良好与否和塔板结构及气液两相相对流动情况有关,后者即是本实验研究的流体力学性能。
1.塔板的组成各种塔板板面大致可分为三个区域,即溢流区、鼓泡区和无效区。
降液管所占的部分称为溢流区。
降液管的作用除使液体下流外,还须使泡沫中的气体在降液管中得到分离,不至于使气泡带入下一塔板而影响传质效率。
因此液体在降液管中应有足够的停留时间使气体得以解脱,一般要求停留时间大于3~5s。
一般溢流区所占总面积不超过塔板总面积的25%,对液量很大的情况,可超过此值。
塔板开孔部分称为鼓泡区,即气液两相传质的场所,也是区别各种不同塔板的依据。
而如图1阴影部分所示则为无效区,因为在液体进图1塔板板面口处液体容易自板上孔中漏下,故设一传质无效的不开孔区,称为进口安定区,而在出口处,由于进降液管的的泡沫较多,也应设定不开孔区来破除一部分泡沫,又称破沫区。

流体力学计算公式流体力学是研究流体的运动规律和性质的一门学科,广泛应用于工程和科学领域中。
在流体力学的研究过程中,有许多重要的计算公式和方程被提出和应用。
下面是一些重要的流体力学计算公式。
1.压力力学方程:压力力学方程是描述流体力学中流体静压力分布和变化的方程。
对于稳定的欧拉流体,方程为:∇P=-ρ∇φ其中,P是压力,ρ是流体的密度,φ是流体的势函数。
2.欧拉方程:欧拉方程用于描述流体的运动,它是流体运动的基本方程之一:∂v/∂t+v·∇v=-1/ρ∇P+g其中,v是流体的速度,P是压力,ρ是流体的密度,g是重力加速度。
3.奇异体流动方程:奇异体流动是流体与孤立涡流动的一种类型,其方程为:D(D/u)/Dt=0其中,D/Dt是对时间的全导数,u是速度向量。
4.麦克斯韦方程:5.纳维-斯托克斯方程:纳维-斯托克斯方程是描述流体的动力学行为的方程,它是流体力学中最重要的方程之一:∂v/∂t+v·∇v=-1/ρ∇P+μ∇²v其中,v是速度矢量,P是压力,ρ是密度,μ是动力黏度。
6.贝努利方程:贝努利方程描述了在不可压缩流体中流体静力学的变化。
贝努利方程给出了伯努利定律,即沿着一条流线上的速度增加,压力将降低,反之亦然。
贝努利方程的公式为:P + 1/2ρv^2 + ρgh = const.其中,P是压力,ρ是密度,v是流体速度,g是重力加速度,h是流体高度。
7.流量方程:流量方程用于描述流体在管道或通道中的流动。
Q=A·v其中,Q是流量,A是截面积,v是流速。
8.弗朗脱方程:弗朗脱方程是描述管道中流体流动的方程,其中考虑了摩擦阻力的影响:hL=f(L/D)(v^2/2g)其中,hL是管道摩擦阻力头损失,f是阻力系数,L是管道长度,D 是管道直径,v是流速,g是重力加速度。
以上是一些重要的流体力学计算公式。
这些公式和方程在流体力学中具有广泛的应用,是工程和科学领域中进行流体流动分析和计算的基础。

现代流体力学数值模拟方法现代流体力学数值模拟方法是一种通过数值计算和模拟来研究流体运动和相互作用的方法。
它在科学研究、工程设计和实际应用中发挥着重要的作用。
本文将介绍现代流体力学数值模拟方法的原理和应用,并探讨其在不同领域中的意义和挑战。
第一部分:现代流体力学数值模拟方法的原理现代流体力学数值模拟方法主要基于数学模型和计算机算法。
在数学模型方面,流体力学方程是数值模拟的基础。
流体力学方程包括连续性方程、动量方程和能量方程。
这些方程描述了流体的运动、压力分布和能量传递等基本特性。
为了解决这些方程,需要使用适当的数值方法来离散化和求解。
在计算机算法方面,现代流体力学数值模拟方法主要使用有限差分法、有限元法和边界元法等。
有限差分法是一种基于差商近似的数值方法,适用于均匀网格的情况。
有限元法和边界元法则是一种基于离散化网格的数值方法,适用于复杂几何形状和非均匀网格的情况。
这些数值方法可以将流体力学方程转化为代数方程组,并通过迭代求解得到数值解。
第二部分:现代流体力学数值模拟方法的应用现代流体力学数值模拟方法在各个领域中都有广泛的应用。
在航空航天领域,数值模拟可以用于研究飞机和火箭的气动性能,优化机翼和机身的设计,提高飞行的安全性和效率。
在汽车工业领域,数值模拟可以用于研究汽车的空气动力学特性,改善车辆的操控性和燃油经济性。
在能源领域,数值模拟可以用于研究风力发电和水力发电的效率,优化能源系统的设计和运行。
在建筑工程领域,数值模拟可以用于研究建筑物的风荷载和地震反应,提高建筑物的抗风抗震性能。
第三部分:现代流体力学数值模拟方法面临的挑战尽管现代流体力学数值模拟方法在各个领域中得到了广泛应用,但仍然面临着一些挑战。
首先,数值模拟需要耗费大量的计算资源和时间。
随着问题规模的增大和模拟精度的提高,计算量会急剧增加,导致计算效率低下。
其次,数值模拟结果的准确性和可靠性需要得到验证。
数值模拟只是一种近似解,其结果需要与实验数据进行对比和验证。


工程流体力学公式1.流体静力学公式:(1) 压强公式:P = ρgh,其中P为压强,ρ为流体密度,g为重力加速度,h为液面高度。
(2)压力公式:P=F/A,其中P为压力,F为作用力,A为受力面积。
2.流体力学基本方程:(1)质量守恒方程:∂(ρ)/∂t+∇·(ρv)=0,其中ρ为密度,t为时间,v为速度矢量。
(2) 动量守恒方程:∂(ρv)/∂t + ∇·(ρvv) = -∇P + ∇·τ +ρg,其中P为压力,τ为应力张量,g为重力加速度。
(3) 能量守恒方程:∂(ρe)/∂t + ∇·(ρev) = -P∇·v +∇·(k∇T) + ρg·v,其中e为单位质量的总能量,T为温度,k为热传导系数。
3.流体动力学方程:(1)欧拉方程:∂v/∂t+(v·∇)v=-∇(P/ρ)+g,其中v为速度矢量,P为压力,ρ为密度,g为重力加速度。
(2)再循环方程:∂v/∂t+(v·∇)v=-∇(P/ρ)+g+F/M,其中F为体积力,M为质量。
4.流体阻力公式:(1) 粘性流体的阻力公式:F = 6πμrv,其中F为阻力,μ为粘度,r为流体直径,v为速度。
(2)粘性流体在管道中的流量公式:Q=(π/8)ΔP(R^4)/(Lμ),其中Q为流量,ΔP为压差,R为半径,L为管道长度,μ为粘度。
5.流体力学定律:(1) Pascal定律:在封闭的液体容器中,施加在液体上的外力将均匀传递到液体的每一个点。
(2) Bernoulli定律:沿着流体流动方向,速度增大则压力减小,速度减小则压力增大。
除了上述公式之外,还有许多与特定问题相关的公式,如雷诺数、流体阻力系数、泵和液力传动公式等。
这些公式是工程流体力学研究和设计的基础,可以帮助工程师分析和解决与流体运动和相互作用有关的问题。

结合案例,写出计算流体力学的模拟步骤
计算流体力学(CFD)的模拟步骤如下:
1. 建立模型:根据实际情况,通过CAD软件建立三维几何模型。
例如,对于汽车行驶时空气流动的模拟,需要建立汽车三维几何模型。
2. 网格划分:将建立的几何模型划分成有限个网格,称为网格划分。
因为CFD 求解需要离散化,将二维或三维的几何模型离散化成网格,每个网格内拥有自己的物理量和数值解。
3. 制定边界条件:边界条件描述物理量(如速度、压力等)在边界网格上的取值。
例如,对于汽车三维几何模型,需要指定路面的速度和发动机的压力等。
4. 选择数值方法:根据计算需要和实际情况的复杂度,选择数值方法。
CFD常用的数值方法包括有限体积法、有限元法和谱方法等。
5. 求解:利用CFD软件进行数值求解,得到各个网格处物理量的数值解,例如压力和速度。
CFD求解的过程中,需要考虑数值格式的准确性、稳定性、收敛性和计算效率等因素。
6. 分析和评估:对CFD模拟的结果进行逐步评估,判断模拟的准确性和可靠性。
例如,对于汽车空气动力学的模拟,需要评估不同的镀铬排气管对汽车空气流动
行为的影响,进而改进汽车的空气动力学设计。
7. 优化设计:根据CFD模拟结果,优化模型设计。
例如,对于汽车空气动力学的模拟,可以优化发动机进气口的设计,降低风阻。
优化设计的目的是改进产品性能和节省成本。

工程流体力学中的流体力学参数计算与分析工程流体力学是研究流体在工程领域中运动与变形规律的科学。
在工程中,流体力学参数的计算与分析是非常重要的,它们能够帮助工程师评估流体的性能和行为,指导工程设计和优化。
在工程流体力学中,流体力学参数的计算与分析主要包括液体的密度、动力粘度、静力粘度、比重、表观粘度和黏度系数等等。
下面将一一介绍这些参数的计算方法及其在工程中的应用。
首先,液体的密度是指单位体积液体的质量。
密度可以通过实验测量或基于液体成分来计算。
在实验测量中,可以使用质量和体积的比值来得到液体的密度。
在基于成分计算中,根据液体的化学成分以及每个成分的密度,可以计算出混合液体的密度。
密度的计算和分析在各种流体流动和储存的工程中都有重要应用,如管道输送、储罐设计和物料分离等。
其次,动力粘度和静力粘度是流体的粘性特征的度量。
动力粘度是指流体在剪切应力作用下的抵抗力,常用单位是帕斯卡秒(Pa·s)。
静力粘度是指流体在静止状态下的抵抗力,其单位为平方速度单位。
这两个参数的计算可以通过实验测量或根据流体的物化性质进行计算。
在工程流体力学中,动力粘度和静力粘度在液体输送、液体流动和润滑油设计等领域发挥重要作用。
比重是指单位体积液体的重量与等体积水的重量的比值。
比重可以通过实验测量或根据液体的质量和密度计算。
比重的计算与分析可以用于液体的浮力和沉降速度的估计,对于液体流动与混合的设计和优化非常关键。
表观粘度是指流体在流动中展现的表面粘度特征,即有效粘度。
它是流体在管道、通道或装置中流动时所表现出来的整体粘度特征。
表观粘度的计算可以通过动力粘度、流体密度和流动速度的组合来实现。
在工程流体力学中,表观粘度的计算与分析可以用于液体流动的压降估计、泵的选择和流量计的校准等。
最后,黏度系数是流体内部分子之间相互作用力的度量。
黏度系数可以通过实验测量或根据流体分子结构和运动理论计算。
黏度系数的计算与分析在聚合物工程、化学工程和油田开发等领域有广泛应用。
流体力学公式大全流体力学是研究流体静力学和流体动力学的学科,涉及到流体的运动规律、压力分布、速度场等内容。
在工程和物理学领域,流体力学有着广泛的应用,包括飞机设计、水利工程、汽车空气动力学等方面。
本文将为大家详细介绍流体力学中常见的公式,希望能够帮助大家更好地理解和应用流体力学知识。
1. 流体静力学公式。
在静止的流体中,压力的分布可以用以下公式表示:\[ P = \rho \cdot g \cdot h \]其中,P为压力,ρ为流体密度,g为重力加速度,h为流体的高度。
2. 流体动力学公式。
在流体运动时,流体的速度场可以用以下公式表示:\[ \frac{Dv}{Dt} = -\frac{1}{\rho} \cdot \nabla P + g \]其中,Dv/Dt表示速度的变化率,ρ为流体密度,∇P为压力的梯度,g为重力加速度。
3. 纳维-斯托克斯方程。
描述了流体运动的基本规律,可以用以下形式表示:\[ \rho \cdot \frac{Dv}{Dt} = -\nabla P + \mu \cdot \nabla^2 v + \rho \cdot g \]其中,μ为流体的动力粘度,∇^2v为速度的散度。
4. 伯努利方程。
描述了流体在不同位置之间的能量转换关系,可以用以下公式表示:\[ P + \frac{1}{2} \cdot \rho \cdot v^2 + \rho \cdot g \cdot h = \text{常数} \]其中,P为压力,ρ为流体密度,v为流体速度,h为流体的高度。
5. 应力张量。
描述了流体内部的应力分布情况,可以用以下矩阵表示:\[ \tau = \begin{bmatrix} \tau_{xx} & \tau_{xy} & \tau_{xz} \\ \tau_{yx} &\tau_{yy} & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & \tau_{zz} \end{bmatrix} \] 其中,τ为应力张量,下标表示不同方向上的应力分量。
计算流体力学教案第一章:计算流体力学简介1.1 课程目标了解计算流体力学的基本概念理解计算流体力学的发展历程掌握计算流体力学的应用领域1.2 教学内容计算流体力学的定义和发展历程计算流体力学的应用领域计算流体力学的方法和步骤1.3 教学方法讲授基本概念和理论知识展示相关实例和应用领域引导学生进行实际操作和思考1.4 教学资源教材和参考书目相关软件和工具网络资源和案例研究1.5 教学评估课堂讨论和问题解答练习题和作业项目研究和报告2.1 课程目标掌握流体力学的基本原理和定律理解流体的性质和行为分析流体的流动和压力分布2.2 教学内容流体的定义和分类流体力学的基本原理和定律流体的性质和行为流体的流动和压力分布2.3 教学方法讲授基本原理和定律进行数值分析和实例解析引导学生进行实验观察和数据分析2.4 教学资源教材和参考书目相关软件和工具实验设备和仪器2.5 教学评估课堂提问和问题解答练习题和作业实验报告和数据分析3.1 课程目标掌握数值方法的基本原理和技巧理解数值方法的适用范围和限制分析数值方法的准确性和稳定性3.2 教学内容数值方法的定义和分类数值方法的原理和技巧数值方法的适用范围和限制数值方法的准确性和稳定性3.3 教学方法讲授数值方法的基本原理和技巧进行数值分析和实例解析引导学生进行实验观察和数据分析3.4 教学资源教材和参考书目相关软件和工具实验设备和仪器3.5 教学评估课堂提问和问题解答练习题和作业实验报告和数据分析第四章:计算流体力学软件介绍4.1 课程目标掌握计算流体力学软件的基本操作和功能理解计算流体力学软件的适用范围和限制分析计算流体力学软件的准确性和稳定性4.2 教学内容计算流体力学软件的定义和分类计算流体力学软件的基本操作和功能计算流体力学软件的适用范围和限制计算流体力学软件的准确性和稳定性4.3 教学方法讲授计算流体力学软件的基本操作和功能进行数值分析和实例解析引导学生进行实验观察和数据分析4.4 教学资源教材和参考书目相关软件和工具实验设备和仪器4.5 教学评估课堂提问和问题解答练习题和作业实验报告和数据分析第五章:计算流体力学应用实例分析5.1 课程目标掌握计算流体力学在实际工程中的应用理解计算流体力学在不同领域的应用案例分析计算流体力学的优势和局限性5.2 教学内容计算流体力学在工程中的应用领域计算流体力学应用案例分析计算流体力学的优势和局限性5.3 教学方法讲授计算流体力学在工程中的应用领域分析计算流体力学应用案例引导学生进行讨论和思考5.4 教学资源教材和参考书目相关软件和工具实际工程案例和数据5.5 教学评估课堂讨论和问题解答练习题和作业项目研究和报告第六章:有限元方法在计算流体力学中的应用理解有限元方法的基本原理和步骤掌握有限元方法在计算流体力学中的应用分析有限元方法的优缺点6.2 教学内容有限元方法的定义和发展历程有限元方法的基本原理和步骤有限元方法在计算流体力学中的应用有限元方法的优缺点6.3 教学方法讲授有限元方法的基本原理和步骤通过实例分析有限元方法在计算流体力学中的应用引导学生进行实验操作和数据分析6.4 教学资源教材和参考书目有限元软件和工具实验设备和仪器6.5 教学评估课堂提问和问题解答练习题和作业实验报告和数据分析第七章:边界层理论和湍流模型理解边界层理论的基本概念掌握湍流模型的发展和应用分析不同湍流模型的特点和适用条件7.2 教学内容边界层理论的基本概念和方程湍流模型的定义和发展常用湍流模型的特点和适用条件边界层理论和湍流模型的关系7.3 教学方法讲授边界层理论的基本概念和方程分析不同湍流模型的特点和适用条件通过实例讲解湍流模型的应用7.4 教学资源教材和参考书目相关软件和工具实验设备和仪器7.5 教学评估课堂讨论和问题解答练习题和作业实验报告和数据分析第八章:多相流和反应流计算理解多相流和反应流的基本概念掌握多相流和反应流的计算方法分析多相流和反应流计算的挑战和限制8.2 教学内容多相流和反应流的定义和分类多相流和反应流的计算方法多相流和反应流计算的挑战和限制多相流和反应流计算的应用领域8.3 教学方法讲授多相流和反应流的基本概念和分类分析多相流和反应流的计算方法通过实例讲解多相流和反应流计算的应用8.4 教学资源教材和参考书目相关软件和工具实验设备和仪器8.5 教学评估课堂讨论和问题解答练习题和作业实验报告和数据分析第九章:计算流体力学的优化和并行计算理解计算流体力学优化的基本概念掌握计算流体力学并行计算的方法和技术分析计算流体力学优化和并行计算的优势和限制9.2 教学内容计算流体力学优化的定义和方法计算流体力学并行计算的基本概念和技术计算流体力学优化和并行计算的应用领域计算流体力学优化和并行计算的优势和限制9.3 教学方法讲授计算流体力学优化的基本概念和方法分析计算流体力学并行计算的方法和技术通过实例讲解计算流体力学优化和并行计算的应用9.4 教学资源教材和参考书目相关软件和工具实验设备和仪器9.5 教学评估课堂讨论和问题解答练习题和作业实验报告和数据分析第十章:计算流体力学的未来发展方向了解计算流体力学当前的研究热点掌握计算流体力学的发展趋势分析计算流体力学在未来的应用前景10.2 教学内容计算流体力学当前的研究热点计算流体力学的发展趋势计算流体力学在未来的应用前景10.3 教学方法讲授计算流体力学当前的研究热点和发展趋势引导学生进行思考和讨论分析计算流体力学在未来的应用前景10.4 教学资源教材和参考书目相关研究报告和论文网络资源和案例研究10.5 教学评估重点和难点解析1. 计算流体力学简介难点解析:流体力学的基本原理和定律的理解,流体的性质和行为的分析,流体的流动和压力分布的计算。
工艺专业塔器水力学计算设计导则在工艺专业中,塔器是常见的设备之一,其用于气体和液体的传质和传热操作。
水力学计算是塔器设计中重要的一环,它涉及流体在塔器内的流动及其性能参数的计算。
本文将介绍工艺专业塔器水力学计算的设计导则。
首先,在塔器水力学计算中,需要确定流体在塔器内的流动方式。
常见的塔器流动方式包括乘法和分流两种情况。
在乘法流动中,流体从上至下依次通过各层填料或板片区域;在分流流动中,流体从上至下分流通过不同的路径。
根据不同的情况选择适当的流动方式,对塔器的设计和性能有着重要的影响。
其次,水力学计算中的重要参数包括液体和气体的流量、压力损失、液体分布以及气液接触面积等。
流量是指单位时间内流过给定截面的液体或气体的体积,可以通过实验测定或计算方法进行估算。
压力损失是指流体在通过塔器时由于阻力而损失的压力,可以利用经验公式或数值模拟方法进行计算。
液体分布是指流体在塔器内各个截面上的分布情况,其均匀性对传质和传热效果有着重要的影响。
气液接触面积是指气体与液体接触的表面积,其越大,传质和传热效果越好。
另外,在水力学计算中,填料或板片的选择和设计也是关键的一步。
填料或板片的选择应考虑到其对流体流动的影响以及材料的耐腐蚀性能。
常见的填料形式有环形填料、层状填料和网状填料等,其选择应根据具体的工艺要求和设计参数进行。
填料或板片的设计应考虑到填料高度、表面积和孔隙度等因素,以达到较好的传质和传热效果。
最后,在水力学计算中,还需要考虑流动的稳定性和流体在塔器内的过流速度等因素。
流动的稳定性是指流体在塔器内是否容易产生不稳定现象,如波动、涡旋等。
通过减小压力损失、优化流道结构和控制流体流动参数,可以提高流动的稳定性。
过流速度是指流体在塔器内的流动速度,过大的过流速度可能导致阻力增大、压力损失加大以及流动的不稳定。
综上所述,工艺专业塔器水力学计算设计导则包括确定流动方式、计算重要参数、选择和设计填料或板片以及考虑流动的稳定性和过流速度等因素。
(四)流体力学验算(塔板校核) 1.计算气体通过塔板压降h P ,教材172页式(7-63)、式(7-64)、式(7-65) 校核p h 是否符合要求:常压、加压塔水柱mm h p 54~27=;减压塔水柱mm h p 20=左右 2.淹塔(液泛)验算液泛有两种形式:降液管液泛和夹带液泛(过量的液沫夹带) 设计中防止液泛的方法:先以不发生过量液沫夹带为原则,限定气速,再校核降液管截面积是否足够。
为防止液泛,在设计时应使: )(W T d h H H +≤φ教材173页式(7-66)、式(7-67)式(7-68)、式(7-69) 3.雾沫(液沫)夹带验算 教材173页式(7-70)在下列泛点率数值范围内,一般可保证雾沫夹带量达到规定指标,即V e 小于0.1㎏液体/㎏气体:大塔 泛点率<80% 直径0.9m 以下的塔 泛点率<70% 减压塔 泛点率<75% (五)绘制塔板负荷性能图 (教材174页)图7-33 塔板负荷性能图在系统物性、塔板结构尺寸已经确定的条件下,要维持塔的正常操作,必须把气液负荷限制在一定范围内,在以S S L V 、分别为纵、横轴的直角坐标系中,标绘各种界限条件下的关系曲线,从而得到允许的负荷波动范围图形,这个图形即称为塔板的负荷性能图。
(1)雾沫夹带上限线 此线表示雾沫夹带量等于0.1㎏液体/㎏气体时的S S L V -关系 (2)液泛线 液泛线表示降液管内泡沫层高度达到最大允许值时的S S L V 与的关系。
(3)液相负荷上限线液相负荷上限线反映了对于液体在降液管内停留时间的起码要求。
(4)液相负荷下限线一般取堰上的液层高度mm h ow 6=作为液相负荷下限条件。
低于此值时,便不能保证板上液流的均匀分布,会降低气液接触效果。
(5)气相负荷下限线(泄漏线)此线表明不发生严重漏液现象的最低气相负荷,是一条平行于横轴的直线,塔板的适宜操作区应在此线的上方。
塔的水力学计算手册1.目的与适用围12.塔设备特性13.名词术语和定义14.浮阀/筛孔板式塔盘的设计15.填料塔的设计11.目的与适用围为提高工艺工程师的设计质量,推广计算机应用而编写本手册。
本手册是针对气液传质塔设备中的普遍性问题而编写。
对于某些具体塔设备的数据(比如:某生产流程中针对某塔设备的板效率而采用的计算关联式,或者对于某吸收填料塔的传质单元高度或等板高度而采用的具体计算公式)则未予收入。
本设计手册以应用为主,主要是指导性的计算方法和步骤,并配合相应的计算程序,具体公式及理论推阐可参考有关文献。
2.塔设备特性作为气(汽)、液两相传质用的塔设备,首先必须能使气(汽)、液两相得到充分的接触,以得到较高的传质分离效率。
此外,塔设备还应具有以下一些特点:(1)当气(汽)、液处理量过大(超过设计值)时,仍不致于发生大量的雾沫挟带或液泛等影响正常操作的现象。
(2)当操作波动(设计值的50%~120%)较大时,仍能维持在较高的传质效率下稳定操作,并具有长期连续操作所必须具备的可靠性。
(3)塔压力降尽量小。
(4)结构简单、耗材少、制造和安装容易。
(5)耐腐蚀、不易堵塞。
(6)塔的滞留液量要小。
3.名词术语和定义3.1塔径(tower diameter),DT塔筒体壁直径,见图3.1-(a)。
3.2板间距(tray spacing),H T塔相邻两层塔盘间的距离,见图3.1-(a)。
3.3降液管(downer),DC各层塔盘之间专供液相流体通过的组件,单溢流型塔盘为侧降液管,双溢流型塔盘有侧降液管和中央降液管,三或多溢流型塔盘有侧降液管、偏侧降液管、偏中央降液管及中央降液管。
3.4 降液管顶部宽度(DC top width),Wd弓形降液管面积的弦高。
掠堰另有算法,见图3.1-(a),-(b)。
3.5 降液管底间隙(DC clearance),ho降液管底部边缘至塔盘(或受液盘)之间的距离,见图3.1-(a)。
1 塔器设计概述1.1 石油化工装置中塔器占有很大的比重。
几乎每种工艺流程都存在蒸馏或吸收等分离单元过程,因此塔器设计至关重要。
往往塔器设计的优劣,决定着装置的先进性和经济性,必须给予重视。
1.2 塔器设计与工艺流程设计有着非常密切的关系,亦即塔器的选型和水力学计算与工艺流程的设计计算是结合在一起的。
有时塔器设计影响着分离流程和操作条件的选择。
例如减小蒸馏塔的回流比,能降低能耗,但塔板数增加,对塔器讲就是减小塔径和增加塔高,其中必有一个最经济条件的选择。
又如真空塔或对釜温有要求的蒸馏塔均对压降要求较严,需要选择压降低的板式塔或填料塔,在塔器水力学计算后,压降数据要返回工艺作釜温核算。
1.3 一般工艺流程基本确定后,进行塔器的选型、设计等工作。
塔器设计涉及到工艺、化学工程、设备、仪表、配管等专业。
化学工程专业的任务及与各专业间关系另有说明。
见化学工程专业工作手册H-P0101-96、H-P0301-96。
1.4 随着石油化工和科技的迅猛发展,蒸馏塔从一般的一股进料、二股产品的常规塔发展为多股进料、多侧线,有中间换热的复杂塔。
要求塔的生产能力大、效率高、塔板数多,即大塔径、多程数、高效、低压降等,对塔器设计提出了更高的要求,并推动了塔器设计工作的发展。
1.5 近年来电子计算机的普及和发展,为工艺与塔器设计提供了有力的工具。
我们可应用PROCESS或PRO/Ⅱ等工艺流程模拟软件进行计算,得到塔的最大和最小汽液负荷、密度等数据,以便进行分段的塔的水力学计算,使工艺和塔的水力学计算能同步进行,并作多方案比较,求得最佳设计。
1.6 设计中主要考虑的问题1.6.1 确定工艺流程(尤其是分离流程)通过工艺流程模拟电算,选定最佳切割方案,其中包括多股进料、侧线采出、进料状态和位置等方面的选择。
1.6.2 塔压的设定考虑到物料能自流输送,釜温的限制要求,冷凝器和再沸器采用冷热介质的条件,以及对塔径或塔板数的影响等方面。