人教版九年级数学下册 28.1 第2课时 余弦函数和正切函数 教案设计2

28．1锐角三角函数第2课时 余弦函数和正切函数1．理解余弦、正切的概念；(重点)2．熟练运用锐角三角函数的概念进行有关计算．(重点)一、情境导入教师提问：我们是怎样定义直角三角形中一个锐角的正弦的？为什么可以这样定义？学生回答后教师提出新问题：在上一节课中我们知道，如图所示，在Rt △ABC 中，∠C ＝90°，当锐角∠A 确定时，∠A 的对边与斜边的比就随之确定了．现在我们要问：其他边之间的比是否也确定了呢？为什么？二、合作探究探究点一：余弦函数和正切函数的定义 【类型一】 利用余弦的定义求三角函数值在Rt △ABC 中，∠C ＝90°，AB ＝13，AC ＝12，则cos A ＝( )A.513B.512C.1213D.125解析：∵Rt △ABC 中，∠C ＝90°，AB ＝13，AC ＝12，∴cos A ＝AC AB ＝1213.故选C.方法总结：在直角三角形中，锐角的余弦等于这个角的邻边与斜边的比值．变式训练：见《学练优》本课时练习“课堂达标训练” 第2题 【类型二】 利用正切的定义求三角函数值如图，在边长为1的小正方形组成的网格中，△ABC 的三个顶点均在格点上，则tan A ＝( )A.35B.45C.34D.43解析：在直角△ABC 中，∵∠ABC ＝90°，∴tan A ＝BC AB ＝43.故选D.方法总结：在直角三角形中，锐角的正切等于它的对边与邻边的比值． 变式训练：见《学练优》本课时练习“课堂达标训练” 第5题 探究点二：三角函数的增减性【类型一】 判断三角形函数的增减性随着锐角α的增大，cos α的值( )A ．增大B ．减小C ．不变D ．不确定解析：当角度在0°～90°之间变化时，余弦值随着角度的增大而减小，故选B. 方法总结：当0°＜α＜90°时，cos α的值随着角度的增大(或减小)而减小(或增大)． 【类型二】 比较三角函数的大小sin70°，cos70°，tan70°的大小关系是( )A ．tan70°＜cos70°＜sin70°B ．cos70°＜tan70°＜sin70°C ．sin70°＜cos70°＜tan70°D ．cos70°＜sin70°＜tan70°解析：根据锐角三角函数的概念，知sin70°＜1，cos70°＜1，tan70°＞1.又∵cos70°＝sin20°，正弦值随着角的增大而增大，∴sin70°＞cos70°＝sin20°.故选D.方法总结：当角度在0°≤∠A ≤90°之间变化时，0≤sin A ≤1，0≤cos A ≤1，tan A ≥0. 探究点三：求三角函数值【类型一】 三角函数与圆的综合如图所示，△ABC 内接于⊙O ，AB 是⊙O 的直径，点D 在⊙O 上，过点C 的切线交AD 的延长线于点E ，且AE ⊥CE ，连接CD .(1)求证：DC ＝BC ；(2)若AB ＝5，AC ＝4，求tan ∠DCE 的值．解析：(1)连接OC ，求证DC ＝BC 可以先证明∠CAD ＝∠BAC ，进而证明DC ︵＝BC ︵；(2)由AB ＝5，AC ＝4，可根据勾股定理得到BC ＝3，易证△ACE ∽△ABC ，可以求出CE 、DE 的长，在Rt △CDE 中根据三角函数的定义就可以求出tan ∠DCE 的值．(1)证明：连接OC .∵OA ＝OC ，∴∠OAC ＝∠OCA .∵CE 是⊙O 的切线，∴∠OCE ＝90°.∵AE ⊥CE ，∴∠AEC ＝∠OCE ＝90°，∴OC ∥AE ，∴∠OCA ＝∠CAD ，∴∠CAD ＝∠BAC ，∴DC ︵＝BC ︵.∴DC ＝BC ；(2)解：∵AB 是⊙O 的直径，∴∠ACB ＝90°，∴BC ＝AB 2－AC 2＝52－42＝3.∵∠CAE＝∠BAC ，∠AEC ＝∠ACB ＝90°，∴△ACE ∽△ABC ，∴EC BC ＝AC AB ，即EC 3＝45，EC ＝125.∵DC ＝BC ＝3，∴ED ＝DC 2－CE 2＝32－（125）2＝95，∴tan ∠DCE ＝ED EC ＝95125＝34.方法总结：证明圆的弦相等可以转化为证明弦所对的弧相等．利用圆的有关性质，寻找或构造直角三角形来求三角函数值，遇到比较复杂的问题时，可通过全等或相似将线段进行转化．变式训练：见《学练优》本课时练习“课后巩固提升” 第5题【类型二】 利用三角形的边角关系求三角函数值如图，△ABC 中，AD ⊥BC ，垂足是D ，若BC ＝14，AD ＝12，tan ∠BAD ＝34，求sin C 的值．解析：根据tan ∠BAD ＝34，求得BD 的长．在直角△ACD 中由勾股定理可求AC 的长，然后利用正弦的定义求解．解：∵在直角△ABD 中，tan ∠BAD ＝BD AD ＝34，∴BD ＝AD ·tan ∠BAD ＝12×34＝9，∴CD＝BC －BD ＝14－9＝5，∴AC ＝AD 2＋CD 2＝122＋52＝13，∴sin C ＝AD AC ＝1213.方法总结：在不同的直角三角形中，要根据三角函数的定义，分清它们的边角关系，结合勾股定理是解答此类问题的关键．变式训练：见《学练优》本课时练习“课后巩固提升”第9题 三、板书设计1．余弦函数的定义；2．正切函数的定义；3．锐角三角函数的增减性．在数学学习中，有一些学生往往不注重基本概念、基础知识，认为只要会做题就可以了，结果往往失分于选择题、填空题等一些概念性较强的题目．通过引导学生进行知识梳理，教会学生如何进行知识的归纳、总结，进一步帮助学生理解、掌握基本概念和基础知识.。

28．1锐角三角函数第2课时 余弦函数和正切函数1．理解余弦、正切的概念；(重点)2．熟练运用锐角三角函数的概念进行有关计算．(重点)一、情境导入教师提问：我们是怎样定义直角三角形中一个锐角的正弦的？为什么可以这样定义？学生回答后教师提出新问题：在上一节课中我们知道，如图所示，在Rt △ABC 中，∠C ＝90°，当锐角∠A 确定时，∠A 的对边与斜边的比就随之确定了．现在我们要问：其他边之间的比是否也确定了呢？为什么？二、合作探究探究点一：余弦函数和正切函数的定义 【类型一】 利用余弦的定义求三角函数值在Rt △ABC 中，∠C ＝90°，AB ＝13，AC ＝12，则cos A ＝( )A.513B.512C.1213D.125解析：∵Rt △ABC 中，∠C ＝90°，AB ＝13，AC ＝12，∴cos A ＝AC AB ＝1213.故选C.方法总结：在直角三角形中，锐角的余弦等于这个角的邻边与斜边的比值．变式训练：见《学练优》本课时练习“课堂达标训练” 第2题 【类型二】 利用正切的定义求三角函数值如图，在边长为1的小正方形组成的网格中，△ABC 的三个顶点均在格点上，则tan A ＝( )A.35B.45C.34D.43解析：在直角△ABC 中，∵∠ABC ＝90°，∴tan A ＝BC AB ＝43.故选D.方法总结：在直角三角形中，锐角的正切等于它的对边与邻边的比值． 变式训练：见《学练优》本课时练习“课堂达标训练” 第5题 探究点二：三角函数的增减性【类型一】 判断三角形函数的增减性随着锐角α的增大，cos α的值( )A ．增大B ．减小C ．不变D ．不确定解析：当角度在0°～90°之间变化时，余弦值随着角度的增大而减小，故选B. 方法总结：当0°＜α＜90°时，cos α的值随着角度的增大(或减小)而减小(或增大)． 【类型二】 比较三角函数的大小sin70°，cos70°，tan70°的大小关系是( )A ．tan70°＜cos70°＜sin70°B ．cos70°＜tan70°＜sin70°C ．sin70°＜cos70°＜tan70°D ．cos70°＜sin70°＜tan70°解析：根据锐角三角函数的概念，知sin70°＜1，cos70°＜1，tan70°＞1.又∵cos70°＝sin20°，正弦值随着角的增大而增大，∴sin70°＞cos70°＝sin20°.故选D.方法总结：当角度在0°≤∠A ≤90°之间变化时，0≤sin A ≤1，0≤cos A ≤1，tan A ≥0. 探究点三：求三角函数值【类型一】 三角函数与圆的综合如图所示，△ABC 内接于⊙O ，AB 是⊙O 的直径，点D 在⊙O 上，过点C 的切线交AD 的延长线于点E ，且AE ⊥CE ，连接CD .(1)求证：DC ＝BC ；(2)若AB ＝5，AC ＝4，求tan ∠DCE 的值．解析：(1)连接OC ，求证DC ＝BC 可以先证明∠CAD ＝∠BAC ，进而证明DC ︵＝BC ︵；(2)由AB ＝5，AC ＝4，可根据勾股定理得到BC ＝3，易证△ACE ∽△ABC ，可以求出CE 、DE 的长，在Rt △CDE 中根据三角函数的定义就可以求出tan ∠DCE 的值．(1)证明：连接OC .∵OA ＝OC ，∴∠OAC ＝∠OCA .∵CE 是⊙O 的切线，∴∠OCE ＝90°.∵AE ⊥CE ，∴∠AEC ＝∠OCE ＝90°，∴OC ∥AE ，∴∠OCA ＝∠CAD ，∴∠CAD ＝∠BAC ，∴DC ︵＝BC ︵.∴DC ＝BC ；(2)解：∵AB 是⊙O 的直径，∴∠ACB ＝90°，∴BC ＝AB 2－AC 2＝52－42＝3.∵∠CAE＝∠BAC ，∠AEC ＝∠ACB ＝90°，∴△ACE ∽△ABC ，∴EC BC ＝AC AB ，即EC 3＝45，EC ＝125.∵DC ＝BC ＝3，∴ED ＝DC 2－CE 2＝32－（125）2＝95，∴tan ∠DCE ＝ED EC ＝95125＝34.方法总结：证明圆的弦相等可以转化为证明弦所对的弧相等．利用圆的有关性质，寻找或构造直角三角形来求三角函数值，遇到比较复杂的问题时，可通过全等或相似将线段进行转化．变式训练：见《学练优》本课时练习“课后巩固提升” 第5题【类型二】 利用三角形的边角关系求三角函数值如图，△ABC 中，AD ⊥BC ，垂足是D ，若BC ＝14，AD ＝12，tan ∠BAD ＝34，求sin C 的值．解析：根据tan ∠BAD ＝34，求得BD 的长．在直角△ACD 中由勾股定理可求AC 的长，然后利用正弦的定义求解．解：∵在直角△ABD 中，tan ∠BAD ＝BD AD ＝34，∴BD ＝AD ·tan ∠BAD ＝12×34＝9，∴CD＝BC －BD ＝14－9＝5，∴AC ＝AD 2＋CD 2＝122＋52＝13，∴sin C ＝AD AC ＝1213.方法总结：在不同的直角三角形中，要根据三角函数的定义，分清它们的边角关系，结合勾股定理是解答此类问题的关键．变式训练：见《学练优》本课时练习“课后巩固提升”第9题 三、板书设计1．余弦函数的定义；2．正切函数的定义；3．锐角三角函数的增减性．在数学学习中，有一些学生往往不注重基本概念、基础知识，认为只要会做题就可以了，结果往往失分于选择题、填空题等一些概念性较强的题目．通过引导学生进行知识梳理，教会学生如何进行知识的归纳、总结，进一步帮助学生理解、掌握基本概念和基础知识.。

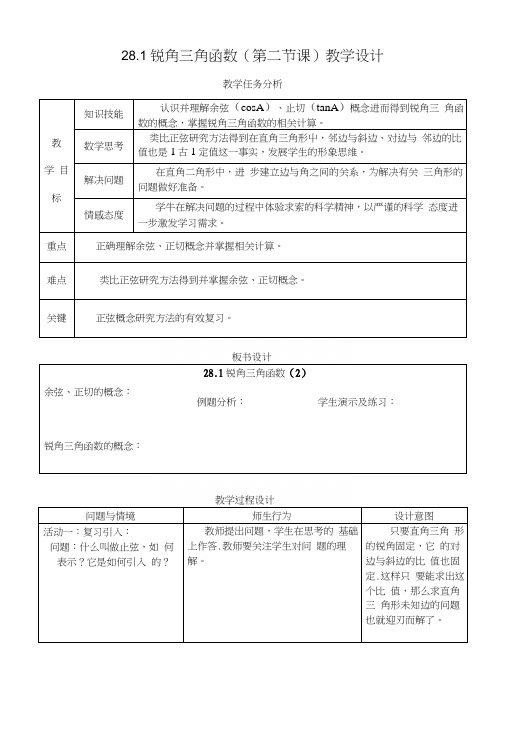
28.1锐角三角函数（第二节课）教学设计教学任务分析教学目标知识技能认识并理解余弦（cosA）、止切（tanA）概念进而得到锐角三角函数的概念，掌握锐角三角函数的相关计算。

数学思考类比正弦研究方法得到在直角三角形屮，邻边与斜边、对边与邻边的比值也是1古1定值这一事实，发展学生的形象思维。

解决问题在直角二角形中，进步建立边与角之间的关系，为解决有关三角形的问题做好准备。

情感态度学牛在解决问题的过程中体验求索的科学精神，以严谨的科学态度进一步激发学习需求。

重点正确理解余弦、正切概念并掌握相关计算。

难点类比正弦研究方法得到并掌握余弦、正切概念。

关键正弦概念研究方法的有效复习。

板书设计余弦、正切的概念：28.1锐角三角函数（2）例题分析：学生演示及练习：锐角三角函数的概念：教学过程设计问题与情境师生行为设计意图活动一：复习引入：问题：什么叫做止弦，如何表示？它是如何引入的？教师提出问题，学生在思考的基础上作答.教师要关注学生对问题的理解。

只要直角三角形的锐角固定，它的对边与斜边的比值也固定.这样只要能求出这个比值，那么求直角三角形未知边的问题也就迎刃而解了。

口答:(1)如图，平面直角坐标 系中，若点P 坐标为(3, 4),则 cosPOQ 二 _____________ ; tan ZP0Q 二 _________ . (2)如图,AABC 中一边 BC 与以AC 为直径的相 切与点C,若BC 二4, AB=5, cosB 二 _________ ; tanA= ___ .问题与情境活动二：探究活动： 如图，在RtAABC 中， ZC=90°,当锐角A 确定 时，ZA 的对边与斜边的比 就随之确定，此时，其他边 之间的比是否也确定了 呢？为什么？师生行为 教师提出问题后，学生认真思 考，若仍不能回答，教师要引导学 生类比上节课的方法(由特殊到一 般的思想)，并沿着正弦的研究轨 迹，学生先研究特殊的30度，45 度角，再用儿何画板研究更一般的 角度，最后用图形的相似论证。

九年级数学下28.1.2余弦、正切函数学案（人教版）28.1.2 余弦、正切函数学案一、新课导入题导入问题：在Rt△ABC中，当锐角A确定时，∠A的对边与斜边的比随之确定.∠A的邻边与斜边的比呢？∠A的对边与邻边的比呢？这节课我们学习余弦和正切.（板书课题）2.学习目标（1）了解锐角三角函数的概念，理解余弦、正切的概念.（2）能依据正弦、余弦、正切的定义进行相关的计算学习重、难点重点：余弦、正切的概念.难点：余弦、正切的求值.二、分层学习第一层次学习1.自学指导（1）自学内容：教材P64探究.（2）自学时间：8分钟.（3）自学方法：完成探究提纲.（4）探究提纲：①∠A是任一个确定的锐角时，是一个固定值, 与三角形的大小无关，那么也是一个固定值吗？呢？②在Rt△ABC 中，∠C=90°，叫做∠A的余弦，记作 cosA ，即cosA③在Rt△ABC 中，∠C=90°，叫做∠A的正切，记作 tanA ，即tanA④锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数 .2.自学：学生可结合自学指导进行自学助学（1）师助生：①明了学情：明了学生是否能弄清正弦、余弦、正切分别表示直角三角形中哪两条边的比.②差异指导：结合图形理解三个三角函数的意义.（2）生助生：小组相互交流、研讨强化：余弦、正切的求值.第二层次学习1.自学指导（1）自学内容：教材P65例2.（2）自学时间：5分钟.（3）自学方法：完成自学参考提纲.④在Rt△ABC 中，∠C=90°，如果各边长都扩大到原来的2倍，那么∠A的正弦、余弦和正切值有变化吗？说明理由∠A的正弦、余弦和正切值没有变化.理由：锐角三角函数值与三角形大小无关.2.自学：学生可结合自学指导进行自学助学（1）师助生：①明了学情：明了学生是否能弄清正弦、余弦、正切分别表示直角三角形中哪两条边的比.②差异指导：根据学情分类指导.（2）生助生：小组内相互交流、研讨强化：（1）已知直角三角形任意两边长，求其锐角的三角函数值问题：可先由勾股定理求出第三条边长，再按三角函数定义求值.（2）点3名学生板演自学参考提纲第②、③题，点1名学生口答自学参考提纲第④题，并点评.三、评价1.学生自我评价:这节课你学到了哪些知识？还有什么问题未解决？2.教师对学生的评价：（1）表现性评价:从学生学习、交流协作以及回答问题等方面进行评价.（2）纸笔评价:课堂评价检测教师的自我评价（教学反思）.本节课的引入采用探究的形式.首先引导学生认知特殊角的余弦、正切，进而引出锐角三角函数的定义.通过作图、猜想论证，配合由浅入深的练习，使学生不但知道对任意给定锐角，它的余弦、正切值是固定值，而且加以论证并会运用.在教学过程中逐步培养学生观察、比较、分析、概括的思维能力，提高学生对几何图形美的认识，感受三角函数的实际应用价值作业评价一、基础巩固（70分）1.(10分)在Rt△ABC中，∠C=90°，∠A、∠B、∠C 所对的边分别为a、b、c，则下列等式中不正确的是（D）A.a=c×sinAB.b=a×tanBC.b=c×sinBD2.(10分)如图，将∠AOB放置在5×5的正方形网格中，则cos∠AOB的值是（C）（C）3.(30分)分别求出下列各图中的∠A、∠B的余弦和正切值.4.(10分)在Rt△ABC中，∠C＝90°，BC＝5，cosA＝，求sinA, tanB的值.解：sinA= , tanB(10分)如图，已知AB是⊙O的直径，点C、D在⊙O上，且AB＝5，sinB= ．求cosD，tanD的值.二、综合应用（20分）6.(10分)如图，在等腰△ABC中,AB=AC=5,BC=6.求sinB,cosB,tanB的值.解：作AD⊥BC于D.∵AB=AC=5，∴BD=DC= B∴在Rt△ABD 中，AD= =4,∴sinB= ,cosB= ,tanB（10分）如图，点P 在∠α的边OA上，且P点坐标为( ，5)．求sinα，cosα和tanα的值.解：sinα= ，cosα= ,tanα三、拓展延伸（10分） 8.(10分) 在Rt△ABC中，∠C＝90°，请利用锐角三角函数的定义及勾股定理探索∠A的正弦、余弦之间的关系。

部审人教版九年级数学下册教学设计28.1 第2课时《余弦函数和正切函数》一. 教材分析人教版九年级数学下册第28.1节《余弦函数和正切函数》是本册教材的重要内容，主要介绍了余弦函数和正切函数的定义、性质及其应用。

通过本节课的学习，学生能够掌握余弦函数和正切函数的基本概念，理解它们的图象和性质，并能运用它们解决实际问题。

本节课的内容为后续学习三角函数的复合函数、三角恒等式等奠定了基础。

二. 学情分析九年级的学生已经学习了函数、三角函数等基本知识，具备一定的数学基础。

但学生在学习过程中，对余弦函数和正切函数的理解和应用仍有困难。

因此，在教学过程中，教师需要关注学生的学习需求，针对学生的薄弱环节进行有针对性的教学，帮助学生克服困难，提高学生的数学素养。

三. 教学目标1.知识与技能目标：让学生掌握余弦函数和正切函数的定义、性质及其应用；2.过程与方法目标：通过观察、分析、归纳等方法，培养学生研究函数问题的能力；3.情感态度与价值观目标：激发学生学习数学的兴趣，培养学生的团队合作意识，使学生在学习过程中体验到成功的喜悦。

四. 教学重难点1.重点：余弦函数和正切函数的定义、性质及其应用；2.难点：余弦函数和正切函数图象的绘制及其性质的推导。

五. 教学方法1.情境教学法：通过生活实例引入余弦函数和正切函数的概念，激发学生的学习兴趣；2.启发式教学法：在讲解过程中，引导学生主动思考、提问，提高学生的参与度；3.小组合作学习：引导学生分组讨论、探究，培养学生的团队合作意识；4.案例教学法：通过典型例题的讲解，使学生掌握余弦函数和正切函数的应用。

六. 教学准备1.准备相关教学课件、PPT等教学资料；2.准备典型例题和练习题；3.准备黑板、粉笔等教学工具；4.提前布置预习任务，让学生预习本节课的内容。

七. 教学过程1.导入（5分钟）教师通过生活实例引入余弦函数和正切函数的概念，激发学生的学习兴趣。

例如，讲解旋转物体在某一角度时的速度、加速度等物理量的变化，引导学生思考这些变化与什么因素有关。

义务教育学校课时教案备课时间：上课时间：课题第二十八章锐角三角函数28.1锐角三角函数第2课时余弦和正切主备人教学目标知识与能力：1.理解余弦、正切的概念，了解锐角三角函数的定义；2.能运用余弦、正切的定义解决问题.过程与方法：逐步培养学生观察、分析、类比、概括的思维能力.情感态度与价值观：在探索结论的过程中，体验探索的乐趣，增强数学学习的信心，感受成功的快乐.德育渗透德育范畴实施建议（具体策略）探索精神通过正弦的学习，鼓励学生自主探究余弦和正切，激发学生学习数学的热情。

教学重点掌握余弦、正切的概念，并能运用它们解决具体问题. 教学难点灵活运用三角函数的有关定义进行计算.学情分析教学过程一、新课导入问题我们是如何得到锐角正弦的概念的？二、推进新课知识点1 余弦、正切的定义探究在Rt△ABC中，当锐角A确定时，∠A的对边与斜边的比随之确定.那∠A的邻边与斜边的比呢？∠A的对边与邻边的比呢？猜想：∠A邻边与斜边的比、对边与邻边的比都是定值.探究：任意画 Rt△ABC 和 Rt△A'B'C'，使得∠C =∠C'=90°．∠A=∠A'，那么ACAB=A CA B''''、BCAC=B CA C''''？时间分配二次备课【归纳结论】余弦：在Rt △ABC 中，∠C =90°，我们把锐角A 的邻边与斜边的比叫做∠A 的余弦，记作cosA ，即cosA =A bc∠的对边＝斜边正切：在RtAABC 中，∠C =90°，我们把锐角A 的对边与邻边的比叫做∠A 的正切，记作tanA ，tanA =A aA b∠的对边＝∠的邻边.锐角A 的正弦、余弦、正切叫做∠A 的锐角三角函数. 练习：1.如图，在Rt △ABC 中，∠C ＝90°，BC ＝6，sinA ＝53， 求cosA 、tanB 的值．知识点2 运用正弦、余弦定义求值例 如图，在 Rt △ABC 中，∠C=90°，AB=10，BC=6，求 sinA ，cosA ，tanA 的值. 思考：若条件不变，你能求出sinB ，cosB ，tanB 的值吗？ 观察前面的结果，你有什么发现？ 若∠A +∠ B = 90°，则sinA = cosB ，tanA ·tanB=1. 练习：1.分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值．2.在Rt △ABC 中，∠C=90°，如果各边长都扩大到原来的2倍，那么∠A 的正弦值、余弦值和正切值有什么变化？ 三、随堂演练1.在Rt △ABC 中，∠C=90°，∠A 、∠B 、∠C 所对的边分别为a 、b 、c ，则下列等式中不正确的是（ ）2.如图，将∠AOB放置在5×5的正方形网格中，则cos∠AOB的值是（）3.如图，在等腰△ABC中，AB=AC=5，BC=6.求sinB,cosB,tanB的值.四、课堂小结板书设计第二十八章锐角三角函数28.1锐角三角函数第2课时余弦和正切作业设计与布置作业类型作业内容试做时长基础性作业基本性作业（必做）习题28.1第一题求余弦值和正切值鼓励性作业（选择）习题28.1第二题第二问、第三问挑战性作业（选择）练习册拓展性作业无作业反馈记录教学反思。

九年级数学下28.1.2余弦、正切函数学案（人教版）1.2余弦、正切函数学案一、新课导入课题导入问题：在Rt△ABc中，当锐角A确定时，∠A的对边与斜边的比随之确定.∠A的邻边与斜边的比呢？∠A的对边与邻边的比呢？这节课我们学习余弦和正切.学习目标了解锐角三角函数的概念，理解余弦、正切的概念.能依据正弦、余弦、正切的定义进行相关的计算.学习重、难点重点：余弦、正切的概念.难点：余弦、正切的求值.二、分层学习层次学习自学指导自学内容：教材P64探究.自学时间：8分钟.自学方法：完成探究提纲.探究提纲：①∠A是任一个确定的锐角时，是一个固定值,与三角形的大小无关，那么也是一个固定值吗？呢？②在Rt△ABc中，∠c=90°，叫做∠A的余弦，记作cosA，即cosA=.③在Rt△ABc中，∠c=90°，叫做∠A的正切，记作tanA，即tanA=.④锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.自学：学生可结合自学指导进行自学.助学师助生：①明了学情：明了学生是否能弄清正弦、余弦、正切分别表示直角三角形中哪两条边的比.②差异指导：结合图形理解三个三角函数的意义.生助生：小组相互交流、研讨.强化：余弦、正切的求值.第二层次学习自学指导自学内容：教材P65例2.自学时间：5分钟.自学方法：完成自学参考提纲.④在Rt△ABc中，∠c=90°，如果各边长都扩大到原来的2倍，那么∠A的正弦、余弦和正切值有变化吗？说明理由∠A的正弦、余弦和正切值没有变化.理由：锐角三角函数值与三角形大小无关.自学：学生可结合自学指导进行自学.助学师助生：①明了学情：明了学生是否能弄清正弦、余弦、正切分别表示直角三角形中哪两条边的比.②差异指导：根据学情分类指导.生助生：小组内相互交流、研讨.强化：已知直角三角形任意两边长，求其锐角的三角函数值问题：可先由勾股定理求出第三条边长，再按三角函数定义求值.点3名学生板演自学参考提纲第②、③题，点1名学生口答自学参考提纲第④题，并点评.三、评价学生自我评价:这节课你学到了哪些知识？还有什么问题未解决？教师对学生的评价：表现性评价:从学生学习、交流协作以及回答问题等方面进行评价.纸笔评价:课堂评价检测.教师的自我评价.本节课的引入采用探究的形式.首先引导学生认知特殊角的余弦、正切，进而引出锐角三角函数的定义.通过作图、猜想论证，配合由浅入深的练习，使学生不但知道对任意给定锐角，它的余弦、正切值是固定值，而且加以论证并会运用.在教学过程中逐步培养学生观察、比较、分析、概括的思维能力，提高学生对几何图形美的认识，感受三角函数的实际应用价值作业评价一、基础巩固在Rt△ABc中，∠c=90°，∠A、∠B、∠c所对的边分别为a、b、c，则下列等式中不正确的是A.a=c×sinAB.b=a×tanBc.b=c×sinBD.c=如图，将∠AoB放置在5×5的正方形网格中，则cos∠AoB的值是分别求出下列各图中的∠A、∠B的余弦和正切值.4.在Rt△ABc中，∠c＝90°，Bc＝5，cosA＝，求sinA,tanB的值.解：sinA=,tanB=.如图，已知AB是⊙o的直径，点c、D在⊙o上，且AB ＝5，sinB=．求cosD，tanD的值.二、综合应用如图，在等腰△ABc中,AB=Ac=5,Bc=6.求sinB,cosB,tanB的值.解：作AD⊥Bc于D.∵AB=Ac=5，∴BD=Dc=Bc=3.∴在Rt△ABD中，AD==4,∴sinB=,cosB=,tanB=.如图，点P在∠α的边oA上，且P点坐标为．求sin α，cosα和tanα的值.解：sinα=，cosα=,tanα=.三、拓展延伸在Rt△ABc中，∠c＝90°，请利用锐角三角函数的定义及勾股定理探索∠A的正弦、余弦之间的关系.。

A B CD 锐角三角函数——余弦和正切一、教学目标1、使学生知道当直角三角形的锐角固定时，它的邻边与斜边、对边与邻边的比值也都固定这一事实．2、逐步培养学生观察、比较、分析、概括的思维能力．二、教学重点、难点 重点：理解余弦、正切的概念 难点：熟练运用锐角三角函数的概念进行有关计算 三、教学过程 （一）复习引入 1、口述正弦的定义 2、（1）如图，已知AB 是⊙O 的直径，点C 、D 在⊙O 上，且AB ＝5，BC ＝3．则sin ∠BAC= ；sin ∠ADC= ．（2）﹙2006成都﹚如图，在Rt △ABC 中，∠ACB ＝90°，CD ⊥AB 于点D 。

已知AC= 5 ，BC=2，那么sin ∠ACD ＝（ ） A3 B ．23 C5D2（二）实践探索一般地，当∠A 取其他一定度数的锐角时，它的邻边与斜边的比是否也是一个固定值？如图：Rt △ABC 与Rt △A`B`C`，∠C=∠C` =90o ，∠B=∠B`=α， 那么与有什么关系？分析：由于∠C=∠C` =90o ，∠B=∠B`=α，所以Rt △ABC ∽Rt △A`B`C`，，即结论：在直角三角形中，当锐角B 的度数一定时，不管三角形的大小如何，∠B 的邻边与斜边的比也是一个固定值。

如图，在Rt △ABC 中，∠C=90o ，把锐角B 的邻边与斜边的比叫做∠B 的余弦，记作cosB 即把∠A 的对边与邻边的比叫做∠A 的正切.记作tanA,即锐角A 的正弦,余弦,正切都叫做∠A 的锐角三角函数.（三）教学互动例2:如图,在中, ,BC=6, 求cos 和tan 的值.B解: ,又例3:(1)如图(1), 在中，,,,求的度数. (2)如图(2),已知圆锥的高AO等于圆锥的底面半径OB 的倍,求.（四）巩固再现1.在中，∠C＝90°，a，b，c分别是∠A、∠B、∠C 的对边，则有（）A ．B ．C ．D．2. 在中，∠C ＝90°，如果那么的值为（）A ．B ．C ．D ．3、如图：P是∠的边OA上一点，且P点的坐标为（3，4），则cos＝_____________.4、P67 练习1、2四、布置作业教后反思：2。