必修三第一章算法初步学案

第1课时辗转相除法与更相减损术、秦九韶算法1．理解辗转相除法与更相减损术的含义，了解其执行过程．2．理解秦九韶算法的计算过程，并了解它提高计算效率的实质．1．辗转相除法与更相减损术(1)辗转相除法①辗转相除法，又叫欧几里得算法，是一种求两个正整数的最大公约数的古老而有效的算法．②辗转相除法的算法步骤第一步，给定两个正整数m，n.第二步，计算m除以n所得的余数r.第三步，m＝n，n＝r.第四步，若r＝0，则m，n的最大公约数等于m；否则，返回第二步．(2)更相减损术的算法步骤第一步，任意给定两个正整数，判断它们是否都是偶数．若是，用2约简；若不是，执行第二步．第二步，以较大的数减去较小的数，接着把所得的差与较小的数比较，并以大数减小数．继续这个操作，直到所得的数相等为止，则这个数(等数)或这个数与约简的数的乘积就是所求的最大公约数．(3)辗转相除法和更相减损术的区别与联系(1)秦九韶算法简介①秦九韶算法要解决的问题是求多项式的值．②秦九韶算法的特点通过一次式的反复计算，逐步得到高次多项式的值，即将一个n次多项式的求值问题归结为重复计算n个一次多项式的值的问题．③秦九韶算法的原理将f(x)＝a n x n＋a n－1x n－1＋…＋a1x＋a0改写为：f(x)＝(a n x n－1＋a n－1x n－2＋…＋a1)x＋a0＝((a n x n－2＋a n－1x n－3＋…＋a2)x＋a1)x＋a0＝…先计算最内层括号内一次多项式的值，即v1＝a n x＋a n－1，再由内向外逐层计算一次多项式v k的值．(2)秦九韶算法的操作方法①算法步骤如下第一步，输入多项式次数n、最高次项的系数a n和x的值．第二步，将v的值初始化为a n，将i的值初始化为n－1.第三步，输入i次项的系数a i.第四步，v＝vx＋a i，i＝i－1.第五步，判断i是否大于或等于0.若是，则返回第三步；否则，输出多项式的值v.②程序框图如图所示③程序如下INPUT “n＝”；nINPUT “an＝”；aINPUT “x＝”；xv＝ai＝n－1WHILE i＞＝0INPUT “ai＝”；av＝v*x＋ai＝i－1WENDPRINT vEND1．实际应用更相减损术时要做的第一步工作是什么？[提示] 先判断a，b是否为偶数，若是，都除以2再进行．2．判断正误．(正确的打“√”，错误的打“×”)(1)辗转相除法的基本步骤是用较大的数除以较小的数．( )(2)求最大公约数的方法除辗转相除法之外，没有其他方法．( )(3)编写辗转相除法的程序时，要用到循环语句．( )[提示] (1)√(2)×(3)√题型一辗转相除法和更相减损术的应用【典例1】用辗转相除法求612与468的最大公约数，并用更相减损术检验所得结果．[思路导引] 将612作为大数，468作为小数，执行辗转相除法和更相减损术的步骤即可.[解] 用辗转相除法：612＝468×1＋144,468＝144×3＋36,144＝36×4，即612和468的最大公约数是36.用更相减损术检验：612和468为偶数，两次用2约简得153和117,153－117＝36,117－36＝81,81－36＝45,45－36＝9,36－9＝27,27－9＝18,18－9＝9，所以612和468的最大公约数为9×2×2＝36.求最大公约数的两种方法步骤(1)利用辗转相除法求给定的两个数的最大公约数，即利用带余除法，用数对中较大的数除以较小的数，若余数不为零，则将余数和较小的数构成新的数对，再利用带余除法，直到大数被小数除尽，则这时的较小数就是原来两个数的最大公约数．(2)利用更相减损术求两个正整数的最大公约数的一般步骤是：首先判断两个正整数是否都是偶数．若是，用2约简，也可以不除以2，直接求最大公约数，这样不影响最后结果．[针对训练1] 用辗转相除法求80与36的最大公约数，并用更相减损术检验你的结果．[解] 80＝36×2＋8，36＝8×4＋4,8＝4×2＋0，即80与36的最大公约数是4.验证：80÷2＝40,36÷2＝18；40÷2＝20,18÷2＝9；20－9＝11,11－9＝2；9－2＝7,7－2＝5；5－2＝3,3－2＝1；2－1＝1,1×2×2＝4；所以80与36的最大公约数为4.题型二求三个正整数的最大公约数【典例2】求325,130,270三个数的最大公约数[思路导引] 求三个数的最大公约数，可先求两个数的最大公约数，再求这个最大公约数与第三个数的最大公约数．[解] 解法一(辗转相除法)：因为325＝130×2＋65,130＝65×2，所以325和130的最大公约数为65.因为270＝65×4＋10,65＝10×6＋5,10＝5×2,所以65和270的最大公约数为5,故325,130,270三个数的最大公约数为5.解法二(更相减损术)：325－130＝195,195－130＝65,130－65＝65.所以325和130的最大公约数是65.270－65＝205,205－65＝140,140－65＝75,75－65＝10,65－10＝55,55－10＝45,45－10＝35,35－10＝25,25－10＝15,15－10＝5,10－5＝5.所以65和270的最大公约数为5，故325,130,270三个数的最大公约数为5.理解辗转相除法的实质，从计算结果上看，辗转相除法是以相除余数为零而得到结果的.[针对训练2] 求三个数175,100,75的最大公约数.[解] 先求175与100的最大公约数：175＝100×1＋75,100＝75×1＋25,75＝25×3,∴175与100的最大公约数是25.再求25与75的最大公约数：75－25＝50,50－25＝25,∴75和25的最大公约数是25.∴175,100,75的最大公约数是25.题型三秦九韶算法【典例3】已知一个5次多项式为f(x)＝4x5＋2x4＋3.5x3－2.6x2＋1.7x－0.8，用秦九韶算法求这个多项式当x＝5时的值.[思路导引] 可根据秦九韶算法的原理，将所给的多项式改写，然后由内到外逐次计算．[解] 将f(x)改写为f(x)＝((((4x＋2)x＋3.5)x－2.6)x＋1.7)x－0.8，由内向外依次计算一次多项式，当x＝5时的值：v0＝4；v 1＝4×5＋2＝22； v 2＝22×5＋3.5＝113.5； v 3＝113.5×5－2.6＝564.9； v 4＝564.9×5＋1.7＝2826.2； v 5＝2826.2×5－0.8＝14130.2.所以当x ＝5时，多项式的值等于14130.2.(1)用秦九韶算法求多项式f (x )当x ＝x 0的值的思路为： ①改写．②计算⎩⎪⎨⎪⎧v 0＝a n ，v k ＝v k －1x 0＋a n －k (k ＝1，2，…，n ).③结论f (x 0)＝v n .(2)应用秦九韶算法计算多项式的值应注意的3个问题 ①要正确将多项式的形式进行改写． ②计算应由内向外依次计算．③当多项式函数中间出现空项时，要以系数为零的齐次项补充．[针对训练3] 用秦九韶算法计算多项式f (x )＝12＋35x －8x 2＋6x 4＋5x 5＋3x 6在x ＝－4时的值时，v 3的值为( )A ．－144B ．－136C ．－57D ．34[解析] 根据秦九韶算法多项式可化为f (x )＝(((((3x ＋5)x ＋6)x ＋0)x －8)x ＋35)x ＋12.由内向外计算v 0＝3；v 1＝3×(－4)＋5＝－7； v 2＝－7×(－4)＋6＝34； v 3＝34×(－4)＋0＝－136.[答案] B课堂归纳小结1.求两个正整数的最大公约数的问题，可以用辗转相除法，也可以用更相减损术．用辗转相除法，即根据a＝nb＋r这个式子，反复相除，直到r＝0为止；用更相减损术，即根据r＝|a－b|这个式子，反复相减，直到r＝0为止．2.秦九韶算法的关键在于把n次多项式转化为一次多项式，注意体会递推的实现过程，实施运算时要由内向外，一步一步执行．1．辗转相除法可解决的问题是( )A．求两个正整数的最大公约数B．多项式求值C．求两个正整数的最小公倍数D．排序问题[解析] 辗转相除法可以求两个正整数的最大公约数.[答案] A2．用辗转相除法求72与120的最大公约数时，需要做除法次数为( )A．4 B．3C．5 D．6[解析] 120＝72×1＋48,72＝48×1＋24,48＝24×2.[答案] B3．用更相减损术求36与134的最大公约数，第一步应为________．[解析] ∵36与134都是偶数，∴第一步应先除以2，得到18与67.[答案] 先分别除以2，得到18与674．用秦九韶算法求f(x)＝2x3＋x－3当x＝3时的值v2＝________.[解析] f(x)＝((2x＋0)x＋1)x－3，v0＝2，v1＝2×3＋0＝6，v2＝6×3＋1＝19.[答案] 195．用秦九韶算法求多项式f(x)＝8x7＋5x6＋3x4＋2x＋1，当x＝2时的值．[解] 根据秦九韶算法，把多项式改写成如下形式：f(x)＝8x7＋5x6＋0·x5＋3·x4＋0·x3＋0·x2＋2x＋1＝((((((8x＋5)x＋0)x＋3)x＋0)x＋0)x＋2)x＋1.而x＝2，所以有v0＝8，v1＝8×2＋5＝21，v2＝21×2＋0＝42，v3＝42×2＋3＝87，v4＝87×2＋0＝174，v5＝174×2＋0＝348，v6＝348×2＋2＝698，v7＝698×2＋1＝1397.所以当x＝2时，多项式的值为1397.算法案例在实际生活中的应用通过算法案例的学习，知道算法的核心是一般意义上的解决问题的策略的具体化．对于一个实际问题，我们在分析、思考后可将之转化为数学问题，从而获得解决它的基本思路.【典例】现有长度为2.4 m和5.6 m两种规格的钢筋若干，要焊接一批棱上无接点的正方体模型，问怎样设计才能保证正方体的体积最大且不浪费材料？[思路导引] 要焊接正方体，就是将两种规格的钢筋截成长度相等的钢筋条．为了保证不浪费材料，应使得每种规格的钢筋截取后没有剩余，因此截取的长度应为2.4与5.6的公约数；为使得正方体的体积最大，因此截取的长度应为2.4与5.6的最大公约数.[解] 用更相减损术来求2.4与5.6的最大公约数：5．6－2.4＝3.2,3．2－2.4＝0.8,2．4－0.8＝1.6,1．6－0.8＝0.8,因此2.4与5.6的最大公约数为0.8.所以使得正方体的棱长为0.8 m时，正方体的体积最大且不浪费材料.[针对训练] 甲，乙，丙三种溶液的质量分别为147 g，343 g，133 g，现要将它们分别全部装入小瓶中，每个小瓶中装入溶液的质量相同，问每瓶最多装多少？[解] 由题意，每个小瓶中装入的溶液的质量应是三种溶液质量的最大公约数．先求147与343的最大公约数：343－147＝196,196－147＝49,147－49＝98,98－49＝49，所以147与343的最大公约数是49.再求49与133的最大公约数：133－49＝84,84－49＝35,49－35＝14,35－14＝21,21－14＝7,14－7＝7，所以147,343,133的最大公约数为7，即每瓶最多装7 g.课后作业(八)(时间45分钟)学业水平合格练(时间25分钟)1．秦九韶算法与直接计算相比较，下列说法错误的是( )A．秦九韶算法与直接计算相比，大大节省了做乘法的次数，使计算量减少，并且逻辑结构简单B．秦九韶算法减少了做乘法的次数，在计算机上也就加快了计算的速度C．秦九韶算法减少了做乘法的次数，在计算机上也就降低了计算的速度D．秦九韶算法避免了对自变量x单独做幂的计算，而且与系数一起逐次增长幂次，从而提高计算的精度[解析] 秦九韶算法减少了做乘法的次数，在计算机上也就加快了计算的速度，故选项C错误．[答案] C2．下列说法中正确的个数为( )①辗转相除法也叫欧几里得算法；②辗转相除法的基本步骤是用较大的数除以较小的数；③求最大公约数的方法，除辗转相除法之外，没有其他方法；④编写辗转相除法的程序时，要用到循环语句．A．1 B．2C．3 D．4[解析] ①、②、④正确，③错误．[答案] C3．利用秦九韶算法求f(x)＝1＋2x＋3x2＋…＋6x5当x＝2时的值时，下列说法正确的是( )A．先求1＋2×2B．先求6×2＋5，第二步求2×(6×2＋5)＋4C．f(2)＝1＋2×2＋3×22＋4×23＋5×24＋6×25直接运算求解D．以上都不对[解析] 利用秦九韶算法应先算a n x＋a n－1，再算(a n x＋a n－1)x＋a n－2，故选B.[答案] B4．中国古代有计算多项式值的秦九韶算法，下图是实现该算法的程序框图．执行该程序框图，若输入的x＝2，n＝2，依次输入的a为2,2,5，则输出的s＝( )A．7 B．12C．17 D．34[解析] 该题考查程序框图的运行及考生的识图能力．由程序框图知，第一次循环：x＝2，n＝2，a＝2，s＝0×2＋2＝2，k＝1；第二次循环：a＝2，s＝2×2＋2＝6，k＝2；第三次循环：a＝5，s＝6×2＋5＝17，k＝3.结束循环，输出s的值为17，故选C.[答案] C5．用更相减损术求117和182的最大公约数时，需做减法的次数是( )A．8 B．7C．6 D．5[解析] ∵182－117＝65,117－65＝52,65－52＝13,52－13＝39,39－13＝26,26－13＝13，∴13是117和182的最大公约数，需做减法的次数是6.[答案] C6．用秦九韶算法求n次多项式f(x)＝a n x n＋a n－1x n－1＋…＋a1x＋a0当x＝x0时的值，求f(x0)需要乘方、乘法、加法的次数分别为( )A.n(n＋1)2，n，n B．n,2n，nC．0,2n，n D．0，n，n[解析] 因为f(x)＝(…((a n x＋a n－1)x＋a n－2)x＋…＋a1)x＋a0，所以乘方、乘法、加法的次数分别为0，n，n.[答案] D7．用秦九韶算法求多项式f(x)＝12＋35x－8x2＋79x3＋6x4＋5x5＋3x6当x＝－4的值时，其中v1的值为________．[解析] ∵f(x)＝12＋35x－8x2＋79x3＋6x4＋5x5＋3x6，∴v0＝a6＝3，v1＝v0x＋a5＝3×(－4)＋5＝－7.[答案] －78．378和90的最大公约数为________．[解析] 378＝90×4＋18,90＝18×5＋0，∴378与90的最大公约数是18.[答案] 189．求1356和2400的最小公倍数．[解] 2400＝1356×1＋1044，1356＝1044×1＋312，1044＝312×3＋108，312＝108×2＋96，108＝96×1＋12，96＝12×8.所以1356与2400的最大公约数为12.则1356与2400的最小公倍数为(1356×2400)÷12＝271200.10．用秦九韶算法求多项式f(x)＝7x7＋6x6＋5x5＋4x4＋3x3＋2x2＋x当x＝3时的值．[解] f(x)＝((((((7x＋6)x＋5)x＋4)x＋3)x＋2)x＋1)·x，所以v0＝7，v1＝7×3＋6＝27，v2＝27×3＋5＝86，v3＝86×3＋4＝262，v4＝262×3＋3＝789，v5＝789×3＋2＝2369，v6＝2369×3＋1＝7108，v7＝7108×3＝21324.故x＝3时，多项式f(x)＝7x7＋6x6＋5x5＋4x4＋3x3＋2x2＋x的值为21324.应试能力等级练(时间20分钟)11．下列哪组的最大公约数与1855,1120的最大公约数不同( )A．1120,735 B．385,350C．385,735 D．1855,325[解析] ∵(1855,1120)→(735,1120)→(735,385)→(350,385)→(350,35)，∴1855与1120的最大公约数是35，由以上计算过程可知选D.[答案] D12．用秦九韶算法计算多项式f(x)＝3x6＋4x5＋5x4＋6x3＋7x2＋8x＋1，当x＝0.4时的值时，需要做乘法和加法的次数分别是( )A．6,6 B．5,6C．5,5 D．6,5[解析] 根据秦九韶算法，把多项式改写为f(x)＝(((((3x＋4)x＋5)x＋6)x＋7)x＋8)x＋1，∴需要做6次加法运算，6次乘法运算，故选A.[答案] A13．已知a＝333，b＝24，则使得a＝bq＋r(q，r均为自然数，且0≤r≤b)成立的q 和r的值分别为________．[解析] 用333除以24，商即为q，余数就是r.333÷24的商为13，余数是21.∴q＝13，r＝21.[答案] 13,2114．用秦九韶算法求多项式f(x)＝1－5x－8x2＋10x3＋6x4＋12x5＋3x6当x＝－4时的值时，v0，v1，v2，v3，v4中最大值与最小值的差是________．[解析] 多项式变形为f(x)＝3x6＋12x5＋6x4＋10x3－8x2－5x＋1＝(((((3x＋12)x＋6)x＋10)x－8)x－5)x＋1，v0＝3，v1＝3×(－4)＋12＝0，v2＝0×(－4)＋6＝6，v3＝6×(－4)＋10＝－14，v4＝－14×(－4)－8＝48，所以v4最大，v3最小，所以v4－v3＝48＋14＝62.[答案] 6215．用辗转相除法和更相减损术两种方法求三个数72,120,168的最大公约数．[解] (辗转相除法)：先求120,168的最大公约数．因为168＝120×1＋48，120＝48×2＋24,48＝24×2，所以120,168的最大公约数是24.再求72,24的最大公约数．因为72＝24×3，所以72,24的最大公约数为24，即72,120,168的最大公约数为24.(更相减损术)：先求120,168的最大公约数．168－120＝48,120－48＝72，72－48＝24,48－24＝24，所以120,168的最大公约数为24.再求72,24的最大公约数．72－24＝48,48－24＝24，所以72,24的最大公约数为24，即72,120,168的最大公约数为24.。

算法初步导学案一、导：知识提要：算法的含义、程序框图、基本算法语句，辗转相除法、更相减损术、秦久韶算法与进位制。

1．算法的含义：在数学中算法通常是指按照一定规则解决某一类问题的明确和有限的步骤．算法的特点：（1）有限性（一个算法的步骤是有限的，必须在有限操作之后停止，不能是无限的.（2）确定性（算法的每一步骤和次序应当是确定的。

（3）有效性(算法的每一步骤都必须是有效的)。

2. 程序框、流程线的名称与功能3（1）.基本算法语句：输入语句、输出语句、赋值语句、条件语句、循环语句（2）.三种基本逻辑结构：顺序结构、条件结构、循环结构（3）.循环语句分while 型语句和for 型语句，设计循环语句程序时要注意：①循环语句中的变量一般需要进行一定的初始化操作；②循环语句在循环的过程中需要有“结束”的机会；③循环的过程中变量的变化规律。

4．算法案例学习辗转相除法与更相减损术、秦久韶算法、进位制时，必须了解其历史背景，理解解题原理，掌握解题步骤.二、学：学法指导1．规范基本语句一般格式【方法点拨】输入语句中提示内容与变量之间用分号“；”隔开，若输入多个变量，变量与变量之间用逗号“，”隔开。

输出语句显示算法的输出结果功能，输出语句输出常量、变量或表达式的值或字符。

赋值语句将表达式所代表的值赋给变量，赋值语句左边只能是变量名字，而不是表达式，右边表达式可以是一个数据、常量和算式。

【案例分析】 判断下列给出的语句是否正确，将错误的语句改正过来？（1）、INPUT c b a ;; （2）、INPUT 3=x （3）、PRINT 4=A（4）、B =3 （5）、0=+y x （6）、4==B A否用forwhile 型【解析】：在WHILE 型程序里面i=1 、sum=1，控制循环的条件为i<=100，按此算法最后得到的结果应为1001312111+++++ ，所以应将sum=1改为sum=0； 4．注重算法的实践应用【方法点拨】用算法处理应用问题的基本思路是：分析实际问题－－建立数学模型－－写算法步骤－－画程序框图－－编制算法程序。

人教版高中必修3第一章算法初步教学设计一、教学目标1.1 知识目标•掌握算法的基本概念和算法设计的流程；•能够正确理解和应用算法中的常用术语和符号；•学习并实现常见的算法，如冒泡排序、选择排序等。

1.2 能力目标•培养学生分析问题、解决问题的能力；•培养学生运用算法设计解决实际问题的能力；•培养学生的团队合作精神，提高学生的学习兴趣和学习效果。

二、教学内容2.1 什么是算法？•算法的定义；•算法与计算的关系；•算法的特点。

2.2 算法设计的流程•算法设计的步骤；•算法设计时需要考虑的问题。

2.3 常见算法•冒泡排序；•选择排序；•插入排序；•快速排序。

三、教学过程3.1 任务型学习1.让学生自己搜索和学习算法的定义，掌握算法的基本概念；2.将学生分为小组，分别针对冒泡排序、选择排序、插入排序、快速排序这四个常见算法进行深入学习；3.鼓励学生在小组内交流讨论，互相帮助，通过任务型学习的方式掌握每一种算法的实现过程和应用场景。

3.2 理论讲解1.讲解算法设计的流程，强调算法设计的基本思想；2.结合具体算法进行详细介绍；3.帮助学生掌握常用术语和符号的意义和用法。

3.3 多媒体展示1.利用计算机多媒体技术对算法的基本概念、算法设计的流程和常见算法进行展示；2.通过多媒体展示帮助学生理解算法中的关键点和难点。

3.4 实践操作1.让学生利用所学知识，对一些简单的排序问题进行解决；2.鼓励学生在实践中发现问题和总结经验；3.引导学生在实践中培养合作精神，培养团队意识。

四、教学评价4.1 测试评价1.设计一份测试题，测评学生对算法设计的基本概念、设计思想、常见算法等方面的掌握情况；2.给出具体的分值和评分标准。

4.2 成果展示1.让学生利用所学知识，针对一些复杂实际问题进行算法设计和实现；2.要求学生用合适的方式进行成果展示和说明；3.通过成果展示，评价学生团队合作精神和算法设计能力。

五、教学反思通过本次教学，学生基本掌握了算法的定义、算法设计的基本流程和常见算法的实现方法。

数学必修3 第一章算法初步第一章算法初步§1.1算法与程序框图§1.1.1算法的概念【学习目标】1 •确理解算法的概念，掌握算法的基本特点.2 •通过例题学习，会设计算法的基本思路.【学习重点】【学习难点】算法的含义及应用. 写出解决一类问题的算法.、自主学习(阅读课本2—5页，完成下列问题)1.解二元一次方程组有几种方法？2•结合教材实例J X~2y= ~1,(1)总结用加减消元法解二元一次方程组的步骤.mv,(2)x — 2v = —1 (1)3 •结合教材实例丿总结用代入消元法解二元一次方程组的步骤.fx + y", (2)4 •算法的定义：广义的算法是 _____________________________________________在数学中，算法通常是______________________________________________________现在，算法通常可以________________________________________________________5.算法的特征：(1) 确定性：算法的每一步都应当做到准确无误、不重不漏.不重”是指不是可有可无的，甚至无用的步骤，不漏”是指缺少哪一步都无法完成任务.(2) 顺序性与正确性：算法从开始的第一步”直到最后一步”之间做到环环相扣，分工明确，前一步”是后一步”的前提，后一步”是前一步”的继续，并且每一步都准确无误，才能解决问题.⑶有限性：算法要有明确的开始和结束，当到达终止步骤时所要解决的问题必须有明确的结果，也就是说必须在有限步内完成任务，不能无限制地持续进行.(4)不唯一性：求解某一问题的算法不一定是唯一的，对于同一个问题，可有不同的算法.、合作探究例1 : (1)设计一个算法，判断7是否为质数.(2)设计一个算法，判断35是否为质数.例2 :请写出判断n(n>2)是否为质数的算法.例3:写出用二分法"求方程x2-2=0 (x>0)的近似解的算法二、达标检测1•已知直角三角形两直角边长为a, b，求斜边长c的一个算法分下列三步：①计算c二a2b2；②输入直角三角形两直角边长a,b的值；③输出斜边长c的值,其中正确的顺序是()A. ①②③B.②③①C.①③②D.②①③2. 若f x在区间l.a, b 1内单调，且f a|_f b ：：：0,则f x在区间l.a,b 1内( )A.至多有一个根B.至少有一个根C.恰好有一个根D.不确定3. 已知一个学生的语文成绩为89,数学成绩为96，外语成绩为99.求他的总分和平均成绩的一个算法为：第一步：取A=89 ,B=96 ,C=99 ;第二步：______________________________________________ ;第三步：______________________________________________ ;第四步：输出计算的结果.4. 写出1疋X3 X4 >5 >6的一个算法.数学必修3 第一章算法初步四、学习小结算法概念及特征§1.1.2程序框图及算法的基本逻辑结构(1)【学习目标】1•了解什么是程序框图，知道学习程序框图的意义.2 •理解程序框的画法和功能.3•掌握基本逻辑结构的应用，并能解决有关的程序框图问题.【学习重点】掌握程序框的画法和功能.【学习难点】掌握基本逻辑结构的应用，并能解决有关的程序框图问题. 【学习过程】-、自主学习(阅读课本6—20页，完成下列问题)1 •什么是程序框图？图形符号名称功能二1二7>IF i、合作探究例1 :右图所示的是一个算法的流程图，已知a1=3,输出的b=7,求a2的值.例2:已知一个三角形三条边的边长分别为a, b, c,利用海伦—秦九韶公式设计一个计算三角形面积的算法，并画出程序框图表示.(已知三角形三边边长分别为a,b,c ,则三角形的面积为i------------------------------ a + b 十cS= ... p(p-a)(p-b)( p-c)),其中p= •这个公式被称为海伦一秦九韶公式)数学必修3 第一章算法初步二、达标检测1 •在算法的逻辑结构中 ，要求进行逻辑判断，并根据结果进行不同处理的是哪种结构（）A.顺序结构C.顺序结构和条件结构 2 •算法共有三种逻辑结构，即顺序逻辑结构，条件逻辑结构和循环逻辑结构，下列说法正确的是（）A. 一个算法只能含有一种逻辑结构 B •—个算法最多可以包含两种逻辑结构 C.一个算法必须含有上述三种逻辑结构D •—个算法可以含有上述三种逻辑结构的任意组合四、学习小结1 •程序框图概念2 •基本逻辑结构有哪些?B.条件结构和循环结构 D.没有任何结构3 •给出以下一个算法的程序框图 （如下图所示）,该程序框图的功能是（ A.求输出a,b,c 三数的最大数 B. 求输出a,b,c 三数的最小数 C. 将a,b,c 按从小到大排列 D.将a, b, c 按从大到小排列4 •右边的程序框图 件是（）（如下图所示 B. x =0?），能判断任意输入的数 x 的奇偶性：其中判断框内的条 D. m = 1?C.x =1?§1.1.2程序框图及算法的基本逻辑结构（2）【学习目标】1 •理解程序框的画法和功能.3 •能解决有关的程序框图问题.【学习重点】能解决有关的程序框图问题.【学习难点】掌握基本逻辑结构的应用，并能解决有关的程序框图问题. 【学习过程】-、自主学习1 •什么是程序框图？2•程序框图的图形符号及各自的功能是什么?3 •算法的基本逻辑结构有哪些？分别有什么作用?、合作探究3 3A.⑴n > 1000 ?⑵n v 10003 3B.⑴ n < 1000 ? ⑵ n > 10003 3C.⑴n v 1000 ?⑵n > 10003 3D.⑴n v 1000 ? ⑵n v 1000例1:如图⑴、⑵,它们都表示的是输出所有立方小于1000的正整数的程序框图，那么数学必修3 第一章算法初步二、达标检测1 .执行如图所示的程序框图23A . 1B .C .—3 212 .阅读如图所示的程序框图i =，输出的S值为（610D .987，运行相应的程序.若输入m的值为2,则输出的结果开始i =0, S =12S 1S = -------2S 1i」屮否>2是. 输出S结束3,则输出S的值是（），若输入n的值为D. 73 .执行如图1所示的程序框图A. 1 B . 2 C . 44 .阅读如下程序框图，如果输出i=4,那么空白的判断框中应填入的条件是A . S v 8B . S v 9 D. S v 11( ).C. S v 10§1.2基本算法语句§121输入语句、输出语句和赋值语句【学习目标】1 •理解学习基本算法语句的意义.2•学会输入语句、输出语句和赋值语句的基本用法.3•理解算法步骤、程序框图和算法语句的关系，学会算法语句的写法. 【学习重点】输入语句、输出语句和赋值语句的基本用法.【学习难点】算法语句的写法.【学习过程】-、自主学习（阅读课本21 —24页，完成下列问题）1 •指出输入语句的格式、功能、要求.2 •指出输出语句的格式、功能、要求.3 •指出赋值语句的格式、功能、要求.4 •指出三种语句与框图的对应关系.二、合作探究例1:用描点法作函数y=x3+3x2-24x+30的图象时，需要求出自变量和函数的一组对应值.画出程序框图并编写程序.例2 :给一个变量重复赋值.数学必修3 第一章算法初步例3 :交换两个变量的值，并输出交换前后的值.二、达标检测1. P24练习题第1题、第4题.2.将两个数a =8,b =7交换，使a =7 ,b =8,使用赋值语句正确的一组（）A . a = b ,b = aB .C . b = a , a = bD .3写出两图中程序框图的运行结果：开始图1中输出S= _______________ ；图2中输出a = _______________c =b ,b = a ,a = c a = c ,c =b ,b =a四、学习小结三种语句的格式、功能、要求以及与框图的对应关系.数学必修3 第一章算法初步§122条件语句【学习目标】1 •理解学习基本算法语句的意义.2 •学会条件语句的基本用法.3•理解算法步骤、程序框图和算法语句的关系，学会算法语句的写法. 【学习重点】条件语句的基本用法【学习难点】算法语句的写法【学习过程】-、自主学习（阅读课本25—28页，完成下列问题）1 •回忆程序框图中的两种条件结构.2•指出条件语句的格式及功能.3. 指出两种条件语句的相同点与不同点.4 •指出条件语句与程序框图的对应关系.、合作探究例1 :编写一个程序，求实数x的绝对值.例2:把前面求解一元二次方程ax2+bx+c=0的程序框图转化为程序.例3:编写程序，使任意输入的3个整数按从大到小的顺序输出.二、达标检测1. P29练习题第2题、第4题.2 •有如下程序运行后输出结果是（）A . 3 4 5 6B . 4 5 6C . 5 6D . 63.第3题程序运行后输出结果是______________________ .四、学习小结条件语句的格式、功能以及与程序框图的对应关系.数学必修3 第一章算法初步§123循环语句【学习目标】1 •理解学习基本算法语句的意义.2 •学会循环语句的基本用法.3•理解算法步骤、程序框图和算法语句的关系，学会算法语句的写法.【学习重点】循环语句的基本用法.【学习难点】循环语句的写法学习过程一、自主学习（阅读课本29—32页，完成下列问题）1 •试用程序框图表示循环结构.2 •指出循环语句的格式及功能.3.指出两种循环语句的相同点与不同点.4 •指出循环语句与程序框图的对应关系.二、合作探究例1:修改前面编写过的求函数y=x3+3x2-24x+30的值的程序，连续输入11个自变量的取值，输出相应的函数值.例2:教材中的用二分法”求方程x2-2=0 （x>0）的近似解的程序框图（见教材图1 • 120）包含了顺序结构、条件结构和循环结构•下面，我们把这个程序框图转化为相应的程序.111 1例3 :设计算法求的值•要求画出程序框图，写出1 x2 2x3 3汉4 99 汉100用基本语句编写的程序.二、达标检测1. 直到型循环结构为数学必修3 第一章算法初步四、学习小结指出循环语句的格式、功能以及与程序框图的对应关系.§.3算法案例【学习目标】1 •理解辗转相除法与更相减损术的含义，了解其执行过程. 2•理解秦九韶算法飞计算过程，并了解它提高计算效率的实质. 3.理解进位制的概念，能进行不同进位制间的转化. 【学习重点】1. 掌握辗转相除法，更相减损术求公约数的方法.2. 能用秦九韶算法求多项式的值.C2. P 32练习题第1题、第2题.()D3. 能进行不同进位制间的转化.【学习难点】理解上述算法的含义.学习过程一、自主学习(阅读课本34—45页，了解以下问题)1. 怎样用短除法求最大公约数？2. 怎样用辗转相除法求最大公约数？3. 怎样用更相减损术求最大公约数？4. 秦九韶算法如何求多项式的值？5. 如何把k进制的数化为十进制数？6. 把十进制数化为k进制数的方法叫什么？具体如何转化？二、合作探究例1:用辗转相除法求8 251与6 105的最大公约数，写出算法分析，画出程序框图，写出算法程序.例2 :用更相减损术求98与63的最大公约数.例3:已知一个5次多项式为f (x) =5X5+2X4+3. 5x3-2. 6x2+1 . 7x-0. 8,用秦九韶算法求这个多项式当x=5时的值.例4:将下列各进制数按要求转化为其它进位制数.数学必修3 第一章算法初步（1）101101（2）= ____ （化为 10 进制）（2）10303（4）= _______ （化为 10 进制） （3）19仁 ____________ （化为5进制） （4） 1234（5 = ________ （化为8进制） 三、达标检测1 •分别用辗转相除法与更相减损术求123和48的最大公约数.2.用秦九韶算法求多项式 f （x ）=7x 7+6x 6+5x 5+4x 4+3x 3+2x 2+x 当x=3时的值.3•以下给出的各数中不可能是八进制数的是 （）A . 312B . 10110C . 82D . 74574. 完成下列进位制之间的转化.10110012= ------------------------------- 10 = --------------------- 55. 下列各数中最小的数是四、学习小结1. 辗转相除法与更相减损术求最大公约数.2. 用秦九韶算法求多项式值的方法.3. 不同进位制的转化.10=2021210A . 111111B . 210 6D . 8193125=第一章算法初步测试题一、选择题1 .已知直角三角形两直角边长为a,b,求斜边长c的一个算法分下列三步:①计算c = •. a b :②输入直角三角形两直角边长 a ,b的值;③输出斜边长C的值，其中正确的顺序是A .①②③B.②③① C .①③②2.如果执行下面的程序框图，那么输出的A . 2 450D.②①③S等于( )C. 2 550 D . 2 652B . 2 5003. 右边的程序框图A. m =0?4. 将两个数a=8,b=7交换，使a =7A . a = b ,b =aC . b = a, a = b5. 下列给出的输入语句、⑴输出语句INPUT(3)赋值语句3=B 则其中正确的个数是，A . 0 个B .(如上图所示),能判断任意输入的数X的奇偶性：其中判断框内的条件是B.X =0 ? C . X=1? D . m=1?,b=8,使用赋值语句正确的一组c=b ,b = a,a= ca = c,c=b ,b = a输出语句和赋值语句a;b ；c (2)输入语句INPUTx=3⑷赋值语句A=B=2C.6. 三位七进制的数表示的最大的十进制的数是A. 322 B . 332 C . 3427. 下边程序执行后输出的结果是A . -1B . 0C . 1&当x =2时,下面的程序段结果是D . 352数学必修3 第一章算法初步C. 15D. 179 •下面为一个求20个数的平均数的程序在横线上应填充的语句为A.i >20 B . i c20 C . i=20 D . i20n =5i =1S = 0s = 0s = 0i =1WHILE sc15WHILE i<=4DOs= s + n s = s* x + 1INPUT xn = n —1i =i +1S = S + x WEND WEND i =i +1PRINT n PRINT s LOOP UNTIL _END END a = S/20PRINT a第7题程序第8题程序END第9题程序10 . 下列各数中最小的数是(A . 1111112B. 2106C. 10004D . 819二、填空题11•如图⑵程序框图箭头a指向①处时，输出s= _________ .箭头a指向②处时，输出s= ___________ .INPUT xIF x>9 AND x<100 THENa=x\10b=x MOD 10 x=10*b+aPRINT xEND IFEND第13题程序13 •若输入的数字是“ 37输出的结果是14. 2183和1947的最大公约数是___三、解答题12 .此题程序运行结果为_____________X2-1 15.已知f X = 22x2-5（X'0）画出程序框图，并编写一个程序，对每输入的一个X X 0值,都得到相应的函数值.16.某次考试，满分100分,按规定x _80者为良好，60 _ x ：：： 80者为及格，小于60者不及格，画出当输入一个同学的成绩x时，输出这个同学属于良好、及格还是不及格的程序框图.数学必修3 第一章算法初步17.铁路托运行李，从甲地到乙地，按规定每张客票托运行李不超过50 kg时,每千克0.2元,超过50 kg时，超过部分按每千克0.25元计算，画出计算行李价格的算法框图.18.用秦九韶算法计算函数 f x = 2x4■ 3x3■ 5x-4在x=2时的函数值.主备：顾斌元修订：杨志福马宇鲲审阅：顾斌元党继雄21。

《算法初步》学案一、学习目标1．了解《算法初步》的知识构建。

2．掌握本学案的例题题型。

二、重点与难点重点：知识构建与例题。

难点：例题。

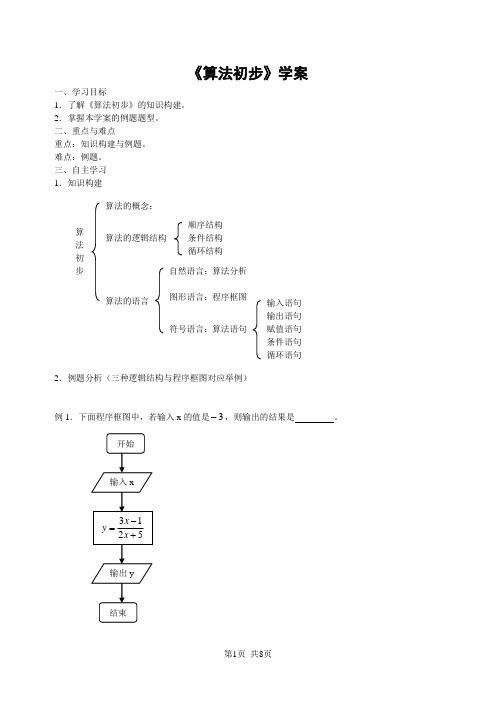
三、自主学习1．知识构建2．例题分析（三种逻辑结构与程序框图对应举例）例1．下面程序框图中，若输入x 的值是3-，则输出的结果是 。

算法初步算法的概念： 算法的语言 自然语言：算法分析 图形语言：程序框图 符号语言：算法语句 输入语句输出语句赋值语句条件语句循环语句算法的逻辑结构 顺序结构 条件结构 循环结构答案：10 点评：本程序框图体现的是顺序结构，其作用是求函数5213+-=x x y 的函数值的算法。

例2．下面程序框图中，若输入x 的值是4，则输出的结果是 。

答案：3-点评：本程序框图体现的是条件结构，其作用是求分段函数⎪⎪⎩⎪⎪⎨⎧≥-<+=0,5210,321x x x x y 的函数值的算法。

变式：下面程序框图中，若输入x 的值分别是2,0,2-，则对应的输出值之和是 。

答案：1-例3．下面的程序框图中输出的结果是。

答案：30点评：本程序框图体现的是直到型循环结构，如果用当型循环结构表示，则程序框图如下：3．练习巩固（1）某程序框图如图所示，该程序运行后输出的k 的值是 () A ．4 B ．5 C ．6 D ．7（2）在下图的程序框图中，输出的s 的值为 ( )A ． 12B ． 14C ． 15D ． 20开始1=nn a 5=输出a1+=n n6≤n ？ 结束是否（3）某流程如下图所示,现输入如下四个函数,则可以输出的函数是（）． A ．2)(x x f = B ．x x f 1)(=C ．62ln )(-+=x x x fD ．3)(x x f =（4）如图所示，是关于判断闰年的流程图，则以下年份是闰年的为 () A ．1996年 B ．1998年C ．2010年D ．2100年（5）下图是计算201614121+⋅⋅⋅+++的值的一个程序框图，则判断框内应填入的条件是（ ） A.i>10 B.i<10 C.i>20 D.i<20（6）按下面的程序框图运算．若输入8x =，则输出k = ；若输出2k =，则输入x 的取值范围是 ．答案：（1）A （2）C （3）D （4）A（5）A （6）4，(]28,57。

人教版高中必修3第一章算法初步课程设计课程目标本课程旨在帮助学生了解算法的基本概念和常用算法的实现方式，以及培养学生的编程思维能力和解决问题的能力。

教学内容1.算法的基本概念2.常用排序算法：冒泡排序、选择排序、插入排序、快速排序3.常用查找算法：顺序查找、二分查找4.算法的复杂度分析教学重点和难点教学重点•算法的基本概念和特点•常用排序算法和查找算法的原理和实现方式教学难点•快速排序的原理和实现方式•算法的复杂度分析教学方法本课程采用“理论讲授+案例分析+编程实践”的教学方法，具体如下：1.理论讲授：教师通过讲解PPT、示意图等形式，介绍算法的基本概念、常用算法的原理和实现方式。

2.案例分析：教师通过具体的案例，让学生在实践中理解算法的应用和优化。

3.编程实践：教师通过提供一些编程练习题，让学生进行算法实现和分析。

并在课堂上展示部分学生的优秀代码。

课程安排本课程共计4个课时，具体安排如下：1.第1课时：算法的基本概念。

介绍算法的定义、特点、效率和正确性等基本概念。

2.第2-3课时：排序算法。

介绍冒泡排序、选择排序、插入排序、快速排序的实现方式和时间复杂度分析。

3.第4课时：查找算法和复杂度分析。

介绍顺序查找、二分查找的实现方式和时间复杂度分析，以及算法的复杂度分析方法。

课程评价本课程考核方式为闭卷笔试和编程实践，笔试占60%，编程实践占40%。

针对学生的不同水平，编程实践的难度分为初级和高级两个难度级别，学生可以自主选择挑战。

同时，教师也将根据学生的课堂表现和编程作业进度，对学生进行平时成绩评价。

总结本课程以算法初步为主要内容，重点介绍了排序算法和查找算法，并通过编程实践提高学生的编程能力和解决问题的能力。

希望学生能通过本课程的学习，了解算法的概念和特点，掌握常用算法的实现方式，培养良好的编程思维和解决问题的能力，为后续专业学习打下基础。

1)) ) 高中数学(必修3)第一章(算法初步)知识点导学一、算法的概念:1.算法概念:在数学上,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成。

2.算法的特点:(1)有限性:一个算法的步骤序列是有限的,必须在有限步操作之后停止,不能是无限的,(2)确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不应当是模棱两可的,(3)顺序性与正确性:算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后继步骤,前一步是后一步的前提,只有执行完前一步才能进行下一步,并且每一步都准确无误,才能完成问题,(4)不唯一性:求解某一个问题的解法不一定是唯一的,对于一个问题可以有不同的算法,(5)普遍性:很多具体的问题,都可以设计成合理的算法去解决,如:心算,计算器计算都要经过有限步事先设计好的步骤加以解决。

二、程序框图:1.程序框图的概念:程序框图又称流程图,是一种用规定的图形,指向线及文字说明来准确,直观地表示算法的图形,一个程序框图包括以下几部分:表示相应操作的程序框,带箭头的流程线,程序框外必要的文字说明,3.学习这部分知识的时候,要掌握各个图形的形状,作用及使用规则,画程序框图的规则如下:①使用标准的图形符号,②框图一般按从上到下,从左到右的方向画,③除判断框外,大多数流程图符号只有一个进入点和一个退出点,判断框是具有超过一个退出点的唯一符号,④判断框分两大类,一类是对“是”与“否”两个分支的判断,而且有且仅有两个结果,另一类是多分支判断,有几种不同的结果,⑤在图形符号内描述的语言要非常简练清楚。

4.算法的三种基本逻辑结构:顺序结构,条件结构,循环结构。

(1)顺序结构:顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的,它是由若干个依次执行的处理步骤组成的,它是任何一个算法都离不开的一种基本算法结构,顺序结构 在程序框图中的体现就是用流程线将程序框自上而下地连接起来,按顺序执行算法步骤,如图1,A 框和B 框是依次执行的,只有在执行完A 框指定的操作后,才能接着执行B 框所指定的操作。

示范教案整体设计教学分析前面学习了算法、程序框图与几种算法语句，本节课作为本章的小结，旨在和学生一起站在全章的高度，以算法思想为灵魂，以问题解决为主线，以典型例题为操作平台，以巩固知识、发展能力、提高素养为目的对本章作全面的复习总结，帮助学生进一步提高对算法的理解和认识，优化知识结构．三维目标1．对本章知识形成知识网络，提高学生的逻辑思维能力，培养学生的归纳能力．2．熟练应用算法、程序框图与基本算法语句来解决问题，培养学生的分析问题和解决问题的能力，逐步学会用数学方法去认识世界、改造世界．重点难点教学重点：应用算法、程序框图与基本算法语句解决问题．教学难点：形成知识网络．课时安排1课时教学过程导入新课思路1(情境导入)．大家都熟悉围棋高手“石佛”李昌镐吧，他曾经打遍天下无敌手，你知道他最令人可怕的地方吗？他的技术很全面，但他最厉害的技术是“官子”，他的“官子”层次分明，可以说滴水不漏，堪称世界第一．我们的这次复习也要像围棋中的“官子”，也要做到层次分明、滴水不漏．思路2(直接导入)．前面我们学习了算法、程序框图与基本算法语句等内容，今天我们对本章知识、方法、数学思想进行全面、系统的总结与复习．推进新课新知探究提出问题(1)请同学们自己梳理本章知识结构.(2)回顾算法的定义及特征.(3)回忆程序框图的三种逻辑结构.(4)总结算法语句.讨论结果：(1)本章知识结构如下图．(2)算法的定义：广义的算法是指完成某项工作的方法和步骤，那么我们可以说洗衣机的使用说明书是操作洗衣机的算法，菜谱是做菜的算法等等．在数学中，算法通常是指按照一定规则解决某一类问题的明确有限的步骤．现在，算法通常可以编成计算机程序，让计算机执行并解决问题．算法的特征：①确定性：算法的每一步都应当做到“准确无误、不重不漏”“不重”是指不是可有可无的、甚至无用的步骤，“不漏”是指缺少哪一步都无法完成任务．②逻辑性：算法从开始的“第一步”直到“最后一步”之间做到环环相扣、分工明确，“前一步”是“后一步”的前提，“后一步”是“前一步”的继续．③有穷性：算法要有明确的开始和结束，当到达终止步骤时所要解决的问题必须有明确的结果，也就是说必须在有限步内完成任务，不能无限制地持续进行．(3)顺序结构、条件分支结构、循环结构．(4)赋值语句：变量＝表达式．输入语句：变量＝input.输出语句：print(%io(2)，变量)．条件语句：格式1：if表达式语句序列1；else语句序列2；end格式2：if表达式语句序列1；end循环语句：for语句：for循环变量＝初值：步长：终值循环体；endwhile语句：while表达式循环体；end应用示例例1如下图所示，该程序框图输出的结果为________．解：该程序框图的运行过程是：A＝1；S＝1；S＝1＋9＝10；A＝1＋1＝2；A≤2，成立；S＝10＋9＝19；A＝2＋1＝3；A＝3≤2，不成立；输出S＝19.答案：19点评：解决同一个问题，可以有多种算法，那么就有多种程序框图和语句，再就是不同版本的教材算法语句的语言形式也不相同，因此高考试题中通常不会考查画程序框图或编写程序．由于学习本章的目的是体会算法的思想，所以已知程序框图或程序，判断其结果是高考考查本章知识的主要形式，这也是课程标准和考试说明对本章的要求．其判断方法是具体∴y ＝π2×2－5＝π－5. 例2到银行办理个人异地汇款(不超过100万元)，银行收取一定的手续费．假设汇款额不超过100元，收取1元手续费；超过100元但不超过5 000元，按汇款额的1%收取；超过5 000元，一律收取50元手续费．试用程序框图描述汇款额为x 元时，银行收取手续费y 元的过程．分析：这是一个实际问题，故应先建立数学模型，y ＝⎩⎪⎨⎪⎧ 1(0<x ≤100)，0.01x (100<x ≤5 000)，50(5 000<x ≤1 000 000).由此看出，要求手续费，需先判断x 的范围．解：程序框图如下图：点评：条件分支结构经常与分段函数有密切的关联；判断框里要写明分支的条件，从而决定下一步该作出怎样的选择．例3已知函数y ＝⎩⎪⎨⎪⎧ 2x －1，x ≤－1，log 3(x ＋1)，－1<x<2，x 4，x ≥2，试设计一个算法，输入x 的值，求对应的函数值．分析：对输入x 的值与－1和2比较大小，即分类讨论．解：算法如下：S1 输入x 的值；S2 当x ≤－1时，计算y ＝2x －1，否则执行下一步；S3 当x ≥2时，计算y ＝x 4，否则执行下一步；S4 计算y ＝log 3(x ＋1)；S5 输出y.点评：分段函数是高考考查的重点，在考虑算法步骤时，要用到分类讨论思想，这为复习程序框图和算法语句打好了基础.知能训练1．下面程序框图输出的结果是( )A ．11B ．12C ．132D ．1 320分析：该程序框图的运行过程是：i ＝12；s ＝1；i ＝12≥10，成立；s ＝1×12＝12；i ＝12－1＝11；i ＝11≥10，成立；s ＝12×11＝132；i ＝11－1＝10；i ＝10≥10，成立；s ＝132×10＝1 320；i ＝10－1＝9；i ＝9≥10，不成立；输出s ＝1 320.答案：D2．下图是表示求解方程x 2－(a ＋1)x ＋a ＝0(a ∈R ，a 是常数)过程的程序框图．请在标有序号(1)(2)(3)(4)处填上你认为合适的内容将框图补充完整．(1)____________；(2)____________；(3)____________；(4)____________．解析：所解方程是一元二次方程，先计算判别式Δ＝(a ＋1)2－4a ＝(a －1)2，所以(1)处填(a －1)2；计算判别式Δ的大小后，再判断其符号，由于Δ＝(a －1)2，则只需判断a 是否等于1即可，则(2)有两种填法a ＝1或a ≠1，当(2)处填a ＝1时，(3)处填x 1＝x 2＝1，(4)处填x 1＝a ，x 2＝1；当(2)处填a ≠1时，(3)处填x 1＝a ，x 2＝1，(4)处填x 1＝x 2＝1.答案：(1)(a －1)2 (2)a ＝1 (3)x 1＝x 2＝1 (4)x 1＝a ，x 2＝1或(1)(a －1)2 (2)a ≠1(3)x 1＝a ，x 2＝1 (4)x 1＝x 2＝13．下列程序的功能是________．s ＝0；for i ＝1：1：100s ＝s ＋1/i ；endprint(%io(2)，s)；解析：该程序的执行过程是：s ＝0；i ＝1，s ＝0＋11＝1； i ＝2，s ＝1＋12；i ＝3，s ＝1＋12＋13； ……i ＝100，s ＝1＋12＋13＋…＋1100. 答案：计算1＋12＋13＋…＋1100的值 拓展提升数学的美是令人惊异的！如三位数153，它满足153＝13＋53＋33，即这个整数等于它各位上的数字的立方的和，我们称这样的数为“水仙花数”．请您设计一个算法，找出大于100，小于1 000的所有“水仙花数”．(1)写出算法步骤；(2)画出程序框图．分析：由于需要判断大于100，小于1 000的整数是否满足等于它各位上的数字的立方的和，所以需要用循环结构．解：(1)算法步骤如下：S1 i ＝101；S2 如果i 不大于999，则执行第3步，否则算法结束；S3 若这个数i 等于它各位上的数字的立方的和，则输出这个数；S4 i ＝i ＋1，返回第2步．(2)程序框图如下图所示．课堂小结(1)复习了本章知识，形成了知识网络．(2)判断算法的功能或输出结果．作业本章小结Ⅲ.巩固与提高 4、5.设计感想本节通过大量生动活泼的例题对本章进行系统的总结，通过精彩的点评渗透算法的基本思想，使学生的知识得到进一步巩固，使学生的思想方法不断升华．备课资料人机大战的启示人类的许多进步之所以产生，多半是发明了一个更好、更有力的工具．物质工具使工作速度加快并使人们从重体力劳动中解脱出来，而信息工具则扩大人们的智力．物质工具如犁、起重机、推土机、内燃机、电动机等等，是人的四肢的延伸，而计算机是人的大脑的延伸．它最初只能进行数值计算，但随着其发展，应用范围不断扩大．它不仅能够进行计算，还能进行记忆、判断、推理、设计、控制、自动化处理等等．一句话，只要是能输入计算机里的信息，它都能按照人的要求对信息进行迅速而圆满的处理．因此，计算机也被称为电脑．在短短十几年的时间里，我们经历了计算机深入生活每一个角落的过程，深深感受到了计算机多方面的强大的功能．其中，国际象棋大师卡斯帕罗夫与IBM“深蓝”的人机大战的结果曾引起世人瞩目和激烈讨论，留下了有关计算机与人的关系的种种思考．1989年，美国IBM公司成立了“深蓝”(Deep Blue)项目小组，开始着手研究有关计算机下棋方面的技术，其实就是设计下棋的算法．其目的是证明它具有能够处理复杂博弈模式的能力，而真正的意图是，以此作为一个模型，将并行技术深入到其他各种复杂应用领域.1988年，“深蓝”的前身“深思”(Deep Thought)在华裔科学家许峰雄等人的开发下，已经具备与人进行国际象棋比赛的能力．“深蓝”在开始设计时就以超越“深思”为目的，特别在运算速度与处理能力部分．经过不断的努力，1996年2月，当今最优秀的国际象棋棋手、世界冠军卡斯帕罗夫与“深蓝”计算机展开了第一次真正的角逐．比赛为六局对抗赛．虽然卡斯帕罗夫最终以4∶2的比分取胜，但今天计算机所达到的能力，也着实让全世界吃了一惊．尤其是第一局，“深蓝”以获胜来了个“开门红”．卡斯帕罗夫在赛后承认，“深蓝”是必须认真对待的劲敌，他说：“我没有料到它如此难以对付，我输掉第一局非常幸运，因为那是给我发出的最严重警告．”由于卡斯帕罗夫战胜“深蓝”，他预言“在严肃、经典的比赛中，计算机在本世纪没有赢棋的机会．”然而，卡斯帕罗夫对计算机技术的飞速发展估计错了．仅仅一年后，“深蓝”就战胜了这位大师.1997年5月人机大战重开．前五局战平，5月11日第六局决胜局的比赛，卡斯帕罗夫仅走了19步便向“深蓝”认输．“深蓝”的重量达1.4吨，拥有32个节点，每一节点有8块专门为进行国际象棋对弈设计的处理器，从而拥有每秒运算超过2亿步的惊人速度．为了使“深蓝”能拥有更多的资源规划棋步，开发小组汇集了一个开放棋局的数据库，输入了100年来世界顶级棋手的棋局，此外还有残局数据库，即最后五步时的走法，形成了汇集10亿个棋局的数据库．自1996年在输给卡斯帕罗夫之后，美国特级大师本杰明加盟“深蓝”，将他对象棋的理解编成语句输入“深蓝”，且在1997年的比赛中，每场对局结束后，小组都会根据卡斯帕罗夫的情况相应地修改特定的参数．“深蓝”在比赛中，不会疲倦、不会有心理和情绪上的起伏，只是不动声色地进行高速准确的运算．因此，卡斯帕罗夫的对手并不是“深蓝”主机，而是一群人如何运用电脑的硬、软件来向一个人的智慧和反应挑战．电脑的胜利说到底是人脑的胜利．但是“深蓝”的这次胜利，毕竟标志着计算机技术又上了一个新台阶，更准确地说，这次“深蓝”胜利，是人脑经过电脑胜过人脑．它也反过来让人们思考，什么是思维的本质？它第一次让人类如此真切地感受到了电脑与人的相异却又能够与人对抗的能力，这种力量还会从人们今后的努力中得到滋养从而不断壮大．有人曾将人机大战称为捍卫人类尊严的比赛，此次“深蓝”获胜，绝不意味人类的尊严丧失殆尽．许峰雄博士说得好：“棋王卡斯帕罗夫的胜利是为人类的过去赢了一盘棋；今年，‘深蓝’胜卡斯帕罗夫，是为人类的未来赢了一盘棋．”另外，深具意义的是，“深蓝”证明了人类的极限．超越人类的极限是一件很大的事情，人类就是在不断超越自己的极限中而进步的．。

1．1 算法与程序框图1．1.1算法的概念内容标准学科素养1。

通过回顾解二元一次方程组的方法，了解算法的思想。

2。

了解算法的含义和特征。

3.会用自然语言表述简单的算法。

提升数学运算发展逻辑推理应用数学抽象授课提示:对应学生用书第1页［基础认识]知识点一算法的概念预习教材P2－3,思考并完成以下问题一个大人和两个小孩一起渡河,渡口只有一条小船，每次只能渡1个大人或两个小孩，他们三人都会划船,但都不会游泳．（1)试问他们怎样渡过河去?提示：第一步,两个小孩同船过河去；第二步，一个小孩划船回来；第三步，一个大人划船过河去;第四步，对岸的小孩划船回来;第五步，两个小孩同船渡过河去．（2）设计的过河方法有什么特点？提示:由于船小，不能同时坐三个人，这样就需要遵循这一规则，然后按照一定的步骤一步一步的把三人运到河对岸．知识梳理在数学中，算法通常是指按照一定规则解决某一类问题的明确和有限的步骤．现在,算法通常可以编成计算机程序，让计算机执行并解决问题．知识点二算法与计算机知识梳理计算机解决任何问题都要依赖于算法．只有将解决问题的过程分解为若干个明确的步骤,即算法，并用计算机能够接受的“语言”准确地描述出来，计算机才能够解决问题．思考：与一般的解决问题的过程相比，算法最重要的特征是什么？提示：最重要的特征是步骤的有序性、明确性和有限性．［自我检测］下列叙述不能称为算法的是(）A．从北京到上海先乘汽车到飞机场，再乘飞机到上海B．解方程4x＋1＝0的过程是先移项再把x的系数化成1C．利用公式S＝πr2计算半径为2的圆的面积得π×22D．解方程x2－2x＋1＝0解析：A、B两选项给出了解决问题的方法和步骤，是算法．C项，利用公式计算也属于算法．D项，只提出问题没有给出解决的方法，不是算法．答案：D授课提示：对应学生用书第2页探究一算法的概念［例1]下列关于算法的说法，正确的个数为(）①求解某一类问题的算法是唯一的；②算法必须在有限步操作之后停止；③算法的每一步操作必须是明确的，不能有歧义或模糊；④算法执行后一定产生确定的结果．A．1B．2C．3 D．4［解析］由于算法具有有限性、确定性、输出性等特点,因而②③④正确，而解决某类问题的算法不一定唯一，从而①错．［答案］ C方法技巧1。