指数及指数函数知识点及习题

高中数学必修1知识点总结—指数及指数函数1、 根式na （一般的，如果n x a =，那么x 叫做a 的n 次方根，其中*1,n n N >∈且.）35325325n n n ⎧=⎪⎨-=-⎪⎩正数的次方根是正数如当是奇数时，负数的次方根是负数如20,n a n an ⎧>±⎪⎨⎪⎩正数的次方根有个，且互为相反数如：则次方根为当是偶数时，负数没有偶次方根0的任何次方根都是0，记作0n2、nna的讨论 n nn a a =当是奇数时，；,0,0n n a a n a a a a ≥⎧==⎨-≤⎩当是偶数时， （2）分数指数幂的概念）分数指数幂的概念①正数的正分数指数幂的意义是：(0,,,mnmna a a m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是：11()()(0,,,m mmnnnaa m n N a a-+==>∈且1)n >．0的负分数指数幂没有意义．义． 注意口诀：底数取倒数，指数取相反数．底数取倒数，指数取相反数． （3）分数指数幂的运算性质）分数指数幂的运算性质①(0,,)rsr saa aa r s R +⋅=>∈ ②()(0,,)r s rsa a a r s R =>∈③()(0,0,)rr rab a b a b r R =>>∈一、 指数计算公式：()Q s r a ∈>,,0_____=⋅s r a a ________=sraa _____)(=s r a ______)(=r ab )1,,0_______(>∈>=*n N n m a anm，________=n na 练习 计算下列各式的值：计算下列各式的值：（1）)4()3)((636131212132b a b a b a ÷- （2）()322175.003129721687064.0+⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛---（3）421033)21(25.0)21()4(--⨯+-- （4）33)3(625π-+-2．已知31=+-x x ，则=+-22x x 已知23=a,513=b，则=-ba 23＝____________. 3. 若21025x x =，则10x x-等于_________________【2.1.2】指数函数及其性质（4）指数函数）指数函数函数名称函数名称指数函数指数函数定义定义函数(0x y a a =>且1)a ≠叫做指数函数叫做指数函数图象图象1a >01a <<定义域定义域 R 值域值域(0,)+∞过定点过定点 图象过定点(0,1)，即当0x=时，1y =．奇偶性奇偶性 非奇非偶非奇非偶单调性单调性在R 上是增函数上是增函数在R 上是减函数上是减函数函数值的函数值的 变化情况变化情况1(0)1(0)1(0)x x x a x a x a x >>==<< 1(0)1(0)1(0)x x x a x a x a x <>==>< a 变化对变化对 图象的影响图象的影响 在第一象限内，a 越大图象越高；在第二象限内，a 越大图象越低．越大图象越低．题型1、求函数经过的点 1、2)(f 1-=+x a x )10(≠>a a 且过定点______________2、函数y=4+a x -1的图象恒过定点P 的坐标是________________3.已知指数函数图像经过点)3,1(-p ，则=)3(f题型2、 图像问题1.下列说法中：下列说法中：①任取x ∈R 都有3x >2x ； ②当a >1时，任取x ∈R 都有a x >a －x ；③函数y =(3)－x 是增函数；④函数y =2|x |的最小值为1 ；⑤在同一坐标系中，y =2x 与y =2－x 的图象对称于y 轴。

指数与指数函数知识讲解一、指数运算1.根式的概念：①定义：若一个数的n 次方等于),1(*∈>N n n a 且，则这个数称a 的n 次方根．即若a x n =，则x 称a 的n 次方根)1*∈>N n n 且，1）当n 为奇数时，n a 的次方根记作n a ；2）当n 为偶数时，负数a 没有n 次方根，而正数a 有两个n 次方根且互为相反数，记作)0(>±a a n ．②性质：1）a a n n =)(；2）当n 为奇数时，a a n n =； 3）当n 为偶数时，⎩⎨⎧<-≥==)0()0(||a a a a a a nn．2.幂的有关概念①规定：1）∈⋅⋅⋅=n a a a a n( N*；N 个 2）)0(10≠=a a ； 3）∈=-p aap p(1Q ，4）m a a a n m n m ,0(>=、∈n N* 且)1>n ． ②性质：1）r a a a a sr s r ,0(>=⋅+、∈s Q ）；2）r a a a s r s r ,0()(>=⋅、∈s Q ）；3）∈>>⋅=⋅r b a b a b a r r r ,0,0()( Q ）． 注：上述性质对r s R ∈、均适用．二、指数函数1.定义：函数)1,0(≠>=a a a y x 且称指数函数，1）函数的定义域为R ； 2）函数的值域为),0(+∞；3）当10<<a 时函数为减函数，当1>a 时函数为增函数．2.函数图像：1）指数函数的图象都经过点（0，1），且图象都在第一、二象限；2）指数函数都以x 轴为渐近线（当10<<a 时，图象向左无限接近x 轴，当1>a 时，图象向右无限接近x 轴）；指数函数在同一直角坐标系中的图像的相对位置与底数大小的关系是：在y 轴右侧，图像从上到下相应的底数由大变小，在y 轴的左侧，图像从下到上相应的底数由大变小．3）无奇偶性，是非奇非偶函数，但对于相同的)1,0(≠>a a a 且，函数x x a y a y -==与的图象关于y 轴对称，x x y a y a ==-与的图象关于x 轴对称；log xa y a y x ==与的图象关于直线y x =对称．f x () =12( = 2x4）有两个特殊点：零点(0,1)，不变点(1,)a ．5）抽象性质： ()()(),()()/()f x y f x f y f x y f x f y +=⋅-=3函数值的变化特征：典型例题一．选择题（共8小题）1．（2017春•东河区校级期末）函数y=2x（x≤0）的值域是（）A．（0，1） B．（﹣∞，1）C．（0，1]D．[0，1）2．（2016秋•黄陵县校级期末）下列函数一定是指数函数的是（）A．y=2x+1B．y=x3 C．y=3•2x D．y=3﹣x3．（2017秋•罗湖区校级期中）若函数f（x）=（a2﹣2a﹣2）a x是指数函数，则a的值是（）A．﹣1 B．3 C．3或﹣1 D．24．（2017秋•定州市校级期末）如果a＞1，b＜﹣1，那么函数f（x）=a x+b的图象在（）A．第一、二、三象限B．第一、三、四象限C．第二、三、四象限D．第一、二、四象限5．（2017秋•历下区校级期末）已知函数g（x）=3x+t的图象不经过第二象限，则t的取值范围为（）A．t≤﹣1 B．t＜﹣1 C．t≤﹣3 D．t≥﹣36．（2018•全国模拟）若2m＞2n，则下列结论一定成立的是（）A．＞B．m|m|＞n|n|C．ln（m﹣n）＞0 D．πm﹣n＜1 7．（2018•凯里市校级二模）已知a=0.52.1，b=20.5，c=0.22.1，则a、b、c的大小关系是（）A．a＜c＜b B．b＞a＞c C．b＜a＜c D．c＞a＞b8．（2017秋•天心区校级期末）某品牌电脑投放市场的第一个月销售100台，第二个月销售200台，第三个月销售400台，第四个月销售790台，则下列函数模型中能较好反映销售量y与投放市场月数x之间的关系的是（）A．y=100x B．y=50x2﹣50x+100C．y=50×2x D．y=10x+100二．填空题（共3小题）9．（2016•南昌县自主招生）函数的定义域是．10．（2016•长宁区一模）方程9x+3x﹣2=0的解是．11．（2014秋•嘉定区期末）若函数f（x）=（a﹣1）x是指数函数，则实数a的取值范围是．三．解答题（共3小题）12．已知指数函数f（x）=a x（a＞0，且a≠1）的图象过点（﹣2，），求函数的解析式．13．若指数函数的图象经过点（，4），求该函数的解析式及f（﹣）的值．14．比较a=（）0.2与b=2的大小．。

课时 4 指数函数一 . 指数与指数幂的运算（ 1）根式的观点①假如xna, a R, x R, n 1，且 nN ，那么 x 叫做 a 的 n 次方根． 当 n 是奇数时， a 的 n 次方根用符号 na 表示；当 n 是偶数时，正数 a 的正的 n 次方根用符号na 表示，负的 n 次方根用符号na表示； 0 的 n 次方根是 0；负数 a 没有 n 次方根．②式子 n a 叫做根式，这里 n 叫做根指数， a 叫做被开方数．当n 为奇数时， a 为随意实数；当 n 为偶数时， a．③根式的性质： (na )n a ；当 n 为奇数时， n a n a ；当 n 为偶数时， n a n | a |a (a 0) ．a (a 0)（ 2）分数指数幂的观点mna m (a①正数的正分数指数幂的意义是：a n 0, m,n N , 且 n 1) ．0 的正分数指数幂等于0．②m(1m1 ) m( a正数的负分数指数幂的意义是：a n)n n (0, m, n N , 且 n1) ．0 的负分数指aa数幂没存心义． 注意口诀： 底数取倒数，指数取相反数．（ 3）分数指数幂的运算性质①a r a s a r s (a 0, r , s R)② (ar) sa rs (a 0, r , s R)③(ab)ra rb r (a0,b 0, rR)二 . 指数函数及其性质（ 4）指数函数函数名称指数函数定义函数 ya x (a 0 且 a1) 叫做指数函数a 1a 1yy a xya xy图象y1y1(0,1)(0,1)OxOx定义域 R值域（0,+ ∞）过定点 图象过定点（0,1 ），即当 x=0 时， y=1．奇偶性非奇非偶单一性在 R 上是增函数在 R 上是减函数函数值的 y ＞ 1(x ＞ 0), y=1(x=0), 0＜ y ＜ 1(x ＜ 0)y ＞ 1(x ＜ 0), y=1(x=0), 0＜ y ＜ 1(x ＞ 0)变化状况a 变化对在第一象限内， a 越大图象越高，越凑近 y 轴； 在第一象限内， a 越小图象越高，越凑近 y 轴； 图象影响在第二象限内，a 越大图象越低，越凑近x 轴．在第二象限内，a 越小图象越低，越凑近x 轴．三 .例题剖析1.设 a 、 b 知足 0<a<b<1,以下不等式中正确的选项是 ( C)A.a a <a bB.b a <b bC.a a <b aD.b b <a b 分析： A 、B 不切合底数在 (0,1) 之间的单一性 ; C 、 D 指数同样 , 底小值小 . 应选 C. 2.若 0<a<1,则函数 y=a x 与 y=(a-1)x 2 的图象可能是 (D )分析： 当 0<a<1 时 ,y=a x 为减函数 ,a-1<0, 因此 y=(a-1)x2张口向下 , 应选 D.3.设指数函数 f(x)=a x (a>0 且 a ≠ 1),则以下等式中不正确的选项是 ( D )A.f(x+y)=f(x)f(y)f (x)B.f(x-y)=f ( y)C.f(nx)= ［ f(x) ］ nD.f ［ (xy) n ］ =［ f(x) ］ n ［ f(y) ］ n (n ∈ N * )分析： 易知 A 、 B 、 C 都正确 .对于 D,f ［(xy)n］ =a (xy)n , 而［ f(x) ］ n ·［f(y) ］ n =(a x ) n ·(a y ) n =a nx+ny , 一般状况下 D 不建立 .11 34.设 a= ( 3) 3,b= ( 4)4,c= ( 3) 4,则 a 、b 、 c 的大小关系是 ( B )43 2A.c<a<b3分析： a= ( )B.c<b<aC.b<a<cD.b<c<a1 111(8133( 4)3 ( 4) 4=b, b=(4) 4)4(3) 4 =c.∴ a>b>c.3 332725.设 f(x)=4 x -2x+1,则 f -1 (0)=______1____________. 分析： 令 f -1 (0)=a, 则 f(a)=0 即有 4a -2 · 2a =0.2a · (2 a -2)=0, 而 2a >0,∴ 2a =2 得 a=1.6.函数 y=a x-3 +4(a>0 且 a ≠ 1)的反函数的图象恒过定点 ______(5,3)____________.分析： 因 y=a x 的图象恒过定点 (0,1), 向右平移 3 个单位 , 向上平移 4 个单位获得 y=a x-3 +4 的图象 , 易知恒过定点 (3,5).故其反函数过定点 (5,3).10 x 10 x.证明 f(x) 在 R 上是增函数 .7.已知函数 f(x)=x10 x10x1010x102x1,设 x 1<x 2∈ R,则f(x 1)-f(x2)=10x 1 1010x 1 10x 110x 210 x 2102 x 11 102 x 21 2(102 x 1102 x2).x 110x2 10x2 102 x1 1102 x21(102 x11)(102 x 2 1)∵ y=10 x是增函数 ,∴ 10 2x 1 10 2x 2 <0.而 10 2x 1 +1>0, 102 x 2 +1>0,故当 x <x 时 ,f(x)-f(x )<0,1212即 f(x 1)<f(x 2). 因此 f(x) 是增函数 .8.若定义运算 a b=b, ab,则函数 f(x)=3 x3-x 的值域为 ( A )a, a b,A.(0,1]B. ［ 1,+∞ )C.(0,+ ∞ )D.(- ∞ ,+∞ )分析： 当 3x ≥3-x , 即 x ≥ 0 时 ,f(x)=3-x∈(0,1 ］ ;x-x, 即 x<0 时 ,f(x)=3x∈ (0,1).3 x , x 0, 当 3<3∴ f(x)=x值域为 (0,1).3x ,0,9.函数 y=a x 与 y=-a -x (a>0,a ≠1) 的图象 ( C )A. 对于 x 轴对称B.对于 y 轴对称C.对于原点对称D.对于直线 y=-x 对称分析： 可利用函数图象的对称性来判断两图象的关系.10.当 x ∈［ -1,1］时 ,函数 f(x)=3 x-2 的值域为 _______［ -5,1 ］ ___________.3分析： f(x) 在［ -1,1 ］上单一递加 .11.设有两个命题 :(1)对于 x 的不等式 x 2+2ax+4>0对全部 x ∈ R 恒建立 ;(2) 函数 f(x)=-(5-2a) x是减函数 .若命题 (1)和 (2)中有且仅有一个是真命题 ,则实数 a 的取值范围是 _______(- ∞ ,-2)__________.分析： (1) 为真命题=(2a) 2-16<0-2<a<2. (2)为真命题 5-2a>1 a<2.若 (1) 假 (2) 真 , 则 a ∈ (- ∞ ,-2]. 若 (1) 真 (2) 假, 则 a ∈ (-2,2)∩［ 2,+ ∞］=.故 a 的取值范围为 (- ∞ ,-2).12.求函数 y=4 -x -2-x +1,x ∈［ -3,2］的最大值和最小值 .解： 设 2-x=t, 由 x ∈［ -3,2 ］得 t ∈［ 1,8 ］ , 于是 y=t 2-t+1=(t-1)2+3. 当 t= 1时 ,y3 .424有最小值 这时 x=1.当 t=8 时 ,y 有最大值57.这时 x=-3.2413.已知对于 x 的方程 2a2x-2-7a x-1 +3=0 有一个根是 2,求 a 的值和方程其他的根 . 解： ∵ 2 是方程 2a2x-2-9a x-1+4=0 的根 , 将 x=2 代入方程解得 a= 1或 a=4.2(1) 当 a= 1时 , 原方程化为 2· ( 1)2x-2-9(1) x-1 +4=0.①222x-1 2令 y=( 1) , 方程①变成 2y -9y+4=0,2解得 y 1=4,y 2= 1.∴ ( 1) x-1 =42x=-1,2( 1 ) x-1 = 1x=2.22(2) 当 a=4 时 , 原方程化为 2· 42x-2 -9 · 4x-1 +4=0. ②令 t=4 x-1 , 则方程②变成 2t 2-9t+4=0. 解得 t 1=4,t 2= 1.x-12=4x=2,∴44x-1 = 1x=- 1 .22故方程此外两根是当 a= 1时 ,x=-1;1 .2当 a=4 时 ,x=-214.函数 y= (1) 3 4xx 2的单一递加区间是 ( D )3A. ［ 1,2］B.［ 2,3］C.(-∞ ,2]D.［ 2,+∞ )分析： 由于 y=3x2-4x+3 , 又 y=3t 单一递加 ,t=x 2-4x+3 在 x ∈［ 2,+ ∞ ) 上递加 , 故所求的递加区间为［ 2,+ ∞ ).15.已知 f(x)=3 x-b (2≤ x ≤ 4,b 为常数 ) 的图象经过点 (2,1), 则 F(x)=f 2(x)-2f(x) 的值域为 ( B )A. ［ -1,+∞ )B. ［ -1,63)C.［ 0,+∞ )D.(0,63 ］分析： 由 f(2)=1, 得 32-b =1,b=2,f(x)=3 x-2.∴ F (x)= ［ f(x)-1 ］2-1=(3 x-2 -1) 2-1. 令 t=3 x-2 ,2 ≤x ≤4.2∴g(t)=(t-1) - 1,t ∈［ 1,9 ］.2.1 指数函数练习1．以下各式中建立的一项A ． ( n)71n 7 m 7B ．12 ( 3)433m3C ． 4 x 3y 3( x y) 4D ．393321111 1 52．化简 (a 3 b 2 )( 3a 2 b 3 ) ( a 6 b 6 ) 的结果3D ． 9a 2 A ． 6aB ． aC ． 9a3．设指数函数 f ( x)a x ( a 0, a1) ，则以下等式中不正确的选项是f (x) A ． f(x+y)=f(x) ·f(y)B ． f （ x y ）f ( y)C ． f (nx)[ f ( x)]n (nQ )D ． f ( xy) n [ f ( x)] n ·[f ( y)] n1 4．函数 y (x5) 0 ( x 2)2A ． { x | x 5, x 2}B ． { x | x 2}C ． { x | x 5}D ． { x | 2 x 5或 x 5}（）（）（）(n N )（ ）5．若指数函数 y a x 在 [－ 1,1]上的最大值与最小值的差是1，则底数 a 等于 （）A ．15 B ．1 5 C ．15D ．5 122 226．当 a0 时，函数 y axb 和 yb ax 的图象只可能是（）7．函数 f ( x)2 |x| 的值域是（）A ． (0,1]B ． (0,1)C ． (0, )D ． R8．函数 f ( x)2 x 1, x 0，知足 f ( x)1的 x 的取值范围1x 2 , x（）A ． ( 1,1)B ． ( 1, )C ． { x | x 0或 x2}D ． { x | x 1或 x1}9．函数 y(1) x 2x2得单一递加区间是2（）A ．[ 1,1]B ． ( , 1]C ．[2,)D ．[ 1,2]2exe x210．已知 f ( x)（）2 ，则以下正确的选项是A ．奇函数，在 R 上为增函数B ．偶函数，在 R 上为增函数C ．奇函数，在 R 上为减函数D ．偶函数，在 R 上为减函数11．已知函数 f (x)的定义域是（1， 2），则函数 f (2 x ) 的定义域是.12．当 a ＞0 且 a ≠1 时，函数 f (x)=a x －2－ 3 必过定点.三、解答题：13．求函数 y1的定义域 .x5 x 1114．若 a ＞0， b ＞ 0，且 a+b=c ，求证： (1) 当r ＞1时， a r +b r ＜ c r ； (2) 当r ＜ 1时， a r +b r ＞ c r .a x 1 15．已知函数 f ( x)(a ＞1) .a x1（ 1）判断函数 f (x) 的奇偶性；（ 2）证明 f (x)在 (－∞， +∞ )上是增函数 .xa16．函数 f(x) ＝ a (a>0 ，且 a ≠1) 在区间 [1,2] 上的最大值比最小值大2，求 a 的值．参照答案一、 DCDDD AADDA二、 11． (0,1)；12． (2，－ 2) ；三、 13． 解：要使函数存心义一定：x 1 0x 1x0 x 0x 1∴ 定义域为 ： x xR 且 x0, x 1a rrrb r此中a1,0b114． 解：ba，c rcccc.r ＞1 ，a rb ra b 1，r r r当因此+b＜ c ；时c c c crrrrr当 r ＜ 1 时， aba b1， 因此 a +b ＞c .ccc c15． 解 ：(1)是奇函数 .(2) 设x ＜x ，则 f (x 1 )ax11 ax21 。

指数与指数函数知识点与题型归纳1．根式(1)根式的概念：若x n ＝a ，则x 叫做a 的n 次方根，其中n ＞1且n ∈N *.式子na 叫做根式，这里n 叫做根指数，a 叫做被开方数．(2)a 的n 次方根的表示；x n＝a ⇒⎩⎨⎧x ＝ n a (当n 为奇数且n >1时)，x ＝±n a (当n 为偶数且n >1时).2．有理数指数幂3a 变化对图象的影响 在第一象限内，从逆时针方向看图象，a 逐渐增大；在第二象限内，从逆时针方向看图象，a 逐渐减小．（1）画指数函数图象的三个关键点画指数函数y ＝a x (a >0，且a ≠1)的图象，应抓住三个关键点：(1，a )，(0,1)，⎪⎭⎫ ⎝⎛-a 1,1. （2）指数函数的图象与底数大小的比较如图是指数函数(1)y ＝a x ，(2)y ＝b x ，(3)y ＝c x ，(4)y ＝d x 的图象， 底数a ，b ，c ，d 与1之间的大小关系为c >d >1>a >b .由此我们可得到以下规律：在y 轴右(左)侧图象越高(低)，其底数越大．（3）指数函数y ＝a x (a ＞0，a ≠1)的图像和性质跟a 的取值有关，要特别注意应分a ＞1与0＜a ＜1来研究．题型一 指数幂的化简与求值1．化简3a a 的结果是________．2．若(2a －1)2＝3(1－2a )3，则实数a 的取值范围为________． 3.=+3-2-233___________4．已知24714===cba，则cb a 111+-＝________. 5. 已知14x x-+=，求1122x x -+及1x x --的值．题型二 指数函数的图象及应用类型一 与指数函数有关的图象辨析 6．函数|1|--=x ey |的大致图象是( )7．函数||1)(x e x f -=的图象大致是( )8．函数12+=x y 的图象是________(填序号)．类型二 指数函数图象的应用9．函数b a y x-=(a >0且a ≠1)的图象经过第二、三、四象限，则a b 的取值范围为( )A ．(1，＋∞)B ．(0，＋∞)C ．(0,1)D ．无法确定 10．函数33+=-x ay (a >0，且a ≠1)的图象过定点________．11. 若曲线13-=x y 与直线y ＝m 有两个不同交点，则实数m 的取值范围是________． 12．若条件变为：方程m x =-13||有两个不同实根，则实数m 的取值范围是________．13．若条件变为：函数m 13+-=x y 的图像不经过第二象限，则实数m 的取值范围是________． 14．函数xa y =(a >0且a ≠1)与函数y ＝(a －1)x 2－2x －1在同一个坐标系内的图象可能是( )15．已知函数xa y ⎪⎭⎫ ⎝⎛-=421的图象与指数函数xa y =的图象关于y 轴对称，则实数a 的值是___16．设函数⎩⎨⎧>≤+=0,20,1)(x x x x f x,则满足1)1()(>-+x f x f 的x 的取值范围是________． 17．已知实数a ，b 满足等式ba20202019=，下列五个关系式：①0＜b ＜a ；②a ＜b ＜0；③0＜a ＜b ；④b ＜a ＜0；⑤a ＝b .其中不可能成立的关系式有________(填序号)． 18．设2m ＝3n ，则m ，n 的大小关系一定是（ ）A ．m ＞nB ．m ＜nC ．m ≥nD ．以上答案都不对题型三 指数函数的性质及应用类型一 比较指数式大小19．已知2.12=a ，2.021-⎪⎭⎫⎝⎛=b ，2log 25=c ，则a ，b ，c 的大小关系为( )A ．b <a <cB ．c <a <bC ．c <b <aD ．b <c <a 20．已知xxx f --=22)(，4197-⎪⎭⎫ ⎝⎛=a ，5179⎪⎭⎫⎝⎛=b ，97log 2=c ，则f (a )，f (b )，f (c )的大小关系为( )A ．f (b )<f (a )<f (c )B ．f (c )<f (b )<f (a )C ．f (c )<f (a )<f (b )D ．f (b )<f (c )<f (a ) 21.设函数axx f -=2)(与xa x g =)((a ＞1且a ≠2)在区间(0，＋∞)上具有不同的单调性，则M ＝(a －1)0.2与1.01⎪⎭⎫⎝⎛=a N 的大小关系是( )A ．M ＝NB ．M ≤NC ．M ＜ND ．M ＞N 类型二 解不等式与方程 22．不等式1472-->x x a a(0<a <1)的解集为____________．23．设函数⎪⎩⎪⎨⎧≥<-⎪⎭⎫ ⎝⎛=0,0,721)(x x x x f x,若1)(<a f ，则实数a 的取值范围是( )A ．(－∞，－3)B ．(1，＋∞)C ．(－3,1)D ．(－∞，－3)∪(1，＋∞)24．当x ∈(－∞，－1]时，不等式024)(2<-⋅-xxm m 恒成立，则实数m 的取值范围是( )A ．(－2,1)B ．(－4,3)C ．(－3,4)D ．(－1,2) 25.方程11214=-+xx 的解为________．26. 若不等式0421>⋅++a xx在x ∈(－∞，1]时恒成立，则实数a 的取值范围是________．类型三 与指数函数有关的函数最值问题 27．函数y ＝3x 2－2x的值域为________．28．函数12221)(++-⎪⎭⎫ ⎝⎛=x x x f 的递减区间是________，值域是________．29．函数12141+⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛=xxy 在区间[－3,2]上的值域是________．类型四 与指数函数有关的函数单调性问题 30. 函数124)(+-=x xx f 的单调增区间是________．31. 已知函数|2|2)(m x x f -=(m 为常数)，若f (x )在区间[2，＋∞)上单调递增，则m 的取值范围是________． 32．函数221)(x x x f -⎪⎭⎫⎝⎛=的单调递增区间是( )A.⎥⎦⎤ ⎝⎛∞-21, B.⎥⎦⎤⎢⎣⎡21,0 C.⎪⎭⎫⎢⎣⎡+∞,21D.⎥⎦⎤⎢⎣⎡1,2133．若函数f (x )＝a |2x －4|(a >0，且a ≠1)，满足f (1)＝19，则f (x )的单调递减区间是( )A ．(－∞，2]B ．[2，＋∞)C ．[－2，＋∞)D ．(－∞，－2]34．设xe xf =)(，0＜a ＜b ，若()ab fp =，⎪⎭⎫⎝⎛+=2b a f q ，)()(b f a f r =，则下列关系式中正确的是( )A ．q ＝r ＜pB ．p ＝r ＜qC ．q ＝r ＞pD ．p ＝r ＞q35．若函数f (x )＝a x (a x －3a 2－1)(a >0，且a ≠1)在区间[0，＋∞)上是增函数，则实数a 的取值范围是( )A.⎥⎦⎤⎝⎛32,0 B.⎪⎪⎭⎫⎢⎣⎡1,33 C ．(]3,1 D.⎪⎭⎫⎢⎣⎡+∞,23 36．已知定义域为R 的函数abx f x x ++-=+122)(是奇函数．(1)求a ，b 的值；(2)若对任意的t ∈R ，不等式0)2()2(22<-+-k t f t t f 恒成立，求k 的取值范围．37．已知函数3241)(1+-=-x x x f λ(－1≤x ≤2)． (1)若23=λ，求函数)(x f 的值域； (2)若函数)(x f 的最小值是1，求实数λ的值．38．函数()4426xx f x +=--，其中[]0,3x ∈（1）求()f x 的最大值与最小值；（2）若存在[]00,3x ∈使()00f x a -≤成立，求实数a 的范围.39．设指数函数xm x f )2()(+=，幂函数32)1()(x m m x g ++=． （1）求m ；（2）设a ＜0，如果存在x 1，x 2∈[﹣2，2]，使得)()(21x g x af >，求a 的取值范围．2.解析：2a －12＝|2a －1|，31－2a3＝1－2a .因为|2a －1|＝1－2a .故2a －1≤0，所以a ≤12.3.解析：原式22(33)2(33)2(33)3324232(31)+++===-----22(33)2(1263)2266(33)(33)+===-+4.解析：由题设可得21a ＝14,21b＝7,21c ＝4，则2-11a b＝147＝2，∴2-+111a b c ＝2×4＝23，∴1a －1b ＋1c ＝3.5.解析：因为14x x-+=，所以 x ＞0，则112122()2426x x x x --+=++=+=，则11226x x-+=因为 1222()216x x x x --+=++=，则2214x x -+=，所以 1222()214212x x x x ---=+-=-=，所以11223x x--==±6.解析：因为－|x －1|≤0，所以0<e －|x －1|≤e 0，即0<y ＝e－|x －1|≤1，故选B.7.解析：选A 由f (x )＝1－e |x |是偶函数，其图象关于y 轴对称，排除B 、D.又e |x |≥1，所以f (x )的值域为 (－∞，0]，排除C.8.解析：由y ＝2x 的图象向左平移1个单位可得y ＝2x＋1的图象．答案：①9.解析：因为函数y ＝a x －b 的图象经过第二、三、四象限，所以函数y ＝a x －b 单调递减且其图象与y 轴的交点在y 轴的负半轴上．令x ＝0，则y ＝a 0－b ＝1－b ，由题意得⎩⎪⎨⎪⎧ 0<a <1，1－b <0，解得⎩⎪⎨⎪⎧0<a <1，b >1，故a b ∴(0,1)，故选C.10.解析：因为指数函数y ＝a x (a >0，且a ≠1)的图象过定点(0,1)，所以在函数y ＝a x －3＋3中， 令x －3＝0，得x ＝3，此时y ＝1＋3＝4，即函数y ＝a x －3＋3的图象过定点(3,4)．11.解析：曲线y ＝|3x －1|的图像是由函数y ＝3x 的图像向下平移一个单位长度后，再把位于x 轴下方的图像沿x 轴翻折到x 轴上方得到的，而直线y ＝m 的图像是平行于x 轴的一条直线，它的图像如图所示，由图像可得，如果曲线y ＝|3x －1|与直线y ＝m 有两个公共点，则m 的取值范围是(0,1)．12.解析：作出函数y ＝3|x |－1与y ＝m 的图像如图所示，数形结合可得m 的取值范围是(0，＋∞)．]13.解析：作出函数y ＝|3x －1|＋m 的图像如图所示．由图像知m ≤－1，即m ∴(－∞，－1]．14.解析：选C ；两个函数分别为指数函数和二次函数，其中二次函数过点(0，－1)，故排除A 、D ；二次函数的对称轴为直线x ＝1a －1，当0<a <1时，指数函数递减，1a －1<0，C 符合题意；当a >1时，指数函数递增，1a －1>0，B 不符合题意，选C. 15.解析：由两函数的图象关于y 轴对称，可知12a －4与a 互为倒数，即a2a －4＝1，解得a ＝4.16.解析：画出函数f (x )的大致图象如图所示，易知函数f (x )在(－∞，＋∞)上单调递增．又x >x －1，且x －(x －1)＝1，f (0)＝1，所以要使f (x )＋f (x －1)>1成立，结合函数f (x )的图象知只需x －1>－1，解得x >0.故所求x 的取值范围是(0，＋∞)．17.解析：作出y ＝2 019x 及y ＝2 020x 的图像如图所示，由图可知a ＞b ＞0，a ＝b ＝0或a ＜b ＜0时，有2 019a ＝2 020b ，故③④不可能成立．18.解：当m ＞n 时，因为函数y ＝2x 在R 上单调递增，所以2m ＝3n ＞2n ，所以（）n ＞1，所以m ＞n ＞0， 当m ＝n 时，（）n ＝1，所以m ＝n ＝0，当m ＜n 时，因为函数y ＝2x 在R 上单调递增，所以2m ＝3n ＜2n ， 所以（）n ＜1，所以n ＜0，则m ＜n ＜0，故选：D ．19.解析：因为2.021-⎪⎭⎫⎝⎛=b ＝20.2<21.2＝a ，所以a>b>1.又因为c ＝2log 52＝log 54<1，所以c<b<a.选C20.解析：易知f(x)＝2x －2－x 在R 上为增函数，又0797997514141>=⎪⎭⎫⎝⎛>⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=-b a ，c ＝log 279<0， 则a>b>c ，所以f(c)<f(b)<f(a)． 21.因为f (x )＝x 2－a与g (x )＝a x (a ＞1且a ≠2)在区间(0，＋∞)上具有不同的单调性，所以a ＞2，所以M ＝(a －1)0.2＞1，111.0<⎪⎭⎫⎝⎛=a N ，所以M ＞N .故选D.22.解析：因为y ＝a x (0<a <1)为减函数，所以2x －7<4x －1，解得x >－3；答案为(－3，＋∞)点评：(1)a f(x)＝a g(x)⇔f(x)＝g(x)．(2)a f(x)＞a g(x)，当a ＞1时，等价于f(x)＞g(x)；当0＜a ＜1时，等价于f(x)＜g(x)．23.解析：当a <0时，不等式f (a )<1可化为1721<-⎪⎭⎫ ⎝⎛a ，即821<⎪⎭⎫ ⎝⎛a ，即32121-⎪⎭⎫⎝⎛<⎪⎭⎫ ⎝⎛a ，因为0<12<1，所以a>－3，此时－3<a<0；当a≥0时，不等式f(a)<1可化为a<1，所以0≤a<1. 故a 的取值范围是(－3,1)．24.解析：因为(m 2－m )·4x －2x <0在(－∞，－1]上恒成立．所以(m 2－m )<12x 在x ∴(－∞，－1]上恒成立．因为y ＝12x 在(－∞，－1]上单调递减，所以当x ∴(－∞，－1]时，y ＝12x ≥2，所以m 2－m <2，所以－1<m <2.选D25.解析：当x ≥0时，原方程化为4x ＋2x －12＝0，即(2x )2＋2x －12＝0.∴(2x －3)(2x ＋4)＝0，所以2x ＝3，即x ＝log 23.当x ＜0时，原方程化为4x －2x －10＝0.令t ＝2x ，则t 2－t －10＝0(0＜t ＜1)．由求根公式得t ＝1±1＋402均不符合题意，故x ＜0时，方程无解．26.解析：从已知不等式中分离出实数a ，得⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛->x x a 2141.因为函数x y ⎪⎭⎫ ⎝⎛=41和xy ⎪⎭⎫⎝⎛=21在R 上都是减函数，所以当x ∴(－∞，1]时，4141≥⎪⎭⎫ ⎝⎛x，2121≥⎪⎭⎫ ⎝⎛x，所以4321412141=+≥⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛xx，从而得432141-≤⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-x x .故实数a 的取值范围为a ＞－34.即⎪⎭⎫⎝⎛+∞-,4327.解析：设u ＝x 2－2x ，则y ＝3u ，u ＝x 2－2x ＝(x －1)2－1≥－1，所以y ＝3u ≥3－1＝13，所以函数y ＝3x 2－2x 的值域是⎪⎭⎫⎢⎣⎡+∞,31.28.解析：令u ＝－x 2＋2x ＋1，则u ＝－(x －1)2＋2.又uy ⎪⎭⎫ ⎝⎛=21在R 上是减函数，则函数12221)(+=-⎪⎭⎫ ⎝⎛=x x x f 的递减区间为函数u ＝－x 2＋2x ＋1的增区间．由此函数f (x )的递减区间为(－∞，1]．因为u ≤2，则4121)(2=⎪⎭⎫⎝⎛≥x f ，即函数f (x )的值域为⎪⎭⎫⎢⎣⎡+∞,41。

指数与指数函数知识点与例题讲解【基础知识回顾】一、指数1、根式：当n 为奇数，a a n n =；当n 为偶数，⎩⎨⎧<-≥==00a a a a a a n n ，，.2、指数运算 (1)分数指数幂()10>∈>=*n N n m a a a n mnm，且，，； ()1011>∈>==*-n N n m a a aanmnm nm ，且，，.(2)指数幂的运算性质①()Q s r a aa a sr sr∈>=•+，，0； ②()Q s r a a aa s r s r∈>=-，，0；③()()Q s r a a a rs sr∈>=，，0； ④()()Q r b a b a ab r r r∈>>=，，00.二、指数函数1、定义：一般地，函数()10≠>=a a a y x ，且叫做指数函数，其中x 是自变量，函数的定义域是R .2、图像和性质1>a 10<<a图像性质定义域： 值域：过定点 ，即当0=x 时，1=y在R 上是在R 上是非奇非偶函数3、同底的指数函数x a y =与对数函数x y a log =互为反函数，它们的图像关于直线x y =对称. 三、立方和差公式()()2233y xy x y x y x +-+=+，()()2233y xy x y x y x ++-=-.【课前小测】1、233等于（ ） A 、2 B 、33 C 、327 D 、27 2、52-a等于（ ） A 、52-aB 、25aC 、52aD 、25a -3、下列函数是指数函数的是（ ） A 、2x y = B 、x y 2= C 、12+=x y D 、x y 23⨯=4、函数32-=x y 的定义域为（ ） A 、[)+∞,3 B 、R C 、()+∞,3 D 、()+∞,05、使代数式041)73()2(-+--x x 有意义，则x 取值范围是 .考点一 ：比较大小例1、比较下列各题中两个数的大小：⑴8.03 7.03 ⑵1.075.0- 1.075.0 ⑶6.08.1 6.18.0 ⑷3231-⎪⎭⎫ ⎝⎛ 532-【解析】⑴因为x y 3=在R 上是增函数，且7.08.0>，所以>8.037.03。

选版指数及指数函数1、指数与指数幂的运算 （1）根式的概念①如果,,,1n x a a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．当n 是奇数时，a 的n当n 是偶数时，正数a 的正的n n 次方根用符号 0的n 次方根是0；负数a 没有n 次方根．根式，这里n 叫做根指数，a 叫做被开方数． 当n 为奇数时，a 为任意实数；当n 为偶数时，0a ≥． ③根式的性质：n a =；当n a =；当n 为偶数时，(0)|| (0) a a a a a ≥⎧==⎨-<⎩． （2）分数指数幂的概念①正数的正分数指数幂是：0,,,m na a m n N +=>∈且1)n >.②正数的负分数指数幂是： 1()0,,,mm n n aa m n N a -+==>∈且1)n >． 0的正分数指数幂等于0, 0的负分数指数幂没有意义． （3）分数指数幂的运算性质①(0,,)r s r s a a a a r s R +⋅=>∈ ②r a ÷s a =r s a -()0,,a r s R >∈； ③()rs a =rs a ()0,,a r s R >∈；④()rab =r r a b ⋅()0,0,a b r R >>∈； 2、指数函数及其性质定义函数(0x y a a =>且1)a ≠叫做指数函数图象1a >01a <<定义域 R 值域 （0,+∞）过定点 图象过定点（0,1），即当x=0时，y=1．奇偶性 非奇非偶单调性在R 上是增函数在R 上是减函数函数值的 变化情况y ＞1(x ＞0), y=1(x=0), 0＜y ＜1(x ＜0)y ＞1(x ＜0), y=1(x=0), 0＜y ＜1(x ＞0)a 变化对 图象的影 响 在第一象限内，a 越大图象越高，越靠近y 轴；在第二象限内，a 越大图象越低，越靠近x 轴．在第一象限内，a 越小图象越高，越靠近y 轴；在第二象限内，a 越小图象越低，越靠近x 轴．例题讲解 一、指数1、化简［32)5(-］43的结果为 （ ）A ．5B ．5C ．－5D ．－52、2115113366221()(3)()=3a b a b a b -÷__________.二、指数函数3、已知指数函数图像经过点)3,1(-p ，则=)3(f 4xa y =xy(0,1)O1y =x a y =xy(0,1)O1y =5.6、若21(5)2x f x -=-，则(125)f = . 三、指数函数的图像问题7、若函数(1)(0,1)x y a b a a =-+>≠的图像经过第一、三、四象限，则一定有（ ） A ．01>>b a 且 B ．010<<<b a 且C ．010><<b a 且D ．11>>b a 且8、函数()2()1xf x a =-在R 上是减函数，则a 的取值范围是（ ） A 、1>a B 、2<a C 、2a < D 、12a <<9、当a ≠0时，函数y ax b =+和y b ax =的图象只可能是（ ）四、定义域与值域问题 10、求下列函数的定义域和值域 （1）x xy 212+= （2）222)31(-=x y （4）2221++-⎪⎭⎫ ⎝⎛=x x y （5）1121+-⎪⎭⎫⎝⎛=x x y11、下列函数中，值域为()+∞,0的函数是（ ）xy A 23.= 12.-=x y B 12.+=x y C xy D -⎪⎭⎫⎝⎛=221.12、设集合2{|3,},{|1,}x S y y x R T y y x x R ==∈==-∈，则S T 是 （ ）A 、∅B 、TC 、SD 、有限集 13、若函数()1222-=--aax xx f 的定义域为R ，则实数a 的取值范围 .14、若函数0322≤--x x ，求函数x x y 4222⋅-=+的最大值和最小值.五、比较大小问题15、设.)32(,)32(2.15.1-==b a 那么实数a 、b 与1的大小关系正确的是 ( )A. 1<<a bB. 1<<b aC. a b <<1D. b a <<116、比较大小3221）（，3251）（，3121）（六、定点问题17、函数)10(33≠>+=-a a a y x 且的图象恒过定点___________. 七、单调性问题18、函数xx y 2221-⎪⎭⎫⎝⎛=的单调增区间为_____________19、函数)10()(≠>=a a a x f x 且在区间]2,1[上的最大值比最小值大2a，则=a ________ 20、函数1)1(222)(+--=x a x x f 在区间),5[+∞上是增函数，则实数a 的取值范围是 ( )A. [6,+)∞B. ),6(+∞C. ]6,(-∞D. )6,(-∞ 21、设01a <<，解关于x 的不等式22232223xx xx a a -++->.22、已知函数22513x x y ++⎛⎫= ⎪⎝⎭，求其单调区间及值域.八、函数的奇偶性问题23、函数2121x x y -=+是（ ）A 、奇函数B 、偶函数C 、既奇又偶函数D 、非奇非偶函数24、2()1()(0)21x F x f x x ⎛⎫=+⋅≠ ⎪-⎝⎭是偶函数，且()f x 不恒等于零，则()f x ( )A 、是奇函数B 、可能是奇函数，也可能是偶函数C 、是偶函数D 、不是奇函数，也不是偶函数 25、若函数141)(++=xa x f 是奇函数，则=a _________ 26、如果函数)(x f 在区间[]a a 24,2--上是偶函数，则a =_________（一）指数与指数函数1．根式（1）根式的概念（2）．两个重要公式①⎪⎩⎪⎨⎧⎩⎨⎧<-≥==)0()0(||a a a a a aa nn ；②a a n n =)(（注意a 必须使n a 有意义）。

指数及指数函数（一）指数与指数幂的运算1．根式的概念一般地，如果a x n=，那么x 叫做a 的n 次方根，其中n >1，且n ∈N *．当n 是奇数时，正数的n 次方根是一个正数，负数的n 次方根是一个负数．此时，a 的n 次方根用符号n a 表示．式子n a 叫做根式，这里n 叫做根指数，a 叫做被开方数．当n 是偶数时，正数的n 次方根有两个，这两个数互为相反数．此时，正数a 的正的n 次方根用符号n a 表示，负的n 次方根用符号－n a 表示．正的n 次方根与负的n 次方根可以合并成±n a （a >0）．由此可得：负数没有偶次方根；0的任何次方根都是0，记作00=n ． 结论：当n 是奇数时，a a n n =当n 是偶数时，⎩⎨⎧<≥-==)0()0(||a a a a a a n n2．分数指数幂)1,,,0(*>∈>=n N n m a a an m nm)1,,,0(11*>∈>==-n N n m a a aanmnm nm0的正分数指数幂等于0，0的负分数指数幂没有意义 3．有理指数幂的运算性质 （1）r a ·sr r aa += ),,0(Q s r a ∈>；（2）rssr a a =)( ),,0(Q s r a ∈>； （3）srra a ab =)(),0,0(Q r b a ∈>>．（一）指数函数的概念一般地，函数)1a ,0a (a y x≠>=且叫做指数函数，其中x 是自变量，函数的定义域为R ．注意：○1 指数函数的定义是一个形式定义 ○2 注意指数函数的底数的取值范围，底数为什么不能是负数、零和1．（二）指数函数的图象和性质注意内容：定义域、值域、特殊点、单调性、最大（小）值、奇偶性．指数函数的图象如右图：4图象特征函数性质1a > 1a 0<< 1a > 1a 0<<向x 、y 轴正负方向无限延伸 函数的定义域为R 图象关于原点和y 轴不对称 非奇非偶函数函数图象都在x 轴上方 函数的值域为R +函数图象都过定点（0，1） 1a 0=自左向右看， 图象逐渐上升 自左向右看， 图象逐渐下降 增函数减函数在第一象限内的图象纵坐标都大于1 在第一象限内的图象纵坐标都小于1 1a ,0x x >> 1a ,0x x <>在第二象限内的图象纵坐标都小于1 在第二象限内的图象纵坐标都大于1 1a ,0x x <<1a ,0x x ><图象上升趋势是越来越陡图象上升趋势是越来越缓函数值开始增长较慢，到了某一值后增长速度极快；函数值开始减小极快，到了某一值后减小速度较慢；利用函数的单调性，结合图象还可以看出：（1）在[a ，b]上，)1a 0a (a )x (f x≠>=且值域是)]b (f ),a (f [或)]a (f ),b (f [； （2）若0x ≠，则1)x (f ≠；)x (f 取遍所有正数当且仅当R x ∈； （3）对于指数函数)1a 0a (a )x (f x ≠>=且，总有a )1(f =； （4）当1a >时，若21x x <，则)x (f )x (f 21<；指数与指数函数练习题一、选择题：1、化简1111132168421212121212-----⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，结果是（ ） A 、11321122--⎛⎫- ⎪⎝⎭B 、113212--⎛⎫- ⎪⎝⎭ C 、13212-- D 、1321122-⎛⎫- ⎪⎝⎭2、44等于（ ） A 、16a B 、8a C 、4a D 、2a3、若1,0a b ><,且b b a a -+=则b b a a --的值等于（ ）A 、6B 、2±C 、2-D 、24、函数()2()1xf x a =-在R 上是减函数，则a 的取值范围是（ ）A 、1>a B 、2<a C、a <、1a <<5、下列函数式中，满足1(1)()2f x f x +=的是( )A 、 1(1)2x +B 、14x + C 、2x D 、2x -6、已知01,1a b <<<-,则函数xy a b =+的图像必定不经过（ ） A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限7、一批设备价值a 万元，由于使用磨损，每年比上一年价值降低%b ，则n 年后这批设备的价值为（ ）A 、(1%)na b -B 、(1%)a nb -C 、[1(%)]n a b -D 、(1%)na b -8、若103,104x y ==，则10x y -= 。

指数及指数函数 （一）指数与指数幂的运算1．根式的概念一般地，如果a x n =，那么x 叫做a 的n 次方根，其中n >1，且n ∈N *． 当n 是奇数时，正数的n 次方根是一个正数，负数的n 次方根是一个负数．此时，a 的n 次方根用符号n a 表示．式子n a 叫做根式，这里n 叫做根指数，a 叫做被开方数．当n 是偶数时，正数的n 次方根有两个，这两个数互为相反数．此时，正数a 的正的n 次方根用符号n a 表示，负的n 次方根用符号－n a 表示．正的n 次方根与负的n 次方根可以合并成±n a （a >0）． 由此可得：负数没有偶次方根；0的任何次方根都是0，记作00=n ．结论：当n 是奇数时，a a n n =当n 是偶数时，⎩⎨⎧<≥-==)0()0(||a a a a a a n n 2．分数指数幂0的正分数指数幂等于0，0的负分数指数幂没有意义3．有理指数幂的运算性质（1）r a ·s r r aa += ),,0(Q s r a ∈>； （2）rs s r a a =)( ),,0(Q s r a ∈>；（3）s r r a a ab =)(),0,0(Q r b a ∈>>． （一）指数函数的概念一般地，函数)1a ,0a (a y x≠>=且叫做指数函数，其中x 是自变量，函数的定义域为R ． 注意：○1 指数函数的定义是一个形式定义 ○2 注意指数函数的底数的取值范围，底数为什么不能是负数、零和1．（二）指数函数的图象和性质注意内容：定义域、值域、特殊点、单调性、最大（小）值、奇偶性．指数函数的图象如右图：4．指数函数的性质利用函数的单调性，结合图象还可以看出：（1）在[a ，b]上，)1a 0a (a )x (f x ≠>=且值域是)]b (f ),a (f [或)]a (f ),b (f [；（2）若0x ≠，则1)x (f ≠；)x (f 取遍所有正数当且仅当R x ∈；（3）对于指数函数)1a 0a (a )x (f x ≠>=且，总有a )1(f =；（4）当1a >时，若21x x <，则)x (f )x (f 21<；指数与指数函数练习题一、选择题：1、化简1111132168421212121212-----⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，结果是（ ） A 、11321122--⎛⎫- ⎪⎝⎭B 、113212--⎛⎫- ⎪⎝⎭C 、13212--D 、1321122-⎛⎫- ⎪⎝⎭ 2、44等于（ ） A 、16a B 、8a C 、4a D 、2a 3、若1,0ab ><,且b b a a -+=则b b a a --的值等于（ ）A 、6B 、2±C 、2-D 、24、函数()2()1xf x a =-在R 上是减函数，则a 的取值范围是（ ） A 、1>a B 、2<a C、a <、1a <<5、下列函数式中，满足1(1)()2f x f x +=的是( )A 、 1(1)2x +B 、14x + C 、2x D 、2x - 6、已知01,1a b <<<-,则函数x y a b =+的图像必定不经过（ ） A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限7、一批设备价值a 万元，由于使用磨损，每年比上一年价值降低%b ，则n 年后这批设备的价值为（ ）A 、(1%)na b -B 、(1%)a nb -C 、[1(%)]n a b -D 、(1%)n a b - 8、若103,104x y ==，则10x y -= 。

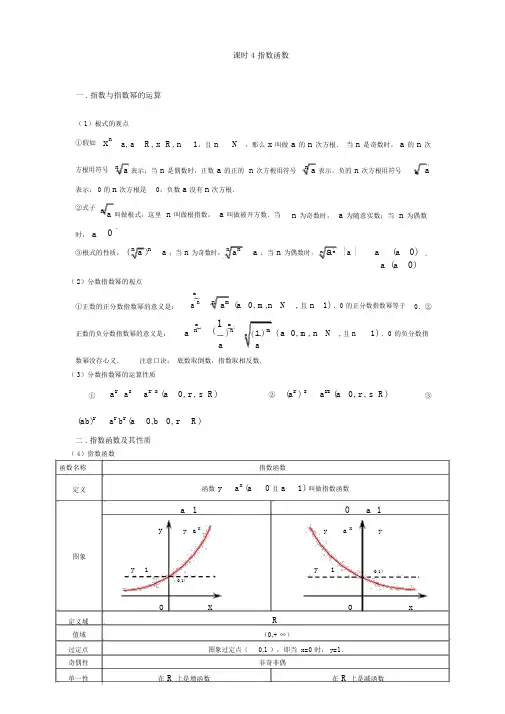
课时4指数函数一. 指数与指数幂的运算（1）根式的概念 ①如果,,,1nxa a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．当n 是奇数时，a 的n表示；当n 是偶数时，正数a 的正的nn次方根用符号0的n 次方根是0；负数a 没有n 次方根．n 叫做根指数，a 叫做被开方数．当n 为奇数时，a 为任意实数；当n 为偶数时，0a ≥．③根式的性质：n a =；当na =；当n(0)|| (0)a a a a a ≥⎧==⎨-<⎩．（2）分数指数幂的概念①正数的正分数指数幂的意义是：0,,,m naa m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是： 1()0,,,m m nn aa m n N a -+==>∈且1)n >．0的负分数指数幂没有意义．注意口诀：底数取倒数，指数取相反数． （3）分数指数幂的运算性质①(0,,)rs r s aa a a r s R +⋅=>∈②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r r ab a b a b r R =>>∈二.指数函数及其性质（4）指数函数a 变化对图象影响在第一象限内，a 越大图象越高，越靠近y 轴； 在第二象限内，a 越大图象越低，越靠近x 轴． 在第一象限内，a 越小图象越高，越靠近y 轴； 在第二象限内，a 越小图象越低，越靠近x 轴．三.例题分析1.设a 、b 满足0<a<b<1,下列不等式中正确的是(C) A.a a <a b B.b a <b b C.a a <b a D.b b <a b解析：A 、B 不符合底数在(0,1)之间的单调性;C 、D 指数相同,底小值小.故选C. 2.若0<a<1,则函数y=a x 与y=(a-1)x 2的图象可能是(D)解析：当0<a<1时,y=a x为减函数,a-1<0,所以y=(a-1)x 2开口向下,故选D.3.设指数函数f(x)=a x (a>0且a ≠1),则下列等式中不正确的是(D) A.f(x+y)=f(x)f(y)B.f(x-y)=)()(y f x f C.f(nx)=［f(x)］n D.f ［(xy)n ］=［f(x)］n ［f(y)］n (n ∈N *) 解析：易知A 、B 、C 都正确. 对于D,f ［(xy)n］=a(xy)n,而［f(x)］n·［f(y)］n=(a x )n·(a y)n=anx+ny,一般情况下D 不成立.4.设a=31)43(-,b=41)34(-,c=43)23(-,则a 、b 、c 的大小关系是(B)A.c<a<bB.c<b<aC.b<a<cD.b<c<a解析：a=413131)34()34()43(>=-=b,b=434141)23()278()34(-=>=c.∴a>b>c.5.设f(x)=4x -2x+1,则f -1(0)=______1____________. 解析：令f -1(0)=a,则f(a)=0即有4a-2·2a=0.2a·(2a-2)=0,而2a>0,∴2a=2得a=1.6.函数y=a x-3+4(a>0且a ≠1)的反函数的图象恒过定点______(5,3)____________.解析：因y=a x的图象恒过定点(0,1),向右平移3个单位,向上平移4个单位得到y=a x-3+4的图象,易知恒过定点(3,5).故其反函数过定点(5,3).7.已知函数f(x)=xx xx --+-10101010.证明f(x)在R 上是增函数.证明：∵f(x)=1101101010101022+-=+---x x xx x x , 设x 1<x 2∈R ,则f(x 1)-f(x 2)=)110)(110()1010(21101101101101010101010101010212122112222111122222222++-=+--+-=+--+-----x x x x x x x x x x x x x x x x . ∵y=10x 是增函数, ∴21221010x x -<0. 而1210x +1>0,2210x +1>0, 故当x 1<x 2时,f(x 1)-f(x 2)<0, 即f(x 1)<f(x 2). 所以f(x)是增函数.8.若定义运算a ⊗b=⎩⎨⎧<≥,,,,b a a b a b 则函数f(x)=3x ⊗3-x 的值域为(A)A.(0,1]B.［1,+∞)C.(0,+∞)D.(-∞,+∞)解析：当3x ≥3-x ,即x ≥0时,f(x)=3-x ∈(0,1］;当3x<3-x,即x<0时,f(x)=3x∈(0,1).∴f(x)=⎩⎨⎧<≥-,0,3,0,3x x x x 值域为(0,1).9.函数y=a x 与y=-a -x (a>0,a ≠1)的图象(C) A.关于x 轴对称B.关于y 轴对称 C.关于原点对称D.关于直线y=-x 对称解析：可利用函数图象的对称性来判断两图象的关系.10.当x ∈［-1,1］时,函数f(x)=3x -2的值域为_______［-35,1］___________. 解析：f(x)在［-1,1］上单调递增.11.设有两个命题:(1)关于x 的不等式x 2+2ax+4>0对一切x ∈R 恒成立;(2)函数f(x)=-(5-2a)x 是减函数.若命题(1)和(2)中有且仅有一个是真命题,则实数a 的取值范围是_______(-∞,-2)__________.解析：(1)为真命题⇔Δ=(2a)2-16<0⇔-2<a<2.(2)为真命题⇔5-2a>1⇔a<2.若(1)假(2)真,则a ∈(-∞,-2].若(1)真(2)假,则a ∈(-2,2)∩［2,+∞］=∅. 故a 的取值范围为(-∞,-2).12.求函数y=4-x -2-x +1,x ∈［-3,2］的最大值和最小值. 解：设2-x =t,由x ∈［-3,2］得t ∈［41,8］,于是y=t 2-t+1=(t-21)2+43.当t=21时,y 有最小值43.这时x=1.当t=8时,y 有最大值57.这时x=-3. 13.已知关于x 的方程2a 2x-2-7a x-1+3=0有一个根是2,求a 的值和方程其余的根. 解：∵2是方程2a 2x-2-9a x-1+4=0的根,将x=2代入方程解得a=21或a=4. (1)当a=21时,原方程化为2·(21)2x-2-9(21)x-1+4=0.① 令y=(21)x-1,方程①变为2y 2-9y+4=0, 解得y 1=4,y 2=21.∴(21)x-1=4⇒x=-1,(21)x-1=21⇒x=2. (2)当a=4时,原方程化为2·42x-2-9·4x-1+4=0.② 令t=4x-1,则方程②变为2t 2-9t+4=0.解得t 1=4,t 2=21. ∴4x-1=4⇒x=2, 4x-1=21⇒x=-21. 故方程另外两根是当a=21时,x=-1; 当a=4时,x=-21. 14.函数y=243)31(x x -+-的单调递增区间是(D) A.［1,2］B.［2,3］C.(-∞,2]D.［2,+∞)解析：因为y=3x2-4x+3,又y=3t 单调递增,t=x 2-4x+3在x∈［2,+∞)上递增,故所求的递增区间为［2,+∞).15.已知f(x)=3x-b (2≤x ≤4,b 为常数)的图象经过点(2,1),则F(x)=f 2(x)-2f(x)的值域为(B) A.［-1,+∞)B.［-1,63) C.［0,+∞)D.(0,63］解析：由f(2)=1,得32-b =1,b=2,f(x)=3x-2. ∴F(x)=［f(x)-1］2-1=(3x-2-1)2-1. 令t=3x-2,2≤x≤4.∴g(t)=(t -1)2-1,t∈［1,9］. ∴所求值域为［-1,63］.2.1指数函数练习1．下列各式中成立的一项（）A ．7177)(m n mn= B ．31243)3(-=-C ．43433)(y x y x +=+D ．3339=2．化简)31()3)((656131212132b a b a b a ÷-的结果（）A ．a 6B ．a -C ．a 9-D ．29a3．设指数函数)1,0()(≠>=a a a x f x ，则下列等式中不正确的是（） A ．f (x +y )=f(x )·f (y ) B ．)()(y f x f y x f =-）（ C ．)()]([)(Q n x f nx f n∈=D ．)()]([·)]([)(+∈=N n y f x f xy f n n n4．函数21)2()5(--+-=x x y（）A ．}2,5|{≠≠x x xB ．}2|{>x xC ．}5|{>x xD ．}552|{><<x x x 或5．若指数函数x a y =在[－1,1]上的最大值与最小值的差是1，则底数a 等于 （）A ．251+B ．251+- C ．251± D ．215± 6．当a ≠0时，函数y ax b =+和y b ax =的图象只可能是 （）7．函数||2)(x x f -=的值域是（）A ．]1,0(B ．)1,0(C ．),0(+∞D ．R8．函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ，满足1)(>x f 的x 的取值范围 （）A ．)1,1(-B ．),1(+∞-C ．}20|{-<>x x x 或D ．}11|{-<>x x x 或9．函数22)21(++-=x x y 得单调递增区间是 （）A ．]21,1[-B ．]1,(--∞C ．),2[+∞D ．]2,21[10．已知2)(xx e e x f --=，则下列正确的是 （）A ．奇函数，在R 上为增函数B ．偶函数，在R 上为增函数C ．奇函数，在R 上为减函数D ．偶函数，在R 上为减函数 11．已知函数f (x )的定义域是（1，2），则函数)2(x f 的定义域是. 12．当a ＞0且a ≠1时，函数f (x )=a x －2－3必过定点. 三、解答题：13．求函数y x x =--1511的定义域.14．若a ＞0，b ＞0，且a +b =c ，求证：(1)当r ＞1时，a r +b r ＜c r ；(2)当r ＜1时，a r +b r ＞c r .15．已知函数11)(+-=x x a a x f (a ＞1).（1）判断函数f (x )的奇偶性；（2）证明f (x )在(－∞，+∞)上是增函数.16．函数f(x)＝a x(a>0，且a ≠1)在区间[1,2]上的最大值比最小值大，求a 的值．参考答案一、DCDDDAADDA二、11．(0,1)；12．(2，－2)； 三、13．解：要使函数有意义必须：∴定义域为：{}x x R x x ∈≠≠且01,14．解：rrrrr c b c a c b a ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+，其中10,10<<<<cbc a . 当r ＞1时，1=+<⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr，所以a r +b r ＜c r； 当r ＜1时，1=+>⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr ，所以a r +b r ＞c r . 15．解：(1)是奇函数.(2)设x 1＜x 2，则1111)()(221121+--+-=-x x x x a a a a x f x f 。

指数及指数函数（一）指数与指数幂的运算1．根式的概念一般地，如果a x n=，那么x 叫做a 的n 次方根，其中n >1，且n ∈N *．当n 是奇数时，正数的n 次方根是一个正数，负数的n 次方根是一个负数．此时，a 的n 次方根用符号n a 表示．式子n a 叫做根式，这里n 叫做根指数，a 叫做被开方数．当n 是偶数时，正数的n 次方根有两个，这两个数互为相反数．此时，正数a 的正的n 次方根用符号n a 表示，负的n 次方根用符号－n a 表示．正的n 次方根与负的n 次方根可以合并成±n a （a >0）．由此可得：负数没有偶次方根；0的任何次方根都是0，记作00=n ． 结论：当n 是奇数时，a a n n =当n 是偶数时，⎩⎨⎧<≥-==)0()0(||a a a a a a n n2．分数指数幂)1,,,0(*>∈>=n N n m a a an m nm)1,,,0(11*>∈>==-n N n m a a aanmnm nm0的正分数指数幂等于0，0的负分数指数幂没有意义 3．有理指数幂的运算性质 （1）r a ·sr r aa += ),,0(Q s r a ∈>；（2）rssr a a =)( ),,0(Q s r a ∈>； （3）srra a ab =)(),0,0(Q r b a ∈>>．（一）指数函数的概念一般地，函数)1a ,0a (a y x≠>=且叫做指数函数，其中x 是自变量，函数的定义域为R ．注意：○1 指数函数的定义是一个形式定义 ○2 注意指数函数的底数的取值范围，底数为什么不能是负数、零和1．（二）指数函数的图象和性质注意内容：定义域、值域、特殊点、单调性、最大（小）值、奇偶性．指数函数的图象如右图：4图象特征函数性质1a > 1a 0<< 1a > 1a 0<<向x 、y 轴正负方向无限延伸 函数的定义域为R 图象关于原点和y 轴不对称 非奇非偶函数函数图象都在x 轴上方 函数的值域为R +函数图象都过定点（0，1） 1a 0=自左向右看， 图象逐渐上升 自左向右看， 图象逐渐下降 增函数减函数在第一象限内的图象纵坐标都大于1 在第一象限内的图象纵坐标都小于1 1a ,0x x >> 1a ,0x x <>在第二象限内的图象纵坐标都小于1 在第二象限内的图象纵坐标都大于1 1a ,0x x <<1a ,0x x ><图象上升趋势是越来越陡图象上升趋势是越来越缓函数值开始增长较慢，到了某一值后增长速度极快；函数值开始减小极快，到了某一值后减小速度较慢；利用函数的单调性，结合图象还可以看出：（1）在[a ，b]上，)1a 0a (a )x (f x≠>=且值域是)]b (f ),a (f [或)]a (f ),b (f [； （2）若0x ≠，则1)x (f ≠；)x (f 取遍所有正数当且仅当R x ∈； （3）对于指数函数)1a 0a (a )x (f x ≠>=且，总有a )1(f =； （4）当1a >时，若21x x <，则)x (f )x (f 21<；指数与指数函数练习题一、选择题：1、化简1111132168421212121212-----⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，结果是（ ） A 、11321122--⎛⎫- ⎪⎝⎭B 、113212--⎛⎫- ⎪⎝⎭ C 、13212-- D 、1321122-⎛⎫- ⎪⎝⎭2、44等于（ ） A 、16a B 、8a C 、4a D 、2a3、若1,0a b ><,且b b a a -+=则b b a a --的值等于（ ）A 、6B 、2±C 、2-D 、24、函数()2()1xf x a =-在R 上是减函数，则a 的取值范围是（ ）A 、1>a B 、2<a C、a <、1a <<5、下列函数式中，满足1(1)()2f x f x +=的是( )A 、 1(1)2x +B 、14x + C 、2x D 、2x -6、已知01,1a b <<<-,则函数xy a b =+的图像必定不经过（ ） A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限7、一批设备价值a 万元，由于使用磨损，每年比上一年价值降低%b ，则n 年后这批设备的价值为（ ）A 、(1%)na b -B 、(1%)a nb -C 、[1(%)]n a b -D 、(1%)na b -8、若103,104x y ==，则10x y -= 。