中考数学一轮复习第15讲二次函数与一元二次方程导学1案22

教学重点：探索一次函数图象与一元二次方程的关系，理解抛物线与x轴交点情况。

教学难点：函数方程x轴交点，三者之间的关系的理解与运用。

当球飞行0秒和4秒时，它的高度为0米.
即0秒时球地面飞出，4秒时球落回地面.
5.一般地，从二次函数
y=ax2+bx+c的
图象可知：如果抛物线y=与x轴有公共点（x0，0），那么x0就是方程
ax2+bx+c=0的
一个根。

抛物线与x轴的三种位置关系：没有公共点，有一个公共点，有两个公共点。

这对应着一元二次方程根的三种情况：没有实数根，有两个相等的实数根，有两个不等的实数根。

环节3
当堂练习
1.若抛物线
26
y x x m
=-+与x轴1.学生独立完成。

2.小组交流讨论
1.展示学生实
践结果。

预设：部分
学生在做的
过程中遇到。

备课时间：2017、8、28 授课时间：2017、9、4备课人：郭艳玲（主备）母东文课型：新授课 教具:多媒体课件 教法：启发式 学法：自主合作探究22.2 二次函数与一元二次方程导学目标：1、理解二次函数与一元二次方程的关系，掌握方程与函数间的转化。

2、会利用数形结合的方法判断抛物线与x 轴的交点个数。

3、培养合作意识和探索数学知识间联系的好习惯，体验二次函数的应用。

导学重点：探索一次函数图象与一元二次方程的关系，理解抛物线与x 轴交点情况。

难点：函数→方程→x 轴交点，三者之间的关系的理解与运用。

导学方法:先由学生自学课本，经历自主探究总结的过程，并独立完成自主学习部分，然后学习小组交流讨论，形成知能，最后完成当堂训练题。

导学过程:一、创设情境，引入新课二次函数的223y x x =--的图象如图所示。

根据图象回答：（1）x 为何值时, 0y =？（2）你能根据图象，求方程2230x x --=的根吗？（3）二次函数223y x x =--与方程2230x x --=之间有何关系呢？二、自主学习，固知提能1、二次函数与一元二次方程之间的关系【探究】教材P43问题：如图，以40m/s 的速度将小球沿与地面成30°角的方向击出时，球的飞行路线将是一条抛物线。

如果不考虑空气阻力，球的飞行高度h （单位：m ）与飞行时间t （单位：s ）之间具有关系：2205h t t =-。

考虑以下问题：（1）球的飞行高度能否达到15m ？如能，需要多少飞行时间？（2）球的飞行高度能否达到20m ？如能，需要多少飞行时间？（3）球的飞行高度能否达到20.5m ？为什么？（4）球从飞出到落地需要多少时间？【归纳】二次函数与一元二次方程有如下关系：二次函数与一元二次方程之间有如下关系①函数2y ax bx c =++,当函数值y 为某一确定值m 时,对应自变量x 的值就是方程2ax bx c m ++=的根.②特别是0y =时，对应自变量x 的值就是方程20ax bx c ++=的根。

第二十二章二次函数22.2 二次函数与一元二次方程学习目标：1.通过探索,理解二次函数与一元二次方程(不等式)之间的联系.2.能运用二次函数及其图象、性质确定方程的解或不等式的解集.3.了解用图象法求一元二次方程的近似根.重点：能运用二次函数及其图象、性质确定方程的解或不等式的解集.难点：通过探索,理解二次函数与一元二次方程(不等式)之间的联系.一、知识链接1.如何用判别式b2－4ac来判断一元二次方程20ax bx c++=(a≠0)根的情况.2.写出二次函数223y x x=--的图象的顶点坐标、对称轴,并画出它的图象.然后观察图象,x 为何值时,y=0？二、要点探究探究点1：二次函数与一元二次方程的关系问题如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气的阻力,球的飞行高度h(单位：m)与飞行时间t(单位：s)之间具有关系：h=20t－5t2,考虑以下问题：(1) 球的飞行高度能否达到15m？如果能,需要多少飞行时间？(2) 球的飞行高度能否达到20m？如果能,需要多少飞行时间？(3) 球的飞行高度能否达到20.5m？为什么？(4) 球从飞出到落地要用多少时间？要点归纳：一般地,当y取定值且a≠0时,二次函数为一元二次方程.典例精析例1 如图,丁丁在扔铅球时,铅球沿抛物线26810105xy x=-++运行,其中x是铅球离初始位置的水平距离,y是铅球离地面的高度.自主学习课堂探究(1) 当铅球离地面的高度为2.1m时,它离初始位置的水平距离是多少？(2) 铅球离地面的高度能否达到2.5m,它离初始位置的水平距离是多少？(3) 铅球离地面的高度能否达到3m？为什么？探究点2：利用二次函数深入讨论一元二次方程思考观察思考下列二次函数的图象与x轴有公共点吗？如果有,公共点的横坐标是多少？当x取公共点的横坐标时,函数的值是多少？由此你能得出相应的一元二次方程的根吗？(1)y=x2－x+1；(2) y=x2－6x+9；(3)y=x2+x－2.要点归纳：二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次方程ax2+bx+c=0根的关系：一元二次方程ax2+bx+c=0的根b2－4ac二次函数y=ax2+bx+c的图象与x轴交点有两个交点有两个不相等的实数根b2－4ac＞0有两个重合的交点有两个相等的实数根b2－4ac=0没有交点没有实数根b2－4ac＜0例2 已知关于x的二次函数y＝mx2－(m＋2)x＋2(m≠0)．(1)求证：此抛物线与x轴总有两个交点；(2)若此抛物线与x轴总有两个交点,且它们的横坐标都是整数,求正整数m的值．【变式题】已知：抛物线y＝x2＋ax＋a－2.(1)求证：不论a取何值时,抛物线y＝x2＋ax＋a－2与x轴都有两个不同的交点；(2)设这个二次函数的图象与x轴相交于A(x1,0),B(x2,0),且x1、x2的平方和为3,求a的值．探究点3：利用二次函数求一元二次方程的近似解例3 利用函数图象求方程x2-2x-2=0的实数根(结果保留小数点后一位).方法总结：一元二次方程x²－2x－2=0 的根就是抛物线y=x²－2x－2 与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标,这种解一元二次方程的方法叫做图象法.例4 已知二次函数y＝ax2＋bx＋c的图象如图所示,则一元二次方程ax2＋bx＋c＝0的近似根为()A．x1≈－2.1,x2≈0.1B．x1≈－2.5,x2≈0.5C．x1≈－2.9,x2≈0.9D．x1≈－3,x2≈1方法总结：解答本题首先需要根据图象估计出一个根,再根据对称性计算出另一个根,估计值的精确程度,直接关系到计算的准确性,故估计尽量要准确．探究点4：二次函数与一元二次不等式的关系(拓展)问题1 函数y=ax2+bx+c的图象如图①,那么：方程ax2+bx+c=0的根是；不等式ax2+bx+c>0的解集是；不等式ax2+bx+c<0的解集是.图① 图①拓广探索：函数y=ax2+bx+c的图象如图①,那么：方程ax2+bx+c=2的根是______________；不等式ax2+bx+c>2的解集是___________；不等式ax2+bx+c<2的解集是_________.问题2 如果不等式ax2+bx+c>0（a≠0）的解集是x≠2的一切实数,那么函数y=ax2+bx+c的图象与x轴有个交点,坐标是.方程ax2+bx+c=0的根是.问题3 如果方程ax2+bx+c=0(a≠0)没有实数根,那么函数y=ax2+bx+c的图象与x轴有______个交点；不等式ax2+bx+c<0的解集是多少？试一试：利用函数图象解下列方程和不等式.(1) ①－x2+x+2=0；①－x2+x+2>0；①－x2+x+2<0.(2) ①x2－4x+4=0；①x2－4x+4>0；①x2－4x+4<0.(3) ①－x2+x－2=0；①－x2+x－2>0；①－x2+x－2<0.要点归纳：二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次不等式的关系：二次函数y =ax 2+bx +c 的图象与x 轴交点 a ＞0a ＜0有两个交点x 1,x 2 (x 1＜x 2)y ＜0,x 1＜x ＜x 2； y ＞0,x ＞x 2或x ＜x 1y ＞0,x 1＜x ＜x 2； y ＜0,x ＞x 2或x ＜x 1.有一个交点x 0y ＞0,x 0之外的所有实数；y ＜0,无解y ＜0,x 0之外的所有实数；y ＞0,无解. 没有交点 y ＞0,所有实数； y ＜0,无解y ＜0,所有实数； y ＞0,无解三、课堂小结判别式Δ=b 2－4acΔ>0 Δ＝0 Δ＜0二次函数y =ax 2+bx +c (a >0)的图象一元二次方程ax 2+bx +c =0(a ≠0)的根 x 1；x 2 x 1=x 2＝-2ba没有实数根不等式ax 2+bx +c >0(a >0)的解集 x <x 1或x >x 2x ≠ -2ba 的一切实数 所有实数不等式ax 2+bx +c <0(a >0)的解集 x 1<x <x 2 无解无解1.根据下列表格的对应值：x 3.23 3.243.253.26y =ax 2+bx +c－0.06 －0.020.03 0.09 判断方程 ax 2+bx +c =0 (a ≠0,a ,b ,c 为常数)一个解x 的范围是( )A. 3< x < 3.23B. 3.23< x < 3.24C. 3.24 <x < 3.25D. 3.25 <x < 3.26 2.若一元二次方程20x mx n -+=无实根,则抛物线2y x mx n =-+的图象位于( )A.x 轴上方B.第一、二、三象限C.x 轴下方D.第二、三、四象限 3.二次函数y ＝kx 2－6x ＋3的图象与x 轴有交点,则k 的取值范围是( )A.k <3B.k <3且k ≠0C.k ≤3D.k ≤3且k ≠04.若二次函数y =－x 2+2x +k 的部分图象如图所示,且关于x 的一元二次方程 －x 2+2x +k =0的一个解x 1=3,则另一个解x 2= .当堂检测5.一元二次方程3x2+x－10=0的两个根是x1=－2 ,x2=53,那么二次函数y=3x2+x－10与x轴的交点坐标是.6.已知二次函数268y x x=-+的图象,利用图象回答问题：(1)方程2680x x-+=的解是什么？(2) x取什么值时,y>0 ？(3) x取什么值时,y<0 ？7.已知函数y＝(k-3)x2＋2x＋1的图象与x轴有交点,求k的取值范围．8.某学校初三年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时距地面209米,与篮框中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行轨迹为抛物线,篮框距地面3米．(1)建立如图所示的平面直角坐标系,问此球能否准确投中？(2)此时,若对方队员乙在甲面前1米处跳起盖帽拦截,已知乙的最大摸高为3.1米,那么他能否获得成功？参考答案自主学习知识链接1.当b 2－4ac ＞0时,方程有两个不相等的实数根；当b 2－4ac =0时,方程有两个相等的实数根；当b 2－4ac ＜0时,方程无实数根.2.解：y =x 2-2x -3=(x -1)2-4,则y =x 2-2x -3的图象的顶点坐标为（1,-4）,对称轴为直线x =1,画图略,当x =3或-1时,y =0. 课堂探究二、要点探究探究点1：二次函数与一元二次方程的关系 问题 解：（1）解方程：15=20t -5t 2,t 2-4t +3=0,t 1=1,t 2=3.①当球飞行1s 或3s 时,它的高度为15m. （2）解方程：20=20t -5t 2,t 2-4t +4=0,t 1=t 2=2.当球飞行2s 时,它的高度为20m.（3）解方程：20.5=20t -5t 2,t 2-4t +4.1=0,因为(-4)2-4 ×4.1<0,所以方程无解.即球的飞行高度达不到20.5m.(4)0=20t -5t 2,t 2-4t =0,t 1=0,t 2=4.当球飞行0s 和4s 时,它的高度为0m 即0s 时小球从地面飞出,4s .例1 解 ：（1）由抛物线的表达式得268 2.1,10105x x -++=即x 2-6x +5=0,解得x 1=1,x 2=5. 即当铅球离地面的高度为2.1m 时,它离初始位置的水平距离是1m 或5m.（2）由抛物线的表达式得268 2.5,10105x x -++=即x 2-6x +9=0,解得x 1=x 2=3.即当铅球离地面的高度为2.5m 时,它离初始位置的水平距离是3m.（3）由抛物线的表达式得2683,10105x x -++=即x 2-6x +14=0,因为Δ=(-6)2-4×1×14＜0,所以方程无实根.所以铅球离地面的高度不能达到3m.探究点2：利用二次函数深入讨论一元二次方程 思考 解：（1）y =x 2－x +1的图象与x 轴无交点,则相应的一元二次方程为x 2－x +1=0无实数根.(2) y =x 2－6x +9的图象与x 轴有1个交点,交点的横坐标为3,则相应的一元二次方程为 x 2－6x +9=0,其根为x 1=x 2=3.(3) y =x 2+x －2的图象与x 轴有2个交点,交点的横坐标分别为-2,1,则相应的一元二次方程为x 2+x －2=0,其根为x 1=1,x 2=-2.例2 (1)证明：①m ≠0,①Δ＝(m ＋2)2－4m ×2＝m 2＋4m ＋4－8m ＝(m －2)2. ①(m －2)2≥0,①Δ≥0,①此抛物线与x 轴总有交点.(2)解：令y ＝0,则(x －1)(mx －2)＝0,所以 x －1＝0或mx －2＝0,解得 x 1＝1,x 2＝2.m当m 为正整数1或2时,x 2为整数,即抛物线与x 轴总 有两个交点,且它们的横坐标都是整数．所以正整数m 的值为1或2.【变式题】(1)证明：①Δ＝a 2－4(a －2)＝(a －2)2＋4＞0,①不论a 取何值时,抛物线y ＝x 2＋ax ＋a －2与x 轴都有两个不同的交点.(2)解：①x 1＋x 2＝－a ,x 1·x 2＝a －2,①2212x x +＝(x 1＋x 2)2－2x 1·x 2＝a 2－2a ＋4＝3,①a ＝1.探究点3：利用二次函数求一元二次方程的近似解例3 解：画出函数 y =x ²-2x -2 的图象（如下图）,由图象可知,方程有两个实数根,一个在-1与0之间,另一个在2与3之间.先求位于-1到0之间的根,由图象可估计这个根是-0.8或-0.7,利用计算器进行探索,见下表：观察上表可以发现,当x 分别取-0.8和-0.7时,对应的y 由负变正,可见在-0.8与-0.7之间肯定有一个x 使y =0,即有y =x 2-2x -2的一个根,题目只要求精确到0.1,这时取x =-0.8或x =-0.7都符合要求.但当x =-0.7时更为接近0.故x 1≈-0.7. 同理可得另一近似值为x 2≈2.7. 例4 B探究点4：二次函数与一元二次不等式的关系(拓展) 问题1 x 1=-1,x 2=3 x ＜-1或x ＞3 -1＜x ＜3 拓广探索： x 1=-2,x 2=4 x ＜-2或x ＞4 -2＜x ＜4 问题2 1 （2,0） x =2问题3 0 （1）当a >0时, ax 2+bx +c <0无解;（2）当a ＜0时, ax 2+bx +c <0的解集是一切实数.试一试：解：（1）①x 1=-1 , x 2=2 ①-1 ＜ x ＜2 ①x ＜-1或 x ＞2 （2）①x 1= x 2=2 ①x ≠2的一切实数 ① x 无解 （3）①x 无解 ①x 无解 ① x 为全体实数 当堂检测1.C2.A3.D4.-15.（-2,0）,5,03⎛⎫ ⎪⎝⎭6.解：（1）x 1=2,x 2=4; （2）x <2或x >4; （3）2<x <4.7.解：当k ＝3时,函数y ＝2x ＋1是一次函数．①一次函数y ＝2x ＋1与x 轴有一个交点, ①k ＝3；当k ≠3时,y ＝(k －3)x 2＋2x ＋1是二次函数．①二次函数y ＝(k －3)x 2＋2x ＋1的图象与x 轴有交点,①Δ＝b 2－4ac ≥0.①b 2－4ac ＝22－4(k －3)＝－4k ＋16,①－4k ＋16≥0.①k ≤4且k ≠3.综上所述,k 的取值范围是k ≤4.8. 解：(1)由条件可得到出手点、最高点和篮框的坐标分别为A 200,9⎛⎫ ⎪⎝⎭, B (4,4),C (7,3).其中B 是抛物线的顶点．设二次函数关系式为y ＝a (x －4)2＋4,将点A 的坐标代入,可得y ＝－19(x －4)2＋4.将点C 的坐标代入上式,得左边＝3,右边＝－19(7－4)2＋4＝3,左边＝右边,即点C 在抛物线上．所以此球一定能投中.(3) 将x ＝1代入函数关系式,得y ＝3.因为3.1＞3,所以盖帽能获得成功．。

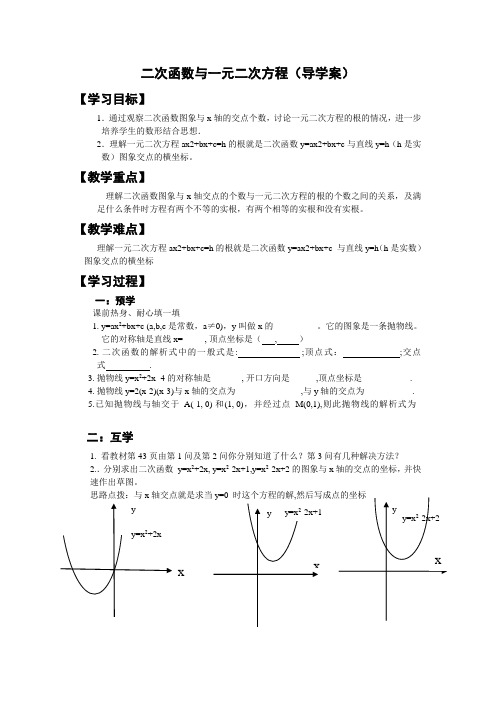
二次函数与一元二次方程（导学案）【学习目标】1．通过观察二次函数图象与x轴的交点个数，讨论一元二次方程的根的情况，进一步培养学生的数形结合思想．2．理解一元二次方程ax2+bx+c=h的根就是二次函数y=ax2+bx+c与直线y=h（h是实数）图象交点的横坐标。

【教学重点】理解二次函数图象与x轴交点的个数与一元二次方程的根的个数之间的关系，及满足什么条件时方程有两个不等的实根，有两个相等的实根和没有实根。

【教学难点】理解一元二次方程ax2+bx+c=h的根就是二次函数y=ax2+bx+c 与直线y=h（h是实数）图象交点的横坐标【学习过程】一：预学课前热身、耐心填一填1. y=ax2+bx+c (a,b,c是常数，a≠0)，y叫做x的__________。

它的图象是一条抛物线。

它的对称轴是直线x=_____, 顶点坐标是（, ）2. 二次函数的解析式中的一般式是: ;顶点式：;交点式.3. 抛物线y=x2+2x- 4的对称轴是_______, 开口方向是______,顶点坐标是___________.4. 抛物线y=2(x-2)(x-3)与x轴的交点为_______________,与y轴的交点为___________.5.已知抛物线与轴交于A(-1, 0) 和(1, 0)，并经过点M(0,1),则此抛物线的解析式为_______________二：互学1. 看教材第43页由第1问及第2问你分别知道了什么？第3问有几种解决方法？2.．分别求出二次函数y=x2+2x, y=x2-2x+1,y=x2-2x+2的图象与x轴的交点的坐标，并快速作出草图。

y=0时这个方程的解,（1）观察下列二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象，每个图象与x 轴有几个交点？（2）一元二次方程x2+2x=0,x2-2x+1=0有几个根?（3）验证一下一元二次方程x2-2x+2=0有根吗?（4）说说二次函数y=ax2+bx+c 的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?3．归纳整理a.二次函数y=ax2+bx+c的图象和x轴交点有三种情况:(1)、有两个交点,(2)、有一个交点,(3)、没有交点b.当二次函数y=ax2+bx+c的图象和x轴有交点时交点的横坐标就是当y=0时自变量x 的值, 即一元二次方程ax2+bx+c=0的根c.完成下列表格，观察二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程2【例】一个足球被从地面向上踢出，它距地面的高度h（m）可以用公式h=－4.9t＋19.6t 来表示．其中（s）表示足球被踢出后经过的时间．（1）当t=1时，足球的高度是多少？（2）t为何值时，h最大？（3）经过多长时间球落地？（4）方程－4.9t2＋19.6t =0的根的实际意义是什么？你能在图上表示吗?（5）方程14.7=－4.9t2＋19.6t 的根的实际意义是什么？你能在图上表示吗?三：评学1.开拓创新：已知二次函数y=kx2－7x－7的图象与x轴有两个交点，则k的取值范围为什么? 2．课堂小结3.随堂检测（1）．抛物线y=-3（x－2）（x＋5）与x轴的交点坐标为_______（2）．抛物线y=x2－2x＋3与两坐标轴交点的个数为个．（3）．抛物线y=2x2＋8x＋m与x 轴只有一个交点，则m= ____________。

九年级数学上册：二次函数与一元二次方程导学案学习目标：1．探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系．2．理解二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系,理解何时方程有两个不等的实根、两个相等的实数和没有实根．3．理解一元二次方程的根就是二次函数与y＝h(h是实数)交点的横坐标．一、基础扫描1一元二次方程ax2＋bx＋c＝0根的判别式当△＞0时当△﹤0时当△=0时2一元一次方程kx＋b＝0(k≠0)和一次函数y＝kx＋b(k≠0)后,讨论了它们之间的关系．当一次函数中的函数值y＝0时,一次函数y＝kx＋b就转化成了一元一次方程_______,且一次函数y＝kx＋b(k≠0)的图象与x轴交点的横坐标即为一元一次方程_______的解．二、探究1一元二次方程ax2＋bx＋c＝0(a≠0)和二次函数y＝ax2＋bx＋c(a≠0),它们之间是否也存在一定的关系呢?函数：①y＝x2＋2x ② y＝x2－2x＋1 ③y＝x2－2x＋2图象：一元二次方程：⑴x2＋2x＝0 ⑵x2－2x＋1＝0 ⑶x2－2x＋2＝0一元二次方程根的形式：⑴△__0有_______ ⑵△__0 有_______ ⑶△__0 有_______ 一元二次方程的解：⑴___________ ⑵___________ ⑶___________函数与x轴交点的个数：①___________ ② ___________ ③___________函数与x轴交点的坐标：①___________ ②___________ ③___________结合元二次方程根的形式和函数与x轴交点的个数得出的结论是：结合一元二次方程的解和函数与x轴交点的坐标得出的结论是：(3)二次函数y＝ax2＋bx＋c的图象和x轴交点的坐标与一元二次方程ax2＋bx＋c＝0的根有什么关系?探究2我们已经知道,竖直上抛物体的高度h(m)与运动时间t(s)的关系可以用公式h＝－5t2＋v 0t＋h表示,其中h0(m)是抛出时的高度,v0(m/s)是抛出时的速度．一个小球从地面被以40m/s的速度竖直向上抛起,小球的高度h(m)与运动时间t(s)的关系如下图所示,那么(1)h与t的关系式是什么?(2)小球经过多少秒后落地?你有几种求解方法?与同伴进行交流．(3)在本节一开始的小球上抛问题中,何时小球离地面的高度是60m?你是如何知道的?三、知识超市1．抛物线y=a（x－2）（x＋5）与x轴的交点坐标为．2．抛物线y=2x2＋8x＋m与x轴只有一个交点,则m= ．3．二次函数y=kx2＋3x－4的图象与x轴有两个交点,则k的取值范围．4．抛物线y=x2－2x＋3的顶点坐标是抛物线y=x2－2x＋3可变形为y=（x－__）（x＋__）且与x轴交点的坐标与y轴交点的坐标,5画出函数y=x2－2x＋3的草图6．已知抛物线y=mx2＋（3－2m）x＋m－2（m≠0）与x轴有两个不同的交点．（1）求m的取值范围；（2）判断点P（1,1）是否在抛物线上；（3）当m=1时,求抛物线的顶点Q及P点关于抛物线的对称轴对称的点P′的坐标,并过P′、Q、P三点,画出抛物线草图．四、课后总结：。

数学九年级上册《二次函数与一元二次方程的关系》导学案设计人：审核人：【学习目标】1、能准确说出二次函数图像与相应一元二次方程之间联系；2、能够切实体会数形结合的数学思想；3、提高自身合作交流的意识和能力。

【学习重点】二次函数图像和一元二次方程之间的关联；【学习难点】二次函数与X轴的交点个数与一元二次方程根的判别式之间的关系。

【学习方法】自学过程中认真观察不同二次函数图像与坐标轴交点的个数，从而初步认识二次函数图像与相应一元二次方程之间的联系，并能为同伴释疑，通过练习加强记忆。

自学阅读课本43-45页，完成下列问题。

一、二次函数y=x2+2x, y=x2-2x+1, y=x2-2x+2(1)、每个图象与x轴分别有___、___、____个交点。

(2)、一元二次方程x2+2x=0,x2-2x+1=0有几个根?验证一下一元二次方程x2-2x+2=0有根吗?二、1、求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标。

x，2x与A、B的坐标有什么联系？2、你发现方程x2-3x+2=0的解1总结：二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?二次函数y=ax2+bx+c 的图象和x轴交点个数一元二次方程ax2+bx+c=0的根的情况一元二次方程ax2+bx+c=0根的判别式b2-4ac三、再观察下列三幅图。

（1）（2）（3）1、(1)中抛物线y=x2+2x与X轴有2个公共点，公共点的横坐标是-2、0那么当x=-2时函数的值是______，当x=0时函数的值是________________.也就是x=-2、0是方程________________的根。

(2)中抛物线y=x2-2x+1与X轴有一个公共点，公共点的横坐标是1，那么当x=1时函数的值是_______。

就是x=1是方程________的根。

(3)中抛物线y=x2-2x+2与X轴无交点，就是函数值不可能是_______.那么方程__________就无实数根。

二次函数与一元二次方程小试牛刀1．一次函数36y x =-与x 轴的交点坐标为，与y 轴的交点坐标为。

2．画出函数36y x =-的图象，从图象直接观察写出：当x 取何值时，0y >；当x 取何值时，0y <？锦囊妙计要点一、二次函数与一元二次方程的关系1.二次函数图象与x 轴的交点情况决定一元二次方程根的情况求二次函数2y ax bx c =++(a ≠0)的图象与x 轴的交点坐标，就是令y ＝0，求20ax bx c ++=中x 的值的问题．此时二次函数就转化为一元二次方程，因此一抛物线与直线的交点问题抛物线与x 轴的两个交点的问题实质就是抛物线与直线的交点问题．我们把它延伸到求抛物线2y ax bx c =++(a ≠0)与y 轴交点和二次函数与一次函数1y kx b =+(0)k ≠的交点问题．抛物线2y ax bx c =++(a ≠0)与y 轴的交点是(0，c)．抛物线2y ax bx c =++(a ≠0)与一次函数1y kx b =+(k ≠0)的交点个数由方程组12,y kx b y ax bx c =+⎧⎨=++⎩的解的个数决定． 当方程组有两组不同的解时⇔两函数图象有两个交点； 当方程组有两组相同的解时⇔两函数图象只有一个交点； 当方程组无解时⇔两函数图象没有交点．总之，探究直线与抛物线的交点的问题，最终是讨论方程(组)的解的问题． 要点二、利用二次函数图象求一元二次方程的近似解 用图象法解一元二次方程的步骤：1.作二次函数的图象，由图象确定交点个数，即方程解的个数；2. 确定一元二次方程的根的取值范围．即确定抛物线与x 轴交点的横坐标的大致范围；3. 在(2)确定的范围内，用计算器进行探索.即在(2)确定的范围内，从大到小或从小到大依次取值，用表格的形式求出相应的y 值．4.确定一元二次方程的近似根．在(3)中最接近0的y 值所对应的x 值即是一元二次方的近似根．要点三、抛物线与不等式的关系二次函数2y ax bx c =++(a ≠0)与一元二次不等式20ax bx c ++>(a ≠0)及20ax bx c ++<(a ≠0)之间的关系如下12()x x <：注：a ＜0的情况请同学们自己完成．衣钵相传模块一、二次函数图象与坐标轴交点例1．将抛物线y=x 2﹣1向下平移8个单位长度后与x 轴的两个交点之间的距离为（ ） A ．4B ．6C ．8D ．10【答案】B【解析】解：将抛物线y=x 2﹣1向下平移8个单位长度， 其解析式变换为：y=x 2﹣9而抛物线y=x 2﹣9与x 轴的交点的纵坐标为0， 所以有：x 2﹣9=0 解得：x 1=﹣3，x 2=3，则抛物线y=x2﹣9与x轴的交点为（﹣3，0）、（3，0），所以，抛物线y=x2﹣1向下平移8个单位长度后与x轴的两个交点之间的距离为6沙场点兵1．二次函数y＝x2－3x＋2，当x＝1时，y＝________；当y＝0时，x＝_______ 。

22.2二次函数与一元二次方程 学习目标：1.探索二次函数与一元二次方程、一元二次不等式之间的关系．2.掌握一元二次方程(组)的图象解法．重点、难点1.重点：探索二次函数与一元二次方程、一元二次不等式之间的关系．2.难点：掌握一元二次方程(组)的图象解法．导学过程：阅读教材P16 — 19 , 完成课前预习【课前预习】1：准备知识（1） 一元二次方程根的情况：（2）一次函数与一元一次方程的关系：2：探究1以40米/秒的速度将小球沿与地面成300角的方向击出时，球的飞行路线将是一条抛物线。

如果不考虑空气阻力，球的飞行高度h 米与飞行时间t 秒之间具有关系2520t t h -=。

考虑以下问题：（1） 球的飞行高度能否达到15米？如能，需要多少飞行时间？（2） 球的飞行高度能否达到20米？如能，需要多少飞行时间？（3） 球的飞行高度能否达到20.5米？为什么？（4） 球从飞出到落地需要用多少时间？探究2给出三个二次函数：（1）232+-=x x y ；（2）12+-=x x y ；（3）122+-=x x y ．它们的图象分别为观察图象与x 轴的交点个数，分别是 个、 个、 个．你知道图象与x 轴的交点个数与什么有关吗？另外，能否利用二次函数c bx ax y ++=2的图象寻找方程)0(02≠=++a c bx ax ，不等式)0(02≠>++a c bx ax 或)0(02≠<++a c bx ax 的解？3：结论一般的，从二次函数c bx ax y ++=2的图象可知，（1） 如果抛物线c bx ax y ++=2与x 轴有公共点，公共点的横坐标是x 0,那么当x= 时，函数的值是0，因此x= 就是方程)0(02≠=++a c bx ax 的一个根。

（2） 二次函数的图象与x 轴的位置关系有三种：没有公共点，有一个公共点，有两个公共点。

这对应着一元二次方程根的三种情况： 实数根，有 的实数根，有 的实数根。

第15讲 二次函数与一元二次方程一、知识梳理二次函数与一元二次方程的关系 抛物线y ＝ax 2＋bx ＋c 与x 轴的交点个数 判别式Δ＝b 2－4ac 的符号方程ax 2＋bx ＋c ＝0有实根 的个数 2个Δ>0 两个________实根 1个Δ＝0 两个________实根 没有 Δ<0 ________实根二次函数y ＝ax2＋bx ＋c(a≠0)的图象特征与a 、b 、c 及判别式b2－4ac 的符号之间的关系字母的符号 图象的特征 aa>0 开口向上 a<0开口向下 b b ＝0对称轴为y 轴 ab>0(b 与a 同号)对称轴在y 轴左侧 ab<0(b 与a 异号)对称轴在y 轴右侧 c c ＝0经过原点 c>0与y 轴正半轴相交 c<0与y 轴负半轴相交 b 2－4ac b 2－4ac ＝0与x 轴有惟一交点(顶点) b 2－4ac>0 与x 轴有两个不同交点b 2－4ac<0 与x 轴没有交点 特殊关系当x ＝1时，y ＝a ＋b ＋c当x ＝－1时，y ＝a －b ＋c若a ＋b ＋c>0，即x ＝1时，y>0若a －b ＋c>0，即x ＝－1时，y>0二次函数图象的平移将抛物线y ＝ax 2＋bx ＋c(a ≠0)用配方法化成y ＝a(x －h)2＋k(a ≠0)的形式，而任意抛物线y ＝a(x －h)2＋k 均可由抛物线y ＝ax 2平移得到，具体平移方法如图二、题型、技巧归纳考点1二次函数与一元二次方程例1 抛物线y＝x2－4x＋m与x轴的一个交点的坐标为(1，0)，则此抛物线与x轴的另一个交点的坐标是________．技巧归纳：一元二次方程ax2+bx+c=0的两个根为x1,x2 ,则抛物线 y=ax2+bx+c与x轴的交点坐标是(x1,0),(x2,0)考点2二次函数的图象的平移例2 将抛物线y＝x2＋1先向左平移2个单位，再向下平移3个单位，那么所得抛物线的函数关系式是( ) A．y＝(x＋2)2＋2 B．y＝(x＋2)2－2C．y＝(x－2)2＋2 D．y＝(x－2)2－2技巧归纳：1．采用由“点”带“形”的方法．图形在平移时，图形上的每一个点都按照相同的方向移动相同的距离，抛物线的平移问题往往可转化为顶点的平移问题来解决．2．平移的变化规律可为：(1)上、下平移：当抛物线y＝a(x－h)2＋k向上平移m(m>0)个单位后，所得的抛物线的关系式为y＝a(x－h)2＋k＋m；当抛物线y＝a(x－h)2＋k向下平移m(m>0)个单位后，所得的抛物线的关系式为y＝a(x－h)2＋k－m.(2)左、右平移：当抛物线y＝a(x－h)2＋k向左平移n(n>0)个单位后，所得的抛物线的关系式为y＝a(x－h ＋n)2＋k；当抛物线y＝a(x－h)2＋k向右平移n(n>0)个单位后，所得的抛物线的关系式为y＝a(x－h－n)2＋k.例3 如图把抛物线y＝0.5x2平移得到抛物线m. 抛物线m经过点A(－6,0)和原点(0,0)，它的顶点为P，它的对称轴与抛物线y＝0.5x2交于点Q，则图中阴影部分的面积为________．。