正态分布t分布课件

格式：ppt
大小：2.63 MB
文档页数：10

下载文档原格式

正态分布 t分布

未知时，以样本标准差 S 代替 σ 所得到的统计量
xμ S/ n
态分布，而是服从 t 分布(t-distribution)。它的概率分布密度函数如下：
t 分布概率密度曲线特点: 1、t 分布受自由度的制约，每一个自由度都有一条 t 分布概率密度曲线。 2、t 分布概率密度曲线以纵轴为对称轴，左右对称，且在t＝0时，取得最大值。 3、与标准正态分布曲线相比，t 分布曲线顶部略低，两尾部稍高而平。df 越小这种趋势越明显。df 越大，t 分布越趋近于标准正态分布。当n >50时，t 分布与标准正态分布的区别很小；n >100时，t 分布基本与标准正态分布相同；n→+∞时，t 分布与标准正态分布完全一致。
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
x=
1 2
x
-3 -2 -1 0
x=
1 2 3 x
x=
不同均数均值反映随机变量的平均水平（位置参数），向右平移表示逐渐增大，向左平移表示逐渐减小。
（1）曲线在x 轴的上方，与x 轴永不相交（2）曲线是单峰的,它关于直线 x=μ对称 1 （3）曲线在 x=μ 处达到峰值(最高点) σ 2π （4）曲线与横轴 x所夹面积为1
例3 某地1986年120名8岁男孩身高均数为 X =123.02cm ，标准差为S=4.79cm，试估计: (1)该地8岁男孩身高在130cm以上者占该地8 岁男孩总数的百分比； (2)身高在120cm～128cm者占该地8岁男孩总数的百分比; (3)该地80%的男孩身高集中在哪个范围？
t 分布
利用公式，查附表得： (1) P(x＜1.64) =Φ(1.64) =0.9495 (2) P (x≥2.58) =1-Φ(2.58) =1-0.9951 =0.0049 (3) P (│x│≥2.56) =2-2Φ(2.56) =2-2×0.9948 =0.0104 (4) P (0.34＜x≤1.53) =Φ(1.53)-Φ(0.34) = 0.9370-0.6331=0.3039 (5) P(x＜-1.82) =1-Φ(1.82) =1-0.9656 =0.0344

统计学中的正态分布和t分布

统计学中的正态分布和t分布统计学是研究随机现象的规律性和概率统计方法的学科。

在统计学中，使用概率分布来描述随机变量的分布规律。

其中，正态分布和t分布是统计学中非常重要的两种概率分布。

正态分布，也叫高斯分布，是一种连续的概率分布。

在正态分布中，均值、中位数和众数三者相等，分布是左右对称的，呈钟形曲线。

正态分布在数理统计中起着非常重要的作用，因为如果一个随机变量的分布近似为正态分布，则其数据分析的效果往往更加准确。

t分布，是一种与正态分布有关的概率分布。

在实际应用中，由于总体标准差未知或样本容量较小，使得正态分布难以直接应用，因而使用t分布更为恰当。

t分布具有以下特点：t分布是在样本量较小的情况下被应用的，当样本量大的时候，t分布与正态分布趋于相同；t分布的形状取决于自由度，自由度越大，t分布越接近于正态分布，自由度越小，t分布越扁平。

正态分布和t分布的应用场景非常广泛。

在生产工厂中，对于产品的质量控制，需要对产品的重量或尺寸等指标进行检测，这时可以使用正态分布或t分布作为数据分析手段。

在金融领域中，对于股票的价格变化、股票风险等方面，也可以使用正态分布和t 分布进行数据分析。

在医学领域中，研究某种药物的不良反应出现的概率，使用t分布的方法进行分析，提高研究结果的可信度。

结论正态分布和t分布是统计学中非常重要的两种概率分布。

正态分布在数据分析中起着非常重要的作用，可以对随机变量的分布进行描述。

而t分布则适用于样本量较小的情况下的数据分析。

正态分布和t分布在很多领域都有广泛的应用，包括生产工厂、金融领域以及医学领域等。

掌握正态分布和t分布的知识，可以帮助我们更加准确地进行数据分析和决策。

正态分布课件

在气象中，某地每年七月份的平均气温、平均湿度以及降雨量等，水文中的水位；
总之，正态分布广泛存在于自然界、生产及科学技术的许多领域中。
正态分布在概率和统计中占有重要地位。
4、正态曲线的性质
（1）曲线在x轴的上方，与x轴不相交.
（μ－σ，μ＋σ]
0.6826
（μ－2σ，μ＋2σ]
0.9544
（μ－3σ，μ＋3σ]
0.9974
（2）曲线是单峰的,它关于直线x=μ对称.
（4）曲线与x轴之间的面积为1.
（3）曲线在x=μ处达到峰值(最高点)
（5）若固定, 随值的变化而沿x轴平移, 故称为位置参数
（6）当μ一定时，曲线的形状由σ确定 .σ越大，曲线越“矮胖”，表示总体的分布越分散；σ越小，曲线越“瘦高”，表示总体的分布越集中.
5、特殊区间的概率:
m-a
m+a
x=μ
若X~N ,则对于任何实数a>0,概率为如图中的阴影部分的面积，对于固定的和而言，该面积随着的减少而变大。这说明越小, 落在区间的概率越大，即X集中在周围概率越大。
4
0.04
[0.5,1)
8
0.08
[1,1.5)
15
0.15
[1.5,2)
22
0.22
[2,2.5)
25
0.25
[2.5,3)
14
0.14
[3,3.5)
6
0.06
[3.5,4)
4
0.04
[4,4.5)
2
0.02
11
高尔顿钉板实验的频率分布直方图
这条曲线具有 “中间高，两头低” 的特征，像这种类型的曲线, 就是（或近似地是）以下函数的图像:

统计学正态分布及t分布32页PPT

40、人类法律，事物有规律，这是里的人，才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭，生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍，就是一下子不要学很多。——洛克
统计学正态分布及t分布
36、如果我们国家的法律中只有某种神灵，而不是殚精竭虑将神灵揉进宪法，总体上来说，法律就会更好。—— 马克·吐温 37、纲纪废弃之日，便是暴政兴起之时。— —威·皮物特
38、若是没有公众舆论的支持，法律是丝毫没有力量的。 ——菲力普斯 39、一个判例造出另一个判例，它们迅速累聚，进而变成法律。 ——朱尼厄斯

《正态分布》ppt课件

《正态分布》ppt课件
目录
CONTENTS
• 正态分布基本概念 • 正态分布在统计学中应用 • 正态分布在自然科学领域应用 • 正态分布在社会科学领域应用 • 正态分布计算方法及工具介绍 • 正态分布在实际问题中案例分析
01 正态分布基本概念
CHAPTER
定义与性质
定义
对称性
正态分布是一种连续型概率分布，描述了许多自然现象的概率分布情况。在统计学中，正态分布又被称为高斯分布。
系统误差与随机误差
正态分布可以帮助区分系统误差和随机误差。系统误差是由于实验装置或方法本身的缺陷引起的，而随机误差则是由于各种不可控因素引起的。通过正态分布分析，可以对这两类误差进行识别和纠正。
化学中浓度分布规律研究
01
溶液浓度的正态分布
在化学实验中，溶液的浓度分布往往符合正态分布。通过测量不同位置
利用SPSS的图形功能，可以绘制多种统计图表，包括频率分布直方图、正态分布曲线图等。
SPSS提供了丰富的统计分析方法，如参数估计、假设检验、方差分析等，可以根据研究需求选择合适的方法进行分析。
06 正态分布在实际问题中案例分析
CHAPTER
质量控制过程中产品合格率评估
质量控制图
利用正态分布原理，通过绘制质量控制图，可以直观地展示产品质量的波动情况，从而及时发现并处理异常波动，确保产品合格
数据输入与整理
在Excel中输入数据，并进行必要的整理，如删除重复值、处理缺失值等。
使用内置函数计算均值和标准差
Excel提供了丰富的内置函数，可以直接计算数据集的均值（AVERAGE函数）和标准差（STDEV函数）。
绘制图表
利用Excel的图表功能，可以根据数据快速生成频率分布直方图和正态分布曲线图。

正态分布课件课件

医学研究
正态分布经常被用来描述人体的生理指标，例如血压、体重、心率和血糖等。
工程技术
正态分布在工程技术中也有着很重要的应用，例如在质量控制和可靠性分析中。
正态分布在数据分析中的应用
偏度和峰度
使用偏度和峰度帮助了解正态分布的形状和分布。偏度描述了平均值分布在曲线的何处，而峰度则描述了曲线的陡峭程度。
正态分布在适用性和排除异常值方面存在一些限制。如果样本不符合正态分布，此时用正态分布进行分析可能会导致错误的结论。
Hale Waihona Puke 正态分布的常用假设及检验假设检验
假设检验是指在一定的显著水平下，对总体参数提出假设，并根据样本数据的分布，用统计学方法判断原假设是否成立。
P值
P值是在假设检验中使用的一个统计量，通常一起出现的是显著性水平。 p值是落在拒绝域的概率，越小说明差异越显著。
正态分布优缺点
1 优点
2 缺点
正态分布具有左右对称性，易于使用和理解，广泛适用于各行各业的数据分析。
中心极限定理
中心极限定理告诉我们，样本均值的分布逼近于正态分布，无论样本分布如何。这意味着我们可以在特定条件下使用正态分布来预测总体分布。
置信区间
使用正态分布来计算置信区间。在数据分析中，置信区间是指根据样本数据计算出的一个区间，以此来推测总体参数的范围。
正态分布的概率计算方法
1
累积分布函数
正态性检验方法
正态Q-Q图
Q-Q图是通过将样本数据分布和正态分布进行比较来检验正态性的。如果点的分布趋近于一条直线，则样本数据符合正态分布。
Shapiro-Wilk检验
Shapiro-Wilk检验是一种经典的正态性检验方法。该检验基于样本数据的偏度、峰度、样本大小和简单随机抽样的原则，可以判断样本数据是否符合正态分布。

统计学正态分布及t分布

正态分布2�样本有几个特别重要的数字特征，这些数字是描述样本频率分布特征的，称之为样本特征数�而在生物统计学中，样本特征数使用频繁的有以下几个）。

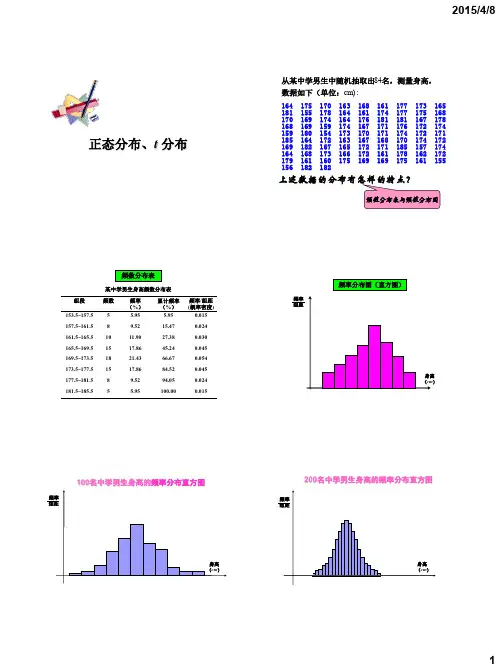
�1.算术平均数，简称平均数（36•正态分布的概念•如果把数值变量资料编制频数表后绘制频数分布图（又称直方图，它用矩形面积表示数值变量资料的频数分布，每条直条的宽表示组距，直条的面积表示频数（或频率）大小，直条与直条之间不留空隙。

），若频数分布呈现中间为最多，左右两侧基本对称，越靠近中间频数越多，离中间越远，频数越少，形成一个中间频数多，两侧频数逐渐减少且基本对称的分布，那我们一般认为该数值•变量服从或近似服从•数学上的正态分布。

7•当n →∞，直方条面积(频率)→各自的概率•然后组距→０时，直方条的宽度→０，直方条→垂直线，各个直方条顶点间的连线构成一条光滑的曲线，即：概率密度曲线，而曲线下(直方条)的总面积始终为１，在区间[a,b a,b]]的概率＝对应曲线段下的面积(直方条面积)。

8正态分布的概念在σ不变的情况下函数曲线形状不变，若μ变大时，曲线位置向右移；若变小时，曲线位置向左移，故称μ为位置参数。

11121σ2σ3σ在μ不变的情况下函数曲线位置不变，若σ变大时，曲线形状变的越来越“胖”和“矮”；若σ变小时，曲线形状变的越来越“瘦”和“高”，故称σ为形态参数或变异度参数。

13012-1-2xy-3μ= -1σ=0.5012-1-2x y -33μ=0σ=1012-1-2x y -334μ=1σ=2正态曲线的性质（1）曲线在x 轴的上方，与x 轴不相交.（2）曲线是单峰的,它关于直线x =μ对称.（3）曲线在x =μ处达到峰值(最高点)（4）曲线与x 轴之间的面积为1（5）当 x <μ时,曲线上升;当x >μ时,曲线下降.并且当曲线向左、右两边无限延伸时, 以x 轴为渐近线,向它无限靠近.(6)当μ一定时，曲线的形状由σ确定 .σ越大，曲线越“矮胖”，表示总体的分布越分散；σ越小，曲线越“瘦高”，表示总体的分布越集中.14�而整个正态分布则应该是各区间密度函数的累计积分.�一种连续的分布不可能求某项(某点)的概率,而只能求某个区间的概率.�任意两点x 1，x 2且(x 1≤x 2)，X 在 (x 1, x 2)范围内取值的概率P,即正态分布曲线在(x 1, x 2)下面积2221()212x x x P e dxµσπσ−−=∫15标准正态分布正态分布由μ和σ所决定，不同的μ、σ值就决定了不同的正态分布密度函数，因此在实际计算中很不方便的。

正态分布ppt精品课件

结果解释
根据检验结果，解释两组数据是否存在显著差异，并结合实
际背景进行讨论。
06
正态分布在生活中的应用举例
质量控制领域应用举例
01
产品规格设定
在制造业中，正态分布用于设定产品规格。通过对产品特性进行统计分
析，可以确定产品特性的均值和标准差，进而设定合理的上下规格限。
02 03
过程能力分析
正态分布也用于评估生产过程的能力。通过计算过程能力指数（如Cp 和Cpk），可以了解生产过程是否稳定，并确定是否需要采取改进措施。
多元方差分析（MANOVA）与多元回归分析（ Multiple Regression Analysis）：当涉及多个自变量或多个因变量时，可以使用多元方差分析或多元回归分析来探究它们之间的关系。
回归分析（Regression Analysis）：用于探究自变量与因变量之间的线性或非线性关系，通过拟合回归方程来预测因变量的取值。
概率密度函数性质 f(x)≥0，对于所有x∈R。
02
正态分布在统计学中应用
描述性统计量计算
均值（Mean）：表示数据的“中心 ”或“平均”水平，计算方法是所有数值之和除以数值个数。
偏度（Skewness）：描述数据分布形态的偏斜程度，正偏态表示数据向右偏，负偏态表示数据向左偏。
标准差（Standard Deviation）：衡量数据分布的离散程度，即数据偏离均值的程度，计算方法是方差的平方根。
实例分析：两组数据是否存在显著差异
数据描述
给出两组数据的描述性统计量，如均值、标准差等。
假设检验步骤
按照上述假设检验步骤，对两组数据进行假设检验。
结果解释
根据检验结果，判断两组数据是否存在显著差异，并给出相应的

T分布（近似标准正态分布）

T分布（近似标准正态分布）1.1 定义定义：假设X服从标准正态分布N（0,1），Y服从卡⽅分布，那么的分布称为⾃由度为n的t分布,记为。

T分布密度函数其中，Gam(x)为伽马函数。

可⽤于两组独⽴计量资料的假设检验。

由于在实际⼯作中，往往σ（总体⽅差）是未知的，常⽤s（样本⽅差）作为σ总体⽅差的估计值，为了与u变换（正态化变换）区别，称为t变换，统计量t 值的分布称为t分布。

【u分布也叫标准正态分布】u变换：[(X-µ)/σ]转化成标准正态变量u，以使原来各种形态的正态分布都转换为µ=0，σ=1的标准正态分布（standard normaldistribution），亦称u分布。

在和中，t-分布（t-distribution）⽤于根据⼩样本来估计呈且⽅差未知的总体的均值。

如果总体⽅差已知（例如在样本数量⾜够多时），则应该⽤正态分布来估计总体均值。

经常应⽤在对呈的总体的进⾏估计。

它是对两个差异进⾏测试的学⽣t测定的基础。

t检定改进了Z检定（en:Z-test），不论样本数量⼤或⼩皆可应⽤。

在样本数量⼤（超过120等）时，可以应⽤Z检定，但Z检定⽤在⼩的样本会产⽣很⼤的误差，因此样本很⼩的情况下得改⽤学⽣t检定。

t分布曲线形态与n（确切地说与⾃由度df）⼤⼩有关。

与标准正态分布曲线相⽐，⾃由度df越⼩，t分布曲线愈平坦，曲线中间愈低，曲线双侧尾部翘得愈⾼；⾃由度df愈⼤，t分布曲线愈接近正态分布曲线，当⾃由度df=∞时，t分布曲线为标准正态分布曲线。

当总体的是未知的但却⼜需要估计时，我们可以运⽤t-分布。

【特征】：（1）以0为中⼼，左右对称的单峰分布；（2）其数学期望E(Z) = 0，n>1;⽅差D(Z)=n/n-2 , n>2 。

（3）t分布是⼀簇曲线，其形态变化与n（确切地说与df）⼤⼩有关。

⾃由度df越⼩，t分布曲线越低平；⾃由度df越⼤，t分布曲线越接近标准正态分布（u分布）曲线；（4）随着⾃由度逐渐增⼤，t分布逐渐接近标准正态分布。

《数学正态分布》PPT课件

A.f (x)
1
( x )2
e 22
2
C.f (x)
1
( x 1)2
e4
2 2
B.f (x)
2
e
x2 2
2
D.f (x)
1
x2
e2
2
2.设随机变量 ~ N (2,2),则 D( 1 )的值为( C ).
2
A. 1 B. 2 C. 1 D. 4 2
2。正态分布的图像
当时 0, 1，正态总体称为标准正态总体，相应的函数
F( 2 ) F( 2 ) (2) (2) 0.954 正态总体 N(, 2 )在( 3 , 3 )内取值的概率是
F( 3 ) F( 3 ) (3) (3) 0.997
上述计算结果可用下表来表示:
区间
取值概率
( , )
( 2 , 2 )
图
( 3 , 3 )
解:(Ⅰ）设此次参加竞赛得人数为N，竞赛成绩为x，则x服从N（70，100）
设
z
x70 10
，则z服从标准正态分布N（0，1）
∴P（x≥90）=1-P（x＜90）191 0700=1-Φ(2)
查正态分布表知Φ(2)=
∴P（x≥90）=
12 ∴N=526 N
（Ⅱ）设设奖的分数线约为a分
p(xa)1p(xa)1 (a1 70)0
5 52 0 60.095 1a1 7000.9049
查正态分布表知Φ
a17001.31
∴a=
∴设奖的分数线约为分
4。标准正态分布 ~ N(0,1) 在标准正态分布表中相应于x0的值 ( x0 )是
指总体取值小于x0的概率，即 ( x0 ) P( x x0 )

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

标准误是样本均数的标准差，即描述样本均数的抽样误差。凡同性质的资料，标准误大说明抽样误x 差大，用样本均数估计总体均数的可靠性小；而标准误小，说明抽样误差小，用样本均数估计总体均数的可靠性大。
标准误与标准差的区别
µ
x3
x1 s x2
xs
µ
x1
s x3 x
x2
x sx
(二)样本均数的正态分布（中心极限定理）
由抽样而引起的样本均数与总体均数之间的差别及样本均数与样本均数之间的差别称为抽样误差。
从正态分布的同一总体中随机抽取例数相等的若干个样本，分别计算它们的均数，这些样本均数的标准差称为标准误。
标准误与标准差的区别
标准差描述个体变量值间的变异程度。凡同性质的资料，标准差大表示个体变量值变异大，样本均数对个体的代表性差。标准差小表示个体变量值变异小，样本均数对个体的代表性好。
u x
x
t x
sx
（五）t 分布特征
t 值自由度( )
t 分布特征 t界值 t值与自由度的关系 t界值与概率的关系单侧、双侧t界值
t 值自由度( )
从一个总体中抽取200个样本，每一个样本含量n=6则200个样本可计算出200个样本均数 x 每一个样本均数可计算出一个t
估计，t值就是样本均数 x 与总体均数µ的差数
除以 sx 所得之商 t x / sx
SUCCESS
THANK YOU
2019/8/29
实际工作中 x 用 sx 估计，这时对
正态变量 x 采用的不是u变换，而是t
变换。如果从一个正态总体中，抽取样本含量为n的许多样本，分别计算其样本均数和标准误，然后再求出每一个t值，这样可有许多t值，其频数分布是一种连续型分布，这就是统计学上的t分布。
正态分布的特征
正态分布曲线以均数为中心，左右对称。正态分布曲线下的面积分布有一定的规
律正态分布曲线在横轴上方均数处最高。正态分布曲线有两个参数：均数µ 为位
置参数，标准差ơ 为形状参数。
（二）正态分布曲线下的面积分布规律
数理统计证明：正态分布曲线下与横轴之间的整体面积为1或100%。以µ为总体均数，ơ为总体标准差，则正态分布曲线下面积的分布规律经积分法计算有如下规律（图2）
布就是标准正态分布。
u= x -μ/σ x
(四)t值 t分布
对于任何一个横轴变量为 x均数为µ ，标准误为 x的正态分布，都可以通过变换，使之成为µ=0， x =1的标准正态分布。变换的方法是将变量值 x变换为u，u=x- µ / x ，u值的分
布就是标准正态分布。实际工作中 x 常用 sx
一、正态分布
（一）正态分布的概念
正态分布又称高斯分布，是一种很重要的连续型分布，应用甚广。在医学卫生领域中有许多变量的频数分布资料可绘制成直方图而且频数分布是中间（靠近均数处）频数多，两边频数少，且左右对称。
可以设想，如果将观察人数逐渐增多，组段不断分细，图中直条将逐渐变窄，其顶端的中点的连线将逐渐接近于一条光滑的曲线，这条曲线略呈钟型，两头低，中间高，左右对称，近似于数学上的正态分布曲线（图1）
（三）正态分布曲线的两个参数
均数µ决定曲线在横轴上的位置是正态分布曲线的位置参数（图3.1）。
标准差ơ决定曲线的形状是正态分布曲线的形状参数（变异度参数）（图3.2）。
（四）标准正态分布
对于任何一个均数为µ ，标准差为ơ 的正态分布，都可以通过变换，使之成为µ=0, ơ=1的标准正态分布。变换的方法是将变量值x变换为u，u=x- µ / ơ ， u值的分布就是标准正态分布。
µ+ 1ơ范围内的面积占正态曲线下总面积的68.27%，即有68.27%的变量值分布在此范围内；
µ+ 1.96ơ范围内的面积占正态曲线下总面积的95.00%，即有95.00%的变量值分布在此范围内；
µ+ 2.58ơ范围内的面积占正态曲线下总面积99.00%，即有99.00%的变量值分布在此范围内
从一个呈正态分布的总体中随机抽取样本含量相等的许多样本，分别计算出它们的样本均数。这些样本均数的频数分布仍是以总体均数为中心的正态分布。
µ
x1
x3 x
x2
(三)样本均数的标准正态分布
对于任何一个横轴变量为 x 均数为µ ，标准误为 x 的正态分布，都可以通过变换，使之成为µ=0、 x =1的标准正态分布。变换的方法是将变量值x 变换为u，u= x- µ / x ，u值的分
计量资料统计分析
正态分布 t分布
正态分布 t分布
计量资料的统计推断是以正态分布、标准正态分布、t分布为理论基础。
正态分布、标准正态分布、 t分布的相互关系是参数估计和假设检验的理论基础。
本课件主要学习正态分布、标准正态分布、 t分布的概念、分布特征、相互关系。
Байду номын сангаас
正态分布 t分布
一、正态分布（一）正态分布的概念（二）正态分布曲线下的面积分布规律（三）正态分布曲线的两个参数（四）标准正态分布（五）标准正态分布曲线下的面积分布规律二、 t分布（一）均数的抽样误差（二）样本均数的正态分布（中心极限定理）（三）样本均数的标准正态分布（四）t值、t分布（五）t分布特征
u=-1.96,u=1.96 范围内的面积占正态曲线下总面积的 95.00%，即有95.00%的变量值分布在此范围内；
u=-2.58,u=2.58范围内的面积占正态曲线下总面积99.00%，即有99.00%的变量值分布在此范围内。
二、t 分布
(一)均数的抽样误差标准误
在总体中随机抽取一部分个体作为样本，进行调查研究以推论总体的方法，称为抽样研究方法。
u=x-μ/σ
(五)标准正态分布曲线下的面积分布规律
标准正态分布曲线以u值为横轴变量，位置参数µ=0，形状参数ơ=1，标准正态分布曲线与横轴之间的整体面积为1或100%。标准正态分布曲线下面积的分布规律有如下规律（图5）
u=-1,u=1范围内的面积占正态曲线下总面积的68.27%，即有68.27%的变量值分布在此范围内；

正态分布t分布课件

合集下载