07-极坐标、圆锥曲线、导数tm

圆锥曲线的极坐标方程及其推导过程嘿，咱今儿来聊聊圆锥曲线的极坐标方程及其推导过程，这可有意
思啦！
你想啊，圆锥曲线，那可是数学世界里的大明星呢！椭圆、双曲线、抛物线，各有各的特点，各有各的魅力。

那极坐标又是啥呢？简单说，就是用距离和角度来描述一个点的位置。

这就好比你在一个大广场上，别人问你在哪，你可以说离某个标
志多远，然后朝哪个方向。

那圆锥曲线的极坐标方程咋来的呢？咱就拿椭圆来说吧。

想象一下，有个点在椭圆上跑来跑去，那它到一个定点（焦点）的距离和到一条
定直线（准线）的距离，是不是有个固定的比例呀？嘿，这就是关键！通过这个关系，咱就能捣鼓出椭圆的极坐标方程啦。

具体咋推导呢？咱先设椭圆上那个点的极坐标是（ρ，θ），焦点到
原点的距离是 c，椭圆的长半轴是 a。

然后根据那些关系，一顿操作猛
如虎，就能算出ρ 啦！是不是很神奇？
双曲线其实也差不多，就是那个比例关系有点不一样。

抛物线呢，
就更特别啦，它只有一个焦点和一条准线。

你说这圆锥曲线的极坐标方程有啥用？用处可大啦！比如在一些物理问题里，像天体运动啥的，就经常用到。

而且在数学里，这可是研究圆锥曲线的重要工具呢！
你看，通过这么一个看似简单的极坐标方程，咱就能把圆锥曲线的各种性质都给搞清楚，这多厉害呀！这就好比你有了一把钥匙，能打开圆锥曲线这个神秘宝盒的大门。

所以啊，别小看这圆锥曲线的极坐标方程，它里面蕴含的知识可深着呢！咱可得好好琢磨琢磨，把它弄明白。

不然，那可就亏大啦！你说是不是？。

极坐标圆锥曲线的应用
极坐标圆锥曲线是一种描述平面上点的轨迹的数学工具，它由直角坐标系中的圆锥曲线变换而来。

极坐标圆锥曲线有很多重要的应用，下面介绍其中几个：
1. 极坐标圆锥曲线在天文学中的应用：天文学家使用极坐标圆
锥曲线来描述行星、卫星、彗星等天体的运动轨迹。

例如，地球绕太阳公转的轨迹就是一个椭圆。

天文学家通过观测行星的位置和速度，可以确定它们的轨道参数，如轨道离心率、轨道倾角等。

2. 极坐标圆锥曲线在工程中的应用：工程师使用极坐标圆锥曲
线来设计各种机械和电子设备。

例如，螺旋线是一种常见的极坐标圆锥曲线，在机械加工中广泛应用。

另外，极坐标圆锥曲线还可以用来描述电磁波的传播路径和天线的辐射特性等。

3. 极坐标圆锥曲线在物理学中的应用：物理学家使用极坐标圆
锥曲线来描述粒子在电场和磁场中的运动轨迹。

例如，质谱仪利用粒子在磁场中的轨迹来分析物质的成分。

此外，极坐标圆锥曲线还可以用来描述电荷在电场中的受力情况和天体运动的动力学过程等。

总之，极坐标圆锥曲线是一种非常重要的数学工具，在天文学、工程、物理学等领域都有广泛的应用。

掌握它的基本原理和应用方法，对于相关专业的学生和从事相关工作的人员都是非常有帮助的。

- 1 -。

圆锥曲线方程知识点总结一、圆锥曲线的基本方程椭圆的标准方程如下：$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1. (a > b > 0)$$其中椭圆的长轴为$2a$，短轴为$2b$，焦距为$\sqrt{a^2 - b^2}$，离心率为$c/a$。

双曲线的标准方程如下：$$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1. (a > 0, b > 0)$$其中双曲线的两个分支的焦点到中心的距离为$c = \sqrt{a^2 + b^2}$。

抛物线的标准方程如下：$$x^2 = 4ay. (a > 0)$$其中抛物线的焦点为$(0, a)$，顶点为$(0, 0)$。

二、圆锥曲线的参数方程圆锥曲线还可以用参数方程表示。

以椭圆为例，其参数方程为：$$\begin{cases}x = a \cos \theta, \\y = b \sin \theta. \\\end{cases}$$其中$\theta$的取值范围为$[0, 2\pi]$。

双曲线和抛物线的参数方程也可以类似地表示。

三、圆锥曲线的极坐标方程圆锥曲线还可以用极坐标方程表示。

以椭圆为例，其极坐标方程为：$$r = \frac{ab}{\sqrt{a^2 \sin^2 \theta + b^2 \cos^2 \theta}}.$$其中$r$为极径，$\theta$为极角。

双曲线和抛物线的极坐标方程也可以类似地表示。

四、圆锥曲线的性质1. 圆锥曲线关于坐标轴的对称性：- 椭圆关于$x$轴和$y$轴都对称；- 双曲线关于$x$轴和$y$轴都对称；- 抛物线关于$y$轴对称。

2. 圆锥曲线的焦点、直径、离心率等：- 椭圆的焦点到中心的距离为$c = \sqrt{a^2 - b^2}$，离心率为$e = c/a$；- 双曲线的焦点到中心的距离为$c = \sqrt{a^2 + b^2}$，离心率为$e = c/a$；- 抛物线的焦点到中心的距离为$c = a$，离心率为$e = 1$。

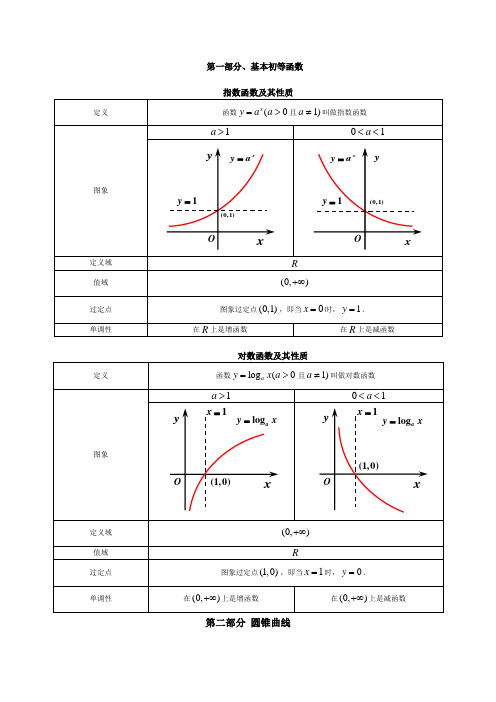
第一部分、基本初等函数第二部分圆锥曲线椭圆1、平面内与两个定点1F ，2F 的距离之和等于常数（大于12F F ）的点的轨迹称为椭圆． 即：|)|2(,2||||2121F F a a MF MF >=+。

这两个定点称为椭圆的焦点，两焦点的距离称为椭圆的焦距． 2、椭圆的几何性质：焦点的位置 焦点在x 轴上焦点在y 轴上图形标准方程()222210x y a b a b +=>> ()222210y x a b a b +=>> 范围a x a -≤≤且b y b -≤≤b x b -≤≤且a y a -≤≤顶点()1,0a A -、()2,0a A()10,b B -、()20,b B()10,a A -、()20,a A ()1,0b B -、()2,0b B 轴长 短轴的长2b = 长轴的长2a =焦点 ()1,0F c -、()2,0F c()10,F c -、()20,F c焦距 ()222122F F c c a b ==-对称性 关于x 轴、y 轴、原点对称离心率)01c e e a ==<<双曲线3、平面内与两个定点1F ，2F 的距离之差的绝对值等于常数（小于12F F ）的点的轨迹称为双曲线．即：|)|2(,2||||||2121F F a a MF MF <=-。

这两个定点称为双曲线的焦点，两焦点的距离称为双曲线的焦距．4、双曲线的几何性质：焦点的位置 焦点在x 轴上焦点在y 轴上 图形标准方程()222210,0x y a b a b -=>> ()222210,0y x a b a b -=>> 范围 x a ≤-或x a ≥，y R ∈y a ≤-或y a ≥，x R ∈顶点 ()1,0a A -、()2,0a A ()10,a A -、()20,a A 轴长 虚轴的长2b = 实轴的长2a =焦点 ()1,0F c -、()2,0F c()10,F c -、()20,F c焦距 ()222122F F c c a b ==+对称性 关于x 轴、y 轴对称，关于原点中心对称离心率)1c e e a ==>渐近线方程b y x a=±a y x b=±5、实轴和虚轴等长的双曲线称为等轴双曲线．抛物线6、平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹称为抛物线．定点F 称为抛物线的焦点，定直线l 称为抛物线的准线．7、抛物线的几何性质：标准方程22y px =()0p >22y px =- ()0p > 22x py = ()0p > 22x py =-()0p >图形对称轴x 轴y 轴焦点,02p F ⎛⎫ ⎪⎝⎭ ,02p F ⎛⎫- ⎪⎝⎭ 0,2p F ⎛⎫ ⎪⎝⎭0,2p F ⎛⎫- ⎪⎝⎭准线方程2px =-2px =2p y =-2p y =离心率1e =第三部分 导数及其应用1、函数()f x 从1x 到2x 的平均变化率：()()2121f x f x x x --2、导数定义：()f x 在点0x 处的导数记作xx f x x f x f y x x x ∆-∆+='='→∆=)()(lim)(00000；．3、函数()y f x =在点0x 处的导数的几何意义是曲线()y f x =在点()()00,x f x P 处的切线的斜率．4、常见函数的导数公式：①'C 0=；②1')(-=n n nx x ； ③x x cos )(sin '=；④x x sin )(cos '-=；⑤a a a x x ln )('=；⑥x x e e =')(； ⑦a x x a ln 1)(log '=；⑧xx 1)(ln '= 5、导数运算法则：()1 ()()()()f x g x f x g x '''±=±⎡⎤⎣⎦；()2 ()()()()()()f x g x f x g x f x g x '''⋅=+⎡⎤⎣⎦； ()3()()()()()()()()()20f x f x g x f x g x g x g x g x '⎡⎤''-=≠⎢⎥⎡⎤⎣⎦⎣⎦．6、在某个区间(),a b 内，若()0f x '>，则函数()y f x =在这个区间内单调递增； 若()0f x '<，则函数()y f x =在这个区间内单调递减．7、求函数()y f x =的极值的方法是：解方程()0f x '=．当()00f x '=时：()1如果在0x 附近的左侧()0f x '>，右侧()0f x '<，那么()0f x 是极大值； ()2如果在0x 附近的左侧()0f x '<，右侧()0f x '>，那么()0f x 是极小值．8、求函数()y f x =在[],a b 上的最大值与最小值的步骤是：()1求函数()y f x =在(),a b 内的极值；()2将函数()y f x =的各极值与端点处的函数值()f a ，()f b 比较，其中最大的一个是最大值，最小的一个是最小值．。

圆锥曲线简化计算技巧
圆锥曲线是解析几何中一个重要的部分，它包括椭圆、双曲线和抛物线等。

在解决圆锥曲线问题时，掌握一些简化计算的技巧是非常有帮助的。

以下是一些常用的圆锥曲线简化计算技巧：
1. 参数方程法：对于一些复杂的圆锥曲线问题，可以通过引入参数来简化计算。

参数方程可以将圆锥曲线的几何性质转化为代数方程，从而方便求解。

2. 极坐标法：对于一些与极坐标有关的圆锥曲线问题，使用极坐标可以简化计算。

极坐标可以将圆锥曲线的方程转化为极坐标形式，从而方便求解。

3. 对称性质：圆锥曲线具有对称性质，可以利用这些性质来简化计算。

例如，在椭圆中，关于长轴和短轴的对称性可以用来简化计算。

4. 切线性质：对于一些与切线有关的圆锥曲线问题，可以利用切线的性质来简化计算。

例如，在抛物线中，切线的斜率等于该点的导数。

5. 数形结合：在解决圆锥曲线问题时，可以将代数方程与几何图形结合起来，从而方便求解。

数形结合可以帮助我们更好地理解问题的本质，从而找到更有效的解决方案。

6. 整体代换：在一些复杂的圆锥曲线问题中，可以通过整体代换来简化计算。

整体代换可以将复杂的代数表达式转化为简单的代数表达式，从而方便求解。

7. 逐步化简：在解决圆锥曲线问题时，可以通过逐步化简来简化计算。

逐步化简可以将复杂的代数方程逐步化简为简单的代数方程，从而方便求解。

以上是一些常用的圆锥曲线简化计算技巧，掌握这些技巧可以帮助我们更有效地解决圆锥曲线问题。

圆锥曲线与极坐标极坐标在平⾯内取⼀个定点O，叫极点，引⼀条射线Ox，叫做极轴，再选定⼀个长度单位和⾓度的正⽅向（通常取逆时针⽅向）。

对于平⾯内任何⼀点M，⽤ρ表⽰线段OM的长度（有时也⽤r表⽰），θ表⽰从Ox到OM的⾓度，ρ叫做点M的极径，θ叫做点M的极⾓，有序数对 (ρ,θ) 就叫点M的极坐标，这样建⽴的坐标系叫做极坐标系。

极坐标系⽤长度和⾓度取代了⼆维的坐标，相对于⼀般的直⾓坐标为下⾯的优点：便于处理⾓度的关系便于表⽰和计算长度设M为平⾯上的⼀点，它的直⾓坐标为 (x,y)，极坐标为 (ρ,θ)，易得互化公式：x=ρcosθy=ρsinθorρ2=x2+y2 tanθ=yx (x≠0)p，由圆锥曲线的统⼀定义知ρd=e，由图形可得d=p+ρcosθ，代⼊得ρ=ep1−e cosθ当e=0 时，轨迹为圆；0<e<1 时，轨迹为椭圆；e=1 时，轨迹为抛物线；e>1 时，轨迹为双曲线。

（2）以坐标原点为极点在这⾥只考虑椭圆与双曲线的情况，抛物线也可类⽐：椭圆或双曲线的标准⽅程（焦点在x轴上）为：x2a2±y2b2=1 {{Processing math: 100%代⼊x=ρcosθ，y=ρsinθ得：ρ2cos2θa2±ρ2sin2θb2=1，提取ρ2得：1ρ2=cos2θa2±sin2θb2，此⽅程表⽰椭圆或双曲线的轨迹。

取加号时，轨迹为椭圆；取减号时，轨迹为双曲线。

⼀些结论如图，F为圆锥曲线E的焦点，过F的直线交E与A,B两点，设直线AB的倾斜⾓为α，则|AF|=ep1−e cosα, |BF|=ep1+e cosα|AB|=ep1−e cosα+ep1+e cosα=2ep1−e2cos2α（看成以F为极点的极坐标系，由圆锥曲线⽅程ρ=ep1−e cosθ，令θ=α可得A点的ρ，即 |AF|；同理，令θ=α+π得到B的，再⽤诱导公式 cos(θ+π)=−cosθ）当椭圆与双曲线以标准⽅程表⽰时，焦准距p=b2c，离⼼率e=ca，那么|AF|=b2a−c cosα, |BF|=b2a+c cosα|AB|=2ab2a2−c2cos2α若|AF||BF|=λ，则1+e cosα1−e cosα=λ，解出e cosα=λ−1λ+1已知e,λ时，可⽤上式求倾斜⾓。

圆锥曲线解题技巧应用极坐标方程解题在数学中，圆锥曲线是与一个双曲线、抛物线或椭圆相关的二维曲线。

解决圆锥曲线问题通常需要熟悉各种曲线的性质和方程。

其中，极坐标方程是一种经常应用的解题技巧。

本文将介绍圆锥曲线解题时应用的极坐标方程以及相关技巧和例题。

一、极坐标方程的基本概念极坐标是一种描述平面上点的坐标系，其中每个点由极径和极角确定。

在极坐标系中，点的坐标表示为(r, θ)，其中r 是点到原点的距离，θ 是点与极轴的夹角。

圆锥曲线的极坐标方程通常可以写成以下形式：1. 椭圆：r = a(1 - e*cosθ)2. 双曲线：r = a(1 + e*cosθ)3. 抛物线：r = a(1 - e*sinθ)其中 a 是焦点到准线的距离（也称为半焦距），e 是离心率。

二、极坐标方程解题技巧1. 确定曲线类型：首先通过曲线的方程判断是椭圆、双曲线还是抛物线。

根据方程中的参数，可以判断曲线的形状和特征。

2. 确定半焦距和离心率：通过方程中给出的参数，可以计算出椭圆、双曲线或抛物线的半焦距和离心率。

这些值将在后续的解题过程中提供重要的信息。

3. 根据极坐标方程绘制图形：利用计算机或手绘的方式，在极坐标系中绘制出曲线的形状。

这有助于直观地理解曲线的性质和特征，并准备后续解题的步骤。

4. 求解相关问题：根据具体的题目要求，利用极坐标方程和曲线性质进行解题。

可以通过求交点、切线、曲率等来解决各种问题。

三、应用实例例题一：求给定双曲线极坐标方程r = 2/(1 + 3cosθ) 的离心率和半焦距。

解析：根据双曲线的极坐标方程r = a(1 + e*cosθ) 可知，此题中的 a = 2，即半焦距为 2。

要求离心率 e，可以将方程转换为标准形式，得到2/(1 + 3cosθ) = a/(1 + e*cosθ)。

比较系数可知 e = 3。

例题二：给定椭圆极坐标方程 r = 4/(2 - cosθ)，求椭圆的焦距。

解析：根据椭圆的极坐标方程 r = a(1 - e*cosθ) 可知，此题中的 a = 4。

圆锥曲线的极坐标方程与参数方程解析极坐标方程与参数方程是圆锥曲线的两种常用表示形式。

在研究圆锥曲线时，利用这两种方程形式可以更加直观地描述曲线的特征与性质。

本文将详细介绍圆锥曲线的极坐标方程和参数方程的解析过程，并通过具体的例子来进一步说明。

一、圆锥曲线的极坐标方程圆锥曲线的极坐标方程可以用极坐标系中的极径r和极角θ来表示。

对于圆锥曲线而言，其极坐标方程的一般形式如下：r = f(θ)其中，函数f(θ)代表了曲线的性质与形状，具体形式根据不同的圆锥曲线类型而异。

以下是几种常见的圆锥曲线的极坐标方程及其解析过程：（一）圆的极坐标方程圆是一种特殊的圆锥曲线，其极坐标方程可以表示为：r = a其中，a代表圆的半径。

（二）椭圆的极坐标方程椭圆的极坐标方程形式如下：r = a(1 - ε²) / (1 - εcosθ)其中，a代表椭圆的半长轴长度，ε代表椭圆的离心率。

（三）双曲线的极坐标方程双曲线的极坐标方程可以写为：r = a(1 + εcosθ) / (1 - εcosθ)其中，a代表双曲线的焦距，ε代表双曲线的离心率。

（四）抛物线的极坐标方程抛物线的极坐标方程可以表示为：r = a / (1 + cosθ)其中，a代表抛物线的焦点到准线的距离。

通过以上例子可以看出，圆锥曲线的极坐标方程形式多样，每一种形式代表了不同的曲线类型和特征。

研究圆锥曲线时，可以根据需要选择不同的极坐标方程进行分析。

二、圆锥曲线的参数方程除了极坐标方程外，参数方程也是描述圆锥曲线常用的一种形式。

在参数方程中，圆锥曲线的坐标可以通过参数t的取值得到。

一般来说，圆锥曲线的参数方程具有以下形式：x = f(t)y = g(t)其中，函数f(t)和g(t)分别表示曲线的x坐标与y坐标，具体形式根据不同的圆锥曲线类型而定。

以下是几种常见圆锥曲线的参数方程及其解析过程：（一）圆的参数方程圆的参数方程可以表示为：x = acos(t)y = asin(t)其中，a代表圆的半径，t取值范围通常为0到2π。