全国I卷近十年(2010-2019)高考文科数学真题分类汇编合集

专题06平面向量历年考题细目表历年高考真题汇编1．【2019年新课标1文科08】已知非零向量，满足||＝2||，且（）⊥，则与的夹角为（）A．B．C．D．【解答】解：∵（）⊥，∴，∴，∵，∴．故选：B．2．【2018年新课标1文科07】在△ABC中，AD为BC边上的中线，E为AD的中点，则（）A．B．C．D．【解答】解：在△ABC中，AD为BC边上的中线，E为AD的中点，（），故选：A．3．【2015年新课标1文科02】已知点A（0，1），B（3，2），向量（﹣4，﹣3），则向量（）A．（﹣7，﹣4）B．（7，4）C．（﹣1，4）D．（1，4）【解答】解：由已知点A（0，1），B（3，2），得到（3，1），向量（﹣4，﹣3），则向量（﹣7，﹣4）；故选：A．4．【2014年新课标1文科06】设D，E，F分别为△ABC的三边BC，CA，AB的中点，则（）A．B．C．D．【解答】解：∵D，E，F分别为△ABC的三边BC，CA，AB的中点，∴（）+（）（），故选：A．5．【2010年新课标1文科02】平面向量，已知（4，3），（3，18），则夹角的余弦值等于（）A．B．C．D．【解答】解：设（x，y），∵a＝（4，3），2a+b＝（3，18），∴∴cosθ，故选：C．6．【2017年新课标1文科13】已知向量（﹣1，2），（m，1），若向量与垂直，则m＝．【解答】解：∵向量（﹣1，2），（m，1），∴（﹣1+m，3），∵向量与垂直，∴（）•（﹣1+m）×（﹣1）+3×2＝0，解得m＝7．故答案为：7．7．【2016年新课标1文科13】设向量（x，x+1），（1，2），且⊥，则x＝．【解答】解：∵；∴；即x+2（x+1）＝0；∴．故答案为：．8．【2013年新课标1文科13】已知两个单位向量，的夹角为60°，t（1﹣t）．若•0，则t＝．【解答】解：∵，，∴0，∴t cos60°+1﹣t＝0，∴10，解得t＝2．故答案为2．9．【2012年新课标1文科15】已知向量夹角为45°，且，则．【解答】解：∵， 1∴∴|2|解得故答案为：310．【2011年新课标1文科13】已知a与b为两个垂直的单位向量，k为实数，若向量与向量k垂直，则k＝．【解答】解：∵∴∵垂直∴即∴k＝1故答案为：1考题分析与复习建议本专题考查的知识点为：平面向量的线性运算，平面向量基本定理及坐标表示，平面向量的数量积，平面向量的综合应用等.历年考题主要以选择填空题型出现，重点考查的知识点为：平面向量的线性运算，平面向量基本定理及坐标表示，平面向量的数量积等，预测明年本考点题目会比较稳定，备考方向以知识点平面向量的线性运算，平面向量的数量积，平面向量的综合应用等为重点较佳.最新高考模拟试题1．在ABC ∆中，，，若，则（ ）A ．3y x =B ．3x y =C ．3y x =-D ．3x y =-【答案】D 【解析】 因为，所以点D 是BC 的中点，又因为，所以点E 是AD 的中点，所以有：，因此，故本题选D.2．已知非零向量a ,b 的夹角为60,且满足22a b -=,则a b ⋅的最大值为( ) A ．12B ．1C ．2D ．3【答案】B 【解析】因为非零向量a ,b 的夹角为60,且满足22a b -=, 所以，即，即，又因为，当且仅当2a b =时，取等号；所以，即2a b ≤；因此，.即a b ⋅的最大值为1. 故选B3．设a ，b 均为单位向量，则“a 与b 夹角为2π3”是“||3a b +=”的( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【答案】D 【解析】因为a ，b 均为单位向量， 若a 与b 夹角为2π3，则；因此，由“a 与b 夹角为2π3”不能推出“||3a b +=”； 若||3a b +=，则，解得1cos ,2a b =，即a 与b 夹角为π3， 所以，由“||3a b +=”不能推出“a 与b 夹角为2π3” 因此，“a 与b 夹角为2π3”是“||3a b +=”的既不充分也不必要条件. 故选D4．在矩形ABCD 中，4AB =uu u r,2AD =．若点M ，N 分别是CD ，BC 的中点，则AM MN ⋅=（ ）A ．4B ．3C ．2D ．1【答案】C 【解析】由题意作出图形，如图所示：由图及题意，可得：，.∴.故选：C ．5．已知P 为等边三角形ABC 所在平面内的一个动点，满足，若2AB =，则（ ）A ．B ．3C ．6D ．与λ有关的数值【答案】C 【解析】如图：以BC 中点为坐标原点O ，以BC 方向为x 轴正方向，OA 方向为y 轴正方向，建立平面直角坐标系，因为2AB =，则3AO =，因为P 为等边三角形ABC 所在平面内的一个动点，满足，所以点P 在直线BC ，所以AP uu u r在AO 方向上的投影为AO ， 因此.故选C6．已知向量，且()a a b ⊥-，则m 的值为（ ）A ．1B ．3C ．1或3D ．4【答案】B 【解析】 因为，所以，因为()a a b ⊥-，则，解得3m =所以答案选B.7．已知向量a 、b 为单位向量，且a b +在a 1，则向量a 与b 的夹角为（ ） A ．6π B ．4π C ．3π D ．2π 【答案】A 【解析】设向量a 与b 的夹角为θ， 因为向量a 、b 为单位向量，且a b +在a 1+， 则有，变形可得：，即，又由0θπ≤≤，则6πθ=，故选A ．8．在矩形ABCD 中，与BD 相交于点O ，过点A 作AE BD ⊥，垂足为E ，则AE EC ⋅=（ ）A ．725B ．14425C ．125D ．1225【答案】B 【解析】 如图：由3AB =，4=AD 得：，又AE BD ⊥又本题正确选项：B9．已知直线y=x+m 和圆x 2+y 2=1交于A 、B 两点，O 为坐标原点，若，则实数m=（ ）A ．1±B ．2±C ．2±D ．12±【解析】联立221y x m x y =+⎧⎨+=⎩ ，得2x 2+2mx+m 2-1=0， ∵直线y=x+m 和圆x 2+y 2=1交于A 、B 两点，O 为坐标原点，∴△=4m 2+8m 2-8=12m 2-8＞0，解得m 或m ＜，设A （x 1，y 1），B （x 2，y 2），则x 1+x 2=-m ，，y 1y 2=（x 1+m ）（x 2+m ）=x 1x 2+m （x 1+x 2）+m 2，AO =（-x 1，-y 1），AB =（x 2-x 1，y 2-y 1），∵+y 12-y 1y 2=1+m 2-m 2=2-m 2=32，解得m= 故选：C ．10．已知菱形ABCD 的边长为2，，点E ，F 分别在边BC ，DC 上，3BC BE =，DC DF λ=，若1AE AF ⋅=，则λ的值为（ ）A ．3B ．2C ．23 D ．52【答案】B 【解析】 由题意可得：，且：，故，解得：2λ=.11．已知正ABC ∆的边长为4，点D 为边BC 的中点，点E 满足AE ED =，那么EB EC ⋅的值为（ ） A ．83- B ．1-C ．1D ．3【答案】B 【解析】由已知可得：，又所以所以故选：B ．12．在ABC ∆中，3AC =，向量AB 在AC 上的投影的数量为，则BC =( )A ．5B ．C ．29D ．【答案】C 【解析】∵向量AB 在AC 上的投影的数量为2-，∴．① ∵3ABC S ∆=，∴，∴．②由①②得tan1A=-，∵A为ABC∆的内角，∴34Aπ=，∴．在ABC∆中，由余弦定理得，∴BC=故选C．13．在△ABC中，，则λμ+=（）A．1-3B．13C．1-2D．12【答案】A【解析】因为所以P为ABC∆的重心，所以, 所以,所以因为，所以故选：A14．在ABC∆中，，则（）A．9:7:8B．C．6:8:7D．【答案】B【解析】设所以，所以，所以，得所以故选：B15．在平行四边形ABCD中，若则ADC∠=( )A．56πB．34πC．23πD．2π【答案】C【解析】如图所示,平行四边形ABCD中, ,，，,因为,所以, ，所以，故选C.16．已知△ABC中，．点P为BC边上的动点，则的最小值为（）A．2 B．34-C．2-D．2512-【答案】D【解析】以BC的中点为坐标原点，建立如图的直角坐标系，可得，设，由，可得，即，则，当16a =时，的最小值为2512-． 故选：D ．17．如图Rt ABC ∆中，2ABC π∠=，2AC AB =，BAC ∠平分线交△ABC 的外接圆于点D ，设AB a =，AC b =，则向量AD =（ ）A ．a b +B ．12a b +C ．12a b +D ．23a b +【答案】C 【解析】解：设圆的半径为r ，在Rt ABC ∆中，2ABC π∠=，2AC AB =， 所以3BAC π∠=，6ACB π∠=，BAC ∠平分线交ABC ∆的外接圆于点D ，所以， 则根据圆的性质，又因为在Rt ABC ∆中，，所以四边形ABDO 为菱形，所以．故选：C ．18．在ABC ∆中，90A ∠=︒，1AB =，2AC =，设点D 、E 满足AD AB λ=， ()AC R λ∈，若5BE CD ⋅=，则λ=（ ） A ．13- B ．2 C ．95D ．3【答案】D 【解析】因为90A ∠=︒，则，所以.由已知，345λ-=，则3λ=. 选D .19．已知点C 为扇形AOB 的弧AB 上任意一点，且，若，则λμ+的取值范围为（ ）A ．[2,2]-B ．C ．D ．[1,2]【答案】D 【解析】解：设半径为1，由已知可设OB 为x 轴的正半轴，O 为坐标原点，建立直角坐标系，其中A （12-，B （1，0），C （cos θ，sin θ）（其中∠BOC ＝θ有（λ，μ∈R ）即：（cos θ，sin θ）＝λ（12-+μ（1，0）；整理得：12-λ+μ＝cos θ；2λ＝sin θ，解得：λ=，μ＝cos θ，则λ+μ=cos θsin θ+cos θ＝2sin （θ6π+），其中；易知λ+μ=+cos θsin θ+cos θ＝2sin （θ6π+），由图像易得其值域为[1，2]20．在同一平面内，已知A 为动点，B ，C 为定点，且∠BAC=3π，2ACB π∠≠，BC=1，P 为BC 中点．过点P 作PQ⊥BC 交AC 所在直线于Q ，则AQ 在BC 方向上投影的最大值是（ ） A ．13B ．12CD ．23【答案】C 【解析】建立如图所示的平面直角坐标系，则B （-12，0），C （12，0），P （0，0）， 由BAC 3π∠=可知，ABC 三点在一个定圆上，且弦BC 所对的圆周角为3π，所以圆心角为23π.圆心在BC 的中垂线即y 轴上，且圆心到直线BC的距离为12tan 3BCπ=即圆心为(0,6，半径为.所以点A 的轨迹方程为：，则213x ≤，则，由AQ 在BC 方向上投影的几何意义可得：AQ 在BC 方向上投影为|DP|=|x|， 则AQ 在BC方向上投影的最大值是3， 故选：C ． 21．已知圆的弦AB 的中点为(1,1)-，直线AB 交x 轴于点P ，则PA PB ⋅的值为______．【解析】设(1,1)M -，圆心(2,0)C -，∵，根据圆的性质可知，1AB k =-， ∴AB 所在直线方程为，即22gR r，联立方程可得，，设11(,)A x y ，22(,)B x y ，则，令0y =可得(0,0)P ，，故答案为：-5． 22．已知向量，若，则λ=______．【答案】12【解析】 解：；；；；解得12λ=．故答案为：12． 23．向量()1,2a =-，()1,0b =-，若，则λ=_________.【答案】13【解析】向量()1,2a =-，()1,0b =-， 所以，又因为， 所以，即，解得13λ=，故答案为13. 24．设向量12,e e 的模分别为1,2，它们的夹角为3π，则向量21e e -与2e 的夹角为_____． 【答案】6π 【解析】又∴向量21e e -与2e 的夹角为：6π 本题正确结果：6π 25．已知平面向量a ，m ，n ，满足4a =r，，则当m n -=_____，则m 与n 的夹角最大．【解析】设a ，m ，n 的起点均为O ，以O 为原点建立平面坐标系，不妨设(4,0)a =，(,)m x y =，则，4a m x ⋅=，由可得，即，∴m 的终点M 在以(2,0)为半径的圆上，同理n 的终点N 在以(2,0)显然当OM ，ON 为圆的两条切线时，MON ∠最大，即m ，n 的夹角最大．设圆心为A ，则AM =，，∴， 设MN 与x 轴交于点B ，由对称性可知MN x ⊥轴，且2MN MB =，∴.26．如图，已知P 是半径为2，圆心角为3π的一段圆弧AB 上一点，2A B B C =，则P C P A ⋅的最小值为_______．【答案】5﹣【解析】设圆心为O,AB 中点为D,由题得.取AC 中点M ，由题得, 两方程平方相减得，要使PC PA ⋅取最小值，就是PM 最小，当圆弧AB 的圆心与点P 、M 共线时，PM 最小.此时DM=,所以PM 有最小值为2，代入求得PC PA ⋅的最小值为5﹣故答案为：5﹣27．如图，在边长为2的正三角形ABC 中，D 、E 分别为边BC 、CA 上的动点，且满足CE mBD =（m 为定常数，且(0,1]m ∈），若AD DE ⋅的最大值为34-，则m =________.【答案】12【解析】以BC 中点为坐标原点O ，OC 方向为x 轴正方向，OA 方向为y 轴正方向，建立如图所示平面直角坐标系，因为正三角形ABC 边长为2，所以(1,0)B -，(1,0)C ，A ，则(2,0)BC =，，因为D 为边BC 上的动点，所以设BD tBC =，其中01t ≤≤，则，所以(21,0)D t -；又，所以，因此， 所以，，故，因为(0,1]m ∈，所以，又01t ≤≤， 所以当且仅当324m t m -=+时，AD DE ⋅取得最大值，即，整理得，解得12m =或8m =（舍） 故答案为1228．在ABC ∆中，已知AB 边上的中线1CM =，且1tan A ，1tan C ，1tan B 成等差数列，则AB 的长为________.【答案】3【解析】因为1tan A ，1tan C ，1tan B成等差数列， 所以，即， 所以，由正弦定理可得， 又由余弦定理可得，所以，故， 又因为AB 边上的中线1CM =，所以1CM =，因为， 所以，即，解c =.即AB29．如图，在平面四边形ABCD 中，，30ACD ∠=︒，AB BC =，点E 为线段BC 的中点．若 (,R λμ∈)，则λμ的值为_______．【解析】以A 为原点，建立如图所示的平面直角坐标系，不妨设AB ＝BC ＝2，则有A （0,0），B （2,0），C （2,2），E （2,1），AC ＝，AD ＝×tan30°＝3，过D 作DF⊥x 轴于F ，∠DAF＝180°－90°－45°＝45°， DF＝3sin45°＝，所以D（3-，3）， AC ＝（2,2），AD＝（3-），AE ＝（2,1），因为， 所以，（2,2）＝λ（）+μ（2,1）， 所以，，解得：343λμ⎧=⎪⎪⎨⎪=⎪⎩λμ30．在平面直角坐标系xOy 中，已知()11,A x y ，()22,B x y 为圆221x y +=上两点，且．若C 为圆上的任意一点，则CA CB 的最大值为______． 【答案】32【解析】因为C 为圆x 2+y 2＝1上一点，设C （sin θ，cos θ），则，∵()11,A x y ，()22,B x y 为圆221x y +=上两点，∴，又，∴，其中，∵sin()θϕ+∈[﹣1，1]， ∴当sin()θϕ+＝1时，CA CB ⋅的最大值为32． 故答案为：32．。

专题07数列历年考题细目表历年高考真题汇编1．【2015年新课标1文科07】已知{a n}是公差为1的等差数列，S n为{a n}的前n项和，若S8＝4S4，则a10＝（）A．B．C．10 D．122．【2013年新课标1文科06】设首项为1，公比为的等比数列{a n}的前n项和为S n，则（）A．S n＝2a n﹣1 B．S n＝3a n﹣2 C．S n＝4﹣3a n D．S n＝3﹣2a n3．【2012年新课标1文科12】数列{a n}满足a n+1+（﹣1）n a n＝2n﹣1，则{a n}的前60项和为（）A．3690 B．3660 C．1845 D．18304．【2019年新课标1文科14】记S n为等比数列{a n}的前n项和．若a1＝1，S3，则S4＝．5．【2015年新课标1文科13】在数列{a n}中，a1＝2，a n+1＝2a n，S n为{a n}的前n项和，若S n＝126，则n ＝．6．【2012年新课标1文科14】等比数列{a n}的前n项和为S n，若S3+3S2＝0，则公比q＝．7．【2019年新课标1文科18】记S n为等差数列{a n}的前n项和．已知S9＝﹣a5．（1）若a3＝4，求{a n}的通项公式；（2）若a1＞0，求使得S n≥a n的n的取值范围．8．【2018年新课标1文科17】已知数列{a n}满足a1＝1，na n+1＝2（n+1）a n，设b n．（1）求b1，b2，b3；（2）判断数列{b n}是否为等比数列，并说明理由；（3）求{a n}的通项公式．9．【2017年新课标1文科17】记S n为等比数列{a n}的前n项和．已知S2＝2，S3＝﹣6．（1）求{a n}的通项公式；（2）求S n，并判断S n+1，S n，S n+2是否成等差数列．10．【2016年新课标1文科17】已知{a n}是公差为3的等差数列，数列{b n}满足b1＝1，b2，a n b n+1+b n+1＝nb n．（Ⅰ）求{a n}的通项公式；（Ⅱ）求{b n}的前n项和．11．【2014年新课标1文科17】已知{a n}是递增的等差数列，a2，a4是方程2﹣5+6＝0的根．（1）求{a n }的通项公式； （2）求数列{}的前n 项和．12．【2013年新课标1文科17】已知等差数列{a n }的前n 项和S n 满足S 3＝0，S 5＝﹣5． （Ⅰ）求{a n }的通项公式； （Ⅱ）求数列{}的前n 项和．13．【2011年新课标1文科17】已知等比数列{a n }中，a 1，公比q ．（Ⅰ）S n 为{a n }的前n 项和，证明：S n（Ⅱ）设b n ＝log 3a 1+log 3a 2+…+log 3a n ，求数列{b n }的通项公式． 14．【2010年新课标1文科17】设等差数列{a n }满足a 3＝5，a 10＝﹣9． （Ⅰ）求{a n }的通项公式；（Ⅱ）求{a n }的前n 项和S n 及使得S n 最大的序号n 的值． 考题分析与复习建议本专题考查的知识点为：数列的概念与简单表示法，等差数列及其前n 项和，等比数列及其前n 项和，数列求和，数列求通项等.历年考题主要以选择填空或解答题题型出现.重点考查的知识点为：等差数列及其前n 项和，等比数列及其前n 项和，数列求和，数列求通项等.预测明年本考点题目会比较稳定，备考方向以知识点等差数列及其前n 项和，等比数列及其前n 项和，数列求和，数列求通项为重点较佳.最新高考模拟试题1．等差数列{}n a ，等比数列{}n b ，满足111a b ==，53a b =，则9a 能取到的最小整数是（ ） A ．1-B ．0C ．2D ．32．中国古代数学名著《九章算术》中有这样一个问題今有牛、马、羊食人苗，苗主责之粟五斗，羊主曰“我羊食半马、“马主曰“我马食半牛，”今欲衰偿之，问各出几何?此问题的译文是今有牛、马、羊吃了别人的禾苗，禾苗主人要求赔偿5斗粟、羊主人说“我羊所吃的禾苗只有马的一半，”马主人说“我马所吃的禾苗只有牛的一半，“打算按此比例偿还，他们各应偿还多少？该问题中，1斗为10升，则马主人应偿还( )升粟？ A ．253B ．503C ．507D ．10073．我国古代的《洛书》中记载着世界上最古老的一个幻方：如图，将1，2，…，9填入33⨯的方格内，使三行，三列和两条对角线上的三个数字之和都等于15.一般地，将连续的正整数21,2,3,,n L 填入n n ⨯个方格中，使得每行，每列和两条对角线上的数字之和都相等，这个正方形叫做n 阶幻方.记n 阶幻方的对角线上的数字之和为n N ，如图三阶幻方的315N =，那么 9N 的值为（ ）A ．41B ．45C ．369D ．3214．设数列{}n a 的前n 项和为n S ，且11a = 2(1)()n n S a n n N n *=+-∈，则数列13n S n ⎧⎫⎨⎬+⎩⎭的前10项的和是（ ） A ．290B ．920C ．511D ．10115．意大利数学家列昂那多·斐波那契以兔子繁殖为例，引入“兔子数列”：1,1,2,3,5,8,13,21,34,55,L L ，即()()()()()121,12F F F n F n F n ===-+-()3,n n N*≥∈，此数列在现代物理“准晶体结构”、化学等都有着广泛的应用．若此数列被2整除后的余数构成一个新数列{}n a ，则数列{}n a 的前2019项的和为（ ） A ．672B ．673C ．1346D ．20196．已知数列{}n a 是等比数列，数列{}n b 是等差数列，若261033a a a ⋅⋅=16117b b b π++=，则21039tan1b b a a +-⋅的值是（ ）A ．1B．2C．2-D．7．已知数列{}n a 满足2*123111()23n a a a a n n n N n ++++=+∈L ，设数列{}n b 满足：121n n n n b a a ++=，数列{}n b 的前n 项和为n T，若*()1n n N T n nλ<∈+恒成立，则实数λ的取值范围为（ ） A ．1[,)4+∞B ．1(,)4+∞C ．3[,)8+∞D ．3(,)8+∞8．已知函数()y f x =的定义域为R ，当0x <时()1f x >，且对任意的实数,x y R ∈，等式()()()f x f y f x y =+成立，若数列{}n a 满足()()1111n n f a f n N a *+⎛⎫=∈ ⎪+⎝⎭，且()10a f =，则下列结论成立的是（ ） A ．()()20162018f a f a > B ．()()20172020f a f a > C ．()()20182019f a f a > D ．()()20162019f a f a >9．在数列{}n a 中，1111,,(*)2019(1)n n a a a n N n n +==+∈+，则2019a 的值为______． 10．已知正项等比数列{}n a 满足5432a a a +=，若存在两项m a ，n a，使得1a =，则91m n+的最小值为__________． 11．已知数列{}n a 满足对*,m n N ∀∈，都有m n m n a a a ++=成立，72a π=，函数()f x =2sin 24cos2xx +，记()n n y f a =，则数列{}n y 的前13项和为______．12．已知数列{}n a 的前n 项和为n S ，满足22()n n S a n n N *=+∈，则n a =_____．13．等差数列{}n a 中，410a =且3a ，6a ，10a 成等比数列，数列{}n a 前20项的和20S =____ 14．已知正项等比数列{}n a 的前n 项和为n S ．若9362S S S =+，则631S S +取得最小值时，9S 的值为_______．15．设数列{}n a 的前n 项和为n S ，且满足11222n n a a a n -++⋯+=，则5S =____．16．已知数列{}n a 满足112(1)0,4n n n a na a ++-==，则数列(1)(2)na n n ⎧⎫⎨⎬++⎩⎭的前n 项和为___________.17．定义：从数列{}n a 中抽取(,3)m m N m ∈≥项按其在{}n a 中的次序排列形成一个新数列{}n b ，则称{}n b 为{}n a 的子数列；若{}n b 成等差（或等比），则称{}n b 为{}n a 的等差（或等比）子数列. （1）记数列{}n a 的前n 项和为n S ，已知21n n S =-. ①求数列{}n a 的通项公式；②数列{}n a 是否存在等差子数列，若存在，求出等差子数列；若不存在，请说明理由. （2）已知数列{}n a 的通项公式为()n a n a a Q +=+∈，证明：{}n a 存在等比子数列. 18．在等差数列{}n a 中，已知公差2d =，2a 是1a 与4a 的等比中项 （1）求数列{}n a 的通项公式； （2）若数列{}n b 满足3122331313131n n n b b b ba =++++++++L ，求数列{}nb 的通项公式； （3）令()*4n nn a b c n N =∈，数列{}n c 的前n 项和为n T . 19．已知等差数列{}n a 满足32421,7a a a =-=，等比数列{}n b 满足()35242b b b b +=+，且()2*22n n b b n =∈N .（1）求数列{}n a ，{}n b 的通项公式；（2）记数列{}n a 的前n 项和为n S ，若数列{}n c 满足()*1212n n nc c c S n b b b ++⋯+=∈N ，求{}n c 的前n 项和为n T .20．等差数列{}n a 前n 项和为n S ，且432S =，13221S =． （1）求{}n a 的通项公式n a ；（2）数列{}n b 满足()*1n n n b b a n N+-=∈且13b =，求1n b ⎧⎫⎨⎬⎩⎭的前n 项和n T ． 21．设{}n a 是单调递增的等比数列，n S 为数列{}n a 的前n 项和．已知313S =，且13a +，23a ，35a +构成等差数列． （1）求n a 及n S ；（2）是否存在常数λ．使得数列{}n S λ+是等比数列?若存在，求λ的值；若不存在，请说明理由． 22．对于无穷数列{}n a ，{}n b ，若{}{}1212max ,,,min ,,,k k k b a a a a a a =-L L ，1,2,3,k =L ，则称{}n b 是{}n a 的“收缩数列”.其中{}12max ,,,k a a a L ，{}12min ,,,k a a a L 分别表示12,,,k a a a L 中的最大数和最小数.已知{}n a 为无穷数列，其前n 项和为n S ，数列{}n b 是{}n a 的“收缩数列”. （1）若21n a n =+，求{}n b 的前n 项和； （2）证明：{}n b 的“收缩数列”仍是{}n b ；（3）若121(1)(1)(1,2,3,)22n n n n n n S S S a b n +-+++=+=L L 且11a =，22a =，求所有满足该条件的{}n a .。

专题07数列历年考题细目表历年高考真题汇编1．【2015年新课标1文科07】已知{a n}是公差为1的等差数列，S n为{a n}的前n项和，若S8＝4S4，则a10＝（）A．B．C．10 D．122．【2013年新课标1文科06】设首项为1，公比为的等比数列{a n}的前n项和为S n，则（）A．S n＝2a n﹣1 B．S n＝3a n﹣2 C．S n＝4﹣3a n D．S n＝3﹣2a n3．【2012年新课标1文科12】数列{a n}满足a n+1+（﹣1）n a n＝2n﹣1，则{a n}的前60项和为（）A．3690 B．3660 C．1845 D．18304．【2019年新课标1文科14】记S n为等比数列{a n}的前n项和．若a1＝1，S3，则S4＝．5．【2015年新课标1文科13】在数列{a n}中，a1＝2，a n+1＝2a n，S n为{a n}的前n项和，若S n＝126，则n ＝．6．【2012年新课标1文科14】等比数列{a n}的前n项和为S n，若S3+3S2＝0，则公比q＝．7．【2019年新课标1文科18】记S n为等差数列{a n}的前n项和．已知S9＝﹣a5．（1）若a3＝4，求{a n}的通项公式；（2）若a1＞0，求使得S n≥a n的n的取值范围．8．【2018年新课标1文科17】已知数列{a n}满足a1＝1，na n+1＝2（n+1）a n，设b n．（1）求b1，b2，b3；（2）判断数列{b n}是否为等比数列，并说明理由；（3）求{a n}的通项公式．9．【2017年新课标1文科17】记S n为等比数列{a n}的前n项和．已知S2＝2，S3＝﹣6．（1）求{a n}的通项公式；（2）求S n，并判断S n+1，S n，S n+2是否成等差数列．10．【2016年新课标1文科17】已知{a n}是公差为3的等差数列，数列{b n}满足b1＝1，b2，a n b n+1+b n+1＝nb n．（Ⅰ）求{a n}的通项公式；（Ⅱ）求{b n}的前n项和．11．【2014年新课标1文科17】已知{a n}是递增的等差数列，a2，a4是方程2﹣5+6＝0的根．（1）求{a n }的通项公式； （2）求数列{}的前n 项和．12．【2013年新课标1文科17】已知等差数列{a n }的前n 项和S n 满足S 3＝0，S 5＝﹣5． （Ⅰ）求{a n }的通项公式； （Ⅱ）求数列{}的前n 项和．13．【2011年新课标1文科17】已知等比数列{a n }中，a 1，公比q ．（Ⅰ）S n 为{a n }的前n 项和，证明：S n（Ⅱ）设b n ＝log 3a 1+log 3a 2+…+log 3a n ，求数列{b n }的通项公式． 14．【2010年新课标1文科17】设等差数列{a n }满足a 3＝5，a 10＝﹣9． （Ⅰ）求{a n }的通项公式；（Ⅱ）求{a n }的前n 项和S n 及使得S n 最大的序号n 的值． 考题分析与复习建议本专题考查的知识点为：数列的概念与简单表示法，等差数列及其前n 项和，等比数列及其前n 项和，数列求和，数列求通项等.历年考题主要以选择填空或解答题题型出现.重点考查的知识点为：等差数列及其前n 项和，等比数列及其前n 项和，数列求和，数列求通项等.预测明年本考点题目会比较稳定，备考方向以知识点等差数列及其前n 项和，等比数列及其前n 项和，数列求和，数列求通项为重点较佳.最新高考模拟试题1．等差数列{}n a ，等比数列{}n b ，满足111a b ==，53a b =，则9a 能取到的最小整数是（ ） A ．1-B ．0C ．2D ．32．中国古代数学名著《九章算术》中有这样一个问題今有牛、马、羊食人苗，苗主责之粟五斗，羊主曰“我羊食半马、“马主曰“我马食半牛，”今欲衰偿之，问各出几何?此问题的译文是今有牛、马、羊吃了别人的禾苗，禾苗主人要求赔偿5斗粟、羊主人说“我羊所吃的禾苗只有马的一半，”马主人说“我马所吃的禾苗只有牛的一半，“打算按此比例偿还，他们各应偿还多少？该问题中，1斗为10升，则马主人应偿还( )升粟？ A ．253B ．503C ．507D ．10073．我国古代的《洛书》中记载着世界上最古老的一个幻方：如图，将1，2，…，9填入33⨯的方格内，使三行，三列和两条对角线上的三个数字之和都等于15.一般地，将连续的正整数21,2,3,,n L 填入n n ⨯个方格中，使得每行，每列和两条对角线上的数字之和都相等，这个正方形叫做n 阶幻方.记n 阶幻方的对角线上的数字之和为n N ，如图三阶幻方的315N =，那么 9N 的值为（ ）A ．41B ．45C ．369D ．3214．设数列{}n a 的前n 项和为n S ，且11a = 2(1)()n n S a n n N n *=+-∈，则数列13n S n ⎧⎫⎨⎬+⎩⎭的前10项的和是（ ） A ．290B ．920C ．511D ．10115．意大利数学家列昂那多·斐波那契以兔子繁殖为例，引入“兔子数列”：1,1,2,3,5,8,13,21,34,55,L L ，即()()()()()121,12F F F n F n F n ===-+-()3,n n N*≥∈，此数列在现代物理“准晶体结构”、化学等都有着广泛的应用．若此数列被2整除后的余数构成一个新数列{}n a ，则数列{}n a 的前2019项的和为（ ） A ．672B ．673C ．1346D ．20196．已知数列{}n a 是等比数列，数列{}n b 是等差数列，若261033a a a ⋅⋅=16117b b b π++=，则21039tan1b b a a +-⋅的值是（ ）A ．1B．2C．2-D．7．已知数列{}n a 满足2*123111()23n a a a a n n n N n ++++=+∈L ，设数列{}n b 满足：121n n n n b a a ++=，数列{}n b 的前n 项和为n T，若*()1n n N T n nλ<∈+恒成立，则实数λ的取值范围为（ ） A ．1[,)4+∞B ．1(,)4+∞C ．3[,)8+∞D ．3(,)8+∞8．已知函数()y f x =的定义域为R ，当0x <时()1f x >，且对任意的实数,x y R ∈，等式()()()f x f y f x y =+成立，若数列{}n a 满足()()1111n n f a f n N a *+⎛⎫=∈ ⎪+⎝⎭，且()10a f =，则下列结论成立的是（ ） A ．()()20162018f a f a > B ．()()20172020f a f a > C ．()()20182019f a f a > D ．()()20162019f a f a >9．在数列{}n a 中，1111,,(*)2019(1)n n a a a n N n n +==+∈+，则2019a 的值为______． 10．已知正项等比数列{}n a 满足5432a a a +=，若存在两项m a ，n a，使得1a =，则91m n+的最小值为__________． 11．已知数列{}n a 满足对*,m n N ∀∈，都有m n m n a a a ++=成立，72a π=，函数()f x =2sin 24cos2xx +，记()n n y f a =，则数列{}n y 的前13项和为______．12．已知数列{}n a 的前n 项和为n S ，满足22()n n S a n n N *=+∈，则n a =_____．13．等差数列{}n a 中，410a =且3a ，6a ，10a 成等比数列，数列{}n a 前20项的和20S =____ 14．已知正项等比数列{}n a 的前n 项和为n S ．若9362S S S =+，则631S S +取得最小值时，9S 的值为_______．15．设数列{}n a 的前n 项和为n S ，且满足11222n n a a a n -++⋯+=，则5S =____．16．已知数列{}n a 满足112(1)0,4n n n a na a ++-==，则数列(1)(2)na n n ⎧⎫⎨⎬++⎩⎭的前n 项和为___________.17．定义：从数列{}n a 中抽取(,3)m m N m ∈≥项按其在{}n a 中的次序排列形成一个新数列{}n b ，则称{}n b 为{}n a 的子数列；若{}n b 成等差（或等比），则称{}n b 为{}n a 的等差（或等比）子数列. （1）记数列{}n a 的前n 项和为n S ，已知21n n S =-. ①求数列{}n a 的通项公式；②数列{}n a 是否存在等差子数列，若存在，求出等差子数列；若不存在，请说明理由. （2）已知数列{}n a 的通项公式为()n a n a a Q +=+∈，证明：{}n a 存在等比子数列. 18．在等差数列{}n a 中，已知公差2d =，2a 是1a 与4a 的等比中项 （1）求数列{}n a 的通项公式； （2）若数列{}n b 满足3122331313131n n n b b b ba =++++++++L ，求数列{}nb 的通项公式； （3）令()*4n nn a b c n N =∈，数列{}n c 的前n 项和为n T . 19．已知等差数列{}n a 满足32421,7a a a =-=，等比数列{}n b 满足()35242b b b b +=+，且()2*22n n b b n =∈N .（1）求数列{}n a ，{}n b 的通项公式；（2）记数列{}n a 的前n 项和为n S ，若数列{}n c 满足()*1212n n nc c c S n b b b ++⋯+=∈N ，求{}n c 的前n 项和为n T .20．等差数列{}n a 前n 项和为n S ，且432S =，13221S =． （1）求{}n a 的通项公式n a ；（2）数列{}n b 满足()*1n n n b b a n N+-=∈且13b =，求1n b ⎧⎫⎨⎬⎩⎭的前n 项和n T ． 21．设{}n a 是单调递增的等比数列，n S 为数列{}n a 的前n 项和．已知313S =，且13a +，23a ，35a +构成等差数列． （1）求n a 及n S ；（2）是否存在常数λ．使得数列{}n S λ+是等比数列?若存在，求λ的值；若不存在，请说明理由． 22．对于无穷数列{}n a ，{}n b ，若{}{}1212max ,,,min ,,,k k k b a a a a a a =-L L ，1,2,3,k =L ，则称{}n b 是{}n a 的“收缩数列”.其中{}12max ,,,k a a a L ，{}12min ,,,k a a a L 分别表示12,,,k a a a L 中的最大数和最小数.已知{}n a 为无穷数列，其前n 项和为n S ，数列{}n b 是{}n a 的“收缩数列”. （1）若21n a n =+，求{}n b 的前n 项和； （2）证明：{}n b 的“收缩数列”仍是{}n b ；（3）若121(1)(1)(1,2,3,)22n n n n n n S S S a b n +-+++=+=L L 且11a =，22a =，求所有满足该条件的{}n a .。

十年高考真题分类汇编（2010—2019）数学专题01 集合1.(2019•全国1•理T1)已知集合M={x|-4<x<2},N={x|x2-x-6<0},则M∩N=( )A.{x|-4<x<3}B.{x|-4<x<-2}C.{x|-2<x<2}D.{x|2<x<3}【答案】C【解析】由题意得N={x|-2<x<3},则M∩N={x|-2<x<2},故选C.2.(2019•全国1•文T2)已知集合U={1,2,3,4,5,6,7},A={2,3,4,5},B={2,3,6,7},则B∩∁U A=( )A.{1,6}B.{1,7}C.{6,7}D.{1,6,7}【答案】C【解析】由已知得∁U A={1,6,7},∴B∩∁U A={6,7}.故选C.3.(2019•全国2•理T1)设集合A={x|x2-5x+6>0},B={x|x-1<0},则A∩B=( )A.(-∞,1)B.(-2,1)C.(-3,-1)D.(3,+∞)【答案】A【解析】由题意,得A={x|x<2,或x>3},B={x|x<1},所以A∩B={x|x<1},故选A.4.(2019•全国2•文T1)已知集合A={x|x>-1},B={x|x<2},则A∩B=( )A.(-1,+∞)B.(-∞,2)C.(-1,2)D.⌀【答案】C【解析】由题意,得A∩B=(-1,2),故选C.5.(2019•全国3•T1)已知集合A={-1,0,1,2},B={x|x2≤1},则A∩B=( )A.{-1,0,1}B.{0,1}C.{-1,1}D.{0,1,2}【答案】A【解析】A={-1,0,1,2},B={x|-1≤x≤1},则A∩B={-1,0,1}.故选A.6.(2019•北京•文T1)已知集合A={x|-1<x<2},B={x|x>1},则A∪B=( )A.(-1,1)B.(1,2)C.(-1,+∞)D.(1,+∞)【答案】C【解析】∵A={x|-1<x<2},B={x|x>1},∴A∪B=(-1,+∞),故选C.7.(2019•天津•T1)设集合A={-1,1,2,3,5},B={2,3,4},C={x∈R|1≤x<3},则(A∩C)∪B=( )A.{2}B.{2,3}C.{-1,2,3}D.{1,2,3,4}【答案】D【解析】A∩C={1,2},(A∩C)∪B={1,2,3,4},故选D.8.(2019•浙江•T1)已知全集U={-1,0,1,2,3},集合A={0,1,2},B={-1,0,1},则(∁U A)∩B=( )A.{-1}B.{0,1}C.{-1,2,3}D.{-1,0,1,3}【答案】A【解析】∁U A={-1,3},则(∁U A)∩B={-1}.9.(2018•全国1•理T2)已知集合A={x|x2-x-2>0},则∁R A=( )A.{x|-1<x<2}B.{x|-1≤x≤2}C.{x|x<-1}∪{x|x>2}D.{x|x≤-1}∪{x|x≥2}【答案】B【解析】A={x|x<-1或x>2},所以∁R A={x|-1≤x≤2}.10.(2018•全国1•文T1)已知集合A={0,2},B={-2,-1,0,1,2},则A∩B=( )A.{0,2}B.{1,2}C.{0}D.{-2,-1,0,1,2}【答案】A【解析】由交集定义知A∩B={0,2}.11.(2018•全国2•文T2,)已知集合A={1,3,5,7},B={2,3,4,5},则A∩B=( )A.{3}B.{5}C.{3,5}D.{1,2,3,4,5,7}【答案】C【解析】集合A、B的公共元素为3,5,故A∩B={3,5}.12.(2018•全国3•T1)已知集合A={x|x-1≥0},B={0,1,2},则A∩B=( )A.{0}B.{1}C.{1,2}D.{0,1,2}【答案】C【解析】由题意得A={x|x≥1},B={0,1,2},∴A∩B={1,2}.13.(2018•北京•T1)已知集合A={x||x|<2},B={-2,0,1,2},则A∩B=( )A.{0,1}B.{-1,0,1}C.{-2,0,1,2}D.{-1,0,1,2}【答案】A【解析】∵A={x|-2<x<2},B={-2,0,1,2},∴A∩B={0,1}.14.(2018•天津•理T1)设全集为R,集合A={x|0<x<2},B={x|x≥1},则A∩(∁R B)=( )A.{x|0<x≤1}B.{x|0<x<1}C.{x|1≤x<2}D.{x|0<x<2}【答案】B【解析】∁R B={x|x<1},A∩(∁R B)={x|0<x<1}.故选B.15.(2018•天津•文T1)设集合A={1,2,3,4},B={-1,0,2,3},C={x∈R|-1≤x<2},则(A∪B)∩C=( )A.{-1,1}B.{0,1}C.{-1,0,1}D.{2,3,4}【答案】C【解析】A∪B={-1,0,1,2,3,4}.又C={x∈R|-1≤x<2},∴(A∪B)∩C={-1,0,1}.16.(2018•浙江•T1)已知全集U={1,2,3,4,5},A={1,3},则∁U A=( )A.⌀B.{1,3}C.{2,4,5}D.{1,2,3,4,5}【答案】C【解析】∵A={1,3},U={1,2,3,4,5},∴∁U A={2,4,5},故选C.17.(2018•全国2•理T2,)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为( )A.9B.8C.5D.4【答案】A【解析】满足条件的元素有(-1,-1),(-1,0),(-1,1),(0,1),(0,0),(0,-1),(1,-1),(1,0),(1,1),共9个。

专题03函数概念与基本初等函数历年考题细目表历年高考真题汇编1．【2019年新课标1文科03】已知a＝log20.2，b＝20.2，c＝0.20.3，则（）A．a＜b＜c B．a＜c＜b C．c＜a＜b D．b＜c＜a【解答】解：a＝log20.2＜log21＝0，b＝20.2＞20＝1，∵0＜0.20.3＜0.20＝1，∴c＝0.20.3∈（0，1），∴a＜c＜b，故选：B．2．【2018年新课标1文科12】设函数f（），则满足f（+1）＜f（2）的的取值范围是（）A．（﹣∞，﹣1] B．（0，+∞）C．（﹣1，0）D．（﹣∞，0）【解答】解：函数f（），的图象如图：满足f（+1）＜f（2），可得：2＜0＜+1或2＜+1≤0，解得∈（﹣∞，0）．故选：D．3．【2016年新课标1文科08】若a＞b＞0，0＜c＜1，则（）A．log a c＜log b c B．log c a＜log c bC．a c＜b c D．c a＞c b【解答】解：∵a＞b＞0，0＜c＜1，∴log c a＜log c b，故B正确；∴当a＞b＞1时，0＞log a c＞log b c，故A错误；a c＞b c，故C错误；c a＜c b，故D错误；故选：B．4．【2015年新课标1文科10】已知函数f（），且f（a）＝﹣3，则f（6﹣a）＝（）A．B．C．D．【解答】解：由题意，a≤1时，2α﹣1﹣2＝﹣3，无解；a＞1时，﹣log2（a+1）＝﹣3，∴α＝7，∴f（6﹣a）＝f（﹣1）＝2﹣1﹣1﹣2．故选：A．5．【2015年新课标1文科12】设函数y＝f（）的图象与y＝2+a的图象关于y＝﹣对称，且f（﹣2）+f（﹣4）＝1，则a＝（）A．﹣1 B．1 C．2 D．4【解答】解：∵与y＝2+a的图象关于y＝对称的图象是y＝2+a的反函数，y＝log2﹣a（＞0），即g（）＝log2﹣a，（＞0）．∵函数y＝f（）的图象与y＝2+a的图象关于y＝﹣对称，∴f（）＝﹣g（﹣）＝﹣log2（﹣）+a，＜0，∵f（﹣2）+f（﹣4）＝1，∴﹣log22+a﹣log24+a＝1，解得，a＝2，故选：C．6．【2014年新课标1文科05】设函数f（），g（）的定义域都为R，且f（）是奇函数，g（）是偶函数，则下列结论正确的是（）A．f（）•g（）是偶函数B．|f（）|•g（）是奇函数C．f（）•|g（）|是奇函数D．|f（）•g（）|是奇函数【解答】解：∵f（）是奇函数，g（）是偶函数，∴f（﹣）＝﹣f（），g（﹣）＝g（），f（﹣）•g（﹣）＝﹣f（）•g（），故函数是奇函数，故A错误，|f（﹣）|•g（﹣）＝|f（）|•g（）为偶函数，故B错误，f（﹣）•|g（﹣）|＝﹣f（）•|g（）|是奇函数，故C正确．|f（﹣）•g（﹣）|＝|f（）•g（）|为偶函数，故D错误，故选：C．7．【2013年新课标1文科12】已知函数f（），若|f（）|≥a，则a的取值范围是（）A．（﹣∞，0] B．（﹣∞，1] C．[﹣2，1] D．[﹣2，0]【解答】解：由题意可作出函数y＝|f（）|的图象，和函数y＝a的图象，由图象可知：函数y＝a的图象为过原点的直线，当直线介于l和轴之间符合题意，直线l为曲线的切线，且此时函数y＝|f（）|在第二象限的部分解析式为y＝2﹣2，求其导数可得y′＝2﹣2，因为≤0，故y′≤﹣2，故直线l的斜率为﹣2，故只需直线y＝a的斜率a介于﹣2与0之间即可，即a∈[﹣2，0]故选：D．8．【2012年新课标1文科11】当0＜时，4＜log a，则a的取值范围是（）A．（0，）B．（，1）C．（1，）D．（，2）【解答】解：∵0＜时，1＜4≤2要使4＜log a，由对数函数的性质可得0＜a＜1，数形结合可知只需2＜log a，∴即对0＜时恒成立∴解得a＜1故选：B．9．【2011年新课标1文科10】在下列区间中，函数f（）＝e+4﹣3的零点所在的区间为（）A．（，）B．（，0）C．（0，）D．（，）【解答】解：∵函数f（）＝e+4﹣3∴f′（）＝e+4当＞0时，f′（）＝e+4＞0∴函数f（）＝e+4﹣3在（﹣∞，+∞）上为f（0）＝e0﹣3＝﹣2＜0f（）1＞0f（）20∵f（）•f（）＜0，∴函数f（）＝e+4﹣3的零点所在的区间为（，）故选：A．10．【2011年新课标1文科12】已知函数y＝f（）的周期为2，当∈[﹣1，1]时f（）＝2，那么函数y＝f（）的图象与函数y＝|lg|的图象的交点共有（）A．10个B．9个C．8个D．1个【解答】解：作出两个函数的图象如上∵函数y＝f（）的周期为2，在[﹣1，0]上为减函数，在[0，1]上为增函数∴函数y＝f（）在区间[0，10]上有5次周期性变化，在[0，1]、[2，3]、[4，5]、[6，7]、[8，9]上为增函数，在[1，2]、[3，4]、[5，6]、[7，8]、[9，10]上为减函数，且函数在每个单调区间的取值都为[0，1]，再看函数y＝|lg|，在区间（0，1]上为减函数，在区间[1，+∞）上为增函数，且当＝1时y＝0；＝10时y＝1，再结合两个函数的草图，可得两图象的交点一共有10个，故选：A．11．【2011年新课标1文科03】下列函数中，既是偶函数又在（0，+∞）上单调递增的函数是（）A．y＝23B．y＝||+1 C．y＝﹣2+4 D．y＝2﹣||【解答】解：对于A．y＝23，由f（﹣）＝﹣23＝﹣f（），为奇函数，故排除A；对于B．y＝||+1，由f（﹣）＝|﹣|+1＝f（），为偶函数，当＞0时，y＝+1，是增函数，故B正确；对于C．y＝﹣2+4，有f（﹣）＝f（），是偶函数，但＞0时为减函数，故排除C；对于D．y＝2﹣||，有f（﹣）＝f（），是偶函数，当＞0时，y＝2﹣，为减函数，故排除D．故选：B．12．【2010年新课标1文科06】如图，质点P在半径为2的圆周上逆时针运动，其初始位置为P0（，），角速度为1，那么点P到轴距离d关于时间t的函数图象大致为（）A．B．C．D．【解答】解：通过分析可知当t＝0时，点P到轴距离d为，于是可以排除答案A，D，再根据当时，可知点P在轴上此时点P到轴距离d为0，排除答案B，故选：C．13．【2010年新课标1文科09】设偶函数f（）满足f（）＝2﹣4（≥0），则{|f（﹣2）＞0}＝（）A．{|＜﹣2或＞4} B．{|＜0或＞4} C．{|＜0或＞6} D．{|＜﹣2或＞2}【解答】解：由偶函数f（）满足f（）＝2﹣4（≥0），可得f（）＝f（||）＝2||﹣4，则f（﹣2）＝f（|﹣2|）＝2|﹣2|﹣4，要使f（|﹣2|）＞0，只需2|﹣2|﹣4＞0，|﹣2|＞2解得＞4，或＜0．应选：B．14．【2010年新课标1文科12】已知函数，若a，b，c互不相等，且f（a）＝f （b）＝f（c），则abc的取值范围是（）A．（1，10）B．（5，6）C．（10，12）D．（20，24）【解答】解：作出函数f（）的图象如图，不妨设a＜b＜c，则ab＝1，则abc＝c∈（10，12）．故选：C．15．【2018年新课标1文科13】已知函数f（）＝log2（2+a），若f（3）＝1，则a＝．【解答】解：函数f（）＝log2（2+a），若f（3）＝1，可得：log2（9+a）＝1，可得a＝﹣7．故答案为：﹣7．16．【2014年新课标1文科15】设函数f（），则使得f（）≤2成立的的取值范围是．【解答】解：＜1时，e﹣1≤2，∴≤ln2+1，∴＜1；≥1时，2，∴≤8，∴1≤≤8，综上，使得f（）≤2成立的的取值范围是≤8．故答案为：≤8．17．【2012年新课标1文科16】设函数f （）的最大值为M ，最小值为m ，则M +m ＝ ．【解答】解：函数可化为f （），令，则为奇函数，∴的最大值与最小值的和为0．∴函数f （）的最大值与最小值的和为1+1+0＝2．即M +m ＝2． 故答案为：2． 考题分析与复习建议本专题考查的知识点为：函数，函数的单调性与最值，函数的奇偶性与周期性，幂函数与二次函数，指数函数，对数函数，分段函数，函数的图象，函数与方程等.历年考题主要以选择填空题型出现，重点考查的知识点为：函数的单调性与最值，函数的奇偶性与周期性，指数函数，对数函数，分段函数，函数的图象，函数与方程等.预测明年本考点题目会比较稳定，备考方向以知识点函数的单调性与最值，函数的奇偶性与周期性，指数函数，对数函数，分段函数，函数的图象，函数与方程等为重点较佳.最新高考模拟试题1．已知()21f x ax bx =-+是定义域为[a ，a +1]的偶函数，则2b a a -＝（ ）A ．0B ．34C 2D ．4【答案】B 【解析】∵f （）在[a ，a +1]上是偶函数， ∴﹣a ＝a +1⇒a 12=-， 所以f （）的定义域为[12-，12]， 故：f （）12=-2﹣b +1， ∵f （）在区间[12-，12]上是偶函数，有f （12-）＝f （12），代入解析式可解得：b ＝0；∴2b a a -13144=-=．故选：B ．2．已知函数()y f x =的定义域为R ,)1(+x f 为偶函数,且对121x x ∀<≤,满足()()01212<--x x x f x f .若(3)1f =,则不等式()2log 1f x <的解集为（ ）A ．1,82⎛⎫ ⎪⎝⎭B ．)8,1(C ．10,(8,)2⎛⎫⋃+∞ ⎪⎝⎭D ．(,1)(8,)-∞⋃+∞【答案】A 【解析】因为对121x x ∀<≤,满足()()01212<--x x x f x f ，所以()y f x =当1≤x 时，是单调递减函数，又因为)1(+x f 为偶函数，所以()y f x =关于1x =对称，所以函数()y f x =当1>x 时，是增函数，又因为(3)1f =，所以有1)1(=-f ，当2log 1x ≤时，即当02x <≤时，()()222log 1log (11log 2221)1f x f x x x x f <⇒<-⇒>-⇒>∴<≤当2log 1x >时，即当2x >时，()()222log 1log (3)log 3828x x f x f x f x <⇒<⇒∴<<⇒<<，综上所述：不等式()2log 1f x <的解集为1,82⎛⎫ ⎪⎝⎭，故本题选A.3．函数22()log (34)f x x x =--的单调减区间为（ ）A ．(,1)-∞-B ．3(,)2-∞-C ．3(,)2+∞D ．(4,)+∞【答案】A 【解析】函数()()22log 34f x x x =--,所以 2340(4)(1)04x x x x x -->⇒-+>⇒>或1x <-，所以函数()f x 的定义域为4x >或1x <-，234y x x =--当3(,)2-∞时，函数是单调递减，而1x <-，所以函数()()22log 34f x x x =--的单调减区间为(),1-∞-，故本题选A 。

专题01集合历年考题细目表历年高考真题汇编1．【2019年新课标1文科02】已知集合U＝{1，2，3，4，5，6，7}，A＝{2，3，4，5}，B＝{2，3，6，7}，则B∩∁U A＝（）A．{1，6} B．{1，7} C．{6，7} D．{1，6，7}【解答】解：∵U＝{1，2，3，4，5，6，7}，A＝{2，3，4，5}，B＝{2，3，6，7}，∴∁U A＝{1，6，7}，则B∩∁U A＝{6，7}故选：C．2．【2018年新课标1文科01】已知集合A＝{0，2}，B＝{﹣2，﹣1，0，1，2}，则A∩B＝（）A．{0，2} B．{1，2}C．{0} D．{﹣2，﹣1，0，1，2}【解答】解：集合A＝{0，2}，B＝{﹣2，﹣1，0，1，2}，则A∩B＝{0，2}．故选：A．3．【2017年新课标1文科01】已知集合A＝{|＜2}，B＝{|3﹣2＞0}，则（）A．A∩B＝{|} B．A∩B＝∅C．A∪B＝{|} D．A∪B＝R【解答】解：∵集合A＝{|＜2}，B＝{|3﹣2＞0}＝{|}，∴A∩B＝{|}，故A正确，B错误；A∪B＝{||＜2}，故C，D错误；故选：A．4．【2016年新课标1文科01】设集合A＝{1，3，5，7}，B＝{|2≤≤5}，则A∩B＝（）A．{1，3} B．{3，5} C．{5，7} D．{1，7}【解答】解：集合A＝{1，3，5，7}，B＝{|2≤≤5}，则A∩B＝{3，5}．故选：B．5．【2015年新课标1文科01】已知集合A＝{|＝3n+2，n∈N}，B＝{6，8，10，12，14}，则集合A∩B中元素的个数为（）A．5 B．4 C．3 D．2【解答】解：A＝{|＝3n+2，n∈N}＝{2，5，8，11，14，17，…}，则A∩B＝{8，14}，故集合A∩B中元素的个数为2个，故选：D．6．【2014年新课标1文科01】已知集合M＝{|﹣1＜＜3}，N＝{|﹣2＜＜1}，则M∩N＝（）A．（﹣2，1）B．（﹣1，1）C．（1，3）D．（﹣2，3）【解答】解：M＝{|﹣1＜＜3}，N＝{|﹣2＜＜1}，则M∩N＝{|﹣1＜＜1}，故选：B．7．【2013年新课标1文科01】已知集合A＝{1，2，3，4}，B＝{|＝n2，n∈A}，则A∩B＝（）A．{1，4} B．{2，3} C．{9，16} D．{1，2}【解答】解：根据题意得：＝1，4，9，16，即B＝{1，4，9，16}，∵A＝{1，2，3，4}，∴A∩B＝{1，4}．故选：A．8．【2012年新课标1文科01】已知集合A＝{|2﹣﹣2＜0}，B＝{|﹣1＜＜1}，则（）A．A⊊B B．B⊊A C．A＝B D．A∩B＝∅【解答】解：由题意可得，A＝{|﹣1＜＜2}，∵B＝{|﹣1＜＜1}，在集合B中的元素都属于集合A，但是在集合A中的元素不一定在集合B中，例如∴B⊊A．故选：B．9．【2011年新课标1文科01】已知集合M＝{0，1，2，3，4}，N＝{1，3，5}，P＝M∩N，则P的子集共有（）A．2个B．4个C．6个D．8个【解答】解：∵M＝{0，1，2，3，4}，N＝{1，3，5}，∴P＝M∩N＝{1，3}∴P的子集共有22＝4故选：B．10．【2010年新课标1文科01】已知集合A＝{|||≤2，∈R}，B＝{|4，∈}，则A∩B＝（）A．（0，2）B．[0，2] C．{0，2} D．{0，1，2}【解答】解：∵A＝{|||≤2}＝{|﹣2≤≤2}B＝{|4，∈}＝{0，1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16}则A∩B＝{0，1，2}故选：D．考题分析与复习建议本专题考查的知识点为：集合关系及其运算，历年考题主要以选择填空题型出现， 重点考查的知识点为：交并补运算，预测明年本考点题目会比较稳定，备考方向以知识点交并补运算为重点较佳.最新高考模拟试题1．若集合{}5|2A x x =-<<，{}|||3B x x =<，则A B =I （ ）A ．{}|32x x -<<B ．{}|52x x -<<C ．{}|33x x -<<D ．{}|53x x -<<【答案】A【解析】解：{}{}333||B x x x x =<=-<<，则{}|32A B x x ⋂=-<<，故选：A ．2．已知集合2{|560}A x x x =-+≤，{|15}B x Z x =∈<<，则A B =I （ ）A ．[2,3]B ．(1,5)C ．{}2,3D ．{2,3,4}【答案】C【解析】2560(2)(3)023x x x x x -+≤⇒--≤⇒≤≤Q ，{}23A x x ∴=≤≤，又{}{|15}2,3,4B x Z x =∈<<=，所以{}2,3A B ⋂=，故本题选C.3．已知集合{3,2,1,0,1,2,3}A =---，{}2|450B x x x =∈--≤R ，则A B =I （ ）A ．{3,2,1,0}---B ．{}1,0,1,2,3-C ．{}3,2--D ．{}3,2,1,0,1,2,3---【答案】B【解析】 因为{}2|450B x x x =∈--≤R {|15}x x =-≤≤， {3,2,1,0,1,2,3}A =---∴{}1,0,1,2,3A B ⋂=-．故选B ．4．已知全集U =R ，集合{}|24,{|(1)(3)0}x A x B x x x =>=--<，则()U A B =I ð（ ） A ．(1,2)B ．(]1,2C ．(1,3)D ．(,2]-∞ 【答案】B【解析】由24x >可得2x >， (1)(3)0x x --<可得13x <<，所以集合(2,),(1,3)A B =+∞=,(,2]U A =-∞ð，所以()U A B =I ð(]1,2，故选B.5．已知集合{}(,)|1,A x y y x x R ==+∈，集合{}2(,)|,B x y y x x R ==∈，则集合A B ⋂的子集个数为（ ）A ．1B ．2C ．3D ．4 【答案】D【解析】由题意得，直线1y x =+与抛物线2y x =有2个交点，故A B ⋂的子集有4个.6．已知集合{}2log (1)2M x x =+＜，{1,0,1,2,3}N =-，则()R M N ⋂ð=（ ）A ．{-1，0，1，2，3}B ．{-1，0，1，2}C ．{-1，0，1}D ．{-1，3} 【答案】D【解析】 由题意，集合{}2log (1)2{|13}M x x x x =+<=-<<，则{|1R M x x =≤-ð或3}x ≥又由{1,0,1,2,3}N =-，所以(){1,3}R M N ⋂=-ð，故选D.7．已知集合{}lg(1)A x y x ==-，{}1,0,1,2,3B =-，则()R A B I ð=( )A ．{}1,0-B ．{}1,0,1-C ．{}1,2,3D ．{}2,3【答案】B【解析】 因为{}{}lg(1)1A x y x x x ==-=>，所以{}1R C A x x =≤，又{}1,0,1,2,3B =-，所以{}()1,0,1R C A B =-I .故选B8．已知R 是实数集，集合{}1,0,1A =-，{}210B x x =-≥，则()A B =R I ð（）A ．{}1,0-B ．{}1C ．1,12⎡⎤⎢⎥⎣⎦D ．1,2⎛⎫-∞ ⎪⎝⎭【答案】A【解析】1|2B x x 禳镲=?睚镲铪Q1|2R C B x x 禳镲\=<睚镲铪即(){1,0}R A C B ?-故选A 。

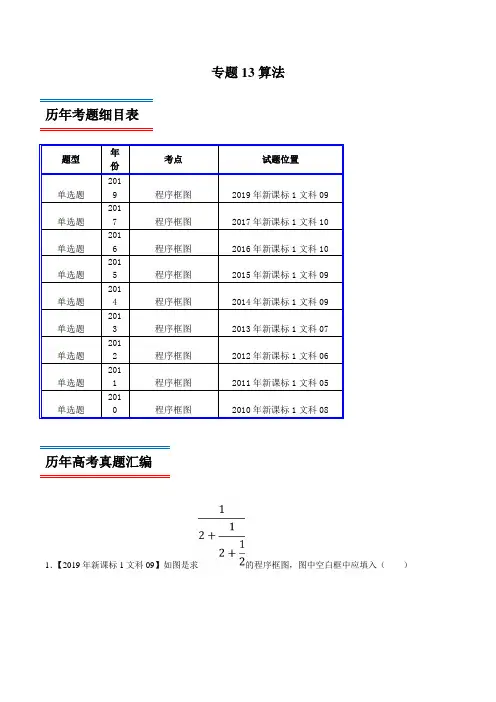
专题13算法历年考题细目表题型年份考点试题位置单选题2019 程序框图2019年新课标1文科09单选题2017 程序框图2017年新课标1文科10单选题2016 程序框图2016年新课标1文科10单选题2015 程序框图2015年新课标1文科09单选题2014 程序框图2014年新课标1文科09单选题2013 程序框图2013年新课标1文科07单选题2012 程序框图2012年新课标1文科06单选题2011 程序框图2011年新课标1文科05单选题2010 程序框图2010年新课标1文科08历年高考真题汇编1．【2019年新课标1文科09】如图是求的程序框图，图中空白框中应填入（）A．A B．A＝2 C．A D．A＝12．【2017年新课标1文科10】如图程序框图是为了求出满足3n﹣2n＞1000的最小偶数n，那么在和两个空白框中，可以分别填入（）A．A＞1000和n＝n+1 B．A＞1000和n＝n+2C．A≤1000和n＝n+1 D．A≤1000和n＝n+23．【2016年新课标1文科10】执行下面的程序框图，如果输入的＝0，y＝1，n＝1，则输出，y的值满足（）A．y＝2 B．y＝3 C．y＝4 D．y＝54．【2015年新课标1文科09】执行如图所示的程序框图，如果输入的t＝0.01，则输出的n＝（）A．5 B．6 C．7 D．85．【2014年新课标1文科09】执行如图的程序框图，若输入的a，b，分别为1，2，3，则输出的M＝（）A．B．C．D．6．【2013年新课标1文科07】执行程序框图，如果输入的t∈[﹣1，3]，则输出的s属于（）A．[﹣3，4] B．[﹣5，2] C．[﹣4，3] D．[﹣2，5]7．【2012年新课标1文科06】如果执行右边的程序框图，输入正整数N（N≥2）和实数a1，a2，…，a n，输出A，B，则（）A．A+B为a1，a2，…，a n的和B．为a1，a2，…，a n的算术平均数C．A和B分别是a1，a2，…，a n中最大的数和最小的数D．A和B分别是a1，a2，…，a n中最小的数和最大的数8．【2011年新课标1文科05】执行如图的程序框图，如果输入的N是6，那么输出的p是（）A．120 B．720 C．1440 D．50409．【2010年新课标1文科08】如果执行如图的框图，输入N＝5，则输出的数等于（）A．B．C．D．考题分析与复习建议本专题考查的知识点为：算法的逻辑结构，顺序结构、条件结构、循环结构，程序框图和算法思想，求程序框图中的执行结果和确定控制条件.历年考题主要以选择题型出现，重点考查的知识点为：算法的循环结构，程序框图和算法思想.预测明年本考点题目会比较稳定，备考方向以算法的循环结构，程序框图和算法思想为重点较佳.最新高考模拟试题1．我国古代数学专著《九章算术》中有一个“两鼠穿墙题”，其内容为：“今有垣厚五尺，两鼠对穿，大鼠日一尺，小鼠也日一尺，大鼠日自倍，小鼠日自半．问何日相逢？各穿几何？”如图的程序框图于这个题目，执行该程序框图，若输入=20，则输出的结果为（ ）A ．3B ．4C ．5D ．62．如图所示的程序框图，若=5,则运算多少次停止( )A ．2B ．3C ．4D ．53．正整数n 除以m 后的余数为，记为r n MOD m =，如4195MOD =.执行如图的程序框图，则输出的数n 是( )A．19B．22C．27D．47 4．执行如图所示的程序框图，输出n的值为（）A．6B．7C．8D．95．为了计算11111123420192020S=-+-++-L，设计如图所示的程序框图，则在空白框中应填入（）A ．1i i =+B ．2i i =+C ．3i i =+D ．4i i =+6．如图程序框图的算法思路于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a ，b 分别为16，20，则输出的a =（ ）A ．14B ．4C ．2D ．07．执行如图所示的程序框图，则输出的S 值为( )A．4B．5 C．8D．98．某程序框图如图所示，若该程序运行后输出的值是95，则a的值是（）A．7B．6C．5D．4 9．执行如图的程序框图，如果输出的S=3，则输入的t=（）A ．1? -B ．3?- C ．1或3 D ．1或3-10．如图是一个算法流程图，则输出的结果是（ ）A ．3B ．4C ．5D ．611．《九章算术》中有如下问题“今有牛、羊、马食人苗，苗主责之粟五斗，主日‘我羊食半马.’马主日‘ 我马食半牛.’今欲衰偿之，问各出几何?”翻译为今有牛、马、羊吃了别人的禾苗，禾苗主人要求赔偿5斗粟.羊主人说“我羊所吃的禾苗只有马的一半.”马主人说“我马吃的禾苗只有牛的一半”打算按此比率偿还，问牛、马、羊的主人各应赔偿多少粟?已知1斗=10升，针对这一问题，设计程序框图如图所示，若输出k 的值为2，则m =（ ）A ．503B ．507．C ．103D ．100712．在如图所示的计算1592017++++L 程序框图中，判断框内应填入的条件是（ ）A ．2017?i ≤B ．2017?i <C ．2013?i <D ．2021?i ≤ 13．如图所示的程序框图所实现的功能是（ ）A ．输入a 的值，计算()2021131a -⨯+ B ．输入a 的值，计算()2020131a -⨯+ C ．输入a 的值，计算()2019131a -⨯+D ．输入a 的值，计算()2018131a -⨯+ 14．执行如图所示的程序框图，如果输入的]2,0[∈x ，那么输出的y 值不可能为A．1 B．0C．1D．215．阅读如图所示的程序框图，则输出的（）A．30B．29C．90D．5416．执行如图所示的程序框图，若输出的，则判断框内应填入的条件是（）A．B．C．D．17．执行如图所示的程序框图，则输出的（）A．3B．4C．5D．618．执行下面程序框图，若输入的的值分别为0和44，则输出的值为（）A．4B．7C．10D．1319．执行如图所示的程序框图，若输出结果为1，则可输入的实数值的个数为（）A．1B．2C．3D．420．运行程序框图，如果输入某个正数后，输出的，那么的值为（）A．3B．4C．5D．6。

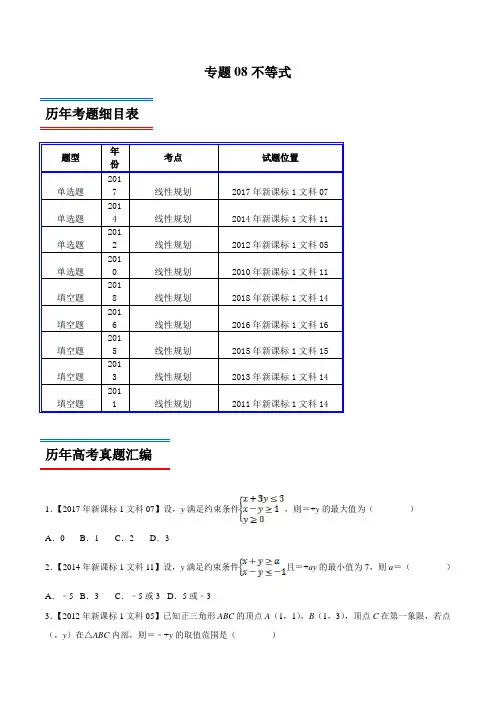
专题08不等式历年考题细目表题型年份考点试题位置单选题2017 线性规划2017年新课标1文科07单选题2014 线性规划2014年新课标1文科11单选题2012 线性规划2012年新课标1文科05单选题2010 线性规划2010年新课标1文科11填空题2018 线性规划2018年新课标1文科14填空题2016 线性规划2016年新课标1文科16填空题2015 线性规划2015年新课标1文科15填空题2013 线性规划2013年新课标1文科14填空题2011 线性规划2011年新课标1文科14历年高考真题汇编1．【2017年新课标1文科07】设，y满足约束条件，则＝+y的最大值为（）A．0 B．1 C．2 D．32．【2014年新课标1文科11】设，y满足约束条件且＝+ay的最小值为7，则a＝（）A．﹣5 B．3 C．﹣5或3 D．5或﹣33．【2012年新课标1文科05】已知正三角形ABC的顶点A（1，1），B（1，3），顶点C在第一象限，若点（，y）在△ABC内部，则＝﹣+y的取值范围是（）A ．（1，2）B ．（0，2）C ．（1，2）D ．（0，1）4．【2010年新课标1文科11】已知▱ABCD 的三个顶点为A （﹣1，2），B （3，4），C （4，﹣2），点（，y ）在▱ABCD 的内部，则＝2﹣5y 的取值范围是（ ）A ．（﹣14，16）B ．（﹣14，20）C ．（﹣12，18）D ．（﹣12，20） 5．【2018年新课标1文科14】若，y 满足约束条件，则＝3+2y 的最大值为 ．6．【2016年新课标1文科16】某高科技企业生产产品A 和产品B 需要甲、乙两种新型材料．生产一件产品A 需要甲材料1.5g ，乙材料1g ，用5个工时；生产一件产品B 需要甲材料0.5g ，乙材料0.3g ，用3个工时，生产一件产品A 的利润为2100元，生产一件产品B 的利润为900元．该企业现有甲材料150g ，乙材料90g ，则在不超过600个工时的条件下，生产产品A 、产品B 的利润之和的最大值为 元． 7．【2015年新课标1文科15】若，y 满足约束条件，则＝3+y 的最大值为 ．8．【2013年新课标1文科14】设，y 满足约束条件，则＝2﹣y 的最大值为 ．9．【2011年新课标1文科14】若变量，y 满足约束条件，则＝+2y 的最小值为 ．考题分析与复习建议本专题考查的知识点为：不等关系与不等式，一元二次不等式及其解法，二元一次不等式组与简单的线性规划问题，基本不等式及其应用等.历年考题主要以选择填空题型出现，重点考查的知识点为：一元二次不等式及其解法，二元一次不等式组与简单的线性规划问题，基本不等式及其应用等，预测明年本考点题目会比较稳定，备考方向以知识点一元二次不等式及其解法，二元一次不等式组与简单的线性规划问题，基本不等式及其应用等为重点较佳.最新高考模拟试题1．已知11x y -≤+≤，13x y ≤-≤，则182yx⎛⎫⋅ ⎪⎝⎭的取值范围是（ ） A ．82,2⎡⎤⎣⎦B ．81,22⎡⎤⎢⎥⎣⎦C ．72,2⎡⎤⎣⎦D ．71,22⎡⎤⎢⎥⎣⎦2．已知点()2,1A ，动点(),B x y 的坐标满足不等式组2023603260x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩，设为向量OB uuu v 在向量OA u u u v 方向上的投影，则的取值范围为（ ） A．55⎡⎢⎣⎦ B．55⎡⎢⎣⎦ C ．[]2,18D ．[]4,183．已知实数x ，y ，满足约束条件13260x x y x y ≥⎧⎪-≤⎨⎪+-≤⎩，若2z x y =-+的最大值为（ ）A ．-6B ．-4C ．2D ．34．若直线()1y k x =+与不等式组243322y x x y x y -≤⎧⎪-≤⎨⎪+≥⎩表示的平面区域有公共点，则实数k 的取值范围是（ ）A ．(],1-∞B ．[]0,2C ．[]2,1-D ．(]2,2-5．已知,x y 满足约束条件20,20,20,x y x y -≤⎧⎪-≤⎨⎪+-≥⎩，则2z x y =+ 的最大值与最小值之和为（ ）A ．4B ．6C ．8D ．106．设0.231log 0.6,log 20.6m n ==，则（ ） A ．m n mn m n ->>+ B ．m n m n mn ->+> C ．mn m n m n >->+D ．m n m n mn +>->7．若x ，y 满足约束条件42y x x y y ≤⎧⎪+≤⎨⎪≥-⎩，则2z x y =+的最大值是（ ）A ．8B ．4C ．2D ．68．“2a =”是“0x ∀>，1x a x+≥成立”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件9．已知函数()ln(1)f x x =-，若f （a ）＝f （b ），则a+2b 的取值范围为（ ） A ．（4，+∞）B．[3)++∞C ．[6，+∞）D．(4,3+10．已知正项等比数列{a n }满足：a 7=a 6+2a 5，若存在两项a m 、a n ，使得a m a n =16a 12，则1m +9n的最小值为（ ） A ．32B ．83C ．114D ．不存在11．若正数,m n 满足21m n +=，则11m n+的最小值为（ ） A ．322+ B ．32+C ．222+D ．312．若实数满足，则的最大值是（ ）A ．-4B ．-2C ．2D ．4 13．已知，则取到最小值时（ ） A ．B ．C ．D ． 14．已知函数，若，则的最小值为（ ）A ．B ．C ．D ．15．在平面直角坐标系中，分别是轴正半轴和图像上的两个动点，且，则的最大值是A ．B ．C ．4D ．16．定义：区间的长度均为，若不等式的解集是互不相交区间的并集，设该不等式的解集中所有区间的长度之和为，则（ ）A ．当时，B ．当时，C ．当时，D ．当时，17．关于的不等式的解集为，则的取值范围为 （ ）A ．B ．C ．D ．18．若关于的不等式上恒成立，则实数a 的取值范围是A ．B ．C ．D ．19．已知函数的导函数为的解集为,若的极小值等于-98,则a 的值是（ ） A ．- B ． C ．2 D ．520．在R 上定义运算⊗：(1)x y x y ⊗=-，若不等式()()1x a x a -⊗+<对任意实数x 恒成立，则实数a 的取值范围为（ ） A ．11a -<<B ．1322a -<< C ．3122a -<< D ．02a <<21．在ABC ∆中，,,a b c 分别为角,,A B C 所对边的长，S 为ABC ∆的面积．若不等式22233kS b c a ≤+-恒成立，则实数k 的最大值为______．22．已知实数,x y 满足约束条件2020x y x y x a +-≥⎧⎪-+≥⎨⎪≤⎩，若2(0)z ax y a =->的最大值为1-，则实数a 的值是______23．已知实数,x y 满足不等式组201030y x y x y -≤⎧⎪--≤⎨⎪+-≥⎩，则yx 的取值范围为__________．24．若x ，y 均为正实数，则221(2)x y x y+++的最小值为_______.25．点(),M x y 在曲线C ：224210x x y -+-=上运动，22+1212150t x y x y a =+---，且t 的最大值为b ，若,a b R +∈，则111a b++的最小值为_____. 26．已知实数,x y 满足约束条件222020x x y x y ≤⎧⎪-+≥⎨⎪++≥⎩，则3xz y =-+的最大值为_____27．已知实数x ，y 满足342y x x y x ≥⎧⎪+≤⎨⎪≥⎩，则3z x y =+的最大值是__________．28．设x ,y 满足约束条件360200,0x y x y x y --≤⎧⎪-+≥⎨⎪≥≥⎩,若目标函数(0,0)z ax by a b =+>>的值是最大值为12,则23a b+的最小值为______． 29．若,x y 满足约束条件40,20,20,x y x x y -+≤⎧⎪-≤⎨⎪+-≥⎩则2z x y =+的最小值为__________．30．在ABC ∆中，内角,,A B C 的对边分别为,,a b c ，若222a b ab c ++=，且ABC ∆，则ab最小值为_______．。

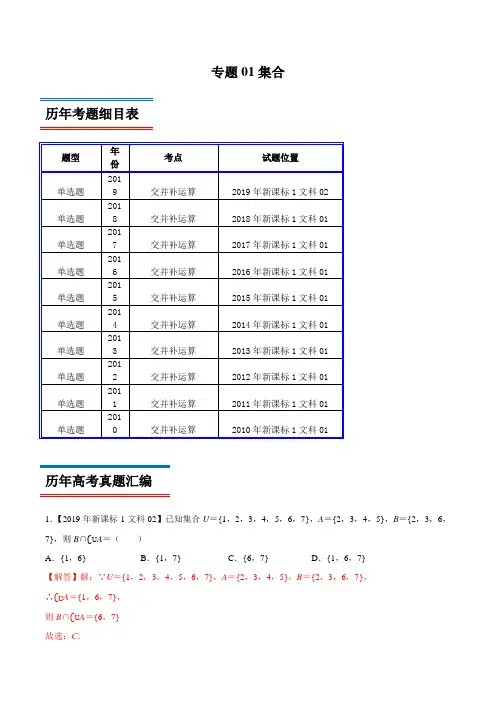
专题01集合历年考题细目表历年高考真题汇编1．【2019年新课标1文科02】已知集合U＝{1，2，3，4，5，6，7}，A＝{2，3，4，5}，B＝{2，3，6，7}，则B∩∁U A＝（）A．{1，6} B．{1，7} C．{6，7} D．{1，6，7}【解答】解：∵U＝{1，2，3，4，5，6，7}，A＝{2，3，4，5}，B＝{2，3，6，7}，∴∁U A＝{1，6，7}，则B∩∁U A＝{6，7}故选：C．2．【2018年新课标1文科01】已知集合A＝{0，2}，B＝{﹣2，﹣1，0，1，2}，则A∩B＝（）A．{0，2} B．{1，2}C．{0} D．{﹣2，﹣1，0，1，2}【解答】解：集合A＝{0，2}，B＝{﹣2，﹣1，0，1，2}，则A∩B＝{0，2}．故选：A．3．【2017年新课标1文科01】已知集合A＝{|＜2}，B＝{|3﹣2＞0}，则（）A．A∩B＝{|} B．A∩B＝∅C．A∪B＝{|} D．A∪B＝R【解答】解：∵集合A＝{|＜2}，B＝{|3﹣2＞0}＝{|}，∴A∩B＝{|}，故A正确，B错误；A∪B＝{||＜2}，故C，D错误；故选：A．4．【2016年新课标1文科01】设集合A＝{1，3，5，7}，B＝{|2≤≤5}，则A∩B＝（）A．{1，3} B．{3，5} C．{5，7} D．{1，7}【解答】解：集合A＝{1，3，5，7}，B＝{|2≤≤5}，则A∩B＝{3，5}．故选：B．5．【2015年新课标1文科01】已知集合A＝{|＝3n+2，n∈N}，B＝{6，8，10，12，14}，则集合A∩B中元素的个数为（）A．5 B．4 C．3 D．2【解答】解：A＝{|＝3n+2，n∈N}＝{2，5，8，11，14，17，…}，则A∩B＝{8，14}，故集合A∩B中元素的个数为2个，故选：D．6．【2014年新课标1文科01】已知集合M＝{|﹣1＜＜3}，N＝{|﹣2＜＜1}，则M∩N＝（）A．（﹣2，1）B．（﹣1，1）C．（1，3）D．（﹣2，3）【解答】解：M＝{|﹣1＜＜3}，N＝{|﹣2＜＜1}，则M∩N＝{|﹣1＜＜1}，故选：B．7．【2013年新课标1文科01】已知集合A＝{1，2，3，4}，B＝{|＝n2，n∈A}，则A∩B＝（）A．{1，4} B．{2，3} C．{9，16} D．{1，2}【解答】解：根据题意得：＝1，4，9，16，即B＝{1，4，9，16}，∵A＝{1，2，3，4}，∴A∩B＝{1，4}．故选：A．8．【2012年新课标1文科01】已知集合A＝{|2﹣﹣2＜0}，B＝{|﹣1＜＜1}，则（）A．A⊊B B．B⊊A C．A＝B D．A∩B＝∅【解答】解：由题意可得，A＝{|﹣1＜＜2}，∵B＝{|﹣1＜＜1}，在集合B中的元素都属于集合A，但是在集合A中的元素不一定在集合B中，例如∴B⊊A．故选：B．9．【2011年新课标1文科01】已知集合M＝{0，1，2，3，4}，N＝{1，3，5}，P＝M∩N，则P的子集共有（）A．2个B．4个C．6个D．8个【解答】解：∵M＝{0，1，2，3，4}，N＝{1，3，5}，∴P＝M∩N＝{1，3}∴P的子集共有22＝4故选：B．10．【2010年新课标1文科01】已知集合A＝{|||≤2，∈R}，B＝{|4，∈}，则A∩B＝（）A．（0，2）B．[0，2] C．{0，2} D．{0，1，2}【解答】解：∵A＝{|||≤2}＝{|﹣2≤≤2}B＝{|4，∈}＝{0，1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16}则A∩B＝{0，1，2}故选：D．考题分析与复习建议本专题考查的知识点为：集合关系及其运算，历年考题主要以选择填空题型出现， 重点考查的知识点为：交并补运算，预测明年本考点题目会比较稳定，备考方向以知识点交并补运算为重点较佳.最新高考模拟试题1．若集合{}5|2A x x =-<<，{}|||3B x x =<，则A B =I （ ）A ．{}|32x x -<<B ．{}|52x x -<<C ．{}|33x x -<<D ．{}|53x x -<<【答案】A【解析】解：{}{}333||B x x x x =<=-<<，则{}|32A B x x ⋂=-<<，故选：A ．2．已知集合2{|560}A x x x =-+≤，{|15}B x Z x =∈<<，则A B =I （ ）A ．[2,3]B ．(1,5)C ．{}2,3D ．{2,3,4}【答案】C【解析】2560(2)(3)023x x x x x -+≤⇒--≤⇒≤≤Q ，{}23A x x ∴=≤≤，又{}{|15}2,3,4B x Z x =∈<<=，所以{}2,3A B ⋂=，故本题选C.3．已知集合{3,2,1,0,1,2,3}A =---，{}2|450B x x x =∈--≤R ，则A B =I （ ）A ．{3,2,1,0}---B ．{}1,0,1,2,3-C ．{}3,2--D ．{}3,2,1,0,1,2,3---【答案】B【解析】 因为{}2|450B x x x =∈--≤R {|15}x x =-≤≤， {3,2,1,0,1,2,3}A =---∴{}1,0,1,2,3A B ⋂=-．故选B ．4．已知全集U =R ，集合{}|24,{|(1)(3)0}x A x B x x x =>=--<，则()U A B =I ð（ ） A ．(1,2)B ．(]1,2C ．(1,3)D ．(,2]-∞ 【答案】B【解析】由24x >可得2x >， (1)(3)0x x --<可得13x <<，所以集合(2,),(1,3)A B =+∞=,(,2]U A =-∞ð，所以()U A B =I ð(]1,2，故选B.5．已知集合{}(,)|1,A x y y x x R ==+∈，集合{}2(,)|,B x y y x x R ==∈，则集合A B ⋂的子集个数为（ ）A ．1B ．2C ．3D ．4 【答案】D【解析】由题意得，直线1y x =+与抛物线2y x =有2个交点，故A B ⋂的子集有4个.6．已知集合{}2log (1)2M x x =+＜，{1,0,1,2,3}N =-，则()R M N ⋂ð=（ ）A ．{-1，0，1，2，3}B ．{-1，0，1，2}C ．{-1，0，1}D ．{-1，3} 【答案】D【解析】 由题意，集合{}2log (1)2{|13}M x x x x =+<=-<<，则{|1R M x x =≤-ð或3}x ≥又由{1,0,1,2,3}N =-，所以(){1,3}R M N ⋂=-ð，故选D.7．已知集合{}lg(1)A x y x ==-，{}1,0,1,2,3B =-，则()R A B I ð=( )A ．{}1,0-B ．{}1,0,1-C ．{}1,2,3D ．{}2,3【答案】B【解析】 因为{}{}lg(1)1A x y x x x ==-=>，所以{}1R C A x x =≤，又{}1,0,1,2,3B =-，所以{}()1,0,1R C A B =-I .故选B8．已知R 是实数集，集合{}1,0,1A =-，{}210B x x =-≥，则()A B =R I ð（）A ．{}1,0-B ．{}1C ．1,12⎡⎤⎢⎥⎣⎦D ．1,2⎛⎫-∞ ⎪⎝⎭【答案】A【解析】1|2B x x 禳镲=?睚镲铪Q1|2R C B x x 禳镲\=<睚镲铪即(){1,0}R A C B ?-故选A 。

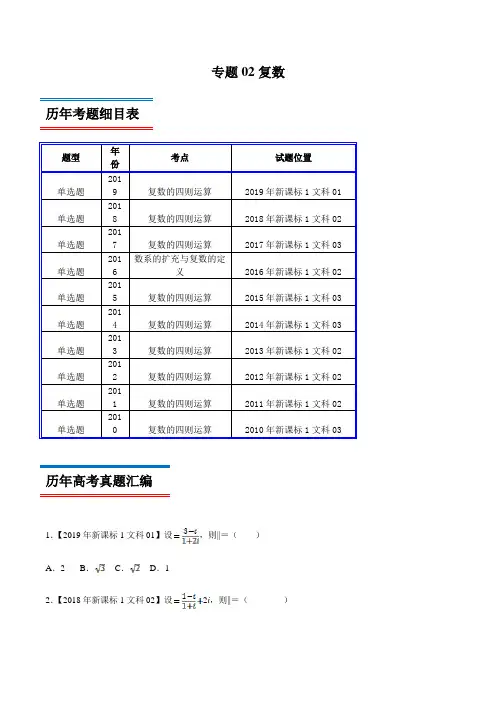
专题02复数历年考题细目表题型年份考点试题位置单选题2019 复数的四则运算2019年新课标1文科01单选题2018 复数的四则运算2018年新课标1文科02单选题2017 复数的四则运算2017年新课标1文科03单选题2016数系的扩充与复数的定义2016年新课标1文科02单选题2015 复数的四则运算2015年新课标1文科03单选题2014 复数的四则运算2014年新课标1文科03单选题2013 复数的四则运算2013年新课标1文科02单选题2012 复数的四则运算2012年新课标1文科02单选题2011 复数的四则运算2011年新课标1文科02单选题2010 复数的四则运算2010年新课标1文科03历年高考真题汇编1．【2019年新课标1文科01】设，则||＝（）A．2 B．C．D．12．【2018年新课标1文科02】设2i，则||＝（）A．0 B．C．1 D．3．【2017年新课标1文科03】下列各式的运算结果为纯虚数的是（）A．i（1+i）2 B．i2（1﹣i）C．（1+i）2D．i（1+i）4．【2016年新课标1文科02】设（1+2i）（a+i）的实部与虚部相等，其中a为实数，则a等于（）A．﹣3 B．﹣2 C．2 D．35．【2015年新课标1文科03】已知复数满足（﹣1）i＝1+i，则＝（）A．﹣2﹣i B．﹣2+i C．2﹣i D．2+i6．【2014年新课标1文科03】设i，则||＝（）A．B．C．D．27．【2013年新课标1文科02】（）A．﹣1i B．﹣1i C．1i D．1i8．【2012年新课标1文科02】复数的共轭复数是（）A．2+i B．2﹣i C．﹣1+i D．﹣1﹣i9．【2011年新课标1文科02】复数（）A．2﹣i B．1﹣2i C．﹣2+i D．﹣1+2i10．【2010年新课标1文科03】已知复数，则||＝（）A．B．C．1 D．2考题分析与复习建议本专题考查的知识点为：复数的基本概念(复数的实部、虚部、共轭复数、复数的模等)，复数相等的充要条件，考查复数的代数形式的四则运算，重点考查复数的除法运算，与向量结合考查复数及其加法、减法的几何意义等，历年考题主要以选择题题型出现，重点考查的知识点为复数的基本概念(复数的实部、虚部、共轭复数、复数的模等)，复数相等的充要条件，考查复数的代数形式的四则运算，重点考查复数的除法运算等，预测明年本考点题目会比较稳定，备考方向以知识点复数的基本概念(复数的实部、虚部、共轭复数、复数的模等)，复数相等的充要条件，考查复数的代数形式的四则运算为重点较佳.最新高考模拟试题1．复数52iz =-在复平面上的对应点位于（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．设i z a b =+（a ，b ∈R ，i 是虚数单位），且22i z =-，则有（ ） A ．1a b +=- B ．1a b -=- C ．0a b -= D ．0a b +=3．若复数1i1ia z +=+为纯虚数，则实数a 的值为( ) A ．1B ．1-C ．0D ．24．复数i （1+i ）的虚部为（ ）AB ．1C ．0D ．1-5．已知复数11z i =-+，复数2z 满足122z z =-，则2z = ( )A ．2B CD ．106．已知复数312i z i=+，则复数的实部为（ ）A ．25-B ．25i -C ．15-D ．15i -7．复数122ii-=+（ ）A ．1i -B ．i -C ．iD ．1i +8．已知i 为虚数单位,复数满足：()z 12i i +=-，则在复平面上复数对应的点位于（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限9．设复数z a i =+，z 是其共轭复数，若3455z i z =+，则实数a =（ ） A ．4B ．3C ．2D ．110．已知i 是虚数单位，复数满足2(1)1i i z-=+，则z =（ ）AB ．2C ．1D 11．复数()()21z i i =+-，其中i 为虚数单位，则的实部是（ ） A ．-1B ．1C ．2D ．312．已知复数(1)1z i i -=+，则复数z =（ ） A ．2i +B ．2i -C ．iD ．i -13．已知i 为虚数单位，若1(,)1a bi a b R i=+∈-，则b a =（ ）A ．1B C D ．214．已知复数满足2(1i)(3i)z +=+，则||z =（ ）A BC ．D ．815．已知i 是虚数单位，则复数11i i -+在复平面上所对应的点的坐标为（ ） A ．()0,1B ．()1,0-C ．()1,0D ．()0,1-16．若复数满足(1i)|1|z +=+，则在复平面内的共轭复数对应的点位于（ ） A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限17．已知复数满足12iz i =+，则的虚部是（ ） A ．1-B ．i -C ．2D ．2i18．已知31iz i-=-（其中i 为虚数单位），则z 的虚部为( ) A ．i -B ．1-C ．1D ．219．复数2(1)41i z i -+=+的虚部为( )A ．1-B ．3-C ．1D ．220．已知复数()11z ai a R =+∈，212z i =+（i 为虚数单位），若12z z 为纯虚数，则a =（ ）A ．2-B ．2C ．12-D ．1221．设复数满足2ii z+=，则z =（ ） A ．1BC ．3D ．522．已知复数1i z i=-，则z +在复平面内对应的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限23．复数满足(1)2z i i -=，则复数z =（ ） A ．1i -B ．12i +C ．1i +D ．1i --24．若复数2(1)z m m m i =+++是纯虚数，其中m 是实数，则1z=（ ） A ．iB ．i -C ．2iD ．2i -25．设i 为虚数单位，则复数22iz i-=+的共扼复数z =（ ） A ．3455i + B ．3455i - C ．3455i -+ D ．3455i -- 26．已知复数1z 、2z在复平面内对应的点关于虚轴对称，11z =，则12z z =( ) A ．2BCD ．127．已知复数1＝1+2i ，2＝l ﹣i ，则12z z =（ ） A ．13i 22-- B ．13i 22-+ C ．13i 22- D ．13i 22+ 28．在复平面内，复数(2i)z -对应的点位于第二象限，则复数可取（ ） A ．2B ．-1C ．iD ．2i +29．已知i 为虚数单位，则复数3(1)iz i i+=-的虚部为（ ）A ．1B ．2C ．1-D ．2-30．已知复数(i)(1i)z a =+-（i 为虚数单位）在复平面内对应的点在直线2y x =上，则实数a 的值为（ ）A ．0B ．1-C ．1D ．13-。

专题15不等式选讲历年考题细目表题型年份考点试题位置解答题2019 不等式选讲2019年新课标1文科23解答题2018 综合测试题2018年新课标1文科23解答题2017 综合测试题2017年新课标1文科23解答题2016 综合测试题2016年新课标1文科24解答题2015 综合测试题2015年新课标1文科24解答题2014 综合测试题2014年新课标1文科24解答题2013 综合测试题2013年新课标1文科24解答题2012 综合测试题2012年新课标1文科24解答题2011 综合测试题2011年新课标1文科24解答题2010 综合测试题2010年新课标1文科24历年高考真题汇编1．【2019年新课标1文科23】已知a，b，c为正数，且满足abc＝1．证明：（1）a2+b2+c2；（2）（a+b）3+（b+c）3+（c+a）3≥24．2．【2018年新课标1文科23】已知f（）＝|+1|﹣|a﹣1|．（1）当a＝1时，求不等式f（）＞1的解集；（2）若∈（0，1）时不等式f（）＞成立，求a的取值范围．3．【2017年新课标1文科23】已知函数f（）＝﹣2+a+4，g（）＝|+1|+|﹣1|．（1）当a＝1时，求不等式f（）≥g（）的解集；（2）若不等式f（）≥g（）的解集包含[﹣1，1]，求a的取值范围．4．【2016年新课标1文科24】已知函数f（）＝|+1|﹣|2﹣3|．（Ⅰ）在图中画出y＝f（）的图象；（Ⅱ）求不等式|f（）|＞1的解集．5．【2015年新课标1文科24】已知函数f（）＝|+1|﹣2|﹣a|，a＞0．（Ⅰ）当a＝1时，求不等式f（）＞1的解集；（Ⅱ）若f（）的图象与轴围成的三角形面积大于6，求a的取值范围．6．【2014年新课标1文科24】若a＞0，b＞0，且．（Ⅰ）求a3+b3的最小值；（Ⅱ）是否存在a，b，使得2a+3b＝6？并说明理由．7．【2013年新课标1文科24】已知函数f（）＝|2﹣1|+|2+a|，g（）＝+3．（Ⅰ）当a＝﹣2时，求不等式f（）＜g（）的解集；（Ⅱ）设a＞﹣1，且当∈[，]时，f（）≤g（），求a的取值范围．8．【2012年新课标1文科24】已知函数f（）＝|+a|+|﹣2|①当a＝﹣3时，求不等式f（）≥3的解集；②f（）≤|﹣4|若的解集包含[1，2]，求a的取值范围．9．【2011年新课标1文科24】设函数f （）＝|﹣a |+3，其中a ＞0．（Ⅰ）当a ＝1时，求不等式f （）≥3+2的解集（Ⅱ）若不等式f （）≤0的解集为{|≤﹣1}，求a 的值．10．【2010年新课标1文科24】设函数f （）＝|2﹣4|+1．（Ⅰ）画出函数y ＝f （）的图象：（Ⅱ）若不等式f （）≤a 的解集非空，求a 的取值范围． 考题分析与复习建议本专题考查的知识点为：解绝对值不等式、证明不等式、利用不等式恒成立求参数的值或范围，求含有绝对值的函数最值也是考查的热点．求解的一般方法是去掉绝对值，也可以借助数形结合求解.历年考题主要以解答题题型出现，重点考查的知识点为解绝对值不等式、证明不等式、利用不等式恒成立求参数的值或范围，求含有绝对值的函数最值也是考查的热点．预测明年本考点题目会比较稳定，备考方向以知识点解绝对值不等式、利用不等式恒成立求参数的值或范围，证明不等式为重点较佳. 最新高考模拟试题 1．已知函数()22()f x x a x a R =-+-∈.（1）当2a =时，求不等式()2f x >的解集；（2）若[2,1]x ∈-时不等式()32f x x ≤-成立，求实数a 的取值范围． 2．已知()221f x x x =-++．（1）求不等式()6f x <的解集；（2）设m 、n 、p 为正实数，且()3m n p f ++=，求证：12mn np pm ++≤．3．[选修4—5：不等式选讲]已知函数()|||2|(0)f x x m x m m =--+>.（1）当1m =，求不等式()1f x ≥的解集；（2）对于任意实数,x t ，不等式()21f x t t <++-恒成立，求实数m 的取值范围.4．选修4-5不等式选讲已知关于x 的不等式20x m x -+≤的解集为{|2}x x ≤-，其中0m >.（1）求m 的值；（2）若正数a ，b ，c 满足a b c m ++=，求证：2222b c a a b c++≥. 5．选修4-5：不等式选讲 已知函数()13f x x x a =+++（1）当1a =-时，解不等式()2f x ≥；（2）若存在0x 满足00()211f x x ++<，求实数a 的取值范围.6．已知函数()|2|f x ax =-.（Ⅰ）当4a =时，求不等式()|42|8f x x ++≥的解集；（Ⅱ）若[2,4]x ∈时，不等式()|3|3f x x x +-≤+成立，求a 的取值范围.7．已知函数()21f x x x a =-++，()2g x x =+．（1）当1a =-时，求不等式()()f x g x <的解集；（2）设12a >-，且当1,2x a ⎡⎫∈-⎪⎢⎣⎭，()()f x g x ≤，求a 的取值范围． 8．已知函数()|2|f x x =-．（Ⅰ）求不等式()|1|f x x x <++的解集；（Ⅱ）若函数5log [(3)()3]y f x f x a =++-的定义域为R ，求实数a 的取值范围．9．已知函数()123f x x x =-+-．（Ⅰ）解关于x 的不等式()4f x ≤；（Ⅱ）若()20f x m m -->恒成立，求实数m 的取值范围．10．已知函数()211f x x x =-++.（Ⅰ）解不等式()3f x ≥；（Ⅱ）记函数()f x 的最小值为m ，若,,a b c 均为正实数，且232a b c m ++=，求222a b c ++的最小值. 11．已知函数()12f x x a x =+++.（Ⅰ）求1a =时，()3f x ≤的解集；（Ⅱ）若()f x 有最小值，求a 的取值范围，并写出相应的最小值.12．选修4-5：不等式选讲已知函数()|23||1|f x x x =--+.（1）求不等式()6f x ≤的解集；（2）设集合M 满足：当且仅当x M ∈时，()|32|f x x =-，若,a b M ∈，求证：228223a b a b -++≤. 13．[选修4—5：不等式选讲]已知函数()31f x x m x m =----（1）若1m =，求不等式()1f x <的解集.（2）对任意的x R ∈，有()(2)f x f ≤，求实数m 的取值范围.14．已知()21f x x x =+-．（1）证明()1f x x +≥；（2）若,,a b c +∈R ，记33311134abc a b c +++的最小值为m ，解关于x 的不等式()f x m <． 15．选修4—5：不等式选讲已知函数()11f x x mx =++-，m R ∈。

专题09立体几何历年考题细目表质17解答题2013垂直关系的判定与性质2013年北京文科17解答题2012垂直关系的判定与性质2012年北京文科16解答题2011空间角与空间距离2011年北京文科17解答题2010垂直关系的判定与性质2010年北京文科17历年高考真题汇编1．【2018年北京文科06】某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为( ）A．1 B．2 C．3 D．4【解答】解:四棱锥的三视图对应的直观图为：PA⊥底面ABCD，AC,CD，PC＝3，PD＝2,可得三角形PCD不是直角三角形．所以侧面中有3个直角三角形，分别为：△PAB，△PBC，△PAD．故选：C．2．【2017年北京文科06】某三棱锥的三视图如图所示，则该三棱锥的体积为（）A．60 B．30 C．20 D．10【解答】解：由三视图可知:该几何体为三棱锥，该三棱锥的体积10．故选：D．3．【2015年北京文科07】某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为（）A．1 B．C．D．2【解答】解：由三视图知：几何体是四棱锥，且四棱锥的一条侧棱与底面垂直,底面为正方形如图：其中PB⊥平面ABCD，底面ABCD为正方形∴PB＝1，AB＝1，AD＝1，∴BD,PD．PC═该几何体最长棱的棱长为：故选：C．4．【2013年北京文科08】如图,在正方体ABCD﹣A1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有（)A．3个B．4个C．5个D．6个【解答】解:建立如图所示的空间直角坐标系，不妨设正方体的棱长｜AB｜＝3,则A（3,0，0），B（3，3，0），C（0,3,0），D（0,0，0），A1（3，0，3），B1（3，3,3）,C1（0,3,3）,D1（0，0,3)，∴（﹣3，﹣3，3），设P（x,y,z)，∵(﹣1，﹣1,1）,∴（2，2,1）．∴｜PA|＝｜PC|＝|PB1|，｜PD｜＝｜PA1|＝｜PC1｜，|PB｜，|PD1｜．故P到各顶点的距离的不同取值有,3,，共4个．故选：B．5．【2012年北京文科07】某三棱锥的三视图如图所示，该三棱锥的表面积是（）A．28+6B．30+6C．56+12D．60+12【解答】解：三视图复原的几何体是底面为直角边长为4和5的三角形，一个侧面垂直底面的等腰三角形，高为4,底边长为5，如图，所以S底10，S后,S右10，S左6．几何体的表面积为：S＝S底+S后+S右+S左＝30+6．故选：B．6．【2011年北京文科05】某四棱锥的三视图如图所示，该四棱锥的表面积是（）A．16B．16+16C．32D．16+32【解答】解：由已知中的三视力可得该几何体是一个四棱锥，棱锥的底面边长为4，故底面面积为16,棱锥的高为2,故侧面的高为：2，则每个侧面的面积为：4,故棱锥的表面积为：16+16,故选：B．7．【2010年北京文科05】一个长方体去掉一个小长方体，所得几何体的正视图与侧(左）视图分别如图所，则该几何体的俯视图为( )A．B．C．D．【解答】解：由正视图可知去掉的长方体在正视线的方向，从侧视图可以看出去掉的长方体在原长方体的左侧，由以上各视图的描述可知其俯视图符合C选项．故选:C．8．【2010年北京文科08】如图，正方体ABCD﹣A1B1C1D1的棱长为2,动点E、F在棱A1B1上．点Q是CD的中点,动点P在棱AD上，若EF＝1，DP＝x，A1E＝y（x，y大于零）,则三棱锥P﹣EFQ的体积（）A．与x，y都有关B．与x，y都无关C．与x有关，与y无关D．与y有关,与x无关【解答】解：三棱锥P﹣EFQ的体积与点P到平面EFQ的距离和三角形EFQ的面积有关，由图形可知，平面EFQ与平面CDA1B1是同一平面，故点P到平面EFQ的距离是P到平面CDA1B1的距离，且该距离就是P到线段A1D 的距离,此距离只与x有关，因为EF＝1，点Q到EF的距离为线段B1C的长度，为定值，综上可知所求三棱锥的体积只与x有关，与y无关．故选：C．9．【2019年北京文科12】某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示．如果网格纸上小正方形的边长为l,那么该几何体的体积为．【解答】解：由三视图还原原几何体如图，该几何体是把棱长为4的正方体去掉一个四棱柱，则该几何体的体积V．故答案为：40．10．【2019年北京文科13】已知l，m是平面α外的两条不同直线．给出下列三个论断：①l⊥m；②m∥α；③l⊥α．以其中的两个论断作为条件,余下的一个论断作为结论，写出一个正确的命题：．【解答】解：由l，m是平面α外的两条不同直线，知：由线面平行的判定定理得：若l⊥α,l⊥m，则m∥α．故答案为：若l⊥α，l⊥m，则m∥α．11．【2016年北京文科11】某四棱柱的三视图如图所示，则该四棱柱的体积为．【解答】解:由已知中的三视图可得：该几何体上部是一个以俯视图为底面四棱柱，棱柱的底面面积S(1+2）×1，棱柱的高为1，故棱柱的体积V，故答案为：12．【2014年北京文科11】某三棱锥的三视图如图所示，则该三棱锥最长棱的棱长为．【解答】解：由主视图知CD⊥平面ABC，设AC中点为E，则BE ⊥AC，且AE＝CE＝1；由主视图知CD＝2，由左视图知BE＝1，在Rt△BCE中，BC，在Rt△BCD中,BD，在Rt△ACD中，AD＝2．则三棱锥中最长棱的长为2．故答案为：2．13．【2013年北京文科10】某四棱锥的三视图如图所示，该四棱锥的体积为．【解答】解：几何体为底面边长为3的正方形，高为1的四棱锥，所以体积．故答案为：3．14．【2019年北京文科18】如图，在四棱锥P﹣ABCD中,PA⊥平面ABCD，底面ABCD为菱形，E为CD的中点．（Ⅰ）求证：BD⊥平面PAC；（Ⅱ）若∠ABC＝60°,求证:平面PAB⊥平面PAE；（Ⅲ）棱PB上是否存在点F,使得CF∥平面PAE?说明理由．【解答】证明：（Ⅰ）∵四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD为菱形,∴BD⊥PA,BD⊥AC，∵PA∩AC＝A，∴BD⊥平面PAC．(Ⅱ）∵在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD为菱形，E为CD的中点，∠ABC＝60°,∴AB⊥AE，PA⊥AE,∵PA∩AB＝A，∴AE⊥平面PAB，∵AE⊂平面PAE，∴平面PAB⊥平面PAE．解:（Ⅲ)棱PB上是存在中点F，使得CF∥平面PAE．理由如下:取AB中点G,连结GF，CG，∵在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD为菱形，E为CD的中点，∴CG∥AE，FG∥PA，∵CG∩FG＝G,AE∩PA＝A，∴平面CFG∥平面PAE，∵CF⊂平面CFG，∴CF∥平面PAE．15．【2018年北京文科18】如图,在四棱锥P﹣ABCD中,底面ABCD 为矩形，平面PAD⊥平面ABCD，PA⊥PD，PA＝PD，E,F分别为AD，PB的中点．（Ⅰ）求证：PE⊥BC；（Ⅱ）求证：平面PAB⊥平面PCD；(Ⅲ）求证：EF∥平面PCD．【解答】证明：（Ⅰ）PA＝PD,E为AD的中点，可得PE⊥AD，底面ABCD为矩形，可得BC∥AD，则PE⊥BC；（Ⅱ）由于平面PAB和平面PCD有一个公共点P，且AB∥CD,在平面PAB内过P作直线PG∥AB，可得PG∥CD，即有平面PAB∩平面PCD＝PG，由平面PAD⊥平面ABCD，又AB⊥AD，可得AB⊥平面PAD,即有AB⊥PA,PA⊥PG;同理可得CD⊥PD，即有PD⊥PG，可得∠APD为平面PAB和平面PCD的平面角，由PA⊥PD，可得平面PAB⊥平面PCD；（Ⅲ）取PC的中点H，连接DH，FH，在三角形PCD中，FH为中位线，可得FH∥BC，FH BC,由DE∥BC，DE BC,可得DE＝FH,DE∥FH，四边形EFHD为平行四边形,EF⊄平面PCD,DH⊂平面PCD,即有EF∥平面PCD．16．【2017年北京文科18】如图，在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA＝AB＝BC＝2，D为线段AC的中点，E为线段PC上一点．(1)求证：PA⊥BD;（2)求证：平面BDE⊥平面PAC；（3）当PA∥平面BDE时，求三棱锥E﹣BCD的体积．【解答】解：（1）证明：由PA⊥AB，PA⊥BC，AB⊂平面ABC，BC⊂平面ABC，且AB∩BC＝B，可得PA⊥平面ABC，由BD⊂平面ABC，可得PA⊥BD；（2)证明：由AB＝BC,D为线段AC的中点,由PA⊥平面ABC，PA⊂平面PAC，可得平面PAC⊥平面ABC，又平面PAC∩平面ABC＝AC，BD⊂平面ABC，且BD⊥AC，即有BD⊥平面PAC，BD⊂平面BDE，可得平面BDE⊥平面PAC；（3）PA∥平面BDE，PA⊂平面PAC，且平面PAC∩平面BDE＝DE，可得PA∥DE，又D为AC的中点,可得E为PC的中点，且DE PA＝1,由PA⊥平面ABC,可得DE⊥平面ABC,可得S△BDC S△ABC2×2＝1，则三棱锥E﹣BCD的体积为DE•S△BDC1×1．17．【2016年北京文科18】如图,在四棱锥P﹣ABCD中，PC⊥平面ABCD,AB∥DC,DC⊥AC．（1）求证：DC⊥平面PAC；（2）求证：平面PAB⊥平面PAC；（3）设点E为AB的中点，在棱PB上是否存在点F，使得PA∥平面CEF？说明理由．【解答】（1）证明:∵PC⊥平面ABCD，DC⊂平面ABCD，∴PC⊥DC,∵DC⊥AC，PC∩AC＝C，∴DC⊥平面PAC;（2）证明：∵AB∥DC，DC⊥AC，∴AB⊥AC，∵PC⊥平面ABCD,AB⊂平面ABCD，∴PC⊥AB，∵PC∩AC＝C,∴AB⊥平面PAC，∵AB⊂平面PAB，∴平面PAB⊥平面PAC；（3）解：在棱PB上存在中点F,使得PA∥平面CEF．∵点E为AB的中点，∴EF∥PA，∵PA⊄平面CEF,EF⊂平面CEF，∴PA∥平面CEF．18．【2015年北京文科18】如图，在三棱锥V﹣ABC中,平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC＝BC，O,M分别为AB，VA的中点．（1）求证：VB∥平面MOC；（2）求证:平面MOC⊥平面VAB（3）求三棱锥V﹣ABC的体积．【解答】（1）证明：∵O,M分别为AB,VA的中点，∴OM∥VB，∵VB⊄平面MOC,OM⊂平面MOC，∴VB∥平面MOC;（2)∵AC＝BC，O为AB的中点，∴OC⊥AB，∵平面VAB⊥平面ABC,OC⊂平面ABC，∴OC⊥平面VAB，∵OC⊂平面MOC，∴平面MOC⊥平面VAB（3)在等腰直角三角形ACB中，AC＝BC,∴AB＝2，OC＝1，∴S△VAB，∵OC⊥平面VAB,∴V C﹣VAB•S△VAB，∴V V﹣ABC＝V C﹣VAB．19．【2014年北京文科17】如图，在三棱柱ABC﹣A1B1C1中，侧棱垂直于底面,AB⊥BC，AA1＝AC＝2，BC＝1,E、F分别为A1C1、BC 的中点．（1）求证：平面ABE⊥平面B1BCC1；(2)求证：C1F∥平面ABE；（3）求三棱锥E﹣ABC的体积．【解答】解：(1）证明：∵三棱柱ABC﹣A1B1C1中，侧棱垂直于底面,∴BB1⊥AB，∵AB⊥BC，BB1∩BC＝B，BB1，BC⊂平面B1BCC1,∴AB⊥平面B1BCC1，∵AB⊂平面ABE,∴平面ABE⊥平面B1BCC1；（Ⅱ）证明：取AB中点G，连接EG，FG，则∵F是BC的中点，∴FG∥AC，FG AC，∵E是A1C1的中点，∴FG∥EC1，FG＝EC1，∴四边形FGEC1为平行四边形，∴C1F∥EG，∵C1F⊄平面ABE,EG⊂平面ABE，∴C1F∥平面ABE；（3）解：∵AA1＝AC＝2，BC＝1，AB⊥BC,∴AB，∴V E﹣ABC S△ABC•AA1（1)×2．20．【2013年北京文科17】如图，在四棱锥P﹣ABCD中,AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD．E和F 分别是CD和PC的中点,求证：(Ⅰ）PA⊥底面ABCD;(Ⅱ)BE∥平面PAD；（Ⅲ）平面BEF⊥平面PCD．【解答】解：（Ⅰ)∵PA⊥AD，平面PAD⊥平面ABCD，平面PAD ∩平面ABCD＝AD，由平面和平面垂直的性质定理可得PA⊥平面ABCD．（Ⅱ）∵AB∥CD，AB⊥AD，CD＝2AB，E和F分别是CD和PC 的中点，故四边形ABED为平行四边形,故有BE∥AD．又AD⊂平面PAD，BE不在平面PAD内,故有BE∥平面PAD．(Ⅲ）平行四边形ABED中，由AB⊥AD可得，ABED为矩形，故有BE⊥CD①．由PA⊥平面ABCD，可得PA⊥AB，再由AB⊥AD可得AB⊥平面PAD，∴CD⊥平面PAD，故有CD⊥PD．再由E、F分别为CD和PC的中点，可得EF∥PD，∴CD⊥EF②．而EF和BE是平面BEF内的两条相交直线，故有CD⊥平面BEF．由于CD⊂平面PCD，∴平面BEF⊥平面PCD．21．【2012年北京文科16】如图1，在Rt△ABC中,∠C＝90°，D，E分别为AC，AB的中点，点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置，使A1F⊥CD,如图2．（1）求证：DE∥平面A1CB；(2)求证：A1F⊥BE；(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ？说明理由．【解答】解：（1）∵D,E分别为AC，AB的中点，∴DE∥BC,又DE⊄平面A1CB，∴DE∥平面A1CB．(2)由已知得AC⊥BC且DE∥BC，∴DE⊥AC,∴DE⊥A1D，又DE⊥CD，∴DE⊥平面A1DC,而A1F⊂平面A1DC,∴DE⊥A1F，又A1F⊥CD，∴A1F⊥平面BCDE，∴A1F⊥BE．（3)线段A1B上存在点Q，使A1C⊥平面DEQ．理由如下：如图,分别取A1C，A1B的中点P，Q，则PQ∥BC．∵DE∥BC,∴DE∥PQ．∴平面DEQ即为平面DEP．由（Ⅱ)知DE⊥平面A1DC，∴DE⊥A1C,又∵P是等腰三角形DA1C底边A1C的中点，∴A1C⊥DP，∴A1C⊥平面DEP,从而A1C⊥平面DEQ，故线段A1B上存在点Q，使A1C⊥平面DEQ．22．【2011年北京文科17】如图,在四面体PABC中,PC⊥AB,PA⊥BC，点D，E，F，G分别是棱AP，AC,BC,PB的中点．(Ⅰ）求证:DE∥平面BCP；（Ⅱ）求证：四边形DEFG为矩形;(Ⅲ)是否存在点Q，到四面体PABC六条棱的中点的距离相等？说明理由．【解答】证明：(Ⅰ）∵D,E分别为AP,AC的中点，∴DE∥PC,∵DE⊄平面BCP，∴DE∥平面BCP．（Ⅱ）∵D，E,F,G分别为AP，AC，BC,PB的中点，∴DE∥PC∥FG，DG∥AB∥EF∴四边形DEFG为平行四边形,∵PC⊥AB，∴DE⊥DG，∴四边形DEFG为矩形．(Ⅲ）存在点Q满足条件，理由如下：连接DF，EG，设Q为EG的中点，由（Ⅱ）知DF∩EG＝Q,且QD＝QE＝QF＝QG EG，分别取PC，AB的中点M，N，连接ME，EN，NG，MG，MN，与（Ⅱ）同理，可证四边形MENG为矩形,其对角线交点为EG的中点Q，且QM＝QN EG，∴Q为满足条件的点．23．【2010年北京文科17】如图，正方形ABCD和四边形ACEF所在的平面互相垂直．EF∥AC，AB，CE＝EF＝1．（Ⅰ）求证：AF∥平面BDE;(Ⅱ）求证：CF⊥平面BDE．【解答】证明：（Ⅰ）设AC于BD交于点G．因为EF∥AG，且EF＝1,AG AC＝1，所以四边形AGEF为平行四边形,所以AF∥EG，因为EG⊂平面BDE，AF⊄平面BDE，所以AF∥平面BDE．(Ⅱ）连接FG．因为EF∥CG,EF＝CG＝1，且CE＝1，所以平行四边形CEFG为菱形．所以CF⊥EG．因为四边形ABCD为正方形，所以BD⊥AC．又因为平面ACEF⊥平面ABCD，且平面ACEF∩平面ABCD＝AC,所以BD⊥平面ACEF．所以CF⊥BD．又BD∩EG＝G，所以CF⊥平面BDE．考题分析与复习建议本专题考查的知识点为：空间几何体的结构、三视图和直观图，空间几何体的表面积与体积,空间点、直线、平面之间的位置关系，直线、平面平行、垂直的判定与性质，空间向量及其运算，立体几何中的向量方法(证明平行与垂直、求空间角和距离）等.历年考题主要以选择填空或解答题题型出现，重点考查的知识点为：三视图和直观图，空间几何体的表面积与体积，直线、平面平行、垂直的判定与性质,立体几何中的向量方法（证明平行与垂直、求空间角和距离)等.预测明年本考点题目会比较稳定，备考方向以知识点三视图和直观图,空间几何体的表面积与体积，直线、平面平行、垂直的判定与性质，立体几何中的向量方法(证明平行与垂直、求空间角和距离)等为重点较佳.最新高考模拟试题1．在正方体中, 1AD与BD所成的角为( ）A．45?B．90C．60D．120【答案】C【解析】如图,连结BC1、BD和DC1,在正方体ABCD-A1B1C1D1中，由AB=D1C1，AB∥D1C1，可知AD1∥BC1，所以∠DBC1就是异面直线AD1与BD所成角，在正方体ABCD—A1B1C1D1中，BC1、BD和DC1是其三个面上的对角线，它们相等．所以△DBC1是正三角形，∠DBC1=60°故异面直线AD1与BD所成角的大小为60°．故选：C．2．在正方体中，用空间中与该正方体所有棱成角都相等的平面 去截正方体,在截面边数最多时的所有多边形中,多边形截面的面积为S，周长为l，则( ）A．S为定值，l不为定值B．S不为定值，l为定值C．S与l均为定值D．S与l均不为定值【答案】C【解析】正方体的所有棱中，实际上是3组平行的棱，每条棱所在直线与平面α所成的角都相等，如图：与面1A BD平行的面且截面是六边形时满足条件，不失一般性设正方体边长为1，即六边形EFGHMN，其中分别为其所在棱的中点，由正方体的性质可得2EF=，2∴六边形的周长l为定值32．∴六边形的面积为，由正方体的对称性可得其余位置时也为正六边形,周长与面积不变，故S与l均为定值，故选C.3．在四面体P ABC-中，ABCPA=,4∆为等边三角形，边长为3，3PC=，PB=，5则四面体P ABC-的体积为（）A．3B．23C．11D．10【答案】C【解析】如图,延长CA至D，使得3AD=，连接,DB PD，因为，故ADB∆为等腰三角形，又，故，所以即,故CB DB⊥，因为，所以，所以CB PB⊥，因，DB⊂平面PBD,PB⊂平面PBD，所以CB⊥平面PBD,所以，因A为DC的中点，所以，因为，故PDC∆为直角三角形,所以,又，而4∆为直角三角形，PB=,故即PBD所以,所以，故选C。

1-
A.1+2i
B.-1+2i
C.1-2i
D.-1-2i
1
42.(2014·全国 1·文 T3)设 z=1+ +i,则|z|=( )
1
√2
√3
A.2
B. 2
C. 2
D.2
43.(2013·全国 1·理 T2)若复数 z 满足(3-4i)z=|4+3i|,则 z 的虚部为( )
A.-4
4
B.-5
4
C.4
D.√2
1+2i
8.(2018·全国 2·理 T1) =( )
1-2i
4
A.-5
−
3
5i
4
B.-5
+
3
5i
3
C.-5
−
4
5i
3
D.-5
+
4
5i
9.(2018·全国 2·文 T1)i(2+3i)=( )
A.3-2i
B.3+2i
1
C.-3-2i
D.-3+2i
10.(2018·全国 3·理 T2 文 T2)(1+i)(2-i)=( )
A.√3
B.√5
C.3
D.5
4.(2019·全国 2·文 T2)设 z=i(2+i),则 =( )
A.1+2i
B.-1+2i
C.1-2i
D.-1-2i
5.(2019·全国 1·理 T2)设复数 z 满足|z-i|=1,z 在复平面内对应的点为(x,y),则( )
A.(x+1)2+y2=1
B.(x-1)2+y2=1

专题15不等式选讲历年考题细目表题型年份考点试题位置解答题2019 不等式选讲2019年新课标1文科23解答题2018 综合测试题2018年新课标1文科23解答题2017 综合测试题2017年新课标1文科23解答题2016 综合测试题2016年新课标1文科24解答题2015 综合测试题2015年新课标1文科24解答题2014 综合测试题2014年新课标1文科24解答题2013 综合测试题2013年新课标1文科24解答题2012 综合测试题2012年新课标1文科24解答题2011 综合测试题2011年新课标1文科24解答题2010 综合测试题2010年新课标1文科24历年高考真题汇编1．【2019年新课标1文科23】已知a，b，c为正数，且满足abc＝1．证明：（1）a2+b2+c2；（2）（a+b）3+（b+c）3+（c+a）3≥24．2．【2018年新课标1文科23】已知f（）＝|+1|﹣|a﹣1|．（1）当a＝1时，求不等式f（）＞1的解集；（2）若∈（0，1）时不等式f（）＞成立，求a的取值范围．3．【2017年新课标1文科23】已知函数f（）＝﹣2+a+4，g（）＝|+1|+|﹣1|．（1）当a＝1时，求不等式f（）≥g（）的解集；（2）若不等式f（）≥g（）的解集包含[﹣1，1]，求a的取值范围．4．【2016年新课标1文科24】已知函数f（）＝|+1|﹣|2﹣3|．（Ⅰ）在图中画出y＝f（）的图象；（Ⅱ）求不等式|f（）|＞1的解集．5．【2015年新课标1文科24】已知函数f（）＝|+1|﹣2|﹣a|，a＞0．（Ⅰ）当a＝1时，求不等式f（）＞1的解集；（Ⅱ）若f（）的图象与轴围成的三角形面积大于6，求a的取值范围．6．【2014年新课标1文科24】若a＞0，b＞0，且．（Ⅰ）求a3+b3的最小值；（Ⅱ）是否存在a，b，使得2a+3b＝6？并说明理由．7．【2013年新课标1文科24】已知函数f（）＝|2﹣1|+|2+a|，g（）＝+3．（Ⅰ）当a＝﹣2时，求不等式f（）＜g（）的解集；（Ⅱ）设a＞﹣1，且当∈[，]时，f（）≤g（），求a的取值范围．8．【2012年新课标1文科24】已知函数f（）＝|+a|+|﹣2|①当a＝﹣3时，求不等式f（）≥3的解集；②f（）≤|﹣4|若的解集包含[1，2]，求a的取值范围．9．【2011年新课标1文科24】设函数f （）＝|﹣a |+3，其中a ＞0．（Ⅰ）当a ＝1时，求不等式f （）≥3+2的解集（Ⅱ）若不等式f （）≤0的解集为{|≤﹣1}，求a 的值．10．【2010年新课标1文科24】设函数f （）＝|2﹣4|+1．（Ⅰ）画出函数y ＝f （）的图象：（Ⅱ）若不等式f （）≤a 的解集非空，求a 的取值范围． 考题分析与复习建议本专题考查的知识点为：解绝对值不等式、证明不等式、利用不等式恒成立求参数的值或范围，求含有绝对值的函数最值也是考查的热点．求解的一般方法是去掉绝对值，也可以借助数形结合求解.历年考题主要以解答题题型出现，重点考查的知识点为解绝对值不等式、证明不等式、利用不等式恒成立求参数的值或范围，求含有绝对值的函数最值也是考查的热点．预测明年本考点题目会比较稳定，备考方向以知识点解绝对值不等式、利用不等式恒成立求参数的值或范围，证明不等式为重点较佳. 最新高考模拟试题 1．已知函数()22()f x x a x a R =-+-∈.（1）当2a =时，求不等式()2f x >的解集；（2）若[2,1]x ∈-时不等式()32f x x ≤-成立，求实数a 的取值范围． 2．已知()221f x x x =-++．（1）求不等式()6f x <的解集；（2）设m 、n 、p 为正实数，且()3m n p f ++=，求证：12mn np pm ++≤．3．[选修4—5：不等式选讲]已知函数()|||2|(0)f x x m x m m =--+>.（1）当1m =，求不等式()1f x ≥的解集；（2）对于任意实数,x t ，不等式()21f x t t <++-恒成立，求实数m 的取值范围.4．选修4-5不等式选讲已知关于x 的不等式20x m x -+≤的解集为{|2}x x ≤-，其中0m >.（1）求m 的值；（2）若正数a ，b ，c 满足a b c m ++=，求证：2222b c a a b c++≥. 5．选修4-5：不等式选讲 已知函数()13f x x x a =+++（1）当1a =-时，解不等式()2f x ≥；（2）若存在0x 满足00()211f x x ++<，求实数a 的取值范围.6．已知函数()|2|f x ax =-.（Ⅰ）当4a =时，求不等式()|42|8f x x ++≥的解集；（Ⅱ）若[2,4]x ∈时，不等式()|3|3f x x x +-≤+成立，求a 的取值范围.7．已知函数()21f x x x a =-++，()2g x x =+．（1）当1a =-时，求不等式()()f x g x <的解集；（2）设12a >-，且当1,2x a ⎡⎫∈-⎪⎢⎣⎭，()()f x g x ≤，求a 的取值范围． 8．已知函数()|2|f x x =-．（Ⅰ）求不等式()|1|f x x x <++的解集；（Ⅱ）若函数5log [(3)()3]y f x f x a =++-的定义域为R ，求实数a 的取值范围．9．已知函数()123f x x x =-+-．（Ⅰ）解关于x 的不等式()4f x ≤；（Ⅱ）若()20f x m m -->恒成立，求实数m 的取值范围．10．已知函数()211f x x x =-++.（Ⅰ）解不等式()3f x ≥；（Ⅱ）记函数()f x 的最小值为m ，若,,a b c 均为正实数，且232a b c m ++=，求222a b c ++的最小值. 11．已知函数()12f x x a x =+++.（Ⅰ）求1a =时，()3f x ≤的解集；（Ⅱ）若()f x 有最小值，求a 的取值范围，并写出相应的最小值.12．选修4-5：不等式选讲已知函数()|23||1|f x x x =--+.（1）求不等式()6f x ≤的解集；（2）设集合M 满足：当且仅当x M ∈时，()|32|f x x =-，若,a b M ∈，求证：228223a b a b -++≤. 13．[选修4—5：不等式选讲]已知函数()31f x x m x m =----（1）若1m =，求不等式()1f x <的解集.（2）对任意的x R ∈，有()(2)f x f ≤，求实数m 的取值范围.14．已知()21f x x x =+-．（1）证明()1f x x +≥；（2）若,,a b c +∈R ，记33311134abc a b c +++的最小值为m ，解关于x 的不等式()f x m <． 15．选修4—5：不等式选讲已知函数()11f x x mx =++-，m R ∈。

十年高考真题分类汇编（2010—2019）数学专题01 集合1.(2019•全国1•理T1)已知集合M={x|-4<x<2},N={x|x2-x-6<0},则M∩N=( )A.{x|-4<x<3}B.{x|-4<x<-2}C.{x|-2<x<2}D.{x|2<x<3}【答案】C由题意得N={x|-2<x<3},则M∩N={x|-2<x<2},故选C.2.(2019•全国1•文T2)已知集合U={1,2,3,4,5,6,7},A={2,3,4,5},B={2,3,6,7},则B∩∁U A=( )A.{1,6}B.{1,7}C.{6,7}D.{1,6,7}【答案】C由已知得∁U A={1,6,7},∴B∩∁U A={6,7}.故选C.3.(2019•全国2•理T1)设集合A={x|x2-5x+6>0},B={x|x-1<0},则A∩B=( )A.(-∞,1)B.(-2,1)C.(-3,-1)D.(3,+∞)【答案】A由题意,得A={x|x<2,或x>3},B={x|x<1},所以A∩B={x|x<1},故选A.4.(2019•全国2•文T1)已知集合A={x|x>-1},B={x|x<2},则A∩B=( )A.(-1,+∞)B.(-∞,2)C.(-1,2)D.⌀【答案】C由题意,得A∩B=(-1,2),故选C.5.(2019•全国3•T1)已知集合A={-1,0,1,2},B={x|x2≤1},则A∩B=( )A.{-1,0,1}B.{0,1}C.{-1,1}D.{0,1,2}【答案】AA={-1,0,1,2},B={x|-1≤x≤1},则A∩B={-1,0,1}.故选A.6.(2019•北京•文T1)已知集合A={x|-1<x<2},B={x|x>1},则A∪B=( )A.(-1,1)B.(1,2)C.(-1,+∞)D.(1,+∞)【答案】C∵A={x|-1<x<2},B={x|x>1},∴A∪B=(-1,+∞),故选C.7.(2019•天津•T1)设集合A={-1,1,2,3,5},B={2,3,4},C={x∈R|1≤x<3},则(A∩C)∪B=( )A.{2}B.{2,3}C.{-1,2,3}D.{1,2,3,4}【答案】DA∩C={1,2},(A∩C)∪B={1,2,3,4},故选D.8.(2019•浙江•T1)已知全集U={-1,0,1,2,3},集合A={0,1,2},B={-1,0,1},则(∁U A)∩B=( )A.{-1}B.{0,1}C.{-1,2,3}D.{-1,0,1,3}【答案】A∁U A={-1,3},则(∁U A)∩B={-1}.9.(2018•全国1•理T2)已知集合A={x|x2-x-2>0},则∁R A=( )A.{x|-1<x<2}B.{x|-1≤x≤2}C.{x|x<-1}∪{x|x>2}D.{x|x≤-1}∪{x|x≥2}【答案】BA={x|x<-1或x>2},所以∁R A={x|-1≤x≤2}.10.(2018•全国1•文T1)已知集合A={0,2},B={-2,-1,0,1,2},则A∩B=( )A.{0,2}B.{1,2}C.{0}D.{-2,-1,0,1,2}【答案】A由交集定义知A∩B={0,2}.11.(2018•全国2•文T2,)已知集合A={1,3,5,7},B={2,3,4,5},则A∩B=( )A.{3}B.{5}C.{3,5}D.{1,2,3,4,5,7}【答案】C集合A、B的公共元素为3,5,故A∩B={3,5}.12.(2018•全国3•T1)已知集合A={x|x-1≥0},B={0,1,2},则A∩B=( )A.{0}B.{1}C.{1,2}D.{0,1,2}【答案】C由题意得A={x|x≥1},B={0,1,2},∴A∩B={1,2}.13.(2018•北京•T1)已知集合A={x||x|<2},B={-2,0,1,2},则A∩B=( )A.{0,1}B.{-1,0,1}C.{-2,0,1,2}D.{-1,0,1,2}【答案】A∵A={x|-2<x<2},B={-2,0,1,2},∴A∩B={0,1}.14.(2018•天津•理T1)设全集为R,集合A={x|0<x<2},B={x|x≥1},则A∩(∁R B)=( )A.{x|0<x≤1}B.{x|0<x<1}C.{x|1≤x<2}D.{x|0<x<2}【答案】B∁R B={x|x<1},A∩(∁R B)={x|0<x<1}.故选B.15.(2018•天津•文T1)设集合A={1,2,3,4},B={-1,0,2,3},C={x∈R|-1≤x<2},则(A∪B)∩C=( )A.{-1,1}B.{0,1}C.{-1,0,1}D.{2,3,4}【答案】CA∪B={-1,0,1,2,3,4}.又C={x∈R|-1≤x<2},∴(A∪B)∩C={-1,0,1}.16.(2018•浙江•T1)已知全集U={1,2,3,4,5},A={1,3},则∁U A=( )A.⌀B.{1,3}C.{2,4,5}D.{1,2,3,4,5}【答案】C∵A={1,3},U={1,2,3,4,5},∴∁U A={2,4,5},故选C.17.(2018•全国2•理T2,)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为( )A.9B.8C.5D.4【答案】A满足条件的元素有(-1,-1),(-1,0),(-1,1),(0,1),(0,0),(0,-1),(1,-1),(1,0),(1,1),共9个。

A．1
B．2
C．3
D．4
31（. 2017Ⅲ理 1）已知集合 A = (x, y) x2 + y2 = 1 ，B = (x, y) y = x ，则 A I B 中元素的个数为( )
A．3
B．2
C．1
D．0
32.（2018Ⅰ文 1）已知集合 A = 0，2 ， B = -2，-1，0，1，2 ，则 A I B = ( )
A．（-14，16）
B．（-14，20）
C．（-12，18）
D．（-12，20）
x-3 2.（2010Ⅱ文 2）不等式 0 的解集为( )
x+2
A．{x｜-2< x<3} B．{ x｜x<-2}
C．{ x｜x<-2,或 x>3} D．{ x∣x>3}
x -1
3.(2010Ⅱ文
5
理
3）若变量
x，y
1.集合
1.（2010Ⅰ文理 1）已知集合 A = x | x 2，x R，B = x | x 4，x Z ,则 A I B ＝( )
A．（0，2）
B．[0，2]
C．{0，2}
D．{0，1，2}
2.（2010Ⅱ文 1）设全集 U= x N * | x 6 ,集合 A＝{1，3}，B＝{3，5}，则 CU A U B ＝( )
A．{-1，0}
B．{0，1}
C．{-1，0，1}
D．{0，1，2}
20.（2016Ⅰ文 1）设集合 A={1，3，5，7}，B＝{x| 2 x 5}，则 A∩B=( )
A．{1,3}
B．{3,5}
C．{5,7}
D．{1,7}
21.（2016Ⅰ理 1）设集合 A＝{x|x2－4x+3＜0}，B＝{x|2x－3＞0}，则 A I B = ( )

十年高考真题分类汇编（2010—2019）数学专题空间向量1. （2014 •全国2 •理T11）直三棱柱ABC-A6C 、中，N%4R00 ,MN 分别是A £, A6的中 点,则6y 与4V 所成角的余弦值为（） r 同 u.— 102. （2013 •北京•文T8）如图，在正方体被〃中，尸为对角线做的三等分点，尸到各顶点的距离的不同取值有（）3. （2012 •陕西•理T5）如图,在空间直角坐标系中有直三棱柱板。

1二8与纸则直线与直线必夹角的余弦值为（4. （2010 •大纲全国•文T6）直三棱柱ABC-ABQ 中，若NBAC =90° ,AB=AC=AA1，则异面直线BA ： 与AQ 所成的角等于（）A. 30°B. 45°C. 60°D. 90°5. (2019 •天津•理 T17)如图,AE,平面 ABCD, CF 〃AE ， AD 〃BC, AD_LAB, AB=AD=1, AE=BC 二2.(1)求证:BF 〃平面ADE;B -l B. 4个C 5个 D.6个A.3个 C.这⑵求直线CE与平面BDE所成角的正弦值;⑶若二面角E-BD-F的余弦值为京求线段CF的长.EB6.（2019 •浙江• T 19）如图，已知三棱柱ABC-A&C,平面 4月平面ABC, ZABC^0° , Z 区灰＞30° ,4月引。

泡尸分别是〃;43的中点.（1）证明:年J_6C;⑵求直线房与平面46。

所成角的余弦值.7.（2019 •全国1•理T18）如图，直四棱柱极〃的底面是菱形，例=1,止2, N 员切40° ,EM,V分别是比破,4。

的中点.⑴证明：/V〃平面C、DE;（2）求二面角力T4M的正弦值.8.（2019 •全国2 •理T17）如图，长方体力用a-4£4〃的底面月颜是正方形，点£在棱前［上，龙LEG.⑴证明:麻山平面微a；⑵若AE=A^求二面角B-EC-C的正弦值.9.（2019 •全国3 •理T19）图1是由矩形ADEB,Rt^ABC和菱形BFGC组成的一个平面图形，其中AB=1, BE=BF=2, ZFBC=60° .将其沿AB, BC折起使得BE与BF重合,连接DG,如图2.（1）证明：图2中的A, C, G, D四点共面,且平面ABC_L平面BCGE;（2）求图2中的二面角B-CG-A的大小.10.（2018 •浙江• T 8）已知四棱锥S-ABCD的底面是正方形，侧棱长均相等,E是线段AB 上的点（不含端点）.设SE与BC所成的角为01,SE与平面ABCD所成的角为82,二面角S-AB-C的平面角为83,则（）A.01<02<03B.03<02<61C.01<O3<02D.92<03<0111.（2018 •全国3 •理T19）如图,边长为2的正方形4加9所在的平面与半圆弧曲所在平面垂直,"是曲上异于的点.（1）证明：平面AMD_L平面BMC;⑵当三棱锥M-ABC体积最大时,求面MAB与面MCD所成二面角的正弦值.12.（2018 •北京•理T16）如图，在三棱柱ABC-A瓜&中，CC_L平面ABCM & F, G分别为44：, AQ 4Q 能的中点，AB二BC二遍,AC=AA尸2.⑴求证:AC_L平面BEF;（2）求二面角B-CD-G的余弦值;16.(2018 •浙江• T9)如图，已知多面体ABCA瓜心, 44 £5 均垂直于平面ABC, Z板=120° , A.A^ GC=1, AB=BC=B-.B=^.(1)证明:四_L平面4A4;⑵求直线月a与平面月期所成的角的正弦值.17.(2018 •上海，T17)已知圆锥的顶点为P,底面圆心为0,半径为2.(1)设圆锥的母线长为4,求圆锥的体积；(2)设P0=4, 0A, 0B是底面半径,且NA0B=90° , M为线段AB的中点，如图,求异面直线PM与0B 所成的角的大小.18.(2017 •北京•理T16)如图，在四棱锥P-ABCD中，底面ABCD为正方形,平面PAD,平面ABCD, 点M在线段PB上,PD〃平面MAC, PA=PD二遍,AB=4.⑴求证:M为PB的中点；(2)求二面角B-PD-A的大小；⑶求直线MC与平面BDP所成角的正弦值.19.（2017 •全国 1 •理 T18）如图，在四棱锥 P-ABCD 中,AB〃CD,且NBAP=NCDP=90。