线段计算专题(3)

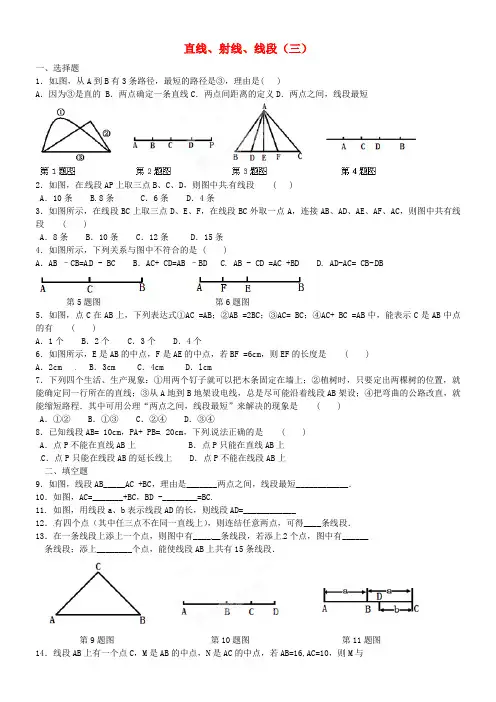
直线、射线、线段（三）一、选择题1．如图，从A到B有3条路径，最短的路径是③，理由是( )A．因为③是直的 B．两点确定一条直线C．两点间距离的定义D．两点之间，线段最短2．如图，在线段AP上取三点B、C、D，则图中共有线段 ( )A．10条 B.8条 C．6条 D．4条3．如图所示，在线段BC上取三点D、E、F，在线段BC外取一点A，连接AB、AD、AE、AF、AC，则图中共有线段 ( )A．8条 B．10条 C．12条 D．15条4．如图所示，下列关系与图中不符合的是 ( )A．AB –CB=A D - BC B．AC+ CD=AB –BD C. AB - CD =AC +BD D. AD-AC= CB-DB第5题图第6题图5．如图，点C在AB上，下列表达式①AC =AB；②AB =2BC；③AC= BC；④AC+ BC =AB中，能表示C是AB中点的有 ( )A．1个 B．2个 C．3个 D．4个6．如图所示，E是AB的中点，F是AE的中点，若BF =6cm，则EF的长度是 ( )A．2cm B．3cm C．4cm D．lcm7．下列四个生活、生产现象：①用两个钉子就可以把木条固定在墙上；②植树时，只要定出两棵树的位置，就能确定同一行所在的直线；③从A地到B地架设电线，总是尽可能沿着线段AB架设；④把弯曲的公路改直，就能缩短路程．其中可用公理“两点之间，线段最短”来解决的现象是 ( )A．①② B．①③ C．②④ D．③④8．已知线段AB= 10cm，PA+ PB= 20cm，下列说法正确的是 ( )A．点P不能在直线AB上 B．点P只能在直线AB上C．点P只能在线段AB的延长线上 D．点P不能在线段AB上二、填空题9．如图，线段AB_____AC +BC，理由是_______两点之间，线段最短____________．10．如图，AC=_______+BC，BD -________=BC.11. 如图，用线段a、b表示线段AD的长，则线段AD=____________12．有四个点（其中任三点不在同一直线上），则连结任意两点，可得____条线段．13．在一条线段上添上一个点，则图中有______条线段，若添上2个点，图中有______ 条线段；添上________个点，能使线段AB上共有15条线段．第9题图第10题图第11题图N的距离是________.15．延长线段AB到C，使BC = 12AB，若AB =8cm，则AC=______第16题图第17题图第19题图16．如图，C、D、E为线段AB上的点，且AC= CD= DE=EB，那么图中有______个点是线段的中点。

专题八：线段计算（3）——分类讨论思想方法点睛几何问题中没给出图形，或给出图形但已知点的位置没给出来，或动点经过“关键点”前后，往往需要考虑分类讨论。

典例精讲1．点A、B、C在同一条直线上，AB＝6cm，BC＝2cm，点M是线段AC的中点，求AM的长．举一反三2．如图，已知线段AB＝4，延长AB到点C，使得AB＝2BC，反向延长AB到点D，使AC ＝2AD．（1）求线段CD的长；（2）若Q为AB的中点，P为线段CD上一点，且BP=12BC，求线段PQ的长．3．已知点C在线段AB上，AC＝2BC，点D、E在直线AB上，点D在点E的左侧．若AB ＝18，DE＝8，线段DE在线段AB上移动．①如图1，当E为BC中点时，求AD的长；②点F（异于A，B，C点）在线段AB上，AF＝3AD，CE+EF＝3，求AD的长．专题过关4．已知线段AB＝10cm，直线AB上有一点C，且BC＝4cm，M是线段AC的中点，则AM 的长（）A．7cm B．3cm C．3cm或7cm D．7cm或9cm5．已知线段AB＝12，在AB上有C、D、M、N四点，且AC：CD：DB＝1：2：3．AM=12AC，DN =14BD ，求线段MN 的长．6．如图，C 为线段AB 上一点，D 为AC 的中点，E 为BC 的中点，F 为DE 的中点．（1）若AC ＝4，BC ＝6，求CF 的长；（2）若AB ＝16CF ，求AC CB 的值．7．已知线段AB ．（1）M 是线段AB 上一点，且此时所有线段之和为20，求线段AB 的长；（2）直线AB 上有一点C ，且BC ＝4，N 是AC 的中点，求AN 的长．8．点A ，B ，C 在同一直线上，（1）若AB ＝8，AC ：BC ＝3：1，求线段AC 的长度；（2）若AB ＝m ，AC ：BC ＝n ：1（n 为大于1的整数），求线段AC 的长度．9．动点A 从原点出发向数轴负方向运动，同时，动点B 也从原点出发向数轴正方向运动，3秒后，两点相距18个单位长度．已知动点A 、B 的速度比是1：2（速度单位：单位长度/秒）．（1）求出两个动点运动的速度，并在数轴上标出A 、B 两点从原点出发运动3秒时的位置；（2）若A 、B 两点从（1）中的位置同时向数轴负方向运动时，另一动点C 和点B 同时从B 点位置出发向A 运动，当遇到A 后，立即返回向B 点运动，遇到B 点后又立即返回向A 点运动，如此往返，直到B 追上A 时，C 立即停止运动．若点C 一直以20单位长度/秒的速度匀速运动，那么点C 从开始运动到停止运动，行驶的路程是多少个单位长度？（3）若A 、B 两点是（1）中的位置，点P 是AB 两点间的一动点，沿A →B →A 以4单位长度/秒的速度往返运动1次，运动时间为t 秒．①用含t 的代数式表示AP 的长度；②在运动过程中，若BP 中点为Q ，且AQ ＝3AP ，求t 的值．【参考答案】1．解：如图1，当点C在线段AB的延长线上时，∵AB＝6cm，BC＝2cm，∴AC＝8cm，∵点M是线段AC的中点，∴AM=12AC＝4cm，如图2，当点C在线段AB上时，∵AB＝6cm，BC＝2cm，∴AC＝4cm，∵点M是线段AC的中点，∴AM=12AC＝2cm，答：AM的长为2cm或4cm．2．解：（1）∵AB＝4，AB＝2BC，∴BC＝2，∴AC＝AB+BC＝6，∵AC＝2AD，∴AD＝3，∴CD＝AC+AD＝6+3＝9；（2）∵Q为AB中点，∴BQ=12AB＝2，∵BP=12BC，∴BP＝1，当点P在B、C之间时，PQ＝BP+BQ＝2+1＝3；当点P在A、B之间时，PQ＝BQ﹣BP＝2﹣1＝1．即PQ的长为1或3．3．解：①AC＝2BC，AB＝18，∴BC＝6，AC＝12，如图1，∵E为BC中点，∴CE＝BE＝3，∵DE＝8，∴BD＝DE+BE＝8+3＝11，∴AD＝AB﹣DB＝18﹣11＝7；②Ⅰ、当点E在点F的左侧，如图2，或∵CE+EF＝3，BC＝6，∴点F是BC的中点，∴CF＝BF＝3，∴AF＝AB﹣BF＝18﹣3＝15，∴AD=13AF＝5；∵CE+EF＝3，故图2（b）这种情况求不出；Ⅱ、如图3，当点E在点F的右侧，或∵AC＝12，CE+EF＝CF＝3，∴AF＝AC﹣CF＝9，∴AF＝3AD＝9，∴AD＝3．∵CE+EF＝3，故图3（b）这种情况求不出；综上所述：AD的长为3或5．4．C．5．解：当C 点在线段AB 上：∵AB ＝12，AC ：CD ：DB ＝1：2：3，∴AC =16×12＝2，CD =26×12＝4，DB =36×12＝6，∴AM =12AC ＝1，DN =14BD =32，①当点N 在点D 右侧时，如图1，MN ＝MC +CD +DN ＝2﹣1+4+32=132；②当点N 在点D 左侧时，如图2，MN ＝MC +CD ﹣DN ＝2﹣1+4−32=72．综上所述，线段MN 的长为72或132．6．解：（1）∵D 为AC 的中点，∴AD ＝CD =12AC ＝2∵E 为BC 中点，∴CE ＝BE =12BC ＝3∴DE ＝DC +CE ＝5∵F 为DE 中点∴DF =12DE =52∴CF ＝DF ﹣DC =52−2=12（2）如图：设AD ＝CD ＝x ，CE ＝BE ＝y ，则DF =12DE =12（x +y ）∴CF ＝DF ﹣DC =12（y ﹣x ）∴由AB ＝16CF 得：2（x +y ）＝8（y ﹣x ），∴5x ＝3y∴AC BC =2x 2y =x y=35 答：AC BC 的值为35．7．解：（1）如图1所示：根据题意可知：AM +MB +AB ＝20．∵AM +MB ＝AB ，∴2AB ＝20．∴AB ＝10．（2）如图2所示：点C 在AB 的延长线上．∵AB ＝10，BC ＝4，∴AC ＝AB +BC ＝10+4＝14．∵N 是AC 的中点，∴AN =12AC =12×14=7． 如图3所示；点C 在AB 上．∵AB ＝10，BC ＝4，∴AC ＝10﹣4＝6．∵N 是AC 的中点，∴AN =12AC =12×6=3．∴AN 的长为3或7．8．解：（1）当点C 在线段AB 上时，∵AB ＝8，AC ：BC ＝3：1，∴AC ＝6，当点B 在线段AC 上时，∵AB ＝8，AC ：BC ＝3：1，∴BC ＝4，∴AC＝AB+BC＝12；（2）当点C在线段AB上时，∵AB＝m，AC：BC＝n：1，∴AC=nmn+1，当点B在线段AC上时，∵AB＝m，AC：BC＝n：1，∴BC=mn−1，∴AC＝AB+BC＝m+mn−1=mnn−1．9．解：（1）设点A的速度为x单位长度/秒，则点B的速度为2x单位长度/秒，由题意，得3x+6x＝18，解得：x＝2，∴点B的速度为4个单位长度/秒，∴点A的位置是﹣6，点B的位置是12．如图：（2）设B追上A的时间是m秒，由题意，得4m＝2m+18，解得：m＝9，∴点C行驶的路程是：20×9＝180个单位长度；（3）①当0＜t≤4.5时，AP＝4t，当4.5＜t≤9时，AP＝36﹣4t；②当0＜t≤4.5时，4t+18−4t2=3×4t，t=9 10；当4.5＜t≤9时，18−(36−4t)2+36﹣4t＝3（36﹣4t）t=81 10．答：BP中点为Q，且AQ＝3AP时，t的值是910或81 10．。

2019 年七年级数学上册线段的计算专题练习一、解答题：1、如图，己知线段 AB=80，M为 AB的中点， P在MB上， N为 PB的中点，且 NB=14，（1）求 MB的长；（ 2）求 PB的长；（ 3）求 PM的长．2、如图，点 C、D是线段 AB上两点，点 D 是 AC的中点，若 BC=6cm，BD=10cm，求线段 AB的长度．3、如图，已知点 C是线段 AB的中点，点 D 是线段 AC的中点，点 E是线段 BC的中点．（1）若线段 DE=9cm，求线段 AB的长．（ 2）若线段 CE=5cm，求线段 DB的长．AB=8，AC： BC=3：1，求线段 BC的长度．4、点 A，B， C 在同一直线上，5、如图所示，线段 AB=8cm，E 为线段 AB的中点，点 C为线段 EB上一点，且 EC=3cm，点 D为线段 AC的中点，求线段 DE的长度．6、如图，已知线段 AB=32，C为线段 AB上一点，且 3AC=BC，E 为线段 BC的中点， F为线段 AB的中点，求线段 EF 的长．7、如图， M是线段 AC中点，点 B 在线段 AC上，且BC=2AB，求线段 MC和线段 BM的长．AB=4cm，8、如图，线段 AC=8 cm，线段 BC=18 cm，点 M是 AC的中点，在 CB上取一点 N，使得 CN∶NB=1∶2. 求 MN的长．9、如图，已知 BC= AB= CD，点 E，F 分别是 AB，CD的中点，且 EF=60厘米，求 AB，CD的长．10、如图，B是线段AD上一动点，沿A→D→A以2cm/s的速度往返运动1次，C是线段BD的中点，AD=10cm，设点 B 运动时间为 t 秒（ 0≤t ≤ 10）．（1）当 t=2 时，① AB= cm．②求线段 CD的长度．（2）用含 t 的代数式表示运动过程中 AB的长．（3）在运动过程中，若AB中点为E，则EC的长是否变化？若不变，求出EC的长；若发生变化，请说明理由．11、如图，点 B 、 C 在线段 AD 上， CD=2AB ＋ 3．（1）若点 C 是线段 AD 的中点，求 BC －AB 的值；（2）若 4BC=AD ，求 BC － AB 的值；＋3b.13、如图，点 C 在线段 AB 上， AC=8cm ， CB=6cm ，点 M 、 N 分别是 AC 、 BC 的中点．（1）求线段 MN 的长；（2）若 C 在线段 AB 的延长线上，且满足 AC ﹣ BC=bcm ，M 、N 分别为 AC 、BC 的中点，你能猜想出 MN 的长度 吗？请画出图形，并说明理由．14、如图，线段 AC=6cm ，线段 BC=15cm ，点 M 是 AC 的中点，在 CB 上取一点 N ，使得 CN ：NB=1： 2，求 MN 的长．3）若线段 AC 上有一点 P （不与点 B 重合） AP ＋ AC=DP ，求 BP 的长．12、 A 、B 、C 、D 四个车站的位置如图所示， B 、C 两站之间的距离 BC=2a ＋b ，B 、 D 两站之间的距离 BD=4a 求：⑴ ⑵ C 、 若D 两站之间的距离 CD ； C 站到 A 、D 两 站的距离相等，则 A 、 B 两站之间的距离 AB 是多少？15、如图，数轴上 A， B两点对应的有理数分别为 10和 15，点 P从点 A出发，以每秒 1个单位长度的速度沿数轴正方向运动，点 Q同时从原点 O出发，以每秒 2 个单位长度的速度沿数轴正方向运动，设运动时间为 t 秒．（1）当 0< t < 5 时，用含 t 的式子填空： BP= ，AQ= ；（2）当 t=2 时，求 PQ的值；（3）当 AB=2PQ时，求 t 的值．16、如图，已知点 C在线段 AB上，点 M、 N 分别是 AC、 BC的中点 .（1）若 AC=6 ，CB=4 ，求线段 MN的长；（2）若点 C 为线段 AB 上任一点，其它条件不变，你能猜想线段 MN与 AB的数量关系吗？并说明你的理由；（3）若点 C 在线段 AB 的延长线上，其它条件不变，你上述猜想的结论是否仍然成立？请画出图形，写出你的结论，并说明你的理由；17、如图， P 是线段 AB上一点， AB=12cm，C、 D两点分别从 P、B出发以 1cm/s、2cm/s 的速度沿直线 AB向左运动（ C在线段 AP上， D在线段 BP上），运动的时间为 ts ．1）当 t=1 时， PD=2AC，请求出 AP 的长；2）当 t=2 时， PD=2AC，请求出 AP 的长；3）若 C、D 运动到任一时刻时，总有 PD=2AC，请求出 AP的长；4）在（ 3）的条件下， Q是直线 AB上一点，且 AQ﹣ BQ=PQ，求 PQ的长．18、已知数轴上有 A、 B、 C三点，分别表示有理数﹣ 26，﹣ 10， 10，动点 P从 A出发，以每秒 1 个单位的速度向终点 C移动，设点 P 移动时间为 t 秒．（1）用含 t 的代数式表示 P 点对应的数 : ；用含 t 的代数式表示点 P 和点 C的距离： PC=（2）当点 P运动到 B点时，点 Q从 A点出发，以每秒 3 个单位的速度向 C点运动， Q点到达 C 点后，再立即以同样的速度返回点 A.①点 P、 Q同时运动运动的过程中有处相遇，相遇时 t= 秒．②在点 Q开始运动后，请用 t 的代数式表示 P、 Q两点间的距离．19、如图，线段 AB=12，动点 P从 A出发，以每秒 2个单位的速度沿射线 AB运动， M为 AP的中点．（1）出发多少秒后， PB=2AM？（2）当 P在线段 AB上运动时，试说明 2BM﹣ BP为定值．（3）当 P在 AB延长线上运动时， N为 BP的中点，下列两个结论：① MN长度不变；② MA+PN的值不变，选择一个正确的结论，并求出其值．20、探索性问题：已知： b是最小的正整数，且 a、b满足（ c﹣5）2+|a+b|=0 ，请回答问题：（1）请直接写出 a、b、c 的值． a= ， b= ，c= ；（2）数轴上 a、b、c 三个数所对应的点分别为 A、B、 C，点 A、 B、C同时开始在数轴上运动，若点 A 以每秒 1 个单位长度的速度向左运动，同时，点 B 和点 C 分别以每秒 1 个单位长度和 3 个单位长度的速度向右运动，假设 t 秒钟过后，若点 B与点 C之间的距离表示为 BC，点 A 与点 B之间的距离表示为 AB，点 A与点 C 之间的距离表示为 AC．①t 秒钟过后， AC 的长度为（用 t 的关系式表示）；②请问： BC﹣ AB 的值是否随着时间 t 的变化而改变？若变化，请说明理由；若不变，请求其值．参考答案1、解：（ 1）∵ M 是 AB 的中点∴ MB=40（2）∵ N 为 PB 的中点，且 NB=14 ∴ PB=2NB=2× 14=28 （3）∵ MB=40， PB=28 ∴ PM=M ﹣B PB=40﹣ 28=122、解：已知 BC=6cm ， BD=10cm ，∴ DC=BD ﹣BC=4cm ，又点 D 是 AC 的中点，∴ DA=DC=4cm ，所以 AB=BD+DA=10+4=1（4 cm ）． 答：线段 AB 的长度为 14cm ．3、解：（ 1）∵ DE=9cm ，∴ DC+CE=9cm ．∵点 D 是线段 AC 的中点，点 E 是线段 BC 的中点，∴ AC=2CD ，BC=2CE ． ∵AB=AC+BC=（2 CD+CE ） =2DE=18cm ；（2）点 C 是线段 AB 的中点，∴ AB=ACB ．∵点 E 是线段 BC 的中点，∴ BC=2CE=10cm ． ∵点 D 是线段 AC 的中点，∴ DC= AC= BC=5cm ．∴ DB=DC+CB=5+10=15c ．mBC=3： 1，设 BC=x ，则 AC=3xC 在线段 AB 上时， AC+BC=A ．B3x+x=8 解得 x=2 所以 BC=2 C 在 AB 的延长线上时， AC ﹣BC=AB 3x ﹣ x=8 解得 x=4 所以 BC=4 2或 4．∴BC=BE ﹣ EC=4﹣ 3=1cm ，∴ AC=AB ﹣ BC=8﹣ 1=7cm ，∵点 D 为线段 AC 的中点，∴ CD=3.5cm ，∴ DE=CD ﹣ EC=3.5﹣ 3=0.5cm ．6、解：∵ F 为线段 AB 的中点，∴ BF= AB=16， ∵E 为线段 BC 的中点，∴BE=12，∴ EF=BF ﹣BE=16﹣12=4．7、解：∵ AB=4cm ， BC=2AB ，∴ BC=8cm ，∴ AC=AB+BC=4+8=12c ，mMC=AM= AC=6cm ，∴ BM=AM ﹣ AB=6﹣ 4=2cm ．8、解： BC=18cm 所以 CN=18×1÷ (1+2)=6mM 是 AC 中点所以 MC=AC/2=4cm 所以 MN=MC+CN=4+6=10cm 9、解：设 BC=x 厘米，由题意得： AB=3x ， CD=4x∵E ，F 分别是 AB ，CD 的中点∴ BE= AB= x ，CF= CD=2x ∴EF=BE+CF ﹣BC= x+2x ﹣x 即 x+2x ﹣x=60，解得 x=24 ∴AB=3x=72（厘米）， CD=4x=96（厘米）． 答：线段 AB 长为 72 厘米，线段 CD 长为 96 厘米．10、解：（ 1）①∵ B 是线段 AD 上一动点，沿 A →D →A 以2cm/s 的速度往返运动， ∴当 t=2 时， AB=2×2=4cm ．故答案为： 4；②∵ AD=10cm ， AB=4cm ，∴ BD=10﹣ 4=6cm ，∵ C 是线段 BD 的中点，∴ CD= BD= × 6=3cm ；AC ： 当点 所以 当点所以4、解：由于 第一种情况： 因为 AB=8， 第二种情况： 因为 AB=8， 综上， BC 的长为 5、解：∵线段 AB=8cm ， E 为线段 AB 的中点，∴BE4cm ， ∵ AC= BC ，∴ BC= AB=24，∵M 是线段 AC 中点，（2）∵ B是线段 AD上一动点，沿 A→D→A以 2cm/s 的速度往返运动，∴当 0≤t≤5时，AB=2t；当 5<t≤10时，AB=10﹣（2t﹣10）=20﹣2t；（3）不变．∵ AB中点为 E，C 是线段 BD的中点，∴ EC= （AB+BD）= AD= × 10=5cm．11、解：12、解：⑴ CD=（4a＋3b）－（2a＋b）=2a＋2b 答： C、 D两站之间的距离 CD为（ 2a＋2b）⑵ AB=AC－BC=CD－BC=（2a＋2b）－（ 2a＋b）=b 答： A、 B两站之间的距离 AB是 b.13、解：（ 1）∵点 M、N 分别是 AC、BC的中点，∴CM= AC=4cm， CN= BC=3cm，∴ MN=CM+CN=4+3（=7cm）；即线段 MN的长是 7cm．（2）能，理由如下：如图所示，∵点M、N分别是 AC、BC的中点，∴ CM= AC，CN= BC，∴MN=CM+CN=（ AC﹣ BC） = cm．14、解：∵ M是 AC的中点， AC=6，∴ MC=3，又因为 CN∶NB=1∶2，BC=15，∴ CN=5，∴MN=M＋C CN=3＋ 5=8，∴ MN的长为 8 cm15、解：16、解：17、解：18、解：（ 1） P点对应的数为﹣ 26+t；PC=36﹣t ；故答案为：﹣ 26+t ；36﹣t ；（2）①有2 处相遇；分两种情况：Q返回前相遇： 3（t﹣16）﹣ 16=t ﹣ 16，解得： t=24， Q返回后相遇： 3（ t ﹣ 16） +t=36 ×2．解得： t=30．综上所述，相遇时 t=24 秒或 30 秒．故答案为： 24 或 30；②当 16≤t≤24时 PQ=t ﹣3（t ﹣16）=﹣2t+48，当24<t≤28时 PQ=3（ t ﹣16）﹣ t=2t ﹣48，当 28<t≤30时 PQ=72﹣ 3（ t ﹣ 16）﹣ t=120 ﹣4t，当30<t≤36时 PQ=t ﹣ [72 ﹣ 3（ t ﹣16） ]=4t ﹣120，当 36<t≤40时 PQ=3（ t ﹣16）﹣36=3t ﹣84．19、解：20、解：。

专题1.3运用勾股定理证明线段间的平方关系线段之间的平方和或平方差的关系，通常是将它们转换同一个直角三角形中求解，或转换到具有公共边的直角三角形中求解。

类型一直接运用勾股定理探究线段间的平方关系【例1】如图，四边形ABCD中，BD⊥AC．求证：AD2+BC2＝AB2+CD2．【答案】略【解答】解：∵BD⊥AC，∴∠AED＝∠AEB＝∠BEC＝∠DEC＝90°，∴在Rt△AED中，AD2＝AE2+DE2，在Rt△AEB中，AB2＝AE2+BE2，在Rt△BEC中，BC2＝BE2+CE2，在Rt△CED中，CD2＝CE2+DE2，∴AD2+BC2＝AE2+DE2+BE2+CE2，AB2+CD2＝AE2+BE2+CE2+DE2，∴AD2+BC2＝AB2+CD2．【变式1】（2019秋•宿州期末）如图，在Rt△ABC中，∠C＝90°，AM是中线，MN⊥AB，垂足为点N，求证：AN2﹣BN2＝AC2．【答案】略【解答】证明：∵MN⊥AB于N，∴BN2＝BM2﹣MN2，AN2＝AM2﹣MN2∴BN2﹣AN2＝BM2﹣AM2，又∵∠C＝90°，∴AM2＝AC2+CM2∴BN2﹣AN2＝BM2﹣AC2﹣CM2，又∵BM＝CM，∴BN2﹣AN2＝﹣AC2，即AN2﹣BN2＝AC2．【变式2】（2020春•塔河县校级期末）如图，∠C＝90°，AM＝CM，MP⊥AB于点P，求证：BP2＝AP2+BC2．【答案】略【解答】证明：连接BM，∵△ABC是直角三角形，∠C＝90°，∴AB2＝BC2+AC2，则AB2﹣AC2＝BC2．又∵在直角△AMP中，AP2＝AM2﹣MP2，∴AB2﹣AC2+（AM2﹣MP2）＝BC2+（AM2﹣MP2）．又∵AM＝CM，∴AB2﹣AC2+（AM2﹣MP2）＝BC2+（MC2﹣MP2），①∵△APM是直角三角形，∴AM2＝AP2+MP2，则AM2﹣MP2＝AP2，②∵△BPM与△BCM都是直角三角形，∴BM2＝BP2+MP2＝MC2+BC2，MC2+BC2﹣MP2＝BM2﹣MP2＝BP2，③把②③代入①，得AB2﹣AC2+AP2＝BP2，即BP2＝AP2+BC2．【变式3】（2020春•海阳市期中）如图：△ABC中，∠C＝90°，D是AC中点，求证：AB2+3BC2＝4BD2．【答案】略【解答】证明：∵D是AC中点，∴AC＝2CD，在Rt△BCD中，CD＝，∴AC＝2，在Rt△ABC中，AB2＝AC2+BC2，即AB2＝4BD2﹣4BC2+BC2，∴AB2+3BC2＝4BD2．类型二构造直角三角形探究线段间的平方关系【例2】如图，P长方形ABCD内的一点，PA＝3，PB＝4，PC＝5，求PB²+PD²的值。