渗流固结理论

二、课程的基本要求学完“土力学”后，应达到以下基本要求：①认识土为松散体这一特点，并以此解释土的变形规律、渗透性质、强度特性；②掌握土的物理性质及其基本指标，土的分类，确定土的物理状态和土的定名，以及土的物理性质指标和土的强度和变形的关系；③掌握土中应力分布，地基变形，一维渗透固结理论，库仑——莫尔强度理论；④要求掌握库仑、朗金土压力计算理论及适用范围，以及几种常见情况的土压力计算；⑤掌握土坡稳定的一些基本概念和土坡稳定计算的条分法，了解摩擦圆法和增加土坡稳定的一些措施。

三、课程的基本内容以及重点难点绪论介绍“土力学”的主要内容、任务和工程应用成就。

第一章土的物理力学性质讲授内容：土的生成，土的粒径组成和矿物成分，土中的水和气体，土的三相含量指标，土的物理状态及指标，土的工程分类。

自学内容：土的结构及其联结，土的膨胀、收缩及冻胀。

重点：土的组成，三相含量指标和物理状态指标的计算，土的分类。

上述实验方法和资料整理。

难点：认识土的物理指标和状态指标的变化对土性质的影响。

第二章土的渗透性及水的渗流、第三章土中应力和地基应力分布讲授内容：土中一点的应力状态和应力平衡方程，土的渗透性，饱和土的有效压力和孔隙水压力，在简单受力条件下地基中应力分布，基底的接触应力，刚性基础基底压力简化算法，弹性半无限体内的应力分布。

自学内容：部分饱和土的孔隙压力及有效压力，孔隙压力系数。

重点：土的渗透性和有效压力的概念，饱和土的有效压力和孔隙水压力计算，弹性半无限体内的应力分布计算。

难点：在渗透条件下，土的有效压力和孔隙水压力计算。

第四章土的变形性质及地基沉降计算讲授内容：土的弹性变形性质，土的压缩性，饱和粘土的渗透固结和太沙基一维固结理论，试验方法测定土的变形模量，地基沉降计算，沉降差与倾斜，饱和粘土的沉降过程。

自学内容：太沙基一维固结方程的详细推导和固结度公式的推导。

重点：土的压缩性和压缩性指标，土的固结概念，地基沉降的计算。

电渗法中排水固结理论与实践的若干问题曹永华，高志义（中交天津港湾工程研究院有限公司，港口岩土工程技术交通行业重点实验室，天津市港口岩土工程技术重点实验室，天津300222摘要：从工程应用的角度，对地基处理中的电渗法加固机理、适用性、等效加固荷载、电极材料、与其它方法的联合及相关实用技术进行了讨论。

从排水固结考虑，电渗法适合加固的是电渗透系数和电阻率较大、水力渗透系数适中的土体。

电渗加固中，无恒定的等效加固荷载。

电渗常常需要与常规排水固结法联合以提高加固效果。

研制不腐蚀的材料对电渗加固具有重要意义。

电极转换和间歇通电有利于减少电能在电极与土体接触面的消耗，提高电能利用率。

关键词：电渗法；排水固结；地基处理；技术难点中图分类号：TU472文献标识码：A文章编号：1003-3688（2010）03-0022-03Some Problems on Theory and Application of Drainage Consolidationin Electroosmotic for Ground ImprovementCAO Yong-hua ，GAO Zhi-yi（CCCC-Tianjin Port Engineering Institute Co.，Ltd.；Key Laboratory of Port Geotechnical Engineering ，Ministry ofCommunication ；Key Laboratory of Port Geotechnical Engineering of Tianjin ，Tianjin 300222，China ）Abstract ：For engineering application ，some problems of drainage consolidation in electroosmotic for ground improvement were discussed.These problems includes improvement mechanism ，applicability ，equivalent load ，material of electrode ，combination with other methods and some practical technique.In aspects of drainage consolidation methods ，electroosmotic is suitable for soils which have larger electroosmotic permeability ，larger electrical resistively and moderate hydraulic permeability.There is no unique equivalent load in electroosmotic process.It will be better to adopt other soil improvement methods in combination with electroosmosis.Electrodes made of incorrosive material are important for electroosmosis.Electrodes reversal and intermittent current are favourable to reduce the power consumption on the contact surface between electrode and soils ，and improve the efficiency of the power.Key words ：electroosmotic ；drainage consolidation ；ground improvement ；technical problems 中国港湾建设China Harbour Engineering2010年6月第3期总第167期Jun.，2010Total 167，No.3收稿日期：2009-09-08修回日期：2009-12-16作者简介：曹永华（1977—），男，湖南澧县人，博士，高级工程师，从事岩土工程的科研与检测工作。

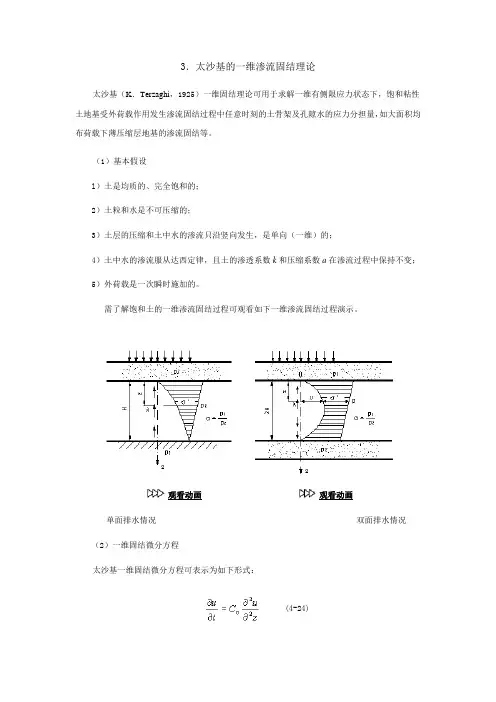
3．太沙基的一维渗流固结理论太沙基（K．Terzaghi，1925）一维固结理论可用于求解一维有侧限应力状态下，饱和粘性土地基受外荷载作用发生渗流固结过程中任意时刻的土骨架及孔隙水的应力分担量，如大面积均布荷载下薄压缩层地基的渗流固结等。

（1）基本假设l）土是均质的、完全饱和的；2）土粒和水是不可压缩的；3）土层的压缩和土中水的渗流只沿竖向发生，是单向（一维）的；4）土中水的渗流服从达西定律，且土的渗透系数k和压缩系数a在渗流过程中保持不变； 5）外荷载是一次瞬时施加的。

需了解饱和土的一维渗流固结过程可观看如下一维渗流固结过程演示。

观看动画观看动画单面排水情况双面排水情况（2）一维固结微分方程太沙基一维固结微分方程可表示为如下形式：(4-24)式中C V称为土的竖向固结系数，cm2/s，其值为：上述固结微分方程可以根据土层渗流固结的初始条件与边界条件求出其特解,当附加应力σz 沿土层均匀分布时孔隙水压力υ(z,t)的解答如下：(4-25)式中m为奇正整数（1，3，5，……）；T V为时间因数，即：H为孔隙水的最大渗径，单面排水条件下为土层厚度，双面排水条件下为土层厚度之半。

一维固结的初始条件与边界条件1. 单面排水土层中的初始条件与边界条件当初始孔隙水压力沿深度为线性分布时，定义土层边界应力比为式中p1为排水面边界处应力，p2为不排水面边界处应力。

序号时间坐标条件1 t=0 0≤z≤H2 0<t≤∞ z=0 υ=03 0≤t≤∞ z=Ht=∞0≤z≤Hυ=02. 双面排水土层中的初始条件与边界条件当初始孔隙水压力沿深度为线性分布时，定义土层边界应力比为式中p1为上边界处应力，p2为下边界处应力。

序号时间坐标条件1 t=0 0≤z≤H2 0<t≤∞ z=0 υ=03 0≤t≤∞ z=Hυ=0。

第四节 饱和粘性土地基沉降与时间的关系前面介绍的方法确定地基的沉降量，是指地基土在建筑荷载作用下到达压缩稳定后的沉降量，因而称为地基的最终沉降量。

然而，在工程实践中，常常需要预估建筑物完工及一般时间后的沉降量和到达某一沉降所需要的时间，这就要求解决沉降与时间的关系问题，下面简单介绍饱和土体依据渗流固结理论为基础解决地基沉降与时间的关系。

一、饱和土的有效应力原理用太沙基渗透固结模型很能说明问题。

当t ＝0时，u =σ，0='σ 当t ﹥0时，u +'=σσ，0≠'σ当t ＝∞时，σσ'=，u ＝0结论：u +'=σσ'，饱和土的渗透固结过程就是孔隙水压力向有效力应力转化的过程。

在渗透固结过程中，伴随着孔隙水压力逐渐消散，有效应力在逐渐增长，土的体积也就逐渐减小，强度随着提高。

二、饱和土的渗流固结整个模型〔饱和土体〕⎪⎩⎪⎨⎧→→→土的渗透性活塞小孔的大小孔隙水水固体颗粒骨架弹簧三、太沙基一维渗流固结理论〔最简单的单向固结〕——1925年太沙基提出 一．基本假设：将固结理论模型用于反映饱和粘性土的实际固结问题，其基本假设如下： 1．土层是均质的，饱和水的2．在固结过程中，土粒和孔隙水是不可压缩的； 3．土层仅在竖向产生排水固结〔相当于有侧限条件〕； 4．土层的渗透系数k 和压缩系数a 为常数；5．土层的压缩速率取决于自由水的排出速率，水的渗出符合达西定律； 6．外荷是一次瞬时施加的，且沿深度z 为均匀分布。

二．固结微分方程式的建立在饱和土体渗透固结过程中，土层内任一点的孔隙水应力),(t z u 所满足的微分方程式称为固结微分方程式。

在粘性土层中距顶面z 处取一微分单元，长度为dz ，土体初始孔隙比为e 1，设在固结过程中的某一时刻t ，从单元顶面流出的流量为q ＋dz zq∂∂则从底面流入的流量将为q 。

于是，在dt 时间内，微分单元被挤出的孔隙水量为：dzdt zqdt q dz z q q dQ )(])[(∂∂=-∂∂+= 设渗透固结过程中时间t 的孔隙比为e t ， 孔隙体积为：dz e e V tv 11+=在dt 时间内，微分单元的孔隙体积的变化量为：dzdte e dt dz e et dt t V dV ttt v v ∂∂+=+∂∂=∂∂=1111)1(由于土体中土粒，水是不可压缩的，故此时间内流经微分单元的水量变化应该等于微分单元孔隙体积的变化量，即：v dV dQ = 或 dzdt t e e dzdt z q t∂∂+=∂∂111)(即：te e z q t∂∂+=∂∂111 根据渗流满足达西定律的假设zu r k z h kki VA q w ∂∂=∂∂=== 式中：A 为微分单元在渗流方向上的载面积，A ＝1；i ：为水头梯度，zhi ∂∂=其中h 为侧压管水头高度 μ：为孔隙水压力， 0h r u w = 根据压缩曲线和有效应力原理，dpde a -= 而u p u z -=-=σσ' 所以：tua t e t ∂∂=∂∂ 并令w ar e k Cv )1(1+=则得t uzu Cv ∂∂=∂∂22此式即为饱和土体单向渗透固结微分方程式 。

渗流理论与比奥固结理论的分析作者：程敬珍程晓柱来源：《城市建设理论研究》2012年第32期摘要：目前的基坑、边坡工程中的流固耦合分析大部分以比奥固结理论为基础。

本文分析了渗流分析的控制方程与固结理论中的渗流方程的异同。

关键词：渗流分析； Biot固结理论Abstract：The analysis on flow-deformation coupling of foundation pit and side slope almost bases on Biot’s consolidation theory. The difference between seepage equations in seepage analysis and consolidation is searched in this paper.Key words：seepage analysis; Biot’s consolidation theory中图分类号：O357.3文献标识码：A 文章编号：2095-2104（2012）1引言土体具有被流体透过的性能称为土体的渗透性。

在水头差的作用下，流体可以透过土体孔隙而产生流动，这种现象称为渗流。

渗流分析的目的是研究渗流域内的水头分布、水流速度和方向，以及孔隙水应力的分布。

渗流问题是岩土工程中一个重要的课题，如边坡、堤坝、地基中的渗流以及基坑渗流等等。

工程中常见的砂沸、流土、管涌等岩土破坏现象皆与土的渗流有关，渗流对土体的强度、变形还具有重要的影响，如土体固结的快慢、荷载作用下土体中有效应力随时间增加的情况、荷载作用下土体强度变化等皆与土体的渗透性有关。

土体在荷载作用下，孔隙水缓慢流出，体积逐渐压缩，土体中有效应力逐步增大，超静孔隙水压力逐步消散直至完全消失，这一过程称为“固结”。

土的固结是土力学学科中最主要的课题之一。

工程中常常应用固结过程的特性，通过排水固结法对软土地基进行改良，减小完工后沉降。

太沙基一维渗流固结理论的基本假设
费尔特-太沙基一维渗流固结理论是地质工程领域中重要的理论之一。

詹斯·费尔特-太沙基是二十世纪1939年提出了这一理论,他根据实际项目对渗流固结数值模拟进行了深入分析,最终发展出此理论。

它从空间分布出发,估计离散等效渗流。

费尔特-太沙基一维渗流固结理论的基本假设是：首先，假设岩样具有线性改变的参数，例如渗流速度，泥沙率和岩样的组成等，不受外界的影响。

其次，可以忽略水位变化对渗流速率的影响，并假设区域压力为零。

最后，假设岩样内部的渗流发生的过程是一维的，沿着形态等效的一维渗流水道渗流运动，以及空气在定域中占有的体积比例。

费尔特-太沙基一维渗流固结方程有助于估计岩样空气，水和砂沙在连续空间和混合空间中的分布，以及准确确定不同条件下的梯度变化，进而得出水位、压力梯度和岩样的实际变形情况及其特性。

在工程应用中，费尔特-太沙基一维渗流固结理论应用广泛，可以有效计算岩样内不同物质之间的速度比和流体流量状态。

在岩石成因机理，岩石力学和岩石失稳性研究中，它也发挥着巨大的作用，为研究岩石及其低应力破坏规律提供了可靠的理论依据。