运算律简便运算复习
- 格式:ppt
- 大小:205.00 KB
- 文档页数:43

运算律和简便运算(一)加减法运算定律1、加法交换律定义:两个加数交换位置,和不变 字母表示:a b b a +=+例如:16+23=23+16 546+78=78+5462、加法结合律定义:先把前两个数相加,或者先把后两个数相加,和不变。
字母表示:)()(c b a c b a ++=++ 注意:加法结合律有着广泛的应用,如果其中有两个加数的和刚好是整十、整百、整千的话,那么就可以利用加法交换律将原式中的加数进行调换位置,再将这两个加数结合起来先运算。
3、减法的性质 注意:这些都是由加法交换律和结合律衍生出来的。
减法性质①:如果一个数连续减去两个数,那么后面两个减数的位置可以互换。
字母表示:b c a c b a --=--减法性质②:如果一个数连续减去两个数,那么相当于从这个数中减去后面两个数的和。
字母表示:)(c b a c b a +-=--4、拆分、凑整法简便计算拆分法:当一个数比整百、整千稍微大一些的时候,我们可以把这个数拆分成整百、整千与一个较小数的和,然后利用加减法的交换、结合律进行简便计算。
例如:103=100+3,1006=1000+6,…凑整法:当一个数比整百、整千稍微小一些的时候,我们可以把这个数写成一个整百、整千的数减去一个较小的数的形式,然后利用加减法的运算定律进行简便计算。
例如:97=100-3,998=1000-2,…注意:拆分凑整法在加、减法中的简便不是很明显,但和乘除法的运算定律结合起来就具有很大的简便了。
(二)乘除法运算定律1.乘法交换律定义:交换两个因数的位置,积不变。
字母表示:a b b a ⨯=⨯例如:85×18=18×85 23×88=88×232、乘法结合律定义:先乘前两个数,或者先乘后两个数,积不变。
字母表示:)()(c b a c b a ⨯⨯=⨯⨯ 乘法结合律的应用基于要熟练掌握一些相乘后积为整十、整百、整千的数。
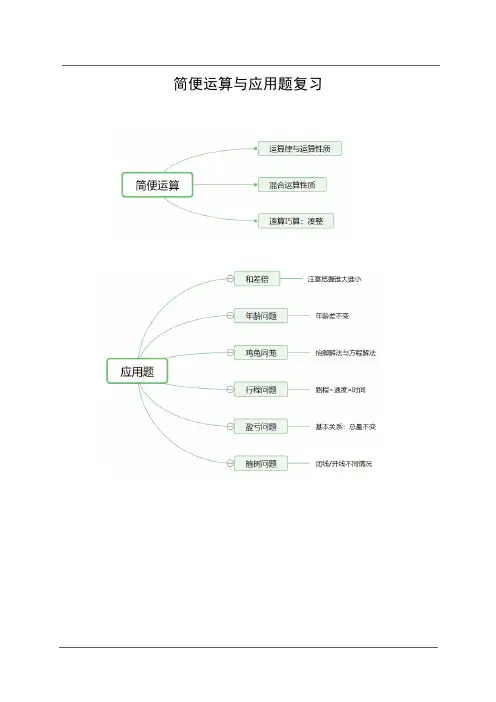
简便运算与应用题复习简便运算一、运算律与运算性质1、加法{交换律:a +b =b +a结合律:(a +b )+c =a +(b +c)2、减法减法运算性质:a −(b +c )=a −b −c ,a −(b −c )=a −b +c3、乘法 {交换律:a ×b =b ×a 结合律:(a ×b )×c =a ×(b ×c ) 分配律:(a +b )×c =a ×c +b ×c 积不变性质:a ×b =(a ×c )×(b ÷c )=(a ÷c )×(b ×c)4、除法除法运算性质:a ÷(b ×c )=a ÷b ÷c ,a ÷(b ÷c )=a ÷b ×c 二、乘、除法混合运算的性质1、商不变性质:被除数和除数乘(或除)以同一个非零数,其商不变2、在连除时,可以交换除数的位置,商不变,即a ÷b ÷c =a ÷c ÷b3、在乘、除混合运算中,被乘数、乘数或除数可以连同运算符号一起交换位置(或称“带着符号搬家”)a ×b ÷c =a ÷c ×b =b ÷c ×a4、在乘、除混合运算中,去或添括号的规则:去或添括号时,括号前是“×”时,“×”“÷”不变号;括号前是“÷”时,去或添括号后,括号中“×”变为“÷”,“÷” 变为“×”5、两个数之积除以两个数之积,可以分别相除后再相乘. (a ×b )÷(c ×d )=(a ÷c )×(b ÷d )=(a ÷d )×(b ÷c) 三、速算巧算的核心思想和本质:凑整 1、分组凑整法.2、拆补凑整法.有些算式中直接凑整不明显,这时可“借数”或“拆数”凑整.3、数值原理法.先把加在一起为整十、整百、整千……的数相加,然后再与其它的数相加.4、“基准数”法.当几个比较接近于某一整数的数相加时,选这个整数为“基准数”(要注意把多加的数减去,把少加的数加上)【例1】 直接写出得数0.2+2.6= 3.2-2.2 = 0.7×2= 0.6÷2= 4.6-3= 2.1×3= 25+15×2= 64÷8×8 = (10-2)÷(20-12=)【例2】递等式计算,能简便计算就简便计算(1) 23.4-0.8-13.4-7.2(2) 12.78-(4.97+2.78)(3) 12.5×0.4×2.5×8(4) 63.4÷2.5÷0.4(5) 35÷(0.35×2)(6) 9+99+999+9999+99999【例3】计算,并将得数用“四舍五入”法凑整到百分位(1)6.8×0.79 (2)4.04×0.52(3)3.14÷0.3 (4)7.356÷2.5【例4】递等式计算(能用简便方法的用简便方法计算)(1)7.8÷2.5×4 (2)(0.8+4)×12.5×2.5 (3)146.5-(23+46.5) (4)6.73×4.8+5.2×6.73(5)1.4×3.8+6.2×(4.2-2.8) (6)[5.6-(1.6+1.6÷4)]÷0.12【例5】列式计算(1)一个数的5倍加上3.2,和是38.2,求这个数。

人教版数学四年级下册《总复习》(四则运算、运算定律与简便计算)说课稿一. 教材分析人教版数学四年级下册《总复习》主要包括四则运算、运算定律与简便计算这两个部分。
这一单元是对整个学期所学内容的回顾与总结,目的是让学生巩固和掌握基本的运算方法和运算定律,提高运算速度和准确性。
二. 学情分析四年级的学生已经掌握了加、减、乘、除四则运算的基本方法,对运算定律也有了一定的了解。
但在实际操作中,部分学生可能会存在运算速度慢、准确性不高、对运算定律运用不熟练等问题。
因此,在教学过程中,需要针对这些问题进行针对性的指导。
三. 说教学目标1.知识与技能:使学生掌握四则运算的基本方法,熟练运用运算定律进行简便计算。
2.过程与方法:培养学生的运算能力,提高运算速度和准确性。
3.情感态度与价值观:激发学生学习数学的兴趣,培养学生的团队合作意识和探究精神。
四. 说教学重难点1.教学重点:四则运算的基本方法,运算定律的运用。
2.教学难点:运算定律在实际计算中的应用,提高运算速度和准确性。
五. 说教学方法与手段1.教学方法:采用讲解、示范、练习、讨论、小组合作等教学方法。
2.教学手段:利用多媒体课件、黑板、粉笔等教学工具。
六. 说教学过程1.导入:通过一个有趣的数学故事引入本节课的主题,激发学生的学习兴趣。
2.讲解与示范:讲解四则运算的基本方法,示范运算定律的运用。
3.练习与讨论:学生进行练习,小组内讨论解决问题。
4.小组合作:学生分组进行合作,运用运算定律进行简便计算。
5.总结与拓展:总结本节课所学内容,提出拓展问题,激发学生的探究精神。
七. 说板书设计板书设计要清晰、简洁,突出重点。
主要包括四则运算的基本方法和运算定律的运用。
八. 说教学评价1.课堂表现:观察学生在课堂上的参与程度、提问回答情况等,了解学生的学习状态。
2.练习完成情况:检查学生完成的练习题,评价学生的掌握程度。
3.小组合作:评价学生在小组合作中的表现,包括沟通能力、合作精神等。








学情分析③乘法结合律和分配律容易混淆使用。
在学生练习后,教师从中提炼出具有典型性、启发性的学生错例进行剖析,分析学生的错因,了解学生的知识掌握情况。
现将学生答题的整体情况做简要分析:错因归类错例诊断分析凑整思想的僵化,未能根据数字的特点合理选择拆分方法一个数拆成两个数之和的思想对个别学生而言已根深蒂固,关注到99可以拆成909,进而使用乘法分配律,没有考虑到是否还有更简便的拆分方法。
凑整思想的僵化,造成生搬硬套。
对于这个学生而言,他是清楚如何拆数才能更简便,没有考虑到等号左右两侧必须相等,书写错误。
乘法结合律的算理理解不到位。
学生对乘法结合律与分配律的算理理解不到位,导致乘法结合律与分配律混淆。
学情分析乘法结合律和分配律混淆,造成过程混乱。
学生未理解算理,没有从本质上理解递等式的含义,纯粹在模范算法,导致计算混乱。
拆数过程少了是否简便的思考。
在进行拆数之前,学生缺乏对算式中的数如何能更简便计算的思考,没有准确分析算式中的数字的特点,缺乏数感。
乘法分配率和乘法结合律混淆学生未能真正辨析和理解乘法结合律与分配律的区别,在解题时思路特别容易受表面形式的干扰,造成运算定律的误用和运算过程的混乱。
目标与重难点教学目标:1通过分类与整理,将各运算定律建立联系,形成一定的知识网络,系统掌握运算定律;2学会从错例中反思,分析错因,能根据题目的具体情况合理使用运算定律进行简便计算,进一步提升综合运用知识的能力;3能根据数字特点及运算符号编制简便计算的题目,建立数感。
教学重难点:1重点:整理运算定律以及熟练运用运算定律进行简便计算。
2难点:合理、灵活地运用运算定律进行简算。
过程设计(1)123-6832(2)123-68-32(3)56×99(4)125×88(5)4×25÷25×4(6)25×(9×4)(7)125×32×25(8)75×(2562)师:第(5)题大家极容易算错?你猜算错的答案是几?为什么会出现这样的错误?正确的答案是几?如何计算?2.判断能使用运算定律简便计算的题都分别使用了哪些运算定律。
一,循凑十凑百原则。
特别注意在乘法中看到4和25得100要放一起或者8和125得1000要放一起上面的加法交换律和乘法交换律差不多, 下面的加法结合律和乘法结合律差不多。
特殊形式一: 特殊形式二: 特殊三:两律都用接近整百整千数 分成相乘是整百整千数 加法交换律与结合律都有 乘法交换律与结合律378—99 125×32×25 65+28+35+7225×125×4×8=378-(100-1) =125×(8×4)×25 =(65+35)+(28+72) =(25×4)×(125×8)=378-100+1 = (125×8)×(4×25) =100+100 =100+100 =278+1 =1000×100交换律结合律练习一12×25 138×25×4 25×32×125 125×13×8 32×125 43+189+57=94+38+106+62 25×64×125 625+98 848+103 165+299 456-199=二、 连续减法简便运算例子:一个数连续减去两个数等于减去两个数的和。
)a+b= b+a :两个或多个数相加,交换加数位置,和不变。
如:84+57+43+16,把84+16和57+43放在一起先算时。
a ×b=b ×a 两个或多个数相乘,交换乘数位置,积不变。
如: 125×99×8把99和8互换位置先算125×8=1000 (a+b) +c = a+(b+c ) :三个数相加,先算前两个数再加第三个数,等于先算后两个数再加第一个数,和不变。
可配合交换律主要先算“凑十528—65—35 528—89—128528—(150+128)=528—(65+35) =528—128—89 =528—128—150=528—100 =400—89=400—150=428 =311=250三、连续除法简便运算例子:一个数连续除于两个数等于除于两个数的积。
苏教版四年级数学下册《运算律与简便计算的整理与复习》教学设计一. 教材分析苏教版四年级数学下册《运算律与简便计算的整理与复习》这一章节,主要让学生复习和掌握加法、减法、乘法、除法的运算律,并能够运用运算律进行简便计算。
教材通过例题和练习题,让学生在实际计算中感受运算律的重要性,提高计算的效率和准确性。
二. 学情分析学生在之前的学习中已经接触过运算律,对加法、减法、乘法、除法的运算律有一定的了解。
但在实际计算中,部分学生可能还没有形成运用运算律进行简便计算的习惯。
因此,在教学过程中,需要引导学生将所学的运算律运用到实际计算中,培养他们运用运算律进行简便计算的能力。
三. 教学目标1.知识与技能:学生能够掌握加法、减法、乘法、除法的运算律,并能够运用运算律进行简便计算。
2.过程与方法:学生通过自主学习、合作交流,培养运用运算律进行简便计算的能力。
3.情感态度与价值观:学生体验到运用运算律进行简便计算的优越性,提高学习数学的兴趣。
四. 教学重难点1.重点:学生能够掌握加法、减法、乘法、除法的运算律,并能够运用运算律进行简便计算。
2.难点:学生能够在实际计算中灵活运用运算律,提高计算的效率和准确性。
五. 教学方法1.引导发现法:教师引导学生发现运算律,并引导学生将运算律运用到实际计算中。
2.案例分析法:教师通过例题和练习题,分析运用运算律进行简便计算的方法。
3.小组合作法:学生分组讨论,合作完成练习题,培养团队合作能力。
六. 教学准备1.教材:苏教版四年级数学下册。
2.课件:教师准备相关的课件,用于辅助教学。
3.练习题:教师准备一些练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)教师通过提问方式,引导学生回顾加法、减法、乘法、除法的运算律,激发学生的学习兴趣。
2.呈现(10分钟)教师通过课件展示加法、减法、乘法、除法的运算律,让学生直观地了解运算律的形式和意义。
3.操练(10分钟)教师给出一些算式,让学生运用所学的运算律进行简便计算。