下载文档原格式
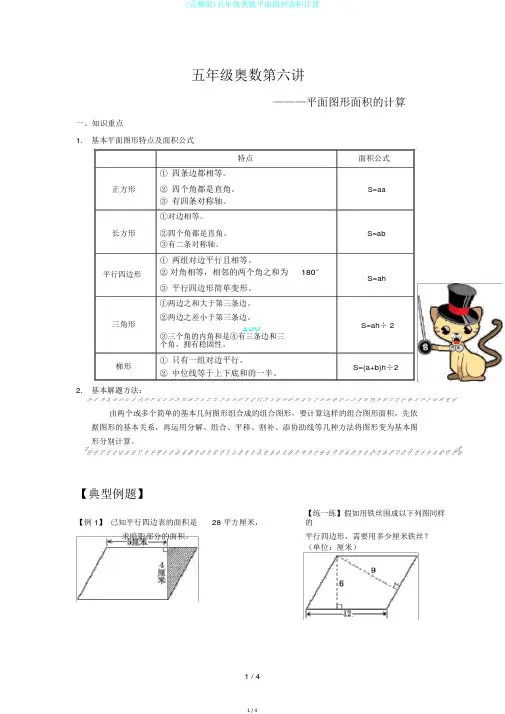
1 / 4五年级奥数第六讲———平面图形面积的计算一、知识重点1. 基本平面图形特点及面积公式特点面积公式① 四条边都相等。
正方形② 四个角都是直角。
S=aa③ 有四条对称轴。
①对边相等。
长方形②四个角都是直角。
S=ab③有二条对称轴。
平行四边形三角形梯形① 两组对边平行且相等。
② 对角相等，相邻的两个角之和为180°③ 平行四边形简单变形。
①两边之和大于第三条边。
②两边之差小于第三条边。
③三个角的内角和是④有三条边和三个角，拥有稳固性。
① 只有一组对边平行。
② 中位线等于上下底和的一半。
S=ahS=ah ÷ 2S=(a+b)h ÷22. 基本解题方法：由两个或多个简单的基本几何图形组合成的组合图形，要计算这样的组合图形面积，先依据图形的基本关系，再运用分解、组合、平移、割补、添协助线等几种方法将图形变为基本图形分别计算。
【典型例题】【例 1】 已知平行四边表的面积是28 平方厘米，【练一练】假如用铁丝围成以下列图同样的求暗影部分的面积。
平行四边形，需要用多少厘米铁丝？（单位：厘米）1 / 4180°。
【例 2】求图中暗影部分的面积。
【练一练】下列图中甲和乙都是正方形，求暗影部分（单位：厘米）的面积。
（单位：厘米）【例 3】以下图，甲三角形的面积比【练一练】平行四边形ABCD 的边长乙三角形的面积大 6 平方厘米，求CE 的长度。
BC=10 厘米，直角三角形 BCE 的直角边 EC 长 8 厘米，已知暗影部分的面积比三角形 EFG 的面积大10 平方厘米。
求 CF 的长。
【例 4】两条对角线把梯形 ABCD 切割成四个三角形。
【练一练】下边的梯形 ABCD 中，下底是已知两个三角形的面积（以下图），求另两个三角形上底的 2 倍， E 是 AB 的中点，求梯形 ABCD 的面积各是多少？（单位：厘米）的面积是三角形EDB 面积的多少倍？B【练一练】【练一练】计算下边图形的面积。
同学个性化教学设计年级：教师: 科目：
班主任：日期: 时段:
【例 1】 在梯形中阴影部分面积是150平方厘米，求梯形面积。
【巩固】如图，已知平行四边形面积是48平方厘米，求阴影部分面积。
【例 2】 如图，是两个完全相同的直角三角形叠在一起，求阴影部分的面积。
（单位：分米）
【例 3】 如图，将长为9厘米、宽为6厘米的长方形划分成四个三角形，其面积分别为1S 、2S 、3S 、
4S ，且4321S S S S +==,求4S 。
【巩固】如图，四年级ABCD是直角三角形，其中AD=12厘米，AB=8厘米，BC=15厘米，且△ADE 四边形DEBF及△CDF的面积相等，求三角形EBF的面积。
【例 4】如图，AE=5厘米，CF=2厘米，AB=6厘米，CD=4厘米，∠B=∠D=90°。
求四边形AFCE 的面积。
【巩固】如图，四边形ABCD中，AE=5厘米，AB=10厘米，FC=12厘米，∠B=∠D=90°，求四边形AFCE的面积。
【例 5】如图，求图示长方形中阴影部分的面积。
（单位：厘米）
【例 6】如图，平行四边形ABCD的边长BC=10厘米，直角三角形BCE的直角边CE长8厘米。
已知阴影部分的面积比三角形FEG的面积大10平方厘米。
求CF的长。
【巩固】如图，正方形ABCD的边长是12厘米，已知DE是EC的长度的2倍。
求（1）△DEF的面积；(2)CF的长。
学生签字：__________
教研组长签字：____
_______。
